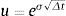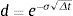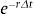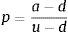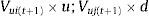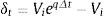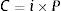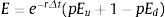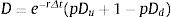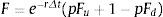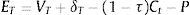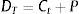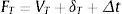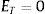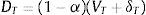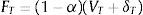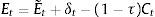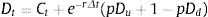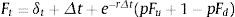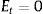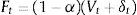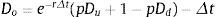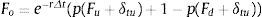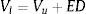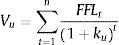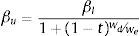En este documento se propone un modelo binomial para valorar empresas, proyectando y condicionando escenarios de continuidad o liquidación de la firma. El modelo se basa en la Teoría de Opciones Reales para estimar el valor de la firma, que resulta de un balance explícito de las ventajas y riesgos de tomar deuda. El trabajo se estructura de la siguiente manera: Primeramente, la introducción y desarrollo del modelo teórico; luego se ilustra mediante un caso de aplicación, comparando los resultados obtenidos con el modelo de descuento de flujos de fondos. Se sensibilizan variables como: endeudamiento, tasa de impuesto y volatilidad para analizar el impacto en el valor de la empresa. Finalmente, se describen las ventajas del modelo propuesto.
This paper proposes a binomial model for company valuation, projecting scenarios of continuity or insolvency of the company, and comparing it with the discounted cash flow model. The Real Option Theory is used for estimating the value of the company, which results in an explicit trade-off between the advantages and the risk of taking on debts. The work is organized as follows: the model is introduced and developed, and then it is illustrated with the application of a case, comparing the results obtained with the discounted cash flow model. Variables like: leverage, tax rate and volatility are sensitive when analyzing the impact on the value of the company. Finally, the document describes the advantages of the proposed model.
El método de Descuento de Flujo de Fondos (DFF) es uno de los que presentan mayor difusión para la valoración de activos reales, reconociendo variantes1 en función de cómo se plantea el impacto de la estructura de capital en el valor de la firma (Fernández, 2012). En principio, el método no contempla la flexibilidad estratégica de la firma para reaccionar frente a diferentes estados contingentes que impactan en el valor de la misma y respecto de los cuales la gerencia tiene posibilidad de incidir, asumiendo irreversibilidad en las decisiones y estados proyectados. Es así que, como complemento del DFF, surgen los modelos de valoración provistos por la Teoría de Opciones Reales.
Algunos de los estados contingentes que potencialmente inciden en el valor del proyecto son los escenarios de insolvencia-solvencia, motivados por la insuficiencia-suficiencia de flujos de fondos libres frente a los flujos de fondos de la deuda y, eventualmente, condicionando la continuidad-liquidación de la empresa. En su clásica formulación, el DFF supone un balance entre los efectos positivos y negativos de la deuda financiera de la empresa (por ejemplo, ahorros fiscales, costos de emisión y costos de disolución ponderados por su posibilidad de acaecimiento etc.), partiendo del concepto de empresas en marcha. Es claro que frente a incrementos en el apalancamiento financiero se incrementan los beneficios y los costos del mismo, llegando a niveles donde el valor de la firma se ve reducido por el impacto negativo del exceso de costos sobre los beneficios, situación contemplada en la estimación del valor por el DFF. Debe plantearse si el método, en su clásica formulación y para un mismo nivel de apalancamiento financiero, incorpora en la estimación de valor intrínseco los posibles estados contingentes de continuación o liquidación de la firma frente a un fracaso financiero. La respuesta es negativa, producto de la necesidad de trabajar con herramientas analíticas propias de un modelo dinámico de valoración, que englobe los diferentes escenarios proyectados, situación que pretende contemplar los modelos de valoración basados en la Teoría Opciones Reales.
Es por ello que el presente trabajo propone un modelo alternativo de valoración al clásico modelo DFF, en su modalidad Valor Presente Ajustado, donde son explicitados posibles escenarios de suficiencia-insuficiencia de flujos de fondos libres para atender los pagos de deuda. La propuesta se caracteriza por ser dinámica, plantearse en tiempo discreto, teniendo como principal motivación la valoración de empresas o proyectos, considerando los probables impactos derivados de las decisiones de financiamiento. En efecto, la decisión de financiamiento tiene como principal efecto condicionar el valor estimado de los activos de la firma y el capital propio, a la generación estocástica de flujo de fondos libres para atender los pagos originados por la deuda de la firma. En tal sentido, no se abandona la clásica concepción de considerar el valor del patrimonio neto como una opción de compra (Black y Scholes, 1973) suponiendo dos escenarios: (a) flujos de fondos libres superiores a los pagos de deuda, cuya consecuencia es la continuidad de la firma; (b) insuficiencia de flujos de fondos libres que deriva en la liquidación automática de la empresa y cancelación de los pasivos con los activos disponibles. El modelo supone que el comportamiento de las variables aleatorias sigue un proceso estocástico geométrico browniano (GBM) en tiempo discreto, por lo tanto el planteo analítico se basa en el clásico modelo binomial CRR (Cox, Ross y Rubinstein, 1979) y en el desarrollo propuesto por Broadie y Kaya (2007). Adicionalmente, supone la existencia de dos imperfecciones de mercado vinculadas a las decisiones de financiamiento y con impacto en el valor de la empresa: impuestos corporativos a la renta y costos de liquidación. (Existen otros trabajos como Broadie et al., 2007, donde se analizan y se brinda una solución numérica a las diferentes etapas en los procesos de negociación de deuda, liquidación y quiebra de la firma).
Cabe destacar que si bien existe una rica literatura sobre los efectos de las decisiones de estructura de capital sobre el valor de la firma, estas escapan del objetivo del presente trabajo. Cabe destacar que si bien existe una rica literatura sobre los efectos de las decisiones de estructura de capital sobre el valor de la firma, estas escapan del objetivo del presente documento. Desde los trabajos seminales (Modigliani y Miller, 1958); (Modigliani y Miller, 1963) se ha desarrollado un conjunto de investigaciones tendientes a explicar los efectos de las decisiones de estructura de capital sobre el valor de la firma. Los trabajos avanzaron sobre la compatibilidad de los postulados y el enfoque del modelo CAPM (Capital Assets Pricing Model) (Rubinstein, 1973); la existencia de impuestos a la renta personal de los tenedores de bonos (Miller, 1977). Estos no afectaron las clásicas proposiciones sobre el comportamiento de la estructura de capital y el valor de la firma. No obstante, los estudios sobre la existencia de asimetría de información revisan los clásicos postulados. Estos se pueden clasificar entre aquellos que estudian la existencia de asimetría de información antes y después del contrato. Antes del contrato constitutivo se tiene: (1) señalización: (a) rol de señalización de la deuda (Ross, 1977), (b) jerarquía financiera (Leland y Pyle, 1977), (Myers, 1984) (Myers y Majluf, 1984) y (2) detección (Stiglitz y Weiss, 1981). Después del contrato: (1) problemas de agencia; algunos de sus modelos: (a) costos de agencia de las acciones y las deudas (Jensen y Meckilng, 1976); (b) costos de agencia de los flujos de fondos libres (Jensen, 1986); (c) teoría de coinversión de los stakeholders (Titman, 1984) y (2) enfoque del ciclo de vida de la firma (Berger y Udell, 1998). Paralelamente se puede citar los estudios sobre la teoría de la estrategia corporativa y sus efectos en las decisiones de financiamiento de la firma (Brander y Lewis, 1986). Existen trabajos que resumen las diferentes teorías sobre la estructura de capital, asimetría de información y costos de agencia, (Copeland, Weston y Shastri, 2004).
No obstante, en el presente trabajo, simplemente, se expone el funcionamiento de un modelo numérico binomial que incorpora y explicita en el proceso de valoración probables impactos de las decisiones de financiamiento en el valor de la firma a la luz de la Teoría de Opciones Reales. Consecuentemente, el trabajo se estructura de la siguiente manera: En la siguiente sección se presenta formalmente el conjunto de ecuaciones utilizadas en el modelo. Seguidamente, se ilustra su funcionamiento sobre un proyecto de inversión de un contrato de concesión de explotación petrolera. En esta se compara el valor obtenido con el método del Valor Presente Ajustado y el modelo binomial propuesto. Adicionalmente, se desarrollan ejercicios de sensibilidad entre el valor del proyecto y variables como nivel de apalancamiento financiero y volatilidad, suponiendo la existencia e inexistencia de impuestos a la renta. Finalmente, se presentan las principales conclusiones.
2Modelo numérico binomial para valorar el impacto de la deuda en el valor del proyecto, estados de solvencia-insolvencia y la continuidad-liquidaciónEl modelo binomial se desarrolla en un ambiente neutral al riesgo, esto implica que el mismo permite valorar las opciones en términos de los flujos de fondos esperados, actualizados desde el vencimiento hasta el presente, suponiendo que los flujos crecen a la tasa libre de riesgo. Como consecuencia, la tasa a la cual crece el subyacente no afecta el valor del derivado, pero la volatilidad relacionada con los rendimientos del subyacente cobra significatividad en el valor de la opción. (En la práctica es más complejo estimar la tasa de crecimiento que la volatilidad (Wilmott, 2009)).
La valuación neutral al riesgo en opciones, requiere que exista perfecta correlación entre los cambios en el valor de la opción y del activo subyacente, debido a que las variaciones de este son el único factor de riesgo para el derivado. Por ejemplo, una cartera compuesta por una posición larga en la opción y la adecuada posición corta en el subyacente no debería tener ningún tipo de fluctuación aleatoria, ya que las variaciones en el precio de la acción (posición corta) se balancean con las variaciones en la opción de compra. El resultado de la estrategia precedente es una cartera que genera un rendimiento equivalente al tipo libre de riesgo y la clave para su construcción consistió en determinar la cantidad de acciones a ser vendidas en corto2. Esta cantidad se conoce como “Delta” y se estima a partir de un modelo financiero3.
La valuación neutral al riesgo permite la valuación de derivados, proyectando o simulando recorridos neutrales al riesgo correspondiente al subyacente para calcular los flujos de fondos de la opción. Estos son recursivamente actualizados a la fecha de valoración para, finalmente, ser promediados y obtener el valor intrínseco del derivado; por lo tanto, el valor promedio de los flujos de fondos esperados actualizados de la opción es el valor teórico de la opción4.
Por lo tanto, en la valoración de las opciones reales de una inversión empleando el modelo binomial en un entorno neutral al riesgo, se requiere, primero, estimar los coeficientes de ascenso (u) y descenso (d). Los parámetros indicados son la base para derivar los coeficientes equivalentes ciertos y la rejilla binomial para construir el recorrido estocástico del activo subyacente (valor de la firma y flujo de fondos operativos). Para estimar los coeficientes u y d, es necesario calcular la inobservable volatilidad en el mercado (σ) de los flujos de fondos del proyecto. La Teoría de Opciones Reales supone que esta se obtiene a partir del desvío del activo financiero réplica (gemelo). Para ello, es condición que los flujos de fondos del proyecto se encuentren perfectamente correlacionados con la variabilidad precio del activo financiero gemelo. Un fuerte supuesto de la Teoría de Opciones es que los mercados sean completos. Sin perjuicio de ello, existen diversos enfoques que, partiendo de determinados supuestos, proponen soluciones a la falta de completitud del mercado (distinción entre riesgos de mercado y privados en el proyecto, enfoque MAD, simulaciones). El enfoque de opciones requiere de la existencia de activos financieros que repliquen los movimientos y permita estimar el desvío esperado del flujo de fondos libres correspondientes al activo real objeto de la valoración, suponiendo distribución lognormal de las variables aleatorias. Caso contrario, se deben incorporar momentos estocásticos de orden superior (Milanesi, 2012). Los mercados no son perfectamente completos, constituyendo esta situación una importante debilidad del enfoque de opciones reales (Smith y Nau, 1995), (Wang y Halal, 2010). En particular, para empresas de capital cerrado, proyectos de inversión en nuevas tecnologías y empresas de base tecnológica. En estos casos, el segundo momento estocástico requerido por las ecuaciones anteriores, se supone calculado a través del método MAD (Marketed Asset Disclaimer) (Copeland y Antikarov, 2001).
Los coeficientes se estiman con las siguientes ecuaciones;
La tasa de crecimiento del valor de la empresa (a) surge de la diferencia entre la tasa libre de riesgo (r) y la tasa de pago de flujos de fondos (q);
El factor de actualización continua utilizado en el procedimiento recursivo del árbol es la tasa libre de riesgo,
Finalmente, los coeficientes neutrales al riesgo (p) son obtenidos mediante la siguiente expresión:
Definidos los parámetros básicos del modelo binomial (Jabbour, Kramin y Young, 2001), se procede al planteo del modelo numérico.
Rejilla binomial para estimar el valor no apalancado de la firma: A partir del valor inicial de los activos de la firma sin apalancamiento (Vu;)5 se proyecta la rejilla binomial utilizando los coeficientes de ascenso y descenso (Ec.1 y 2). De esta se construye la proyección binomial correspondiente a la generación de flujos de fondos libre (δ) en cada nodo de la rejilla. Para la primera rejilla, los posibles valores en cada nodo correspondiente al valor del proyecto sin apalancamiento están dados por la siguiente ecuación:
La rejilla correspondiente a los flujos de fondos libres surgen del producto entre el valor de la firma para un nodo (Ec. 6) y la tasa de pago de estos, según la siguiente expresión: Vixq Alternativamente, se puede plantear, conforme se indica en la siguiente ecuación;
Rejilla binomial para estimar el valor de la deuda: En cada nodo se debe calcular el flujo correspondiente a la deuda; para esto, se supone que la empresa emite un bono con pagos periódicos (C) compuesto por intereses y cancelación del principal al final de la vida del bono.
Si se introducen impuestos, el flujo de la deuda está representado por la expresión, (1–τ) C, siendo τ la tasa de impuesto a las ganancias, y ▵τ=ixτ el valor del ahorro fiscal. El flujo de fondos residual es la diferencia entre el flujo de fondos libres y el flujo de fondos de la deuda expresado por (δ-C). Este representa la magnitud de fondos a favor de los propietarios. En caso de que los flujos de fondos libres generados por el proyecto resulten insuficientes, se procede a cancelar los intereses de la deuda y se liquida el patrimonio neto.
Rejilla binomial para estimar el valor del capital propio, deuda y valor de los activos no condicionada a escenarios de insolvencia o continuidad: Se estiman los valores del capital propio (E), deuda (D) y valor total de los activos operativos (F). El valor de los nodos en el último período correspondiente al capital propio (ET), surge de la suma entre el valor final de la firma sin deuda (Ec. 6), más el valor de los flujos de fondos libres (Ec.7), menos el valor del flujo de fondos de la deuda (Ec.8), para cada nodo respectivo. Las ecuaciones empleadas son las siguientes:
Las ecuaciones precedentes permiten obtener el valor del capital propio (E) y de los activos operativos (F) en t=0 no condicionados por los posibles estados: (a) suficiencia de flujos de fondos o continuidad (δ≥C); (b) estados de liquidación de la firma, producto del fracaso financiero (δ).
A continuación, se desarrollan los pasos para estimar el valor total de los activos apalancados, deuda y capital de los propietarios condicionados a la generación de flujos de fondos en cada escenario proyectado. Existen tres momentos para estimar los posibles valores de la firma y el patrimonio neto: (I) horizonte final de proyección de la rejilla (T); (II) nodos intermedios (0) y (III) momento inicial (t=1 →0). Cabe aclarar que los nodos posteriores de la rejilla, según el estado de continuidad o liquidación, condicionan a los precedentes considerando dos escenarios posibles: (a) suficiencia de fondos para el pago de la deuda (la empresa continúa), (b) insuficiencia de fondos para el pago de la deuda (la empresa se liquida).
- (I)
Conjunto de ecuaciones para estimar los valores condicionados en el horizonte final (T):
Continuidad de la empresa (T): El valor de la firma más el flujo de fondos libres es superior o igual al pago de la deuda (interés más capital): VT+δT≥(1−τ)Ct+P. El conjunto de ecuaciones es el siguiente:
Liquidación (T): El valor de la firma más el flujo de fondos libres es insuficiente para el pago de la deuda (interés más capital): VT+δT<(1−τ)CΔt+P. Si se produce la liquidación de la firma, los costos de transacción son representados por α. El conjunto de ecuaciones es el siguiente:
Conjunto de ecuaciones para estimar el valor de los nodos intermedios condicionados (t; t>0):
Empleando la ecuación 9, se parte del valor del patrimonio neto no condicionado al evento de insuficiencia o solvencia en la generación de fondos, que se denota como: E˜=e−rΔt(pEu+1−pEd). Los escenarios posibles son:
Continuidad de la empresa (t; t≥1): No existe riesgo de liquidación de la firma si la suma de flujo de fondos libres y el valor presente del patrimonio neto es suficiente para atender los servicios corrientes de la deuda: E˜t+δt≥(1−τ)CΔt. En este caso, el conjunto de ecuaciones para valorar son las siguientes:
Liquidación (t
Conjunto de ecuaciones para estimar el valor inicial condicionado (t=1 →0).
Finalmente, el valor en t=0 se obtiene una vez calculados los valores finales (T, punto (I)) e intermedios (t
Aplicación del modelo numérico binomial, la posibilidad de insolvencia y análisis de sensibilidad de variables.
A continuación, se procede a ilustrar el funcionamiento del modelo empleando un proyecto de inversión sobre una concesión de explotación petrolífera; caso planteado originalmente por Smith (2005). Se pretende determinar el valor de un proyecto de inversión de un contrato de concesión para la explotación de un yacimiento de petróleo por un período de 3 años. Los estudios técnicos y de factibilidad indican que las reservas totales son de noventa y nueve millones (99 millones) de barriles y para el momento t=0 se espera producir nueve millones (9 millones) de barriles. Se proyecta: (a) decrecimiento de la producción a una tasa anual del 15%; (b) crecimiento del precio del barril de crudo a razón de un 3% anual; (c) crecimiento de los costos de explotación a razón del 2% anual y (d) costos fijos estables (no hay cambio de estructura). En la proyección de los flujos de fondos libres del contrato se emplean las siguientes variables: (a) precio del crudo por barril U$87,28, en donde los costos de producción representan el 77% del precio de venta, siendo de U$67,21 por unidad; (b) costos fijos por cinco millones de dólares anuales (U$5 millones). El proyecto se financia con una estructura de capital integrada por un setenta por ciento (70%) de deuda y treinta por ciento (30%) de capital propio. Las magnitudes de los componentes de la mezcla son determinados sobre el valor del proyecto desapalancado (Vu). Este último determinado por el método del Valor Actual Ajustado (APV, Adjusted Present Value) como variante del método de descuento de flujos de fondos, con la siguiente expresión:
En la ecuación anterior el APV o valor de la firma apalancada (Vl) es la suma del valor de la firma sin deuda (Vu) más los efectos producidos por la deuda. En este caso, se consideran solamente los efectos derivados del ahorro fiscal de intereses, donde la alícuota del impuesto t es del treinta y cinco por ciento (35%).Vu se estima con la siguiente expresión:
En este caso, FFLt representa los flujos de fondos del proyecto y ku la tasa del costo de capital desapalancado. Esta se estima quitando el efecto de la estructura de capital sobre la tasa de costo de capital propio apalancada ke (Fernández, 2012). Suponiendo que no existe riesgo en la deuda, la expresión utilizada es la siguiente:
Para estimar ku, se aplica el modelo CAPM (Capital Assets Princing Model); el coeficiente beta sin deuda (βu) se estima a partir del coeficiente beta apalancado (βl), sustrayendo la incidencia de la estructura de capital del proyecto representada por Wd (proporción deuda) y We (proporción capital propio).
El efecto del endeudamiento (ED) surge del ahorro fiscal, producto del endeudamiento, (txC). En el ejemplo, la deuda se estructura con un bono tipo americano devengando cupón del 5% sobre el 70% de Vu, con rescate de capital al final del tercer año.
En la tabla 1 se exponen los datos correspondientes a las proyecciones del flujo de fondos libres, valor actual de los flujos de fondos y valor de la firma sin deuda (Ec. 28); este último asciende a U$411,67 millones. La tabla 2 presenta los insumos utilizados para la determinación de la tasa de costo del capital sin deuda, a partir de la ecuación 29, que asciende a 10, 92%6.
Proyecciones de variables, flujos de fondos libres y estimación del valor actual de la firma sin deuda
| Proyecciones | 0 | 1 | 2 | 3 |
| Reservas de petróleo (millones) | 99.00 | 90.00 | 81.00 | 73.35 |
| Nivel de producción (millones) | 9.00 | 9.00 | 7.65 | 6.50 |
| Tasa de costo variable operativo (millones) por millón | $ 21 | $ 55 | $ 69.92 | $ 71.32 |
| Precio de crudo (por barril) | $ 87.28 | $ 89.90 | $ 92.60 | $ 95.37 |
| Ingresos por ventas (millones) | $ 809.1 | $ 708.4 | $ 620.2 | |
| Costos de producción (millones) | $ -616.9 | $ -534.9 | $ -463.8 | |
| Costo fijo (millones) | $ -7.0 | $ -7.0 | $ -7.0 | |
| Flujo de fondos libres después de impuestos (millones) | $ 185.1 | $ 166.5 | $ 149.4 | |
| Valor actual flujos de fondos (VA@ku) | $ 166.91 | $ 135.29 | $ 109.47 | |
| Valor del proyecto sin deuda Vu (VA@ku) | $ 411.67 |
| Otros datos | 0 | 1 | 2 | 3 |
| Tasa decrecimiento producción | 15% | 15% | 15% | |
| Tasa crecimiento costos | 2% | 2% | 2% | |
| Tasa de crecimiento de precio del crudo | 3% | 3% | 3% | |
| Costo fijo (millones) | $ 7.00 | $ 7.00 | $ 7.00 |
Elaboración propia.
Variables utilizadas para calcular la tasa de costo de capital sin deuda
| Tasa de costo de capital | Valores |
| Tasa libre de riesgo (1) (Ver nota 11) | 4.69% |
| Rendimiento esperado de mercado (2) (Ver nota 11) | 14.75% |
| ß apalancado observado comparable (Ver nota 11) | 1.24 |
| Estructura de capital empresa comparable (Wd/We) (Ver nota 11) | 1.54 |
| ß desapalancado del proyecto (3) (Ec.30) | 0.61969015 |
| Ku del proyecto (1)+((2)-(1))*(3) | 10.92% |
Elaboración propia.
El valor inicial del proyecto sin deuda (Vu) es de U$411,67 millones, siendo el valor nominal de la deuda emitida (D) del 70% del valor indicado. Consecuentemente, asciende a U$288,17 millones con un cupón del 5%, suponiendo que el modelo de flujo de fondos se sostiene y no se condiciona el valor de la firma a la posibilidad de insolvencia y liquidación.
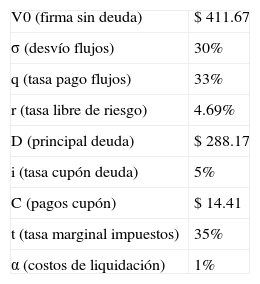
El modelo numérico binomial propuesto permite estimar un valor condicionado a los escenarios de solvencia-insolvencia, producto del apalancamiento financiero de la firma. Las variables de entrada del modelo binomial se exponen en la tabla 3.
Variables del modelo binomial
| V0 (firma sin deuda) | $ 411.67 |
| σ (desvío flujos) | 30% |
| q (tasa pago flujos) | 33% |
| r (tasa libre de riesgo) | 4.69% |
| D (principal deuda) | $ 288.17 |
| i (tasa cupón deuda) | 5% |
| C (pagos cupón) | $ 14.41 |
| t (tasa marginal impuestos) | 35% |
| α (costos de liquidación) | 1% |
Elaboración propia.
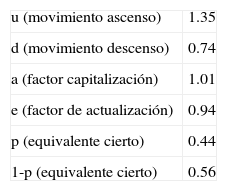
La tasa de pago de flujos de fondos (q) se obtiene a partir del cociente entre la media aritmética de los valores actuales del flujo de fondos libres (tabla 1) y el valor actual del proyecto7. Con las variables de la tabla precedente se está en condiciones de estimar los valores correspondientes a los coeficientes de ascenso, descenso, equivalentes ciertos y factor de capitalización (Ec. 1 a 5), tal como se muestra en la tabla 4.
Las variables de las tablas 3 y 4 permiten proyectar las rejillas para calcular el valor condicionado a escenarios de solvencia-liquidación, producto del riesgo financiero de la deuda. A continuación, se presenta la secuencia de cálculo:
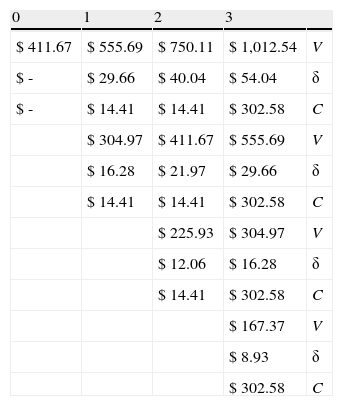
Rejilla binomial proyección Vu, δ, C: Para su construcción se utilizan las ecuaciones 6 a 8. En cada nodo de la rejilla se expone: Valor de firma (Vu;) (primera fila); flujo de fondos libres netos de impuestos (δ) (segunda fila) y los pagos de deuda sin considerar los escudos fiscales (C) (tercera fila), tal como se aprecia en la tabla 5.
Rejilla binomial valores V (valor de la firma sin deuda); δ (flujos de fondos libres después de impuestos); C (flujo de la deuda antes de impuestos)
| 0 | 1 | 2 | 3 | |
| $ 411.67 | $ 555.69 | $ 750.11 | $ 1,012.54 | V |
| $ - | $ 29.66 | $ 40.04 | $ 54.04 | δ |
| $ - | $ 14.41 | $ 14.41 | $ 302.58 | C |
| $ 304.97 | $ 411.67 | $ 555.69 | V | |
| $ 16.28 | $ 21.97 | $ 29.66 | δ | |
| $ 14.41 | $ 14.41 | $ 302.58 | C | |
| $ 225.93 | $ 304.97 | V | ||
| $ 12.06 | $ 16.28 | δ | ||
| $ 14.41 | $ 302.58 | C | ||
| $ 167.37 | V | |||
| $ 8.93 | δ | |||
| $ 302.58 | C |
Elaboración propia.
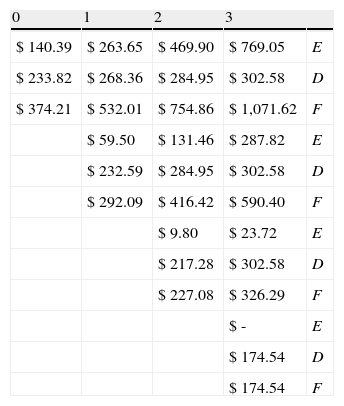
Rejilla binomial proyección (E), (D), (F) no condicionados: A continuación, en la tabla 6, se proyecta la rejilla para estimar el capital propio (E); deuda (D) y valor total de los activos operativos (F) no condicionados por la probabilidad de insolvencia de la firma en los nodos intermedios, utilizando las ecuaciones 9 a 11:
Rejilla binomial sin condicionar valores en nodos intermedios E (valor patrimonio neto); D (valor de la deuda); F (valor de la firma apalancada)
| 0 | 1 | 2 | 3 | |
| $ 140.39 | $ 263.65 | $ 469.90 | $ 769.05 | E |
| $ 233.82 | $ 268.36 | $ 284.95 | $ 302.58 | D |
| $ 374.21 | $ 532.01 | $ 754.86 | $ 1,071.62 | F |
| $ 59.50 | $ 131.46 | $ 287.82 | E | |
| $ 232.59 | $ 284.95 | $ 302.58 | D | |
| $ 292.09 | $ 416.42 | $ 590.40 | F | |
| $ 9.80 | $ 23.72 | E | ||
| $ 217.28 | $ 302.58 | D | ||
| $ 227.08 | $ 326.29 | F | ||
| $ - | E | |||
| $ 174.54 | D | |||
| $ 174.54 | F |
Elaboración propia.
En la rejilla anterior solamente los nodos finales consideran la posibilidad de liquidación de la firma en la medida en que el valor de la deuda sea superior al valor de la firma en su totalidad. El modelo supone que la variable de ajuste es el patrimonio de la empresa (E), siendo la base para proyectar la rejilla que considera los estados contingentes solvencia-liquidación en los nodos finales, intermedios y, consecuentemente, en el valor del proyecto.
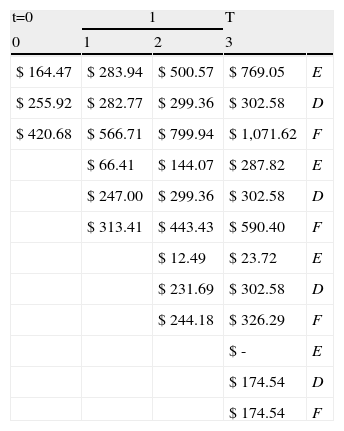
Rejilla binomial proyección (E), (D), (F) condicionados: La tabla 7 presenta los valores que adopta el proyecto considerando estados contingentes de continuidad o liquidación, aplicando: (a) nodos finales (ecuaciones 14 a 17); (b) nodos intermedios (ecuaciones 18 a 23); (c) nodo inicial valor actual (ecuaciones 24 a 26);
Rejilla binomial condicionando valores en nodos intermedios E (valor patrimonio neto); D (valor de la deuda); F (valor de la firma apalancada)
| t=0 | 1 | T | ||
| 0 | 1 | 2 | 3 | |
| $ 164.47 | $ 283.94 | $ 500.57 | $ 769.05 | E |
| $ 255.92 | $ 282.77 | $ 299.36 | $ 302.58 | D |
| $ 420.68 | $ 566.71 | $ 799.94 | $ 1,071.62 | F |
| $ 66.41 | $ 144.07 | $ 287.82 | E | |
| $ 247.00 | $ 299.36 | $ 302.58 | D | |
| $ 313.41 | $ 443.43 | $ 590.40 | F | |
| $ 12.49 | $ 23.72 | E | ||
| $ 231.69 | $ 302.58 | D | ||
| $ 244.18 | $ 326.29 | F | ||
| $ - | E | |||
| $ 174.54 | D | |||
| $ 174.54 | F | |||
Elaboración propia.
Se observa que el valor actual del proyecto con deuda en el momento inicial (F) asciende a U$420,68 millones, el valor actual de la deuda (D) es de U$255,92 millones y el valor actual del patrimonio de la firma (E) U$164,47. Este nodo es el resumen de valores esperados de los nodos futuros ajustados por los coeficientes equivalentes ciertos. Es decir, los valores esperados se encuentran condicionados a la suficiente generación de flujos de fondos libres para atender los pagos de deuda y evitar la liquidación del proyecto.
El valor obtenido con el método del Valor Actual Ajustado (APV), según la ecuación 28, es U$512,53 millones. Este surge de la suma entre el valor de la firma sin deuda y no condicionado a escenarios de solvencia-liquidación (Vu), U$411,67 millones más el valor del ahorro fiscal (ED), U$100,86 millones. La diferencia entre el modelo binomial (U$420,68 millones) y el valor actual ajustado (U$512,53 millones), siendo de U$91,85 millones más para el método tradicional. Esta se explica debido a que el modelo binomial captura el impacto negativo en el valor de la firma, propio de la probabilidad de liquidación, producto de la insuficiencia de los flujos de fondos libres para atender los pagos de la deuda, estado contingente no supuesto por el valor actual ajustado.
Sin perjuicio de la gran variedad de métodos disponibles para la estimación del costo del capital (Pratt y Grabowski, 2008); el método de descuento de flujos de fondos debe utilizar una tasa de actualización que refleje todos los riesgos sistemáticos inherentes a la empresa objeto de valuación. Es común en los procesos de valuación emplear como tasa de costo de capital la tasa de rendimiento requerido para un activo en marcha, sin considerar los riesgos derivados de la posibilidad de liquidación o quiebra de la firma por insuficiencia de fondos (Copeland, Koller y Murrin, 2000). La tasa aludida es utilizada cualquiera sea el escenario proyectado, suponiendo que esta representa todos los estados contingentes en la vida del proyecto. Lo dicho constituye una de las principales falencias metodológicas de los métodos tradicionales de valuación y de los árboles de decisión; estos últimos cuando utilizan la misma tasa ajustada por riesgo para valorar diferentes estrategias proyectadas (Smith et al., 1995; Trigeorgis, 1997).
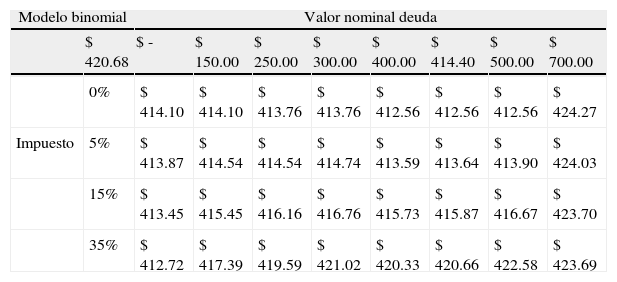
En las tablas 8 y 9 se expone el valor sensibilizado de la firma mediante el modelo numérico binomial y el descuento de flujos de fondos, sensibilizando dos variables: (a) nivel de endeudamiento y (b) alícuota de impuesto.
Tabla de sensibilidad modelo binomial: Valor de la firma-nivel de deuda-tasa de impuesto
| Modelo binomial | Valor nominal deuda | ||||||||
| $ 420.68 | $ - | $ 150.00 | $ 250.00 | $ 300.00 | $ 400.00 | $ 414.40 | $ 500.00 | $ 700.00 | |
| 0% | $ 414.10 | $ 414.10 | $ 413.76 | $ 413.76 | $ 412.56 | $ 412.56 | $ 412.56 | $ 424.27 | |
| Impuesto | 5% | $ 413.87 | $ 414.54 | $ 414.54 | $ 414.74 | $ 413.59 | $ 413.64 | $ 413.90 | $ 424.03 |
| 15% | $ 413.45 | $ 415.45 | $ 416.16 | $ 416.76 | $ 415.73 | $ 415.87 | $ 416.67 | $ 423.70 | |
| 35% | $ 412.72 | $ 417.39 | $ 419.59 | $ 421.02 | $ 420.33 | $ 420.66 | $ 422.58 | $ 423.69 | |
Elaboración propia.
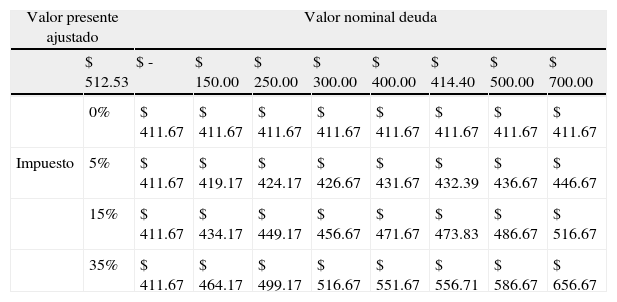
Tabla de sensibilidad descuento de flujos de fondos: Valor de la firma-nivel de deuda-tasa de impuesto
| Valor presente ajustado | Valor nominal deuda | ||||||||
| $ 512.53 | $ - | $ 150.00 | $ 250.00 | $ 300.00 | $ 400.00 | $ 414.40 | $ 500.00 | $ 700.00 | |
| 0% | $ 411.67 | $ 411.67 | $ 411.67 | $ 411.67 | $ 411.67 | $ 411.67 | $ 411.67 | $ 411.67 | |
| Impuesto | 5% | $ 411.67 | $ 419.17 | $ 424.17 | $ 426.67 | $ 431.67 | $ 432.39 | $ 436.67 | $ 446.67 |
| 15% | $ 411.67 | $ 434.17 | $ 449.17 | $ 456.67 | $ 471.67 | $ 473.83 | $ 486.67 | $ 516.67 | |
| 35% | $ 411.67 | $ 464.17 | $ 499.17 | $ 516.67 | $ 551.67 | $ 556.71 | $ 586.67 | $ 656.67 | |
Elaboración propia.
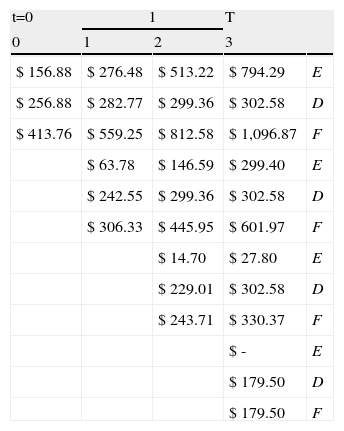
Ahora bien, en un mundo sin impuestos los valores de ambos métodos convergen según se expone en la tabla 10.
Rejilla binomial tasa de impuesto 0%
| t=0 | 1 | T | ||
| 0 | 1 | 2 | 3 | |
| $ 156.88 | $ 276.48 | $ 513.22 | $ 794.29 | E |
| $ 256.88 | $ 282.77 | $ 299.36 | $ 302.58 | D |
| $ 413.76 | $ 559.25 | $ 812.58 | $ 1,096.87 | F |
| $ 63.78 | $ 146.59 | $ 299.40 | E | |
| $ 242.55 | $ 299.36 | $ 302.58 | D | |
| $ 306.33 | $ 445.95 | $ 601.97 | F | |
| $ 14.70 | $ 27.80 | E | ||
| $ 229.01 | $ 302.58 | D | ||
| $ 243.71 | $ 330.37 | F | ||
| $ - | E | |||
| $ 179.50 | D | |||
| $ 179.50 | F | |||
Elaboración propia.
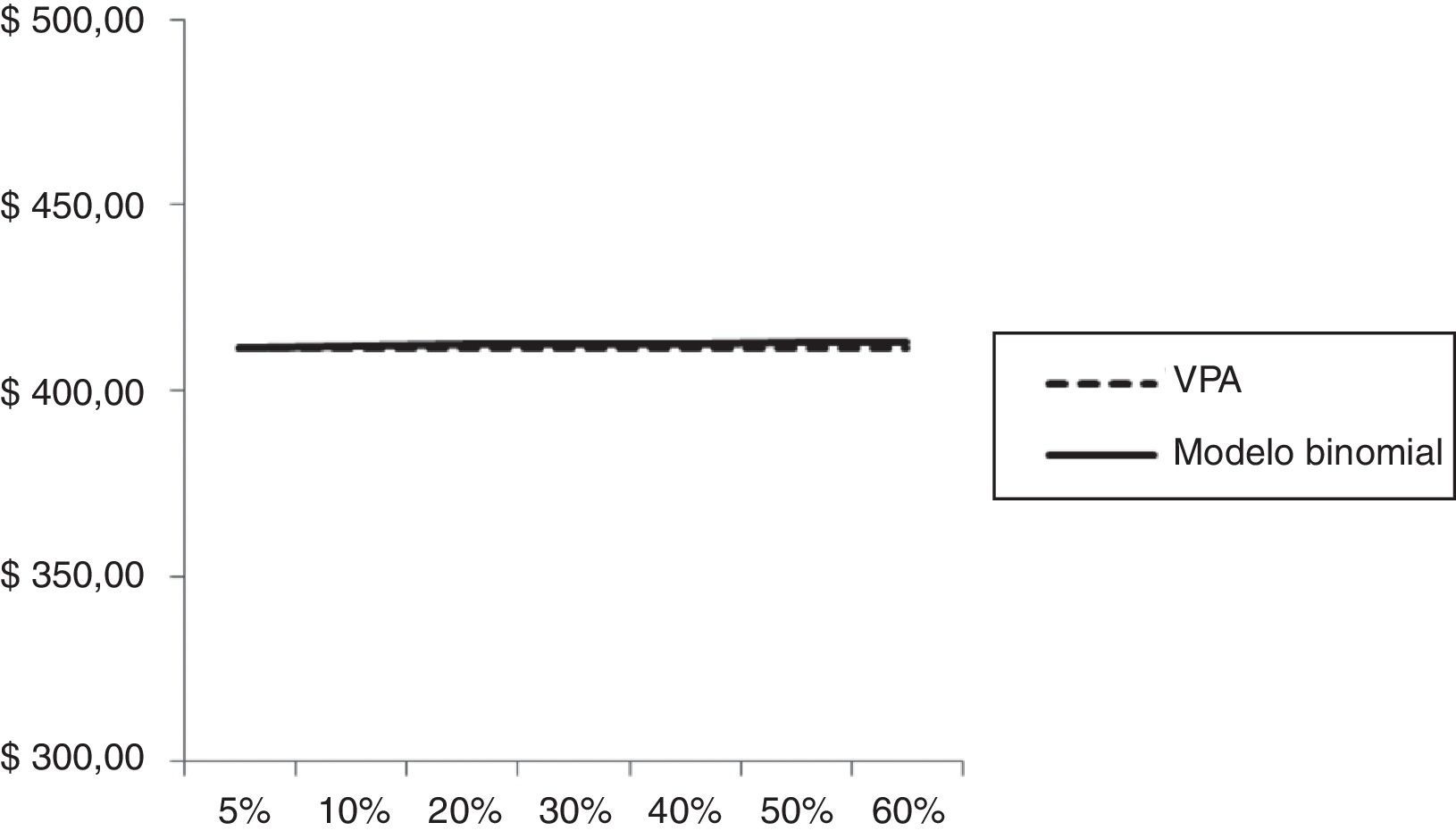
En la figura 1 se puede apreciar la convergencia de ambas medidas cuando no existen impuestos, para diferentes niveles de volatilidad, manteniendo el endeudamiento constante. El método de descuento de flujos de fondos permanece constante con un valor de U$411,67 millones.
El valor estimado, suponiendo una tasa de impuesto del 0% es levemente creciente en función de la relación volatilidad-deuda, producto de considerar la varianza total del valor de la firma y las posibilidades de liquidación, a diferencia del modelo tradicional. Para un nivel de deuda de U$414,40 millones, los valores oscilan entre U$411,40 y U$ 413,01 millones (ver la tabla 11).
Tabla de sensibilidad modelo binomial: Valor de la firma-nivel de deuda-volatilidad tasa de impuesto 0%
| Modelo binomial | Valor nominal deuda | ||||||||
| $ 413.76 | $ - | $ 150.00 | $ 250.00 | $ 300.00 | $ 400.00 | $ 414.40 | $ 500.00 | $ 700.00 | |
| Volatilidad | 5% | $ 414.10 | $ 414.10 | $ 414.10 | $ 414.10 | $ 412.95 | $ 411.40 | $ 410.59 | $ 430.32 |
| 10% | $ 414.10 | $ 414.10 | $ 414.10 | $ 414.10 | $ 411.95 | $ 411.95 | $ 410.86 | $ 427.07 | |
| 20% | $ 414.10 | $ 414.10 | $ 413.66 | $ 413.66 | $ 412.34 | $ 412.34 | $ 412.34 | $ 425.34 | |
| 30% | $ 414.10 | $ 414.10 | $ 413.76 | $ 413.76 | $ 412.56 | $ 412.56 | $ 412.56 | $ 424.27 | |
| 40% | $ 414.10 | $ 413.83 | $ 413.83 | $ 412.73 | $ 412.73 | $ 412.73 | $ 412.73 | $ 423.44 | |
| 50% | $ 414.10 | $ 413.88 | $ 413.88 | $ 412.88 | $ 412.88 | $ 412.88 | $ 412.88 | $ 423.73 | |
| 60% | $ 414.10 | $ 413.92 | $ 413.01 | $ 413.01 | $ 413.01 | $ 413.01 | $ 413.01 | $ 423.09 | |
Elaboración propia.
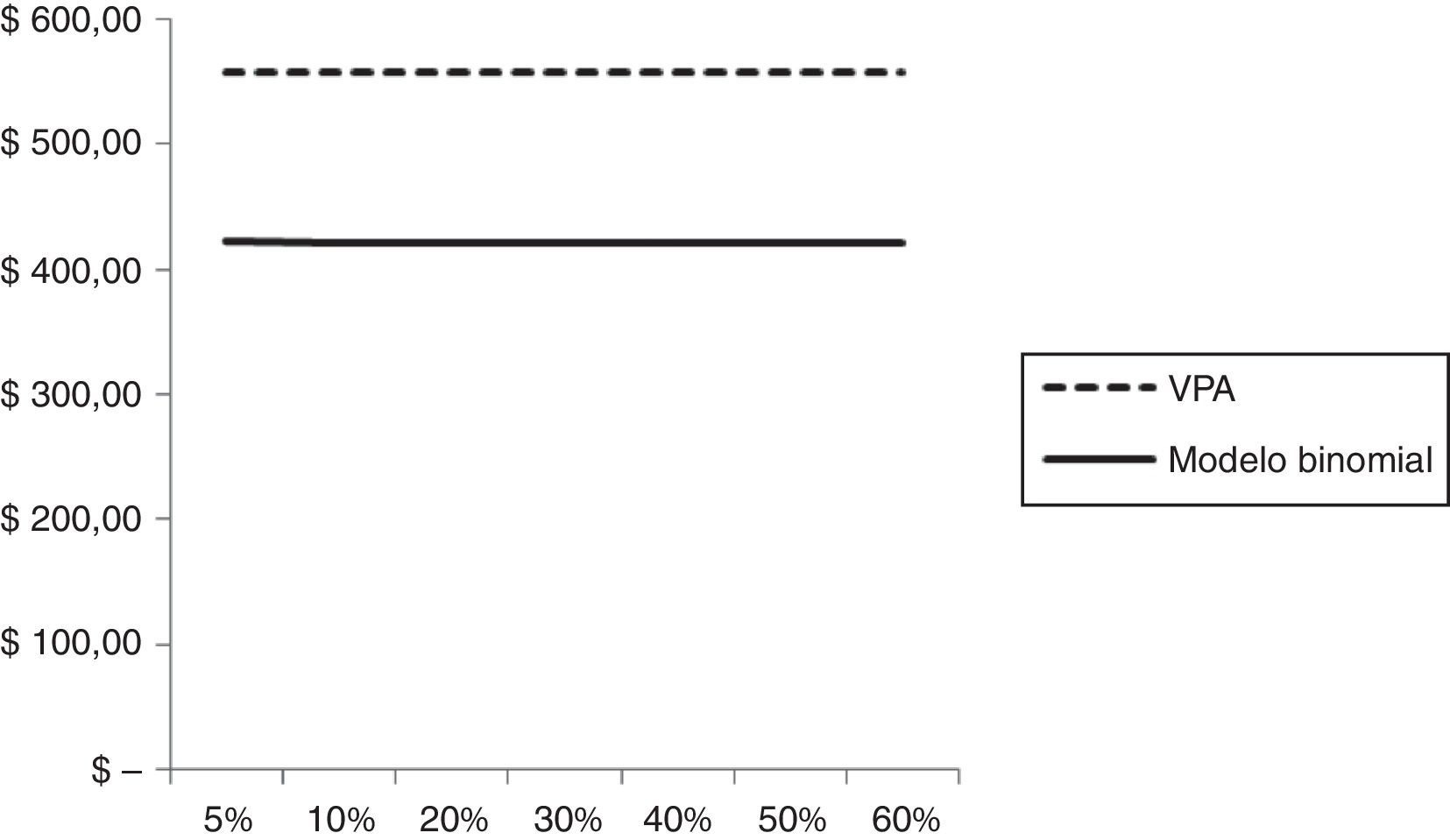
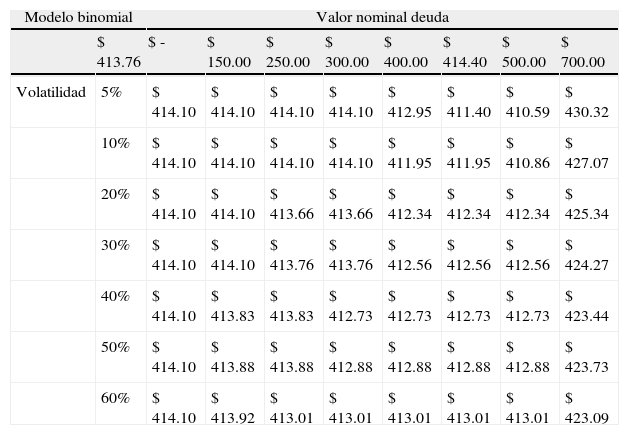
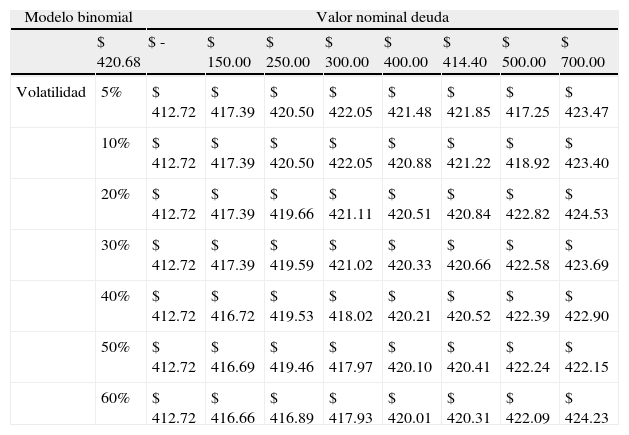
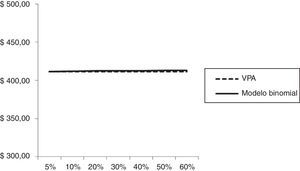
En la figura 2 se estima la sensibilidad valor de la firma-volatilidad, para una tasa de impuesto del 35%.
El valor estimado según el modelo numérico, suponiendo una tasa de impuesto de 35% es levemente decreciente en el modelo binomial (para un nivel de deuda U$414,40, el valor oscila entre U$421,85 y U$420,31), resultado de considerar la varianza total del valor de la firma, conforme se expone en la tabla 12.
Tabla de sensibilidad modelo binomial: Valor de la firma-nivel de deuda-volatilidad, tasa de impuesto 35%
| Modelo binomial | Valor nominal deuda | ||||||||
| $ 420.68 | $ - | $ 150.00 | $ 250.00 | $ 300.00 | $ 400.00 | $ 414.40 | $ 500.00 | $ 700.00 | |
| Volatilidad | 5% | $ 412.72 | $ 417.39 | $ 420.50 | $ 422.05 | $ 421.48 | $ 421.85 | $ 417.25 | $ 423.47 |
| 10% | $ 412.72 | $ 417.39 | $ 420.50 | $ 422.05 | $ 420.88 | $ 421.22 | $ 418.92 | $ 423.40 | |
| 20% | $ 412.72 | $ 417.39 | $ 419.66 | $ 421.11 | $ 420.51 | $ 420.84 | $ 422.82 | $ 424.53 | |
| 30% | $ 412.72 | $ 417.39 | $ 419.59 | $ 421.02 | $ 420.33 | $ 420.66 | $ 422.58 | $ 423.69 | |
| 40% | $ 412.72 | $ 416.72 | $ 419.53 | $ 418.02 | $ 420.21 | $ 420.52 | $ 422.39 | $ 422.90 | |
| 50% | $ 412.72 | $ 416.69 | $ 419.46 | $ 417.97 | $ 420.10 | $ 420.41 | $ 422.24 | $ 422.15 | |
| 60% | $ 412.72 | $ 416.66 | $ 416.89 | $ 417.93 | $ 420.01 | $ 420.31 | $ 422.09 | $ 424.23 | |
Elaboración propia.
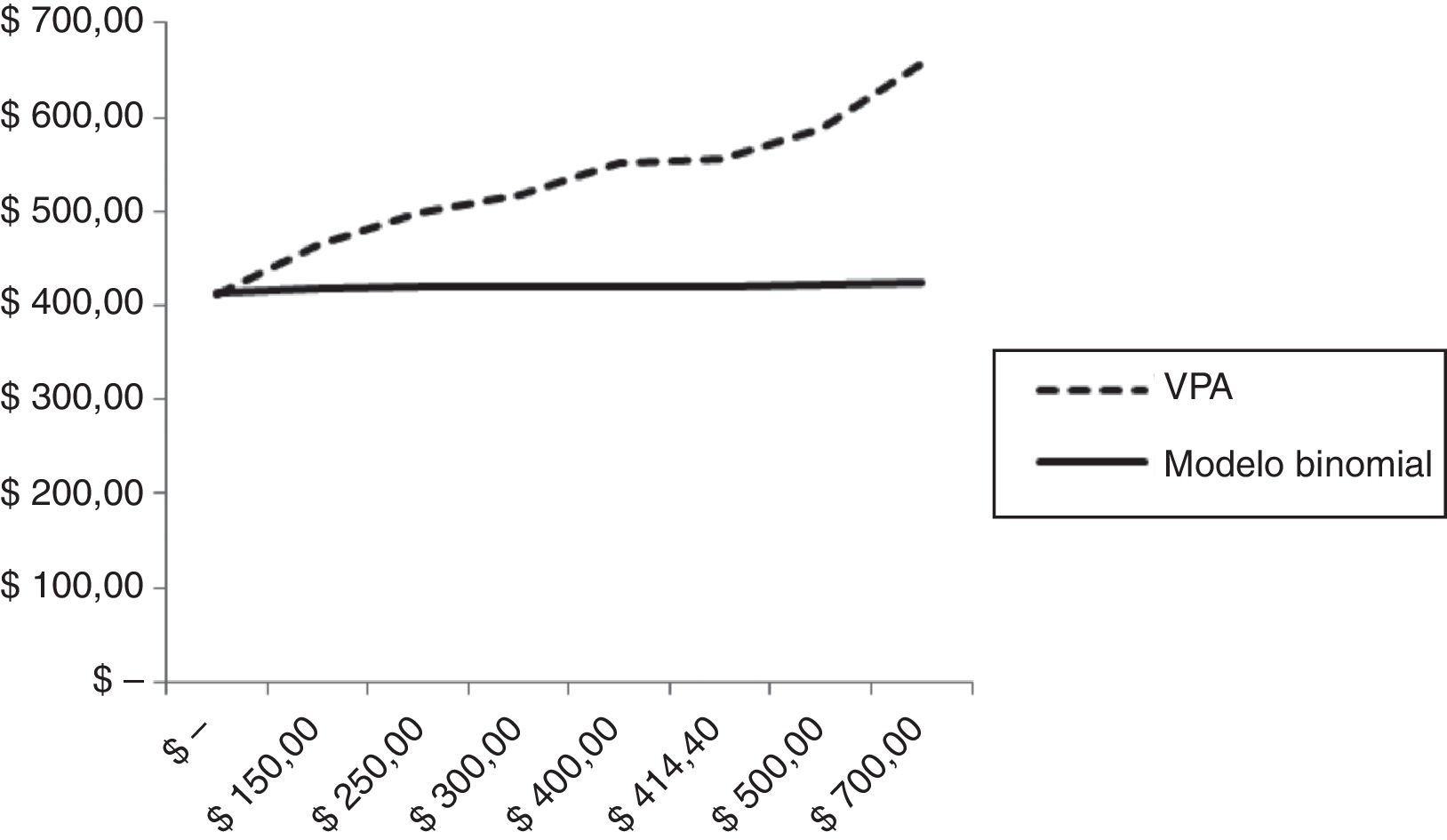
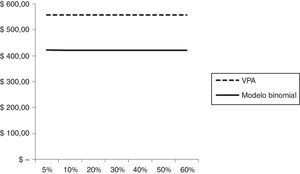
Para diferentes alícuotas tributarias, el valor estimado de la firma mediante el método de descuento de flujo de fondos se incrementa como resultado del impacto positivo propio del ahorro fiscal derivado de la deuda; esto es debido a que no se computan escenarios de insolvencia que afecten el valor intrínseco de la empresa. La diferencia de comportamientos se expone en la figura 3.
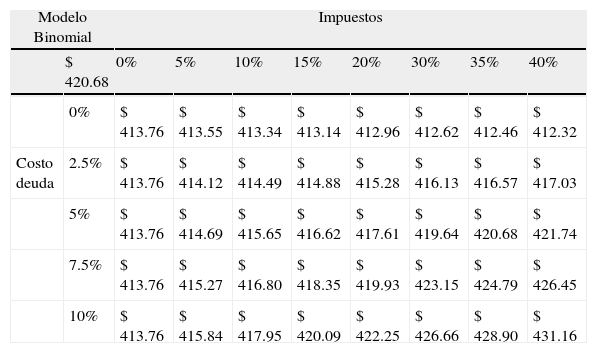
En la tabla 13 se exponen los diferentes valores de la firma, sensibilizando la alícuota impositiva e interés por deuda manteniendo constante el nivel de endeudamiento.
Tabla de sensibilidad modelo binomial: Valor de la firma-tasa de impuesto-costo de la deuda
| Modelo Binomial | Impuestos | ||||||||
| $ 420.68 | 0% | 5% | 10% | 15% | 20% | 30% | 35% | 40% | |
| 0% | $ 413.76 | $ 413.55 | $ 413.34 | $ 413.14 | $ 412.96 | $ 412.62 | $ 412.46 | $ 412.32 | |
| Costo deuda | 2.5% | $ 413.76 | $ 414.12 | $ 414.49 | $ 414.88 | $ 415.28 | $ 416.13 | $ 416.57 | $ 417.03 |
| 5% | $ 413.76 | $ 414.69 | $ 415.65 | $ 416.62 | $ 417.61 | $ 419.64 | $ 420.68 | $ 421.74 | |
| 7.5% | $ 413.76 | $ 415.27 | $ 416.80 | $ 418.35 | $ 419.93 | $ 423.15 | $ 424.79 | $ 426.45 | |
| 10% | $ 413.76 | $ 415.84 | $ 417.95 | $ 420.09 | $ 422.25 | $ 426.66 | $ 428.90 | $ 431.16 | |
Elaboración propia.
Las relaciones entre valor y alícuota impositiva para un mismo nivel de tasa de interés son directas ceteris paribus restantes variables. Si se deja constante la tasa de impuesto y se sensibiliza el interés de la deuda también se obtiene una relación positiva con el valor de la firma. Nuevamente, el modelo no presenta un crecimiento indefinido del valor de la firma; por el contrario, este se ve compensado por la creciente probabilidad de disolución de la firma ante incrementos en los niveles de deuda.
3ConclusionesEl trabajo propuso un modelo numérico binomial para el estudio del impacto de las decisiones de financiamiento sobre el valor a partir de situaciones contingentes de solvencia-insolvencia que condicionan la continuidad o liquidación de la firma. Como resultado, el valor obtenido del proyecto y, consecuentemente, su estructura de capital, resume el abanico de estados contingentes proyectados, considerando situaciones de continuidad de la firma o su liquidación. Es un modelo que complementa al DFF en tanto y en cuanto este supone irreversibilidad de las decisiones y situación de empresa en marcha. De hecho, el DFF no captura las situaciones contingentes y las incorpora en el valor estimado, producto de la incertidumbre a la cual se expone la firma. A menudo, los riesgos de insolvencia y liquidación de la firma no son contemplados, debido al empleo de tasas de costo de capital que suponen comportamientos de empresas en marcha y, por ende, no aplicables a la valoración de situaciones contingentes que dan lugar al planteo de estrategias alternativas (expansión, liquidación, abandono, diferimiento, etc.).
El modelo propuesto no abandona el clásico concepto de equiparar el patrimonio de la empresa a una opción de compra, cuyo precio de ejercicio son los pasivos y el subyacente valor operativo de los activos. La idea precedente es adaptada a un modelo numérico dinámico en tiempo discreto empleando rejillas binomiales. Estas permiten proyectar los diferentes nodos (estados), condicionando la continuidad o liquidación de la firma en la generación de flujos de fondos después de impuestos para atender pagos de deuda, repercutiendo en la estimación del valor de la firma y el patrimonio neto. Los efectos positivos sobre el valor del proyecto, derivados del ahorro fiscal de los intereses, se ven compensados por el impacto negativo que resulta de considerar las probabilidades de insolvencia y posterior liquidación de la firma. Estas aseveraciones son corroboradas en el análisis de sensibilidad presentado, ya que los valores obtenidos para el proyecto y el patrimonio neto se mantienen dentro de un rango a través de un equilibrio entre el efecto positivo del ahorro fiscal y el impacto negativo de la liquidación de la firma.
El método de descuento de flujos de fondos puede clasificarse en tres grandes grupos: (a) Costo promedio ponderado: el valor de la empresa surge de actualizar la corriente de flujos de fondos libres a la tasa del costo promedio ponderado del capital; este incorpora los efectos del ahorro fiscal, producto de la deuda; (b) Valor presente ajustado: el valor de la firma surge de la suma del valor de la empresa sin deuda más el valor actual de los beneficios netos del endeudamiento; (c) Flujos a capital: el valor de la firma surge de actualizar la corriente de flujos de fondos libres más el efecto de la deuda a la tasa del costo promedio ponderado del capital, sin considerar el ahorro fiscal.
Se denominan ventas en corto a las operaciones de apalancamiento donde se obtienen en calidad de préstamo acciones que son vendidas en el mercado para hacerse de liquidez, con la condición de devolver el mismo activo en la fecha de vencimiento estipulada.
Como usualmente se necesita un modelo matemático para calcular la letra griega Delta y los modelos financieros son aproximaciones, no réplicas exactas de la compleja realidad, la eliminación total teórica del riesgo es un ideal difícil de verificar en la práctica. Las principales limitaciones instrumentales de la valuación neutral al riesgo son: (a) requiere un continuo balance de la cobertura, ya que Delta continuamente (no discretamente) cambia, por ende se debe vender-comprar acciones para mantener la posición libre de riesgo; (b) se deben cumplir ciertos supuestos vinculados al proceso estocástico del activo (seguir un movimiento geométrico browniano, sin saltos y con volatilidad conocida y finita).
El ejemplo ilustra la idea detrás de la valuación neutral al riesgo; una acción tiene un precio de mercado de $10,55, creciendo en promedio el 12% por año. Su volatilidad es del 23% y la tasa libre de riesgo es del 4% anual. Se quiere valorar una opción de compra con precio de ejercicio de $11 con fecha de expiración dentro de dos meses. La tasa del 15% de crecimiento es totalmente irrelevante, ya que el crecimiento promedio de la acción no afecta el precio de la opción. En realidad, para valorar el derivado se deben simular recorridos del subyacente desde la fecha de valuación al vencimiento de la opción con crecimiento al tipo libre de riesgo del 4% y volatilidad del 22%. Luego se debe calcular el flujo de fondos correspondientes a los recorridos proyectados, actualizar los flujos al presente y calcular su valor promedio para obtener el valor teórico de la opción (en el modelo binomial no se necesitan todas las simulaciones, se proyectan los recorridos a partir de coeficientes de ascenso y descenso, calculados a desde la volatilidad, los flujos son actualizados al tipo libre de riesgo y ponderados por coeficientes equivalentes ciertos).
Un valor de los activos operativos totales de la empresa independientemente de su estructura de capital.
Se supone que el proyecto de inversión en cuestión genera flujos de fondos correlacionados perfectamente con el precio del petróleo, cuya cotización y comercialización global se expresa en dólares estadounidenses. Los datos utilizados para estimar las variables que integran la tasa de costo de capital fueron obtenidos del sitio web de Aswhat Damodaran: http://pages.stern.nyu.edu/∼adamodar/. Los coeficientes betas apalancados y estructura de capital sectorial (oil/gas production and exploration) fueron obtenidos del cuadro “levered and unlevered betas by sector”. El adicional por riesgo de mercado en dólares para Argentina surge del cuadro “Country default spread and risk premium-Risk premium for others markets”. Finalmente, la tasa libre de riesgo de Estados Unidos 10 Y T-bonds media aritmética 2004-2013 del cuadro “Annual Returns on Stock, T.Bonds and T.Bills: 1928 – Current”
El promedio del valor actual del flujo de fondos en la tabla 1 es de U$137,22; el valor actual del proyecto asciende a U$411,67 millones, la tasa de pago de flujos de fondos (q) es del 33%.