An innovative strategic choice for stakeholders in the chinese traditional commercial street renewal using evolutionary game theory

Abstract

This paper aims to solve the contradiction between the pursuit of economic interests and the protection of historical culture in the renewal of traditional Chinese commercial streets, thus coordinating the interests of the participating subjects. We construct an evolutionary game model of local government, developers, and street owners and explicitly describe the three parties' strategic choices and dynamic processes of evolution. The evolutionarily stable strategy results show that the evolutionary process by which the three parties reach a unique stable strategy set (1,1,1) is “government→developers→owners.” We use system dynamics to simulate the influence of model parameters on the dynamic evolutionary process. The specific results show that the social benefits of local government, the economic benefits of developers, and the supervision costs of street owners are the most sensitive to their respective strategic choices. The incentives and compensation measures formulated by the government can promote the active participation of the government and developers. In addition, the large fines charged by the government can also restrain the bad behavior of developers and achieve a win–win situation for the three parties.

Introduction

With the introduction and application of the concepts of low-carbon cities and healthy cities, urban renewal has ushered in new opportunities. In the 1970s, the United States began to carry out large-scale urban renewal in the modern sense. The main goal of “old city reconstruction” is for it be led by private developers to improve living conditions and the environment (Hunt, 2018). After the 1980s, urban regeneration emphasized urban land reuse, with residents participating in the comprehensive rejuvenation of the community, such that they paid attention to the protection of the community's historical buildings and maintained the community's social fabric (Hui et al., 2020). In China, the “Shenzhen Urban Renewal Measures” promulgated in 2009 first proposed the concept of “urban renewal” based on “old city reconstruction” to strengthen and improve urban functions, upgrade the industrial structure, and promote the sustained development of society. China has entered the era of urban connotative development and high-quality urban development from the extension of urban expansion. The goals of urban renewal are more diversified and integrated, and the participants are more diversified (Zhong, 2020; Chen et al., 2021). “Opinions on strengthening the protection and inheritance of history and culture in urban and rural construction” issued by China in 2021 pointed out that the systematic protection and inheritance of history and cultural heritage is of great significance to the continuation of the historical context, the promotion of high-quality development of city and countryside construction, and the strengthening of cultural self-confidence. However, the renewal of historical streets involves many participants with different interests and demands, leading to other innovative strategic choices according to each participant. Thus, it is difficult to achieve a balanced state of risk-sharing and benefit-sharing among all participants.

Traditional commercial districts are one of the principal parts of urban heritage; as a carrier of historical culture, they have the characteristics of witnessing historical changes, promoting tourism development, and stimulating commercial vitality (Qin & Hu, 2019). With the innovation and development of the city, it has faced loss of historical character, the homogenization and vulgarization of space, the destruction of the traditional business environment, out-of-control government coordination and regulation, and the improper distribution of interests among stakeholders (Mehanna, 2019). At the same time, there have been updated case practices that conflict between the profit-seeking nature of the market economy and the protection of traditional culture. There has also been a lack of commercial heritage. Therefore, coordinating the contradiction between the pursuit of economic interests and the protection of history and culture, balancing the interest demands of the participating subjects, and exploring innovative strategic choices in the cooperation of stakeholders are particularly important.

At present, there are few studies on the innovative strategic choice of stakeholders in urban renewal. The relevant research mainly includes the importance of protecting commercial streets and the protection of urban heritage (Mehanna, 2019), the role of stakeholders in urban renewal (Zhang, Zong, & Chen, 2017), participants’ interest demands and stakeholder cooperation strategies (Zhang, Zhang, & Wu, 2021; Li, Liu &Ye, 2022), interest distribution among participants (Liu, Wei, Zhou, & Liu, 2020), sustainable evaluation of historical district protection (Su, Sigely, & Song, 2020) and performance evaluation (Yang & Li, 2021). The research primarily focuses on the renewal model and renewal evaluation, with little focus on the choice of strategy by various stakeholders, which cannot wholly solve the contradiction between the pursuit of economic interests and the protection of historical culture in the renewal of traditional Chinese commercial blocks. In addition, the failure of the renewal project cannot be avoided. The methods used mainly include literature review, expert interviews, stakeholder analysis, social network analysis, fuzzy analytic hierarchy, cooperative game, and other methods. Existing methods can only analyze the interest demands of stakeholders from a qualitative perspective and cannot quantitatively study the strategic choices of participants. However, the use of evolutionary games can reduce the error of subjective evaluation, and the use of system dynamics can predict the behavior changes and influencing factors of game subjects, combining theory with practice to solve the problem of varying interests of participants.

Based on the contradiction between the pursuit of economic interests and the protection of historical culture in the renewal of traditional commercial streets, we coordinated the distribution of interests of the participating subjects. This paper analyzes the game relationship between stakeholders in the renewal process and their optimal strategy sets. It explores how influencing factors affect the strategic choices of stakeholders. Therefore, this paper first constructs an evolutionary game model to analyze the interested stability of the tripartite parties. Then, system dynamics simulation is used to simulate the influence of exogenous variables on the choice of strategy to explore the impact of each participant's different benefit strategy choices on the stable state of the system (Gao & Zhao, 2020; Xu et al., 2020).

This paper makes the following contributions. (1) In reviewing the literature on the renewal of traditional commercial streets, we found little research on the choice of participants' strategies. Therefore, this paper starts from the perspective of participants' strategy choices and explores the factors that affect the choice of strategies. (2) Research on participants in urban renewal focuses on qualitative analysis of the game process. In this paper, we combined the evolutionary game model and the system dynamics model to study the evolutionary process of the innovative strategy choices of local government, developers, and street owners from a quantitative perspective as well as how to influence strategy selection.

The remaining sections of this paper are as follows. Section 2 describes the literature review on the renewal of traditional commercial streets. Section 3 analyzes the interest demands of stakeholders and the factors affecting their behaviors. In Section 4, we build an evolutionary game model to explore the stable equilibrium. In Section 5, we simulate and analyze the influence of exogenous variables on the choice of third-party strategy. Section 6 puts forward discussions and suggestions. Section 7 presents conclusions and research limitations..

Literature Review

Traditional Commercial Street

The current research on the renewal of traditional commercial streets mainly refers to protecting historical streets (Mehanna, 2019) and the evolution and protection of conventional commercial streets (Wand & Li, 2017; Wang, Li, & Zhang, 2020). Mehanna stated that commercial streets have multiple values such as history, city, architecture, economy, society and are one of the most critical components of urban heritage (Mehanna, 2019). Wang used space syntax to study the spatial structure changes of the Paul Ruins commercial area, and pointed out that the traditional street renewal should focus on the historical preservation area (Wand & Li, 2017). Su pointed out the importance of heritage authenticity protection in urban renewal, and found that the current focus on the material quality of spatial reconstruction has lost the pursuit of authenticity and originality (Su, Sigely, & Song, 2020).

Some studies focus on the sustainable development of historical districts, mainly the evaluation of sustainable development (Wang et al., 2018; Charhardowli et al., 2020), and the reconstruction of historical relic space (Kou et al., 2018; Wang et al., 2018). Because of its two natures of cultural legacy and living community, historical blocks have become important targets for urban renewal and sustainable development. Some studies have provided references for heritage protection and sustainable development research by constructing sustainable evaluation models (Wang et al., 2018). Historical streets pay more attention to the sustainable renewal of economy, society, culture and environment, and maintain the sustainability and regeneration of the historical core of the city. In the background of China's rapid urbanization, we should stress the practical compatibility of urban construction and historical heritage protection (Charhardowli et al., 2020). Policies and regulations, public participation and information openness, and protection of traditional culture are the keys to the project's success.

Stakeholder Game in Urban Renewal

Stakeholders of Urban Renewal

The process of urban regeneration involves multiple stakeholders, such as government departments, developers, and residents, and each stakeholder has a different role in positioning and interest appeal. Each participant's interest balance and game are the main topics of concern. At present, relevant research mainly focuses on the participation of stakeholders in the planning decision-making stage (Zhou, Lan, & Zhou; 2021), interest network structure and governance (Shi, 2018; Qian et al., 2019), stakeholder relationships and demands (Ye et al., 2021; Cheng et al., 2021). Studies have also started to follow with the sustainability of regeneration (Yildiz, Kivark, &Arslan, 2019). Zhou supports stakeholders in participating in the urban renewal decision-making process by constructing an experience-based urban renewal model decision-making system (Zhou, Lan, & Zhou; 2021). In urban renewal decision-making, we should pay attention to stakeholders' knowledge, power, and rights in the decision-making process and determine the relationship and network structure between them (Qian et al., 2019). Shi applied social network analysis methods to study the relationships and demands of stakeholders (Shi, 2018). Yildiz determined the responsibilities of local government, citizens, contractors, architects, engineers, and urban planners in the urban regeneration process (Yildiz, Kivark, &Arslan, 2019). Ye pointed out that in protecting urban history and cultural structure, the interests of local communities and different stakeholders became important (Ye et al., 2021). Cheng pointed out the contradiction between the proportion of potential profit distribution in the process of governing cities in China during the update of Chinese governance cities and the contradiction between the income provided by the district government and developers in public facilities and compromise (Cheng et al., 2021). The focus of resolving social conflicts and interest games in the renewal of historical streets should clarify the roles and interest demands of local government, developers, and owners, formulate relevant policies and regulations, and restrain developers' bad behaviors (Xie & Zhu, 2014).

Application of Evolutionary Game Theory

As a branch of game theory, the evolutionary game theory originates from genetic biology and studies the conflict and cooperative behavior of plants and animals (Wright,1930); the concept of evolutionary stable strategy (ESS) marked the official birth of evolutionary game theory (Smith & Price, 1973). ESS shows that if most populations choose evolutionary stability strategies, then a small part of population invasion is impossible (Smith, 1976). The dynamic replication equation in evolutionary game theory represents the dynamic convergence process of the group (Taylor & Jonker, 1978), and the equilibrium result is a process of continuous adjustment (Foxon, 2006). Since the 1980s, evolutionary game theory has been widespread used in social system changes and industrial evolution, etc. Chu constructed a tripartite evolutionary game framework for the government, developers, and owners in urban renewal. It formulated corresponding subsidy policies to stimulate cooperation between developers and owners to reduce the government's financial burden (Chu et al., 2020). The social conflict caused by the uneven distribution of benefits hinders the implementation of urban renewal. Therefore, Liu investigated the bargaining process between developers and residents regarding the distribution of benefits and suggested that the government should regulate project operations, simplify management procedures, and establish an information-sharing mechanism to ensure that developers and residents live in harmony (Liu et al., 2020). Some scholars have expanded the application field of applied data analysis and game theory. Dong proposes a new aggregator, De-Noising Aggregation (DNAG), which avoids the overfitting phenomenon that occurs when executing Graph Neural Networks (GNNs) on test examples. It has obvious advantages in denoising ability and realizing several graph-structured dataset prediction tasks(Dong et al., 2022). Rasmusen builds a knowledge graph-based model of a consent solicitation user interface and provides a unified consent model to all entities involved in the data sharing process, increasing users' legal awareness (Rasmusen et al., 2022). Li combines machine learning and deep learning to build a Deep Neural Network (DNN) model to improve the quality of alarms in large-scale network security protection, improve false alarm detection effects, and more accurately identify true alarms (Li et al., 2022). Chauhan analyzes the primary factors driving the expansion of the mobile game industry. Use Technology Acceptance Model (TAM) and Machine Learning (ML) techniques from the study of the system and the internal symmetry relationship, and point out that perceived usefulness is an essential parameter of behavioral intentions in the online mobile game industry (Chauhan et al., 2021). Sumathi proposes a dynamic bargaining game method for node selection and data transmission. In the Pareto optimal solution, we consider the reliability and efficiency of the data to select nodes. Then malicious nodes are eliminated according to the principle of node distribution disagreement metrics. It is more resilient than existing methods (Sumathi., 2021).

At present, most of the research on the renewal of traditional commercial streets is the evolution and protection of renewal, the sustainable development of historical blocks, and the responsibilities and benefit distribution of stakeholder relationships in urban renewal. These studies did not build a game model to analyze evolutionary stability strategies. They did not find the factors affecting the renewal project. However, in the renewal process of traditional commercial streets, the interests of stakeholders and their distribution directly affect the implementation of the renewal project. Local government, developers, and street owners are bounded rational people with incomplete information in traditional commercial streets, so use evolutionary game theory to analyze strategy evolution trends and stable equilibrium results, use system dynamics to simulate the factors that affect three stakeholders' strategy choices to promote the three parties' win-win situation.

Methods

Local government, developers, and street owners do not have access to all information, so they are all bounded to rational persons. All stakeholders can learn, think, and imitate. First, they can continuously adjust and refine their strategies by learning from and considering the strategies of other stakeholders. Second, they can build their own body of knowledge, optimize their strategies, and imitate and learn from stakeholders' experiences in similar projects. In reality, during the renewal process of traditional commercial districts, stakeholders need to play multiple rounds of games to achieve the best decision. It is why the evolutionary game model is more suitable for this article.

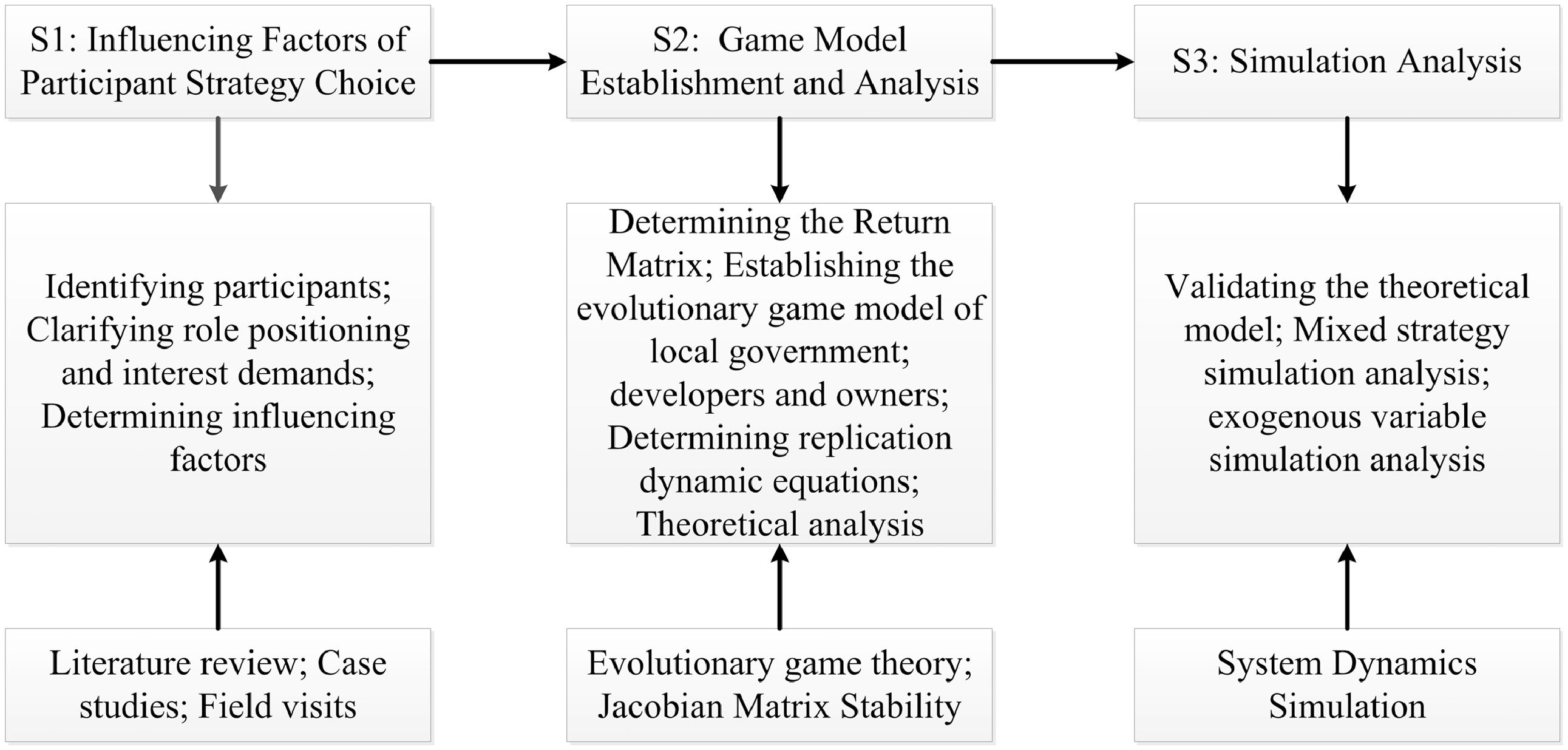
To seek a balanced state of the comprehensive benefits of the three parties in the renewal of traditional Chinese commercial streets and to explore the strategy selection of various stakeholders, the research framework is shown in Figure 1.

Fig. 1.

Research framework

Interest Appeals and Influencing Factors

To achieve a win-win cooperation among the local government, developers and street owners in the traditional Chinese commercial street renewal, this paper studies the innovative strategic decisions from the respective advantages of the three parties. From the standpoint of renewal practice, the environmental benefits of the street are improved compared to before the renewal, so we consider only economic and social benefits.

Analysis of Interests Appeals of Stakeholders

From the perspective of the renewal practice of traditional Chinese commercial streets, the direct stakeholders involved are local government, developers, and street owners.

• (1) Local government

The local government coordinates and regulates the renewal process of traditional commercial streets, coordinating the interests of participants and formulating related policies and regulations to restrict the behavior of the three parties. As a public sector, the government first pays attention to social and public interests, improves the neighborhood environment and public infrastructure, disseminates historical values, and drives urban development. Still, at the same time, the government may also be “short-sighted”, or it may only focus on economic interests, increase fiscal revenue, and promote urban development. Political achievements have dual attributes.

• (2) Developers

As a profit-making organization, the developers are responsible for constructing and operating the updated traditional commercial districts. The fundamental purpose is to maximize economic benefits and have a greater right to speak, which may harm public interests, destroying the social structure and cultural texture. At the same time, developers choose to establish long-term and good cooperative relationships with the government to mention enterprises' popularity to bring public welfare construction to the city.

• (3) Street owners

The street owners refer to the shop's original property owner in the street and obtain the profit dividend after the project operation. Compared with local government, developers are in a disadvantageous position, lack the right to speak, ignore their interests, and have no effective institutional guarantee. They want to receive appropriate financial compensation, which is their benefit, as shown in Table 1.

Table 1.

The role of interests appeals of stakeholders

Stakeholders	Roles	Interest demands
local government	the dual attributes of social interest and economic interest; macro-control, coordination and regulation; a strong voice	improve the street environment and public facilities, stimulate urban development; increase fiscal revenue, improve political performance (Dun, 2016; Yildiz, 2019)
developers	economic interest is the main part, public interest is the auxiliary part; a strong voice (Zhang, Zong, & Chen, 2017; Zhu et al., 2019)	maximize profits; protect part of the public interest (Dun, 2016; Yildiz, 2019)
street owners	individual interest; lack of voice (Zhang, Zong, & Chen, 2017)	obtain financial compensation, optimize the street space (Dun, 2016; Yildiz, 2019)

Determinate the Influencing Factors of Stakeholders’ Innovative strategic choice

Based on a summary analysis of the appeals of urban renewal stakeholders, combined with the field visits and relevant documents, 14 factors that affect the innovative strategic choices of the three stakeholders in the evolutionary game model are determined, as shown in Table 2.

Table 2.

The influencing factors and meaning of stakeholders’ innovative strategic choice

Stakeholders	Influencing factors	Meanings	References
local government	economic benefits	tax revenue during the operating period, etc.
	social benefits	political achievement, public interest, social value, etc.	(Greenwood & Newman, 2010)
	coordinated and regulated costs	manpower, energy, and other costs	(Bagaeen, 2006)
	incentive costs	the cost of incentivizing developers to invest	(Chu et al., 2020)
	compensation costs	compensation given to owners and the cost of encouraging owners to supervise	(Wang, Yang, & Ye, 2019)
developers	normal economic benefits	the operating profit by actively participated	(Wang et al., 2014)
	excessive economic benefits	the sum of legitimate and illegitimate operating profits by excessive pursuit of profit
	social benefits	corporate visibility, reputation, etc.	(Wang et al., 2014)
	investment cost	the cost of renovation and operation
	fine	excessive profit-seeking fines
	public interest	commercialization, loss of historical features, loss of public interest, etc.	(Zhu, et al., 2019)
street owners	economic benefits	part of the profits obtained during the operating period, dividends,
	indirect benefits	Improvement of public facilities, continuation of traditional culture, etc.	(Shi et al.,2016)
	supervision costs	the cost of the developers’ behavior	(Zhuang et al., 2017)

Model Assumption

In the research on the strategic choice of participants in the renewal of traditional commercial streets in China, we mainly focus on the strategic choices of three stakeholders: local governments, developers, and street owners. Therefore, when building an evolutionary game model, it is necessary to fully consider the strategic choices and benefits of the participants to study how to improve the cooperation among stakeholders and achieve a win-win situation for all parties.

The renewal of traditional Chinese commercial streets faces problems such as improper distribution of interests of participants and conflicts between the pursuit of economic interests and traditional culture. Therefore, this paper explicitly studies participants' behaviors from the perspective of evolutionary game theory. In evolutionary game theory, decision-makers are considered bounded rationality, which means that decision-makers do not always aim to maximize their returns. Their strategic choices may be affected by the actions of other players, and they will learn from others and adjust their choices for greater benefit.

The parameters setting of the evolutionary game satisfies the participants' interest demands and influencing factors. Characterize all economic and social costs and benefits. It can solve the problem of coordinating and distributing the interests of participants in the renewal of traditional commercial streets, which is the critical research content of this paper. Based on the behavior of participants in the traditional Chinese commercial district renewal, and determined that we are studying the evolutionary game of three-party dual-strategy and not considering multi-strategy games for the time being. Therefore, studying dual strategies can lay the foundation for multi-agent multi-strategy research.

The local government has two possible strategies: to coordinate and regulate and not to coordinate and regulate. Let α denote the probability that the government chooses the “coordination and regulation” strategy. When the government chooses the “coordinated regulation” strategy, it means that the government will work harder to meet the incentive needs of developers and the compensation of owners. We use C₁ to represent the cost of coordination and regulation, C₂ to represent the cost of incentivizing developers to participate actively, and C₃ to represent the subsidy cost to owners. At the same time, the local government obtains a certain social benefit, R₂. When the government chooses “uncoordinated and unregulated”, C₁ is ignored.

The developers have two possible strategies (active participation and excessive profit-seeking), and β represents the probability that the developers choose the “active participation” strategy. Assuming that the developers participate in the street renewal at the same cost C4 when the developers choose the “active participation” strategy, the essence is to pursue economic interests and obtain a sure financial benefit R₃. At the same time, it will also improve the corporate reputation, reputation, and other social benefits R4. However, there is a possibility of excessive profit-seeking, obtaining economic benefits R₅, and damaging public interestsR8 such as the street's social structure and cultural texture. Therefore, the government's coordination and regulation and the owners' supervision are required. When they find the bad behavior of the developers, the owner can report it to the government, and the developer will be fined C₅.

Street owners also have two possible strategies, the strategy set is (supervised and unsupervised), and γ represents the probability that the owner chooses the “supervised” strategy. The owners participate in the renewal project, regardless of supervision or not, the project operating profit will be R₆. Due to the owners' “minority” thinking, unwilling to pay the cost of supervision, owners choose “no supervision”, which will damage public interest R₈. The government subsidy C₃ promotes the supervision of the owners. To ensure their public interests, the owners will choose the strategy of “supervision”, which will generate supervision costs C₆, and simultaneously obtain indirect benefits such as the continuation of traditional culture R₇. Related evolutionary game model parameters and their settings are shown in Table 3.

Table 3.

Parameters settings and meanings

Parameter	Description
R1	the economic benefits available to local government
R2	the social benefits available to local government
C1	the cost of coordination and regulation by local government
C2	the cost of local government incentives for developers
C3	the compensation from the local government to the owners
R3	the economic benefits for developers to actively participate
R4	the social benefits for developers to increase their visibility
R5	the economic benefits for developers’ excessive profit-seeking
C4	the economic benefits for developers’ excessive profit-seeking
C5	the profit-seeking fines of developers
R6	the economic benefits available to the street owners
R7	the indirect benefits from the supervision of street owners
R8	Excessive profit-seeking by developers brings harm to public interests
C6	the supervision costs of street owners

Construct Evolutionary Game Payoff Matrix

When the local government chooses α, the government gets R₁+R₂ and spends C₁+C₂+C₃. There are two cases for developers and owners. When the developers choose β, they will get R₃+R₄, spend C₄, and also get incentive money C₂; when they select (1-β), they will get R₅, pay C₄, and pay a penalty of C₅. When the street owners choose γ, they will get R₆+R₇, spend C₆, and get government subsidy C₃; when they choose (1-γ), they will get R₆ and pay R₈ for public benefits.

When the government chooses (1-α), the government gets an R₁. There are two cases for developers and owners. When the developers choose β, they will get R₃+R₄ and pay C₄; when they choose (1-β), they will get R₅ and pay C₄. When the block owner chooses γ, they will get R₆+R₇ and pay C₆; when they choose γ, they will get R₆ and pay R₈ for the public interest. we assign the weights of the probability of local government's coordination and regulation(x), the probability of developers' active participation(y), and the probability of block owners' supervision(z) within the interval of (0, 1). The specific income matrix is shown in Table 4:

Table 4.

Evolutionary game payoff matrix of local government, developers and street owners

Game party				local government
				coordinate and regulate (α)	no coordinate and no regulate (1-α)
Developers	actively participate (β)	street owners	Supervise (γ)no supervise (1-γ)	(R1+R2-C1-C2-C3,R3+R4-C4+C2,R6+R7+C3-C6)(R1+R2-C1-C2,R3+R4-C4+C2,R6)	(R1,R3+R4-C4,R6+R7-C6)(R1,R3+R4-C4,R6)
	excessive profit-seeking (1-β)	street owners	Supervise (γ)no supervise (1-γ)	(R1+R2-C1-C3+C5,R5-C4-C5,R6+C3-C6-R8)(R1+R2-C1+C5,R5-C4-C5,R6-R8)	(R1,R5-C4,R6-C6-R8)(R1,R5-C4,R6-R8)

Build and Solve Evolutionary Game Models

Firstly, calculate the expected returns of local government, developers,and street owners under different strategic choices. Using U₁₁ and U₁₂ to represent the strategies of “supervision and regulation” and “unsupervised and unregulated”. The expected payoffs of local government are shown in Equation (1-3):

U₂₁, U₂₂, and U₂ respectively represent the expected income of the developer's active participation, the expected income of excessive profit-seeking, and the average income. The expected payoffs of local government are shown in Equation (4-6):

U₃₁, U₃₂, and U₃ represent the expected returns of the owner's supervision, the unsupervised, and the average returns. The expected payoffs of local government are shown in Equation (7-9):

Secondly, construct the replica dynamic equation of the participating agents to solve the evolutionary stabilization strategies. And we study the evolution process of strategy choice from the perspectives of government, developers, and owners.

First, construct the replication dynamic equation (10) of local government as:

When β=β*=−γC3+R2−C1+C5C2, F_(α)0, indicating that when the developers actively participate in the construction reaches β*, the government's coordinated and regulated behavior reaches a stable equilibrium state, and local government no longer change innovative strategic choices.

When β≠−γC3+R2−C1+C5C2, let F_(α)=0, we can get two stable equilibrium points, α=0 and α=1, that is, if the local government has made a strategy of whether to coordinate and regulate, in the absence of sudden changes, the government will firm up its initial strategy.

According to the nature of the evolutionary game theory, when the derivative of F at the stable equilibrium point is negative, the equilibrium point is the stable strategy of the subject in the evolution process, and the derivative of F(α) can be obtained as shown in equation (11) .

When β≠−γC3+R2−C1+C5C2, we can get dF(α)dα|α=0<0,dF(α)dα|α=1>0. It shows that when α=0, the evolution speed of local government is decreasing. As α increases to 1, the evolution speed of the government increases. At this time, α=0 is the stable equilibrium point of the local government, and its strategy tends to be uncoordinated and unregulated.

When β≠−γC3+R2−C1+C5C2, we can get dF(α)dα|α=0<0,dF(α)dα|α=1>0. It shows that when α=0, the evolution speed of the local government is increasing. As α increases to 1, the evolution speed of the government is decreasing. At this time, α=1 is the stable equilibrium point of the local government, choose the coordinated and regulated strategy.

Second, construct the replication dynamic equation (12) of developers as:

When α=α*=R5−R3−R4C2+C5, F_(β)0, indicating that when the coordination and regulation of the local government reaches α*, the developers’ active participation behavior reaches a stable equilibrium state, and the developers no longer change behavior choices;

When α≠R5−R3−R4C2+C5, let F_(β)=0, two stable equilibrium points, β=0 and β=1, can be obtained, that is if the developers have already made a strategy of whether to actively participate, developers will firm up initial innovative strategic choice in the absence of a sudden change.

Taking the derivative of F(β) can be obtained as shown in the equation (13),

When α≠R5−R3−R4C2+C5, we can get dF(β)dβ|β=0<0,dF(β)dα|β=1>0. It shows that when β=0, the evolution speed of the developers’ behavior is increasing. As β increases to 1, the evolution speed of the developers’ behavior is diminishing. β=1 is the stable equilibrium point for developers, and they choose the strategy of active participation.

When α≠R5−R3−R4C2+C5,we can get dF(β)dβ|β=0>0,dF(β)dβ|β=1<0. It shows that when β=0, the evolution speed of developers’ behavior is decreasing, as β increases to 1, the evolution speed of developers’ behavior is increasing, and developers have reached equilibrium at β=0, β=0 is a stable equilibrium point for developers, choosing an excessive profit-seeking strategy.

Third, construct the replication dynamic equation (14) of street owners as:

When α=α*=C6−βR7C3, F_(γ)0, indicating that when the local government's coordination and regulation efforts reach α*, the supervision behavior of the street owners has reached a stable and equilibrium state, and the owners no longer change their innovative strategic choices.

When α≠C6−βR7C3, let F_(γ)=0, two stable equilibrium points, γ=0 and γ=1, can be obtained, that is, if the street owners has made a strategy of whether to supervise, the owners will firm up their original strategy without a sudden change choose.

Taking the derivative of F_(γ) can be obtained as shown in the equation (15),

When α>C6−βR7C3, we can get dF(γ)dγ|γ=0>0,dF(γ)dγ|γ=1<0. It shows that when γ=0, the evolution speed of street owners’ behavior is increasing. As γ increases to 1, the evolution speed of street owners’ behavior is diminishing, and owners have been evolving toward supervising behavior. At this time, γ= 1 is the stable equilibrium point for owners, and the supervision strategy is selected.

When α0. It shows that when γ=0, the evolution speed of the street owners' behavior is decreasing. As γ increases to 1, the evolution speed of the street owners increases. When γ=0, the equilibrium is reached, and γ=0 is the owners' stabilize equilibrium point and choose an unsupervised strategy.

Evolutionary Stability Analysis of Innovative Strategic

Assuming that the result of copying the dynamic equation is zero, 8 local strategy Nash equilibrium points can be obtained, namely (0,0,0), (0,1,0), (0,0,1), (0, 1, 1), (1,0,0), (1,0,1), (1,1,0) and (1,1,1). Friedman proposed to judge the stability of the local equilibrium point through the Jacobian matrix in the evolutionary model, thereby obtaining the evolutionary stability strategy (ESS) of the system. The Jacobian matrix (16) can be obtained by referring to (10-12).

Use the Jacobian matrix to analyze the stability of 8 local equilibrium points. If all the characteristic roots of the equilibrium point are less than or equal to zero, the point is a stable evolutionary strategy (ESS). If there is a typical root greater than zero or zero multiple roots, then it is unstable. Mark the distinct positive sources as (+), the negative characteristic roots as (-), and the uncertain characteristic roots as (u) to obtain the eight local equilibrium points and their characteristic root analysis, as shown in Table 5. Since the sign of the characteristic root depends on the magnitude of many parameter values, that is, the equilibrium point to reach a stable state cannot be determined, and it can only be analyzed that the system reaches a stable equilibrium under certain conditions.

Table 5.

Detailed table characteristic of local equilibrium points

Equilibrium point	λ1	λ2	λ3	State
E1 (0,0,0)	R2-C1+C5 (+)	R3+R4-R5 (+)	-C6 (-)	saddle point
E2 (1,0,0)	C1-R2-C5 (-)	R3+R4-R5+C2+C5 (+)	C3-C6 (u)	uncertain
E3 (0,1,0)	R2-C1+C5-C2 (+)	R5-R3-R4 (-)	C3-C6 (u)	uncertain
E4 (0,0,1)	R2-C1+C5-C3 (u)	R3+R4-R5 (+)	C6 (+)	uncertain
E5 (1,1,0)	C1+C2-R2-C5 (u)	R5-R3-R4-C2-C5 (-)	C3+R7-C6 (+)	uncertain
E6 (1,0,1)	C1-R2-C3-C5 (-)	R3+R4-R5+C2+C5 (+)	C6-C3 (u)	uncertain
E7 (0,1,1)	R2-C1+C5-C2-C3 (+)	R5-R3-R4 (-)	C6-R7 (-)	uncertain
E8 (1,1,1)	C1+C2+C3-R2-C5 (u)	R5-R3-R4-C2-C5 (-)	C6-C3-R7 (-)	uncertain

In Table 5, since λ_i>0 exists in the equilibrium points E₁-E₇, the necessary and sufficient conditions for stability cannot be satisfied. When C₁+C₂+C₃-R₂-C₅<0, E8(1,1,1) meets the stability requirement . Therefore, C₁+C₂+C₃-R₂-C₅<0 is an important constraint for the stability of the three-player game, which determines the decision-making of participants. In the process of traditional commercial street renewal. in the process of updating traditional commercial streets, the only stable set of strategies for stakeholder games is (coordination and regulation, active participation, and supervision), and the theoretical results are consistent with practice.

First, when both developers and owners have negative strategies (E₁ and E₂), we cannot resolve the contradiction, and the renewal of traditional commercial streets fails. Secondly, when C₁+C₂+C₃-R₂-C₅<0, the local government adopts a coordinated and regulated strategy, encouraging developers to participate in it actively and giving owners subsidies to promote supervision and restrain the developers' destructive behaviors and achieve tripartite cooperation. It is also an important reason local government chooses to coordinate and regulate. When developers choose an excessive profit-seeking strategy, they will harm the public interests of the owners and deepen the contradiction between them. Therefore, the government must also formulate specific punitive measures to restrain the developers. Finally, when the developers also choose the strategy of active participation, the owners will immediately choose the supervision strategy, and the three parties will win together.

From the beginning of evolution to forming a stable policy set, each stakeholder has a time series for starting its stable policy. The local government will first determine its stabilization strategies through evolution. Then, after the local government has entirely determined the stabilization strategy, the developers will gradually evolve the stabilization strategy. Through evolution, street owners will become the last stakeholder to decide their strategic choices. Finally, the stable set of strategies to get the player's game is (1,1,1). Therefore, from a theoretical analysis point of view, the evolution order of the stabilization strategy set is “local government→investors →residents”. This finding can help in studies that improve decision-making efficiency and affect the detailed analysis of the simulation part.

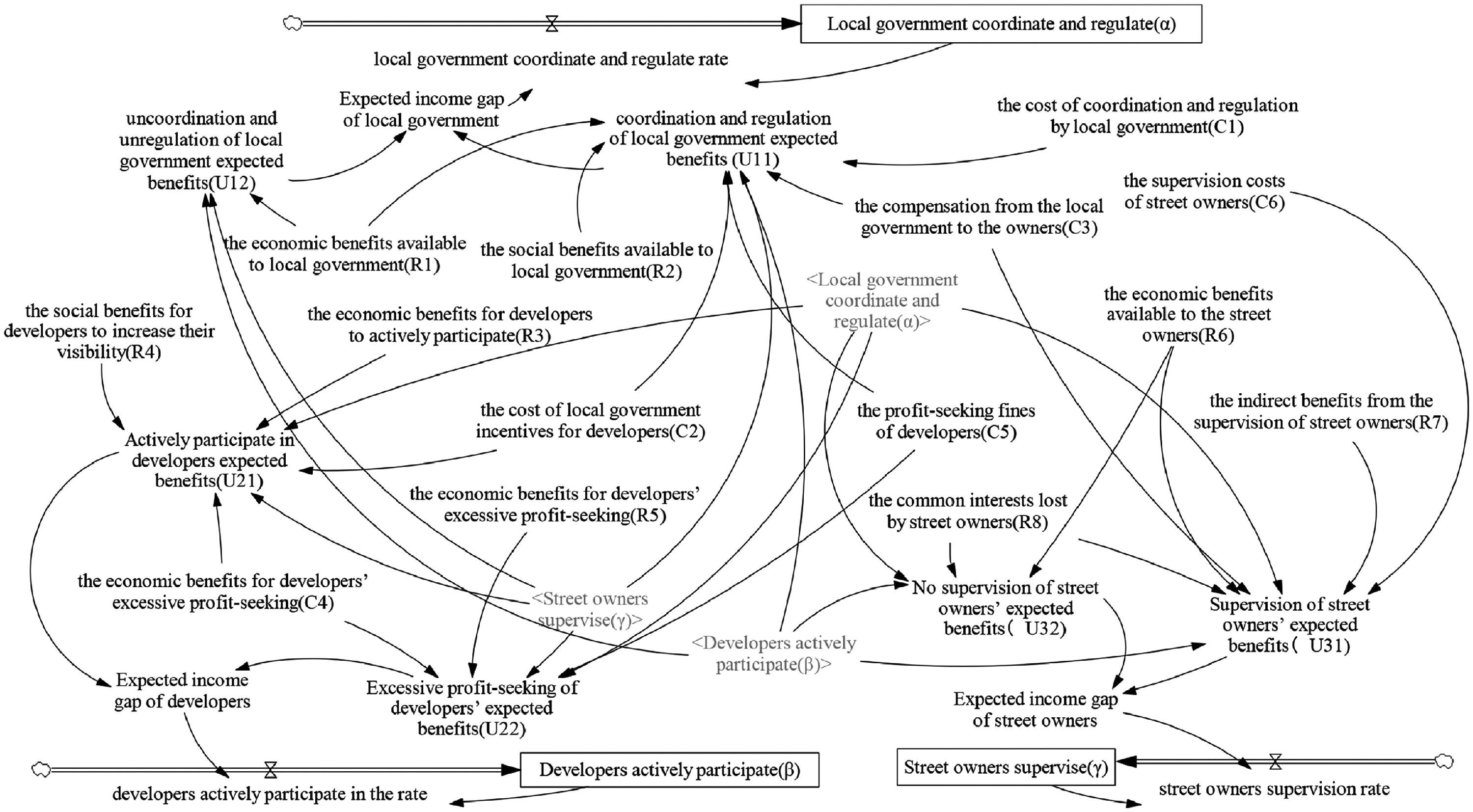
Simulations and Results

SD model of evolutionary game

To study the evolution process of the strategic choice of participants in the renewal of traditional commercial streets and the key factors affecting their behavior, to predict future trends, and to provide a theoretical basis for the formulation of relevant policies. Therefore, this paper uses the Vensim PLE software to establish the dynamic model of the evolutionary game system, as shown in Figure 2.

Fig. 2.

SD models of government, developers, and owners in the traditional commercial street

The SD model comprises three flow variables, three rate change variables, six intermediate variables, and fourteen external variables. The flow variables refer to the behavioral probabilities α, β, and γ of the participating subjects, and the rate variables refer to the behavioral change rates of the participating issues. The exogenous variables refer to the parameters in the evolutionary game process.

This model has many exogenous variables, which are not easy to determine, so we use the simulation experiment method. The setting of the parameters first satisfies that the initial value is greater than zero, and the initial strategy income is greater than zero. Drawing on relevant literature and expert advice, roughly try the parameters to debug the model within the range of parameter value variation, At the same time, use grid search to verify the parameters (Chui et al., 2020). Parameter values are determined when there is no significant change in model behavior, as shown in Table 6. The intermediate variables of the participants satisfy the positive and negative returns in the evolutionary game, and the difference between the expected returns is the difference between the two. Assign a value to a rate variable in combination with a table function, and it is convenient to deal with the nonlinear problems of the simulation process. The specific equation (17-19) are as follows.

Table 6.

Parametric simulation data

Parameter	simulation data	Parameter	simulation data
R1	30	R5	120
R2	60	C4	25
C1	30	C5	30
C2	10	R6	20
C3	5	R7	30
R3	100	R8	10
R4	30	C6	10

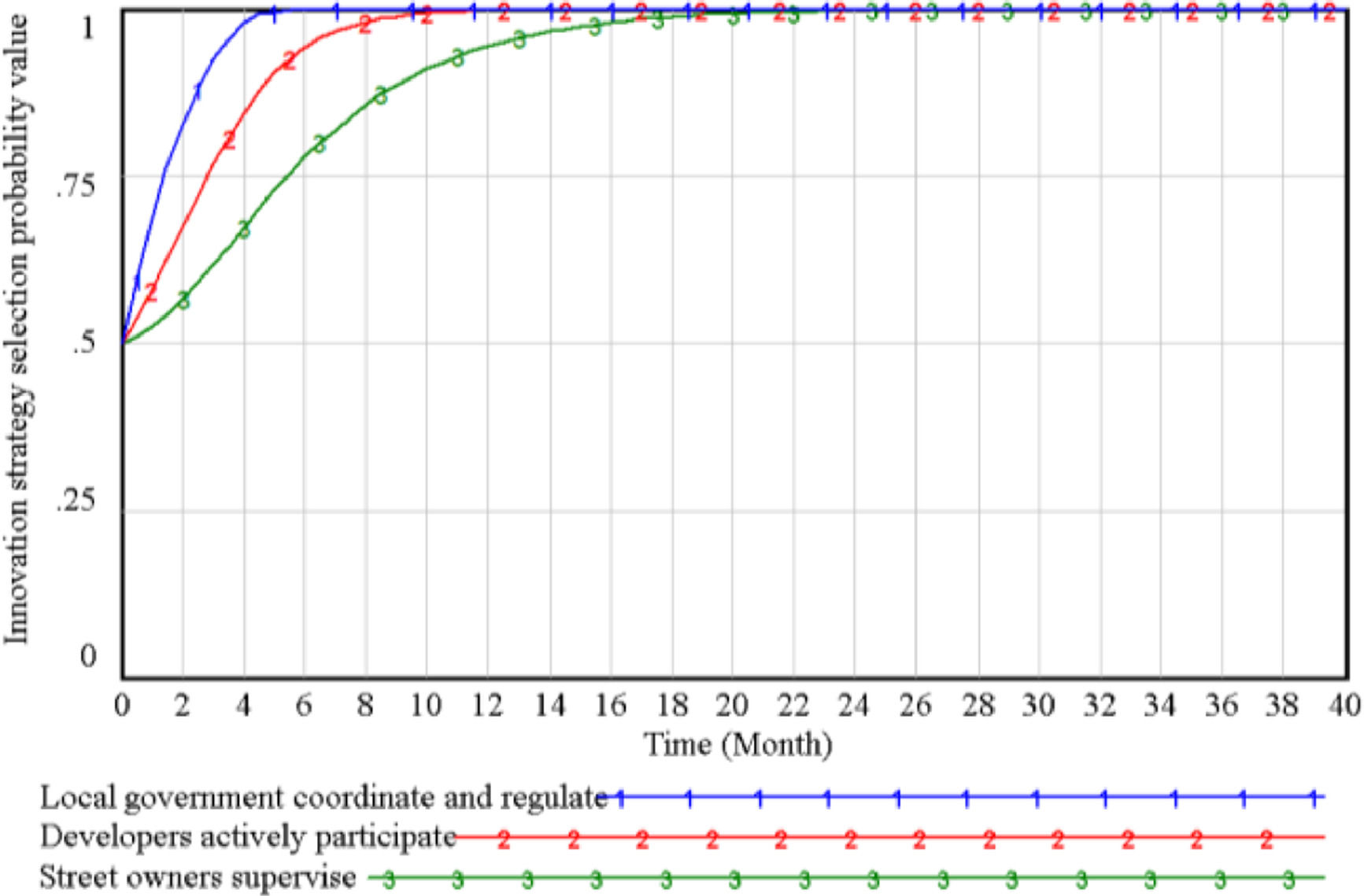
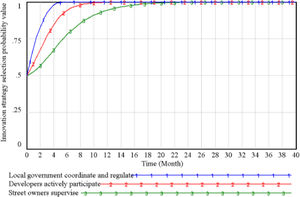
Stability Strategy Simulation Analysis

In the simulation process, set the simulation start time as INITIAL TIME = 0, end time as FINAL TIME = 40, the simulation step length as TIME STEP = 0.5. Firstly, we conduct the simulation analysis of the mixed strategy of the participating subjects. Assuming that the initial willingness of the three parties is x=y=z=0.5. After entering the equations of all other variables, let the local government coordinate and regulate (x) = 0.5, developers actively participate (y) = 0.5, street owners supervise (z) = 0.5, and then simulate the mixed strategy model. The evolution order of the three parties is studied to ensure that the theory is consistent with reality. The result is shown in Figure 3.

Fig. 3.

Probability trend chart of strategy selection for different stakeholders

As shown in Figure 3, local government, developers, and street owners will achieve a stable strategy (1,1,1). The government will reach a stable equilibrium at a faster speed, followed by developers and finally by owners, consistent with the theoretical analysis. It is why the government, as the initiator, should formulate appropriate incentive policies and reward and punishment measures to promote the smooth progress of the renewal project and choose a strategy for coordination and regulation. The developers' capital-profit-seeking nature leads them to choose excessive profit-seeking at the beginning, and the government's incentive policy promotes participation and determines the active participation strategy. At the same time, when the owners see the good actions of the government and developers and choose to supervise under the government's incentives, the system will eventually be in a virtuous cycle.

Simulation Analysis of Exogenous Variables on Stakeholders' Innovative Strategy Choice

The value of exogenous variables will affect the stable equilibrium of stakeholders, so the second step is to study the strategy selection of exogenous variables for participating subjects. The following takes the strategy combination (0,0,0) as an example to discuss how exogenous variables affect the strategy choice of stakeholders.

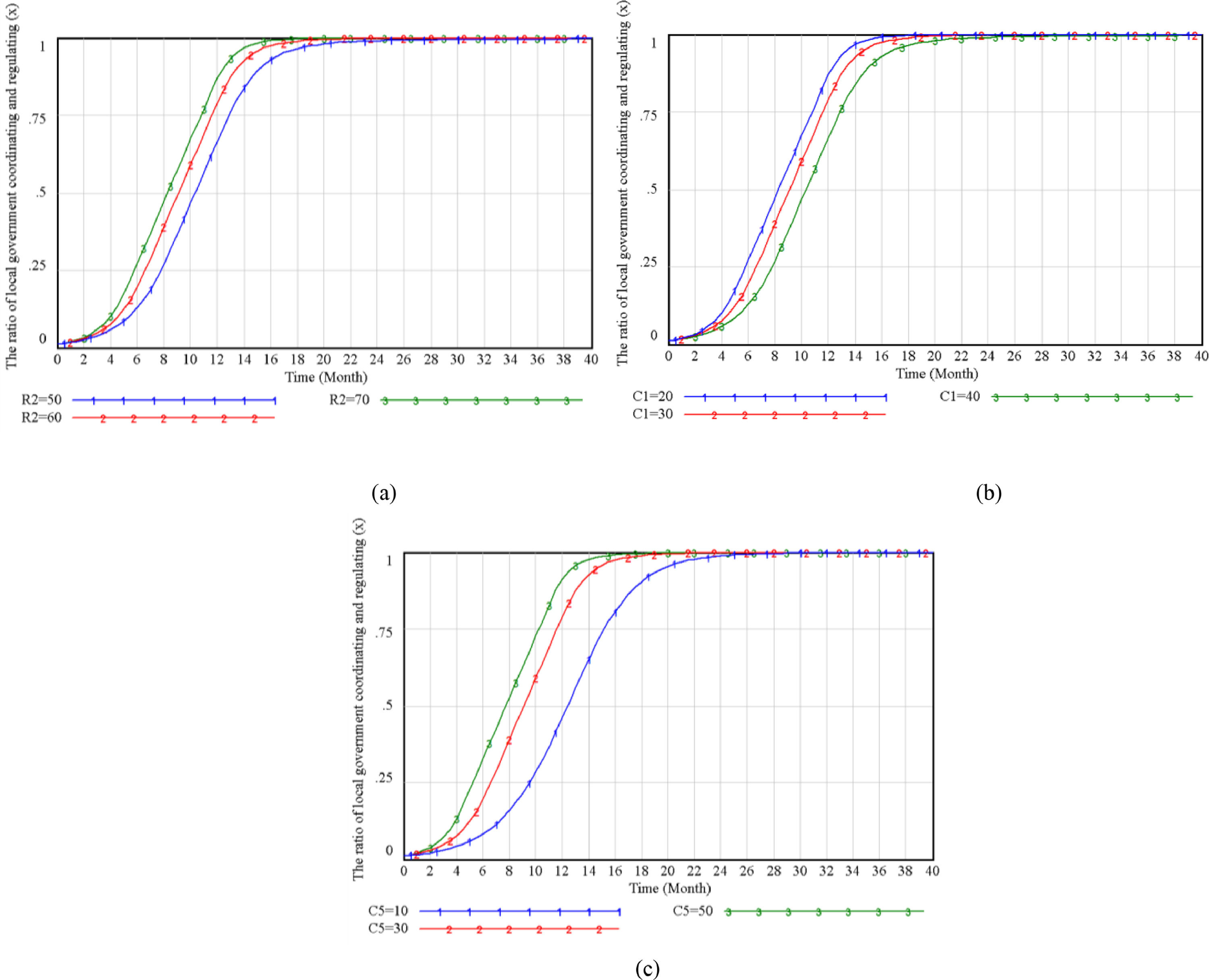
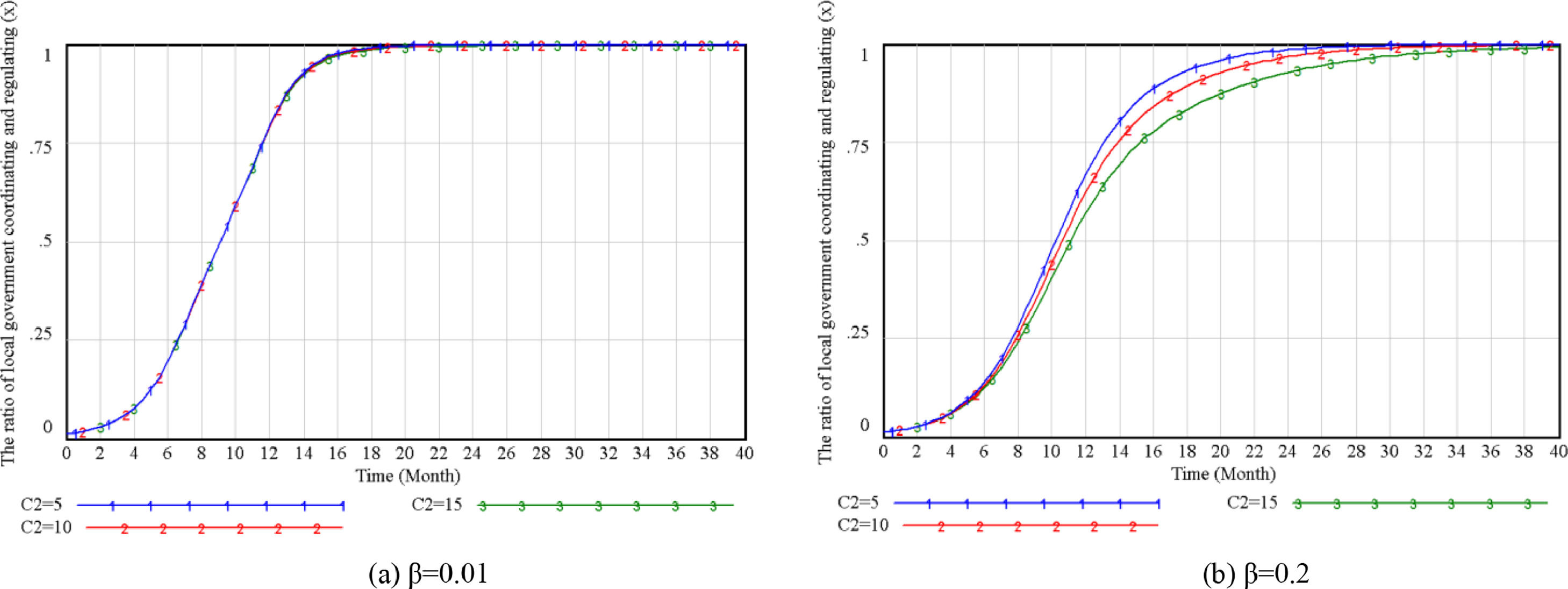
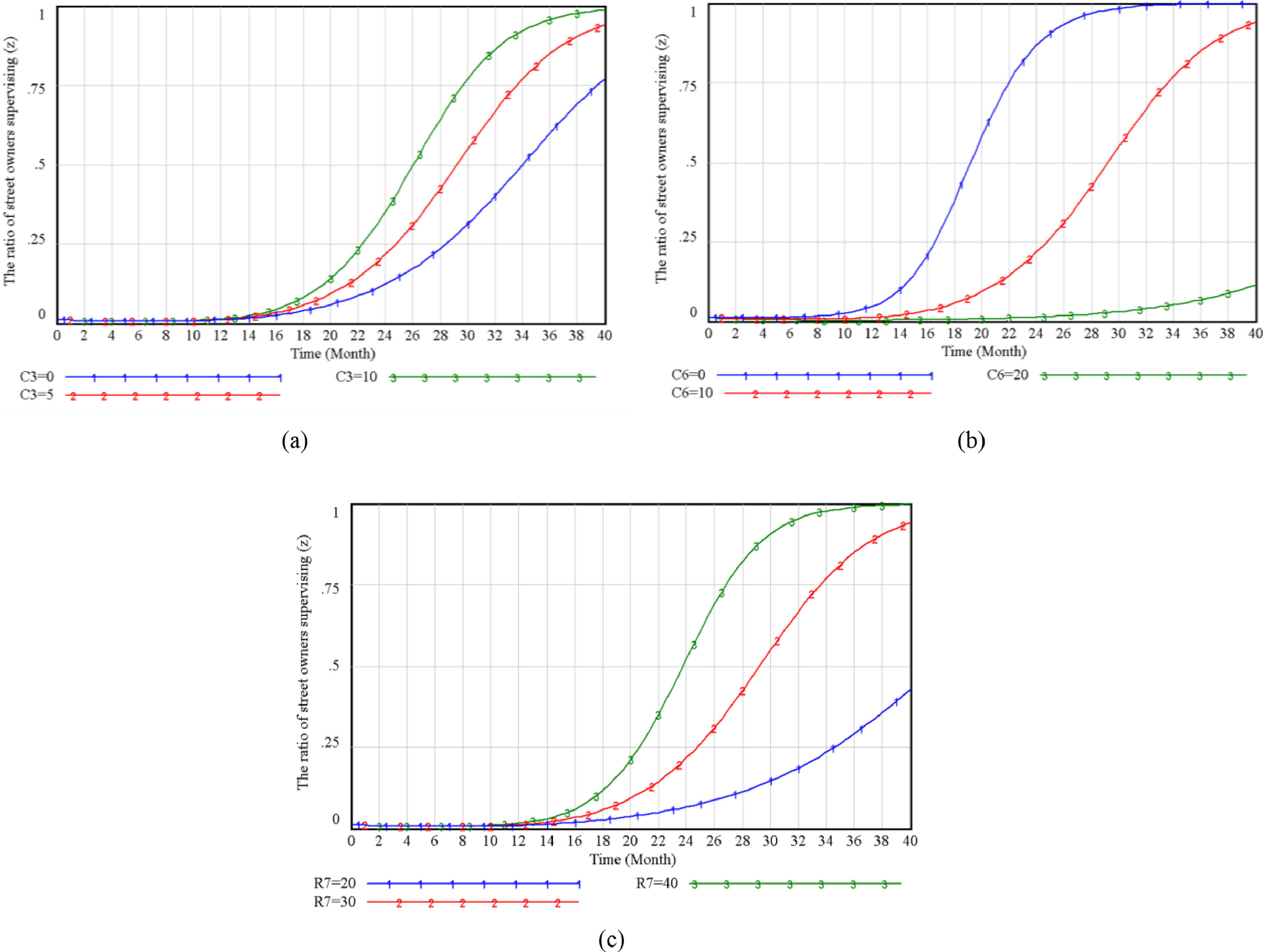
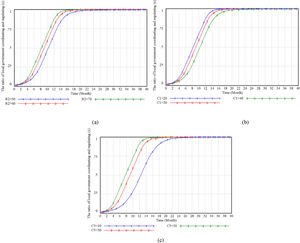
Factors Influencing the Innovative Strategic Choice of Local Government

The initial strategy of the local government is to focus on economic benefits, so it chooses uncoordinated and unregulated strategies. Set α to start to change from 0.01. Simulation analysis shows that the parameters R₂, C₁, and C₅ directly affect the local government's innovative strategic choice, as shown in Figure 4. Affected by β and γ, C₂ and C₃ influence the government's innovative strategic choices, as shown in Figure 5 and Figure 6.

Fig. 4.

the influence of exogenous variables on the government's Innovative strategic choice

Fig. 5.

When β changes, the influence of exogenous variables on the government's innovative strategic choice

Fig. 6.

When γ changes, the influence of exogenous variables on the government's innovative strategic choice

It can be seen from Figure 4 that the evolution trends of R₂, C₁, and C₅ for the choice of government election strategies are similar. When social benefits increase, coordination and regulation costs decrease, and government fines for developers increase, the government tends to choose coordination and regulation. When R₂ increases, the government's convergence speed is accelerated. Because the government is primarily concerned with social interests, it will immediately adopt coordinated and regulated strategies to increase the probability of street renewal. When C₅ decreases, it will significantly reduce the speed at which the government chooses to coordinate and regulate. Because developers choose excessive profit-seeking, the penalty amount is small, government revenue is reduced, and the government needs more time to adjust its strategic choice.

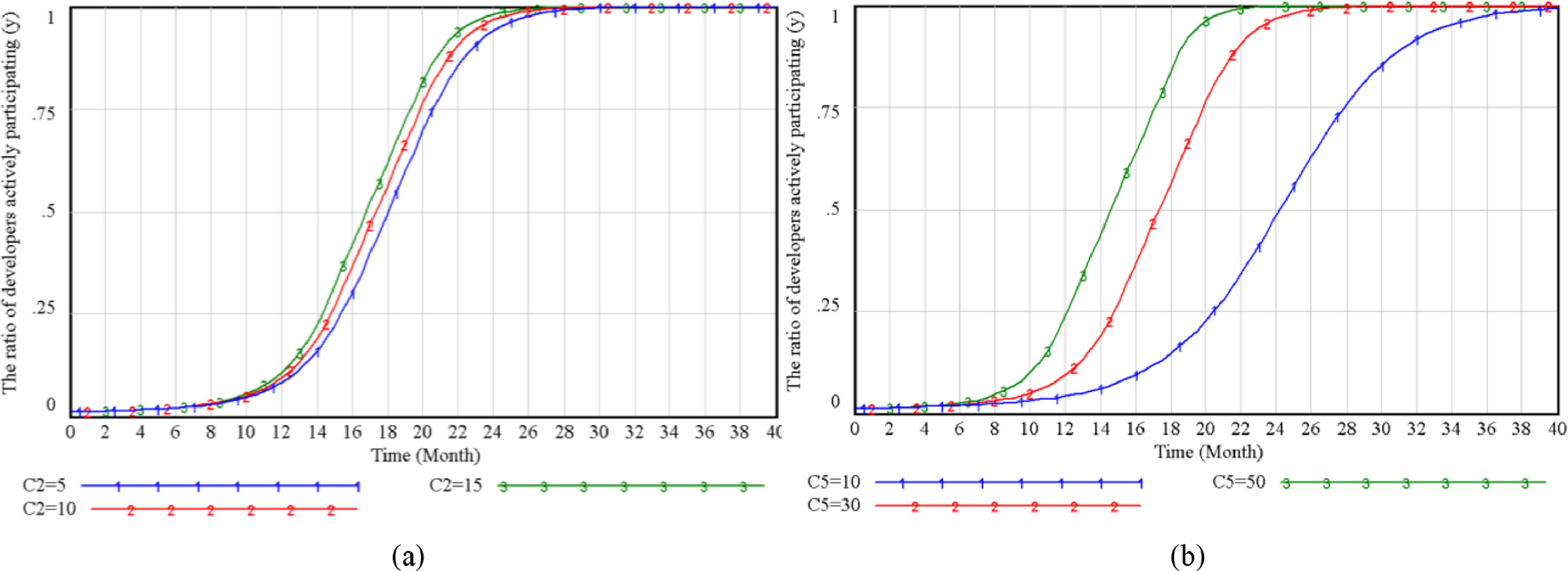
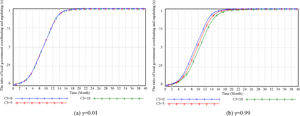
Comparing figures 5, when the developers initial willingness is very low, the change of C₂ has almost no impact on the government innovative strategic choices, but when β increases to a specific value (β=0.2), government spending increases.it will reduce the possibility of government choosing coordination and regulation strategies.

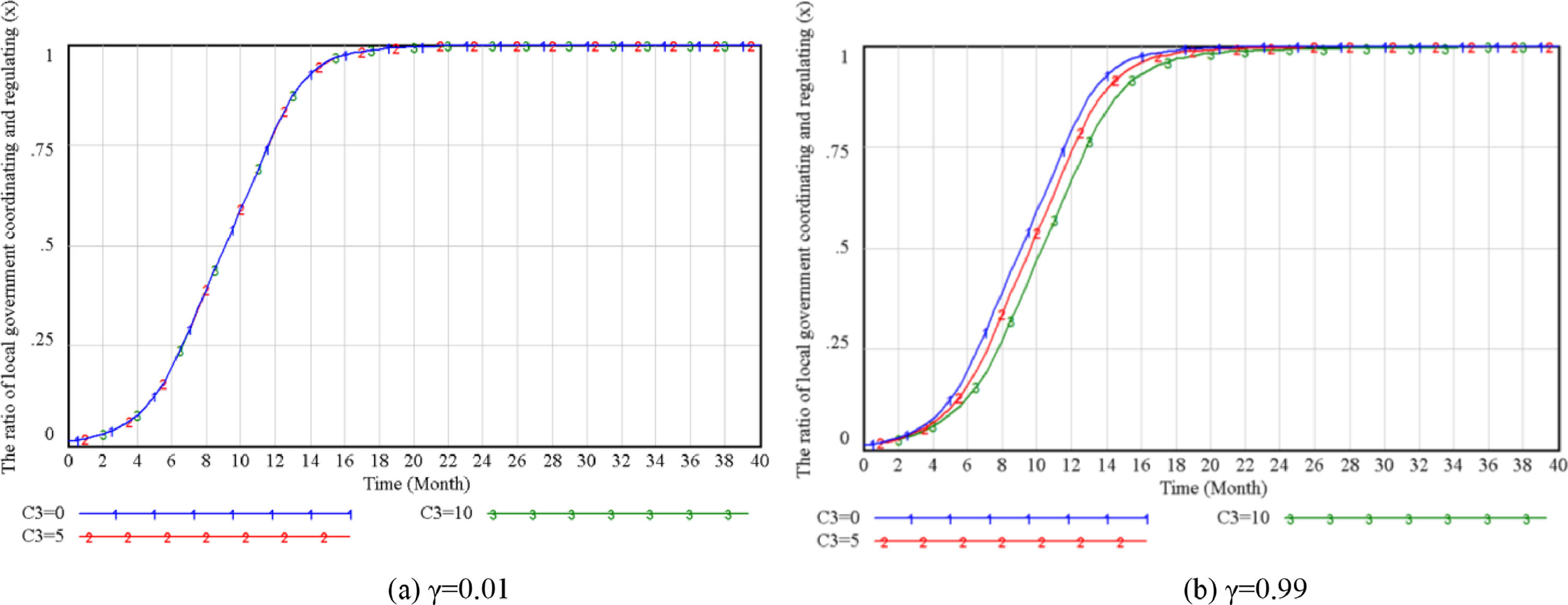
Similarly, comparing figures 6, when the initial willingness of the street owners is very low, the change of C₃ has no impact on the innovative strategic choices of the local government. Still when γ increases to 1, it will affect the government's strategic intention and slow down the government's choice of coordinated supervision. When the values of C₂ and C₃ increase or decrease at the same time, the innovative strategic choice of the developers has the most significant impact on the local government. It also reflects that the developers have a higher status and a more considerable say than the owners.

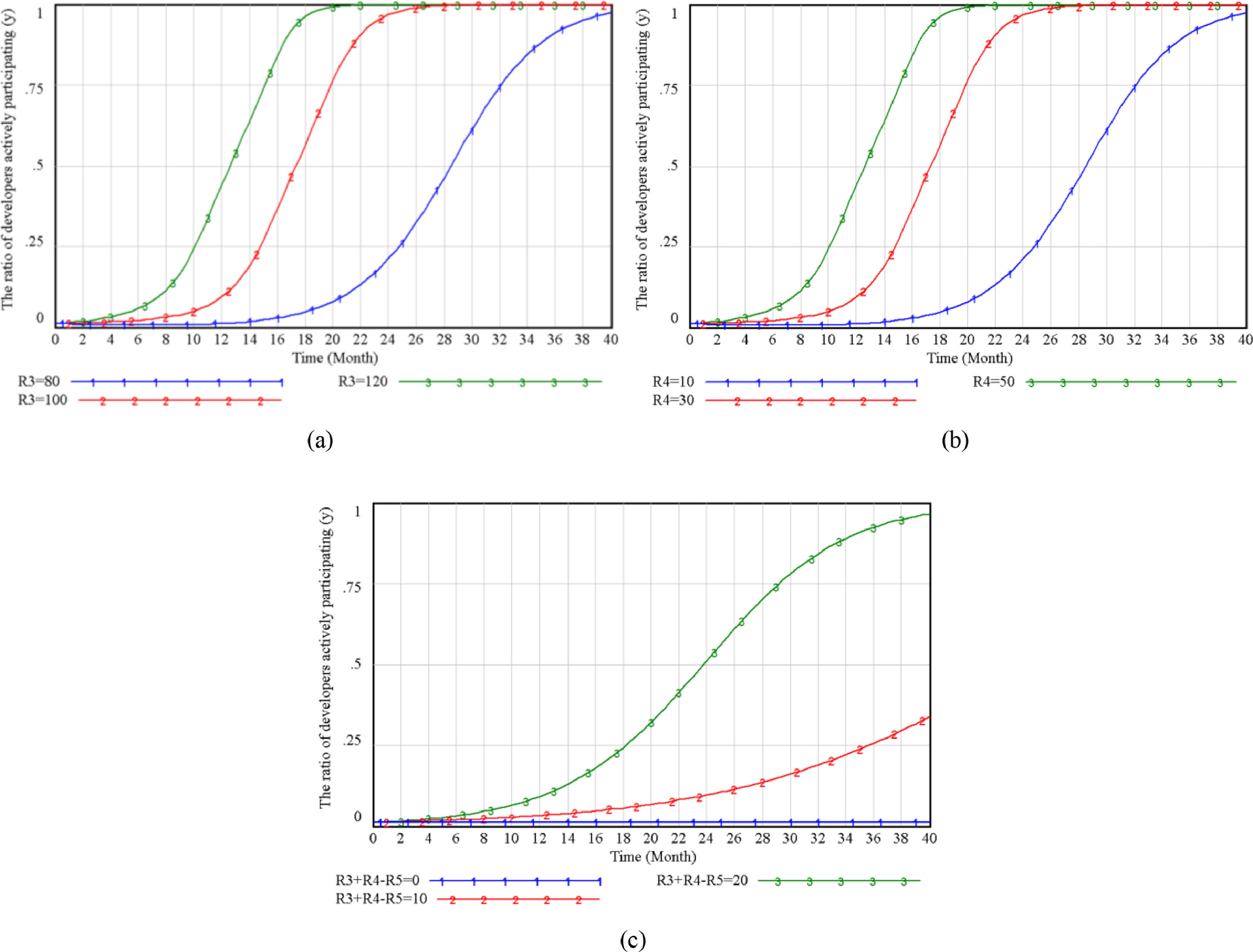
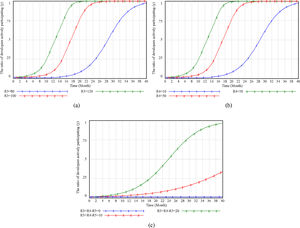
Factors Influencing the Innovative Strategic Choice of Developers

The simulation analysis shows that R₃ and R₄ have the same evolution trend on the developers’ active participation probability, R₃+R₄-R₅ has a more significant impact on the developers’ strategy choice, as shown in Figure 7. C₂ and C₅ can also directly affect the developers’ active participation probability, as shown in Figure 8.

Fig. 7.

the influence of exogenous variables on the developers’ innovative strategic choice

Fig. 8.

The Influence of exogenous variables on the developers’ innovative strategic choice

Figures 7(a) and (b) show that R₃ and R₄ both show a slow S-shaped growth trend for developers' strategic choices, and the numerical changes are more evident for the evolution trend. The probability will soon reach 1. When the profit decreases, the developers need to choose the behavior of active participation for a long time, reflecting the developers' focus on profit maximization. Due to profit-seeking in the capital market, Figure 5(c) shows that when the difference between R₃+R₄-R₅ is zero, developers with the same cost are more likely to choose economic profit rather than implicit income so they will select excessive profit-seeking. The probability of participating in the street renewal is 0.

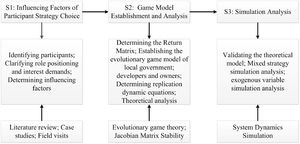
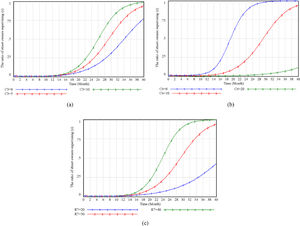
Factors Influencing the Innovative Strategic Choice of Street Owners

Through simulation analysis, C₃, C₆, and R₇ directly impact the probability of street owners' supervision, as shown in Figure 9.

Fig. 9.

The influence of exogenous variables on the street owners’ innovative strategic choice

It can be seen from figures 9(a) and (c) that when the compensation or indirect benefits to street owners increase, the owners tend to supervise. Figure 9(b) shows that when the cost of supervision increases to a certain value, the owners will not supervise because of the “civilian” thinking, and only pay attention to the distributable economic benefits. When it decreases, the owners will converge to 1 at a faster rate. That is to get more benefits with less cost, and at the same time can restrain the bad behavior of developers. All entities have participated in the renewal of traditional business streets with good behaviors, which has promoted a stable and balanced system strategy.

Analysis of Influencing Factors

Through the analysis of the factors that affect the coordination and regulation of local government, the active participation of developers, and the supervision of street owners, they can be divided into three types: key, indirect and irrelevant factors, which are divided into two forms of positive and reverse promotion. The data are shown in Table 7.

Table 7.

Summary of influential factors

	key influencing factors		Indirect influence factors		irrelevant factors
Local government	positive promotion	2	positive promotion	0	1
	reverse promotion	1	reverse promotion	2
Developers	positive promotion	4	0		1
	reverse promotion	0
Street owners	positive promotion	2	0		2
	reverse promotion	1

Discussions and Suggestions

In the evolutionary game system of Chinese traditional commercial street renewal, local government, developers, and street owners will reach a stable equilibrium under certain conditions, and external factors will impact the innovative strategic choice of the three parties. And provide corresponding suggestions to ensure the realization of the comprehensive benefits of the block renewal project and the tripartite win-win goal.

(1) The simulation results show that when the initial strategy of the three parties is (0.5,0.5,0.5), the three parties will reach an evolutionarily stable state (1,1,1) within a certain period, and the rate will be local government> developers> street owners, consistent with the speed of cooperation between the three parties in the actual update process.The non-renewability of traditional commercial streets determines their scarcity attributes, so the government needs to lead. The incentive policies, rewards and punishments, and compensations formulated by the government will affect the choices of developers and owners. The local government chooses coordinated and regulated strategies to guide developers and owners to make positive choices and avoid improper distribution of benefits that obstruct renewal projects.

(2) According to the discussion results of the factors affecting the probability of local government coordination and regulation, the probability of developers' active participation and the probability of street owners' supervision. The social benefit (R₂) of the local government, the economic benefit (R₃)of the developers, and the supervision cost of the street owners (C₆) are the most sensitive to the strategic choice of the stakeholders. The evolution trend changes rapidly when it changes, which is the most critical influencing factor. It is because the government, as a public management department, should first pay attention to social interests. For developers who are profit-making organizations, economic interests are the most fundamental choice. The choice between the two is the opposite. Street owners generally tend to receive financial compensation and profit dividends due to the idea of “small citizens” and are unwilling to pay the cost to supervise the developers. In the actual process, the government's responsibility is also to pay attention to the public interest. Developers are more likely to pursue economic profit maximization. The owners did not supervise for small profits, and the developers harmed the public interests, which led to the deepening of the contradiction between the two parties. The public protested and chose to petition, and the project update failed.

(3) Discuss the simulation results of the incentive cost of the local government to the developers (C₂) and the punishment for the developers' lousy behavior (C₅). When C₂ increases, the rate at which developers reach the equilibrium point of evolutionary stability is faster, prompting developers to join street renewal projects faster. The size of the penalty amount affects the developers' strategy choice: the larger the penalty amount, the more obvious the effect of its active participation. Because traditional commercial street renewal is a weak project, and it isn't easy to attract developers to invest. The government formulates related incentive policies, such as giving preferential treatment to other projects, to promote the smooth progress of the project. But at the same time, owning to the capital profit chasing market, developers may excessively pursue economic interests to the detriment of public goods. The size of the penalty amount affects the developers' innovative strategic choice. The more significant the penalty amount, the more pronounced the effect of their active participation. If the penalty amount is too small, the developers may pursue excessive profit, or it will take a long time to reach 1. Therefore, the government should increase coordination and regulation, formulate corresponding rewards and punishments to enhance the government's deterrence. At the same time, the supervision of the street owners can also discover the bad behavior of the developers and report them to the government. The government's regulation and the owners' supervision point out the direction for the smooth implementation of the renewal project.

(4) According to the discussion simulation results of the owners' supervision cost (C₆), C₆ will directly affect the owners' choice. When C₆ increases to a specific value, the owners will only choose the direct distributed economic profit and choose not to supervise. The government can give appropriate compensation to subsidize the cost of the owners. As the direct beneficiary of the street, they have low voices and status. Therefore, due to the high cost of supervision, they may not directly participate in it but passively accept part of the compensation given by the government. The bad behavior of the developers will lead to the contradiction between the owners and the developers. Therefore, the local government should strengthen public participation awareness, publicize the significance and value of street renewal, improve general supervision channels, promote good cooperation among the three parties, and jointly contribute to the renewal of traditional commercial streets.

Conclusions

This paper establishes a stakeholder game model among local government, developers, and street owners. It solves the contradiction between pursuing economic interests and protecting historical culture in the renewal of traditional commercial streets. Through theoretical analysis, determine the limit condition for the stability of the stakeholder game, that is, C₁+C₂+C₃-R₂-C₅<0. Under limited conditions, the only stable strategy set in the stakeholder game is that the government, developers, and owners choose the strategy of coordination and regulation, active participation, and supervision, respectively. The evolution order of the stable strategy set is “government→developers→owners”. Then, use system dynamics to simulate the correctness of the theoretical results, the evolution order of the stable strategy, and the influence of exogenous variables on its strategy selection. Stakeholders are sensitive to changes in exogenous variables. In particular, the social benefits of local government, the economic and social benefits of developers, and the supervision cost of owners are the key factors that affect the choice of strategies. In addition, the local government's strategy choice probability affects the developers' and owners' choices. Incentives, rewards, and punishments for developers, as well as supervision and compensation for residents, can promote win-win cooperation among the three parties.

This paper has certain limitations. Firstly, to simplify the analysis of the multi-participant game model, this paper only studies the game process of the three leading players' interest strategy selection. Therefore, the model may not fully reflect the multi-party game process. Secondly, the selection of influencing factors in this paper are primarily economic and social benefits, costs, etc., ignoring the influence of ecological and other factors. In the future, we will conduct further studies incorporating these limitations. It is possible to increase the number of participants and explore the evolutionary trend of multiple participants' strategy choices and the factors that affect their strategy choices. And it can expand the scope and proportion of influencing factors and empower them to make the research more comprehensive.

This work was funded by the Shandong Provincial Social Science Planning Office and is based on the research on the factors and countermeasures of the new smart city operating capacity in Shandong Province, grant number 20CSDJ18.

Data Availability

The data used to support the findings of this study are available from the corresponding author upon request.