Optimal Strategy for Corporate International Investment and Consumption Problem with Stochastic Hyperbolic Discounting

Abstract

This study investigates the dynamics of a stochastic hyperbolic discounting model in a continuous-time framework to address the complexities associated with the corporate international investment consumption problem (CIICP). By formulating a dynamic programming equation based on the principles of dynamic programming, we seek to untangle the intricacies of CIICP by incorporating log utility. Our research provides valuable insights into the economic ramifications of the proposed model and presents a comprehensive analysis of numerical sensitivities. This investigation not only contributes to a deeper understanding of the CIICP phenomenon but also contributes to more informed decision-making within the field.

Introduction

Hyperbolic discounting refers to a phenomenon wherein individuals tend to place greater value on immediate benefits compared with future benefits, resulting in a time-inconsistent preference structure that can be categorized into naive or sophisticated. Naive individuals are unaware of their changing preferences over time, leading to inconsistent planning that is not executed practically. In contrast, sophisticated individuals are aware of their time-inconsistent preferences and choose an optimal time-consistent plan. In the context of international investment and consumption for a corporation, this study hypothesizes a continuous-time model with stochastic hyperbolic discounting. Specifically, we propose that corporate managers prefer short-term benefits over future benefits, and this preference structure may have implications for the corporation's investment and consumption decisions, warranting further investigation.

The majority of economic decisions involve a tradeoff between present and future returns, which essentially gives them a time-spanning nature. Discounted utility theory has become the main framework for evaluating intertemporal choices in economics (see, Hajdini, 2012; Mankiw, 2020; Portney & Weyant, 2013). The discount function, which is an essential component of the theory of decision making, values delayed returns in the present. In problems with finite horizons, individuals typically discount short- and long-term utility functions applying the same constant discount rate of their preferences over time. However, experimental studies on time preferences have demonstrated that the time-consistent hypothesis is unrealistic (Ainslie, 1992; Loewenstein & Prelec, 1992; Thaler, 1981) since individuals behave more patiently when both rewards are far removed from the present and more impatiently when both rewards approach the current time. Laibson (1997) proposed a quasi-hyperbolic discount function in which the discount rate decreases over time to capture the phenomenon of time-varying impatience. This type of preference is referred to as present-biased preferences by Palacios-Huerta and Pérez-Kakabadse (2013). Time-inconsistent preferences have been extensively investigated by economists, with a large body of literature exploring hyperbolic discounting models (Ainslie & Haslam, 1992; Ainslie & Herrnstein, 1981; DellaVigna & Malmendier, 2006; Kirby & Herrnstein, 1995; Loewenstein & Prelec, 1992; McClure et al., 2004; Myerson & Green, 1995; Thaler & Shefrin, 1981). These models have been applied to a wide range of economic problems, including Barro (1999), DellaVigna and Malmendier (2004), Grenadier and Wang (2007), O'Donoghue and Rabin (1999), and Palacios-Huerta and Pérez-Kakabadse (2013), among others. However, these models have inherent limitations, as with the assumption of consistent preferences over time and the difficulty of estimating discount rates accurately. Further research is needed to address these limitations and improve our understanding of time-inconsistent preferences.

A surge in research activities regarding corporate international investment has occurred over the years, exploring various aspects of this phenomenon from different perspectives. Choi (1989) examined the evolution of the theory of corporate international investment, focusing on its financial dimension. Bellalah and Wu (2009) proposed a model of corporate investment among international concerns that incorporates stochastic and deterministic elements. The model considers the impact of domestic and foreign prices on firms’ outputs and inputs, along with exchange rate risk and competitiveness between firms. Zhang and Zhang (2012) developed an optimal corporate investment model that accounts for daytime and nighttime differences. Overall, these studies have contributed to our understanding of the factors that influence international investment in corporations; however, some limitations remain. For instance, Choi's (1989) analysis primarily focused on the financial aspects of international investment, neglecting other significant factors such as political and cultural considerations. Bellalah and Wu's (2009) model assumed that firms are rational and profit-maximizing, which might not always be the case in reality. Zhang and Zhang's (2012) model is based on the assumption that daytime and nighttime differences have a significant impact on investment decisions, which might not be true in all contexts. Therefore, future research must address these limitations and provide a more comprehensive understanding of corporations’ international investment.

The literature on firms’ international investment and consumption has included several studies. Wu and Zhang (2006) examined the optimal corporate portfolio and consumption choice problem, in which investors could invest their wealth in bonds (bank accounts) and real projects owned by production. Huang and Wu (2011) focused on the optimal international portfolio and consumption choices for corporations, in which investors could invest their wealth in domestic bonds (bank accounts) or physical projects abroad. Huang and Zhang (2013) proposed a model for firms’ optimal investment and consumption that considered the effects of inflation and differences in market opening and closing. Long and Zeng (2016) investigated an international investment problem for corporations, proposing time-consistent strategies with a mean-variance criterion. Bellalah et al. (2016) conducted a study on corporate international investment and analyzed the impact of information cost, short selling, and taxation on management decision making, finding that these factors have a significant impact on corporate investment decisions. Bellalah and Zhang (2017) investigated the impact of firms’ international investment decisions around market closure on exchange rate risk, incomplete information, and short selling restrictions, determining that these factors had a significant impact on investment. Choi et al. (2018) examined the predictions of real option theory, confirming that it accurately predicts investment decisions. Daszkiewicz (2019) explored the internationalization patterns of family high-tech firms and found that such firms tend to internationalize slowly and cautiously. Glodowska et al. (2019) investigated multinational enterprises’ risk mitigation strategies in emerging markets, finding that these strategies are essential for successful internationalization. Zhu and Sardana (2020) investigated the moderating effect of internationalization motives on Polish firms’ multi- nationalization–performance relationship, determining that such motives had a significant impact on the relationship. Barlozewski and Trapczyzski (2021) examined the impact of foreign exchange rate risk on the expected returns generated by South African investors’ portfolios, demonstrating that this risk has a significant impact on returns. Djemo et al. (2021) examined how small family firms responded to the COVID-19 crisis, finding that such firms adapted and responded to the crisis in various ways. Marjanski & Sulkowski, 2021 examined how new multinational firms structured their foreign direct investment location portfolios and found that such decisions have a significant impact on performance outcomes. Grieco (2021) provided a comprehensive overview of the theories and evidence on foreign investment and development, while Song (2021) examined the conditions under which multinational corporations adjust production volume among subsidiaries. Koren and Vodopyanova (2022) focused on methods to increase transnational corporations’ investment attractiveness, and Li et al. (2022) constructed a proposed mathematical model to study the optimal investment problem. Finally, Nguyen (2023) investigated the relationship between financial constraints and firm productivity in Vietnamese manufacturing industries.

Despite the significant progress made in the field of corporate investment and consumption decisions, some limitations remain in the previous literature. Specifically, the majority of studies have primarily focused on corporations’ optimal investment and consumption choices, while neglecting the potential impact of external factors such as political and economic risks. Furthermore, some studies have solely concentrated on a particular type of investment, such as bonds or physical projects, and have not explored other investment options. To address these limitations, future research should expand on the approaches of previous research by considering a broader range of investment options and external factors to provide more comprehensive insights into firms’ international investment and consumption decisions. As noted, some studies have only focused on specific factors and did not consider other important factors that may affect investment decisions. Additionally, some studies have only focused on specific types of firms or industries, which may limit the generalizability of the findings. Finally, some studies have relied on self-reported data, which could be subject to bias and may not accurately reflect corporations’ actual investment decisions. Therefore, future research must incorporate a more comprehensive set of factors and a broader range of firms and industries to establish a more complete understanding of corporate international investment decision making. In doing so, scholars can gain a deeper understanding of the complex decision making processes that firms engage in when making international investment and consumption decisions and provide more accurate and reliable recommendations for practitioners and policymakers.

As the scope and complexity of problem-solving expands, demand for central processing unit (CPU) resources also rises. To optimize CPU resources, Jararweh et al. (2019) proposed the use of parallelization and vectorization techniques to enhance the performance of the Needleman–Wunsch algorithm; a widely used sequence alignment algorithm in bioinformatics with high computational complexity. The authors suggested distributing the workload to multiple processors using parallelization techniques and optimizing the use of CPU resources using vectorization techniques. They implemented the parallelized and vectorized Needleman–Wunsch algorithm, testing it on a set of DNA sequence data. The results demonstrated that their algorithm significantly improved performance compared with traditional algorithms. This technology has significant implications for future research in this field.

We combine stochastic hyperbolic discounting (SHD) and a corporate international investment and consumption problem (CIICP) to investigate their implications for understanding and solving contemporary economic and financial issues, providing valuable insights for corporate investment and consumption decisions. Our CIICP is constructed referencing Bellalah and Wu (2009), and the SHD method was proposed by Zou et al. (2014). We obtain some interesting results by combining CIICP and SHD. This study makes several notable contributions. First, dynamic programming is applied to formulate a dynamic programming equation (DPE) that describes the optimal corporate international investment strategy and consumption choice for sophisticated individuals. Second, we provide explicit solutions for logarithmic utility. Third, we conduct a sensitivity analysis to examine the volatility parameter of the optimal solution. The results of this study provide valuable insights for CIICP that are of considerable significance for corporate investment and consumption decisions.

The remainder of the paper is organized as follows. Section 2 presents the CIICP market setting and introduces the concept of SHD. Section 3 details the DPE for the problems of international investment and consumption with complex individual corporations. In Section 4, we obtain an explicit solution for log utility. Section 5 provides simulation results to illustrate the impact of volatility parameters on foreign production markets and exchange rates. We present some conclusive and suggested extensions in Section 6. Finally, the Appendix presents the model's technical details.

Model hypotheses

In this section, we present the basic model for the CIICP framework and describe SHD referencing Zou et al. (2014).

Let (Ω,F¯,F,P) denote a filtered probability space, where Ω is a probability space, P is a measurable probability, F¯t represents the information available up to time t, and the filtration F={F¯t},t∈[0,T] satisfies the usual conditions (i.e., {F¯t},t∈[0,T] is right-continuous and P-complete). Here, T represents the terminal horizon. We assume that all stochastic processes and random variables are defined in the filtered probability space (Ω,F¯,F,P). Additionally, let Bt1,Bt2, and Bt3 be three mutually dependent, one-dimensional Brownian motions with correlation coefficients ρ12,ρ13, and ρ23∈[−1,1], respectively, which represent uncertain external sources in the market.

The industrial market model

In this section, we construct a market referencing Bellalah and Wu (2009), considering a “two-country” firm for which domestic (Rt) and foreign (Rt*) static cash flows are denoted as follows:

where Pt,Ct(domestic), Pt* and Ct*(abroad, marked with *) are the output and input production prices. Qt and Qt* represent the amount of production output, β and β* denote positive constants, et represents the exchange rate, which is uncertain, and κ and κ* are the tax rates in home and foreign countries. Choi (1989) assumed the quantity of output (Qt) to be certain and did not consider the tax.

Similar to Choi (1989) and Bellalah and Wu (2009), we assume that the dynamic input and output prices of products and the exchange rate can be expressed in the following form:

and

where the terms μp,μp*,μc,μc*, and μe are constant-bounded and represent the rates that are expected instantaneously for various variables. The terms σ,σ* and σe represent the coefficients of instantaneous fluctuations. The initial values of the above variables are P0,C0,P0*,C0*, and e0, respectively.

The cash flow generated from the domestic market (Rt) is expressed as follows:

with

Similarly, the cash flow (R¯t) in the foreign market that has not yet been remitted is denoted as follows:

where

From R*=etR¯t and Eqs. (3) and (6), the variation in cash flow from abroad (Rt*) is obtained as follows:

where

However, a sunk cost is paid by investors who require extra returns to compensate for the resources with which they engage in the search to obtain information. Information cost has an incremental return dimension, and it is included in the descriptions of the dynamics of different variables and added to the drift. Thus, the actual change in domestic cash flow should be indicated as follows:

where λR represents the rate of information cost in the domestic market.

The real changes in the exchange market are expressed as follows:

where λe represents the rate of information cost in the exchange market.

Then, from R*=etR¯t and Eqs. (8) and (11), the change in cash flow at a specific time coming from the foreign market can be easily obtained as follows:

Wealth process

Let Wt represent corporate wealth and πt denote the proportion of corporate investment abroad at time t≥0. 1−πt is the proportion of home market investment. Referencing the corporate consumption introduced by Sumner (2008), in addition to decision making on investment, the manager can also make consumption decisions to satisfy shareholder demands.

Eqs. (10) and (12) indicate that corporate wealth can be expressed as follows:

where ct is corporate consumption. We assume a positive initial corporate wealth (W0), and π(·) is a measurable process that is almost surely locally bounded.

SHD

We use the framework of Merton (1969) to introduce the stochastic hyperbolic discount function from Harris and Laibson (2013) to examine time-inconsistent individuals’ consumption and investment. Referencing Harris and Laibson (2013), the discount function D(t,s) is expressed as follows:

where [t+τ,+∞) is the forward interval and [t,t+τ) is the closest interval. We assume that the closest interval (τ) has an exponentially distributed duration with parameter λ, and the stationarity assumption is satisfied for the stochastic hyperbolic discount function D(t,s) (i.e., D(t,t+s)=D(0,s)). The expected length of the closest interval is E[τ]=1λ. A lower λ indicates a longer expected duration. The duration of the closest interval is ∞ as λ=0, and the discount function degenerates to a constant exponential discount, and the problem represents Merton's classical case; however, when λ→∞, the closest interval becomes zero, and the discount function is transformed into the following:

A jump occurs at s=t. The parameter η(0<η≤1) shows the present deviation in the degree of preference. A smaller η indicates a larger present deviation. Whenη=1, the present and future intervals are not distinguished and the discount function D(t,s) once again degenerates to an exponential discount function with a discount rate of ρ, and this implies that the problem reduces to Merton's classical case.

CIICP optimization model

This study simultaneously considers firms’ investment and consumption to maximize the utility of wealth by determining the investment strategy and consumption choice. A mature corporate investor with temporally inconsistent preferences is required to allow for future selves in the current decision. The following optimization problems must be solved by complex individual firms for finite and infinite planning periods with SHD to obtain optimal and time-consistent consumption and portfolio policies, respectively:

and

where U(·) is the corporate consumption utility in the investment period, B(·) is the corporate terminal wealth utility, ρ is the manager's time preference in the recent period, η represents the diminished rate of future discounting, and τ represents the length of time of the current phase.

In the next subsection, we first derive the problem for complex individuals, and then extend the analysis to yield DPE that are valid for infinite level problems.

The DPE of the finite horizon problem

Our analytical approach is based on Zou et al. (2014), and has also been used by Karp (2007). Specifically, a continuous-time problem is converted into a discrete-time problem, which we solve using backward induction, obtaining the optimal action of the future self first, and then we obtain the DPE for a finite horizon problem for mature individuals by iterating and passing the problem to the limit of continuous time.

Denoted by V(t,Wt) the value function of Eq. (16) is as follows:

with V(T,WT)=B(T,WT). We assume that V(t,Wt) is of classC1.

Similar to Zou et al. (2014), we deduce the DPE to replace the Hamilton-Jacobi-Bellman (HJB) equation as follows:

where

and ct* satisfies Eq. (19).

Therefore, the DPE for Eq. (16) is Eqs. (19) and (20), for which the boundary conditions for complicated individuals are as follows:

To simplify, we denote the following:

then Eq. (19) is equivalent to the following:

By the first-order conditions, we obtain the optimal solution for Eq. (16) as follows:

Remark 1

• (1)

  The term −VWWWVW is the counterpart to the Pratt–Arrow measure (Pratt, 1976) with respect to risk aversion. This measure reflects how risk-averse a company is toward domestic and foreign investments.

• (2)

  The term Δd3 refers to the variability of investment strategy.

• (3)

  The first term, −VWVWWWΔu2−Δu1Δd3 in πt*, is referred to as “speculative demand” or aggressive demand and is contingent on risk aversion measures.

• (4)

  The second term, −12Δd2Δd3, in πt* is referred to as hedging demand, which covers the demand for foreign investments on a risk hedging basis and is not related to the manager's risk attitude.

Remark 2

Eq. (22) shows that Δu2−Δu1=f*(t)−f(t)+μe+(λR*−λe−λR). Information costs are included in the investment strategy, and this influence is represented by λR*−λe−λR. This expression indicates the information costs involved in cost advantage seeking, wherein managers will not agree to invest abroad until they have obtained some useful information regarding the foreign and exchange markets. Without this information, managers are more inclined to make investments in the local market.

The DPE of the infinite horizon problem

The value function defines V(t,Wt) as in Eq. (17) as follows:

Following Zou et al. (2014), we the DPE can be obtained as follows:

where

We further assume limT→∞ηe−ρ(T−t)B(T,WT)=0. As a consequence, a transversal condition with the boundary condition Eq. (21) becomes the following:

For this reason, the HJB of Eq. (17) is subject to Eq. (13), which is Eq. (26) for sophisticated individuals, and the horizontal condition is Eq. (28).

The explicit solution for CIICP with log utility

In this section, we consider the CIICP with log utility with the following:

We present the following lemma to solve the optimal problem with log utility.

Lemma 1

The solution for the following ODE:

can be characterized as follows:

where αT is a given scalar, and Pt is a given function.

The proof is presented in Appendix A.

From Eq. (23), we have the following:

Theorem 1

Eq. (16) is optimally solved as follows:

and the sophisticated t-agent's value function is as follows:

where αt,βt satisfies the following:

with

and Δu1,Δu2,Δd1,Δd2, and Δd3 are given in Eq. (23).

The proof is presented in Appendix B.

Remark 3

We find that the optimal investment strategy does not determine the wealth process (Wtπ*), but the optimal consumption choice depends on the wealth process (Wtπ*).

Results of simulation and parameter sensitivity

In this section, we examine the impact of parameters with respect to firms’ optimal investment strategies and consumption choices, and supply several numerical examples demonstrating the impact. For the description below, in the absence of any other indication, the fundamental parameters are provided as follows:

(The data are obtained from Bellalah & Wu, 2009).

• (1)

  Based on Theorem 1, we can obtain the portfolio changing over time.

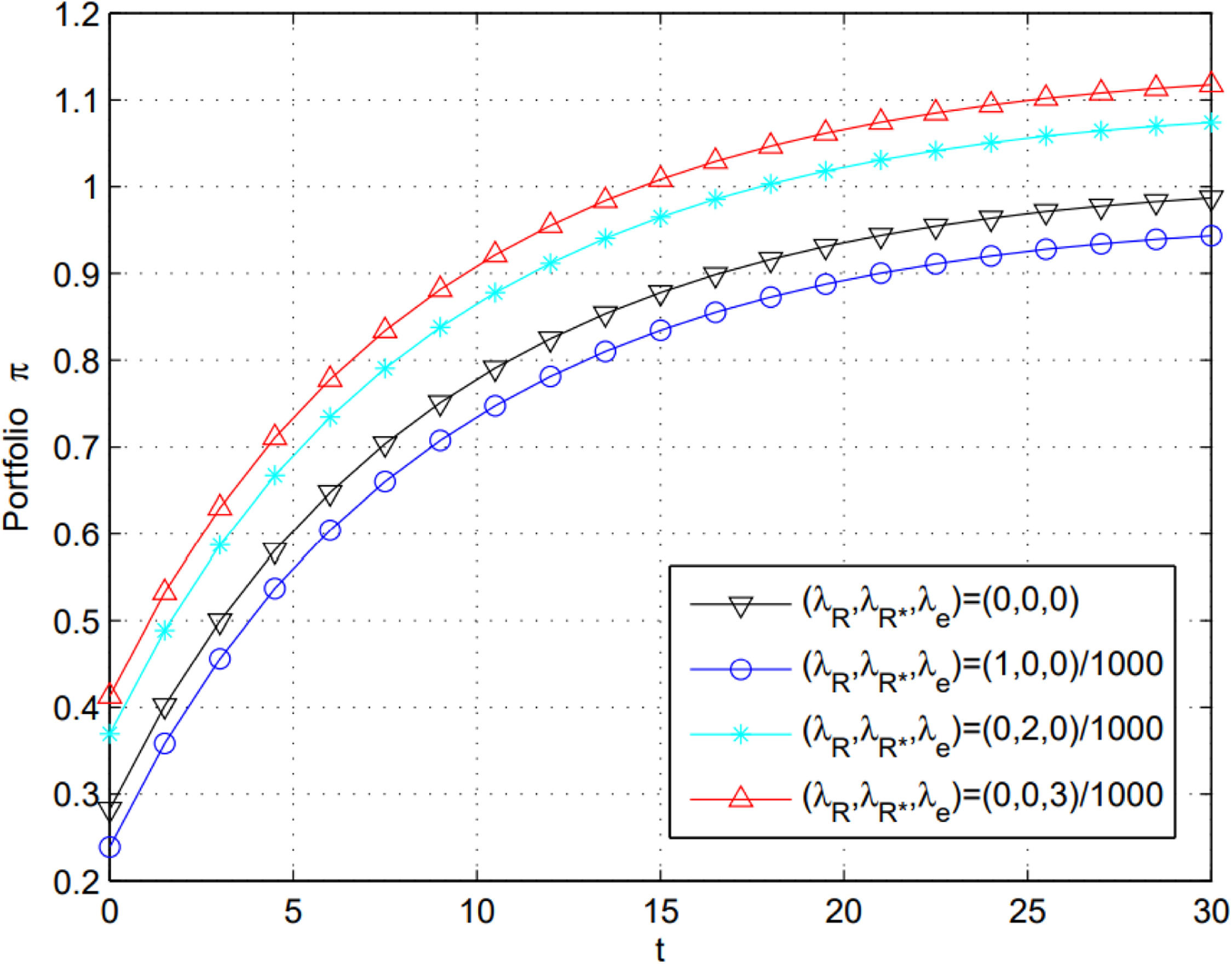
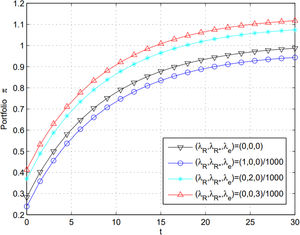
In Fig. 1, (i) letting λR=0.001,λR*=0, and λe=0, we obtain the curve that describes the relationship between the portfolio and information cost in the home market. (ii) Letting λR=0,λR*=0.002, and λe=0, or letting λR=0,λR*=0, and λe=0.003, we obtain a similar curve that describes the relationship between the portfolio and information cost in the home or exchange market. (iii) Letting λR=0,λR*=0, and λe=0, we obtain the curve that demonstrates the portfolio without any information cost.

• (2)

  In Theorem 1, we analyze the sensitivity of information cost rates on optimal investment strategies.

Fig. 1.

Portfolio changes over time.

According to Theorem 1, ∂π*∂λR<0,∂π*∂λR*>0,∂π*∂λe>0 and ∂π*∂μe>0, which means that ∂π*∂λR<0, indicating that the manager should invest less money in the foreign market when the home market's information cost rate (λR) increases and other parameters are fixed. ∂π*∂λR*>0 indicates that more funds should be allocated to the foreign market when other parameters are fixed, and as the information cost rate in the foreign market rises, λR* increases. If managers do not want to spend much on information cost in the foreign market, they choose to invest in the home market. Therefore, information has a central influence on foreign investment and can explain the home bias in international finance. ∂π*∂λe>0 means that more information cost in the exchange market indicates a higher proportion of the total budget is allocated to foreign investment. ∂π*∂μe>0. This suggests that when the exchange rate (μe) increases and other parameters are fixed, the manager should allocate more money to foreign market investment.

It is crucial to determine the relationship between the portfolio and the cost of a single piece of information. We first set λR=0,λR*=0,λe=0,μe=0 for every case. To not show the curves superposed, we let t=1,2,3, and 4. In Fig. 2, (i) letting t=1, we obtain the curve that demonstrates the portfolio changing with λR*. When λR*=0.009, the strategy for achieving the best in the foreign market is π*=0.9735. In this case, the highest proportion of corporate wealth is invested in the foreign market. (ii) Letting t=2, we obtain the curve that demonstrates the portfolio changing with λe. When λe=0.006, the strategy to achieve the best in the foreign market is π*=0.9149. (iii) Letting t=3, we obtain the curve that demonstrates the portfolio changing with μe. When μe=0.01, for the CRRA case, the strategy for achieving the best in the foreign market isπ*=0.9344. (iv) Letting t=4, we obtain the curve that demonstrates the portfolio changing with λR. When λR=0.001, for the CRRA case, the strategy for achieving the best in the foreign market is π*=0.729, indicating that 72.9 % of the corporate wealth is made available for investment in the domestic market.

Fig. 2.

Consumption–wealth ratio c_t/W_t changes over time t.

To compare with the research results from Bellalah and Wu (2009), this study uses the authors’ investment proportion in foreign markets and our own, respectively. When λR*=0.01, their result is x = 0.9073, while our result is about 0.8; when μe=0.01, their result is x = 0.9508, while our result is about 0.8; when λe=0.001, their result is x = 0.7769, while our result is about 0.45; and when λR=0.0095, their result is x = 0.4943, while our result is about 0.25. Considering SHD, the results of this study are generally lower than those of Bellalah and Wu (2009), which indicates that SHD has a significant impact on investment decision making, which is consistent with the hypothesis of time-consistent preferences being unrealistic.

• (3)

  From Theorem 1, we next examine the influence of λ and T on the consumption–wealth ratio.

  • (i)

    The expected duration of the nearest interval goes to zero as λ→∞, and in the case of the stochastic discount function, is changed to Eq. (15) as a deterministic jump function that jumps at t. If T<∞, by Eq. (34), we obtain the following:

    

which leads to

• (ii)

  For an infinite planning horizon, i.e., Eq. (17), by Eq. (34) and letting T→∞, we have αt=λη+ρρ(λ+ρ), and the consumption–wealth ratio can be written as follows:

  

• (4)

  We analyze the sensitivities of parameters λ,η, and time t on the consumption–wealth ratio.

Note that for any x>0,ex>1+x, and taking the partial derivatives of αt w.r.t parameter λ, we can obtain the following:

which means the following:

By taking the derivative of αt in relation to the parameter η, we obtain the following:

Taking the partial derivatives of the above equation in relation to time t, we obtain the following:

which shows that ∂αt∂η is decreasing with respect to time t. Next, we will observe whether ∂αt∂η is negative by its value at t = T. Noting that the parameter ρ∈[0,1], we obtain the following:

Thus, we determine that ∂αt∂η<0, which means the following:

Therefore, the consumption–wealth ratio ct*/Wt is decreasing with respect toη.

According to Eq. (34), we obtain the following:

If ρς−η1−η≥1, then ∂αt∂t≥0, which means ∂∂t(ctWt)=∂∂t(1αt)=−1αt2∂αt∂t≤0. If ρς−η1−η0. Otherwise, if e−λT<ρς−η1−η<1, then when t>T+1λlnρς−η1−η,∂αt∂t<0, or else ∂αt∂t≥0.

Furthermore, λ=0 or η=1 leads to the following:

which means that αt|λ0orη=1=1ρ[1+(ςρ−1)e−ρ(T−t)].

Therefore, the problem reduces to Merton's classical case yielding the following:

By Eq. (32) and for λ>0,0<η<1, we obtain the following:

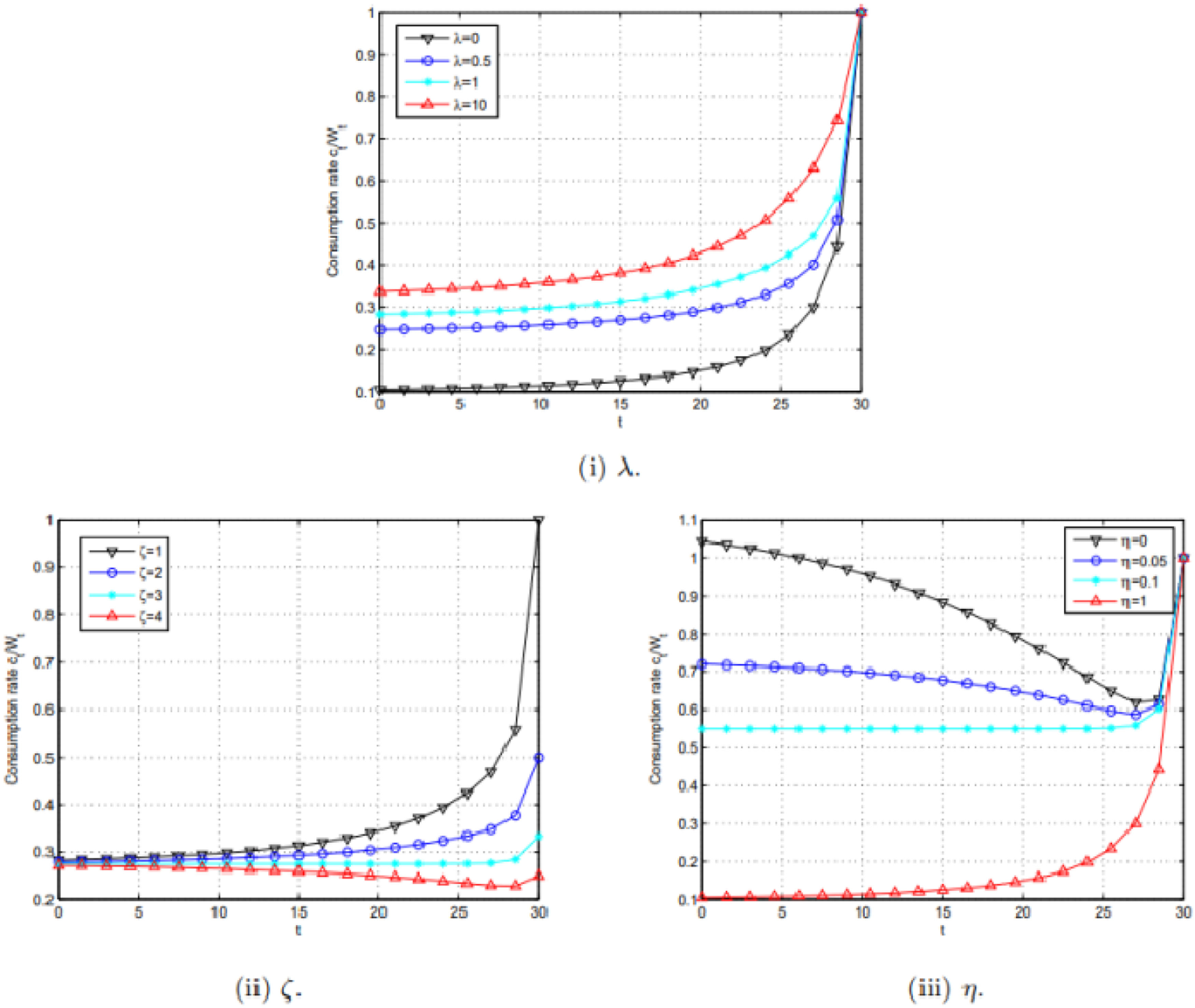
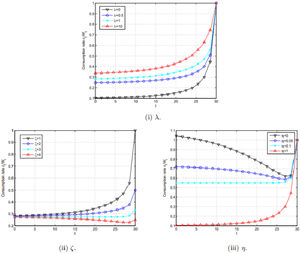
which indicates that the consumption–wealth ratio in this study is larger than Merton's.

In Fig. 2(i), letting ζ1=1 and η1=0.3, we plot the curves with λ1=0,0.5,1, and 10. The results show that the consumption–wealth ratio is increasing with respect to parameter λ.

In Fig. 2(ii), letting λ1=1 and η1=0.3, we plot the curves for ζ1=1,2,3 and 4. The results show that the influence of ζ on the consumption–wealth ratio is significant in the later period.

In Fig. 2(iii), letting λ2=1 and ς1=1, we plot the curves with η1=0,0.05,0.1 and 1. The results show that the influence of η on the consumption–wealth ratio is significant in the early stage.

• (5)

  In Theorem 1, we obtain the figures demonstrating the optimal consumption–wealth ratio (ctWt) changes with the parameters λ and ς.

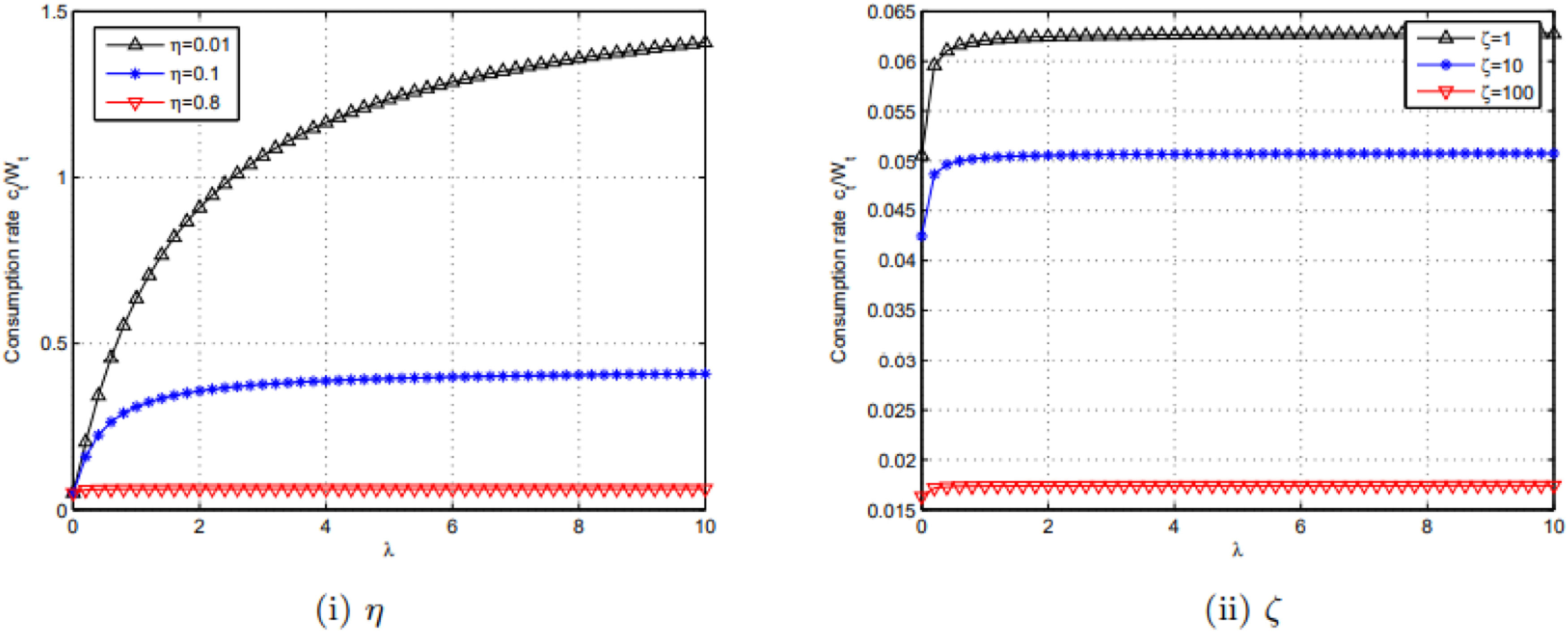
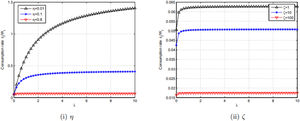
In Fig. 3(i), using three different values of ς with 0.01, 0.1 and 0.8, the results show that the consumption–wealth ratio (ctWt) is scaling up relative to parameter λ.

Fig. 3.

Consumption–wealth ratio c_t/W_t changes with λ.

In Fig. 3(ii), using three different values of ς with 1, 10 and 100, the results show that the consumption–wealth ratio (ctWt) is also scaling up relative to parameter λ.

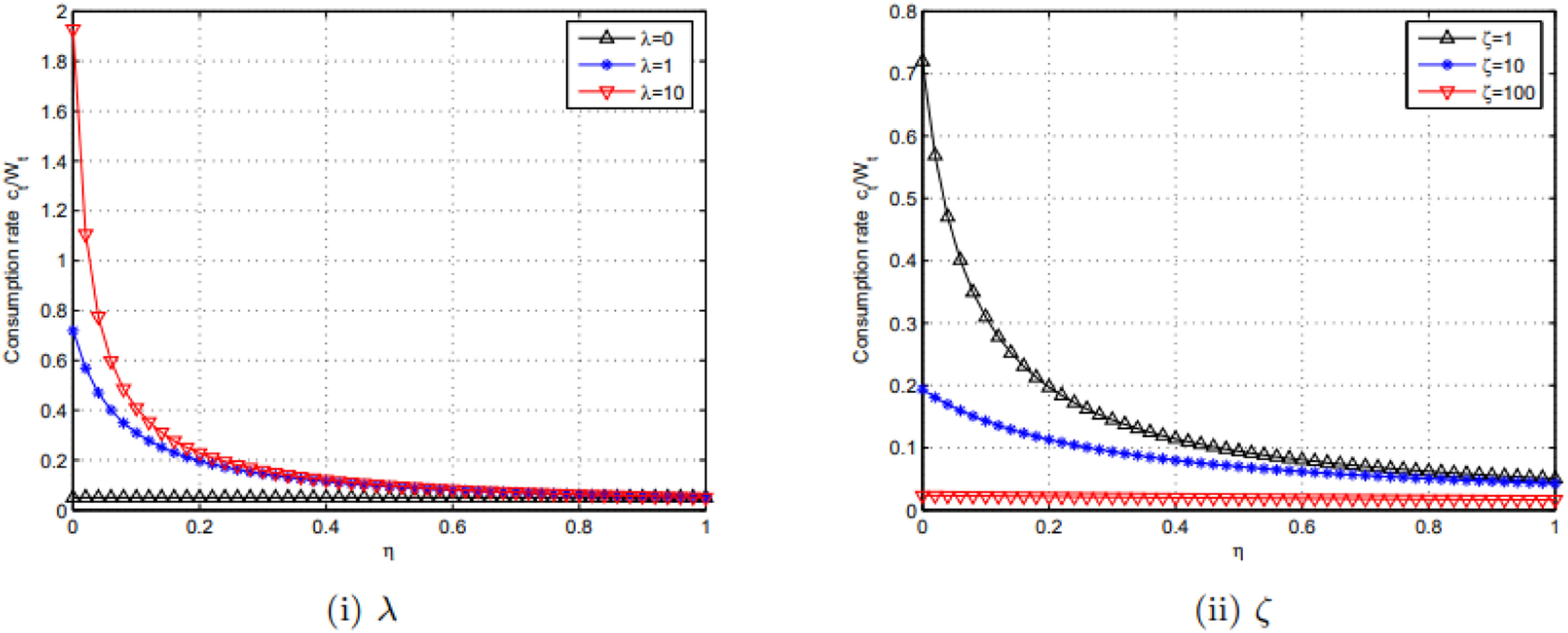
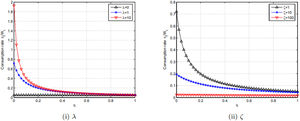
In Fig. 4(i), taking three different values of λ with 0, 1 and 10, the results show that the consumption–wealth ratio (ctWt) is reduced in relation to parameter ς.

Fig. 4.

Consumption–wealth ratio c_t/W_t changes with η.

In Fig. 4(ii), taking three different values of ς with 1, 10 and 100, the results show that the consumption–wealth ratio (ctWt) is also reduced in relation to parameter ς.

Conclusion

This study builds upon the CIICP theory and introduces the concept of SHD based on the prior research conducted by Zou et al. (2014) and Bellalah and Wu (2009). By taking into account the evolving preferences of sophisticated individuals, our study enables the formulation of consumption and investment strategies in a consistent manner over time. We employ a recursive approach to derive explicit solutions for corporate international investment strategy and consumption choices, considering log utility and encompassing both infinite and finite planning periods.

The practical significance of this study lies in its ability to provide more accurate analysis and resolution of issues pertaining to corporate international investment and consumption decisions. By introducing SHD and incorporating dynamic preferences, our dynamic programming approach assists decision-makers in formulating optimal strategies for both the short and long terms. This, in turn, enables more precise predictions and enhanced decision-making support.

Nevertheless, it is important to acknowledge the limitations of this study. Our model is built upon specific assumptions and parameter settings, therefore potentially limiting its applicability to real-world situations. Furthermore, our research does not account for other potential factors and constraints, such as changes in the macroeconomic environment and uncertainties. Thus, future research endeavors should focus on expanding the model to better align with real-world conditions.

Moving forward, future research can expand the model by incorporating additional factors and considering a wider range of constraints. For instance, the inclusion of risk factors and uncertainties could provide insights into the variations observed in optimal strategies within different market environments. Additionally, incorporating the behaviors and strategy choices of other decision-makers, followed by empirical analysis, can help validate the accuracy and applicability of the model. These further research efforts will contribute to a better understanding and resolution of the complex issues surrounding corporate international investment and consumption decisions.

Declaration of generative AI and AI-assisted technologies in the writing process

The author used ChatGPT to assist in modifying the text to improve the readability and grammatical correctness of the article. The author has reviewed and edited the content and is fully responsible for the publication's content.