Rational preference knowledge influence on the evolutionary equilibrium of carbon reduction negotiation: An exploration based on timed petri net

Abstract

In the digital economy age, carbon emission reduction is perhaps the most crucial contribution affecting national activities and international negotiations. In a potential carbon reduction conflict, a rational participant expects to select a suitable strategic opinion to reach another state with improved benefit. Participants’ preferences reflect their priority ranking on multiple possible conflict solutions, directly determining the evolutionary direction and equilibrium solutions. Referring to the potential carbon reduction conflicts, Timed Petri Net for Conflict Analysis (TPNCA) is proposed as a graphical tool to explore participants’ rational preferences, state transformation, and conflict evolutionary equilibrium. The generation rule of TPNCA is designed according to carbon reduction co-operators’ rational preference knowledge. From the long-term perspective, dynamic unilateral improvement is proposed to reflect decision-makers’ strategic initiative willingness to reach end nodes. Dynamic equilibrium conditions are conducted to determine the final stability state for a conflict. This study reveals how participants’ preference knowledge and time constraints influence conflict evolutionary and dynamic equilibria. Climate group should positively engage in carbon reduction negotiations and flexibly adjust national tasks, according to real-time carbon reduction contributions. This study (1) reveals the influence of preference knowledge on conflict evolution, (2) explores the role of time constraints in determining a terminated node, (3) proposes dynamic equilibrium from the long-term perspective, and (4) helps guide participants’ strategic decision-making for mutually solving carbon reduction.

Introduction

As an important milestone in global climate governance, the 26th Conference of the Parties (COP26) released positive and sustainable outcomes for the continuous implementation of the Paris Agreement, such as global carbon reduction consensus (Arora & Mishra, 2021), technology transfer (UNEP - UN Environment Programme, n.d.), climate finance (Wang et al., 2022a), and the cooperative effect (Figures, 2021). Worldwide consensus is that carbon reduction is imperative in addressing global climate change and cooperatively reducing the global carbon footprint. Although developed countries generally utilize sufficient funding (Kim et al., 2022), have advanced green technology (Ibrahim et al., 2022), have developed mature, sustainable industrial systems (Wang et al., 2022b), and utilize complete infrastructure and management systems (Chen et al., 2022); however, their heavy emissions and limited potential result in inefficient margin contribution to carbon reduction. Additionally, some developing countries urgently need to transform the traditional extensive economic development model into a more environmentally friendly, low-energy, and sustainable development model (Chen et al., 2023a), with a remarkable latent capacity for carbon reduction. However, their deficiency in finance and technology may limit their carbon reduction commitment (Dong et al., 2022). To achieve a mutually beneficial effect, climate groups, such as IPCC, are performing as positive bridges, connecting groups to form carbon reduction cooperation (Meinshausen et al., 2022), where developed countries provide funds and green technology as a clean development mechanism (CDM) (Li & Lin, 2021) to assist developing countries. Funded developing countries then take additional portions of carbon reduction from sponsors as the reward. Climate groups act as globally credible organizations to establish and maintain carbon reduction alliances. If controversial issues exist, climate groups will try to negotiate with different countries to find feasible solutions (Chen et al., 2022).

The COVID-19 epidemic has led to a general decline in economic activities around the world (Chen et al., 2023b). Many developing countries, such as India, Thailand, and Vietnam, underwent temporary declines in carbon emissions, allowing them to catch up in their carbon neutrality progress (Ray et al., 2022). However, due to the recovery of circulation and consumption, people's revenge spending, particularly self-driving tourism and barbecue cooking, is returning and causing rapid surges in carbon gas creation. Facing the encouragement of national consumption recovery, some developing countries might encounter the additional pressure of carbon reduction. In this way, the carbon emission pace will be unsustainable or rebound after the COVID-19 pandemic, possibly presenting a significant challenge to realizing carbon reduction targets in 2030 (Roberts et al., 2021). Carbon reduction conflicts may arise among participants, and funded developing countries may be unable to complete the additional carbon reduction mission, possibly requesting to reduce the mission halfway. However, developed countries have already transferred green resources and part of their carbon reduction mission to developing countries. Such countries may insist on previous promises because of the delivered resources. The negative consequence of the conflict will be that developed countries suspend the green support and developing countries stop their carbon reduction behaviour, likely causing a complete failure in the global carbon mission, leading to serious climate crises. As the organizer of the alliance, climate groups can play the role of conflict negotiators to coordinate the appeals of developing and developed countries. Owing to the differential preferences and decision-making process, it is vital to study conflict evolution and explore the possible equilibria of the conflict, which can flexibly adjust carbon reduction missions and avoid serious international dispute beforehand.

The carbon reduction conflict always contains multiple possible states that can be understood as potential solutions. A rational participant is willing to initiate a strategic choice to improve its benefit (Bashar et al., 2014). Among multiple possible states, participants have reference knowledge about the state priority sequence (Kuang et al., 2015). The more preferred state can drive the participant to change their opinion to achieve a benefit better than the current state. The differential preference can induce the participant to consider another direction to resolve the conflict. In ranking states, preference knowledge can be referred to as the collection of preference priority. Different participants have their own preference knowledge for judging whether a strategic opinion should be initiated or not, directly determining the evolutionary direction of the conflict (Huang et al., 2023). Additionally, time factors, such as participant's consideration time and maximum time length, reflect the generation time of strategic decision-making. The time constraint of the decision-making subject affects the negotiation outcome (He, 2022). The participants’ preferences and time-bound knowledge can determine the dynamic equilibrium for guiding players to implement innovative strategic activities in decision sequences and setting maximum negotiation times to realize mutually beneficial states.

This study aims to provide a novel conflict analysis framework driven by preferences and time-bound knowledge, exploring effective suggestions for solving potential carbon reduction conflicts. The contributions of this study include the following conclusions. (1) Timed Petri Net for Conflict Analysis (TPNCA) is designed as an analysis framework to reveal the influence of preference knowledge on conflict evolution. (2) The role of time factors (consideration time and negotiation deadline) is explored to confirm the evolutionary termination condition. (3) Dynamic equilibrium is proposed to provide long-term insights for examining the dynamic stability of a conflict. (4) The effective decision-making sequence and time condition set can induce participants to implement suitable strategic activities to mutually solve carbon reduction conflicts.

The remainder of the paper is organized as follows: Section 2 presents the related existing research and summarizes the research gap. The generation rule of TPNCA and its application to the carbon deduction conflict is proposed in Section 3, driven by participants’ preferences and time-bound knowledge. Section 4 explores the dynamic equilibrium condition from a long-term perspective concerning time constraints. Section 5 shows the detailed process to achieve the potential solutions of the carbon deduction conflict and provides managerial implications. Section 6 provides research conclusions and future aspects.

Literature review

The study explores how preference knowledge affects the conflict evolution of carbon reduction cooperation in the overlapping domains of carbon reduction cooperation, clean development mechanism, and conflict analysis. Therefore, Section 2 provides a brief overview of the following three aspects. The subsection describes the research gap analyzing conflict evolution from a short-term perspective.

Cooperation mechanism in the carbon emission reduction

As a global predicament, carbon reduction emissions cannot be solely overcome through a nation's unilateral efforts. Peng et al. (2023) proposed a four-pole game model to discuss the conflict resolution mechanism of energy investment projects, in which the cooperative carbon-reduction infrastructure was enhanced to provide financial support and oversight for carbon-reduction projects. Wang et al. (2022a) proposed a co-governance mechanism for carbon reduction stakeholders to clarify their roles and reduce emissions. Geng et al. (2022) conveyed that the carbon-reduction collaboration between enterprise alliances and governments should sustainably provide technical support to meet carbon-reduction goals. Zhao et al. (2023) emphasized the contribution of green innovation to the carbon reduction effect, in which collaborative modes performed better.

Clean development mechanism in the carbon emission reduction

To solve increasingly severe climate change caused by carbon emissions, CDMs have emerged as a critical instrument for curbing carbon dioxide emissions (Hong & Rodríguez, 2014). The core objective of CDMs is carbon emission reduction and sustainable development. Cui et al. (2020) examined the positive impact of CDMs on stimulating enterprise-level innovation in renewable energy. Implementing CDMs allows for developing countries to play a more prominent role in global climate governance. Shi et al. (2021) revealed that the implementation of China's CDM projects achieved obvious carbon reducing effects by controlling carbon dioxide emission. In Nigeria, CDMs have effectively curbed natural gas flaring in the oil and gas industry as a policy (Mohammed, 2020). CDMs have played a crucial role in reducing carbon emissions, offering strong support for promoting sustainable development and global climate governance.

Graph model for conflict resolution (GMCR) in environmental issues

In a realistic conflict, several rational Decision Makers (DMs) are present with their own alternative strategic choices and potential solutions in the form of combinations of DMs’ selections and preferences for heterogeneous solutions (Hipel & Fang, 2021). As an effective non-quantitative analytical method for conflict analysis, GMCR has been employed to describe and solve strategic conflicts in many environmental issues (Hipel et al., 2020), such as air carbon emission (He, 2022), greenhouse gas emission (He et al., 2017), brownfield redevelopment (Walker et al., 2012), and water allocation (Yu et al., 2019). GMCR could describe the solution state transacted in the negotiation process, which relies on a DM's rational preference knowledge of states and other DMs' interactive strategic sanctions. The equilibrium states denote the potential solutions of the corresponding conflict.

Research gap and research tasks

Previous research has contributed abundantly to the carbon reduction cooperation mechanism. However, some research gaps remain.

• (1)

  The dispute over carbon reduction was ignored to be explored from a knowledge-driven perspective. Especially in the post-pandemic era, developing countries will face dual pressures from economic recovery and carbon emission perspectives. According to potential carbon reduction disputes, different players may have various preference knowledge on possible states, easily inducing disagreements and behaviour conflicts. The role of preference knowledge should be explored to realize knowledge-driven decision-making.

• (2)

  The influence of time factors on conflict evolution and equilibrium should be deeply examined in carbon reduction conflict. Participants need consideration time to provide strategic opinions for the following activities. The carbon reduction dispute should confirm the maximum time length as the deadline. Time-related knowledge can determine the generation direction and equilibrium of conflict, providing precautionary solutions and management suggestions.

• (3)

  Although previous GMCR introduced time constraints as decision-making time (Inohara, 2016) and time deadlines (He, 2022), related research did not reveal long-term equilibrium solutions, which only concern whether a DM is willing to move to a more preferred adjacent state, while the following DMs may take one or two rounds of counterattack to block it. According to a dynamic evolutionary conflict, whether the state of a DM is stable depends on his preference comparison between the current and terminated states, rather than only the counterattack state. For example, player i prefers to select a strategic decision to move from state s0 to s1, 1≻i0. If another player j, j≠i, chooses one of his strategies and can move to state s2, which will cause player i's preference to be lower than the original state s0, s2≺is0. If this happens for all the players, s0 will be determined as the Sequential Stability or General Metarationality depending on whether s2≻js1 (Hipel & Fang, 2021). However, if all the players select suitable strategy following individual preference knowledge to make unilateral improvements, the conflict will evolve into final state send because of time factors and send≻is0. If so, player i will be willing to move from s0 to send, although there may be some low preferred state in the evolutionary. If it is suitable for all the players, each player's strategic choice for unilateral improvements and long-term equilibrium can be explored, rather than short-term equilibrium only concerns one or two rounds of counterattack behaviours.

Responding to these research gaps, this study proposes a TPNCA framework to explore the driven effect of preference knowledge and the terminated role of time factors. Among various graphic models, the Timed Petri Net contains transition elements to reflect DMs’ consideration time and explore dynamic evolutionary conflicts with time information (Giua & Silva, 2018). When a conflict occurs, knowledge is critical to guide negotiation processes among participants to achieve consensual solutions (Guaita Martínez et al.,2019). Participants’ rational preference knowledge is treated as the driving force to generate TPNCA from quote states, directly determining the development routes. Additionally, the terminated role of time constraints is examined according to time-bound knowledge, describing the relationship between cumulative consideration time and negotiation deadline. Moreover, the carbon reduction conflict among developed country, developing country, and climate group is studied to show the generation of TPN and long-term equilibria exploration processes. Long-term equilibria can be considered a potential beforehand solution for carbon reduction conflicts.

Timed Petri Net and its generation rule for carbon reduction conflict evolutionary

DMs’ strategic choices and state preferences of carbon reduction conflict

DMs in carbon reduction conflict

In the carbon reduction cooperation, the climate group can be regarded as the organizer and manager of the alliance, whose responsibility covers member join-in/out, carbon reduction resource (fund and technology) collection and assignment, carbon reduction mission design and adjustment. As the principal, the developed country designs a carbon reduction project including resource and transferred mission for a developing country. If a developing country undertakes the project, it will receive the carbon reduction resource and promises to undertake the additional carbon reduction mission. All the participants in the cooperation can achieve mutual benefits to accomplish their carbon reduction mission. The developed country successfully reduces its carbon reduction pressure and the developing country can improve its carbon reduction efficiency as well as technology level. Climate group can obtain obvious success on social responsibility and good reputation because of climate improvement.

Although many developing countries reduced the carbon emissions during the COVID-19 pandemic, the prospect of carbon reduction in the next few years is not optimistic. Owing to the transportation recovery and revenge spending, the carbon emission of developing countries will rebound after the COVID-19 pandemic. If a developing country preferentially considers a booming economy, its carbon reduction mission will face significant pressure to be completed. Developing countries may request to reduce the transferred amount in the cooperative process, which will not be simply accepted by developed countries because of resource investment. If the conflict worsens, the developing country will break the carbon reduction cooperation and return the transferred carbon reduction mission to the developed country. If most developing countries abandon the mutual carbon reduction promise, the global carbon reduction behaviour will be ruined, and serious climate crisis may occur.

DMs’ strategic choices and the states of carbon reduction conflict

In the conflict analysis framework, there are three DMs as developed country (Sponsor, Sp), developing country (Agent, A), and climate group (Management, M). The set of DMs N={Sp,A,M}. Suppose that the carbon reduction amount of a developing country is far behind the schedule, the developing country wants to decrease the transferred carbon reduce amount and return it to developed country. The developed country insists that the developing country should strictly follow the contract and complete the promised amount. The climate group can adjust the carbon reduction mission of a related country to avoid serious contract breach.

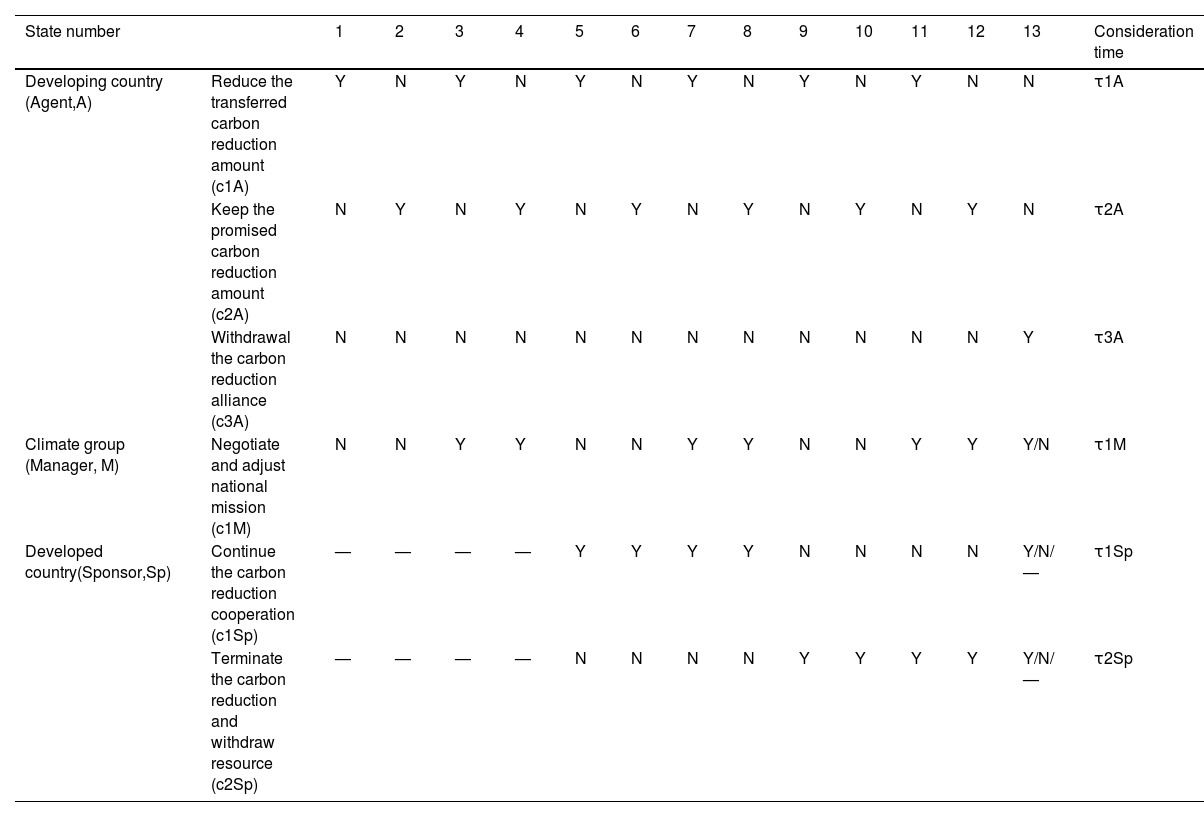
The DMs have their own strategic choices in the negotiation process. The developing country (A) will have three alternative choices as c1A: Reduce the transferred carbon reduction amount to acceptable level and return the reduced amount to the developed country; c2A: Keep the promised higher carbon reduction amount; c3A: quit the carbon reduction alliance and destroy cooperative prospect. The developed country (Sp) will take actions as c1Sp: Continue the carbon reduction cooperation; c2Sp: Terminate carbon reduction cooperation and withdraw green resource. The climate group(M) can determine whether takes c1M: Negotiate and adjust national carbon reduction mission.

As a conflict state is determined by all participants’ strategic selections, Labels Y and N are used to describe the related choice is initiated or not. Symbol — indicates that the developed country has not yet responded to the proposal. Because one participant's alternative choices are exclusive, one strategic selection can be initiated at a time. As shown in Table 1, the developing country has three exclusive opinions (c1A,c2A,c3A), climate group behaves two exclusive selections (c1M or not) and the developed country possesses three exclusive choices (c1Sp,c2Sp or no response). Note that, if a developing country initiates c3A to quit the carbon reduction alliance, whatever selections are adopted by the other participants, the carbon reduction alliance will be terminated. Consequently, 13 states (2×2×3 + 1 = 13) are involved in the conflict. The different combination of DMs’ choices can form conflict states, S={si}, i=1,2,⋯,13, as illustrated in Table 1.

Table 1.

State table of carbon reduction negotiation.

State number		1	2	3	4	5	6	7	8	9	10	11	12	13	Consideration time
Developing country (Agent,A)	Reduce the transferred carbon reduction amount (c1A)	Y	N	Y	N	Y	N	Y	N	Y	N	Y	N	N	τ1A
	Keep the promised carbon reduction amount (c2A)	N	Y	N	Y	N	Y	N	Y	N	Y	N	Y	N	τ2A
	Withdrawal the carbon reduction alliance (c3A)	N	N	N	N	N	N	N	N	N	N	N	N	Y	τ3A
Climate group (Manager, M)	Negotiate and adjust national mission (c1M)	N	N	Y	Y	N	N	Y	Y	N	N	Y	Y	Y/N	τ1M
Developed country(Sponsor,Sp)	Continue the carbon reduction cooperation (c1Sp)	—	—	—	—	Y	Y	Y	Y	N	N	N	N	Y/N/—	τ1Sp
	Terminate the carbon reduction and withdraw resource (c2Sp)	—	—	—	—	N	N	N	N	Y	Y	Y	Y	Y/N/—	τ2Sp

Note: Y, N and — mean “Selection”, “Rejection” and “No reply” respectively.

Suppose that each DM needs discussion time for making a decision, τij denotes DM j’s consideration time for initiating its ith choice, τij>0, as shown in the last column of Table 1. Γ is the maximal time constant of conflict as deadline.

DMs’ preference on the states of carbon reduction conflict

Among 13 states, different participants have different preference knowledge on potential solutions to determine the priorities of ranking. As rational players, participants show a more preferred attitude on the state with more benefit or less cost.

• (1)

  Developing country's preference ranking on states. The most satisfying result for developing country is the reduced request of transferred carbon emission is accepted by the developed country, {s5,s7}, in which s5 is more preferred, 5≻7, owing to no climate group's engagement. The second-best expectation is the waiting states {s3,s1} after raising the reduce request. The climate group's engagement can show its emphasis on the proposal, 3≻1. The third-best condition is developing country keep the promised carbon reduction amount {s8,s2,s4,s6}. Continuous cooperation with climate group's engagement is better than simply waiting, which is better than without climate group's concentration, 8≻2≻4≻6. The fourth-best consequence is the developing country loses the green support from the developed country, {s9,s10,s11,s12}, which can cause the carbon reduction projects sucked in the halfway. Among the states, the conditions developing country loses the green support even it keeps the promise or climate group negotiates are more harmed, 9≻11≻10≻12. The developing country's worst opinion is unilateral withdrawal from the alliance, which will not only be punished by the other participants but also loses the future opportunity because of the dirty record. Consequently, developing country's preference ranking is (5≻7)≻(3≻1)≻(8≻2≻6≻4)≻(9≻11≻10≻12)≻13.

• (2)

  Climate group's preference ranking on states. Climate group greatly expects the carbon reduction cooperation between developing country and developed country can be maintained, especially without negotiation. If they keep the original promises, there will be no adjustment to the mission adjustment. Consequently, climate group's most expected result is the cooperation can be continued, {s5,s6,s7,s8}, in which no climate group's engagement is the better result, 6≻5≻8≻7. Climate group's second-best result is the waiting states {s1,s2,s3,s4} after the reduction proposal is raised by the developing country. Because no engagement or no adjustment is better for climate group, 2≻1≻4≻3. The second-worst consequence for climate group is that the alliance breaks down after developing country changes opinions, {s9,s11,s13}. Because the final result is the same, s9,s11, and s13 are indifferent, (9∼11∼13). The worst situation is that the developed country unilaterally terminates the green support even developing country keeps the promised carbon reduction amount, {s10,s12}. This will greatly destroy the developing country's confidence in participating in a global carbon reduction alliance. Due to the same consequence, s10 is indifferent from s12, s10∼s12. To sum up, climate group's preference ranking is (6≻5≻8≻7)≻(2≻1≻4≻3)≻(9∼11∼13)≻(10∼12).

• (3)

  Developed country's preference ranking on states. Developed country has already transferred funds and green technology to the developing country. Its best result is that developing country can finish the mission without change, {s6,s8}, especially without climate group's intervention, 6≻8. Besides, if the developing country has to change opinion, its unilateral withdrawal will be the better result because developed country can receive liquidated damage and public reputation as intangible asset. The third-best condition is that developed country keep silence on the implement of original promise, {s4,s2}. Climate group's engagement can promote the project progress and effect, 4≻2. Next, once developing country raises the reduce proposal, if the climate group can negotiate and adjust the national task, it will be another good news for developed country. If not, direct rejection of the reduce proposal will show developed country's determination on original promise, 7≻9. Compared to s9 with a clear result, s1 and s3 are temporary states after the raising proposal, which is less preferred than s9. Due to the same result “No response”, s1 and s3 are indifferent to developed country, 1∼3. The second-worst consequence is the developed country has to accept the reduce proposal, {s5,s11}. If so, positive adoption should be better than passive rejection under the pressure from climate group, 5≻11. But if developing country doesn't change but developed country unilaterally terminates the green support, developed country will be globally blamed and definitely lose its reputation. That is the worst consequence for developed country, {s10,s12}. Due to the same negative result, s10∼s12. To sum up, developed country's preference ranking is 6≻8 ≻13 ≻4≻2≻7 ≻9≻(1∼3)≻5≻11≻(10∼12).

DMs’ preference ranking information is shown in Table 2.

Table 2.

State preference ranking information.

DM	State preference ranking (From most preferred to least preferred)
Developing country (Agent, A)	5≻7≻3≻1≻8≻2≻6≻4≻9≻11≻10≻12≻13
Climate group (Manager, M)	6≻5≻8≻7≻2≻1≻4≻3≻(9∼11∼13)≻(10∼12)
Developed country(Sponsor, Sp)	6≻8≻13≻4≻2≻7≻9≻(1∼3)≻5≻11≻(10∼12)

Timed Petri Net for conflict analysis and its generation rule

TPN for conflict analysis and its elements

Suppose that a realistic conflict has DM set N={1,2,⋯}, state set S={s1,s2,⋯} and preference set ∼>.ckj is DM j's kth strategic choose, τkj is the corresponding consideration time and the maximum time length of the process is Γ. The cumulative time consumption of h rounds of the considerations, φh, should not be more than Γ.

To describe conflict evolution concerning consideration time and deadline constraint, TPN for Conflict Analysis (TPNCA) can be employed as a graphic tool. TPNCA contains 4 elements as places, transitions, arcs and consideration time. Place O presents a system state. Let pi(sj) means the ith place in Petri Net presenting the jth state of conflict, Ph={pi(sj)} is the set of places in Petri Net through h rounds of decision-making. Transition ▆ indicates the operations that can change the system state. Suppose ti(ckj) refers to the ith transition in Petri Net presenting DM j implements its kth strategic choose, the corresponding operation time is τkj and Th={ti(ckj)} denotes the set of transitions in Petri Net during htimes of decision-making. Arc, →, connects place with transition and represents the flow direction of process.

Generation rule of TPNCA

Suppose that sα is the initial state and DM i, i∈N, is the next strategic initiator whose choice is cki. If all the participants are rational, a DM will select the strategic choice and moves to another state only If its preference will not be harmed. Due to the time constrain, φh≤Γ. The generation of TPNCA can follow the steps as below.

Step 1. The initial place is p1(sα), h=0, P0={p1(sα)}, T0=∅, φ0=0. DM i can initiate its strategic choice cki driving the conflict comes to adjacent state sβ. If DM i feel higher or indifferent preference, sβ∼≻isα(including sβ≻isα and sβ∼isα) and its consideration time doesn't exceed the deadline, φ0+τki≤Γ, DM i would like to implement strategic choice cki for achieving no worse effect. Consequently, t1(cki) and p2(sβ) are created and TPNCA gets expansion. If so, h=1,P1={p1(sα),p2(sβ)}, T1={t1(cki)}, φ1=τki. Otherwise, there is no DM's strategic choice leads to expansion, h=0, TPNCA will stay in the initial place P0={p1(sα)}.

Step 2. As the same DM cannot make two consecutive moves, DM j (j∈N,j≠i) is the following initiator. DM j may implement strategic choice ck′j and moves from state sβ to next state sγ. If sγ∼≻jsβ and φ2=φ1+τk′j≤Γ, DM j will be willing and have enough time to initiate ck′j and reach state sγ, h=2,P2={P1,p3(sγ)}, T2={T1,t2(ck′j)}. Otherwise, there is no expansion caused by DM's strategic choice, h=1, TPNCA is composed of P1 and T1.

Step 3. Let i=j, k=k′, α=γ and denote j,k′,β,γ=∅, h=h+1.

Step 4. Repeat Step 2 and Step3 until Ph+1=Ph and Th+1=Th. The TPNCA is no further expanded and output the generated graph including Ph+1,Th+1 and arcs.

The flowchart of TPNCA generation can be illustrated by Fig. 1.

Fig. 1.

Flowchart of TPNCA generation.

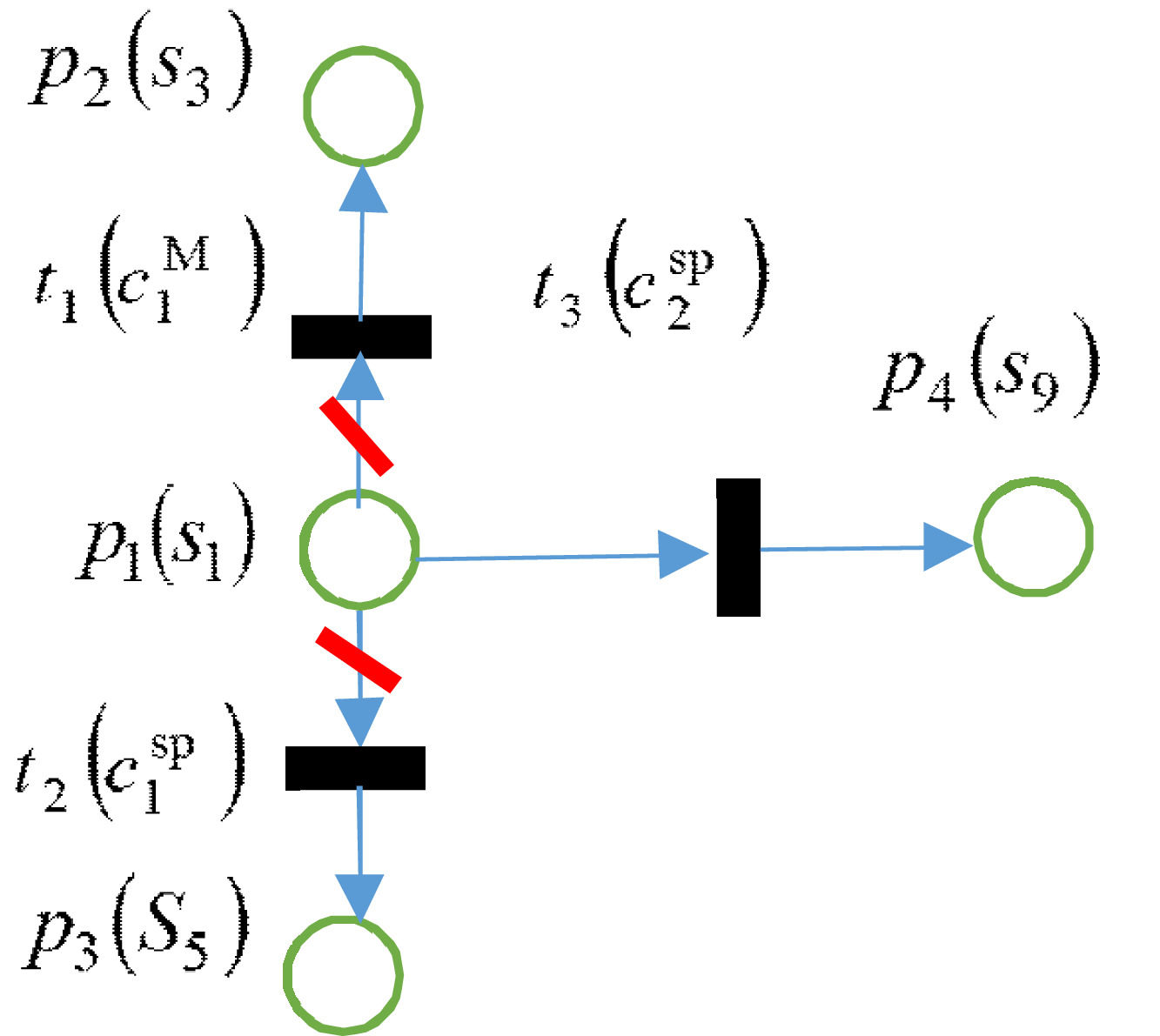
TPNCA for carbon reduction negotiation

According to the description in 2.1, the carbon reduction negotiation starts when a developing country raises the request for reducing the transferred carbon reduction amount. State 1, s1, will be the initial state and the developed country or climate group will be the next actor. The maximum time length is Γ. For TPNCA, P0={p1(s1)}, T0=∅, φ0=0.

Step 1. (1) If climate group(M) is the next actor, it will not implement its strategic choice c1M and drive the negotiation moving to state s3. Because its preference will be lower when it moves, s3≺Ms1.

(2) If developed country (Sp) is the next actor, there will be two choices, c1S and c2S, for consideration. As s9≻Sps1≻Sps5, the developed country prefers to directly reject the developing country's proposal and withdraws the investment, rather than accepting it. It is willing to implement c2S to push the negotiation to state s9.

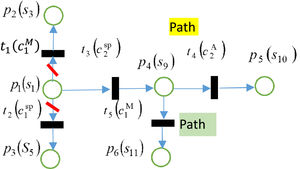
(3) Concerning the developed country's consideration time and overall time constraint, if φ1=τ2S≤Γ, TPNCA will be developed as shown in Fig. 2, in which the infeasible paths are cut marked by \, P1=P0+{p4(s9)}, T1={t3(c2S)}, φ1=τ2S, generation process comes to Step 2. Otherwise, the development of TPNCA is terminated, P0={p1(s1)}, T0=∅, φ0=0.

Fig. 2.

Generation in step 1.

Step 2. After the developed country (Sp) initiates the first choice c2S, developing country or climate group is the next actor, who determines different directions towards negotiation development, as illustrated by Fig. 3.

Fig. 3.

Generation in step 2.

Path 1. The developing country can take choice c2A or c3A to leads the negotiation to s10 or s13, respectively. As s10≻As9≻As13, the developing country will initiate c2A and move to s10, which means that the proposal is withdrawn. If φ2=φ1+τ2A≤Γ, TPNCA will be developed through Path 1 in Fig. 3, P2=P1+{p5(s10)}, T2=T1+{t4(c2A)}, φ2=φ1+τ2A.

Path 2. Climate group can choose, c1M and the conflict comes to s11. Because s11≻Ms9, the climate group will mediate in the dispute and try to give a potential solution. If φ2=φ1+τ1M≤Γ, TPNCA will be developed through Path 2 in Fig. 3, P2=P1+{p6(s11)}, T2=T1+{t5(c1M)}, φ2=φ1+τ1M.

If the time constraint is satisfied φ2≤Γ, generation process comes to the following step. Otherwise, the development of TPNCA is terminated,P1={p1(s1),p4(s9)}, T1={t3(c2S)}, φ1=τ2S.

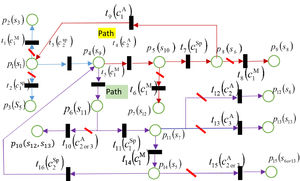
Step 3. If the time constraint is ignored, the above procedures should be repeated and final TPNCA can be obtained as Fig. 4. If the time constraint is considered, the TPNCA is a part of Fig. 4 when cumulative consideration time excesses negotiation deadline.

Fig. 4.

Complete TPNCA without time constraint.

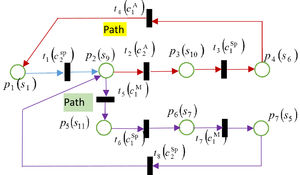
Step 4. Remove the cut branches and output the refined TPNCA with updated element numbers as shown in Fig. 5. In the carbon reduction negotiation, there are two paths, which reflect two kinds of arguments. Path 1 shows that the transferred carbon reduction promise should be kept or not between developed and developing countries. Path 2 reveals that whether climate group should positively negotiation and adjust carbon reduction assignment. DMs’ consideration time and overall negotiation constraint are essential variables for determining the equilibrium of negotiation.

Fig. 5.

Refined TPNCA without time constraint.

Fig. 5 indicates that the TPNCA includes several loops, showing different arguments among a developing country, developed country, and climate group. The specific discussions on different situations should consider the time constraints in different routes.

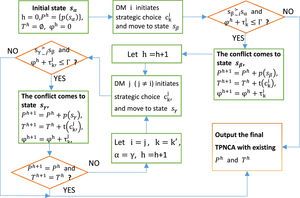
Dynamic equilibrium of TPNCA

Because TPNCA may contain several loops, various routes are displayed with terminated node, which is determined by the time constraint. Suppose that through h^(h^=1,2,⋯) rounds of decision-making, the cumulative consideration time φh^≤Γ and φh^+1>Γ. An evolutionary route is present with initial node and h^ generated nodes. Let Dhi(Sj) be the hth(0≤h≤h^) node in uniflow route presenting the jth state of conflict in which DM i is the next strategy initiator, Dend be the ending node of the route and Rk(Dh) be the DM k's preference of the hth node. According to the generation rule, TPNCA will be evolved and achieved at ending node Dend. For DMs, they should consider whether it is rational moving from halfway node to ending node for preference improvement.

Definition 1. Dynamic unilateral improvement (DUI) is defined as a state transfer for a DM who is willing to move from the current node to the ending node for improving its preference. If DM i is the next strategic initiator and is located at the hth node, its DUI will happen only if Ri(Dh)>Ri(Dend).

Definition 2. Dynamic equilibrium (DE) is defined as the stable situation in which all the DMs are reluctant to leave a node because of no DUI. For DM i, ∀i∈N, the hth node will be DE node only if Ri(Dh)≤Ri(Dend)

According to Definition 2, DE is a kind of Nash equilibrium for determining whether DM prefers to move downstream to the ending node. Different from short-term equilibrium definitions as Sequential Stability (Fraser & Hipel, 1979), General Metarationality and Symmetric Metarationality (Howard, 1971) DE is explored from long-term perspective and concerns time constraints related to ending point.

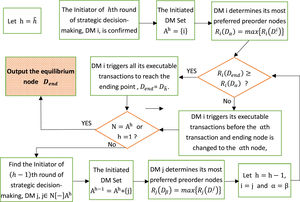
Suppose that DM is rational for pursuing its optimal benefit. According to the route of generated TPNCA, the DE can be explored following inverse derivation process, which is illustrated by Fig. 6.

Fig. 6.

Dynamic equilibrium algorithm.

Step 1. Let h be the sequence number of decision-making activities, h=1,2,⋯,h^. Initially, h=h^.

Step 2. Suppose that DM i is the last strategic initiator before the ending node, who triggers the hth transition (strategic choice) for pushing the conflict evolved from the (h−1)th node Dh−1i to the hth node Dh, Dend=Dh=Dh^. The initiated DM set Ah={i}.

Step 3. Among all the preorder nodes D·i of DM i's strategic choice transitions, the αth (0≤α≤h-1) node is employed to present DM i's strongest preference node, Ri(Dα)=max{Ri(D·i)}.

Step 4. If Ri(Dend)≥Ri(Dα), DM i will trigger all its transitions to guarantee the conflict reaching the ending node. If Ri(Dend)

Step 5. If there is no DM's preference without comparison, N[−]Ah=∅, or the conflict comes to initial node, h=1, output Dend as equilibrium node. If not, go to Step 6.

Step 6. Assume that DM j, j∈N[−]Ah, is the initiator of the (h−1)th, 2≤h≤h^, transition. Denote the βth (0≤β≤h-1) node as DM j's most preferred node adjacent before its executable transitions, Rj(Dβ)=max{Rj(D·j)}. Ah−1=Ah+{j}. Let h=h−1, i=j and α=β, turn back to Step 4.

Dynamic equilibrium of carbon reduction conflict with time constraint

As shown in Fig. 5, the Refined TPNCA includes three basic paths. Let Path0 present the process as p1(s1)→t1(c2Sp)→p2(s9), Path1 refer to the way as t2(c2A)→p3(s10)→t3(c1Sp)→p4(s6)→t4(c1A) and Path2 denote the line as t5(c1M)→p5(s11)→t6(c1Sp)→p6(s7)→t7(c1M)→p7(s5)→t8(c2Sp). The operation time of Path0, Path1 and Path2 are ρ0=τ2Sp, ρ1=τ2A+τ1Sp+τ1A and ρ2=τ1Sp+2τ1M+τ2Sp, respectively.

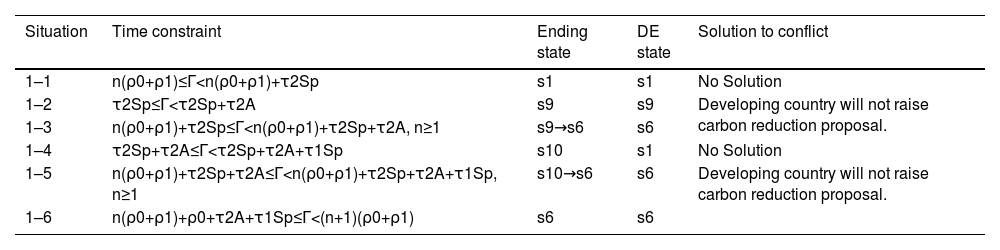
Dynamic equilibrium of carbon reduction negotiation between two DMs

DE analysis on the negotiation between developed country and developing country

In the route only covers the developed country and the developing country, let Route1 present Path0→Path1→Path0→Path1→⋯. Participants focus on the sea-sawing negotiation on whether the developing country raises the transferred carbon reduce amount and whether the developed country rejects the carbon reduce proposal. Because of different maximum time length Γ, the DE analysis of Route1 can be given as the following situations.

• (1)

  If 0≤Γ<τ2Sp=ρ0, after the developing country raises the carbon reduction proposal, there will be no enough time for the developed country to make the counterattack choice. p1(s1) is the ending node, but the conflict is not solved.

• (2)

  If τ2Sp≤Γ<τ2Sp+τ2A, the developed country will select c2Sp and there will be no time for the developing country taking next consideration. So p2(s9) is the ending node, which means that the developed country will directly reject the carbon reduction proposal. Because s1≻As9, the developing country will certainly know that raising carbon reduction proposals will not obtain a positive solution.

• (3)

  If τ2Sp+τ2A≤Γ<τ2Sp+τ2A+τ1Sp, the conflict will come to p3(s10). Because s1≻Sps10, the developed country will not implement c2Sp and deny moving to lower preferred state s10. Consequently, the conflict will remain at an initial state s1 without any progress.

• (4)

  If τ2Sp+τ2A+τ1Sp≤Γ<ρ0+ρ1, the conflict will be stopped at p4(s6). Compare the last DM's (developed country's) preferences between its initiative preorder nodes and ending node, s6≻Sps1≻Sps10. The developed country would prefer to move to state s6. Next, due to s6≻Sps9, the developing country will prefer s6 as well. Consequently, s6 is the dynamic stable state for all the DMs, which can be regarded as DE node. But s1≻As6, the developing country will be not rational to raise carbon reduction proposal, who should keep the original carbon reduction amount.

When Γ continuously increases, the conflict will be looping through Path0→Path 1→Path0→Path 1→⋯. Suppose that the cycle number of Path0→Path 1 is n,n=1,2,3,⋯. In the looping process, the developed country's preorder nodes are s1 and s10, s1≻Sps10. The developing country's preorder nodes cover s9 and s6, s6≻As9.

• (5)

  If n(ρ0+ρ1)≤Γ

• (6)

  If n(ρ0+ρ1)+τ2Sp≤Γ

• (7)

  If n(ρ0+ρ1)+τ2Sp+τ2A≤Γ

• (8)

  If n(ρ0+ρ1)+ρ0+τ2A+τ1Sp≤Γ<(n+1)(ρ0+ρ1), the conflict will come to p4(s6) and the following analysis is same as situation (4).

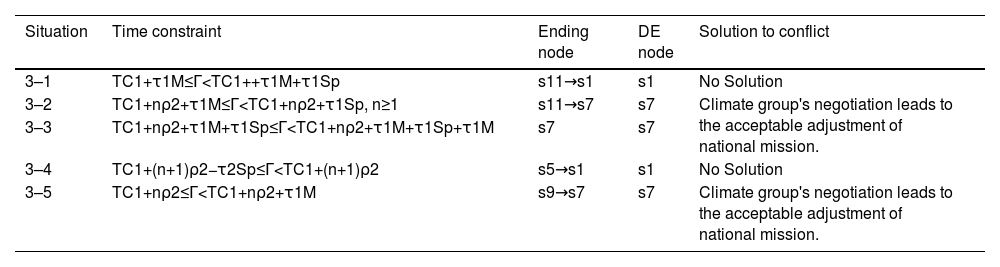
To sum up, the DEs with different time constraints can be found as shown in Table 3, in which n=0,1,2,3,⋯. According to Table 3, whatever the maximum time length Γ is, the conflict will come to DE state s1, s9 or s6. s1 is not beneficial for solving the conflict. s6 and s9 mean developing country should keep the original carbon reduction mission from the contract. If not, its benefit will decrease after developed country's counterattack.

Table 3.

DEs of negotiation in Route1.

Situation	Time constraint	Ending state	DE state	Solution to conflict
1–1	n(ρ0+ρ1)≤Γ	s1	s1	No Solution
1–2	τ2Sp≤Γ<τ2Sp+τ2A	s9	s9	Developing country will not raise carbon reduction proposal.
1–3	n(ρ0+ρ1)+τ2Sp≤Γ	s9→s6	s6
1–4	τ2Sp+τ2A≤Γ<τ2Sp+τ2A+τ1Sp	s10	s1	No Solution
1–5	n(ρ0+ρ1)+τ2Sp+τ2A≤Γ	s10→s6	s6	Developing country will not raise carbon reduction proposal.
1–6	n(ρ0+ρ1)+ρ0+τ2A+τ1Sp≤Γ<(n+1)(ρ0+ρ1)	s6	s6

DE analysis on the negotiation between developed country and climate group

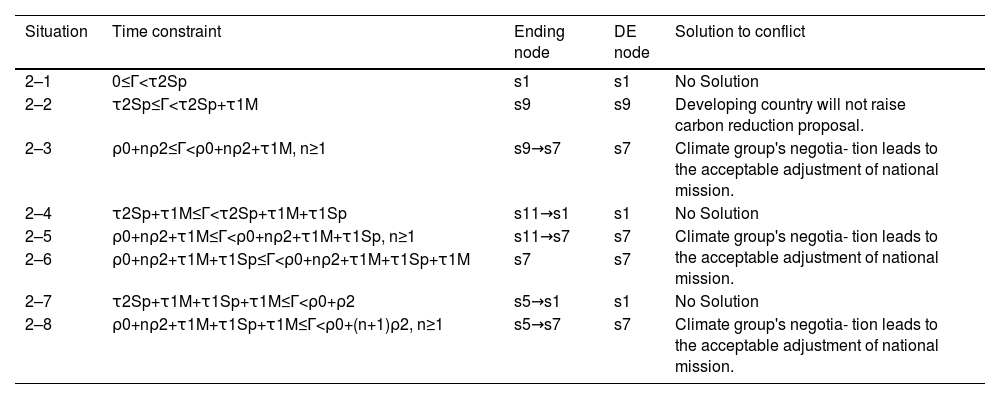
In the Route2 presentingPath0→Path2→Path2→⋯, the developed country decides whether to continue the carbon reduction cooperation as well as climate group determines whether negotiate or not. According to maximum time length Γ, the DE can be analyzed as below.

• (1)

  If 0≤Γ<τ2Sp=ρ0, similar to situation (1) in section 5.1.1, p1(s1) is the ending node, but the conflict is not solved.

• (2)

  If τ2Sp≤Γ<τ2Sp+τ1M, the conflict will come to p2(s9). Similar to situation (2) in section 5.1.1, s9 is the DE node. But the developing country will not raise the carbon reduction proposal because of definite preference decline.

• (3)

  If τ2Sp+τ1M≤Γ<τ2Sp+τ1M+τ1Sp, the negotiation will arrive at p5(s11). Although the climate group prefers moving to s11, s1≻Sps11makes the developed country will stick on s1, which is the DE node.

• (4)

  If τ2Sp+τ1M+τ1Sp≤Γ<τ2Sp+τ1M+τ1Sp+τ1M, the conflict will be terminated at, p6(s7) and the developed country will be the last initiated DM. Because s7≻Sps1≻Sps11, the developed country will be glad to make choices for inducing the conflict evolved to s7. Additionally, s7≻Ms9, the climate ground will prefer the ending node s7 as well, which is the DE node.

• (5)

  If τ2Sp+τ1M+τ1Sp+τ1M≤Γ<ρ0+ρ2, the conflict evolutionary will be stopped at p7(s5) and the last DM is climate group. Because s5≻Ms7≻Ms9, the climate group would like to move to s5. Moreover, s1≻Sps5≻Sps11, the developed country will prefer the initial state s1 as DE node.

• (6)

  When Γ≥ρ0+ρ2, the conflict will be looping through Path0→Path2→Path2→⋯. Suppose that the cycle number of Path 2 is n2,n2=1,2,3,⋯. In the looping process, developed country's preorder nodes are s1,s5 and s11, s1≻Sps5≻Sps11. The climate group's preorder nodes cover s7 and s9, s7≻Ms9.

• (7)

  If ρ0+n2ρ2≤Γ<ρ0+n2ρ2+τ1M, the conflict will come to p2(s9). Because s9≻Sps1≻Sps5≻Sps11, the developed country will prefer to move to s9. Next, due to s7≻Ms9, the climate group will change the ending node to p6(s7) by rejecting the trigger on t7(c2Sp). Additionally, the developed country's preference on s7 is higher than all its preorder nodes, s7≻Sps1≻Sps5≻Sps11. s7 is dynamic stable for all the DMs, which is DE node.

• (8)

  If ρ0+n2ρ2+τ1M≤Γ<ρ0+n2ρ2+τ1M+τ1Sp, the conflict will evolve to p5(s11) and the last DM will be the climate group. Due to s7≻Ms11≻Ms9, the climate group will select s7 as the ending node, rather than directing the conflict to s9. Next, s7 is developed country's most preferred node comparing to its preorder nodes, which is DE node.

• (9)

  If ρ0+n2ρ2+τ1M+τ1Sp≤Γ<ρ0+n2ρ2+τ1M+τ1Sp+τ1M, the conflict will be stopped at s7. s7 is the most preference node of both the developed country and the climate group by comparing to their preorder nodes, which is DE node.

• (10)

  If ρ0+n2ρ2+τ1M+τ1Sp+τ1M≤Γ<ρ0+(n2+1)ρ2, the conflict will be terminated at s5. For the climate group, s5 is the most satisfied node. But the developed country would like to be stopped at s7, because s7≻Sps1≻Sps5≻Sps11. So, the ending node is changed to s7. Similar to situation (8), s7 is the most preference node.

In summary, the DE result concerning time constraints is given in Table 4, n=0,1,2,3,⋯. According to Table 4, situations 2–1, 2–4, 2–7 and 2–2 reveal that there is no constructive solution to the conflict. The effective situations 2–3, 2–5, 2–6 and 2–8 reflect that the climate group should take the responsibility on negotiating and adjusting related national mission to solve the carbon reduce conflict. Comparing the time constraints of the above effective situations, one can find the minimum overall time length is Γmin=ρ0+τ1M+τ1Sp, which happens in situation 2–6, n2=0.

Table 4.

DE of negotiation inRoute2.

Situation	Time constraint	Ending node	DE node	Solution to conflict
2–1	0≤Γ<τ2Sp	s1	s1	No Solution
2–2	τ2Sp≤Γ<τ2Sp+τ1M	s9	s9	Developing country will not raise carbon reduction proposal.
2–3	ρ0+nρ2≤Γ<ρ0+nρ2+τ1M, n≥1	s9→s7	s7	Climate group's negotia- tion leads to the acceptable adjustment of national mission.
2–4	τ2Sp+τ1M≤Γ<τ2Sp+τ1M+τ1Sp	s11→s1	s1	No Solution
2–5	ρ0+nρ2+τ1M≤Γ<ρ0+nρ2+τ1M+τ1Sp, n≥1	s11→s7	s7	Climate group's negotia- tion leads to the acceptable adjustment of national mission.
2–6	ρ0+nρ2+τ1M+τ1Sp≤Γ<ρ0+nρ2+τ1M+τ1Sp+τ1M	s7	s7
2–7	τ2Sp+τ1M+τ1Sp+τ1M≤Γ<ρ0+ρ2	s5→s1	s1	No Solution
2–8	ρ0+nρ2+τ1M+τ1Sp+τ1M≤Γ<ρ0+(n+1)ρ2, n≥1	s5→s7	s7	Climate group's negotia- tion leads to the acceptable adjustment of national mission.

Dynamic equilibrium of carbon reduction negotiation among three DMs

According to Fig. 5, there are two looping routes to reflect the negotiations between developed country and developing country or climate group. If a route includes Path0,Path1 and Path2, there will be a comprehensive route, Route3=Route1·Route2. The negotiation will be made among three DMs, in which the developed country, the developing country and the climate group can make their strategic choices independently.

Suppose that there are n1,n1=1,2,⋯, loops (Path0→Path1) in Route1 and n2,n2=1,2,⋯, circles (Path2) in Route2. In Route3, developed country's preorder nodes present the state s1, s5, s10 and s11, s1≻Sps5≻Sps11≻Sps10; developing country's preorder nodes reveal the state s9 and s6, s6≻As9; climate group's preorder nodes display the state s7 and s9, s7≻Ms9. According to DMs' preorder nodes, the DMs’ most preferred states are sSp*=s1, sA*=s6 and sM*=s7.

DE analysis on the route only through Route1 and terminated in Path2

After n1 loops of Path0→Path1, the conflict first enters Path2 and the time consumption is TC1=n1(ρ0+ρ1)+ρ0.

• (1)

  If TC1+τ1M≤Γ

• (2)

  If TC1+τ1M+τ1Sp≤Γ

• (3)

  If TC1+τ1M+τ1Sp+τ1M≤Γ

• (4)

  Furthermore, suppose that there will be additional n2,n2=1,2,⋯, loops of Path2.

• (5)

  If TC1+n2ρ2≤Γ

• (6)

  If TC1+n2ρ2+τ1M≤Γ

• (7)

  If TC1+n2ρ2+τ1M+τ1Sp≤Γ

• (8)

  If TC1+(n2+1)ρ2−τ2Sp≤Γ

To sum up, DE concerning time constraints is shown in Table 5, in which n=0,1,2,3,⋯. Deferring to Table 5, situations 3–1 and 3–4 show that there is no constructive solution to the conflict. But situations 3–2, 3–3 and 3–5 reflect that the climate group can contribute to the effective solution for negotiation and adjustment. Among time constraints, the minimum overall time length is Γmin=TC1+τ1M+τ1Sp according to situated 3–3, in which n=0.

Table 5.

DE of negotiation route including n1Route1 and terminated inPath2.

Situation	Time constraint	Ending node	DE node	Solution to conflict
3–1	TC1+τ1M≤Γ	s11→s1	s1	No Solution
3–2	TC1+nρ2+τ1M≤Γ	s11→s7	s7	Climate group's negotiation leads to the acceptable adjustment of national mission.
3–3	TC1+nρ2+τ1M+τ1Sp≤Γ	s7	s7
3–4	TC1+(n+1)ρ2−τ2Sp≤Γ	s5→s1	s1	No Solution
3–5	TC1+nρ2≤Γ	s9→s7	s7	Climate group's negotiation leads to the acceptable adjustment of national mission.

DE analysis on the route only through Route2 and terminated node in Path1

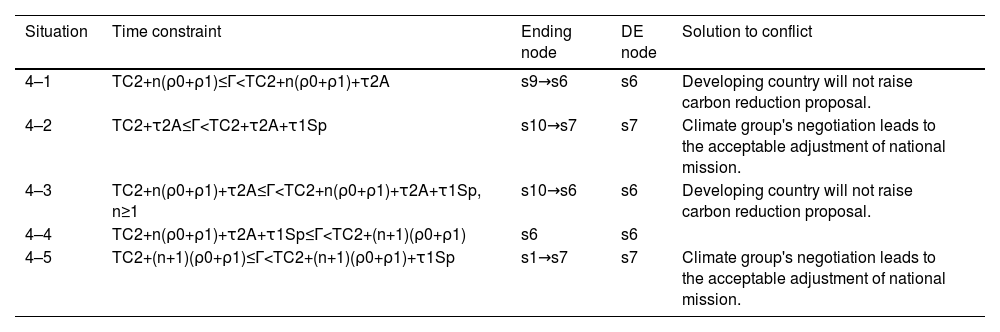
Through Path0 and n2 loops ofPath2, the conflict firstly enters Path1 the time consumption is TC2=ρ0+nρ2.

• (1)

  If TC2+τ2A≤Γ

• (2)

  If TC2+τ2A+τ1Sp≤Γ

• (3)

  If TC2+τ2A+τ1Sp+τ1A≤Γ

If the conflict has n1,n1=1,2,⋯,loops of Path0→Path1, the following steps will be circled in Route1.

• (4)

  If TC2+n1(ρ0+ρ1)≤Γ

• (5)

  If TC2+n1(ρ0+ρ1)+τ2A≤Γ

• (6)

  If TC2+n1(ρ0+ρ1)+τ2A+τ1Sp≤Γ

• (7)

  If TC2+(n1+1)(ρ0+ρ1)≤Γ

To sum up, DE concerning time constraints can be revealed in Table 6, in which n=0,1,2,3,⋯.

Table 6.

DE of negotiation route including n2Route2 and terminated in Path1.

Situation	Time constraint	Ending node	DE node	Solution to conflict
4–1	TC2+n(ρ0+ρ1)≤Γ	s9→s6	s6	Developing country will not raise carbon reduction proposal.
4–2	TC2+τ2A≤Γ	s10→s7	s7	Climate group's negotiation leads to the acceptable adjustment of national mission.
4–3	TC2+n(ρ0+ρ1)+τ2A≤Γ	s10→s6	s6	Developing country will not raise carbon reduction proposal.
4–4	TC2+n(ρ0+ρ1)+τ2A+τ1Sp≤Γ	s6	s6
4–5	TC2+(n+1)(ρ0+ρ1)≤Γ	s1→s7	s7	Climate group's negotiation leads to the acceptable adjustment of national mission.

According to Table 6, there are two DEs, s6 and s7, in the negotiation route. s6 reveals that the developing country should keep the original carbon reduction mission rather than raising reduction proposal, which is not positive to solve the carbon reduction dispute. s7 shows that climate group should perform as negotiation bridge and adjust national mission comprehensively concerning on participants’ contribution and realistic process. The minimum overall time length for achieving s7 is Γmin=TC2+τ2A according to situation 4–2.

DE analysis on the route through Route3 and terminated in Path1

After n1 loops of Path0→Path1 and n2 loops of Path2, the conflict is finally terminated at the node of Path1 and the time consumption is TC3=n1(ρ0+ρ1)ρ0+n2ρ2, n1,n2=1,2,⋯.

• (1)

  If TC3≤Γ

• (2)

  If TC3+τ2A≤Γ

• (3)

  If TC3+τ2A+τ1Sp≤Γ

• (4)

  If TC3+τ2A+τ1Sp+τ1A≤Γ

If the time continues to increase, the conflict will enter various routes. To sum up, DE concerning time constraints can be given in Table 7. According to Table 7, s6 and s7 are DEs in the route terminated in Path1, which includes n1 loops of Path0→Path1 and n2 loops of Path2. As the effective solution, s7 requires climate group's negotiation and adjustment, which needs Γmin=TC3+τ2A+τ1Sp+τ1A at least in situation 5–2.

Table 7.

DE of negotiation route including Route1 and Route2 once terminated in Path1.

Situation	Time constraint	Ending node	DE node	Solution to conflict
5–1	TC3≤Γ	s9→s6	s6	Developing country will not raise carbon reduction proposal.
5–2	TC3+τ2A≤Γ	s10→s6	s6
5–3	TC3+τ2A+τ1Sp≤Γ	s6	s6
5–4	TC3+τ2A+τ1Sp+τ1A≤Γ	s1→s7	s7	Climate group's negotiation leads to the acceptable adjustment of national mission.

DE analysis on the route through Route3 terminated in Path2

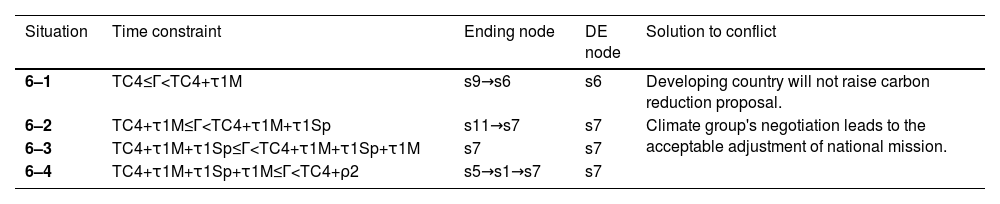
After n1 loops of Path0→Path1 and n2 loops of Path2, the conflict is finally terminated at the node of Path2 and the time consumption is TC4=n1(ρ0+ρ1)ρ0+n2ρ2, n1,n2=1,2,⋯.

• (1)

  If TC4≤Γ

• (2)

  If TC4+τ1M≤Γ

• (3)

  If TC4+τ1M+τ1Sp≤Γ

• (4)

  If TC4+τ1M+τ1Sp+τ1M≤Γ

If the time continues to increase, the conflict will enter previous routes. To sum up, DE concerning time constraints can be given in Table 8. There are two DEs, s6 and s7, in which s6 is the effective solution of carbon reduction conflict. The minimum consideration time Γmin=TC3 can ensure the conflict achieve s6.

Table 8.

DE of negotiation route including Route1 and Route2 once terminated in Path2.

Situation	Time constraint	Ending node	DE node	Solution to conflict
6–1	TC4≤Γ	s9→s6	s6	Developing country will not raise carbon reduction proposal.
6–2	TC4+τ1M≤Γ	s11→s7	s7	Climate group's negotiation leads to the acceptable adjustment of national mission.
6–3	TC4+τ1M+τ1Sp≤Γ	s7	s7
6–4	TC4+τ1M+τ1Sp+τ1M≤Γ	s5→s1→s7	s7

Results analysis

The implication of DE

According to Tables 3-8, the dynamic equilibrium result of carbon reduction conflict can be grouped into three classifications and not all the DEs can provide positive solutions.

• (1)

  DE s1 means the conflict will go to initiative state that developing country raises the carbon reduction proposal but there is no response from other DMs. DE s1 denotes the temporary stability, and the alliance will be easily collapsed once developing countries lose their patience.

• (2)

  DEs s6 and s9 show that developing country will withdraw the carbon reduction proposal because of other DMs’ counterattacks. Once the developing country raises the proposal, the developed country and the climate group will take a series of actions and lead the conflict come to the states which the developing country obtains less preferred state than initiative state. Thus, the developing country will get punishment after it raises the proposal. Although the developing country has to obey their previous promise, the extra carbon reduction press will not be relieved. If the developing country's tolerance excesses its threshold, it will face the huge dissolution risk of alliance (Chen et al., 2022).

• (3)

  DE s7 provides a positive solution for the carbon reduction conflict. The climate group should positively consider the developing country's actual contribution and reasonable appeal, rather than strictly insisting on previous contract or keep blind on the dispute. As a responsible institution, the climate group can actively negotiate with participants in the framework of mutual benefit and equality. Additionally, the climate group can dynamically evaluate and flexibly adjust national carbon reduction mission according to overall progress and individuals’ contributions, which can raise the alliance reputation and realize sustainable development.

The role of time constraint

As the critical determination factor, time constraint can lead the conflict evolved to expected state and determine the original ending node location, which is the anchor point for further discussion. In the carbon reduction conflict, there are several routes to effective DE s7 with time constraint, φh=∑j,kτkj≤Γ. Among the effective routes, the climate group should positively participate in the negotiation for ensuring the conflict can be originally terminated at p7(s5), such as situation 2–6, 3–3, 6–3 or undergo p7(s5). The climate group solving the dispute can require DMs’ consideration time in each step and determine the maximum time length for whole negotiation process. Due to there may be circles in the route, the minimum time consumption for reaching DE s7 is Γmin=ρ0+τ1M+τ1Sp, which happens in situation 2–6, n2=0.

The sequence of DMs’ strategic selections

The sequence of DMs’ strategic selections determines the evolutionary direction in different paths. Only the right evolutionary direction and suitable time constraint can lead to effective DE. The climate group response for dispute can predict the conflict evolutionary direction by setting DMs’ decision-making sequence. Additionally, if a conflict is trapped in a looping condition, determination on the following decision-making order may lead to a satisfied result. Taking situation 3–3 as example, one can find that the decision-making order, the climate group selects c1M first and developed country selects c1Sp second, can help the conflict jump out of n1 loop of Path0→Path1 and come to the expected DE s7.

Managerial implications

• (1)

  Implications to climate group

As the manager and coordinator of the global carbon reduction alliance, climate groups have the responsibility to deal with participants’ disputes and maintain sustainable cooperation. According to the meaning of DE s7, climate groups should positively coordinate the disagreement between participants by flexibly adjusting the national carbon reduction mission. Specifically, once carbon reduction conflict occurs, the climate group can employ participants’ preference knowledge to predict their forthcoming activities towards different states. Additionally, climate group can design the potential evolutionary routes of conflict by setting the participants’ decision-making sequence to achieve the mutual beneficial dynamic equilibrium. The case result shows various routes leading to the expected DE s7. Furthermore, climate groups can utilize negotiation time constraints to induce the conflict to be terminated at the expected state. The time constraints include participants’ consideration time raising the strategic opinions and maximum negotiation time length. According to the meaning of time constraint, the terminated state of conflict is determined by φh+τki≤Γ, which directly provides the maximum decision-making rounds, h. Thus, participants can compare whether it is rational to initiate the following strategic choices for moving to the ending nodes. Inappropriate time constraint could cause the negotiation to be terminated prematurely or ended lately, negatively influencing suitable DEs.

• (2)

  Implications to developing country

Developing countries receive the funds, green technology and the transferred carbon reduction mission from the developed countries. Upon facing the inability to fulfil the transferred emission reduction task, developing countries should proactively present their dilemma and reasonable demand to the alliance and seek assistance from climate groups. As shown by DE s7, climate groups will be willing to negotiate with the developed countries to avoid the bankruptcy of alliances. In using green technology, developing countries should positively implement tracking innovations to realize the follow-up development on green technology according to their own characteristics. If a developing country independently masters advanced green technology, its reliance on developed countries will be weakened and its discourse power will be enhanced in further negotiation. The balance between economic development and carbon emission work should be comprehensively considered, as it is beneficial for the sustainable development of the environment, society and governance.

• (3)

  Implications to developed country

As the designers of transferred carbon reduction task and providers of green resources, the developed countries should emphasize fairness and responsibility in the alliances. According to DE s7, developed countries should avoid the simple strategy of withdrawing or quitting alliances, possibly deterring cooperation. Instead, developed countries can continuously maintain their strong commitment to global carbon emission reduction and avoid policy swings because of some short-sighted behaviours. Developed countries need to collaborate with the climate groups to design carbon emission reduction tasks and launch more mutual beneficial CDM projects, which can establish a more equitable and balanced international framework for carbon emission reduction cooperation.

Conclusions and future works

After the COVID-19 pandemic, many developing countries seized the opportunity to expand their economies. Although the recovery of consumption and transportation greatly contributes to economic development, the extra carbon emissions bring heavy pressure on the completion of the carbon reduction mission. As an important component of carbon reduction alliances, some developing countries have received green funds and technology, transferring carbon reduction amounts from developed countries. However, extra carbon emissions may force developing countries to violate treaties by raising the propose reduction of the transferred carbon reduction amount, causing boycotts and disagreements with developed countries. As the managers of carbon reduction alliances, climate groups can act negotiators by flexibly adjusting the original mission. Additionally, various combinations of DMs’ interactive opinions lead to different ends of disputes influenced by time constraints. Specifically, DMs need to consider strategy and counterattack behaviour according to individuals’ preferences, with a requirement of maximum time length to resolve issues. If the dispute is not effectively solved, the developing country may quit the carbon reduction alliance and cause herd behaviour, breaking the carbon reduction alliance and ruining worldwide carbon reduction agreements. Consequently, driven by DMs' preferences and consideration knowledge, it is vital to describe and display the generation of carbon reduction conflicts from the state quo to the terminated condition. Comprehensively considering the time constraints, the dynamic equilibrium of carbon reduction conflict should be explored, which can be regarded as a potential solution for future development.

To dynamically reflect conflict evolution with time constraints, Timed Petri Net is employed as a graphic tool to describe the generation process of conflict from the state quo to the ending node. The ending node is determined by time constraints, indicating that the sum of existing consideration time should not exceed the total time limit. Carbon reduction disputes among developing countries, developed countries, and climate groups are conducted to show the conflict evolution, driven by DMs’ strategic opinions, state preferences, and rational consideration knowledge. From a long-term perspective, dynamic unilateral improvement is proposed to judge whether a DM will be willing to initiate its following strategic selections to the ending node or determine to stop conflict evolution. If a DM finds that a strategic selection causes the evolution to develop from its most preferred pre-order node to the ending node with lower preference, it will deny initiating the strategic selection and the ending node is changed to the DM's most preferred pre-order node. Concerning ending node shift, dynamic equilibrium can be obtained if an ending state is not one of dynamic unilateral improvement for all the DMs, which can provide potential solutions to the conflict. According to the dynamic equilibrium of carbon reduction conflict, only s7 is a positive solution, requiring a climate group to actually negotiate and flexibly adjust national missions. To achieve s7, DMs’ strategic selection sequence and overall time length should be combined, which can help the conflict evolution trapped in an endless loop. The long-term dynamic equilibrium proposed in this study can provide novel insights to judge conflict stability in a predicted and systematic process.

As critical elements, DM's preferences and consideration time directly influence the generation and dynamic equilibrium of a conflict. Their uncertainty and feasibility analysis should be further investigated. Furthermore, the coalition among DMs in timed Petri net and its impact on dynamic equilibria also deserve discussion.

CRediT authorship contribution statement

Yuan Liu: Methodology, Writing – original draft, Conceptualization. Guoyi Zhang: Resources, Writing – original draft. Yufeng Chen: Conceptualization, Investigation, Writing – review & editing. Jingjing Hao: Investigation, Resources, Visualization.

Acknowledgement

The relevant researches done in this paper are supported by National Natural Science Foundation of China (No. 72071181, No.72174180), Natural Science Foundation of Zhejiang Province (No. LY21G020004), Major Projects of the Key Research Base of Humanities Under the Ministry of Education (No.22JJD790080).