Introducción
Este artículo presenta al lector un marco conceptual para situar las listas de comprobación que le permita integrar los aspectos comunes de todas ellas y diferenciar los específicos para cada tipo de diseño. Para ello, se pretende enlazar los objetivos clínicos y sanitarios que originan la necesidad de una investigación científica con los procedimientos metodológicos que la estadística pone a su disposición.
En el siguiente apartado se expone el propósito de la inferencia y cómo ésta se distingue de los procesos de decisión; en el tercer punto, se distingue entre confirmación de una hipótesis previa y exploración de datos en busca de nuevas ideas; a continuación, se presentan los objetivos habituales de la investigación médica aplicada; en el quinto apartado se clasifican los diseños según la asignación de la causa, la perspectiva temporal y el plan de muestreo, mientras que en el sexto apartado se muestran las herramientas que la estadística ha desarrollado para alcanzar estos objetivos. Finalmente se presentan unas consideraciones prácticas.
Inferencia y decisión
El método científico pretende proponer modelos que representen, a partir de la observación, el entorno que nos rodea. Esta capacidad de ser observado es fundamental, ya que para poder ser considerado científico, un modelo debe ser «falible»1, en el sentido de ser susceptible de entrar en conflicto con datos observables futuros. Este contraste empírico implica que estos modelos son constantemente abandonados en beneficio de otros que los mejoran y matizan. En consecuencia, no se pretende que sean definitivamente ciertos, pero sí que sean útiles y ofrezcan claves para interpretar, adaptar y disfrutar de nuestro entorno. Así, aunque Einstein matizó las leyes de Newton, éstas siguen siendo útiles en muchas situaciones.
El método empírico acepta modestamente que el salto, desde los datos parciales disponibles a los modelos inaccesibles, requiere asumir un riesgo y un margen de error. De esta forma, la información aportada por los datos de una muestra será tanto más válida cuanto menor sea la magnitud de estos errores. En este contexto, la estadística proporciona herramientas para cuantificar y minimizar dicha magnitud. Por ejemplo, con el error típico (standard error) de un estimador se puede cuantificar la magnitud del error aleatorio originado por el proceso de muestreo.
Conviene distinguir, desde el inicio, entre dos grandes objetivos. Por un lado, la inferencia persigue el proceso de adquisición de conocimiento, valorando las pruebas científicas («evidencia») a favor o en contra de los modelos establecidos, para lo que puede utilizar los intervalos de confianza o el valor de p (p-value). Por otro lado, el acto médico, la gestión de recursos2 o el permiso de comercializar un nuevo fármaco implican un proceso de decisión en un marco de incertidumbre, lo que requiere marcar límites para los riesgos asociados a las dos decisiones erróneas (errores de tipo I y tipo II)3. Aunque el proceso de decisión incluye la inferencia y el uso del conocimiento previo disponible, también debe abarcar las consecuencias (utilidad, coste, etc.) de las opciones alternativas en consideración. Así, la decisión de emprender una campaña preventiva sobre los efectos del tabaco depende no sólo del conocimiento disponible, sino también de las consecuencias y los riesgos de las posibles alternativas. Parafraseando a Greenland4, al ver humo en un bosque, es mejor decisión enviar el cuerpo de bomberos para apagar un posible fuego no confirmado que a un grupo de científicos para confirmar que la causa del humo es fuego. O más crudamente, antes de usar el paracaídas en un salto desde mil metros de altura, nadie preguntaría por el ensayo aleatorizado y enmascarado que aporte las pruebas científicas sobre el efecto beneficioso del paracaídas5.
Gran parte de la dificultad en la interpretación del «valor de p» reside en la confusión de estos dos aspectos. Como exponen Hubbard y Bayarri, «la confusión entre las medidas de evidencia y de error está tan profundamente arraigada que ni siquiera es vista como un problema por una gran mayoría de los investigadores. En particular, la mala interpretación de los valores de p redunda en una sobrestimación de la evidencia en contra de la hipótesis nula, que resulta en el elevado número de «efectos estadísticamente significativos» que más tarde se constatan como negligibles»6. Los intervalos de confianza son un método de inferencia que no se confunde con los procedimientos de decisión, por lo que el comité internacional de editores de revistas médicas sugirió su obligatoriedad7 y la declaración CONSORT lo prioriza sobre los valores de p8.
Exploración y confirmación
La inferencia estadística puede desempeñar dos papeles bien diferenciados. En el primero, el investigador explora la muestra con la intención de obtener nuevas ideas que le ayuden a interpretar el fenómeno en estudio. En el segundo, el investigador desea confirmar una idea previamente concebida. Al finalizar un estudio exploratorio, el investigador afirmará, por ejemplo, que «... estos resultados sugieren...»; mientras que al final de un estudio confirmatorio, el investigador podrá afirmar «... se ha establecido, por tanto, que...». Así, un científico que se acerque a los datos desde una perspectiva exploratoria se preguntará «¿cuál es el modelo, más simple, que mejor se ajusta a los datos estudiados?». En cambio, un investigador que desee confirmar sus ideas previas diría «¿los datos estudiados permiten confirmar o rechazar la hipótesis previa?». No todas las especificaciones contenidas en el modelo tendrán la misma importancia. El nombre de hipótesis suele reservarse para las ideas más relevantes y el de premisas para las ideas acompañantes que son necesarias para poder contrastar las hipótesis. De esta forma, un investigador que desee establecer la hipótesis de que un nuevo tratamiento añade un cierto efecto a un tratamiento previo se verá obligado a asumir alguna premisa sobre el comportamiento de dicho efecto en toda la población de pacientes. Por ejemplo, en el caso de un fármaco cuya ficha técnica no establece diferente posología para diversos tipos de pacientes, se está asumiendo implícitamente la premisa de que este efecto es el mismo en todos ellos.
Contrariamente a los estudios exploratorios, un estudio confirmatorio debe establecer previamente la racionalidad y las pruebas empíricas que sustentan las premisas necesarias, para así poder concentrarse en el estudio de la hipótesis planteada. En resumen, a diferencia de los estudios exploratorios en los que «todo vale», los estudios confirmatorios deben concentrarse en el objetivo de contrastar su hipótesis y seguir fielmente el protocolo del estudio que establece, además de la hipótesis, el método de análisis y las premisas que acompañan al modelo. Por tanto, un investigador que desee afirmar «... luego se ha demostrado que...» necesita seguir fielmente el protocolo de investigación. En este sentido, las directrices para el registro de fármacos3 requieren un protocolo detallado antes de iniciar la recogida de datos, y el plan de análisis estadístico, antes de desvelar el código de tratamiento. Por su parte, el grupo de Vancouver requiere, para su posterior publicación, el registro previo de los ensayos clínicos2, no sólo para poder detectar aquellos que se inician pero no se publican, sino también para poder comprobar que los resultados presentados siguen fielmente el plan de análisis previamente especificado, al menos en lo que corresponde a la variable principal en la que se basará la conclusión clave del estudio.
Objetivos habituales de la investigación médica: diagnóstico, pronóstico y tratamiento
Tanto en el diagnóstico como en el pronóstico médico subyace el estudio de la relación entre variables, ya que en ambos se pretende predecir una variable a partir de otra9. Sin embargo, estos dos objetivos se diferencian en que en el primero las variables en estudio pueden ser simultáneas, mientras que en el segundo, el valor del pronóstico será mayor cuanto con más antelación pueda establecerse, y por tanto la predicción se realiza sobre variables futuras. En ambos casos, la calidad de la predicción será mejor cuanto menores sean los errores en la clasificación de los individuos. Para valorar dicha calidad, en el diagnóstico se recurre a los valores de las llamadas probabilidades diagnósticas (sensibilidad, especificidad y valores predictivos), mientras que en el pronóstico, la pregunta de interés es cuánto se reduce la incertidumbre mediante el empleo de la ecuación predictiva. Por ejemplo, si se desea predecir la evolución de un cierto tipo de pacientes, el coeficiente de determinación permite cuantificar, respecto al conjunto de todos los casos, en qué porcentaje se reduce la variabilidad de la evolución gracias a la clasificación, en un mismo grupo, de los casos con características comunes. Nótese, por tanto, que en el diagnóstico, así como en el pronóstico, es más relevante informar sobre la magnitud de la reducción del error de clasificación acompañada del intervalo de confianza que dar el valor de p sobre la relación entre las variables consideradas9.
Además de prever o anticipar acontecimientos futuros, el ejercicio de la medicina implica la intervención mediante el tratamiento o la prevención para cambiar la evolución de los pacientes. Así, establecer una relación de causa y efecto permitirá, mediante intervenciones en la variable causa, modificar el valor futuro de la variable efecto. El establecimiento de la relación causal suele comportar dos pasos sucesivos. En el primero, dado un determinado efecto (una enfermedad, por ejemplo), se desea explorar sus posibles determinantes, sus causas. En el segundo paso, identificada una causa susceptible de ser intervenida, se desea confirmar y cuantificar el efecto que origina su modificación. Recordemos el ejemplo de las epidemias de asma en Barcelona10,11. La respuesta a la pregunta «¿cuáles son las causas del asma?» fue la combinación de descarga de soja en el puerto en un silo defectuoso con ciertas condiciones atmosféricas. El estudio de aquello que era susceptible de intervención y aquello que no lo era llevó a la segunda pregunta: «¿conseguiremos terminar los brotes de agudización del asma reparando el filtro protector del silo durante la descarga de soja?». La pregunta exploratoria del primer paso es retrospectiva: «¿cuáles son las causas de este efecto?». En cambio, la pregunta confirmatoria del segundo paso es prospectiva: «¿qué efecto tiene en la respuesta esta intervención sobre la causa?».
Hay que resaltar desde el primer momento que intervenir significa cambiar algo, lo que implica un mínimo de dos valores para la variable causa. Puede ser el cambio de una opción terapéutica A por otra B; cambiar el protocolo estándar añadiéndole un nuevo tratamiento C, o bien modificar los hábitos higiénico-dietéticos eliminando (o añadiendo) alguno. El procedimiento habitual que se plantea modificar será el punto de referencia, el control, con el que se desea comparar la nueva propuesta en estudio. Usualmente, la misma pregunta que formula la intervención lleva implícita la existencia del procedimiento (o procedimientos) de referencia que se desea modificar. Hay que insistir12 en el término acción como intervención, puesto que atributos como la edad o el sexo pueden ser útiles para hacer un pronóstico o una predicción (por ejemplo, cabe esperar que una mujer viva alrededor de 5 años más que un varón) pero no son modificables y, por tanto, no tiene sentido actuar intervenir sobre ellos («cambie Vd. este hábito de ser varón, hágase mujer y vivirá 5 años más»). En consecuencia, desde un punto de vista práctico, de intervención, es irrelevante preguntarse si el sexo o la edad tienen un efecto causal en, por ejemplo, la supervivencia.
Tipos de variables en un estudio médico
En un estudio médico, conviene distinguir los tres papeles que una variable puede desempeñar. En primer lugar, se puede representar por Y a la respuesta cuya evolución se desea predecir (pronóstico) o modificar (tratamiento, prevención). Ejemplos típicos de respuesta Y serían ciertos síntomas o signos clínicos, la cantidad13 y la calidad de vida14, o el tiempo libre de complicaciones. En segundo lugar, se puede simbolizar con X a la variable en la que se pretende intervenir para modificar la respuesta. El consejo dietético o la prescripción de un fármaco en estudio serían ejemplos característicos. En tercer lugar, se puede notar por Z a las condiciones o atributos con los que las unidades se presentan en el estudio y que podrían predeterminar la respuesta Y. Típicos ejemplos de Z son el sexo, la edad o los hábitos higiénico-dietéticos previos.
Puesto que en un estudio de intervención estos atributos Z no son modificables, se deseará cuantificar los cambios en la respuesta Y (tamaño del efecto o effect size) que siguen a una intervención en la causa X, independientemente del valor de los atributos Z. Si en cambio, el objetivo es predecir, se deseará conocer cómo combinar los valores de estos atributos Z para hacer la «mejor» predicción de la respuesta Y. Es decir, aquella que comporte una mayor reducción en el error de predicción. Por ejemplo, estudios como el de Framingham, REGICOR o SCORE proponen modelos15-17 para predecir el riesgo en un paciente determinado. Es muy atractivo interpretar estos estudios observacionales (de predicción) como si fueran experimentales (de intervención), y poder decir, por ejemplo, que una disminución en el valor de una variable predictiva (pongamos, la presión diastólica) irá seguida de una mejora en la evolución. Debe quedar claro que esta interpretación es meramente tentativa y, por consiguiente, pertenece al terreno de las hipótesis a ser confirmadas en estudios posteriores. Entre los retos que esta extrapolación plantea, destaca que el modelado estadístico habitual asume que puede modificarse la causa X en estudio, manteniendo a nivel fijo las variables Z introducidas en el modelo: ¿se puede disminuir la presión diastólica dejando fija la presión sistólica? o ¿se puede modificar la ingesta de alcohol dejando fija la dieta? Dado que estas condiciones del modelado no son realistas, antes de interpretar un estudio observacional de predicción en términos causales, conviene considerar en el análisis y en la discusión toda la incertidumbre derivada del origen no experimental de los datos, lo que puede hacerse, por ejemplo, con la ayuda de los métodos estadísticos bayesianos18.
Clasificación de los diseños
Según asignación de la causa: experimentación y observación
En los estudios experimentales, el investigador asigna el valor de la intervención a los voluntarios, mientras que en los estudios observacionales, las unidades se presentan con valor en las variables de estudio. Por ejemplo, si se quiere estudiar el efecto de la monitorización de los pacientes hipertensos en el control de su presión, tendremos un estudio de carácter observacional cuando los médicos y los pacientes decidan el número y el momento de las visitas de forma espontánea, mientras que consideraremos que se trata de un estudio experimental si el investigador asigna un número de visitas a cada voluntario. La clave para diferenciar ambos estudios reside, precisamente, en esta asignación.
Las listas de comprobación distinguen claramente entre ambos tipos de diseño. Un estudio experimental deberá regirse por las declaraciones CONSORT19,20 o CONSORT CLUSTER21 si es aleatorizado, o por la TREND22 si la asignación no se decide al azar. En cambio, un estudio observacional deberá regirse por la lista STROBE23.
Nótese que, por respeto al principio de no maleficencia, sólo las intervenciones que pretendan mejorar el estado de salud son, en principio, asignables a las personas. Por ejemplo, no se puede asignar un adolescente al grupo «fumador de tabaco desde los 15 hasta los 50 años». Esto explica la predilección de la epidemiología por los métodos observacionales. En cambio, la pregunta habitual de la farmacología «¿se mejora la evolución con este nuevo tratamiento?» permite la asignación del tratamiento y, por tanto, el diseño experimental. Para recurrir a la asignación, la epidemiología debe revertir primero los efectos negativos en positivos mediante su privación: «¿qué pasará si elimino la exposición a este supuesto tóxico?».
Es bien conocido que asignar la intervención a las unidades abre la posibilidad de utilizar todas las herramientas del diseño de experimentos para minimizar los errores. Pero también es cierto que permite evaluar directamente qué es lo que pasará cuando se asigne la causa en estudio, sin necesidad de asumir que las unidades seguirán fielmente el consejo médico. En el ejemplo anterior de la monitorización observacional de los pacientes hipertensos, la primera asunción que debe hacerse para poder aplicar sus resultados a la intervención futura es que los pacientes se visitarán con la frecuencia acordada con el médico. En cambio, el estudio experimental también permite cuantificar hasta qué punto las unidades siguen las recomendaciones establecidas24.
Según la perspectiva temporal
En un estudio para estimar la capacidad diagnóstica de un indicador, los datos sobre éste y sobre la referencia, o gold standard, pueden recogerse simultáneamente, pero los estudios de predicción y los de intervención requieren un intervalo de tiempo. Si la causa y el efecto se observan en el mismo momento, se habla de estudios transversales, mientras que si la causa acontece previamente al efecto observado, serán longitudinales. Nótese que, por ejemplo, si cierto componente plasmático debe predecir, o bien tener efecto en la enfermedad cardiovascular, el componente debe ser previo en el tiempo a la aparición de sus efectos. Si la determinación analítica se realizara simultáneamente (o incluso con posterioridad) a la aparición de la enfermedad, el valor pronóstico será nulo y la relación de causa-efecto, dudosa, ya que siempre quedará la duda de cuál variable es la causa y cuál la consecuencia.
Los estudios longitudinales en que se recogen las variables causa y efecto en el momento de su aparición se denominan prospectivos, mientras que, si una vez observado el efecto, se investiga en el pasado la causa, se habla de estudios retrospectivos. Como ya se ha comentado en el punto anterior, esta clasificación se suele corresponder con las preguntas prospectivas y retrospectivas.
Además del tipo de pregunta y del orden de recogida de los datos, los términos prospectivo y retrospectivo suelen utilizarse también para indicar si la hipótesis en estudio era previa o posterior a la existencia de los datos. Para evitar esta confusión, Feinstein25 sugiere denominar prolectivos a los estudios en que los datos son posteriores a las hipótesis y retrolectivos a aquellos cuyo contraste se basa en datos pasados. Así, por ejemplo, un estudio sobre una pregunta prospectiva, «¿cuál es el efecto de una intervención?», podría emplear información recogida de forma también prospectiva (primero la causa y luego el efecto) en una base informatizada de datos, pero ser retrolectivo si el objetivo se formula con posterioridad al acontecimiento de los datos. Mientras que el ensayo clínico es prospectivo y también prolectivo, el metaanálisis será retrolectivo si la hipótesis no es previa a la existencia de los datos26 La imposibilidad de demostrar que los datos retrolectivos no han generado la hipótesis dificulta considerar este tipo de estudios como confirmatorios.
Según el plan de muestreo
En los estudios observacionales existen tres principales situaciones según la estrategia de muestreo27. En la primera, se fija el número total de individuos a estudiar, y se observan todas las variables. De esta forma, una muestra aleatoria tenderá a reproducir la distribución de estas variables en la población, lo que permitiría estimar, por ejemplo, qué proporción de casos están expuestos a la causa en estudio y qué proporción presentan o no el efecto. Aplicar esta estrategia de muestreo a los estudios longitudinales prospectivos conduce al denominado estudio de cohortes, en el que se observa una población de unidades (cohorte) durante un tiempo de seguimiento. La desventaja de este muestreo es que no es eficiente, ya que si alguna de las dos variables en estudio tiene muy pocos casos en una categoría, los grupos quedarán descompensados. Por ejemplo, comparar un caso de exposición a un tóxico con 199 no expuestos tendrá un error estándar de estimación mayor que el resultante de la comparación de dos grupos de 100 casos.
La segunda estrategia de muestreo consiste en fijar de antemano el número de casos que presentarán cada valor de la causa en estudio. Es la estrategia habitual en los diseños experimentales, en los que se decide de antemano el número de unidades expuestas a cada alternativa en comparación, lo que permite obtener la máxima potencia y eficiencia estadística mediante la asignación del mismo número de unidades a los dos tratamientos. Como contrapartida, no tendrá sentido afirmar que, en la población origen de las muestras, el porcentaje de casos tratados con cada opción es del 50%. También se puede aplicar esta estrategia para aumentar la eficiencia de los diseños prospectivos observacionales. Si por ejemplo, sólo una pequeña proporción de unidades está expuesta a la causa en estudio, se puede recurrir a seleccionar todas estas unidades (o a dar una elevada probabilidad a su selección) y, en cambio, seleccionar una pequeña proporción de unidades no expuestas a la causa, de forma que el tamaño resultante de los grupos en comparación sea más similar.
La tercera estrategia es similar a la anterior pero aplicada a estudios retrospectivos: en lugar de fijar el número de casos en función de la causa (expuestos y no expuestos), se fija según hayan presentado o no el efecto en estudio (casos y controles). Ahora, es la variable respuesta la que está fija por diseño y, por tanto, no tiene sentido afirmar que la proporción de enfermos estudiados informa sobre la proporción de enfermos en la población. Es bien conocida la consecuencia de esta limitación: no se puede estimar el riesgo atribuible ni el riesgo relativo y debe recurrirse a la odds ratio. Además, los estudios de casos y controles tienen otras limitaciones bien conocidas, como son el reto de encontrar controles que sean comparables con los casos (es decir, que coincidan con ellos en las variables Z) y la dificultad para obtener medidas de la exposición que sean fiables (repetibles, con poco error aleatorio) y libres de sesgo (independientes de la respuesta, es decir, sin error sistemático).
Control del error en el diseño
El método estadístico ayuda a encontrar la mejor información en la que basar la inferencia, entendiendo como mejor aquella que está más libre de errores, tanto sistemáticos como aleatorios. Las herramientas estadísticas pretenden anular los primeros y minimizar los segundos. Se trata de obtener muestras sin errores sistemáticos y que cuantifiquen al error aleatorio y lo hagan tan pequeño como sea posible.
Control del error sistemático
Cuanto más amplio sea el objetivo de la inferencia, mayor es el riesgo de errores. Así, se distingue entre validez interna y validez externa24, la primera hace referencia al grado en que el estudio permite satisfacer los objetivos del investigador. La segunda, al nivel en que estos datos son útiles para otros investigadores cuyas circunstancias puedan diferir de las estudiadas. Cuando el estudio implica la comparación entre grupos de una intervención X, existirá validez interna si los grupos difieren en el valor de esta intervención, pero son iguales en todos los atributos o condiciones Z. Además, existirá validez externa si los atributos Z de los casos estudiados no difieren de los de la nueva población a la que se desea hacer inferencia.
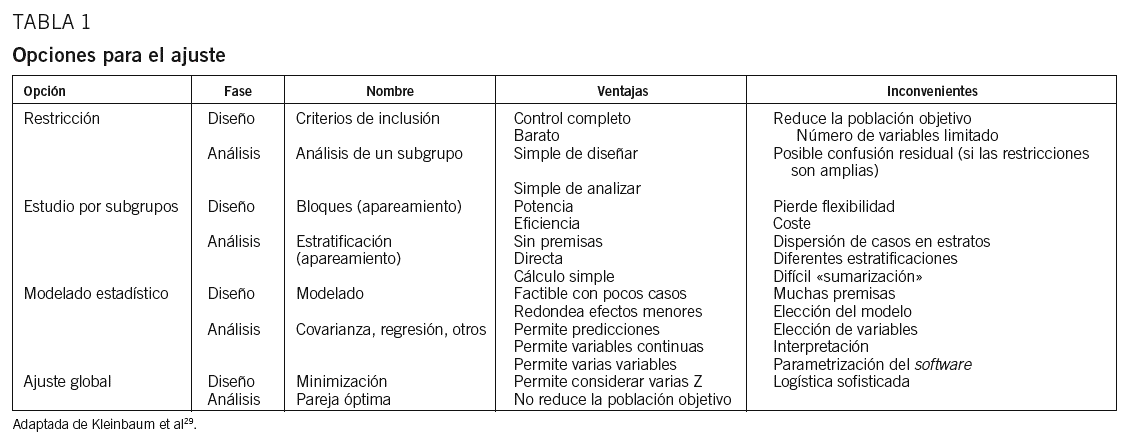
Ya se ha comentado en publicaciones previas28 cómo controlar estos atributos o condiciones Z. Recordemos brevemente que si estos atributos son observables, el método estadístico ofrece cuatro grandes bloques de procedimientos29 (tabla 1): la restricción, los subgrupos, el modelado y el ajuste global. La restricción se aplica, básicamente, mediante los criterios de inclusión y exclusión de pacientes, y representa el método más sencillo para controlar las variables Z, aunque limita la aplicabilidad de los resultados obtenidos a una población más amplia. Formar subgrupos homogéneos respecto a las condiciones Z también permite controlar el error sistemático, así como analizar si el efecto estimado es de magnitud similar en los diferentes subgrupos. Con el método de modelado, generalmente se utilizan las técnicas de regresión para el ajuste de los atributos. En este caso, cuanto más específico sea el protocolo del estudio en describir el método de ajuste que se usará, mayor será su carácter confirmatorio. Finalmente, el ajuste global pretende equilibrar de forma conjunta los efectos de las condiciones Z, de forma que éstos se compensen y el error sistemático asociado sea mínimo, por lo que muchas veces también se denomina método de minimización.
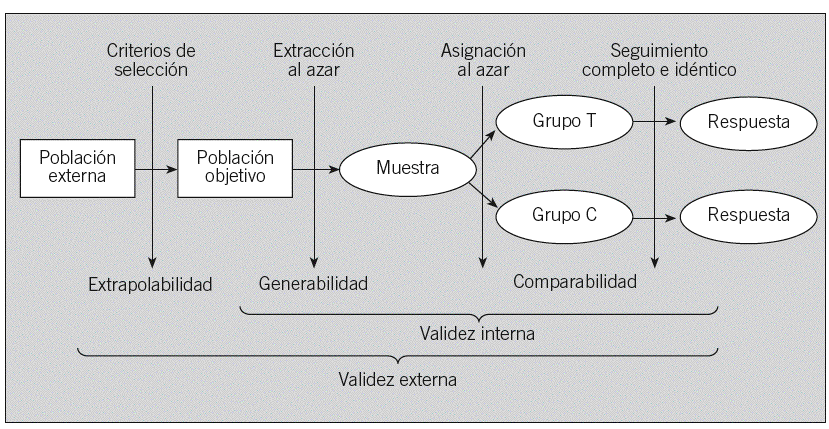
Cuando los atributos o condiciones Z no son observables, quizá porque son desconocidos, la herramienta estadística que debe emplearse es la asignación al azar. La asignación al azar garantiza que todos los voluntarios provienen de la misma población y permite emplear el cálculo de probabilidades para cuantificar el grado de oscilación aleatoria. No debe confundirse la asignación con la obtención al azar (fig. 1): la primera se emplea para obtener grupos inicialmente comparables (validez interna), mientras que la segunda permite generalizar los resultados a la población origen, lo que amplía su representatividad. Dado que la validez externa requiere la existencia previa de validez interna, no tiene sentido eliminar la asignación al azar para aumentar la validez externa30.
Fig. 1. Dos aportaciones del azar a la validez de la inferencia. Tomada de Cobo24.
Es bien conocido que el ensayo clínico aleatorizado recurre al enmascaramiento de las intervenciones8 para mantener a los investigadores cegados, y así conservar la comparabilidad inicial de los grupos obtenida mediante la asignación al azar. No es tan conocido, sin embargo, que también se requiere detallar el enmascaramiento en listas de comprobación de los ensayos no aleatorizados31, de la evaluación de pruebas diagnósticas9 y de los estudios epidemiológicos27.
Control del error aleatorio
El error aleatorio es siempre preferible al sistemático ya que es más fácil de cuantificar. Ya se ha comentado que todas las l por azar mediante el error típico o mediante intervalos de confianza, mientras que dejan a discreción del autor detallar o no el valor de p.
El procedimiento más simple y empleado para minimizar el error aleatorio consiste en aumentar el tamaño de la muestra, método que además de implicar mayores coste y tiempo de seguimiento puede comprometer la calidad de los datos: si la cantidad va en contra de la calidad, por disminuir el error aleatorio se acaba provocando error sistemático, que es menos cuantificable. Por ello, conviene emplear diseños y análisis más eficientes que, sin aumentar el tamaño de la muestra, proporcionen mayor información sobre el objetivo del estudio. Como ya se ha comentado en «Clasificación de los diseños», para un número fijo de casos disponibles, el error de estimación se hace mínimo si ambos grupos tienen el mismo número de casos, es decir, si se distribuye la mitad de casos en cada grupo. Por otro lado, la popularidad del promedio o media muestral radica precisamente en su mayor estabilidad de una muestra a otra, lo que lo hace más eficiente que otros estimadores como la mediana o la proporción de casos por encima de cierto umbral (cutpoint). Un procedimiento habitual para aumentar la eficiencia del estudio consiste en disminuir el error aleatorio mediante el control de la variabilidad de la respuesta (que se divide en entre e intra casos), ya que, a menor variabilidad, mayor información obtenemos de los casos estudiados. La variabilidad entre casos se controla mediante las técnicas de ajuste ya comentadas (restricción, subgrupos y modelado). La variabilidad intracasos se puede controlar estandarizando el proceso de medida, haciendo promedios de medidas repetidas, eliminando valores extremos o, simplemente, empleando la variable más fiable32,33, es decir, la que proporciona valores más cercanos en repetidas determinaciones en las mismas condiciones.
El último procedimiento para aumentar las posibilidades de éxito del estudio ya no se centra en reducir el ruido aleatorio de estimación (error), sino en amplificar la señal proporcionada (efecto). Así, en la medida en que lo permitan los márgenes de seguridad, en el estudio de un fármaco con efectos proporcionales a la dosis, será más eficiente emplear dosis más alejadas, entre las que cabe esperar mayor efecto diferencial. También, en estudios tempranos en los que convenga anteponer la eficiencia y rapidez de resultados a la validez externa, puede recurrirse a seleccionar los casos más sensibles al efecto de la intervención en estudio. En esta misma línea de adelantar la obtención de resultados, estaría el empleo de variables intermedias34, sustitutas de la auténtica respuesta que representa al objetivo sanitario de interés.
Cuantificación del error
Como se acaba de comentar, no todas las fuentes de error presentan las mismas dificultades a la hora de medir su magnitud. Así, el hecho de que la cuantificación de los errores aleatorios se nutra de rutinas ampliamente aceptadas y estandarizadas ha ocasionado que se olvide con facilidad que se puede y se debe describir y medir otras fuentes de error35. El hecho de asumir que únicamente se tienen errores debidos a los procesos aleatorios, olvidando los errores sistemáticos que producen los instrumentos de medida utilizados, los sesgos de los procesos de selección y el error no controlado por variables confusoras desconocidas, en gran parte es causado por el desconocimiento de los métodos existentes para su cuantificación y puede añadir importantes sesgos en nuestros resultados.
La inferencia estadística proporciona las herramientas clásicas para evaluar la magnitud del error aleatorio asociado al muestreo, como la desviación típica o el error estándar. Contrariamente, la evaluación de los errores no aleatorios requiere de otras metodologías. Quizá la forma más intuitiva de acercarse a la cuantificación del error sistemático es la que proporcionan los análisis de sensibilidad36, puesto que permiten responder a la pregunta «¿Cuánto cambia la respuesta cuando modifico en una determinada cantidad alguna de las variables del modelo?». Es decir, estos análisis proporcionan una idea sobre cómo afectarían a la estimación variaciones de los valores iniciales considerados.
Cuando la realidad se muestra más compleja, para considerar las distintas fuentes de error, se requieren modelos más elaborados que describan todos los errores, aleatorios y sistemáticos, de forma conjunta. Para este tipo de modelos más sofisticados, los avances técnicos cada vez proporcionan métodos más asequibles (por ejemplo, los llamados métodos de Monte Carlo, o los muestreos no paramétricos Bootstrap) pero que, a la vez, se alejan de la inferencia clásica, que «suele sustituir los parámetros del modelo por estimaciones como si fuesen los verdaderos valores»37. En este punto, la denominada inferencia bayesiana permite introducir en la estimación del error todo el conocimiento científico previo, asumiendo, de forma natural, nuestra incertidumbre acerca de la magnitud real de los errores que se pretende cuantificar.
Discusión
Las decisiones implícitas en el acto médico deben basarse en conocimiento contrastado empíricamente y en las consecuencias (utilidades, beneficios, costes, etc.) de las alternativas en consideración. Como estas últimas pueden variar fácilmente de un entorno a otro, es difícil establecer decisiones y recomendaciones «universales»2. En cambio, el conocimiento contrastado empíricamente puede ser más generalizable, lo que ha dado lugar a diversas clasificaciones de lo que se ha denominado nivel de evidencia científica38. Sin embargo, como se ha dicho, el acto médico y las decisiones sanitarias abarcan, por lo menos, tres dimensiones diferentes diagnóstico, pronóstico e intervención, por lo que la cantidad de información proporcionada por un estudio, sea original o de revisión sistemática, no puede ser resumida en una única escala.
Las listas de comprobación no deben confundirse con una herramienta para medir la calidad de la investigación. Deben contemplarse como una ayuda para mejorar la calidad de los informes de los estudios científicos en beneficio del autor, pues facilita la redacción del manuscrito; del revisor, para juzgar la aportación del estudio, y del lector, para interpretar correctamente los resultados y sus implicaciones en la práctica clínica.