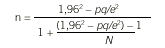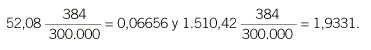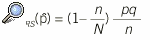La recogida de datos mediante encuesta requiere habitualmente elegir sujetos de una población, para configurar una muestra representativa. La selección muestral, o el diseño muestral, es el procedimiento para determinar qué individuos forman parte de la muestra. Se dice que el diseño de una muestra es complejo si para poder captar buena parte de las características de la población objetivo, la selección se realiza por etapas. La mayoría de las fuentes estadísticas de instituciones oficiales, correspondientes a datos recabados por encuesta, suele ser el resultado de una selección muestral compleja. En ámbitos muy diversos (encuestas de salud, encuestas industriales, encuestas de utilización de servicios o encuestas de la población activa) las estrategias que rigen la elección de entrevistados pueden llegar a revestir un elevado grado de complejidad si la población objetivo es suficientemente grande y heterogénea. Éste es el caso, por ejemplo, del territorio estatal o de una comunidad autónoma.
Las desigualdades territoriales (ya sea en densidad o en estructura de población) y la necesidad de reducir los costes de la recogida de la información son los principales motivos por los que se descarta un proceso de selección muestral aleatoria simple frente a procedimientos más elaborados. En este artículo vamos a trazar las principales líneas relacionadas con las consecuencias prácticas de trabajar con muestras complejas y estableceremos los distintos grados de sofisticación en el proceso de recogida de datos, sus consecuencias y su tratamiento.
En la sección «Material y métodos» indicaremos algunas definiciones básicas sobre los tipos de muestreo, ilustrados con ejemplos. En la sección «Resultados» veremos qué efectos puede tener el diseño muestral y cómo se pueden medir. Finalmente, en la sección «Discusión» se resumirán las principales recomendaciones que deben seguirse.
Material y método
Para poder entender los tipos de muestras posibles, distinguiremos entre diseño simple y diseño complejo. Esta clasificación es mínima pero con ella podemos tener una referencia en la medición de los efectos del diseño. Sin embargo, no vamos a abordar la gran variedad de posibilidades que la teoría de muestras recoge1,2.
Muestra de diseño simple
Decimos que trabajamos con datos obtenidos mediante una muestra aleatoria simple si todos los individuos que conforman la población tienen exactamente la misma probabilidad de haber sido elegidos en la muestra. La mayoría de procedimientos estadísticos estándar (es decir, los que están disponibles en los sistemas informáticos de tratamiento estadístico como el SPSS) supone esta circunstancia, además de requerir que los sujetos individuales (entrevistados) sean independientes.
El marco de referencia en una muestra de diseño simple supone que los individuos de la población pueden ser incluidos en una lista de la que se extraerá una muestra al azar. Este tipo de muestra se denomina muestra aleatoria simple y se abrevia con las siglas SRS (simple random sample).
Muestra de diseño complejo
Diremos que la muestra se ha obtenido mediante un diseño complejo si la probabilidad de elegir un determinado sujeto de la población no es igual para cualquier sujeto3. Es decir, no todos los individuos de la población tienen la misma probabilidad de ser seleccionados para formar la muestra.
Cada sujeto seleccionado en la muestra representará a un determinado número de individuos de la población, posiblemente distinto. De este modo, puede que no todos los entrevistados representen el mismo número de individuos de la población. Además, la elección de los sujetos puede realizarse por etapas, por ejemplo, seleccionando en primer lugar agrupaciones mayores (familias, centros o municipios).
Para cada elemento de la muestra se define su factor de ponderación asociado, que se interpretará como la correspondiente contribución a la muestra en términos del número de sujetos poblacionales a los que el sujeto entrevistado representa.
Hay que distinguir entre lo que se denomina ponderación y lo que se conoce como factor de elevación. Denominamos factor de elevación para cada sujeto al inverso de su probabilidad de ser seleccionado en la muestra. Por lo tanto, la suma de los factores de elevación de todos los individuos muestrales es igual al tamaño poblacional. Lo que habitualmente se conoce como ponderación se obtiene multiplicando el factor de elevación de cada individuo por el tamaño muestral y dividiendo por el tamaño poblacional, de forma que la suma de las ponderaciones individuales es igual al tamaño muestral.
Un ejemplo de las razones por las que a menudo es imprescindible recurrir a un diseño complejo lo podemos encontrar en una situación en la que la población objetivo está formada por diversos tipos de individuos. Además, si la composición de la población responde a tipologías que tienen una frecuencia relativa muy distinta, deberemos prestar atención para seleccionar suficientes individuos de las tipologías minoritarias. Para no complicar la exposición distinguiremos en el ejemplo 1 entre 2 tipos de sujetos, aunque el mismo argumento puede extenderse a más categorías.
Ejemplo 1. Muestra aleatoria simple
Supongamos que una población está formada por 300.000 habitantes. Sabemos que 10.000 viven en un entorno rural y el resto, 290.000, habitan en un entorno urbano. Supongamos que deseamos tomar una muestra de individuos de esta población que sea representativa de su composición. Utilizando la expresión usual para el cálculo del tamaño de la muestra con un intervalo de confianza del 95% y un error máximo esperado del 5% para proporciones con un grado máximo de indeterminación (p = q = 50%), deberíamos tomar una muestra total de 384 individuos. Es decir, el tamaño de muestra necesa-rio que denotamos por n se calcula como
donde e es el error máximo esperado (5%) y N el tamaño de la población (300.000 habitantes).
De acuerdo con la composición de la población el 3% (10.000/300.000), es decir, 13 individuos deberían ser elegidos del ámbito rural y el resto, 371 individuos, se deberían seleccionar entre los que habitan en un entorno urbano. Por lo tanto, la muestra de 384 individuos estaría formada por 13 habitantes de zona rural y 371 habitantes de zona urbana. Ésta sería la composición que debería tener una muestra aleatoria simple en la que todos los individuos de la población tendrían la misma probabilidad de ser seleccionados en la muestra para el estudio. En términos prácticos, podría decirse que cada individuo de la muestra representaría el mismo número de sujetos de la población, aunque por efectos del redondeo los 13 individuos que representan a la población del ámbito rural tendrían un factor de elevación igual a 769,23 y los 371 restantes, al representar un total de 290.000 habitantes, tendrían un factor de elevación igual a 781,67.
El problema principal de la aproximación anterior surge cuando se tiene en cuenta cuál va a ser la utilización posterior de la muestra. Si el investigador desea poder inferir conclusiones sobre la parte de la población que reside en la zona rural, tomará sólo 13 individuos de un total de 10.000, con lo que su margen de error, cuando se estiman proporciones para ese colectivo concreto, posiblemente resultará excesivo, dado que alcanzará un valor aproximadamente igual al 27%.
La muestra del ejemplo 1 refleja un caso de muestra aleatoria simple, con asignación proporcional.
Ejemplo 2. Muestra aleatoria estratificada con asignación no proporcional
Para evitar esta gran pérdida de fiabilidad que se apunta al final del ejemplo 1, manteniendo la misma población y su composición, se sugiere un diseño muestral más elaborado. Supongamos que el investigador puede estar dispuesto a aceptar cotas máximas de error cercanas al 7%. Entonces deberá tomar una muestra de 192 individuos del entorno rural. Ahora bien, supongamos además que sus restricciones de coste de recogida de información no le permiten superar el número total de sujetos a entrevistar, que se había fijado anteriormente en 384, por lo que no tiene otro remedio que tomar otros 192 sujetos del entorno urbano. Ahora la mitad de la muestra está formada por sujetos del entorno rural y la otra mitad por sujetos que residen en un entorno urbano, lo cual no es un fiel reflejo de la realidad, pero permite separar los individuos y realizar inferencias estadísticas desagregadas según el entorno de residencia con valores de fiabilidad aceptables. Además, en ambos subgrupos se alcanza un valor de error máximo esperado inferior al 7% en resultados sobre proporciones para el caso extremo de máxima indeterminación (p = q = 50%).
Esta muestra tiene la ventaja de permitir la separación por ámbitos residenciales (rural o urbano). En términos estadísticos se conoce el diseño muestral que se acaba de describir como muestreo estratificado con asignación no proporcional, porque el número de sujetos seleccionados en cada estrato (el rural o el urbano) no es proporcional al tamaño que tiene el estrato en la población. En la población sólo el 3% de los residentes se localizan en el entorno rural, mientras que en la muestra hemos seleccionado un 50% de individuos de cada zona. Este tipo de diseño estratificado se denomina STR (stratified sampling). Si hubiera sido un diseño estratificado con asignación proporcional, se hubiera denominado PPS (sampling proporcional to size).
Resultados
Si se introduce alguna modificación en la selección muestral que aleja el diseño de un esquema aleatorio simple, se puede incurrir fundamentalmente en 2 alteraciones. La primera afecta al sesgo y la segunda a la varianza.
En el ejemplo 2, puesto que no se ha representado la composición de la población, la muestra tiene una proporción de sujetos del ámbito rural del 50%, cuando en la población este colectivo sólo alcanza el 3%. Cualquier estimación que ataña a una variable cuyo comportamiento no sea idéntico en los colectivos considerados (rural o urbano) estará sesgada, por existir una sobrerrepresentación de los habitantes que residen en zonas rurales. Sin embargo, en el análisis por estratos (es decir, para cada colectivo por separado) se logran mejores cotas de fiabilidad en el segundo diseño que en el del ejemplo 1, ya que el error muestral en el grupo minoritario es mucho menor.
Es de suma importancia valorar si la introducción de sesgo compensa la ganancia en fiabilidad. Sin embargo, en la práctica poco o nada se conoce del comportamiento de las variables en el ámbito poblacional y, por esta misma razón es conveniente valorar el efecto del diseño muestral y, en su caso, corregirlo.
Eliminación de sesgo: uso de ponderaciones individuales
Los diseños basados en una asignación no proporcional pueden corregirse mediante la inclusión de los correspondientes factores de ponderación.
Ejemplo 2 (continuación). Para este ejemplo recordemos que la mitad de la muestra (192 sujetos) representa al 3% de la población. En concreto vemos que cada individuo seleccionado en la muestra que reside en un entorno rural representa a 52,08 individuos de su misma zona de residencia (es decir a 10.000/192). En cambio, un individuo de la muestra que habita en una zona urbana representa a 1.510,42 sujetos de su mismo entorno (es decir a 290.000/192).
Claramente, los factores de elevación, respectivamente 52,08 y 1.510,42, no son idénticos para todos los individuos, ya que los que residen en zonas distintas tienen un factor de elevación diferente. Comprobemos que la suma de todos los factores de elevación proporciona el tamaño poblacional. Por un lado, 192 sujetos tienen un factor de elevación igual a 52,08, lo que implica un resultado total igual a 10.000, al sumar los factores de elevación de esos sujetos. Por otro lado, 192 sujetos tienen un factor de elevación de 1:510,42, lo que implica un resultado final igual a 290.000. La suma de ambos totales es, por tanto, el tamaño poblacional de 300.000.
Para poder calcular las ponderaciones sólo deben realizarse las siguientes operaciones:
De este modo, los individuos que residen en una zona rural deberán tener en la muestra una ponderación igual a 0,06656 y los que pertenecen a la zona urbana una ponderación de 1,93331. Si se suman las ponderaciones de todos los individuos de la muestra se obtiene el tamaño muestral de 384 individuos. Si se utilizan estas ponderaciones en los procedimientos de estimación de magnitudes poblacionales, los resultados no resultarán sesgados, ya que se corregirá la sobrerrepresentación de los individuos residentes en zonas rurales.
Diseños muestrales habituales en encuestas de salud
Los diseños complejos que se utilizan en la actualidad para las encuestas de salud4,5 son elaboraciones más avanzadas de los mismos principios presentados en los ejemplos anteriores. Habitualmente, en las grandes encuestas en las que se abarca un territorio amplio se realiza una selección de municipios en los que se realizarán las entrevistas (lógicamente se trata de un criterio de disminución de costes económicos). Por lo tanto, se definen distintas unidades muestrales. Las denominadas primarias son los municipios (nótese que se usa una muestra de municipios). Una vez situados en el municipio elegido, las unidades muestrales secundarias pueden ser los individuos. En un muestreo complejo, donde se elige una muestra de individuos de una muestra de municipios, se está realizando un diseño bietápico. Obviamente, el diseño puede ser más sofisticado. Por ejemplo, una vez elegida la unidad primaria (el municipio), se pueden elegir domicilios particulares (hogares) en los que se estudiará a todos los miembros que residen en ese mismo hogar. En este caso, se tendría claramente un diseño con conglomerados, ya que al elegir un hogar entero y estudiar a todos los individuos que lo forman, se considera que forman un grupo o cluster. Cuando se toman conglomerados, es importante observar el impacto derivado de llevar a cabo estudios sobre los sujetos individuales. Lo más peligroso, en el ámbito del análisis estadístico, es la interrelación entre los miembros de un mismo hogar, es decir, el comportamiento correlacionado que pueden mostrar. Si esta correlación es muy fuerte, no se puede suponer cierta la hipótesis de independencia entre los sujetos.
Ejemplo 3. Efectos de diseños por conglomerados. Se realiza un muestreo en el que todos los individuos de una misma familia son entrevistados. Si interesa conocer el porcentaje de niños que han acudido a un odontólogo en los últimos 12 meses, es posible que se obtenga un resultado poco fiable, ya que existe un comportamiento altamente correlacionado en las prácticas preventivas inducidas por los padres, por lo que los niños de un mismo hogar tienen respuestas idénticas a esta pregunta. Esto significa que el grado de información que revela la muestra es inferior al que cabría esperar por su tamaño, dada la correlación existente entre las respuestas de sus integrantes.
Medición del efecto del diseño
El muestreo aleatorio simple tiene 2 funciones. En primer lugar, permite tener una base de referencia para poder comparar la eficiencia relativa de otros métodos de muestreo. En segundo lugar, en algún momento de la selección de individuos, ya sea dentro de los estratos o para seleccionar los conglomerados, se utilizará como sistema de aleatorización. Para medir el efecto que tiene el diseño muestral hay que atender a la estimación de la varianza, ya que como se ha visto en la sección «Eliminación de sesgo: uso de ponderaciones individuales», la mayoría de las situaciones prácticas utiliza ponderaciones para evitar la aparición de sesgo. Como las estimaciones de parámetros poblacionales (como la proporción de individuos que presentan una determinada enefermedad o tienen un determinado hábito) puede variar según cuál sea la muestra que se haya seleccionado, se puede medir la varianza de un estimador para concluir sobre el grado de variabilidad de las estimaciones. La varianza del estimador empleado depende del diseño muestral y por esta razón se denomina a veces varianza del diseño. Esta varianza se puede estimar a partir de la información muestral y en este caso se denomina varianza muestral. La raíz cuadrada de esta varianza muestral provoca el error muestral.
La forma de poder evaluar el efecto de un diseño muestral es comparar la varianza de un estimador obtenida mediante ese diseño con la que se obtendría mediante un diseño simple de referencia. Habitualmente se considera muestreo de referencia el obtenido empleando una selección aleatoria simple (como en el ejemplo 1). El cociente entre ambas varianzas se conoce como el efecto del diseño y se denomina DEFF (design effect).
Ejemplo 4. Cálculo del efecto del diseño
En el diseño básico del ejemplo 1 suponíamos que se había elegido una muestra aleatoria simple de individuos de la población (384 individuos, de los que 13 formaban parte del hábitat rural). Supongamos que el 50% del total de individuos encuestados responden que sí a la pregunta ¿ha utilizado un determinado servicio sanitario en el último año? Como el muestreo es aleatorio y simple, la varianza estimada de este promedio se calcularía de la siguiente forma:
En el ejemplo 1, el resultado que se obtiene al sustituir por los valores del tamaño muestral, del tamaño poblacional y si se supone que el producto pq es igual 0,25 es que la varianza es igual a 0,00065. Entonces, al tomar su raíz cuadrada, el error muestral es igual al 0,02550, o del 2,55%. Nótese que, como cabía esperar, el error muestral multiplicado por 1,96 proporciona amplitudes en los intervalos de confianza de ± 5%. En realidad, eso era lo esperado por la forma de calcular el tamaño muestral.
El ejemplo 2 se basa en un diseño estratificado no proporcional en el que disponemos de 192 individuos del entorno rural y 192 del entorno urbano. Aun habiendo incluido ponderaciones individuales, debería emplearse la correspondiente expresión para el cálculo de la varianza muestral. Dentro de cada estrato, como la muestra es aleatoria simple, puede emplearse la fórmula anterior, cambiando el tamaño muestral y el tamaño poblacional. En este caso, obtenemos una estimación de la varianza igual a 0,00128 en el primer estrato y de 0,00130 en el segundo estrato. Como el peso del primer estrato (su tamaño relativo en la población) es del 3%, mientras que el segundo estrato tiene un tamaño relativo del 97%, la varianza final es igual a la combinación de las 2 anteriores teniendo en cuenta esta composición, es decir, (0,03)2 · 0,00128 + (0,97)2 · 0,00130 = 0,00123. Por tanto, la varianza muestral en este segundo diseño tiene el valor de 0,00123. El error muestral es su raíz cuadrada, aproximadamente del 3,5%. Si se divide la varianza muestral en el diseño estratificado no proporcional por la obtenida en el diseño de referencia se obtiene el valor 1,88. Es decir, indicaremos un DEFF igual a 1,88, lo que quiere decir que por efecto del diseño la varianza se ha multiplicado por 1,88.
Como indicación adicional deberemos decir que el efecto del diseño no se debe confundir con la amplitud de los intervalos de confianza, que son una función del error muestral y no de la varianza muestral. Una forma de calcular fácilmente la amplitud del intervalo de confianza para una proporción en el diseño estratificado del ejemplo 2, sabiendo que tiene un efecto del diseño DEFF igual a 1,88, es utilizando su raíz cuadrada multiplicada por la amplitud en la muestra aleatoria simple. Por tanto, en nuestro caso, la amplitud de los intervalos de confianza para proporciones en el ejemplo 2 será aproximadamente igual a (1,88)5%, es decir, del 7%. Ese mismo resultado se obtiene si se toma el verdadero error muestral (3,5%) y se multiplica por 1,96.
Como puede verse, la mayor dificultad para evaluar el efecto de un diseño muestral reside en obtener la correcta estimación de la varianza muestral, de acuerdo con las condiciones de selección de los sujetos de la población que determina este diseño. En el caso utilizado a lo largo de la exposición se ha podido calcular explícitamente, porque se trata de un estadístico sencillo (una proporción) y de un diseño unietápico.
Cuando el estadístico de interés es más complicado (por ejemplo para el coeficiente de una regresión) y el diseño muestral reviste mayor complejidad, no es posible hallar una expresión matemática que permita el cálculo directo de la varianza muestral. Los métodos estadísticos empleados para aproximar este cálculo abarcan desde la linealización de las expresiones hasta los métodos de remuestreo2.
Discusión
Ignorar el diseño muestral puede conducir a estimaciones sesgadas de los parámetros de interés. La inclusión de ponderaciones individuales permite obtener estimaciones puntuales insesgadas, pero los errores estándar pueden quedar subestimados.
Dado que los programas estadísticos utilizados habitualmente incorporan la posibilidad de incluir ponderaciones, realizar esta operación resulta sencillo. Incorporar el diseño completo, y no sólo las ponderaciones, resulta menos asequible, porque no es una opción disponible en los programas de análisis estadístico habituales. Sin embargo, es muy recomendable analizar el efecto del diseño para evaluar el impacto de la selección muestral en la amplitud de los intervalos de confianza que afecten a los resultados de interés. En muchos casos, los diseños muestrales empleados en la práctica introducen asignaciones (sobrerrepresentaciones o subrepresentaciones de colectivos) que pueden distorsionar la fiabilidad al invalidar las hipótesis del diseño muestral aleatorio simple. Estas distorsiones son especialmente graves si el efecto del diseño tiene un valor muy superior a 1, puesto que en este caso la varianza muestral es mayor, igual que las amplitudes de los intervalos de confianza.
Agradecimiento
Las autoras agradecen las ayudas recibidas de SEC2001-3672 y SEC2001-2581-C02-02.