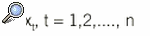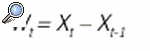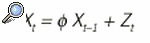Introducción
El seguimiento diario de los pacientes ingresados en una unidad hospitalaria genera información que, procesada adecuadamente, ha de permitir confeccionar un sistema de predicción en tiempo real, mediante el que se pueda detectar posibles cambios en el comportamiento de la situación clínica del paciente. El registro sistemático durante un tiempo determinado de una de las variables del sistema es lo que denominamos una serie temporal. La característica principal de estas observaciones es que no son independientes entre sí, sino que las observaciones consecutivas están relacionadas.
Para averiguar si la bilirrubina provoca toxicidad sobre los centros cerebrales que regulan los ritmos biológicos en recién nacidos sanos a término, Aldana et al1 registran cada 30 minutos, durante las primeras 24 horas de los recién nacidos, los valores de frecuencia cardíaca y respiratoria, temperatura corporal cutánea abdominal y presión arterial sistólica braquial oscilométrica. Los 48 valores obtenidos de cada variable en cada niño constituyen una serie temporal. La serie temporal fue la base del análisis ritmométrico.
El recuento diario de creatinina en sangre, las observaciones monitorizadas procedentes de la presión arterial de un paciente en UCI, el pulso, etc. son ejemplos de series temporales.
Gordon y Smith2 ponen de manifiesto que la naturaleza del proceso de monitorización clínico es tal que necesita procesos on-line capaces de determinar, a partir de los valores precedentes, qué información realmente novedosa aporta la actual observación, lo que debe permitir detectar, lo antes posible, un cambio en la evolución de un paciente.
En una UCI, la detección rápida de estados críticos y de los efectos de las intervenciones es de extrema importancia3. La mayoría de las decisiones está todavía basada en la experiencia y en juicios subjetivos pero no en el análisis estadístico de datos. Además la existencia de sistemas de alarma basados en unos umbrales fijos produce numerosas falsas alarmas cada vez que alguna de estas constantes sobrepasa un umbral superior o cae por debajo de un umbral inferior determinado cuando no se tiene en cuenta la historia previa. Estudios recientes demuestran que el 86% de las alarmas que suenan en una UCI son falsas4. Daumer et al5 y Bauer et al6, entre otros, proponen diferentes procedimientos para la detección y análisis de estos datos atípicos en una UCI. En estas situaciones será de gran utilidad un sistema en tiempo real que permita detectar y tratar estos datos atípicos en las observaciones recogidas a lo largo del tiempo, es decir las diferentes series temporales generadas para cada enfermo en una UCI. Dicho sistema permitirá reducir el número de falsas alarmas. Así, el estudio de las series temporales tiene entre otros objetivos la comprensión y descripción del mecanismo que genera los datos, la previsión de valores futuros y, en ocasiones, es un paso previo para llegar a establecer el control del sistema observado.
Son varias las metodologías matemáticas y estadísticas que se utilizan con la intención de predecir comportamientos futuros de una serie temporal7. En el presente trabajo se incluye una breve introducción a la metodología Box-Jenkins8, a partir de la definición de serie temporal y la presentación de la metodología ARIMA. Como ilustración, se aplica esta metodología a un ejemplo concreto y finalmente, en la discusión, se destacan las ventajas de la utilización de estos modelos.
Definición de serie temporal
Se llama serie temporal a una secuencia ordenada de observaciones de un mismo fenómeno. El orden de llegada de éstas se halla definido por el tiempo en el que se ha obtenido cada una de ellas. Es preciso destacar que este tiempo hace que en una gran mayoría de las situaciones las observaciones sean dependientes (correlacionadas) entre ellas. Esta situación es diferente de lo habitual en otras aplicaciones de la inferencia estadística, en las que es válido asumir que los datos son independientes. En consecuencia, se necesitan herramientas de análisis específicas para el tratamiento de estas observaciones.
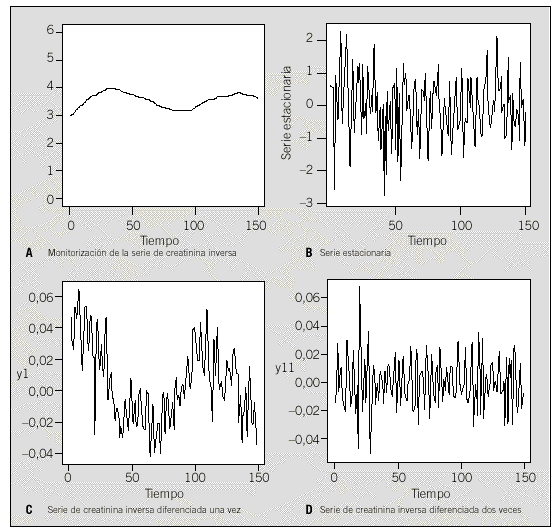
Habitualmente las observaciones se tomarán en instantes equiespaciados, motivo por el que se designa las observaciones de la serie temporal por
Se tratan de la misma forma las dos situaciones siguientes: a) se toma la medida de una variable en instantes sucesivos del tiempo, por ejemplo, se observa el valor de la presión arterial cada hora, o b) se trata de conocer el valor acumulado de una variable en un período definido por dos instantes consecutivos, por ejemplo, las medidas cada 4 horas del flujo urinario. A partir de todo lo precedente, queda claro que se dispone de una única observación en cada instante de tiempo. La representación gráfica de la serie permitirá detectar, además de las componentes de tendencia y/o estacionalidad, anomalías, discontinuidades, cambios de nivel bruscos, observaciones atípicas, etc. Todas estas situaciones se tendrán que estudiar con mucho cuidado para determinar si se corresponden a alguna causa objetiva conocida y buscar la forma más conveniente de tratarlas. En la figura 1a se muestra, como ejemplo, la gráfica de una serie temporal(1) que representa la evolución diaria de la creatinina(2) inversa en sangre en un paciente al que se le ha realizado un trasplante renal.
Figs. 1a-d. A: Monitorización de la serie de creatinina inversa. B: Serie estacionaria. C: Serie de creatinina inversa diferenciada una vez. D: Serie de creatinina inversa diferenciada dos veces.
Idea básica de estacionariedad
Se puede consultar en la bibliografía especializada7-9 la definición formal de estacionariedad; no obstante, en este apartado se presenta una idea intuitiva de este concepto que es fundamental para el tratamiento que se realizará de todo tipo de series. Una serie temporal es estacionaria si sus características estadísticas no cambian con el tiempo, de forma que la media de la serie se mantiene constante a lo largo del tiempo, es decir, no presenta tendencia ni variaciones periódicas (no contiene una componente estacional ni presenta ciclos deterministas) y su variancia también se mantiene constante a lo largo del tiempo. La figura 1b presenta un ejemplo de serie estacionaria, en la que se puede observar que tanto la media como la variancia se mantienen constantes a lo largo del tiempo y no existe un patrón determinado de periodicidad. No obstante, en muchas situaciones aparecen series no estacionarias, como por ejemplo la mostrada en la figura 1a, en la que se aprecia que la media no se mantiene constante a lo largo del tiempo. A menudo la serie, formada por los incrementos o diferencias entre 2 valores consecutivos, llamados primeras diferencias, es estacionaria. Es decir, se sustituye la serie original Xt por una nueva serie Wt obtenida como:
A veces es necesario realizar más de una diferenciación para conseguir una serie estacionaria. En el caso de la serie creatinina inversa en sangre, una primera diferenciación no consigue transformar la serie en estacionaria, y es necesario una segunda diferenciación para conseguir estabilizar la media (figs. 1c y 1d).
Asimismo, también es frecuente que la gráfica de las observaciones muestre una variabilidad que no es constante a lo largo del tiempo. En la práctica, en la mayor parte de los casos será suficiente hacer una transformación logarítmica de los datos para conseguir estabilizar la variancia de la variable9.
Modelos ARIMA
Con el objetivo de conseguir precisión en las previsiones obtenidas a partir de una serie temporal, Box y Jenkins8 propusieron en los setenta una clase de modelos, denominados autorregresivos y de media móvil (ARMA). A título introductorio, comenzaremos por los modelos más simples.
Modelos autorregresivos (AR)
Se puede imaginar que se construye un proceso suponiendo que la observación en el instante t, Xt está relacionada de forma lineal con la observación en el instante t-1, más una componente aleatoria o término de error Zt, es decir
donde * es un parámetro que será estimado a partir de las observaciones disponibles. Es decir, se puede predecir el valor de la inversa de la creatinina en sangre de mañana de un paciente a partir del valor de hoy pero no de forma determinista, sino afectado por un término de error o perturbación aleatoria Zt. Se trata, pues, de un modelo de regresión en el que Xt se explica en función de los datos de su propio pasado; por este motivo lo denominamos proceso autorregresivo de orden 1, de forma abreviada AR(1).
Se considera que las perturbaciones aleatorias Z1,Z2,...,Zn son «ruido blanco», que no contienen información, ya que la información relevante está incluida en la parte determinista del modelo. ¿Y cuándo puede considerarse que son simple ruido? Cuando sean el resultado de la suma de muchos fenómenos, tantos que la influencia de cada uno de ellos sea despreciable, y por lo tanto, con distribución normal. Además, si realmente no aportan información, estos fenómenos actuarán por igual en los diferentes valores de X, por lo que su distribución será idéntica, de igual varianza (homocedástica) a lo largo del tiempo. Finalmente cada término de error Zt no aportará información sobre los restantes: serán entre sí independientes.
Para la identificación de estos modelos, y dado que la principal característica de una serie temporal es que las observaciones no son independientes entre ellas, necesitaremos utilizar una medida del grado de dependencia (lineal) entre las observaciones: la (auto)correlación, que es la correlación de la serie con el valor anterior de la misma. Se pueden definir otras correlaciones aumentando el retardo o distancia entre observaciones consecutivas; todas ellas juntas forman la llamada función de autocorrelación muestral (ACF), que también se denomina correlograma. Es decir, la función de autocorrelación indica el grado de (auto)dependencia (lineal) entre las observaciones para los diferentes retardos. Además de la función de autocorrelación, es necesaria la función de autocorrelación parcial PACF que complementa a la ACF para escoger o identificar el modelo más adecuado a los datos disponibles. Es decir, las relaciones entre las observaciones consecutivas de estos modelos quedan condensadas en las funciones ACF y PACF.
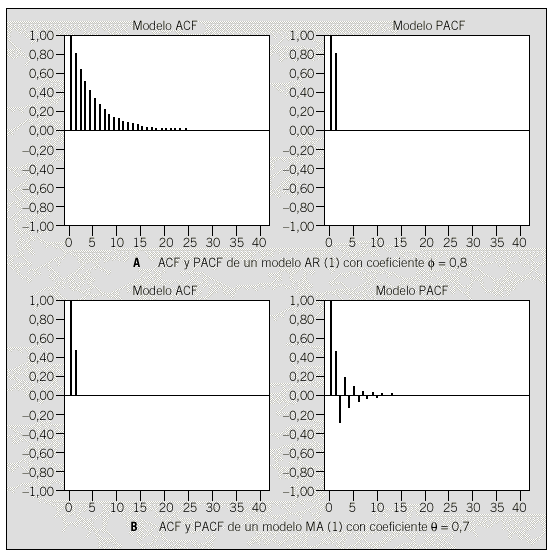
En la figura 2a se halla la representación gráfica de la ACF y PACF del modelo AR(1) con coeficiente * = 0,8. Obsérvese que la ACF decae lentamente mientras que la PACF consta de un único valor.
Figs. 2a y b. A: ACF y PACF de un modelo AR(1) con coeficiente *= 0,8. B: ACF y PACF de un modelo MA(1) con coeficiente *= 0,07.
La generalización de este modelo es el denominado autorregresivo de orden p, en el que para poder predecir un valor determinado, por ejemplo la presión arterial de hoy, necesitamos conocer la presión arterial de este enfermo en los p días anteriores.
Modelos de medias móviles (MA)
Alternativamente podemos expresar Xt como una combinación lineal de dos términos de error consecutivos Zt y Zt-1, es decir Xt = Zt +*Zt-1 donde * también es un parámetro a ser estimado. Este modelo recibe el nombre de media móvil de orden 1, o bien MA(1), que se puede generalizar a uno de media móvil de orden q, si se considera que es la combinación lineal de q términos de error consecutivos.
La figura 2b contiene la representación gráfica de las funciones ACF y PACF para un modelo MA(1), con parámetro * = 0,7. Contrariamente a lo que sucede en el modelo AR(1), la ACF tiene un único valor y la PACF decae lentamente.
Modelos autorregresivos y de medias móviles (ARMA)
Combinando los procesos AR y MA se obtienen los procesos mixtos autorregresivos y de media móvil, es decir los modelos ARMA(p,q), que no son nada más que la combinación de un modelo autorregresivo de orden p y uno de media móviles de orden q. Las características principales de las funciones ACF y PACF de los modelos que acabamos de presentar se hallan expuestas en forma esquemática en la tabla 1.
Modelo autorregresivo integrado de media móvil (ARIMA)
Finalmente, si se pretende ajustar un modelo a unas observaciones que provienen de un modelo no estacionario, después de diferenciarlas, es decir, de trabajar con sus incrementos sucesivos, podremos utilizar un modelo ARMA(p,q), con lo que habremos obviado el problema que se presenta a menudo en la práctica cuando se dispone de datos no estacionarios. En esta situación el modelo se denomina autorregresivo integrado de media móvil (ARIMA)(p,d,q), donde d indica el número de diferenciaciones que han sido necesarias hasta obtener la estacionariedad.
Metodología para la construcción de modelos y sistemática de trabajo
En este apartado se enumeran las diferentes etapas de la metodología desarrollada por Box y Jenkins para construir modelos ARIMA a partir de las observaciones de una serie temporal y se aplican a un caso concreto. Se utilizarán las propiedades de las funciones ACF y PACF de los modelos ARMA vistas en los apartados anteriores.
La metodología consta de las tres etapas presentes en la elaboración de cualquier modelo estadístico:
1. Identificación o propuesta tentativa de uno o varios modelos. Ésta se realiza básicamente a partir de la inspección del gráfico de la serie y de las funciones ACF y PACF para ajustar el orden del modelo. Siempre que sea posible, se tratará de utilizar modelos con pocos parámetros, por el principio de parquedad (parsimony).
2. Estimaciónde los parámetros, mediante cualquier paquete estadístico generalista (MINITAB10, SPSS11, SAS12, etc.) o bien el paquete de libre distribución R13. El software TSW14, también de libre distribución, tiene incorporadas las opciones de identificación automática del modelo, estimación de los parámetros y cálculo de las previsiones.
3. Validacióndel modelo a través de los análisis de los residuos y, si no es adecuado, formulación de un modelo alternativo.
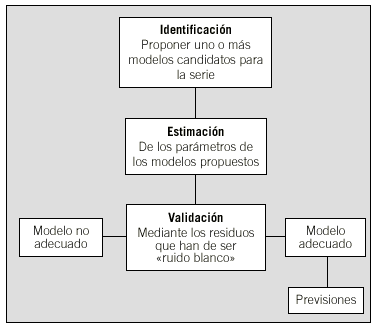
Una vez se dispone de un modelo adecuado, se podrán realizar les previsiones. Los pasos a seguir se pueden ver de forma esquemática en el diagrama de flujos representado en la figura 3.
Fig. 3. Metodología para la construcción de un modelo ARIMA.
Siempre es necesario pensar que no existe «el modelo verdadero» y que, en este proceso, se buscan «modelos útiles».
Aplicación práctica
Como ejemplo ilustrativo de esta sistemática de trabajo se desarrollan los tres puntos propuestos a la modelización de la serie creatinina.
Identificación
Ya se ha comentado en los párrafos precedentes que esta serie no es estacionaria, pues la figura 1a nos muestra que la media no se mantiene constante a lo largo del tiempo, y por el mismo motivo tampoco es estacionaria la primera diferenciación, es decir los sucesivos incrementos de los valores de la creatinina inversa (fig. 1c). Es necesaria una segunda diferenciación para conseguir una serie estacionaria (fig. 1d).
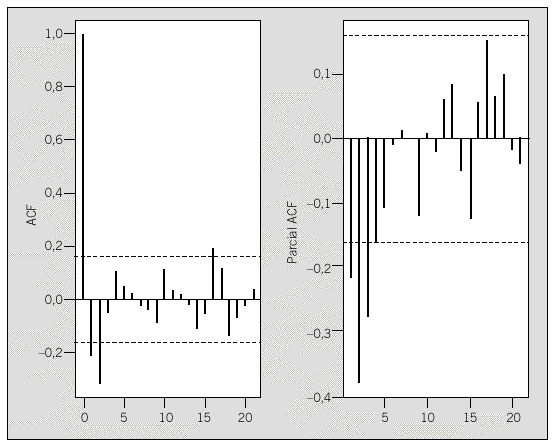
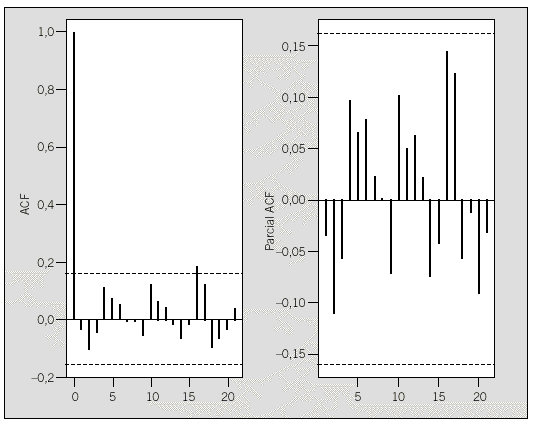
Una vez se ha conseguido una serie estacionaria, la identificación del orden del modelo se decidirá comparando las funciones ACF y PACF muestrales (fig. 4) con las de los posibles modelos teóricos (figs. 2a y b), decantándose en este caso por un modelo MA (de medias móviles) ya que se interpreta que la ACF sólo presenta 2 valores significativos, es decir, 2 valores fuera del intervalo de confianza y la PACF indica un decrecimiento. Para este modelo concreto, el orden de la parte MA se propone de acuerdo con los retardos significativos de la ACF, es decir 2.
Fig. 4. ACF y PACF muestrales de la serie de creatinina inversa diferenciada dos veces. Intervalos de confianza calculados al 95%.
Para expresar este modelo en la metodología ARIMA (p,d,q), recuérdese que d es el número de diferenciaciones necesarias, es decir 2, y que como tentativamente se ha optado por un modelo MA, significa que p = 0. Además del análisis conjunto de las funciones ACF y PACF se ha propuesto que el orden de la parte MA sea 2. Resumiendo, la identificación tentativa para la serie inversa de la creatinina es un modelo ARIMA(0,2,2).
Estimación de los parámetros
En este caso se utiliza el software R. Los resultados de la estimación se pueden hallar en la tabla 2.
Validación
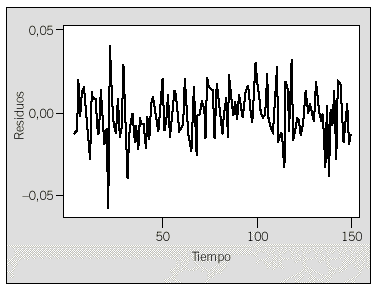
Una vez realizada la estimación de los parámetros del modelo, es necesario verificar que el modelo ajustado es satisfactorio mediante las gráficas de los residuos, así como de su ACF y PACF. En la figura 5 no se detecta que haya valores anómalos ya que corresponde a ruido blanco, es decir, sin ningún patrón detectado a simple vista. En la figura 6 se hallan las correspondientes ACF y PACF de los residuos de este modelo que también cumplen las características correspondientes al ruido blanco, es decir, no hay ningún valor que sobresalga del intervalo de confianza. Por lo tanto, se puede concluir que este modelo es satisfactorio, lo cual representa que será de gran utilidad para realizar el cálculo de futuras previsiones de los valores de creatinina en sangre en dicho paciente.
Fig. 5. Representación gráfica de los residuos del modelo ajustado.
Fig. 6. ACF y PACF de la serie de residuos del modelo ajustado. Intervalos de confianza calculados al 95%.
Discusión
En este artículo, a partir de un caso sencillo se presenta la utilidad para desarrollar un sistema de previsión, mediante la metodología de series temporales, que permita el seguimiento individualizado de un paciente. El ejemplo tratado pone de manifiesto cómo se puede prever un incremento de creatinina en sangre, valor de gran importancia como indicador de inicio de un proceso de rechazo del trasplante renal realizado.
Jo15 presenta un modelo para la arritmia sinusal respiratoria a partir de los datos experimentales (ECG, flujo de aire y presión arterial, etc.) recogidos en posición supina y vertical dejando al sujeto respirar espontáneamente a través de un ventilador pulmonar asistido. Los resultados obtenidos son prometedores ya que sugieren la posibilidad de utilizar esta metodología en condiciones donde el control voluntario de respiración no sea posible, como en el caso de sujetos que están dormidos o anestesiados.
Son varios los autores que demuestran la utilidad de la modelización de series temporales en la vigilancia epidemiológica16,17. Domínguez et al18 han analizado el comportamiento de los indicadores de mortalidad y morbilidad declarada en un área de Barcelona durante diversas temporadas gripales y valorado la utilidad de su modelización para detectar las epidemias de gripe. Para la monitorización del indicador mortalidad se ha desarrollado una aplicación informática instalada en el Servicio de Vigilancia Epidemiológica de la Generalitat de Catalunya y en la Agència de Salut Pública de Barcelona que permite la detección de una causa anómala de mortalidad a partir de la previsión del número de defunciones para la semana siguiente así como su intervalo de confianza. Si la mortalidad real supera el límite superior del intervalo de confianza, será necesario actuar, revisando el resto de la información disponible y alertar la vigilancia para confirmar la presencia de una situación epidémica.
En resumen, se han visto las posibilidades que estas herramientas ofrecen para monitorizar el seguimiento de una población, en el caso de la epidemiología, o de un paciente individual en el caso de la medicina. La monitorización formal de las señales biomédicas obtenidas de un paciente y su análisis bajo la óptica presentada pueden ser de gran utilidad para la previsión de la futura evolución de un paciente.
Agradecimientos
La autora agradece los valiosos comentarios del Dr. Manuel Martí Recober a las versiones previas de este trabajo.