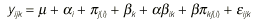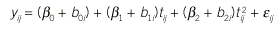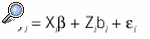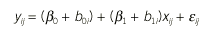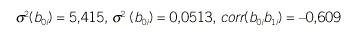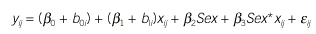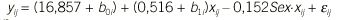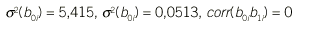Introducción
En medicina clínica es frecuente diseñar ensayos en los que se dispone de varias observaciones del mismo sujeto y se pueden tener además varios grupos de sujetos. Una de las situaciones más frecuentes en estos ensayos consiste en el análisis de datos en los que se dispone de la evolución de alguna variable a lo largo del tiempo para cada individuo (peso de pacientes, crecimiento tumoral, etc.) en diferentes situaciones experimentales (diferentes tratamientos, diferentes dietas, distinguiendo por sexos, etc.) y el objetivo del estudio consiste en realizar la comparación de los grupos mediante la comparación de las curvas obtenidas. En otras situaciones las observaciones repetidas sobre un mismo individuo vienen ocasionadas por el hecho de que se sabe que la variabilidad entre los individuos que se utilizan para realizar un determinado ensayo es muy grande. En este caso, con una observación por individuo será difícil determinar, entre las diferencias entre grupos que se observan, qué componente es debido a los tratamientos administrados y qué componente es debido a la propia variabilidad de la muestra analizada. En estas situaciones suele ser interesante obtener varias medidas del mismo individuo para poder tener una aproximación (en términos estadísticos nos referiremos a control) a esta variabilidad individual.
El concepto de medidas repetidas es un término que engloba las situaciones comentadas anteriormente. En términos generales, se utiliza en aquellas situaciones en las que la variable respuesta en cada unidad experimental se mide en múltiples ocasiones y, posiblemente, en condiciones experimentales distintas. Su ámbito de aplicación es variado, incluyendo la biología, medicina, educación, psicología, econometría, etc.
Como se ha indicado anteriormente, este tipo de análisis suelen plantearse en estudios que son longitudinales por naturaleza, es decir, cuando las medidas se realizan a lo largo del tiempo. En estos casos para cada individuo se dispone de una curva que indica el comportamiento de la variable obtenida a lo largo del tiempo y, por lo tanto, el interés se centra en el modelo matemático que expresa la respuesta como una función del tiempo. Esta función, en general, será no-lineal. En el mejor de los casos, podremos proponer una expresión determinada para esta función teniendo en cuenta las características del proceso que estamos observando. Sin embargo, en muchos casos deberemos considerar modelos más generales (lineal, cuadrático, etc.).
En determinados estudios experimentales, las medidas repetidas corresponderán a la asignación de distintos tratamientos a los sujetos del estudio. En estos casos a cada individuo se le administran todos los tratamientos que se desean estudiar dejando un período prudencial de tiempo entre la administración de dos tratamientos consecutivos para evitar una posible interacción entre ellos. En el análisis de este tipo de situaciones el valor del tiempo en que se realiza cada medida es irrelevante, y el objetivo se centrará en la comparación de los tratamientos teniendo en cuenta que se dispone de una medida de la variabilidad individual al disponer de varias medidas sobre el mismo sujeto. Un caso particular de este tipo de análisis son los diseños cross-over. A modo de resumen, la tabla 1 indica las ventajas y los inconvenientes de este tipo de análisis en su aplicación en estudios clínicos.
Independientemente del diseño experimental con medidas repetidas que se utilice en una situación concreta, una de las características particulares común a todos ellos es la existencia de una estructura de correlaciones muy particular entre los datos: las observaciones de un mismo individuo están correlacionadas, mientras que las observaciones de individuos distintos están incorrelacionadas. Este hecho plantea una serie de problemas desde el punto de vista de análisis estadístico cuya solución, teniendo además en cuenta el tipo de cuestiones a resolver, da lugar a distintas aproximaciones al problema. En este trabajo se van a indicar los métodos más habituales para abordar este tipo de problemas en función del diseño particular y de los objetivos del estudio, haciendo hincapié en la adecuación de cada método a cada situación concreta.
En el ámbito de la investigación médica, este tipo de técnicas proporciona una herramienta de análisis de datos muy interesante. Por ejemplo, se ha aplicado a la evaluación de curvas de glucemia1 y al estudio de la concentración de fármacos en sangre2. El estudio de curvas de crecimiento es otra de las aplicaciones muy frecuentes3. Otros ejemplos de aplicación serían el estudio del efecto de determinados tratamientos en el grosor de la córnea4 o la evaluación de un programa de vacunas de la hepatitis B5.
Desde un punto de vista técnico, y dada la importancia creciente de estas técnicas en medicina, han aparecido distintas revisiones que, desde distintos puntos de vista, analizan los principales métodos estadísticos de forma descriptiva6 o bien con una cierta base estadística7-10.
A pesar de que existe ya abundante información al respecto, no se encuentra una exposición de las distintas aproximaciones al análisis estadístico en estos ensayos en la que se haga más énfasis en el tipo de resultados que se pueden obtener con un ejemplo numérico de cada uno de los métodos que se pueden aplicar. Esta revisión se ha planteado con el objetivo de suplir este vacío.
Definiciones básicas
De cara a una mejor comprensión de los métodos de análisis en los diseños de medidas repetidas es preciso definir algunos conceptos estadísticos que son característicos de estos métodos. Se suele referir como covariables a aquellas variables o factores que pueden afectar a la respuesta. Estas covariables pueden clasificarse en dos categorías:
Internas (inner, within): varían en las observaciones de una misma unidad experimental. Por ejemplo, serían el tiempo, los tratamientos en un diseño cross-over, etc.
Externas (outer, between): se mantienen constantes para todas las observaciones de una misma unidad experimental. Por ejemplo, el sexo, los tratamientos cuando se administran a grupos de unidades experimentales, etc.
Dependiendo del número de medidas repetidas distinguiremos entre:
Diseños equilibrados: con un número fijo de medidas por unidad experimental, tomadas a los mismos instantes de tiempo para todas ellas y sin valores faltantes.
Diseños no equilibrados: con un número variable de medidas en cada unidad experimental, realizadas a distintos instantes de tiempo.
Debido a la multitud de aplicaciones que tiene esta metodología y a que existen diferentes aproximaciones estadísticas para analizar los datos, suele suceder que un mismo concepto aparezca en la bibliografía con distintos nombres. En particular, una primera aproximación al tema puede llevarnos a cierta confusión, tanto en lo que se refiere a la estructura de los datos y al diseño de los estudios como al mismo procedimiento estadístico de análisis de los mismos. Con el objetivo de facilitar la comprensión de los distintos conceptos, en la tabla 2 se definen los utilizados más frecuentemente. A lo largo de esta revisión, trataremos los diferentes métodos para el análisis de datos longitudinales. El estudio de los diseños cross-sectional queda fuera de los objetivos de este trabajo.
Aproximación univariante
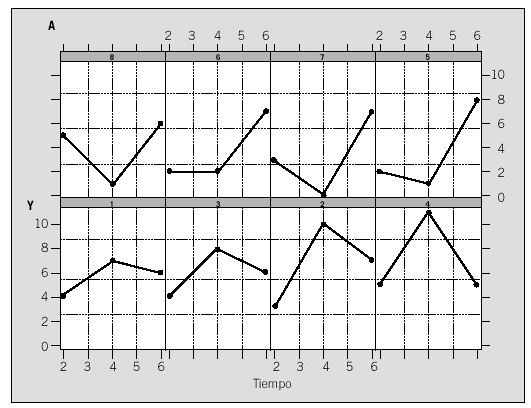
Supongamos que queremos estudiar el efecto de un tratamiento sobre una determinada enfermedad, y que para ello realizamos un ensayo clínico controlado en el que compararemos un grupo de individuos que han recibido el tratamiento respecto a otro grupo control (tabla 3). Cada individuo se ha observado en 3 instantes de tiempo que supondremos iguales para todos los individuos. Una primera aproximación al análisis de estos datos consiste en realizar una representación gráfica. Ésta puede hacerse individualmente (fig. 1a) o bien con un gráfico para cada grupo (fig. 1b).
Utilización del análisis de la varianza (ANOVA)
En el ejemplo de la figura 1 encontramos una situación típica de medidas repetidas en las que se pueden resaltar algunas características:
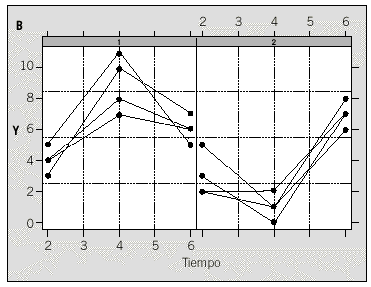
Figs. 1a y b. Representación de los datos de la tabla 3. A: Por individuos. B: por grupos.
Fig. 1b.
El comportamiento de ambos grupos a lo largo del tiempo no es igual. A pesar de que en ambos grupos la función se puede expresar mediante un polinomio de segundo grado, el hecho de que las curvas tengan una orientación opuesta indica que algunos coeficientes de los polinomios tendrán signo opuesto.
El comportamiento de todos los individuos de un mismo grupo es similar, aunque se pueden observar diferencias entre ellos respecto al comportamiento medio del grupo.
En algunos instantes de tiempo la variabilidad es mayor que en otros.
Una primera aproximación al problema consiste en plantear un diseño de análisis de la varianza que refleje de alguna forma la correlación que existe entre las observaciones de un mismo individuo. Un modelo adecuado sería:
donde *i corresponde al efecto del grupo (con i = 1,2 correspondiendo a control y tratamiento, respectivamente), ¼j(i) al efecto del individuo j (j = 1,2,3,4) del grupo i (indicamos entre paréntesis que cada individuo está exclusivamente está anidado en un grupo i), ßk el efecto del tiempo (k = 1,2,3) y los términos *ßik y ß¼kj(i) a las interacciones entre factores. Este tipo de diseño (conocido también como diseño split-plot) ha sido muy utilizado en el análisis de este tipo de datos a pesar de que son necesarios una serie de requisitos de difícil cumplimiento, sobre todo en el ámbito de los estudios clínicos. Estos requisitos son:
1. Homogeneidad de las matrices de covarianzas en cada grupo. Es decir la variabilidad de los datos en cada instante de tiempo tiene que ser la misma en todos los grupos y también la dependencia entre observaciones de un mismo individuo.
2. La matriz de covarianzas debe presentar la propiedad de simetría compuesta (compound symmetry), es decir la correlación entre observaciones alejadas en el tiempo, para un mismo individuo, ha de ser la misma independientemente de la distancia entre las observaciones.
3. El diseño debe ser equilibrado.
4. El número de individuos en cada grupo ha de ser el mismo.
La condición 2 es muy estricta, ya que requiere que exista la misma dependencia tanto entre dos observaciones seguidas en el tiempo como entre dos observaciones alejadas. En el caso particular de nuestro ejemplo se cumplen las condiciones para la aplicación del método univariante, por lo que procedemos a realizar el análisis correspondiente. La tabla 4 contiene los resultados del análisis de la varianza (tabla ANOVA).
A partir de estos resultados podemos concluir que hay diferencias entre los grupos, entre los tiempos y además la interacción entre el tiempo y el grupo también es significativa. Esta interacción se interpreta como un comportamiento distinto, en cada grupo, de la evolución de la variable medida a lo largo del tiempo. Este comportamiento viene expresado en términos de una función matemática. En este caso se ha estudiado si podemos admitir una función lineal o una cuadrática. Tal como se ve en la tabla 4 es la componente cuadrática la que es significativa (como ya se intuía en la fig. 1).
Utilización incorrecta del análisis
Frente a unos datos del tipo del ejemplo anterior, se podría pensar que un análisis válido y sencillo sería realizar una comparación de los grupos en cada instante (por ejemplo, una t de Student en caso de 2 muestras). Esta solución se observa frecuentemente en trabajos de investigación médica con una estructura de datos similar a la de este ejemplo. Sin embargo, los resultados obtenidos mediante esta aproximación no se pueden considerar como válidos debido a las siguientes razones:
No se tiene en cuenta la correlación de los datos para un mismo individuo a lo largo del tiempo.
El error asociado total sería mucho mayor que el que se obtiene cuando se realiza una sola prueba (es decir, estamos frente a un problema de comparaciones múltiples).
La forma de las curvas en cada grupo puede ser distinta (como en nuestro ejemplo) y eso no queda reflejado en el análisis tiempo a tiempo.
Normalmente el número de individuos utilizados en cada grupo es pequeño. Si se realiza un ANOVA, este problema no es grave ya que para realizar los contrastes se utiliza la información de todos los datos. Sin embargo, al realizar las comparaciones a cada instante de tiempo sólo se utilizan los datos de ese tiempo con lo que el análisis acostumbra tener una potencia (capacidad para encontrar diferencias entre grupos) muy baja.
Aproximación multivariante
En la mayoría de las situaciones experimentales relacionados con este tipo de diseño de datos no se cumplen las condiciones de aplicación del análisis anterior. En estos casos será necesario plantear nuevas aproximaciones que permitan resolver el problema de forma eficaz. Una solución consiste en utilizar las ventajas que ofrece el análisis multivariante de la varianza (MANOVA). Esta técnica no precisa de ningún requisito para la forma de la matriz de covarianzas (aunque sí es necesario que las matrices sean iguales entre grupos).
El MANOVA considera que todas la medidas repetidas de un mismo sujeto no son más que una observación multivariante y, por lo tanto, la comparación de grupos se realiza mediante la versión multivariante del análisis de la varianza. Este análisis será apropiado cuando se pretenda detectar diferencias entre grupos a partir del conjunto de medidas repetidas, pero no interesen tanto las medidas individuales a cada instante de tiempo.
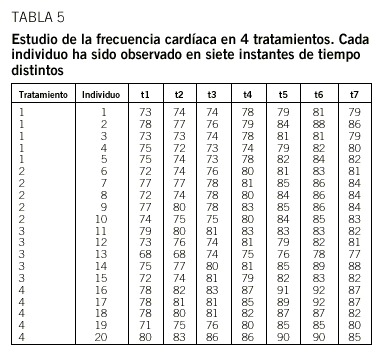
Desde un punto de vista de estructura de datos, y de forma similar al modelo anterior, los instantes de tiempo en los que se realizan las observaciones deben ser iguales para todos los individuos y se deben tener observaciones completas. A modo de ejemplo, la tabla 5 contiene un conjunto de datos acerca de la frecuencia cardíaca (latidos por minuto) medidos en 20 varones asignados al azar a cada uno de 4 tratamientos (5 personas por tratamiento) y medidos cada 5 minutos durante 7 intervalos de tiempo. El conjunto de estas medidas no cumple las condiciones requeridas en el análisis univariante comentadas anteriormente. Por lo tanto aplicaremos el método multivariante.
Análisis de perfiles
En el MANOVA, la forma explícita de realizar la comparación de grupos es mediante el llamado análisis de perfiles. Este análisis estudia la forma de las curvas asociadas a cada sujeto permitiendo profundizar en las causas de las diferencias observadas en las observaciones y obtener resultados similares al estudio univariante. Así se podrá estudiar:
La comparación de grupos, analizando la coincidencia de los perfiles de las curvas de los individuos de cada grupo.
El efecto del tiempo, es decir, la equivalencia de las respuestas a partir de la constancia de los perfiles.
La interacción entre el tiempo y el grupo, a partir del estudio del paralelismo de los perfiles.
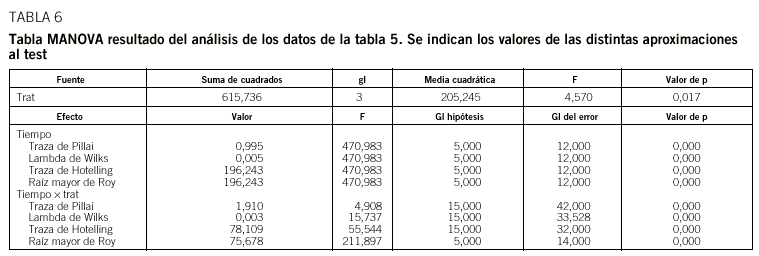
La tabla 6 contiene los resultados de aplicar el análisis MANOVA a los datos del ejemplo de la tabla 5. Para cada uno de los factores analizados aparecen 4 valores de test con su nivel de significación, y se observa que hay diferencias entre tratamientos, entre tiempos y en la interacción. De estos resultados cabe destacar el análisis de la interacción. Como la interacción entre el tiempo y el tratamiento es significativa, podemos concluir que los perfiles no son paralelos y, por lo tanto, el comportamiento de los individuos de los 4 grupos es distinto.
Modelos mixtos
Los 2 métodos anteriores no tienen en cuenta alguna de las características típicas de los datos con medidas repetidas. Estas características se ponían de manifiesto en el ejemplo de la figura 1 y se presentan frecuentemente en medicina. Así, por un lado se observa que existe una curva muy clara en la evolución de las observaciones de ambos grupos a lo largo del tiempo (en el ejemplo comentado, los resultados del gráfico sugieren un polinomio de segundo grado), siendo del mismo tipo para ambos grupos, pero seguramente con coeficientes distintos (la orientación del polinomio es distinta en cada grupo). Por otro lado, dentro de cada grupo se observa una gran variabilidad en las curvas individuales, lo que indica que un modelo que no tenga en cuenta este problema tendrá una variabilidad experimental muy grande, con lo cual no resultará eficaz para realizar el análisis. La aproximación a partir de los modelos mixtos es idónea para hacer frente a estos problemas ya que permite, por un lado, establecer la expresión funcional que explica la evolución de la medida observada a lo largo del tiempo y, por el otro, que los parámetros de esta función puedan variar de sujeto a sujeto. Así, podemos tener modelos lineales, que suponen que la relación se puede expresar mediante la ecuación de una recta o de un polinomio, o bien modelos no lineales que incluyen cualquier otro tipo de función. La decisión sobre el tipo de modelo puede ser un inconveniente en la utilización de estos modelos, ya que no siempre es fácil decidir cuál es la función que mejor se ajusta a nuestros datos.
A pesar de este inconveniente, los modelos mixtos presentan muchas ventajas frente a los modelos anteriores por varias razones:
Se basan en plantear un modelo para un individuo típico, i, al que se han realizado pi observaciones a instantes de tiempo ti1,ti2,...,tipi. En este modelo no es necesario tener los mismos instantes de tiempo para cada individuo ni observaciones completas. Tampoco es necesario que los grupos tengan el mismo número de unidades experimentales.
El modelo individual, con parámetros propios, consiste en una función (lineal o no lineal, aunque en nuestro caso, para simplificar, consideraremos que es lineal) cuyos coeficientes se expresan como una suma de 2 componentes: una componente poblacional, fija para todos los individuos y que representa el valor medio del parámetro dentro del grupo, y una componente aleatoria, distinta para cada individuo, que expresa la parte del parámetro que es propia de cada sujeto. Con ello los modelos mixtos recogen aquellas situaciones en las que los perfiles de los individuos de un mismo grupo puedan diferir entre sí.
Las matrices de covarianzas no tienen por qué tener una estructura concreta y además permiten dar un modelo para explicar la diferente variabilidad de los datos a lo largo del tiempo y para identificar la correlación entre las observaciones a lo largo del tiempo.
Modelo
En nuestro ejemplo, a partir de los gráficos de cada grupo (fig. 1), se puede concluir que un modelo apropiado podría ser un polinomio de segundo grado. El modelo mixto sería:
en el que yij es la respuesta del individuo i a tiempo tij; ß0, ß1 y ß2 corresponden a los parámetros poblacionales y b0i, b1i y b2i a la componente aleatoria de los mismos. El efecto del grupo se incorpora como un elemento más del modelo.
Desde un punto de vista teórico, se supone que b0i, b1i y b2i son variables aleatorias de media 0 y matriz de covarianzas desconocida *, y que los errores siguen una ley normal con una matriz de covarianzas i, con una estructura similar para todos los individuos diferenciándose solamente en la dimensión pues, tal como hemos indicado, cada individuo puede tener un número distinto de observaciones. En esta última matriz se recogen las varianzas a cada instante de tiempo y las covarianzas (correlaciones) entre los tiempos. Aparte de esta matriz, el hecho de que todas las observaciones de un individuo compartan los mismos valores de b0i, b1i y b2i es otra forma de expresar la correlación de los datos.
De forma general se puede expresar el modelo mixto como:
siendo yi el vector de pi observaciones repetidas del individuo i, Xi la matriz de diseño de los efectos fijos, Zi la matriz de diseño de los efectos aleatorios, bi el vector de efectos aleatorios N(0,*) y *i los residuos, N(0, i) siendo estos dos últimos independientes.
Análisis estadístico
El análisis estadístico de los modelos mixtos se basa en deducir y estimar el modelo que, con un mínimo número de parámetros, se ajusta a los datos experimentales. Para esto se sigue una serie de pasos sucesivos:
1. Se estima el modelo propuesto considerando que:
Todos los parámetros tienen una componente fija y aleatoria.
La matriz i tiene la estructura más sencilla posible, consistente en un valor de varianza igual a todos los tiempos (*2) e incorrelación de los datos. Es decir i = *2I.
Con este modelo los parámetros a estimar son: la componente fija de los parámetros (ß0, ß1 y ß2 en nuestro ejemplo), la estimación de los elementos de la matriz *(con lo que será posible conocer la estimación de las componentes aleatorias) y la estimación de *2.
2. A partir de los resultados obtenidos se reajusta el modelo siguiendo los siguientes criterios:
Si la varianza de la componente aleatoria de algún parámetro está cercana a cero, se elimina la componente aleatoria consiguiendo un modelo con menos términos y, por lo tanto, más fácil de interpretar.
Mediante el análisis de un gráfico de residuos del modelo se cambia la matriz i dándole una estructura concreta. Este paso puede presentar alguna dificultad y requiere una cierta experiencia.
3. Cada vez que se considera un nuevo modelo, a partir de la modificación de un modelo previo, es necesario comprobar la validez de la modificación mediante una prueba estadística que certifique la mejora del ajuste con el nuevo modelo. En caso de que el test estadístico indique una mejora significativa, se aceptará la modificación. En este proceso iterativo de mejora del modelo, un punto importante es el estudio de la influencia de las covariables que identifican a los grupos de individuos y que se introducen en el modelo como un factor más. En caso de que el factor sea significativo, podremos confirmar la diferencia entre las curvas experimentales de los distintos grupos.
Ejemplo de modelo mixto
A modo de ilustración, consideraremos un ejemplo clásico analizado por Little y Rubin11 y que corresponde al seguimiento del proceso de crecimiento en 11 niñas y 16 niños. A cada niño se le midió la distancia desde el centro de la pituitaria a la fisura maxilar, a las edades de 8, 10, 12 y 14 años. En este caso, se considera que la relación entre la medida y el tiempo es lineal. Los análisis han sido realizados mediante el paquete estadístico S-Plus12.
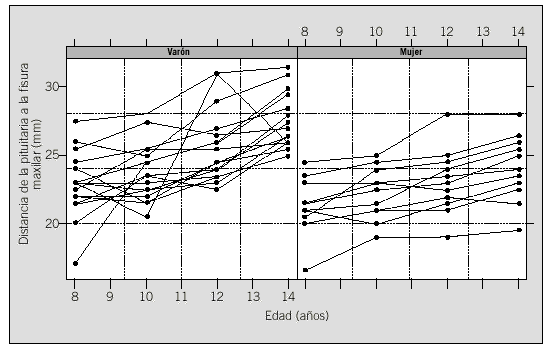
La figura 2 muestra, para cada sexo, la adecuación de un modelo lineal para explicar la relación entre la distancia y la edad. También se observa la presencia de algún niño con un comportamiento errático y que podría ser un candidato a ser excluido, aunque nosotros lo dejaremos en el análisis ya que la exclusión de observaciones debe hacerse en colaboración con el experimentador.
Fig. 2. Representación por sexos de los datos del ejemplo de la tabla 5.
A continuación se detallan los pasos seguidos para obtener el modelo definitivo con los resultados parciales que se han ido obteniendo y que justifican el proceso que se ha seguido. A lo largo del análisis se van a ir planteando distintos modelos que se estimarán y que nos permitirán determinar si se cumplen las hipótesis de igualdad de grupos. El primer ajuste realizado ha sido a un modelo mixto completo, es decir suponiendo que todos los parámetros del modelo tienen parte fija y aleatoria, con la matriz de varianzas y covarianzas de los efectos aleatorios sin una estructura particular que permita simplificar el modelo y con la matriz de varianzas y covarianzas de los errores igual a *2I. Este primer modelo (que llamaremos modelo I) es, por lo tanto:
donde yij es la distancia del niño i medida a la edad j, xij la edad j del niño i. La estimación de los parámetros que caracterizan este modelo son:
1. Para los efectos aleatorios, la estimación de las varianzas de los 2 parámetros y de la correlaciones entre ambos es suficiente para conocer la matriz *:
2. El valor de *2 es 1,716.
3.Para los parámetros fijos: ß0 = 16,7611, ß1 = 0,662, ambos significativos. El hecho de que ß1 sea significativo indica que hay diferencias a lo largo de la edad.
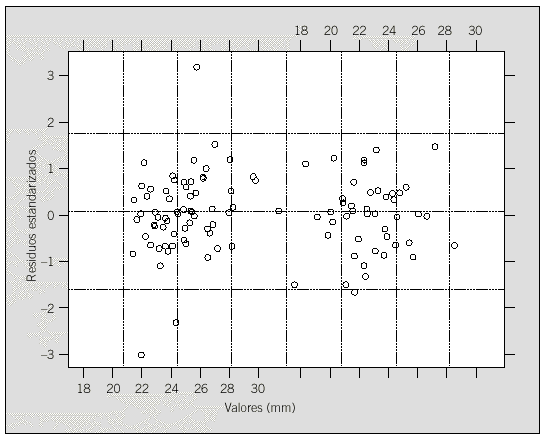
El gráfico de residuos (fig. 3) muestra una mayor variabilidad en los niños que en las niñas, con lo que se sugiere una estructura para la matriz i que incluya esta heterocedasticidad. El modelo propuesto consiste en una matriz en la que la varianza de los residuos toma dos valores: uno para las observaciones de los niños y otro para la de las niñas. A continuación se realiza la estimación de los parámetros anteriores: *2 (niños) = 2,707 y *2 (niñas) = 0,4418, y se ajusta un nuevo modelo (modelo II) corrigiendo el anterior a partir de las estimaciones de las varianzas obtenidas.
Fig. 3. Gráfico de residuos de modelo I correspondiente al análisis mediante la técnica de modelos mixtos (véase texto).
La comparación entre ambos modelos es significativa con un mejor ajuste para el segundo. El gráfico de residuos (que no se indica) muestra que en el modelo corregido los residuos ya no presentan heterocedasticidad. Como no se detecta la presencia de ninguna estructura de correlaciones para los residuos, se decide no analizar con más detalle la estructura de la matriz i.
Debido a que en la figura 2 se observaba que las rectas de los niños parecían distintas de las de las niñas, se continúa el estudio incluyendo la covariable Sex en el modelo inicial. La manera de incluirla consiste en definir el nuevo modelo (modelo III) con dos términos más, uno que recoge la influencia del sexo en las curvas y otro que recoge la interacción entre la edad y el sexo:
El análisis de la significación de los dos términos añadidos es equivalente al estudio del efecto grupo y de la interacción de las aproximaciones univariante y multivariante descritas previamente. Este nuevo modelo ajusta significativamente mejor que el anterior (el valor del estadístico de razón de verosimilitud es 11,75 con un valor de p de 0,0028). Como resultado del ajuste la estimación de los parámetros fijos de este nuevo modelo es:
ß0 = 16,857, ß1 = 0,516, ß2 = 0,632 y ß3 = 0,152, siendo ß2 no significativo.
Este hecho sugiere suprimir este término del modelo y ajustar un cuarto modelo (modelo IV). El nuevo modelo presenta un ajuste equivalente al tercero (el test de razón de verosimilitud es 0,5337 con un valor de p de 0,5021). Como que es más sencillo que el modelo III, ya que tiene un parámetro menos, se decide escoger este último como válido. Al haber excluido el término ß2Sex, se deduce que las rectas de los niños y las niñas tienen aproximadamente la misma ordenada en origen; es decir, no hay diferencias al inicio del ensayo entre ambos grupos, aunque la existencia de un término de interacción Sex*xij indica que la evolución de ambos grupos a lo largo de las distintas edades ha sido distinta.
El siguiente paso consiste en analizar si la parte del modelo propuesta para los efectos aleatorios puede ser simplificada. Recordemos que esto implica analizar con detalle la estructura de la matriz *. Debido a que en los resultados del primer modelo se observaba una correlación baja (0,609) vamos a considerar el caso en que sea nula. Para ello se ajusta un quinto modelo (modelo V) bajo esta suposición. La comparación con el anterior mediante el test de razón de verosimilitud da un estadístico de 0,4505 con un valor de p de 0,5021. Estos resultados muestran que no hay diferencias significativas entre ambos modelos, siendo el último más simple y, por lo tanto, el modelo definitivo escogido. Por lo tanto, el modelo que se ajusta mejor a las observaciones de los niños y las niñas es:
con
La utilización de los modelos mixtos aporta un buen conocimiento del tipo de estructura estadística subyacente a los datos aunque, tal como se observa en este ejemplo, su aplicación requiere conocer adecuadamente el método estadístico y tener una cierta experiencia en su aplicación.
Conclusiones
A lo largo de este trabajo, y mediante la discusión de los ejemplos, se ha intentado dar una visión comparativa de la forma de abordar el análisis de medidas repetidas en función del tipo de datos disponibles. Tal como se ha indicado, la aproximación univariante tiene como principal característica su facilidad de aplicación al poderse utilizar un software estándar para el análisis y, sobre todo, la facilidad de interpretación por la simplicidad de la técnica empleada. El principal inconveniente reside en la restricción que supone en la matriz de covarianzas, lo que delimita seriamente su campo de aplicación a casos muy concretos. Como primera alternativa, el método multivariante no tiene tantas restricciones en cuanto a la matriz de covarianzas, pero requiere que los datos sean equilibrados y completos, aspecto difícil de conseguir en los estudios médicos donde el seguimiento de los pacientes se realiza mediante visitas que no siempre se realizan en la fechas programadas. En este caso también se dispone de software estándar para realizar los análisis aunque la interpretación de los resultados ya no sea tan intuitiva como en el caso anterior.
Los modelos mixtos aportan una potencia de análisis que no permitían los métodos anteriormente indicados. Esta mejora en la capacidad de obtener el máximo de información de los datos va, no obstante, unida a una complejidad del método que determina que un usuario con conocimientos básicos de estadística no pueda realizar el análisis de forma eficiente. En este caso es necesario acudir a un especialista para que, utilizando un software específico, pueda obtener el mejor modelo y nos ayude a explicar el comportamiento de los datos obtenidos.