Aproximación metodológica al uso de redes neuronales artificiales para la predicción de resultados en medicina

En la práctica clínica, existe un gran interés en conseguir modelos de predicción precisos. Dentro de las posibles alternativas técnicas disponibles, las redes neuronales artificiales (RN) se utilizan cada vez más en medicina. En esta revisión realizamos primero una introducción a la metodología de RN, describiendo el funcionamiento del tipo de RN más utilizado, que es el perceptrón multicapa entrenado con algoritmo de retropropagación (MLP). A continuación, comparamos el MLP con la regresión logística (RL) y, finalmente, mediante un ejemplo con datos reales, mostramos un esquema práctico para realizar una aplicación basada en RN. La ventaja principal de las RN es su capacidad de incorporar efectos no-lineales e interacciones entre las variables del modelo sin necesidad de incluirlas a priori. Como mayores desventajas, las RN proporcionan un modelo donde es difícil la interpretación de los parámetros y que necesita de un cierto empirismo en su proceso de construcción y entrenamiento. Las RN son útiles para el cálculo de probabilidad de un resultado en función de un conjunto de variables predictoras y consiguen mejores resultados, en algunas situaciones, que la RL. Las metodologías de RN y RL son complementarias y nos ayudan a conseguir modelos más válidos.

In clinical practice, there is an increasing interest in obtaining adequate models of prediction. Within the possible available alternatives, the artificial neural networks (ANN) are progressively more used. In this review we first introduce the ANN methodology, describing the most common type of ANN, the Multilayer Perceptron trained with backpropagation algorithm (MLP). Then we compare the MLP with the Logistic Regression (LR). Finally, we show a practical scheme to make an application based on ANN by means of an example with actual data. The main advantage of the RN is its capacity to incorporate nonlinear effects and interactions between the variables of the model without need to include them a priori. As greater disadvantages, they show a difficult interpretation of their parameters and large empiricism in their process of construction and training. ANN are useful for the computation of probabilities of a given outcome based on a set of predicting variables. Furthermore, in some cases, they obtain better results than LR. Both methodologies, ANN and LR, are complementary and they help us to obtain more valid models.

Introducción

La toma de decisiones es un punto clave en la práctica médica, tanto en el proceso diagnóstico como en el terapéutico. En cualquier situación, estas decisiones deben estar avaladas por criterios de evidencia y experiencia. Para ello, es preciso recoger y procesar adecuadamente la información referente al estado de salud del paciente (historial, exploración o pruebas diagnósticas, etc.) y confrontarla con la evidencia acumulada en el seguimiento de grupos amplios de pacientes en condiciones controladas. La información disponible se concreta en distintos tipos de variables que reflejan la condición del paciente. A partir de estas variables, es necesario aplicar criterios objetivos que permitan extraer una conclusión adecuada acerca de la posible evolución de la enfermedad, la posibilidad de complicaciones, etc. Considerando la complejidad del problema, la evaluación de la información debe hacerse desde una perspectiva multivariante, de manera que se consideren simultáneamente todas las variables implicadas y se obtenga una generalización adecuada que permita una clasificación apropiada de nuevos casos.

Las técnicas estadísticas multivariantes proporcionan una solución a este tipo de problemas. Así, el análisis discriminante puede utilizarse en la obtención de un criterio diagnóstico a partir de los valores de varias variables, mientras que el análisis de supervivencia permite evaluar convenientemente la contribución de diversas variables a la supervivencia en distintas circunstancias de interés médico. Por otra parte, el análisis de regresión logística (RL) es adecuado cuando se quiere desarrollar un modelo de predicción de un determinado suceso, en general la probabilidad de complicaciones asociadas a un tratamiento o al estado del paciente.

Todas estas técnicas han conocido un auge muy importante en su utilización en medicina. Este auge se justifica, en parte, por su fácil disponibilidad al estar incluidas en casi todos los paquetes estadísticos de uso habitual. Sin embargo, como sucede con cualquier técnica estadística, su utilización debe tener en cuenta las condiciones apropiadas de aplicación, que en general se referirán a la distribución de las variables con las que se trabaja, la independencia entre ellas, etc.

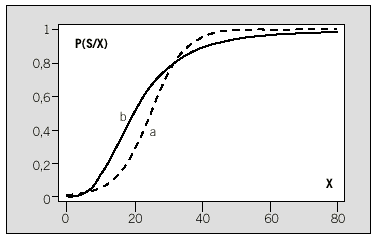
En el caso particular de la regresión logística, ésta tiene unas condiciones específicas de utilización y unas limitaciones en la interpretación de las conclusiones. Básicamente, la RL parte del supuesto de independencia de las variables y considera un modelo específico de asignación de probabilidades (modelo logístico)¹. Cuando estas condiciones no se cumplen, especialmente debido a la dependencia entre las variables consideradas o a efectos no-lineales no incluidos en el modelo, los resultados de la aplicación de esta técnica son discutibles y pueden estar alejados de la realidad (fig. 1). En estas situaciones, es posible utilizar modelos más elaborados que incluyan interacciones entre las variables y efectos no-lineales. Sin embargo, cuando el problema contiene un elevado número de variables predictoras, su complejidad determina que en la práctica se convierta en un problema difícil de abordar y resolver mediante las técnicas habituales. En este caso, una posible alternativa al empleo de este tipo de análisis basados en técnicas estadísticas, más o menos clásicas, la encontramos en metodologías propias de otros campos científicos, como puede ser la inteligencia artificial. En particular, las redes neuronales artificiales (RN) son capaces de desarrollar un modelo de predicción que incorpora automáticamente relaciones entre las variables analizadas sin necesidad de incorporarlas explícitamente en el modelo.

Fig. 1. El modelo logístico. El modelo logístico (a) considera que la función logística representa la relación entre los valores de la variable X y la probabilidad del suceso P(S/X). Si esta relación no se cumple, entonces el método puede proporcionar resultados erróneos. En (b), la P(S/X) se relaciona de manera logística con el Log(X). Si este hecho no se incluye en el modelo, las conclusiones serán erróneas. La RN puede incorporar estas relaciones sin necesidad de formularlas explícitamente.

El objetivo de esta revisión es proporcionar un acercamiento a la metodología de las RN en el contexto de la medicina, tomando como ejemplo su utilización como alternativa a la RL. Empezaremos presentando las ideas generales acerca de las RN y comentando los procedimientos básicos de desarrollo de una red adecuada para el cálculo de probabilidad de un resultado en función de un conjunto de variables predictoras. Mostraremos un esquema práctico para realizar una aplicación basada en esta técnica, y mediante un ejemplo podremos apreciar algunos de los detalles críticos del proceso de entrenamiento y las ventajas e inconvenientes frente a métodos estadísticos alternativos.

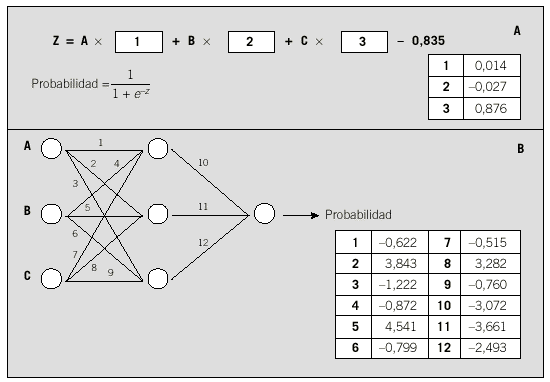
Figs. 8a y b. Número de parámetros. En nuestro ejemplo, el modelo de regresión logística (A) sólo precisa de 3 parámetros (coeficientes de la ecuación logística) para el cálculo de la probabilidad de presentar fracaso renal. La red neuronal (B) ha conseguido mejores resultados, pero necesita 12 parámetros (pesos de las conexiones). (A): edad; (B): valor de presión arterial media, y (C): presencia de infección.

¿Qué son las redes neuronales artificiales?

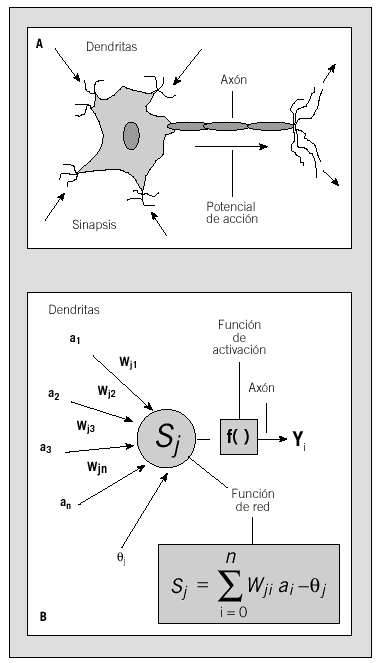
Una RN es un algoritmo de cálculo que se basa en una analogía del sistema nervioso. La idea general consiste en emular la capacidad de aprendizaje del sistema nervioso, de manera que la RN aprenda a identificar un patrón de asociación entre los valores de un conjunto de variables predictoras (entradas) y los estados que se consideran dependientes de dichos valores (salidas). Desde un punto de vista técnico, la RN consiste en un grupo de unidades de proceso (nodos) que se asemejan a las neuronas al estar interconectadas por medio de un entramado de relaciones (pesos) análogas al concepto de conexiones sinápticas en el sistema nervioso. A partir de los nodos de entrada, la señal progresa a través de la red hasta proporcionar una respuesta en forma de nivel de activación de los nodos de salida³. Los valores de salida proporcionan una predicción del resultado en función de las variables de entrada. Desde el punto de vista de implementación práctica, los nodos son elementos computacionales simples que emulan la respuesta de una neurona a un determinado estímulo. Estos elementos, como las neuronas en el sistema nervioso, funcionan como interruptores: cuando la suma de señales de entrada es suficientemente alta (en el caso de una neurona diríamos que se acumula suficiente neurotransmisor), la neurona manda una señal a las neuronas con las que mantiene contacto (se genera un potencial de acción). Esta situación se modela matemáticamente como una suma de pesos de todas las señales de llegada al nodo que se compara con un umbral característico. Si el umbral se supera, entonces el nodo se dispara, mandando una señal a otros nodos, que a su vez procesarán esa información juntamente con la que reciben de nodos adyacentes (fig. 2). Evidentemente, la respuesta de cada nodo dependerá del valor de las interacciones con los nodos precedentes dentro de la estructura de la red. Como en el caso del sistema nervioso, el poder computacional de una RN deriva no de la complejidad de cada unidad de proceso sino de la densidad y complejidad de sus interconexiones⁴.

Figs. 2a y b. Comparación entre la neurona biológica (A) y la neurona artificial (B). (Véase texto.)

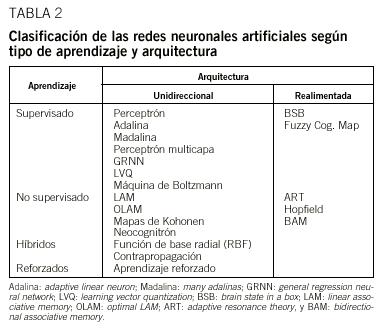
La primera implementación práctica de estas ideas se describe en los trabajos de McCulloch y Pitts en 1946. A partir de este punto, algunos de los hitos principales en la investigación de este tipo de técnicas fueron: el diseño por Widrow y Hoff (1961) de la red conocida como Adalina (capaz de resolver problemas de regresión lineal), el desarrollo de la red con estructura de perceptrón simple en 1959 (con equivalencia al análisis discriminante y regresión logística) y las redes multicapa por Rosenblatt en 1986 (que permiten la resolución de situaciones no lineales). Por otra parte, los trabajos teóricos de Bishop y la aportación sobre redes autoorganizadas de Kohonen dotaron de fundamentos formales a este tipo de técnica⁵. A partir de los trabajos pioneros, el interés sobre esta metodología se ha difundido a casi todos los ámbitos de la ciencia. Los distintos aspectos técnicos y las implicaciones de su utilización han sido investigados desde muchos puntos de vista, interesando, entre otros, a matemáticos, físicos, neurólogos, ingenieros, programadores y filósofos. En medicina las áreas de aplicación se han multiplicado rápidamente en la última década (tabla 1)^6-8, incrementándose continuamente el número de publicaciones que incluyen esta metodología²⁵.

Desde un punto de vista práctico, existen muchos tipos de RN. En la tabla 2 se recogen las más características. Para clasificarlas, podemos considerar dos criterios básicos: el modo de aprendizaje y el flujo de información. En una red, el modo de aprendizaje puede ser supervisado, es decir, la red recibe los patrones de entrada y la respuesta observada que debe aprender; o no supervisado si la red reconoce automáticamente en los datos el patrón que debe aprender. Por otra parte, el flujo de información que manejan puede ser unidireccional, cuando la información sigue una dirección única desde los nodos de entrada a los de salida; o realimentado, donde el flujo de información no es único al incorporar circuitos de realimentación entre capas de la red. En una primera aproximación, indicaremos que las redes unidireccionales con aprendizaje supervisado pueden utilizarse para muchos problemas de interés médico.

El perceptrón multicapa como ejemplo de RN de aplicación en medicina

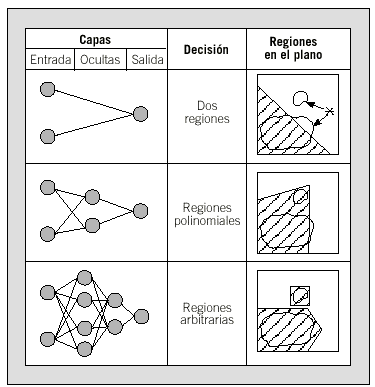
Dentro de las redes supervisadas unidireccionales, la estructura más utilizada es el llamado perceptrón multicapa (MLP, multilayered perceptron). La arquitectura típica de este tipo de red está constituida por varias capas de nodos con interconexión completa entre ellos. El caso más sencillo en este tipo de red consiste en sólo 2 capas de neuronas, las de entrada y las de salida. De esta manera, podemos obtener un modelo adecuado para problemas lineales del tipo de la regresión lineal múltiple. Si queremos analizar problemas no-lineales, es necesario incorporar otras capas de neuronas intermedias u ocultas (hidden units) (fig. 3).

Fig. 3. Capacidad de decisión de las redes neuronales artificiales (perceptrón multicapa). Con 2 variables de entrada, ante un problema de clasificación complejo en el plano (*) una red sin capa oculta no puede resolverlo; el aumento en el número de capas y nodos ocultos permite encontrar la solución.

En este tipo de red, una neurona recibe distintas entradas y activa una función de red (o regla de propagación) con unos pesos de entrada asociados (fig. 2). La computación de estos pesos se sigue de la aplicación de la función de activación que determina el nivel de activación de salida de la neurona. La entrada de las neuronas de la primera capa (entrada) son los valores de las variables predictoras y los niveles de activación de las neuronas de la última capa (salida) son los resultados de la red²⁶. Dentro de los parámetros que definen una red, la función de red más utilizada es de tipo lineal, y como función de activación más empleada está la función sigmoidea.

Proceso de entrenamiento

El entrenamiento consiste en la presentación repetida de un conjunto suficientemente amplio de datos de entrenamiento (training set), formado por las entradas y los valores correspondientes de las variables a predecir, hasta conseguir que los pesos internos (interacciones entre nodos) conduzcan a resultados óptimos en la capa de salida, acercándose lo más posible a los resultados esperados. En un contexto médico, el entrenamiento consistiría en presentar a la red, de forma iterativa, los valores de distintas variables clínicas (en forma de valores de la capa de entrada) de cada paciente y conseguir que la red sea capaz de predecir el estado final observado en cada paciente (indicados por el estado de las capas de salida de la red) de la manera más precisa posible.

En la práctica, el ajuste de los pesos durante el entrenamiento se consigue mediante un proceso iterativo cuya finalidad es minimizar una función de error que cuantifica la discrepancia entre las predicciones de la red y los valores observados en la muestra. La medida más utilizada para evaluar el error en la predicción (función de coste) es la raíz cuadrada del error cuadrático medio (RME, root-mean-square-error) entre los valores de salida de la red y sus valores esperados según los datos disponibles. El proceso comienza calculando el RME asociado a la red con los pesos aleatorios de inicio (red no entrenada). Por ejemplo, en una red con sólo 3 capas (una sola oculta), una vez calculado este error, se modifican, de forma retrógrada, los pesos de entrada de los nodos de salida (tercera capa) y se calcula para cada neurona oculta (segunda capa) un error próximo. Una vez conocido este error vuelven a actualizarse los pesos de entrada para cada neurona oculta. Este proceso se repite cíclicamente para cada iteración del proceso de entrenamiento. La presentación de los datos en cada ciclo puede hacerse con la totalidad de los mismos, siendo esta estrategia la más habitual, o fraccionando en distintos lotes el conjunto de entrenamiento. Esta última estrategia puede conseguir un mejor aprendizaje en algunas aplicaciones. Observamos que en este tipo de red, el flujo de información es unidireccional (de entrada a salida) pero el flujo de actualización del error es retrógrado (backpropagation).

En algunos casos, el proceso de entrenamiento de una red puede llevar a situaciones no deseadas. El riesgo principal consiste en que la red aprenda los ejemplos pero sea incapaz de dar respuestas convenientes en nuevos casos. Para evitar este problema, el proceso de entrenamiento debe considerar otras estrategias adicionales.

Validación cruzada

Para elaborar una red que sea eficaz es conveniente dividir los datos en 3 conjuntos, atendiendo a que cada uno de ellos mantenga la representatividad de la población origen: a) el conjunto de entrenamiento (training set); b) el conjunto de verificación (test set), y c) un conjunto de validación (validation set).

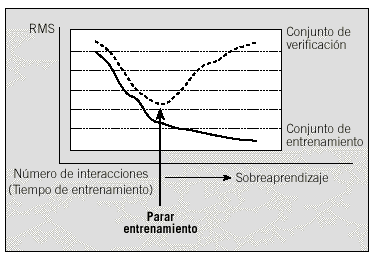
El conjunto de entrenamiento se usa para ajustar los pesos durante la fase de entrenamiento, mientras que el conjunto de verificación se utiliza para decidir cuándo parar el proceso de entrenamiento. Como criterio general, el entrenamiento debe pararse cuando el error del conjunto de verificación sea mínimo. De esta manera, nos aseguramos que la red es capaz de predecir correctamente los resultados de un conjunto de datos que no forman parte de los ejemplos de entrenamiento. Esta técnica se denomina validación cruzada (crossvalidation). Si continuamos el entrenamiento más allá de este punto, la red empieza a aprender de memoria los datos del conjunto de entrenamiento pero pierde capacidad de generalización (fig. 4).

Fig. 4. Criterio de parada del proceso de entrenamiento. RMS: raíz cuadrada del error cuadrático medio.

La búsqueda de una generalización óptima, que es la capacidad de la red de proporcionar una respuesta correcta ante patrones que no han sido empleados en su entrenamiento, requiere que se cumplan tres condiciones: a) que la información recogida en las variables sea suficiente --es decir, una selección apropiada de las variables y una buena calidad en la recogida de datos­; b) que la función que aprenda la red sea suave --pequeños cambios en las variables de entrada produzcan pequeños cambios en las variables de salida­, y c) que el tamaño de la base de datos sea suficiente. De esta manera aseguramos que el conjunto de entrenamiento sea representativo de la población a estudio²⁶. Excepto la segunda condición, el resto de los requisitos son comunes a cualquier técnica multivariante que se emplee.

Una vez finalizado el entrenamiento, la red (entrenada) evalúa el conjunto de validación y produce las correspondientes predicciones con datos que no se han utilizado en el entrenamiento ni en la validación cruzada. Esta prueba final nos aporta un resultado independiente acerca de la capacidad de generalización de la red.

Tamaño y arquitectura de la red

La arquitectura de una red viene determinada por el número de capas y nodos que la forman. La complejidad de la red viene determinada por el número de interconexiones que contiene. En general, no es inmediato establecer de forma exacta cuál será la arquitectura ideal para cada aplicación. Así, problemas de discriminación lineal o de regresión logística pueden solucionarse con redes simples. Los problemas surgen al enfrentarse a modelos más complicados (fig. 3). En aplicaciones médicas, un MLP con una única capa oculta puede ser adecuado en muchos casos. Existen algoritmos evolutivos que determinan, de forma automática, esta arquitectura óptima al aumentar o retirar nodos o capas del modelo. En cualquier caso, la arquitectura óptima debe alcanzarse, en la práctica, mediante un proceso iterativo, validando la capacidad predictiva de las distintas arquitecturas consideradas. Por otra parte, cuanto más compleja sea una red, mayor número de parámetros o pesos deberemos estimar y, por lo tanto, necesitará mayor número de patrones para ser entrenada de manera adecuada.

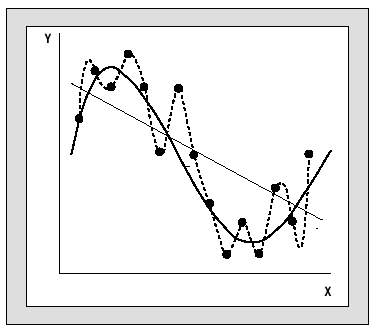
En el otro extremo, la utilización de una red demasiado compleja para solucionar un problema sencillo nos conduce a un sobreajuste (overfitting) que dificulta la capacidad de generalización de la red (fig. 5). Como regla general, para reducir el número de parámetros de una red es conveniente seleccionar apropiadamente las variables de entrada, descartando variables poco informativas. Sin embargo, esta selección no es tan sencilla como en los métodos multivariantes habituales y puede requerir distintas etapas de entrenamiento. Desde un punto de vista más técnico, existen procedimientos propios de la metodología de redes que simplifican la estructura de la red. A modo de ejemplo, algunos de estos métodos consisten en compartir pesos entre varios nodos (weight sharing), realizar un podado de la red (pruning) eliminando los pesos con menor influencia en el resultado del modelo final o aplicar el método de decaimiento de pesos (weight decay), eliminando automáticamente los pesos que tienden a cero²⁶.

Fig. 5. Búsqueda de la generalización. Relación entre complejidad de arquitectura y resultados. En un problema definido por dos variables (x­y). Los puntos representan los datos. La línea recta es el ajuste con una red sin capa oculta. La línea curva representa el ideal de generalización que se ha conseguido con 3 nodos en la capa oculta. La línea de puntos representa un sobreajuste al utilizar una red con 6 nodos en la capa oculta lo que origina una perdida de generalización.

Correspondencia entre redes neuronales artificiales y técnicas estadísticas

En el ámbito de la medicina, la utilización de las RN se ha desarrollado paralelamente a su comparación con técnicas estadísticas. Dependiendo del problema específico estudiado, esta confrontación ha llevado, durante esta última década, a alternar entre el optimismo^27,28 y el pesimismo^29,30 en la utilización de las redes en el entorno de los estudios médicos.

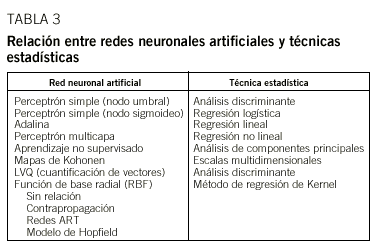
La tabla 3 recoge la correspondencia entre algunas redes y distintos procedimientos estadísticos habitualmente utilizados en medicina. Es interesante apreciar que existen algunos tipos de redes que no poseen una correspondencia concreta con un método estadístico³¹. La comparación más frecuentemente analizada en la literatura se realiza entre el tipo de red más empleada (MLP + backpropagation) y la regresión logística múltiple^32,33. En la tabla 4 se muestran algunos puntos destacando las ventajas y desventajas de las redes de acuerdo con esta comparación. En una revisión de 28 aplicaciones distintas a partir de la bibliografía, Sargent concluye que las redes son, en el peor de los casos, equivalentes o en general ligeramente superiores a la regresión logística múltiple al no tener que depender de exigencias rígidas de independencia de las variables o de los supuestos inherentes al modelo logístico³⁴.

En una aplicación concreta, las redes pueden interpretar de manera distinta la información contenida en las variables respecto a cómo se interpreta esta información en un procedimiento estadístico. Esto nos obliga a analizar cuidadosamente la distinta contribución de cada variable al modelo final y a interpretar sus interdependencias^35-37. A partir de este análisis es posible mejorar los modelos estadísticos (por ejemplo, añadiendo interacciones encontradas entre las variables). De este modo, ambas técnicas pueden colaborar para proporcionar un modelo final adecuado al problema objeto de estudio.

Indicaciones prácticas acerca de la aplicación de una red neuronal artificial en el entorno de predicción de resultados en medicina (cálculo de una probabilidad)

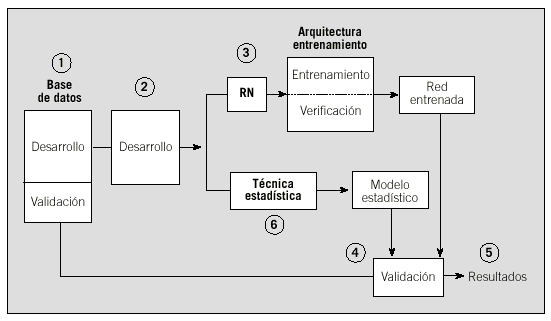
El desarrollo de una RN necesita planificarse adecuadamente para conseguir una red convenientemente entrenada que alcance una precisión óptima³⁸. A modo indicativo, en la figura 6 se muestra un esquema básico de actuación y en la tabla 5 se señalan, de acuerdo con el trabajo de Schwarzer et al, los errores más frecuentes cometidos en trabajos publicados que no han seguido esta planificación³⁹.

Fig. 6. Secuencia del desarrollo de una aplicación basada en red neuronal artificial. RN: red neuronal artificial. (Véase texto.)

Para facilitar una aproximación práctica al uso de esta metodología, planteamos un ejemplo sencillo basado en datos reales con el que seguiremos los distintos pasos. Supongamos que queremos identificar a los pacientes que desarrollarán fracaso renal (definido con criterios estándar) durante su ingreso en una unidad de cuidados intensivos. Para ello, decidimos analizar un modelo que utiliza 3 variables predictoras (simplificamos el problema para hacerlo más didáctico). Las variables consideradas son la edad, el peor valor de tensión arterial media en su primer día de estancia y la identificación de una infección dentro del diagnóstico de entrada. Sabemos que en nuestra serie es más frecuente tener fracaso renal si el paciente tiene más edad, menos presión arterial y diagnóstico de infección. Pero también sospechamos que las variables no son independientes, ya que los pacientes con infección tienden a tener una presión arterial menor, algunos grupos diagnósticos (definidos por su edad) presentan un mayor número de infecciones y la edad condiciona algunos aspectos de la presión arterial. Por lo tanto, debemos buscar un modelo que puede recoger estas relaciones. La variable de resultado será la probabilidad de tener fracaso renal.

Paso 1: base de datos adecuada

El resultado obtenido con una RN depende de los datos que se utilizan para su entrenamiento y, por lo tanto, los sesgos de muestreo pueden influir negativamente el resultado. Aunque se han conseguido buenos resultados con series muy grandes (80.606 pacientes)⁴⁰ o muy pequeñas (sólo 74 casos)⁴¹, se recomienda utilizar, como mínimo, 5-10 observaciones por parámetro estimado, es decir por cada una de las conexiones de la red. Por ejemplo, una red con 17 variables de entrada, 9 nodos en la capa oculta y un nodo de salida (todos plenamente interconectados) tiene 162 parámetros (son 17 por 9 más 9) que exigen un conjunto de entrenamiento mayor de 800 casos⁴².

Para nuestro ejemplo disponemos de una base de datos con 1.000 pacientes, de los que 310 presentaron fracaso renal.

Paso 2: conjuntos de entrenamiento, verificación y validación

La partición de la serie de datos en los conjuntos de desarrollo (entrenamiento y verificación) y el correspondiente conjunto de validación, determina que el tamaño muestral sea suficientemente grande. En aquellos casos en que no sea así, se ha propuesto la utilización de técnicas de remuestreo (bootstrap) con lo que se consigue tener múltiples conjuntos de entrenamiento que aseguran, dentro de las posibilidades y limitaciones de estas técnicas, un proceso de entrenamiento adecuado que conducirá a una buena generalización⁴³. En nuestro ejemplo sobre fracaso renal, la división (de forma aleatoria) aporta 400 pacientes para entrenamiento, 300 para verificación y 300 para validación.

Paso 3: construcción y entrenamiento de la red

Las características de las redes neuronales determinan que su utilización requiera de programas informáticos adecuados. En este punto, existen múltiples opciones comerciales y de libre distribución⁴⁴. Para una referencia actualizada al respecto, el lector interesado puede consultar la página ftp://ftp.sas.com/pub/neural/FAQ.html. En nuestro caso, utilizamos el programa Qnet (Vesta Services Inc). Usando estos programas, podemos empezar a probar qué arquitectura es más conveniente. Ya hemos comentado que este proceso es básicamente empírico. Podemos citar ejemplos que funcionan con estructuras muy simples (19 nodos de entrada/2 nodos ocultos/1 nodo de salida)⁴⁵ o muy complejas (16/35/10/1)¹². En cualquier caso, en la publicación de resultados deben describirse todos los parámetros de construcción (capas, nodos, tipo de interconexiones) y del proceso de entrenamiento (tipo, número de iteraciones, coeficiente de aprendizaje, momento, etc.).

Siguiendo con nuestro ejemplo, utilizamos un perceptrón multicapa entrenado con algoritmo de backpropagation con 3 capas, seleccionando como arquitectura óptima una estructura (3/3/1) con plena interconexión. La función de activación es sigmoidea, parando el entrenamiento, según el criterio de validación cruzada a las 1.500 iteraciones. De acuerdo con esta arquitectura, debemos ajustar 12 parámetros, con lo que los 400 casos del conjunto de entrenamiento son suficientes de acuerdo con el criterio general.

Paso 4: validación de la red

Debe comprobarse la capacidad de generalización de la red enfrentándola a datos distintos de los utilizados en su entrenamiento (conjunto de validación). En este ejemplo, disponemos de 300 casos en el conjunto de validación.

Paso 5: evaluación de los resultados (precisión de la red)

En este ejemplo se trata de predecir la probabilidad de fracaso renal. En este tipo de problemas, donde la predicción es una probabilidad, lo indicado es evaluar la discriminación y la calibración de la red^46,47. Para valorar la discriminación (capacidad de distinguir entre dos estados) se emplean tablas de contingencia eligiendo punto de corte (normalmente 0,5), estableciendo porcentajes de correcta clasificación y analizando las curvas ROC resultantes (especialmente calculando el área bajo la curva ROC)^48,49. Para comprobar la calibración (exactitud del modelo comparando la probabilidad esperada y la observada) se utilizan las pruebas de bondad de ajuste de Hosmer-Lemeshow⁵⁰ que permiten evaluar las curvas de calibración correspondientes a los resultados del método.

Paso 6: comparación de los resultados entre redes neuronales artificiales y regresión logística

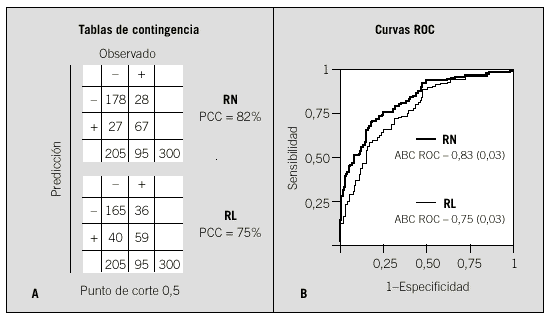
En nuestro ejemplo, comparamos el resultado de la red con los correspondientes a un modelo de regresión logística múltiple que utiliza las 3 variables indicadas anteriormente. Al comparar los resultados (en este caso sólo medimos la propiedad de discriminación con tablas de contingencia y curvas ROC) (fig. 7), podemos comprobar que la red consigue resultados más apropiados. Estos mejores resultados de la red tienen como contrapartida una necesidad de utilizar más parámetros (12) que la regresión logística (3) (fig. 8).

Figs. 7a y b. Resultados de la comparación entre un modelo basado en red neuronal artificial (RN) y otro basado en regresión logística múltiple (RL). Aplicado al conjunto de validación del ejemplo seguido en el texto con 300 pacientes. A: tablas de contingencia donde se evalúa como resultado positivo (+) presentar un fracaso renal; PCC: porcentaje de correcta clasificación. B: curvas ROC; ABC ROC: área bajo la curva ROC (error típico).

Para que la RL se aproxime a los resultados de la RN en este ejemplo, debemos añadir algunos términos de interacción para tener en cuenta la dependencia entre las variables. Sin embargo, es difícil decidir qué términos deben ser incluidos. Si el problema implica más variables, este escollo puede ser difícilmente superable.

Conclusiones

Las RN proporcionan un método general para desarrollar modelos de predicción en medicina. La ventaja principal de esta técnica, si se aplica convenientemente, radica en su capacidad para incorporar interacciones entre las variables sin necesidad de incluirlas a priori. Además, su aplicación no queda restringida a un tipo determinado de distribución de los datos. Como principal desventaja, sin embargo, debemos indicar que proporciona un modelo que es esencialmente una caja negra. La RN es capaz de predecir resultados, pero no disponemos de una interpretación evidente de los parámetros en los mismos términos en que podemos interpretar los resultados de una RL.

En esta revisión hemos considerado fundamentalmente el modelo de red más sencillo. En la actualidad se trabaja con nuevos tipos de redes más potentes y que incorporan técnicas adicionales como son los algoritmos genéticos y los modelos híbridos^52-54. Con ello, se empieza a disponer de herramientas que se fundamentan en el cálculo intensivo y que desafían a los planteamientos estadísticos convencionales. A nuestro entender, lejos de representar una amenaza, estas técnicas proporcionan nuevos puntos de vista que pueden ayudar a obtener herramientas más eficaces en muchas aplicaciones prácticas. Así, el futuro no debería plantearse en términos de competencia entre estos nuevos métodos y la estadística, sino que debería contemplar su acercamiento y complementación para construir modelos de predicción que sean más válidos.