Introducción
En la actualidad, la mayoría de las instituciones y la Administración recogen sistemáticamente información de las regiones de las áreas geográficas que gestionan. Estas bases de datos almacenan sus características ambientales, poblacionales, epidemiológicas, etc. y dan lugar a distintos sistemas de información que pueden estar conectados entre sí por el común denominador de la región geográfica donde se han realizado las medidas. Si las regiones tienen medida su posición geográfica y vinculada a ella su información, los datos están referenciados geográficamente y forman un sistema de información geográfica (SIG).
Los sistemas con información referenciada geográficamente que almacenan datos relacionados con la salud de las comunidades se denominan sistemas de información geográficos sanitarios (SIGS) y su análisis numérico tiene como principales objetivos1,2: a) facilitar la identificación de áreas y/o poblaciones con mayores necesidades insatisfechas de salud, de manera que permita tomar decisiones de una forma ágil y focalizar hacia esos grupos prioritarios las intervenciones; b) facilitar la identificación de los patrones espaciales del riesgo de morbilidad o mortalidad con el propósito de buscar hipótesis sobre sus causas, y c) evaluar la relación entre los niveles de exposición promedio de un factor de riesgo y la carga de morbilidad o mortalidad.
Una parte importante de los datos que almacenan los SIGS son recuentos de la presencia de un episodio en función de las regiones en que se divide el área geográfica de estudio. Pero cuando se analiza esta información, lo más usual es expresar los recuentos de casos en función de la población en que se detectan. En epidemiología esta razón recibe el nombre de tasa y se puede interpretar como una medida de riesgo.
Los procedimientos estadísticos que se deben aplicar para modelar este tipo de datos deben tener en cuenta que, si las tasas siguen patrones de distribución espacial, la información de las regiones próximas estará correlacionada y por tanto se violará la asunción de independencia que exigen los métodos estadísticos clásicos. Las herramientas de análisis numérico que se usan para construir y analizar los modelos de información geográfica se aglutinan con el nombre de estadística espacial, y en este entorno el uso de mapas, particularmente si son computarizados, es el método más efectivo para la transmisión de los resultados de los análisis.
El punto de partida del uso de los modelos de información geográfica en medicina podemos situarlo en 1986, a partir de un trabajo de Gesler3 donde se lleva a cabo una revisión acerca de los usos del análisis espacial en la geografía médica. Desde entonces, y especialmente en los últimos 10 años, se han realizado experiencias que han tenido y tienen como objetivo integrar un conjunto de herramientas en un sistema automatizado capaz de recoger, almacenar, manejar, analizar y visualizar información referenciada geográficamente4. Mientras los sistemas de información se pueden crear usando los paquetes de gestión de bases de datos habituales, por ejemplo Access, FoxPro, etc., los SIG que permiten visualizar la información usando mapas necesitan aplicaciones informáticas como el SIGEpi5 y el ArcGis6.
Este artículo tiene como objetivo presentar y comentar algunos de los métodos estadísticos que se utilizan para analizar datos agrupados (tasas) con correlación espacial. Primero, se enumeran las limitaciones de los procedimientos clásicos y, posteriormente, se presentan las extensiones de éstos para poder realizar análisis geográficos que tengan en cuenta la correlación espacial. Por último, se aplica la metodología expuesta a los datos de incidencia de diabetes tipo 1 en Cataluña para mostrar las diferencias de los resultados. El desarrollo de este ejemplo se ha realizado siguiendo el proceso de análisis necesario para comparar tasas de mortalidad o morbilidad de las regiones de un área y evaluar si presentan un patrón de distribución espacial.
Metodología estadística
Estandarización
Cuando se quieren comparar las tasas de 2 o más poblaciones, el uso de las tasas brutas lleva a resultados incorrectos ya que las diferencias que se pueden observar entre regiones pueden ser imputables no sólo a la intensidad de la característica que se está estudiando, sino también a la estructura de la población respecto a una o más variables, como por ejemplo la edad y el sexo7. Este tipo de variables se conoce como «variables de confusión», debido a que están distorsionando la verdadera intensidad del fenómeno de estudio. La estandarización es un método que permite obtener estimaciones de las tasas eliminando el efecto de las variables de confusión, utilizando para ello las tasas específicas de cada uno de los estratos en que se dividen estas variables.
Existen diferentes tipos de estandarización8, de entre los que destacaremos aquí la estandarización indirecta. Una de las situaciones en la que se utiliza este tipo de estandarización es cuando el número de personas en riesgo es insuficiente para obtener unas tasas específicas representativas, de forma que éstas se pueden obtener internamente utilizando como población de riesgo la de toda el área de estudio o externamente mediante una población de referencia.
Cuando se utiliza la estandarización indirecta, habitualmente se trabaja con la razón estandarizada de mortalidad o morbilidad (SMR) como medida de riesgo. Los SMR se obtienen como el cociente del número de casos observados y el número de casos esperados obtenidos a partir de la estandarización indirecta. De forma que un SMR mayor a 1 indica que existe un riesgo superior en la región de estudio que en la población de referencia; si el SMR es inferior a 1, existe menos riesgo, y si es igual a 1, el riesgo es el mismo. No obstante los SMR de regiones con poca población en riesgo, normalmente rurales, tienden a presentar valores extremos debido a que el número de casos esperados es pequeño. Este hecho provoca que las estimaciones sean muy variables y poco representativas del SMR real de la región.
Un procedimiento que se utiliza para que las estimaciones de los SMR tengan menos variabilidad, es decir sean más estables y así evitar las consecuencias de tener pocos casos esperados, es ajustar los SMR mediante un modelo de regresión.
Modelo de regresión
El modelo de regresión, además de estabilizar los SMR, también permite controlar las estimaciones por posibles variables explicativas, tanto de confusión como factores de riesgo, y por las interacciones que pueden existir entre estas variables.
Cuando se trabaja con tasas o SMR, la variable de estudio corresponde a recuentos, como por ejemplo el número de casos nuevos de una enfermedad en una región y en un período de tiempo determinado. Se asume que los recuentos de cada región se distribuyen bajo una Poisson, por lo que el modelo regresión clásico con residuos distribuidos según una normal no será adecuado, y será preferible utilizar modelos lineales generalizados9, y en particular la regresión de Poisson10.
Si definimos Y = (Y1, ... YN) como el vector de los recuentos en cada una de las N regiones de estudio, y se considera que Y sigue una Poisson con media µ = E * *, donde E es el vector del número de casos esperados obtenidos de la estandarización y * es el vector del riesgo relativo para las N regiones, la regresión de Poisson relaciona la media de los recuentos con las variables explicativas mediante la función logarítmica. Este modelo se expresa mediante la siguiente ecuación:
log(µ) = log(E) + Xß
donde X es la matriz de diseño de las variables explicativas y ß el vector de los coeficientes de regresión de estas variables.
El problema que puede surgir cuando se trabaja con la regresión de Poisson es la presencia del fenómeno conocido como «sobredispersión»11, que se presenta cuando la variabilidad de los datos es superior a la variabilidad asumida por el modelo de Poisson; es decir, cuando la varianza de los recuentos observados es mayor que su media. La sobredipersión puede aparecer por no haber tenido en cuenta variables explicativas relevantes, o por la presencia de correlación espacial entre los SMR de las regiones. En el primer caso se denomina «sobredispersión no estructurada», mientras que en el segundo se habla de «sobredispersión estructurada espacialmente».
La correlación espacial aparece por el hecho de que regiones próximas comparten factores de riesgo desconocidos que no comparten con regiones más alejadas. Estos factores de riesgo pueden asociarse a factores medioambientales, sociales o culturales. Por tanto, esta correlación espacial implica que el riesgo de una región está condicionado por el riesgo de las regiones vecinas, por tanto estas regiones tenderán a presentar riesgos similares.
La principal consecuencia que tiene la presencia de sobredispersión es que las estimaciones, tanto de los SMR como de su error estándar, no serán correctas. Por lo tanto, es necesario utilizar un procedimiento que sea capaz de tener en cuenta esta sobredispersión. Este procedimiento es el modelo lineal generalizado mixto (GLMM)12.
Modelos lineales generalizados mixtos
Los GLMM son una extensión de los modelos lineales generalizados en los que se incorporan efectos aleatorios. En este caso particular, se añade el efecto aleatorio región en la regresión de Poisson, obteniéndose la siguiente ecuación:
log(µ) = log(E) + Xß + Zb,
siendo b el vector de los coeficientes de los efectos aleatorios y Z la matriz de diseño de estos efectos aleatorios. El efecto aleatorio región se añade con la finalidad de capturar la sobredispersión observada. En función del tipo de sobredispersión que se quiere controlar, se pueden especificar 3 modelos para los efectos aleatorios: el de heterogeneidad, el autorregresivo condicional intrínseco (CAR intrínseco)13,14 y el autorregresivo condicional no intrínseco (CAR no intrínseco)15,16.
El modelo de heterogeneidad permite tener en cuenta la sobredispersión no estructurada, el modelo CAR intrínseco, la sobredispersión estructurada espacialmente y el modelo CAR no intrínseco es una conjunción de los 2 modelos anteriores y permite modelar la sobredispersión no estructurada y la sobredispersión estructurada.
Las técnicas de estimación de los parámetros de los GLMM se pueden llevar a cabo bajo dos perspectivas: la bayesiana y la frecuentista.
La estimación de los parámetros mediante la estadística bayesiana se realiza a partir de la distribución conocida como «distribución posterior de los parámetros». Esta distribución se obtiene de combinar la información de la muestra, recogida en la función de verosimilitud, con los conocimientos previos que tiene el investigador de los parámetros desconocidos que se recogen en las distribuciones a priori.
La obtención de la distribución posterior, cuando las integrales a resolver no se pueden obtener de una forma analítica sencilla, se realiza mediante técnicas de simulación, como el Gibbs Sampling17,18. Mediante esta técnica se obtiene una muestra de valores de la distribución posterior de los parámetros sin la necesidad de resolver las integrales y la estimación de los parámetros se realiza a partir de estadísticos descriptivos como, por ejemplo, la media de los valores simulados.
Las estimaciones con la perspectiva frecuentista se obtienen maximizando la función de verosimilitud. Esta maximización no siempre se puede resolver analíticamente. En estos casos se han descrito diferentes métodos para obtener estimaciones de los parámetros entre los que se puede destacar la casi verosimilitud penalizada19.
En la actualidad, para estimar los parámetros de los modelos usando la estadística bayesiana se puede utilizar el programa estadístico de libre distribución WinBUGS. Este programa está disponible para uso público en la página web: http://www.mrc-bsu.cam.ac.uk/bugs/welcome.shtml. En cambio, si deseamos utilizar métodos frecuentistas, es necesario que el propio investigador realice sus programas para obtener las estimaciones.
Para seleccionar el modelo que mejor se ajusta a los datos analizados, se utilizan medidas de bondad de ajuste como por ejemplo el estadístico DIC (Deviance Information Criterion20). Mediante este estadístico el modelo que ajustará mejor a los datos será el que tenga un DIC menor.
Ejemplo: datos de la incidencia de diabetes tipo 1 en la población de menores de 30 años de Cataluña durante el período 1989-1998
En el siguiente ejemplo se analizan los datos de diabetes de tipo 1 de Cataluña. Estos datos corresponden a casos declarados y confirmados en el registro de diabetes entre los años 1989 y 1998 de personas con una edad inferior a 30 años. El objetivo del estudio es analizar la incidencia de la diabetes de tipo 1 a lo largo del territorio. Para ello los datos se han agregado para las 41 comarcas de Cataluña y la población en riesgo para cada comarca se ha obtenido del padrón poblacional del año 1996. Estos datos se han estandarizado para poder eliminar el efecto confusor de las variables género y edad.
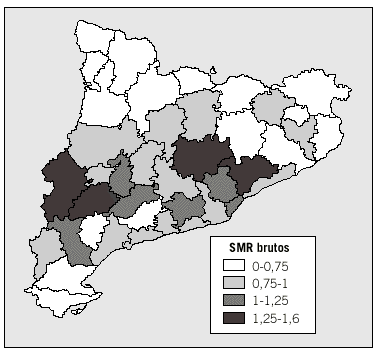
En las figuras 1 y 2 se representan las razones estandarizadas de incidencia para cada comarca y los intervalos de confianza del 95%, que se han construido utilizando la distribución de Poisson21. En relación con la figura 1, se puede observar que aproximadamente la mitad de las comarcas (21) presentan SMR próximos a 1, entre 0,75 y 1,25. Además, se aprecia que la mayoría de las comarcas con menor riesgo (SMR < 0,75) están situadas en el norte de Cataluña y que sólo 4 presentan riesgos mayores de 1,25.
Fig. 1. Distribución espacial de las razones estandarizadas de morbilidad brutas (SMR brutos) de incidencia de diabetes tipo 1 de la población de menores de 30 años durante el período 1989-1998 en las comarcas de Cataluña.
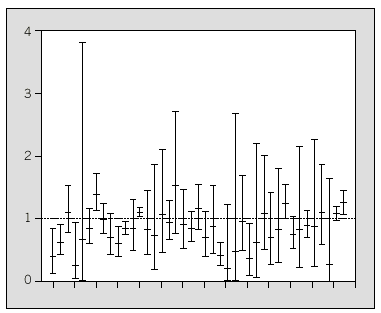
En la figura 2 se observa una gran amplitud en algunos de los intervalos de confianza, lo que indica que estas estimaciones de los SMR brutos presentan mucha variabilidad. Este hecho, tal como se ha explicado en «Metodología estadística», se debe a la diferencia de población en riesgo entre las comarcas. Así, para poder estabilizar y suavizar estas estimaciones es necesario ajustar un modelo de regresión de Poisson.
Fig. 2. Intervalos de confianza del 95% de las razones estandarizadas de morbilidad brutas (SMR brutos) de la incidencia de diabetes tipo 1 de la población de menores de 30 años durante el período 1989-1998 en las comarcas de Cataluña.
A partir del modelo se obtiene una sobredispersión de 3,2, superior a 1, lo que implica que la variabilidad de los datos es superior a la asumida por el modelo. Para tener en cuenta esta sobredispersión se considera un modelo lineal generalizado mixto con un efecto aleatorio comarca. La estimación de este modelo se realiza mediante métodos bayesianos utilizando el programa WinBUGS.
Se consideran los 3 modelos propuestos en «Modelos lineales generalizados mixtos»: heterogeneidad, CAR intrínseco y CAR no intrínseco. Utilizando el DIC como criterio, se llega a la conclusión de que el modelo CAR no intrínseco es el que mejor ajusta los datos (tabla 1). Esto significa que el modelo considera que existe una sobredispersión tanto estructurada espacialmente como no estructurada.
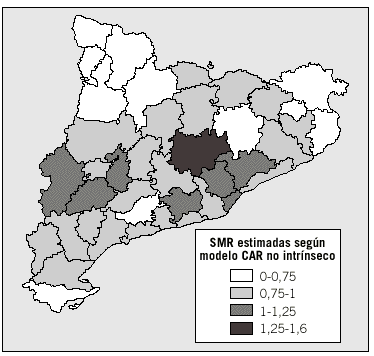
Fig. 3. Distribución espacial de las razones estandarizadas de morbilidad (SMR) de la incidencia de diabetes tipo 1 de la población de menores de 30 años durante el período 1989-1998 en las comarcas de Cataluña estimadas con el modelo autorregresivo condicional no intrínseco (CAR no intrínseco).
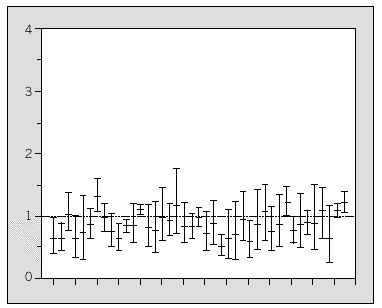
En las figuras 3 y 4 se representan los SMR estimados a partir del modelo CAR no intrínseco y sus intervalos de confianza del 95%. Como se puede observar, los SMR se han suavizado y tan sólo uno de ellos se encuentra en el intervalo de más de 1,25 (fig. 3). Además, también se han obtenido unos intervalos de confianza más precisos, es decir, al haber disminuido la variabilidad de las estimaciones se ha conseguido que éstas sean más representativas del riesgo real.
Fig. 4. Intervalos de confianza del 95% de las razones estandarizadas de morbilidad (SMR) de la incidencia de diabetes tipo 1 de la población de menores de 30 años durante el período 1989-1998 en las comarcas de Cataluña estimadas con el modelo autorregresivo condicional no intrínseco.
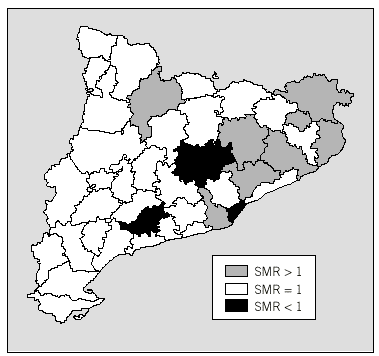
Fig. 5. Distribución espacial de las razones estandarizadas de morbilidad de la incidencia de diabetes tipo 1 de la población de menores de 30 años durante el período 1989-1998 en las comarcas de Cataluña estimadas con el modelo autorregresivo condicional no intrínseco, clasificadas en tres categorías: SMR significativamente mayores de 1, iguales a 1 y menores de 1.
En la figura 5 se representa el mapa de Cataluña en función de si el SMR de cada comarca es significativamente distinto de 1, es decir, que tienen un riesgo significativamente superior o inferior al riesgo general. Mediante esta representación se puede observar que 3 comarcas presentan un SMR significativamente superior a 1, mientras que 8 tienen un SMR significativamente inferior a 1.
La representación de los SMR estimados no muestra claramente un patrón de distribución espacial, debido a que también existe un efecto de heterogeneidad. No obstante, se identifica un agrupamiento de las comarcas con más riesgo.
Discusión y conclusiones
El objetivo de este trabajo ha sido mostrar las técnicas que se emplean para modelar la distribución espacial del riesgo en un área geográfica. En estos casos la estimación bruta del riesgo se ha mostrado muy variable debido a la heterogeneidad de la población en riesgo, provocando que las estimaciones sean poco representativas del riesgo real. Mediante un GLMM, y concretamente una regresión de Poisson con la región como efecto aleatorio, se consigue suavizar las estimaciones, controlar por variables de confusión y tener en cuenta la posible sobredispersión de los datos debida tanto a la heterogeneidad del riesgo en una región como a la presencia de correlación espacial. Así, utilizando este procedimiento se obtienen unas mejores estimaciones del riesgo y de su error estándar.
El riesgo de las regiones sólo presenta un patrón de distribución espacial cuando se incluye en el modelo la sobredispersión estructurada espacialmente. En este caso este componente espacial se puede interpretar como que existen agrupaciones de regiones con un riesgo común. Este hecho viene provocado por la existencia de factores de riesgo que comparten estas regiones.
La representación de las medidas de riesgo mediante un mapa ayuda a la interpretación y a la búsqueda de estas agrupaciones de regiones o la identificación de regiones con mayor riesgo, facilitando la toma de decisiones e intervenciones sanitarias a nivel de región.
Agradecimientos
Nuestro agradecimiento a la Dra. C. Castell y al Dr. R. Tresserras por facilitarnos los datos del Registre de Diabetis mellitus tipo 1 de Catalunya del Consell Assessor sobre la Diabetis a Catalunya del Departament de Sanitat i Seguretat Social y a l'Associació Catalana de Diabetis.