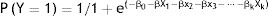Regresión logística

Resumen

La regresión logística es un grupo de técnicas estadísticas que tienen como objetivo comprobar hipótesis o relaciones causales entre una variable dependiente categórica y otras variables independientes que pueden ser categóricas y cuantitativas. Mediante este modelo pretendemos estudiar la probabilidad de que ocurra el evento estudiado en función de unas variables que suponemos que son relevantes o influyentes. En este método es necesario detectar las variables modificadoras de efecto y las de confusión. Sus parámetros se estiman con el método de la máxima verosimilitud a través de un proceso con sucesivas iteraciones.

Abstract

Logistic regression is a group of statistical techniques that aim to test hypotheses or causal relationships between a categorical dependent variable and other independent variables that can be categorical and quantitative. Through this model we intend to study the probability that the event studied will occur based on some variables that we assume are relevant or influential. In this method it is necessary to detect effect modifier and confounding variables. Its parameters are estimated with the maximum likelihood method through a process with successive iterations.

Introducción

La regresión logística es un grupo de técnicas estadísticas que tienen como objetivo comprobar hipótesis o relaciones causales entre una variable dependiente categórica y otras variables independientes que pueden ser categóricas y cuantitativas. Mediante este modelo pretendemos estudiar la probabilidad de que ocurra el evento estudiado (por ejemplo, curar) en función de unas variables que suponemos que son relevantes o influyentes¹ (por ejemplo, tratamiento aplicado, grado de cumplimiento, género, comorbilidad).

Se trata de una función exponencial:

Donde:

• -

  Y es la variable dependiente,

• -

  las k variables explicativas (independientes) se designan por X₁, X₂, X₃,..., X_k,

• -

  β₀, β₁, β₂, β₃,..., β_k son los parámetros del modelo, y

• -

  e indica la función exponencial que corresponde a elevar su número a la potencia de β, X. A su vez, e se corresponde con la constante de Euler, o base de los logaritmos neperianos cuyo valor es aproximadamente 2,718.

La relación entre la variable dependiente y las independientes no queda definida por una recta (lo que correspondería a un modelo lineal), sino que describe una forma sigmoidea (distribución logística)².

Si la variable dependiente es de 2 categorías, es decir, dicotómica (sí/no, curado/no curado, hipertenso/no hipertenso, etc.), decimos que se trata de una regresión logística binaria. Pero también puede suceder que la variable dependiente sea una variable cualitativa de más de 2 categorías, por ejemplo, 1-soltero/2-casado/3-divorciado/4-viudo/5-otro. En este caso, al modelo lo denominamos regresión logística multinomial. En este artículo nos vamos a centrar en la regresión logística binaria.

Los objetivos que nos debemos marcar al realizar una regresión logística son:

• 1.

  Dados los valores de las variables independientes, evaluar la relación entre estas y la variable dependiente para obtener una estimación no sesgada y precisa de la medida de asociación entre ambas.

• 2.

  Estimar la influencia que cada variable independiente tiene sobre la respuesta.

Consideraciones a tener en cuenta

Para poder llevarla a cabo, es necesario primeramente tener presente una serie de peculiaridades:

• 1.

  Hacer el estudio con una muestra suficientemente numerosa y bien distribuida³.

• 2.

  Valorar detenidamente cuáles pueden ser las variables predictoras (independientes) de la variable que queremos predecir (dependiente). Es decir, tener en cuenta todas las variables importantes para explicar la variable respuesta y no introducir variables innecesarias porque estas pueden enmascarar el proceso de modelado y llevar a estimaciones no válidas. Para ello es necesario que revisemos la literatura sobre el tema que queremos investigar y que lo conozcamos bien, y, por supuesto, incluir toda variable que en un análisis univariado previo demuestre una relación estadística con la variable dependiente⁴.

• 3.

  Determinar cuáles pueden ser las variables de confusión. Existe confusión cuando la asociación entre 2 variables difiere significativamente según que se considere, o no, otra variable externa a la relación que se evalúa. Estas variables producen sesgos en la estimación de la medida de asociación. Si no las controlamos y ajustamos, obtendremos una relación que podría ser espuria o artefactada entre las variables independientes y la dependiente. Si no se ha podido controlar o ajustar estas variables en la fase de diseño hay que hacerlo en la de análisis^4–6.

• 4.

  Precisar cuáles son las variables de interacción (modificadoras de efecto). Existe interacción cuando la asociación entre 2 variables varía según los diferentes niveles de otra u otras variables. Según el valor que toman, pueden incrementar la relación que evaluamos (efecto sinérgico), disminuirla (efecto antagónico) e incluso eliminarla (efecto supresivo). A diferencia de la confusión, no produce ningún sesgo en la estimación de esta relación.

Es habitual que estos 2 fenómenos se presenten de forma simultánea y se debe analizar primero la interacción^4,5.

Control y ajuste de variables de confusión e interacción

Hay varias aproximaciones para realizar el control o ajuste de las variables de confusión. En la fase de diseño:

• a)

  Emparejamiento o matching: se trata de seleccionar individuos emparejados por el factor que suponemos de confusión. Es una estrategia empleada en los estudios de caso-control.

• b)

  Restricción: se basa en limitar el estudio al grupo de individuos en los que no esté presente el factor que presumimos de confusión, aunque a costa de perder información y capacidad de generalización de resultados.

• c)

  Asignación aleatoria: la distribución de los individuos a los grupos de comparación de manera aleatoria hace que en muestras grandes se balanceen por igual diferentes factores, de manera que pierdan su capacidad de alterar o mezclar los efectos medidos. Es el mejor procedimiento para controlar la confusión, pero tiene el inconveniente de que solo se puede aplicar a estudios experimentales en donde el investigador manipula o decide la exposición (variable dependiente).

En la fase de análisis se realiza:

• a)

  Análisis estratificado. Estriba en calcular las medidas de asociación entre las 2 variables principales (dependiente e independiente) para cada uno de los estratos de la variable de confusión.

Una vez que obtengamos la relación odds ratio (OR) entre la variable dependiente y la independiente, sin tener en cuenta la variable que suponemos que es de confusión (asociación bruta), se hace lo mismo en cada estrato definido por la presunta variable de confusión y se halla una medida final ajustada (OR global o ponderada de Mantel-Haenszel).

Decimos que existe confusión cuando:

• 1.

  Los valores de las medidas de asociación en cada estrato son similares entre sí, y diferentes de la OR global. En este caso, pueden darse varias posibilidades:

• -

  Relación espuria: la OR global detecta asociación (valor > 1), mientras que las OR en cada estrato no lo detectan, arrojando valores próximos al valor nulo (OR = 1).

• -

  Confusión enmascarando el efecto: la OR global es 1 (no hay asociación), mientras que las OR en cada estrato ponen de manifiesto una asociación (valores > 1).

• -

  Confusión invirtiendo el efecto (paradoja de Simpson): las OR en cada estrato muestran asociación (valores > 1), mientras que la OR global muestra una relación o asociación invertida (valor < 1).

• 2.

  Los valores de las medidas de asociación «ajustadas» divergen en más de un 10% de los de las medidas «brutas».

• 3.

  Deben cumplirse los criterios generales de una variable de confusión, es decir, debe ser un factor de riesgo (o protector) de la variable dependiente, debe estar relacionada con la variable independiente y no ser un paso intermedio en la relación principal evaluada (cronológicamente anterior a la exposición).

Por otra parte, se considera que hay una interacción cuando al estratificar por la variable de interacción los valores de la variable, las OR de cada estrato son muy diferentes entre sí^4,5.

El inconveniente del análisis estratificado es que requiere que la variable por la que se estratifica o ajusta sea de tipo categórico y que el tamaño muestral sea suficientemente grande como para que no existan celdas con pocos representantes. Por ello hoy en día ha sido casi sustituido por las técnicas de análisis multivariante, mucho más eficientes (estimaciones más precisas con menos tamaños muestrales) y que permiten evaluar varios factores de confusión simultáneamente. Sin embargo, el análisis estratificado sigue siendo muy útil para comprender las relaciones entre las variables analizadas.

• b)

  Análisis multivariante con modelos de regresión. Nos permite evaluar simultáneamente las relaciones entre más de 2 variables, con lo cual podemos controlar el efecto de terceras variables^4,5.

Construcción de un modelo de regresión logística

• a)

  Valoramos la interacción con pruebas de significación estadística y mantenemos en el modelo los términos de interacción estadísticamente significativos junto con todas las posibles variables de confusión.

• b)

  Valoramos la confusión sin aplicar pruebas de significación estadística y eliminamos toda variable de este tipo que no produzca un cambio importante en el efecto de la exposición sobre la respuesta cuando se ajusta el modelo sin esa variable. Algunos autores proponen que un cambio clínicamente relevante en la OR debe ser al menos de un 10% y preferiblemente de un 20%.

• c)

  Si al final del proceso se obtiene más de un subconjunto de variables de control que ofrecen un similar grado de ajuste, se debe elegir el que estime con mayor exactitud (menor error estándar o intervalo de confianza más estrecho) el efecto de la exposición sobre la respuesta⁷.

Este proceso debe realizarse siguiendo el principio jerárquico: si se elimina un término cualquiera, todos los términos de mayor orden en los que intervenga deben ser eliminados. Y a la inversa, si se incluye un término cualquiera (con coeficiente no nulo) todos sus términos de menor orden deberán estar presentes en el modelo. Es decir, si un modelo contiene la interacción X*X₁*X₂ también deberá contener las interacciones X*X_1y X*X₂ y la variable exposición X⁶. Por ejemplo, si la interacción es «hipertensión-diabetes», hay que meter también en el modelo las covariables hipertensión y diabetes.

Para llevar a cabo un ajuste estadístico bajo el principio jerárquico, no se pueden utilizar los procedimientos automáticos (hacia adelante –forward– o hacia atrás –backward–) del programa SPSS®, ya que no incorporan la norma jerárquica y eliminan del modelo los términos no significativos, dejando los estadísticamente significativos (coeficientes de regresión no nulos). Por este motivo, en el análisis de regresión con objetivo de ajuste o control de la confusión debe recurrirse al procedimiento intro, que permite al investigador conducir el resultado en función de los resultados que va obteniendo^1,7.

Finalmente, se debe introducir en el modelo la variable dependiente, las independientes o de control, las de interacción estadísticamente significativas y las de confusión ajustadas.

Hay que tener en cuenta que los cálculos de la regresión se hacen mediante el método de máxima verosimilitud con los datos de la muestra; por ello, es necesario ponderar las variables introducidas, porque si son pocas el modelo no predice bien y si son excesivas el modelo es impreciso (meten mucho ruido). Quizá una buena regla es no superar la relación, una variable en el modelo por cada 10 individuos en la muestra analizada¹.

La regresión logística en el programa SPSS®

Activamos la secuencia: Analizar → Regresión → Logística binaria. Se abre un cuadro de diálogo donde indicamos:

• -

  La variable dependiente (es categórica dicotómica, valor 0 y 1).

• -

  La(s) covariable(s) (independientes y de confusión e interactivas que procedan).

• -

  El método: permite especificar cómo se introducen las variables independientes en el análisis. Hay 3 posibilidades:

• 1.

  Intro: el investigador decide qué variables se introducen o extraen del modelo.

• 2.

  Adelante: es un método automático, en donde el programa va introduciendo variables en el modelo, empezando por aquellas que tienen coeficientes de regresión más grandes estadísticamente significativos. Elimina aquellos coeficientes que no considera estadísticamente significativos.

• 3.

  Atrás: también es automático. Parte de un modelo con todas las covariables que se hayan seleccionado en el cuadro de diálogo y va eliminando las que no tienen significación estadística.

A su vez, los métodos Adelante y Atrás permiten elegir entre 3 criterios (condicional, razón de verosimilitud y Wald) con la finalidad de comprobar la significación estadística de cada uno de los coeficientes de regresión del modelo:

• a)

  Hacia adelante: condicional. Selección de variables por pasos. Contrasta la entrada según la significación del coeficiente de regresión y la eliminación basándose en la probabilidad de un estadístico de la razón de verosimilitud que se fundamenta en estimaciones condicionales de los parámetros.

• b)

  Hacia adelante: razón de verosimilitud. Selección por pasos. Contrasta la entrada según la significación del coeficiente de regresión y la eliminación basándose en la probabilidad de un estadístico de la razón de verosimilitud que se fundamenta en estimaciones de la máxima verosimilitud parcial.

• c)

  Hacia adelante: Wald. Selección por pasos. Contrasta la entrada según la significación del coeficiente de regresión y la eliminación basándose en la probabilidad del estadístico de Wald.

• d)

  Hacia atrás: condicional. Selección hacia atrás por pasos. El contraste para la eliminación se basa en la probabilidad del estadístico de la razón de verosimilitud, el cual se fundamenta en las estimaciones condicionales de los parámetros.

• e)

  Hacia atrás: razón de verosimilitud. Selección hacia atrás por pasos. El contraste para la eliminación se basa en la probabilidad del estadístico de la razón de verosimilitud, el cual se fundamenta en estimaciones de la máxima verosimilitud parcial.

• f)

  Hacia atrás: Wald. Selección hacia atrás por pasos. El contraste para la eliminación se basa en la probabilidad del estadístico de Wald⁸.

En el mismo cuadro de diálogo presionamos Categórica, para especificar cuáles de las variables independientes son categóricas. Una vez seleccionadas debemos indicar cuál es el método de contraste (Indicador, por defecto) y cuál es la categoría de referencia (la Última, por defecto). Si deseamos modificar algunos de ellos es necesario aplicar Cambiar.

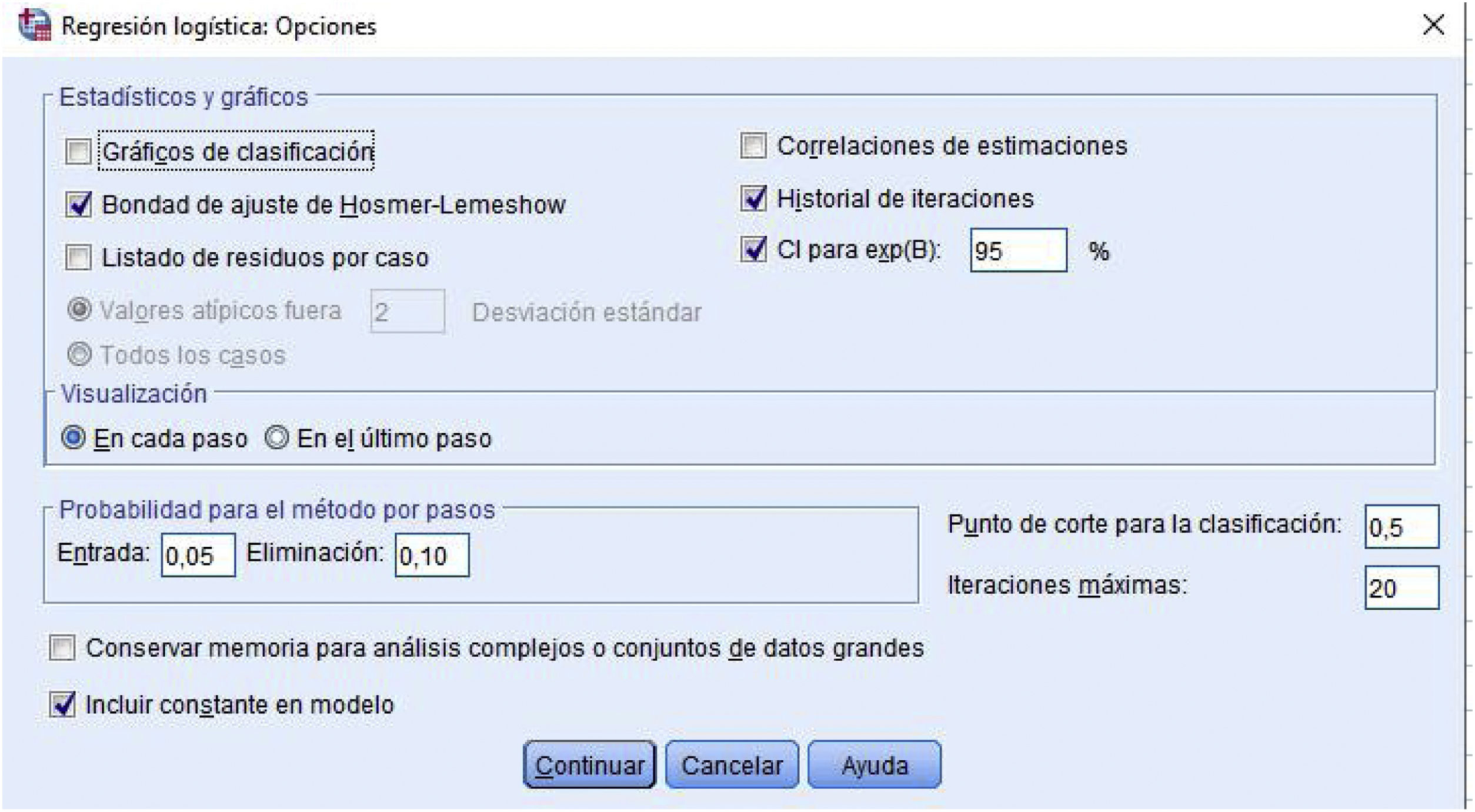
Después Continuar y volvemos al cuadro de diálogo anterior. En Opciones (fig. 1) se pueden elegir diversas tareas y resultados:

• a)

  Estadísticos y gráficos:

• -

  Gráficos de clasificación: histograma de los valores actuales y pronosticados por el modelo para la variable dependiente.

• -

  Bondad de ajuste de Hosmer-Lemeshow: es un método para evaluar el ajuste global del modelo. Se basa en agrupar los casos en deciles de riesgo y comparar la probabilidad observada con la probabilidad esperada dentro de cada decil^1,9.

• -

  Listado de residuos por caso: muestra los residuos no estandarizados, la probabilidad pronosticada y los grupos de pertinencia observado y pronosticado.

• -

  Correlaciones de estimaciones: muestra la matriz de correlaciones de las estimaciones de los parámetros para los términos del modelo.

• -

  Historial de iteraciones. Muestra los coeficientes y el logaritmo de la verosimilitud en cada iteración del proceso de estimación de los parámetros.

• -

  Intervalo de confianza para la OR. Es el rango de valores que el N por ciento de las veces incluye el valor e elevado al valor del coeficiente de regresión logística b. El valor predeterminado es el 95%, pero podemos especificar entre 1 y 99 (los valores habituales son 90, 95 y 99)¹.

• b)

  Visualizaciones. Se puede elegir entre:

• -

  En cada paso: muestra los estadísticos y los gráficos en cada paso.

• -

  En el último paso: muestra el modelo final.

• c)

  Probabilidad para el método por pasos. Nos permite controlar los criterios por los que las variables se introducen y eliminan de la ecuación. Podemos asignar criterios para la Entrada, de modo que una variable se introduce en el modelo si la probabilidad de su estadístico de puntuación es menor que el valor de entrada, y se elimina si la probabilidad de Eliminar es mayor que el valor de salida.

• -

  Punto de corte para la clasificación. Determinamos el punto de corte para clasificar los casos. Los casos con valores pronosticados que han superado este punto de corte elegido se clasifican como positivos (tendrían el resultado o evento que se modeliza), mientras que los menores que el punto de corte, se consideran negativos (no tendrían el resultado que modelizamos). Por defecto, el valor del programa es 0,5, pero nosotros podemos introducir un valor comprendido entre 0,01 y 0,99.

• -

  Iteraciones máximas. En esta casilla podemos elegir el número máximo de veces que el modelo itera antes de finalizar.

• -

  Incluir una constante en el modelo. Podemos decidir si incluimos, o no, una constante en el modelo⁴.

Figura 1.

Regresión logística: opciones.

A continuación: Continuar → Aceptar → Resultados

Interpretación de resultados

Primero aparece un cuadro resumen con el número de casos introducidos, los casos incluidos en el análisis y los casos perdidos. La siguiente tabla nos informa sobre la codificación de la variable dependiente, asignando el programa el valor 0 al menor de los códigos introducidos y 1 al mayor. La tercera tabla muestra la codificación usada en las variables categóricas independientes y la frecuencia absoluta de cada valor.

A continuación el programa nos muestra el Bloque 0 o Bloque de inicio, que consta de:

• -

  Tabla de clasificación: paso 0. El programa nos informa de que la constante está en el modelo y que el valor de corte para clasificar a los individuos es de 5, de manera que a una probabilidad < 0,5 le corresponde 0 y a una > 0,5 el 1.

• -

  Variables en la ecuación: presenta las variables que están en la ecuación y las que no están, a través del parámetro estimado (B), su error estándar (ET), su significación estadística (prueba de Wald, que es un estadístico que sigue una ley chi cuadrado con un grado de libertad) y la estimación de la OR (Exp [B]).

Bloque 1: método avanzar por pasos (razón de verosimilitud)

• -

  Historial de iteraciones: nos indica que en el modelo se incluye la constante, el proceso iterativo de estimación del primer parámetro (b₀) calculado como menos 2 veces el logaritmo neperiano de la verosimilitud inicial (−2LL), y que el proceso ha necesitado n ciclos para estimar correctamente la constante (en nuestro caso fue 7).

• -

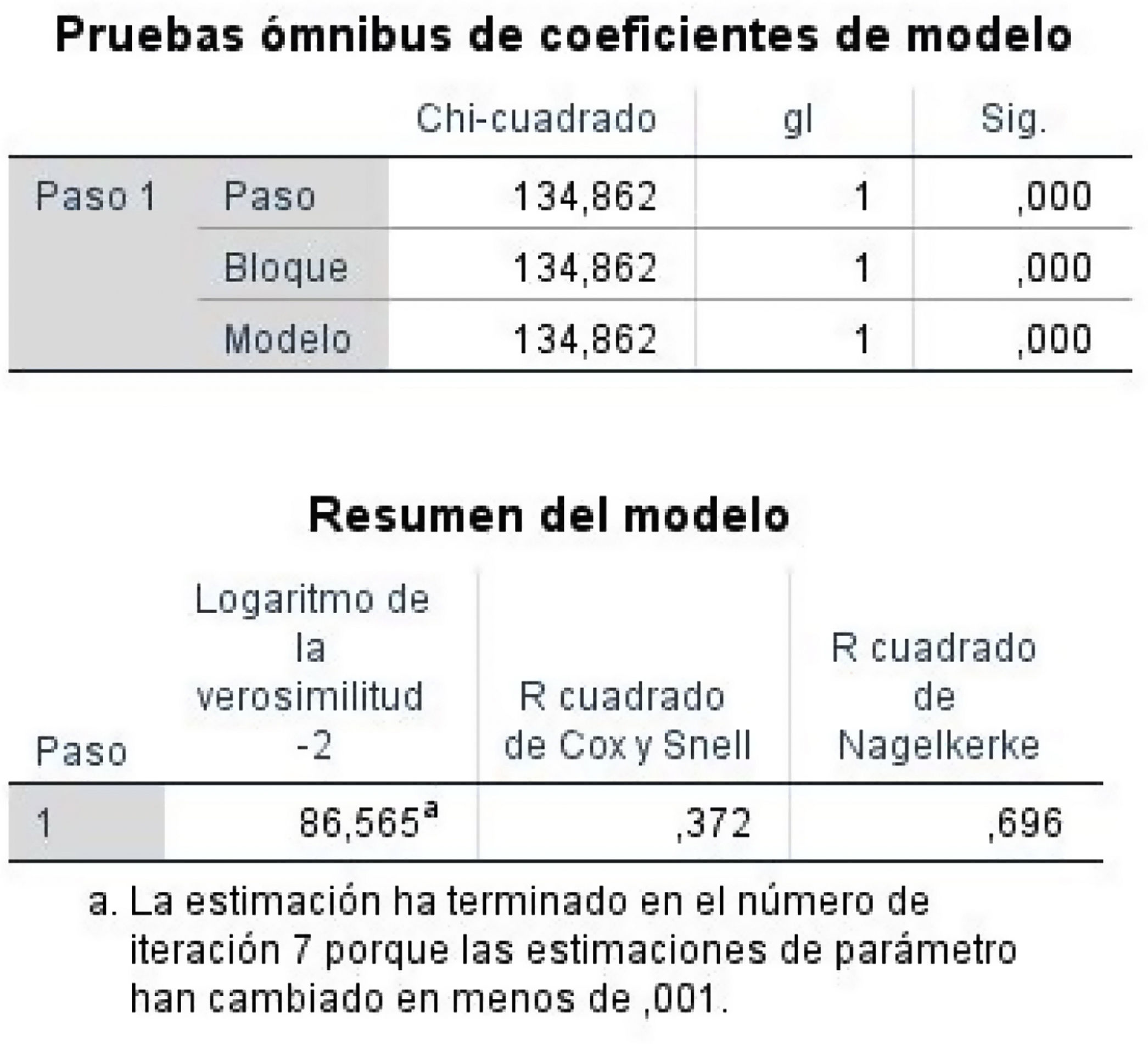
  Prueba ómnibus de coeficiente de modelo: es una prueba que analiza la bondad del modelo mediante una prueba chi cuadrado. Si la significación es menor de 0,05 indica que el modelo ayuda a explicar el evento, es decir, las variables independientes explican la variable dependiente.

El programa nos ofrece 3 entradas:

• •

  Paso: es el cambio de verosimilitud (de −2LL) entre pasos sucesivos en la construcción del modelo.

• •

  Bloque: es el cambio en −2LL entre bloques de entrada sucesivos durante la construcción del modelo.

• •

  Modelo: es la diferencia entre el valor de −2LL para el modelo solo con la constante y el valor −2LL para el modelo actual¹.

En nuestro ejemplo, al haber un único bloque y un único paso, coinciden los 3 valores.

• -

  Resumen del modelo. El programa aporta 3 medidas complementarias a la anterior:

• •

  −2 log de la verosimilitud. Mide hasta qué punto el modelo se ajusta bien a los datos. Al resultado también se le llama «deviación». Cuanto más pequeño sea el valor, mejor será el ajuste.

• •

  R²de Cox y Snell. Indica la parte de la varianza de la variable dependiente explicada por las variables independientes. Sus valores oscilan desde 0 sin llegar a 1 (incluso para un modelo perfecto). Cuanto más alta es la R² más explicativo es el modelo; en nuestro caso es de 0,372, es decir, el 37,2% de la variación de la variable dependiente explica el modelo.

• •

  R²de Nagelkerke. Es una versión corregida de la anterior y cubre el rango completo de 0 a 1. En nuestro ejemplo es de 0,696, que se considera aceptable¹ (fig. 2).

  
  

  Figura 2.

  Prueba ómnibus, de Cox y Snell, y de Nagelkerke.

• -

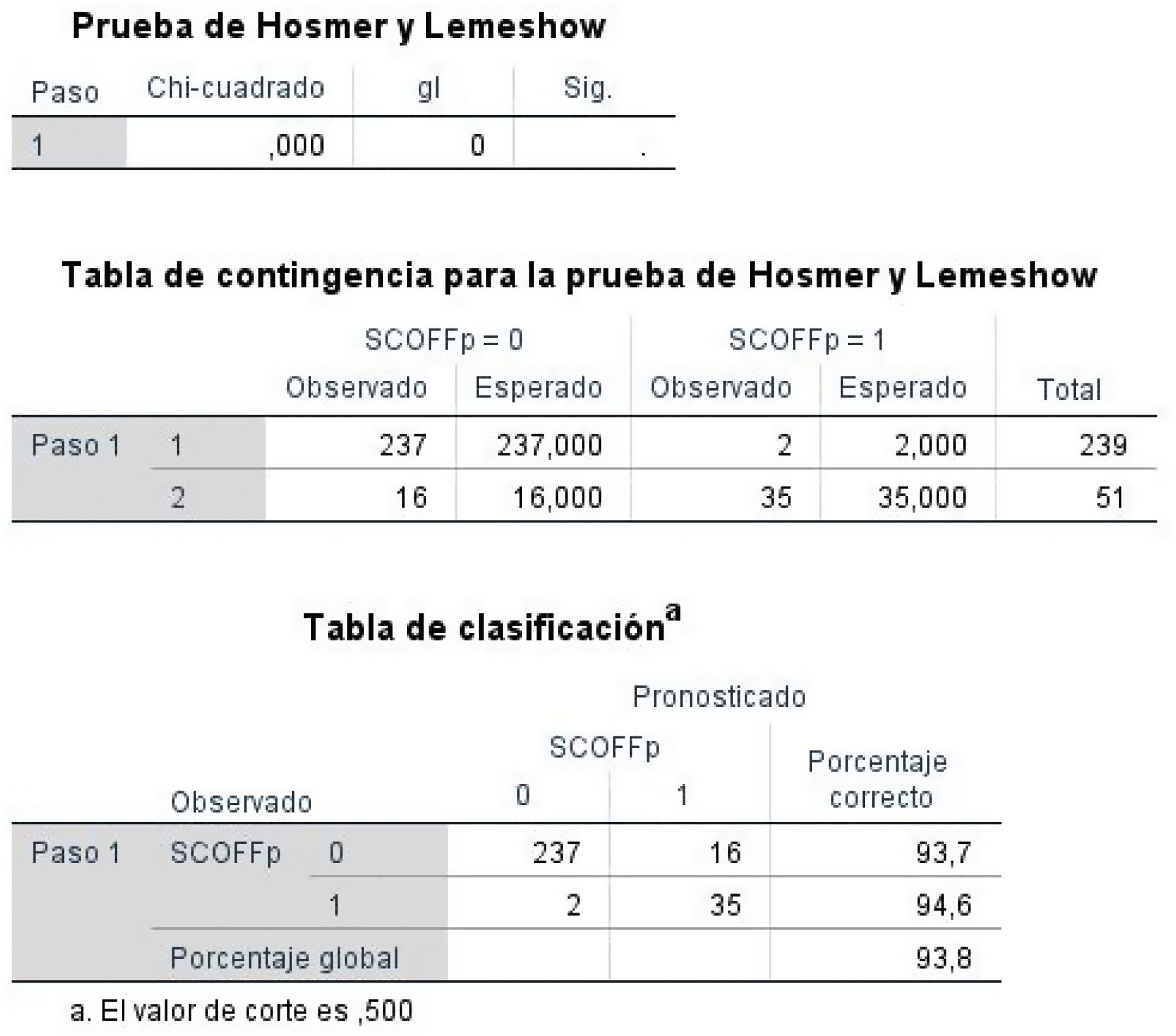
  Prueba de Hosmer-Lemeshow y tabla de clasificación. Es otra prueba para medir la bondad de ajuste de una regresión logística. Consiste en comparar los valores previstos (esperados) por el modelo con los valores realmente observados. Ambas distribuciones, esperada y observada, se contrastan mediante una prueba de chi cuadrado. La hipótesis nula del test de Hosmer-Lemeshow es que no hay diferencias entre los valores observados y los valores pronosticados (el rechazo a este test indicaría que el modelo no está bien ajustado). Otra forma de evaluar el ajuste del modelo es construir una tabla 2 × 2 clasificando a todos los individuos de la muestra según la concordancia de los valores observados con los estimados por el modelo. Una ecuación sin poder de clasificación alguno tendría unos porcentajes de clasificación correcta igual al 50% (por el simple azar). Un modelo puede considerarse aceptable si tiene un nivel alto, de al menos un 75%¹. En nuestro estudio esta concordancia es del 93,8%, lo que significa que el modelo clasifica correctamente el 93,8% de los casos (fig. 3).

  
  

  Figura 3.

  Prueba de Hormer-Lemeshow y tabla de clasificación.
• -

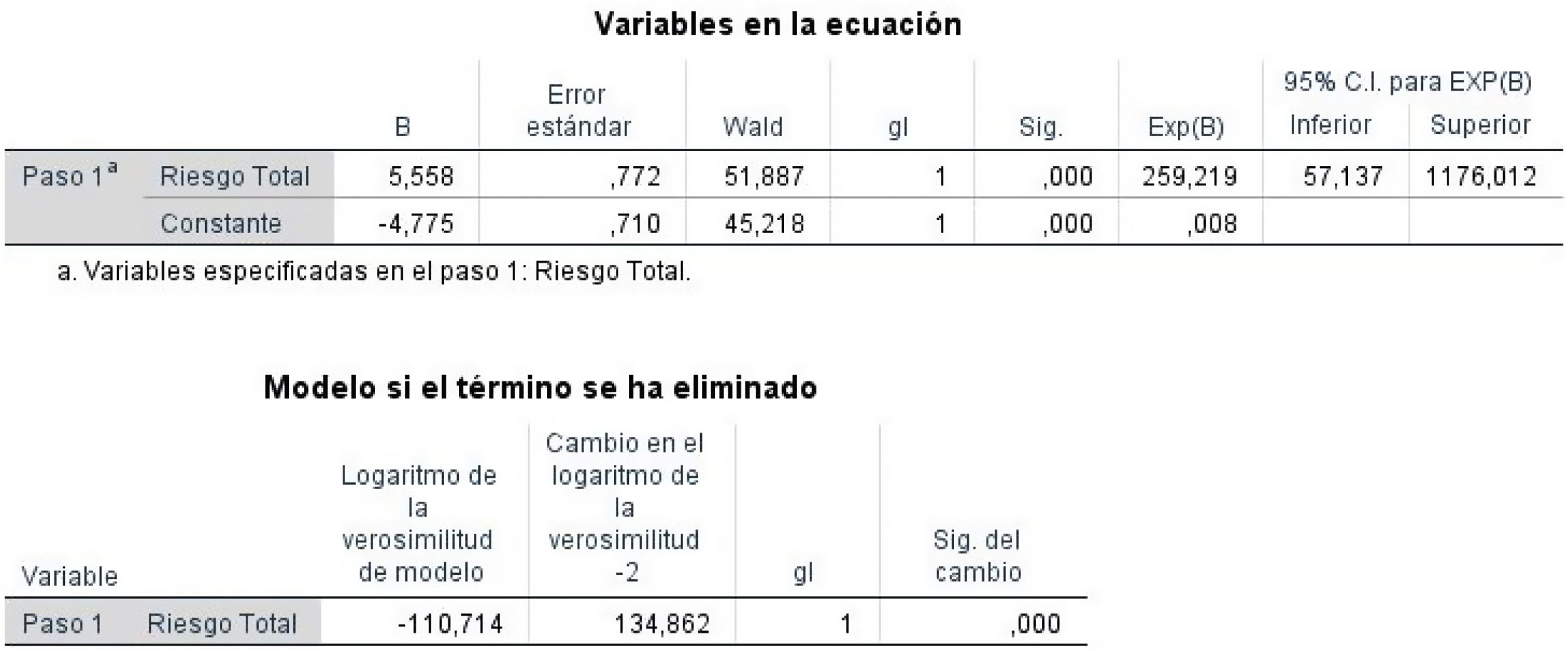
  Variables en la ecuación. El programa nos ofrece las variables que permanecerán en la ecuación, con los siguientes parámetros (fig. 4):

  
  

  Figura 4.

  Variables en la ecuación y modelo si el término se ha eliminado.

• B: coeficiente de regresión. Permite valorar el efecto propio de cada variable independiente sobre la dependiente⁷. Si es positivo, el valor de la variable dependiente aumenta; si es negativo, disminuye.

• ET: error estándar de B.

• Wald: valor del estadístico Wald para evaluar la hipótesis nula (β_i = 0). Si se acepta la hipótesis nula se pueden eliminar del modelo las variables independientes igual a 0; si la rechazamos, debemos incluir en el modelo las variables que no son 0^1,10.

• gl: grados de libertad.

• Sig: significación estadística asociada. Si es menor de 0,05 esa variable independiente estudiada explica la variable dependiente.

• Exp(B): valor de la OR. Expresa la probabilidad de ocurrencia de un evento o enfermedad respecto a la no ocurrencia (cuántas veces más es esta probabilidad).

• IC 95% para Exp(B): intervalo de la OR para un nivel de confianza del 95%.

El programa estadístico también nos enseña las variables que no entran en la ecuación al no ser significativas y por ello no predecir la variable dependiente.

• -

  Modelo si el término se ha eliminado. Se trata de una evaluación de cuánto perdería el modelo si se eliminara cada variable incluida en el mismo (en nuestro ejemplo, una). En aquellas variables en que la significación estadística (sig. del cambio) fuese mayor que el criterio de exclusión establecido, estas se eliminarían del modelo en el paso siguiente¹. En la figura 4 presentamos los cambios en la verosimilitud si se diera esta posibilidad. Como vemos en nuestro caso, el cambio de verosimilitud es significativo (sig. del cambo: 0,000), por lo que dicha variable se queda en el modelo y no se elimina.