Predecir una crisis epiléptica significa la capacidad de determinar de antemano el momento de una crisis con la mayor precisión posible. Un pronóstico correcto de un evento epiléptico en aplicaciones clínicas es un problema típico en procesamiento de señales biomédicas, lo cual ayuda a un diagnóstico y tratamiento apropiado de esta enfermedad. En este trabajo, utilizamos el coeficiente de correlación producto-momento de Pearson a partir de las clases estimadas con un clasificador lineal, usando los parámetros de la distribución Gaussiana generalizada. Esto con el fin de poder pronosticar eventos con crisis y eventos con no-crisis en señales epilépticas. El desempeño en 36 eventos epilépticos de 9 pacientes muestra un buen rendimiento, con un 100% de efectividad para sensibilidad y especificidad superior al 83% para eventos con crisis en todos los ritmos cerebrales. El test de Pearson indica que todos los ritmos cerebrales están altamente correlacionados en los eventos con no-crisis, más no durante los eventos con crisis. Esto indica que nuestro modelo puede escalarse con el coeficiente de correlación producto-momento de Pearson para la detección de crisis en señales epilépticas.
To predict an epileptic event, means the ability to determine in advance the time of the seizure with the highest possible accuracy. A correct prediction benchmark for epilepsy events in clinical applications, is a typical problem in biomedical signal processing that help to an appropriate diagnosis and treatment of this disease. In this work we use Pearson's product-moment correlation coefficient from generalized Gaussian distribution parameters coupled with linear-based classifier to predict between seizure and non-seizure events in epileptic EEG signals. The performance in 36 epileptic events from 9 patients showing a good performance with 100% of effectiveness for sensitivity and specificity greater than 83% for seizures events in all brain rhythms. Pearson's test suggest that all brain rhythms are highly correlated in non-seizure events but no during the seizure events. This suggests that our model can be scaled with the Pearson product-moment correlation coefficient for the detection of epileptic seizures.
El diagnóstico y el tratamiento adecuado de la epilepsia es uno de los principales problemas de la salud pública según la Organización Mundial de la Salud. En todo el mundo hay más de 50 millones de personas que padecen algún tipo de epilepsia, casi el 80% de ellas en regiones en desarrollo, donde 3 cuartas partes no reciben un diagnóstico y tratamiento apropiado1. Los pacientes que presentan esta enfermedad a menudo manifiestan diferentes caracterizaciones fisiológicas, que resultan de la descarga sincrónica y excesiva de un grupo de neuronas en la corteza cerebral. Las crisis epilépticas generalmente tienen un inicio repentino, se extienden en cuestión de segundos y, en la mayoría de los casos, son breves. La manifestación de una crisis depende de la región donde comienza en el cerebro y qué tan rápido se propaga. La correcta identificación de esta información es clave para un tratamiento adecuado de esta enfermedad. La electroencefalografía (EEG) es una modalidad biomédica no invasiva y ampliamente disponible que se puede utilizar para diagnosticar y diseñar un tratamiento correcto de la epilepsia. La EEG captura las principales características que son relevantes de la crisis, lo cual ayuda a discriminar entre actividad cerebral normal y anormal. Las características más estudiadas en la literatura se pueden clasificar en 3 grupos: propiedades espectrales, propiedades morfológicas y descriptores estadísticos. Para un tratamiento integral de estas características véase Schomer y Lopes da Silva2, Osorio et al.3 y Varsavsky et al.4.
Primero vamos a explicar brevemente algunos conceptos usados en este trabajo para desarrollar toda la idea propuesta.
La validación cruzada es una técnica de validación de modelos usada para evaluar cómo los resultados de un algoritmo de análisis estadístico se pueden generalizar a un conjunto de datos independiente. Esto se hace mediante la partición de un conjunto de datos de la siguiente manera: un subconjunto para entrenar el algoritmo y los datos restantes para la prueba o test. Cada ronda de validación cruzada implica la partición aleatoria del conjunto de datos original en un conjunto de entrenamiento y un conjunto de test. El conjunto de entrenamiento luego se usa para entrenar un algoritmo de aprendizaje supervisado y el conjunto de test se usa para evaluar su desempeño. Este proceso se repite varias veces donde el valor de pérdida y el error aparente de la validación cruzada se utilizan como un indicador de rendimiento. Aplicaciones de este método en epilepsia se remontan a la década de los 70 con el trabajo de Lloyd et al.5 usando una técnica llamada template matching6. La importancia de usar la validación cruzada radica en que en muchas aplicaciones biomédicas los datos pueden ser muy limitados para la etapa de entrenamiento y de test, por lo que, si se quieren construir buenos modelos, se debe utilizar la mayor cantidad de datos disponibles para la etapa de entrenamiento. Sin embargo, si el conjunto de validación es pequeño, dará una estimación relativamente ruidosa del rendimiento predictivo7. En la validación cruzada dejando uno fuera, los datos de las particiones usan el enfoque de k-iteraciones, donde k es igual al número total de observaciones en los datos. Véanse Alpaydin et al.8 y Hastie et al.9 para un tratamiento exhaustivo de las propiedades estadísticas y Combrisson y Jerbi10, Sargolzaei et al. 11, Zhang y Parhi12, Stevenson et al.13 y Liang et al.14 para algunos ejemplos en señales EEG.
El coeficiente de correlación producto-momento de Pearson es un test de asociación entre parejas de datos; es usado como una medida del grado de correlación lineal o dependencia entre 2 variables, crisis y no-crisis en nuestro caso. El coeficiente se calcula como el cociente entre la covarianza de las 2 variables y el producto de sus desviaciones típicas. Referimos al lector a Glantz15 para un tratamiento comprensivo de este coeficiente.
En este trabajo estudiamos el coeficiente de correlación producto-momento de Pearson para predecir entre los eventos de crisis y no-crisis, a partir de una clasificación lineal de la estimación de los parámetros de la distribución Gaussiana generalizada, modelo estudiado en nuestros trabajos previos6,16-19. Esta distribución tiene 2 parámetros: escala A y forma B, que se estiman en cada ritmo cerebral, a partir de una descomposición Wavelet. Por lo tanto, tenemos un conjunto de parámetros A y B tanto para eventos de crisis, como para los eventos de no-crisis. Estos parámetros se clasifican a través de un clasificador lineal en 2 clases: crisis o no-crisis. A continuación, el aporte de este trabajo, se estima un coeficiente de correlación producto-momento de Pearson para cada clase; permitiendo un rango de magnitud entre [–1, +1]. Este escalamiento facilita una predicción de la crisis epiléptica en señales de EEG.
Este documento está estructurado de la siguiente manera. La sección 2 describe la metodología propuesta que se usa para describir señales de EEG y discriminar entre un evento de crisis y no-crisis en señales epilépticas. En la sección 3 se muestran los resultados de esta metodología, se aplica y luego se compara con 2 modelos similares en señales reales de EEG de pacientes que presentan crisis epilépticas. La elección de estos 2 modelos es porque usan una metodología similar y están basados en el clásico clasificador de máquinas de vectores de soporte (SVM). Finalmente, las conclusiones se informan en la sección 4.
MetodologíaSea X ∈ ℝNxM la matriz en conjunto de M señales EEG xm ∈ ℝNx1, medidas simultáneamente en diferentes canales en instantes de tiempo discretos N. La metodología propuesta está compuesta de 5 etapas.
La primera etapa divide la señal original X en una serie de segmentos de 2 s con 50% de solapamiento, usando una ventana rectangular Ω=Ω0ω−W−12 con 0≤ω≤W−1, tal que Xi=ΩiX. La segunda etapa consiste en representar cada segmento Xi en su correspondiente representación tiempo-frecuencia, usando una descomposición multirresolución 1D, a través de la Wavelet Daubechies (dB4) con 6 escalas. El propósito de esta descomposición es evaluar la distribución de energía a través de todos los ritmos cerebrales llamados: banda deltaδ: 0,5-4Hz, banda thetaθ:4-8Hz, banda alfaα: 8-13Hz, banda betaβ:13-30Hz y banda gammaγ:> 30Hz.
En la tercera etapa, la distribución estadística de los coeficientes Wavelet es representada usando la distribución generalizada Gaussiana (GGD) de media cero, estudiada en nuestros trabajos previos6,16-19. La GGD tiene una función de densidad de probabilidad dada por:
donde A∈ℝ+ es el parámetro de escala, B∈ℝ+ es el parámetro de forma y Γ. es la función gamma.
Cada escala de la descomposición Wavelet es reducida al estimar los parámetros estadísticos A y B de la distribución Gaussiana generalizada (véase la ecuación fGGD), con el fin de obtener el conjunto de características asociadas a todas las escalas Wavelet para un segmento de 2 s con 50% de solapamiento.
En la cuarta etapa se utiliza un análisis discriminante lineal para clasificar en 2 clases posibles: ωs para los eventos de crisis y ωns para los eventos de no-crisis. Para un vector de características X⌢bi perteneciente a la clase ωs o a la clase ωns, se asume que X⌢bi tiene una distribución normal con valor medio μso μns y matriz de covarianza ∑s∑ μns, entonces:
donde k es la dimensión del vector estimado X⌢bi y P. es la probabilidad de evento en particular. Para el análisis discriminante lineal, se calculan las muestras μso μns de cada clase. Entonces se calcula la muestra ∑so ∑ns al restar primero la muestra μso μns de cada clase a partir de las observaciones de esa clase, y tomando la matriz empírica ∑so ∑ns del resultado. Por lo tanto, el discriminante lineal para el problema de clasificación viene dado por
Finalmente, en la etapa 5, el coeficiente r de correlación producto-momento de Pearson se estima a través de
donde ωS¯Oωns¯ son las medias de cada clase. La magnitud de r describe la fuerza de asociación entre las 2 variables y su signo indica la dirección de esta asociación: r=+1 cuando las 2 variables aumentan juntas, y r=−1 cuando una disminuye y la otra aumenta. Así mismo, también muestra el caso más común de 2 variables que están correlacionadas linealmente. El valor r=0 indica ausencia de correlación, r=+1 indica correlación positiva total y r=−1 indica correlación negativa total.
ResultadosLa metodología propuesta se evaluó mediante la base de datos del Hospital Infantil de Boston, que consta de 36 registros de EEG de sujetos pediátricos con crisis intratables. Las señales EEG son bipolares y están muestreadas a 256Hz para cada sujeto. Cada registro contiene un evento de crisis con un inicio y un final marcado, el cual fue detectado por un neurólogo experimentado. En este trabajo usamos 18 eventos de crisis y 18 eventos de no-crisis de 9 sujetos. Consulte Goldberger et al.20 para obtener más detalles.
Durante la etapa de prepropresamiento se usaron 2 filtros Butterworth IIR en cascada, un filtro pasa-bajo de segundo orden con frecuencia de corte de 100Hz y un filtro pasa-alto de primer orden con una frecuencia de corte de 30Hz21, además se sustrajo el valor medio de cada canal. Consultar Quintero-Rincón et al.22 para un amplio estado del arte en diferentes tipos de artefactos en señales EEG.
La detección de una crisis consta de 2 etapas principales: la extracción de características de la señal EEG y una etapa de clasificación de clases o eventos, basada en un aprendizaje automático, con el fin de caracterizar y cuantificar eventos de crisis o eventos de no-crisis. Usando los mismos datos de entrada, nuestro modelo [Q] fue comparado con 2 modelos similares del estado del arte que trabajan también sobre todos los ritmos cerebrales con una longitud de ventana de 2 s y solapamiento del 50%: [S] Shoeb et al.23,24. Usando una ventana rectangular, la extracción de características se realiza a través del cálculo de las diferencias de energía a nivel espectral/espacial y su relación espectral/temporal utilizando una Wavelet Daubechies (dB4) con 6 escalas junto con la densidad espectral de potencia. [C] Chan et al.25. Usando una ventana Hamming, la extracción de características se estima a través del espectro de potencia usando la transformada de Fourier junto con un periodograma. Ambos modelos usan un clasificador basado en SVM. Cabe resaltar que, en esta comparación, a pesar de que la extracción de características tiene algunas diferencias y la etapa de clasificación es distinta, permite contrastar metodologías similares y el costo computacional que puede ser crucial en implementaciones en tiempo real. Por ejemplo, una solución óptima para el clásico clasificador SVM implica una complejidad del orden de n2 o n3 productos, donde n es el tamaño del conjunto de datos, el cual, por lo general, es grande cuando se analizan señales EEG26,27, mientras que para un clasificador lineal la complejidad es del orden mn +mt+nt, donde m es el número de muestras, n es el número de características y t está dado por t=min(m,n)28.
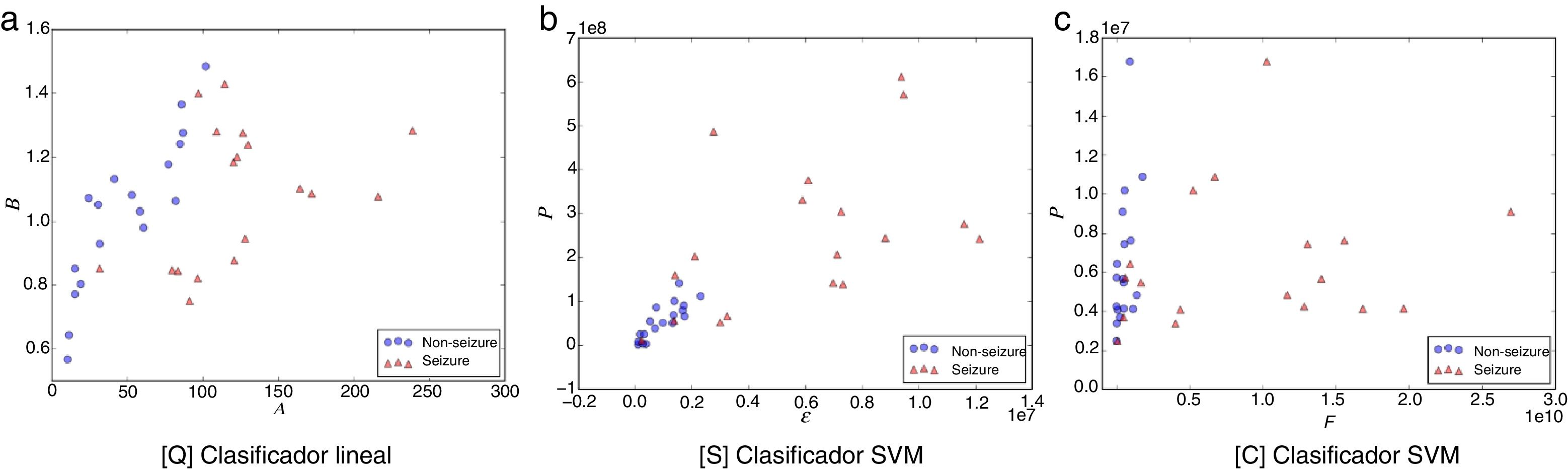
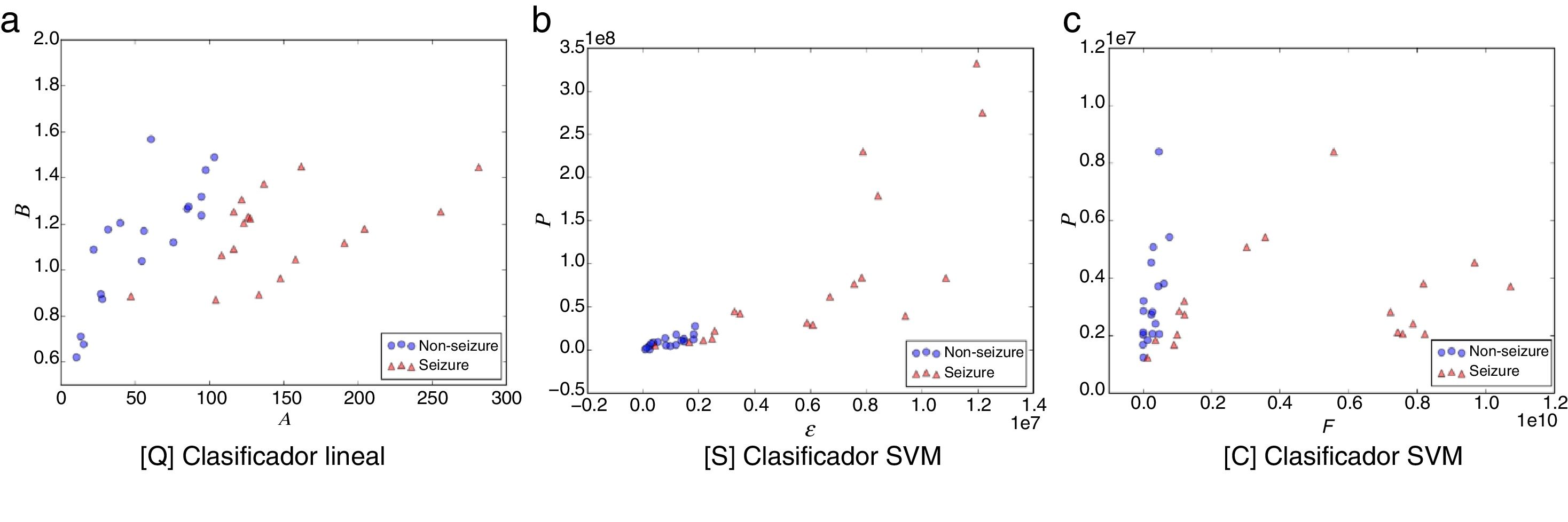
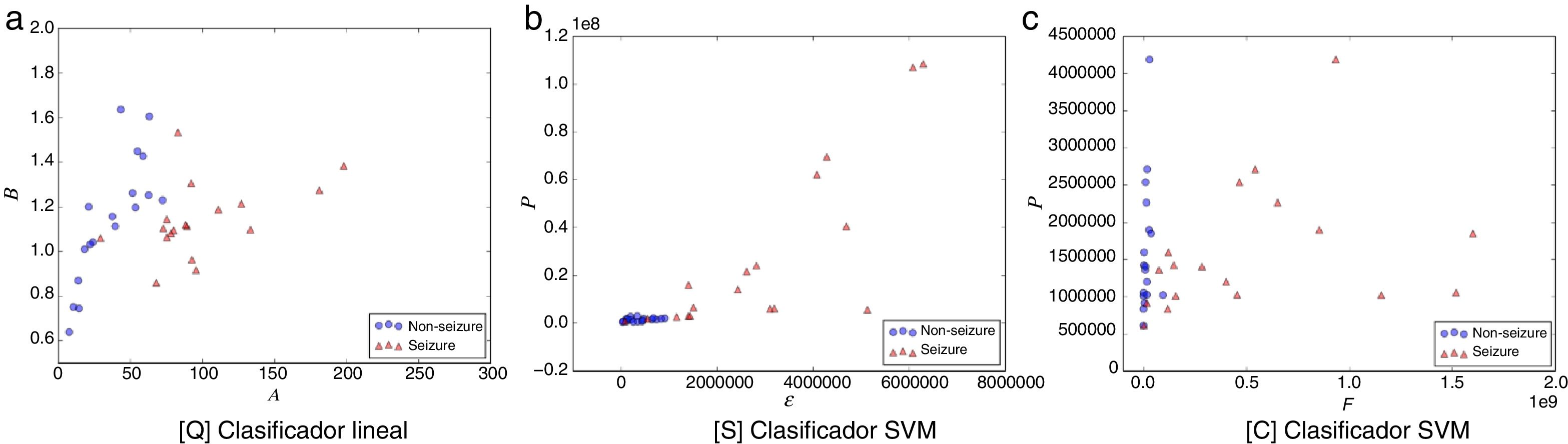
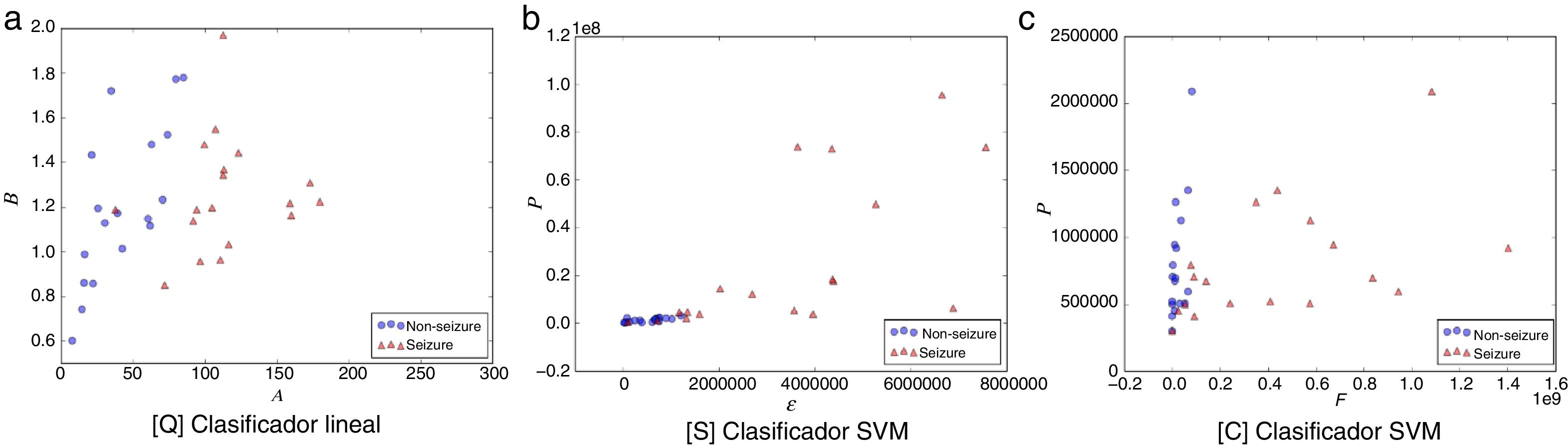
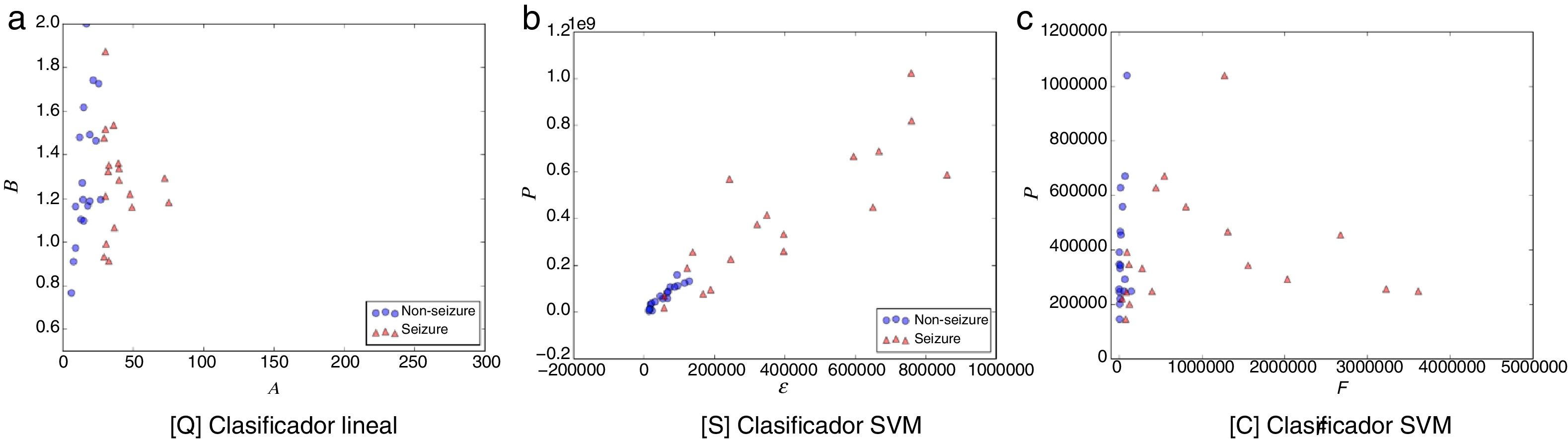
Las figuras 1-5 muestran el rendimiento a través de los diferentes diagramas de dispersión, para todos los ritmos cerebrales de las 2 clases: ωs para crisis y ωns para no-crisis, permitiendo una buena discriminación por inspección visual para todos los modelos. La nomenclatura usada en los diagramas de dispersión, para los ejes x e y, respectivamente, son: escala A y forma B para [Q] usando un clasificador lineal. Energía ɛ y potencia P para [S] y frecuencia F y potencia P para [C], ambos usando un clasificador SVM.
Diagrama de dispersión de la banda delta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.
Diagrama de dispersión de la banda theta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.
Diagrama de dispersión de la banda alfa. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.
Diagrama de dispersión de la banda beta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.
Diagrama de dispersión de la banda gamma. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.
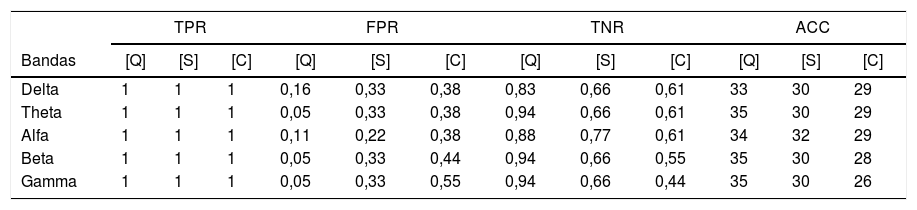
La comparación entre la tabla de contingencia o matriz de confusión presentada en la tabla 1 muestra una sensibilidad o porcentaje de verdaderos positivos del 100% para todos los modelos. Mientras que la especificidad o porcentaje de verdaderos negativos muestra un mejor rendimiento para el modelo basado en el clasificador lineal [Q] con respecto a los otros modelos que están basados en un clasificador SVM, [S] y [C]. Esto nos permite indicar que nuestro modelo basado en un clasificador lineal obtiene la mejor precisión para todos los ritmos cerebrales en los 36 eventos estudiados (18 no-crisis y 18 crisis).
Comparación entre el modelo propuesto [Q] basado en un clasificador lineal, contra 2 modelos similares [S] y [C] que usan un clasificador SVM
| TPR | FPR | TNR | ACC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bandas | [Q] | [S] | [C] | [Q] | [S] | [C] | [Q] | [S] | [C] | [Q] | [S] | [C] |
| Delta | 1 | 1 | 1 | 0,16 | 0,33 | 0,38 | 0,83 | 0,66 | 0,61 | 33 | 30 | 29 |
| Theta | 1 | 1 | 1 | 0,05 | 0,33 | 0,38 | 0,94 | 0,66 | 0,61 | 35 | 30 | 29 |
| Alfa | 1 | 1 | 1 | 0,11 | 0,22 | 0,38 | 0,88 | 0,77 | 0,61 | 34 | 32 | 29 |
| Beta | 1 | 1 | 1 | 0,05 | 0,33 | 0,44 | 0,94 | 0,66 | 0,55 | 35 | 30 | 28 |
| Gamma | 1 | 1 | 1 | 0,05 | 0,33 | 0,55 | 0,94 | 0,66 | 0,44 | 35 | 30 | 26 |
Se estudiaron 36 eventos (18 no-crisis y 18 crisis) para cada ritmo cerebral utilizando la siguiente métrica: sensibilidad o porcentaje de verdaderos positivos (TPR); porcentaje de falsos positivos (FPR); especificidad o porcentaje de verdaderos negativos (TNR) y precisión de clasificación general (ACC).
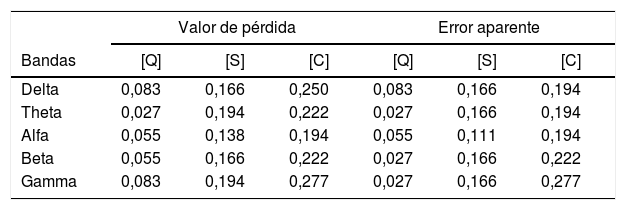
Para cada iteración-k se calcularon el valor de pérdida y el error aparente de los clasificadores, para todas las observaciones usando el modelo entrenado. El valor de pérdida permite determinar la pérdida de clasificación para las observaciones no utilizadas durante el entrenamiento.
El error aparente es la respuesta entre la diferencia de los datos de entrenamiento y las predicciones que hace el clasificador, en función de los datos de entrenamiento de entrada. En otras palabras, es el porcentaje de error cometido sobre la misma muestra empleada para construir el modelo. Valores bajos en ambos métodos significan una gran confianza o exactitud en el clasificador usado. La tabla 2 muestra el rendimiento de los modelos en términos de valor de pérdida y el error aparente. Se puede observar como el modelo [Q] basado en un clasificador lineal tiene los valores de pérdida y error más bajos con respecto a los modelos [S] y [C] basados en un clasificador SVM.
Valor de pérdida y error aparente para los 3 modelos comparados en los 36 eventos (18 no-crisis y 18 crisis) para cada ritmo cerebral
| Valor de pérdida | Error aparente | |||||
|---|---|---|---|---|---|---|
| Bandas | [Q] | [S] | [C] | [Q] | [S] | [C] |
| Delta | 0,083 | 0,166 | 0,250 | 0,083 | 0,166 | 0,194 |
| Theta | 0,027 | 0,194 | 0,222 | 0,027 | 0,166 | 0,194 |
| Alfa | 0,055 | 0,138 | 0,194 | 0,055 | 0,111 | 0,194 |
| Beta | 0,055 | 0,166 | 0,222 | 0,027 | 0,166 | 0,222 |
| Gamma | 0,083 | 0,194 | 0,277 | 0,027 | 0,166 | 0,277 |
Se puede observar que los 3 modelos clasifican correctamente ya que tienen valores bajos, más sin embargo nuestro modelo [Q] basado en la clasificación lineal tiene los mejores valores con respecto a [S] y [C].
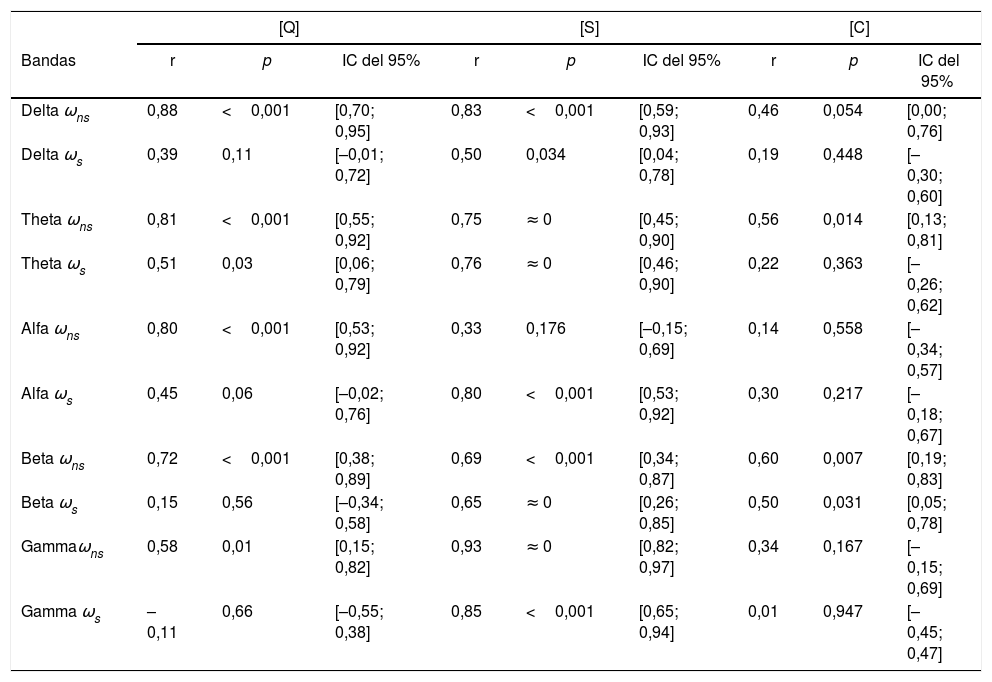
Teniendo toda la información anterior, nosotros nos preguntamos si es posible relacionar los resultados en un rango entre [–1,+1], de tal forma que sirva como una de predicción de las crisis. Para responder a este interrogante, se usó el coeficiente de correlación producto-momento de Pearson para las clases: ωs para los eventos de crisis y ωns para los eventos de no-crisis entre el modelo [Q] basado en el clasificador lineal y los 2 modelos [S] y [Q] basados en un clasificador SVM. El estudio usando 36 eventos (18 crisis y 18 no-crisis) para cada ritmo cerebral, reportado en la tabla 3, indica que nuestro modelo [Q] es potencialmente útil para predecir las crisis en un rango de correlación de [–1,+1], ya que, ωns para las bandas delta, theta, alfa y beta se presenta una alta correlación con un valor de r cercano a 1, excepto para la banda gamma, donde la correlación es media. Todos con un muy buen valor p < 0,05, permitiendo un buen intervalo de confianza. Mientras que para ωs las bandas no están correlacionadas ya que el valor de r es cercano a cero para las bandas delta, theta, alfa y beta, mientras que para la banda gamma la no correlación es máxima. Cabe resaltar que en la comparación entre las 2 clases en la banda theta, el valor de r está en la mitad del intervalo deseado para los eventos de no-crisis, más no tiene un valor muy cercano respecto a los eventos de crisis. Los modelos [S] y [C] presentan en general valores de correlación muy similares, lo cual no permite discriminar claramente entre eventos de crisis y eventos de no-crisis. Estos resultados sugieren que nuestro modelo basado en la distribución Gaussiana generalizada, junto con un clasificador lineal, puede definirse por un valor de escala entre [–1,+1] para discriminar entre eventos de crisis y eventos de no-crisis en todos los ritmos cerebrales, permitiendo definir umbrales a partir del intervalo de confianza para la escala propuesta.
Coeficiente de correlación producto-momento de Pearson entre ωs para un evento de crisis (seizure) y ωns para un evento de no-crisis (non-seizure) sobre los diferentes modelos de clasificación: [Q] basado en un clasificador lineal, [S] y [C] basados en un clasificador SVM
| [Q] | [S] | [C] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Bandas | r | p | IC del 95% | r | p | IC del 95% | r | p | IC del 95% |
| Delta ωns | 0,88 | <0,001 | [0,70; 0,95] | 0,83 | <0,001 | [0,59; 0,93] | 0,46 | 0,054 | [0,00; 0,76] |
| Delta ωs | 0,39 | 0,11 | [–0,01; 0,72] | 0,50 | 0,034 | [0,04; 0,78] | 0,19 | 0,448 | [–0,30; 0,60] |
| Theta ωns | 0,81 | <0,001 | [0,55; 0,92] | 0,75 | ≈ 0 | [0,45; 0,90] | 0,56 | 0,014 | [0,13; 0,81] |
| Theta ωs | 0,51 | 0,03 | [0,06; 0,79] | 0,76 | ≈ 0 | [0,46; 0,90] | 0,22 | 0,363 | [–0,26; 0,62] |
| Alfa ωns | 0,80 | <0,001 | [0,53; 0,92] | 0,33 | 0,176 | [–0,15; 0,69] | 0,14 | 0,558 | [–0,34; 0,57] |
| Alfa ωs | 0,45 | 0,06 | [–0,02; 0,76] | 0,80 | <0,001 | [0,53; 0,92] | 0,30 | 0,217 | [–0,18; 0,67] |
| Beta ωns | 0,72 | <0,001 | [0,38; 0,89] | 0,69 | <0,001 | [0,34; 0,87] | 0,60 | 0,007 | [0,19; 0,83] |
| Beta ωs | 0,15 | 0,56 | [–0,34; 0,58] | 0,65 | ≈ 0 | [0,26; 0,85] | 0,50 | 0,031 | [0,05; 0,78] |
| Gammaωns | 0,58 | 0,01 | [0,15; 0,82] | 0,93 | ≈ 0 | [0,82; 0,97] | 0,34 | 0,167 | [–0,15; 0,69] |
| Gamma ωs | –0,11 | 0,66 | [–0,55; 0,38] | 0,85 | <0,001 | [0,65; 0,94] | 0,01 | 0,947 | [–0,45; 0,47] |
Se usaron 36 eventos (18 crisis y 18 no-crisis) para cada ritmo cerebral; donde r=1 es una correlación total, r=0 es una ausencia de correlación, r=−1 es una no correlación total. IC del 95% es el 95% del intervalo de confianza. [Q] presenta una alta correlación para las bandas delta, theta, alfa y beta, excepto para la banda gamma para los eventos de no-crisis, mientras que para los eventos de crisis presenta una ausencia de correlación. Los modelos [S] y [C] no tienen una correlación clara. Esto sugiere que nuestro modelo [Q] puede estimar los cambios entre eventos crisis y no-crisis en una escala de [–1,+1].
La detección para todos los ritmos cerebrales, basada en el intervalo de confianza (IC del 95%) del coeficiente de correlación producto-momento de Pearson de las señales estudiadas es de: 1 s en promedio antes del inicio de la crisis para el 50%, detección exacta en tiempo del inicio de la crisis para el 30% y el 20% restante tiene una latencia en promedio de 3,07 s.
ConclusionesLos resultados preliminares de este trabajo sugieren que la detección de eventos de crisis en señales EEG, utilizando la distribución Gaussiana generalizada basada en un clasificador lineal junto con el coeficiente de correlación producto-momento de Pearson, es útil para predecir entre un evento de crisis y no-crisis en un valor de escala entre [–1,+1] en todos los ritmos cerebrales. Por lo tanto, es potencialmente interesante para idear algoritmos de detección y predicción de crisis de manera automática en tiempo real en señales EEG.
Las perspectivas para el trabajo futuro incluyen una extensa evaluación de esta metodología, mejorar del tiempo de latencia de la detección de la crisis, realizar un estudio detallado de la confiabilidad de la predicción a medida que se genera la crisis, aplicar nuestra metodología en señales a largo-plazo durante el sueño, hacer pruebas con señales en tiempo real y comparaciones con otros métodos de predicción del estado del arte, que incluyan una alta robustez frente al ruido y control de artefactos, así como la intensidad, la duración y la propagación de las crisis en cada canal.
FinanciaciónParte de este trabajo fue subsidiado por: a) ITBACyT DP.557No.34/2015, Actividades científicas y tecnológicas del departamento de investigación del Instituto Tecnológico de Buenos Aires; b) Protocolo 07/15 del FLENI, y c) Proyecto DynBrain respaldado por el programa internacional STICAmSUD.
Conflicto de interesesLos autores declaran que no tienen ningún conflicto de intereses.






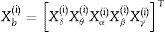
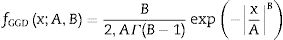
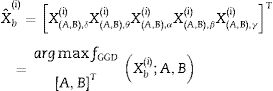
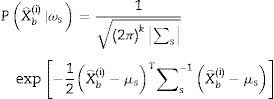
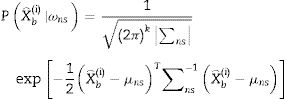
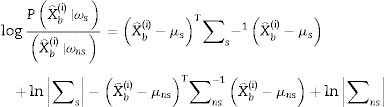
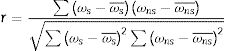
![Diagrama de dispersión de la banda delta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras. Diagrama de dispersión de la banda delta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.](https://static.elsevier.es/multimedia/18530028/0000001000000004/v2_201811280611/S1853002818300466/v2_201811280611/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Diagrama de dispersión de la banda theta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras. Diagrama de dispersión de la banda theta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.](https://static.elsevier.es/multimedia/18530028/0000001000000004/v2_201811280611/S1853002818300466/v2_201811280611/es/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Diagrama de dispersión de la banda alfa. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras. Diagrama de dispersión de la banda alfa. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.](https://static.elsevier.es/multimedia/18530028/0000001000000004/v2_201811280611/S1853002818300466/v2_201811280611/es/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Diagrama de dispersión de la banda beta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras. Diagrama de dispersión de la banda beta. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.](https://static.elsevier.es/multimedia/18530028/0000001000000004/v2_201811280611/S1853002818300466/v2_201811280611/es/main.assets/thumbnail/gr4.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Diagrama de dispersión de la banda gamma. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras. Diagrama de dispersión de la banda gamma. a) [Q] escala A eje-x y forma B eje-y. b) [S] energía ɛ eje-x y potencia P eje-y. c) [C] frecuencia F eje-x y potencia P eje-y. Todos los métodos permiten una discriminación entre eventos de no-crisis (círculos azules, non-seizure) y eventos de crisis (triángulos rojos, seizure). En la edición online podrá consultar los colores de las figuras.](https://static.elsevier.es/multimedia/18530028/0000001000000004/v2_201811280611/S1853002818300466/v2_201811280611/es/main.assets/thumbnail/gr5.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
