El objetivo de este trabajo se centra en verificar, en los estados de Brasil, la correlación existente entre la desigualdad de la renta y el crecimiento económico bajo la hipótesis de la U invertida de Kuznets en el periodo de 1995 a 2012. La suposición de la U invertida –hipótesis de Kuznets (1955)– alude, a corto plazo, que hay una conexión positiva entre la desigualdad de la renta y el nivel de la renta per cápita. Ya, a largo plazo, se percibe una relación de la U invertida, pues hay una inversión de esta relación. El uso de dos tipos de indicadores de la desigualdad de la renta, Gini y Theil, juntamente con la econometría de los datos de panel dinámico, son parte de este trabajo para examinar, empíricamente, la relación entre la desigualdad de la renta y el crecimiento económico. Entre otros resultados, se concluye que la hipótesis de Kuznets es confirmada en los estados brasileños.
This work aims to verify the correlation between income inequality and economic growth in Brazilian states using the Kuznets inverted U hypothesis for the time period from 1995 to 2012. Te assumption of the inverted U hypothesis –Kuznets (1955)– signals that in the short term, there is a positive correlation between income inequality and per capita income levels. In the long term, however, the inverted U relationship emerges, as the relationship is reversed. Tese types of income inequality indicators, as well as the Gini and Theil indices and dynamic panel data econometrics, were included in this work to empirically examine the relationship between income inequality and economic growth. This work confirms the Kuznets hypothesis in Brazilian states, among other findings.
Ce travail se centre sur l’objectif de vérifier la corrélation entre l’inégalité des revenus et la croissance économique dans les états du brésil entre 1995 et 2012, sur la base de l’hypothèse du U inversé de Kuznets (1955). Selon cette hypothèse, à court terme, il y a une connexion positive entre l’inégalité des revenus el le revenu per capita. Par contre, à long terme, on perçoit un rapport inverse. Ce travail comprend l’usage de deux types d’indicateurs de l’inégalité des revenus, Gini y Theil, et l’économétrie des données de panel dynamique, pour examiner, empiriquement, la relation entre l’iné-galité des revenus et la croissance économique. Entre autres résultats, il est conclu que l’hypothèse de Kuznets est confirmée dans les états brésiliens.
O objetivo deste trabalho se centra em verificar, nos estados do Brasil, a correlação existente entre a desigualdade da renda e o crescimento econômico sob a hipótese do U invertido de Kuznets no período de 1995 a 2012. A suposição do U invertido – hipótese de Kuznets (1955) – faz alusão, ao curto prazo, a existência de uma cone-xão positiva entre a desigualdade de renda e o nível de renda per cápita. Já, no longo prazo, se percebe uma relação de U invertido, pois há uma inversão dessa relação. O uso de dois tipos de indicadores da desigualdade de renda, Gini e Theil, conjuntamente com a econometria dos dados de panel dinâmico são parte deste trabalho para examinar, empiricamente, a relação entre a desigualdade de renda e o crescimento econômico. Entre outros resultados, se conclui que a hipótese de Kuznets é confirma-da nos estados brasileiros.
本文的目标是运用库兹涅茨倒U曲线证实1995~2012年巴西收入不平等与, 经济增长的关系。库兹涅茨倒U曲线假设,短期内收入不平等与人均收入, 水平存在正相关关系,但长期而言,将会出现倒U曲线。本文的研究使用, 了库兹涅茨倒U曲线这类收入不平等指标、基尼系数以及面板计量数据, 对收入不平等与经济增长做了经验研究。研究结论认为,巴西经济证实了, 库兹涅茨倒U曲线存在的假设。
Los debates acerca de la relación entre el crecimiento económico y la desigualdad de la renta tuvieron más espacio en las discusiones en 1950, por medio de los trabajos pioneros de Simon Kuznets. Desde entonces, otros estudios y métodos fueron preparados con la finalidad de medir la desigualdad de la renta, tanto en países desarrollados como en países en vías de desarrollo.
En 1955, Simon Kuznets elaboró un referencial teórico con base en el análisis del proceso de cambio de las economías agrícolas para las economías industriales en Inglaterra, Alemania y en los países del Reino Unido. Esta teoría asegura que el proceso de desarrollo económico debía resultar en un periodo inicial de concentración de la renta en el instante en que la migración de personas y recursos pasase de la agricultura a las áreas urbanas e industrializadas, sin embargo, esa tendencia se revertiría en la medida que el proceso de migración fuese atenuado.
Este acontecimiento ocurre por la diferencia de las rentas de la población entre los dos sectores que pueden ser estudiados por medio de la renta per cápita media industrial, de la participación de la renta sectorial en relación a la renta total y de la desigualdad en las participaciones de las poblaciones que tienden a ser superiores en el sector urbano con relación al rural (Salvato et al., 2006).
Kuznets (1955) discute sobre la distribución de la renta, con el objetivo de descubrir si la desigualdad en la distribución de la renta crece o disminuye en el transcurso del crecimiento económico de un país y los factores que la determinan a largo plazo y, si su origen podría estar vinculado al crecimiento económico.
La correlación y ponderación existente entre el crecimiento económico y la desigualdad de la renta es un tema de suma importancia en la historia del pensamiento económico, a pesar de ser un elemento de controversias. Estudios como los de Deininger y Squire (1996, 1998), Ravallion y Chen (1997), Easterly (1999) y Dollar y Kraay (2002) señalan que el crecimiento económico no está relacionado a los altos niveles de la desigualdad de la renta. En contrapartida, Alesina y Rodrick (1994) y Alesina y Perotti (1996) mencionan que la desigualdad de la renta está relacionada al crecimiento económico.
La hipótesis de Kuznets, la U invertida fue probada, también, por algunos autores que utilizaron datos alusivos a Brasil, como son los trabajos de Barros y Gomes (2007), Júnior et al. (2007), Bêrni, Marquetti y Kloeckner (2002) y Salvato et al. (2006).
Las estimativas indicadas varían de acuerdo con las diferentes rentas per cápita en su forma lineal y cuadrática, utilizando el índice de Gini y L de Theil para medir la desigualdad de la renta en todos los métodos econométricos. Frente a eso, el objetivo central del presente artículo es verificar, en los estados de Brasil, la correlación existente entre la desigualdad de la renta y el crecimiento económico bajo la hipótesis de la U invertida de Kuznets, en el periodo de 1995 a 2012, una vez que, aunque la desigualdad en la distribución de la renta en el país sea considerado un problema grave, causante del aumento de la pobreza y de la criminalidad, Brasil ha estado entre las naciones con mejores índices económicos.
Siendo así, todas las unidades federativas de Brasil, incluyendo el Distrito Federal, en el periodo comprendido de 1995 a 2012, serán utilizadas como base de datos en este trabajo, acoplando en su análisis, las informaciones de la desigualdad de la renta –índice de Gini y L de Teil–, renta domiciliar per cápita, años de estudio y expectativa de vida que una persona tiene al nacer. Siendo la base de datos, construida desde la Pesquisa Nacional por Muestra de Domicilios (pnads), concedidos por el Instituto Brasileño de Geografía y Estadística (ibge) y de la base de dados del Instituto de Pesquisa Económica Aplicada (ipeadata).
Diferente de los artículos que antes trabajaron con esta temática, el presente trabajo avanza con respecto al uso de un modelo dinámico para datos de panel, desarrollado por Arellano y Bond (1991), Arellano y Bover (1995) y Blundel y Bond (1998), así como poner al día los datos actuales. Aunque este estudio posea un asunto comúnmente discutido, en el ámbito académico, la evolución de la desigualdad en Brasil se vuelve importante debido a las paradojas que el propio modelo de crecimiento económico implica.
De esta forma, este estudio, además de esta introducción, se estructura en seis secciones. En la segunda sección, será expuesto el referencial teórico y empírico que da fundamento a la problemática sugerida aquí, contando con el artículo de Kuznets (1955) y la revisión de la literatura producida sobre este tema. La tercera sección presenta el modelo econométrico y los métodos de estimación utilizados. A seguir, la cuarta sección, define y discute la base de datos; enseguida, hay un análisis de los resultados logrados de la estimativa del modelo econométrico, en la quinta sección. Y, por fin, completando la estructura de este trabajo, la sexta sección concluye de forma singular con la exposición de las consideraciones finales.
2Propuesta de Kuznets2.1Economic Growth and Income Inequality, el artículoEl ejemplar artículo Economic Growth and Income Inequality, de Simon Kuznets, muestra la relación entre la desigualdad de la renta y el crecimiento económico. Kuznets (1955) desmenuza su trabajo de forma singular haciendo apología al carácter y a las consecuencias de los cambios a largo plazo en la distribución de la renta.
Para el autor, hay por lo menos dos grupos de fuerza para el desarrollo de los países a largo plazo que inducen al crecimiento de la desigualdad en la distribución de la renta–distribución de renta de la estructura industrial y concentración de ahorros en los grupos de renta más elevadas.
Como consecuencia del proceso de industrialización y urbanización la migración rural, buscando mejores condiciones de vida, aconteció de forma significativa. Con eso, para analizarse la distribución de la renta de la población en su totalidad se vuelve imprescindible comprender el método de cómo la renta, en las ciudades y en el campo es compartida, una vez que la desigualdad de la distribución y la renta per cápita media rural son comúnmente menores que la urbana, principalmente como consecuencia de una menor productividad intrínseca a las actividades de cada medio.
Al considerar la desigualdad, en la distribución del ahorro, siendo más elevada que en la distribución de las rentas personales y de los activos, el ahorro acaba limitándose a los grupos más ricos de la sociedad, teniendo como consecuencia, ceteris paribus, una concentración de una proporción creciente de rendimientos en las manos de los grupos de renta más elevados.
Aún en su obra, Kuznets (1955) propone algunas preguntas sobre la distribución de la renta, a saber: ¿será qué la desigualdad en la distribución de la renta se eleva o disminuye en el transcurso del crecimiento económico de un país? ¿Cuáles son los factores que determinan la desigualdad de la renta a largo plazo? Tales preguntas, en líneas generales, comprobaron su preocupación con el grado de desigualdad en la distribución de la renta, cuyo origen podría estar asociado al crecimiento económico.
Según las ideas del autor, las cuestiones arriba citadas son amplias en un campo de estudio que ha tenido pocas definiciones, escasez de datos y las presiones de opiniones fuertemente defendidas. Resalta, aún, que aunque no se puedan evitar completamente las dificultades resultantes se puede auxiliar en las especificaciones características de las distribuciones del tamaño de la renta que se desea examinar y los movimientos que se espera explicar.
Las prominencias empíricas, del estudio de Kuznets, recomiendan que la disminución de la desigualdad en los países desarrollados ocurra, tan sólo, en las últimas fases del proceso de crecimiento y en función de sus beneficios. La sociedad se materializa con un mayor acceso a las redes de salud y educación induciendo, como consecuencia, a un aumento de la productividad, lo que acaba disponiendo los efectos de la rápida industrialización y urbanización. Discurre, también, que conforme las economías experimentan el crecimiento, el acceso a la educación es capaz de suministrar mejores oportunidades, disminuir las desigualdades y las parcelas más pobres de la población volviéndolos más politizados y capaces de modificar las políticas del gobierno.
Las consecuencias del desplazamiento de la revolución agraria para la industrial, juntamente con la elevación poblacional, mediante la rápida declinación en las tasas de mortalidad y mantenimiento, o inclusive, ampliación de la tasa de natalidad que provoca un aumento de la desigualdad principalmente en los periodos iniciales.
La tasa de crecimiento de la población de acuerdo con Kuznets puede ser considerada en parte como causa y en parte como efecto del largo movimiento de la desigualdad de la renta. A parte de todo, vale resaltar que en esta fase incide la preponderancia de factores que benefician el mantenimiento o elevación de los grupos detentores del capital, en la medida en que su posición es estimulada por las ganancias provenientes de las nuevas industrias.
Mediante el contexto anterior, se puede plantear un modelo de dinámica de la desigualdad, dependiente de un régimen específico de crecimiento capaz de caracterizar la estructura secular de la distribución de la renta, en que la desigualdad se acentúa en los momentos iniciales del crecimiento económico, se consolida por un periodo y disminuye en las últimas fases.
Ese modelo temporal es ajustado a la población más pobre, pero los resultados adquiridos mencionan que el proceso de baja de la desigualdad, analizado en los países desarrollados es marcado por la parte creciente trayectoria de la desigualdad a lo largo del tiempo –simulada en la curva de la U invertida.
Varios estudios y métodos fueron preparados con el objetivo de explorar la naturaleza de la relación entre la distribución de la renta y el crecimiento, tanto para los países desarrollados, como para los países en desarrollo. Con el objetivo de explanar la propuesta de este trabajo, la próxima sección se detendrá en la revisión de la literatura de los trabajos antes elaborados sobre la propuesta de Kuznets, revelando sus fundamentos teóricos, bien como las evidencias empíricas encontradas.
2.2Revisión de la literaturaDe acuerdo con Kuznets (1955) es de suma importancia el estudio sobre la tendencia secular de la estructura de la renta, bien como de los factores que la determinan, evaluando las características y procedencias de las alteraciones a largo plazo, una vez que, cualquier percepción adquirida por observación en los cambios de los agregados de algún país, a lo largo del tiempo, será válida, se explicada en términos de movimientos de las divisiones de los variados grupos de la población, pudiendo ser medidos por medio de percentis, decis o quintis.
En Economic Growth and Income Inequality (1955), relativo a la dinámica de la distribución de la renta a lo largo de los procesos de industrialización y urbanización Simon Kuznets ilustró su teoría desde un modelo de economía dualista, trabajando con un sector no agrícola y otro agrícola, con el objetivo de analizar la relación entre la desigualdad de la renta y el crecimiento económico. Se conjeturaba que la desigualdad de la renta aumentaría a corto plazo y, con el crecimiento económico, reduciría –configurando una U invertida.
Permutando la población de un sector para otro, de un tradicional agrícola a un moderno industrializado, se elevaría la desigualdad de la renta, una vez que este sector más dinámico es también más rico y más desigual. Tal fenómeno acontece por la diferencia de las rentas de la población entre los dos sectores, que pueden ser analizados por medio de la renta per cápita media industrial de la participación de la renta sectorial, con relación a la renta total y de la desigualdad en las participaciones poblacionales, que tienden a ser superiores en el sector urbano con relación al rural (Salvato et al., 2006).
Con relación a los datos, Kuznets (1955) atenta para las clasificaciones en distintas categorías de la renta con diversas dimensiones y a los percances consecuentes de la carencia de datos para largos periodos. Para el estudio de esa dinámica, el autor al utilizar series temporales de Estados Unidos, Reino Unido y una limitada muestra para Alemania (Prusia y Sajonia), sugiere que una distribución de la renta relativa, estimada por la incidencia de la renta anual entre las clases, reveló un movimiento de igualdad mayor en la década de 1920, presentándose también, evidencias en el periodo que antecedió al de la Primera Guerra Mundial.
También se percibió que en Estados Unidos la proximidad de las rentas, dentro de los diferentes grupos, aconteció entre la crisis de 1929 y después de la Segunda Guerra Mundial. El mismo acontecimiento fue notado en Inglaterra, entre 1910 y 1947, como consecuencia del empobrecimiento de los estratos de los más ricos, mientras el valor de la renta de los más pobres se mantuvo constante hasta el año de 1919, elevándose en el periodo comprendido entre los años de 1929 a 1947.
Después de la publicación de los trabajos desbravadores de Simon Kuznets en los años de 1950 y 1960, las discusiones sobre la relación entre nivel de la renta per cápita y la desigualdad de la renta presentaron mayor repercusión en el debate económico. Desde entonces, variados estudios y métodos fueron elaborados con el objetivo de medir la desigualdad de la renta, tanto para países desarrollados, como para países en vías de desarrollo (Taques y Mazzutti, 2010).
Fields (2002) asegura que la literatura adoptó dos segmentaciones con los estudios de Kuznets, donde una tiende para los modelos que analizan el formato de la U invertida –desde el nivel de desarrollo económico– y otra que utiliza bases empíricas para corroborar o no la propuesta de Kuznets.
Con la finalidad de probar la hipótesis de la U invertida se realizaron diversas estimativas. Los métodos de cross-section y series de tiempo fueron vastamente usados en estudios de las décadas siguientes a sugerencia de Kuznets, pero sus limitaciones no dejaron de ser apuntadas por otros autores. Como alternativa, la estimativa en datos de panel ha sido ampliamente utilizada y presenta resultados estadísticamente más significantes (Taques y Mazzutti, 2010).
Conforme Bêrni, Marquetti y Kloeckner (2002), los datos de cross-section son favorables para los presentes propósitos porque muestran la posibilidad de identificación de modelos uniformes, que señalan el problema en diferentes países. Con eso, tal identificación, ayuda a establecer promedios, donde los niveles de desigualdad observados, en países específicos, pueden ser comparados.
Fields y Jakubson (1994), al elegir datos de países desarrollados y en vías de desarrollo, asumen que ciertos países pueden estar arriba o abajo del promedio de la curva de Kuznets. Luego, la línea central podría ser estimada por medio de la metodología de efectos fijos. Diversos resultados de los autores discreparon eso desde el método econométrico utilizado, pudiendo la diferencia ser explicada por medio de la observación de los resultados entre países y en un único país.
La mayoría de los estudios empíricos que engloban grupos de países desarrollados y en desarrollo, en la literatura internacional, hacen mención y son favorables a la hipótesis de Kuznets, aunque sean utilizadas metodologías diferenciadas. Siendo así, Kravis (1960), Oshima (1962), Adelman y Morris (1974), Paukert (1973), Ahluwalia (1976), Robinson (1976), Ram (1989), Perotti (1993), Dawson (1997), y Ogwang (2000) y Sylvester (2000), representan un grupo de estudios fundamentados en datos de corte transversal (cross-section) y que reportan evidencias favorables a la hipótesis en cuestión.
Hsing y Smith (1994), utilizando datos de series temporales para la economía americana, no rechazan la hipótesis de Kuznets. Lo mismo ocurre en los estudios de Forbes (2000), Deininger y Squire (1998), Barro (2000) y Tornton (2001) al valerse de datos de panel. Ya Fields y Jakubson (1994), uno de los principales trabajos que no apoya la hipótesis de la U invertida, se basa en estimativas para el panel con efectos fijos.
Otros estudios presentaron diferentes explicaciones para el posible formato de la U invertida para la correlación existente entre la desigualdad y el crecimiento económico, después de los artículos de Kuznets (1955) y de Robinson (1976). En esa línea, Barro (2000) atribuye esa peculiaridad a las deficiencias en el mercado financiero, existentes en economías poco desarrolladas. Las deficiencias en el mercado de crédito afectarían, de forma significativa, la parte más pobre de la población, cuya parcela presenta mayor dificultad de acceso a crédito, disminuyendo su capacidad de conseguir inversiones que implicarían en acúmulo de capital físico o capital humano.
En la esfera nacional, existen trabajos que también parecen evidenciar el comportamiento de la U invertida recomendado por Kuznets. Utilizando datos del Valor Agregado Fiscal (vaf) y del índice de Theil, Bêrni, Marquetti y Kloeckner (2002) evidencian la existencia de una curva de Kuznets para el sector industrial y el de servicios de Rio Grande do Sul en 1991, pero no logra resultados, estadísticamente, relevantes para el sector agropecuario.
Empleando datos de panel para los municipios de Rio Grande do Sul, Bagolin, Gabe y Pontual (2003), también legitiman la relación de la U invertida entre la renta per cápita y el índice de Theil, considerando el periodo de 1970, 1980 y 1991. Jacinto y Tejada (2004) echaron mano de datos cross-section y en panel para las ciudades del noreste brasileño, analizando los años de 1970 y 1991, encontrando también evidencias de la referida curva. Salvato et al. (2006), planteando los años de 1991 y 2000, también obtienen evidencias de que para los municipios de Minas Gerais, la correlación entre la desigualdad de la renta y el desarrollo económico está conforme con la teoría de Kuznets.
Porto Júnior et al. (2007), en sus estimativas para cross-section, las rentas per cápita lineal y cuadrática fueron utilizadas como medidas, objetivando captar alteraciones direccionales en la distribución de la renta de acuerdo con su elevación. Los autores verificaron que para dados de panel, en Rio Grande do Sul, la estimación con efectos fijos alude que el desarrollo inicial fue superado y que la desigualdad de la renta no fue tan elevada, comparándola con el estado de Paraná.
Para las ciudades de Rio Grande do Sul, Bêrni, Marquetti y Kloeckner (2002) observaron la hipótesis de la U invertida de Kuznets en cross-section. Desde un modelo con método no paramétrico de regresión local, emplearon la densidad demográfica municipal y la relación de la renta per cápita sectorial-desigualdad, tanto para la renta agropecuaria cuanto para la industrial y para el sector de servicios. Los resultados confirmaron la U invertida indicado por Kuznets, pero apenas para algunos municipios –cuando esté incluído la variable explicativa de densidad demográfica municipal.
Por lo demás, se destaca que en Brasil, los índices de desigualdad de la economía local crecieron en la década de los setenta y se mantuvieron elevados hasta la mitad de la década de los noventa. Esa situación comenzó a alterarse después de la implantación del “Plano Real”, cuando los índices de desigualdad empezaron a presentar reducción. A pesar de esa baja reciente, la desigualdad de la renta brasileña permanece aún bastante alta. La parte de la renta total apropiada por el 1% más rico de la población es de la misma magnitud que la apropiada por los 50% más pobres (Kakwani et al, 2006).
3MetodologíaCon el objetivo de conocer la correlación existente entre la desigualdad de la renta y sus determinantes, en forma de panel dinámico, se emplearon los estimadores del método de momentos generalizados (mmg-sistema) elaborados en los trabajos de Arellano y Bond (1991), Arellano y Bover (1995) y Blundell y Bond (1998).
En este trabajo, se analizó el comportamiento de la desigualdad de los 27 estados brasileños relacionados con la renta, la educación y en referencia de la expectativa de vida de los individuos de 1995 a 2012.
El modelo supone que el cuadro de la desigualdad de la renta corriente tiende a perpetuarse y/o influenciar el desempeño de la desigualdad en el porvenir. La relación que hay entre la desigualdad de la renta y el crecimiento económico es analizada por medio del modelo de regresión, para dados de panel, con el siguiente formato:
En que, la variable dependiente yit es la medida de desigualdad de la renta (el coeficiente de Gini o índice de Theil); rentait es renta per cápita; eduit son los años medios de estudio de los individuos; eduit es la expectativa de vida de los individuos; ηi son los efectos fijos no observables de los individuos y εit representa los disturbios aleatorios. El subíndice “ i” representa el estado y “t ” el periodo de tiempo.
Arellano y Bond (1991), en su trabajo observan lo ocurrido en dos problemas econométricos, al calcular el modelo por medio de técnicas de estimación tradicionales. Primero, debido a la presencia de los efectos no observables de los individuos, ηi juntamente con la variable dependiente desfasada, yit-1, en el lado derecho de la ecuación. En ese caso, omitir los efectos fijos individuales en el modelo dinámico de panel vuelve a los estimadores de mínimos cuadrados ordinarios (mqo) deformados e inconsistentes. Mientras, el estimador within groups, que corrige para la presencia de efectos fijos, genera una estimativa de β1 sesgada para abajo en paneles con la dimensión temporal pequeña.
Debido a la probable endogeneidad de las variables explicativas. En ese caso, endogeneidad en el lado derecho de la ecuación (2) debe ser tratada para evitar una posible deformación generada por problemas de simultaneidad.
Una de las formas de resolver esos problemas, según Arellano y Bond (1991), es proponiendo el estimador del método de momentos generalizado-diferenciado (mmg-diferenciado), que consiste en la eliminación de los efectos fijos por medio de la primera diferencia de la ecuación (1).
Así, se tiene: en que, para cualquier variable yit, Δyit = yit - yit-1. Se nota que en la ecuación (2), Δyit-1 y Δεit son correlacionados y, así siendo, estimadores de mqo para sus coeficientes serán deformados e inconsistentes. Luego, se hace necesario emplear variables instrumentales para Δyit-1.
La adopción de las hipótesis en la ecuación (1), aluden a que las condiciones de momentos E[Δyit-s Δεit] = 0, para t = 3,4,….T e s ≥ 2, son válidas. Arellano y Bond (1991), basados en esos momentos, indican aplicar yit-s, para t = 3,4,….T e s ≥ 2, como instrumentos para la ecuación (2).
Las otras variables explicativas pueden ser consideradas como: (a) estrictamente exógena, si no es correlacionada con los términos de errores pasados, presentes y futuros; (b) débilmente exógena, si es correlacionada apenas con valores pasados del término de errores, y (c) endógena, si es correlacionada con los términos de errores pasados, presentes y futuros. En el segundo caso, los valores de la variable desfasada en uno o más periodos son instrumentos válidos en la estimativa de la ecuación (2) y, en el último caso, los valores desfasados en dos o más periodos son instrumentos válidos en la estimativa de esa ecuación.
De acuerdo con Arellano y Bover (1995) y Blundell y Bond (1998), tales instrumentos son débiles cuando las variables dependientes y explicativas exhiben fuerte persistencia y/o la variación relativa de los efectos fijos aumenta. De esta forma, producen un estimador mmg-diferenciado no consistente y deformado para paneles con T pequeño.
De esta forma, Arellano y Bover (1995) y Blundell y Bond (1998) recomiendan un sistema que combina el conjunto de ecuaciones en diferencia, ecuación (2), con el conjunto de ecuaciones en nivel, ecuación (1), para reducir ese problema de deformación. Este sistema es designado como método de momentos generalizado-sistema (mmg-sistema).
Para las ecuaciones en diferencias, el conjunto de instrumentos es el mismo anteriormente citado. Para la regresión en nivel, los instrumentos apropiados son las diferencias desfasadas de las respectivas variables. Por ejemplo, asumiendo que las diferencias de las variables explicativas no son correlacionadas con los efectos fijos individuales (para t = 3,4,….T) e E[Δyi2 vi] = 0, para i = 1,2,3,….,N. Entonces, las variables explicativas en diferencias y D yit-1, caso ellas sean exógenas o débilmente exógenas, son instrumentos válidos para ecuación en nivel. Lo mismo ocurre si ellas son endógenas, pero con los instrumentos siendo las variables explicativas en diferencias desfasadas de un periodo y Δyit-1.
Las estimativas del mmg-sistema, expuestas en la próxima sección, derivan de la estimación con estimador corregido por el método de Windmeijer (2005) para evitar que el respectivo estimador de las variancias subestime a las verdaderas variancias en muestra finita.
Siendo así, el estimador empleado fue sugerido por Arellano y Bond (1991) en dos pasos. En la primera etapa, se conjetura que los términos de errores son independientes y homocedásticos en los estados y a lo largo del tiempo. Ya en el segundo periodo, los residuos contraídos en la primera etapa son usados para construir una estimativa consistente de la matriz de variancia-covariancia, relajando, así, las hipótesis de independencia y homocedasticidad. El estimador del segundo periodo es asintóticamente más eficiente con relación al estimador de la primera etapa.
La consistencia del estimador mmg-sistema depende de la suposición de ausencia de correlación serial en el término de errores y de la validez de los instrumentos adicionales. De esta forma, inicialmente, se prueban las hipótesis nulas de ausencia de autocorrelación de primer y segundo orden de los residuos.
Para que los estimadores de los parámetros sean consistentes, la hipótesis de ausencia de autocorrelación de primer orden debe ser rechazada y la de segundo orden aceptada. Posteriormente, se realiza la prueba de Hansen para verificar si los instrumentos adicionales exigidos por el método mmg-sistema son válidos como recomienda Arellano y Bond (1991).
4Base de datosLos datos de este trabajo, para evaluar la relación entre la desigualdad de la renta y el crecimiento económico, fueron obtenidos en la Pesquisa Nacional por Muestra de Domicilios (pnads) y extraídos del Instituto de Pesquisa Económica Aplicada (ipeadata) –y se referen a todos los estados de Brasil y el Distrito Federal, configurando un panel balanceado que abarca de 1995 a 2012.
Según Vanhoudt (2000), los estudios que poseen un alcance mundial comprometen a comparación de los datos, ya que las metodologías investigativas y de colecta de datos son desarrolladas de forma singular en cada país. Siendo así, este trabajo es detentor de una ventaja al hacer uso de la utilización de variables que tienen la misma metodología de cálculo en cada Unidad de la Federación y que posibilita una estimativa más concisa de los indicadores y la comparación de los datos.
El coeficiente de Gini, utilizado como medida de desigualdad es proveniente de la renta domiciliar per cápita. Este índice es frecuentemente usado para expresar el grado de desigualdad de la renta y puede ser asociado a la llamada comba de Lorenz, deliberada por el conjunto de puntos que, desde las rentas ordenadas de forma creciente, relacionan la proporción acumulada de personas y de renta.
Tanto el índice de Gini como el de Theil fueron empleados para observar la evolución de la desigualdad en cada estado brasileño, bien como la robustez de los resultados econométricos. La renta domiciliar per cápita media de la población fue utilizada como medida del nivel de crecimiento económico, siendo las series de estas variables calculadas desde las respuestas a la Pesquisa Nacional por Muestras de Domicilios (pnad/ibge).1
Como variable explicativa, será utilizada la educación que corresponde al promedio de años de estudio de los residentes en los diferentes estados de Brasil, construida a partir de las informaciones de la pnad y la expectativa de vida de los individuos al nacer, obtenidos en el Instituto Brasileño de Geografía y Estadística (ibge).
5Resultados y discusionesEsta sección presenta y discute los resultados logrados en la estimación del modelo econométrico presentado en la sección 4 que relaciona la desigualdad de la renta medida por el índice de Gini y de Theil, y sus determinantes.
Además de los resultados de las estimaciones logradas por mqo y within groups, se presentan también, las estimaciones por medio del método mmg-sistema. Como se vio anteriormente, ese método resulta de una extensión del estimador original de Arellano y Bond (1991), propuesta en Arellano y Bover (1995) y desarrollada en Blundell y Bond (1998).
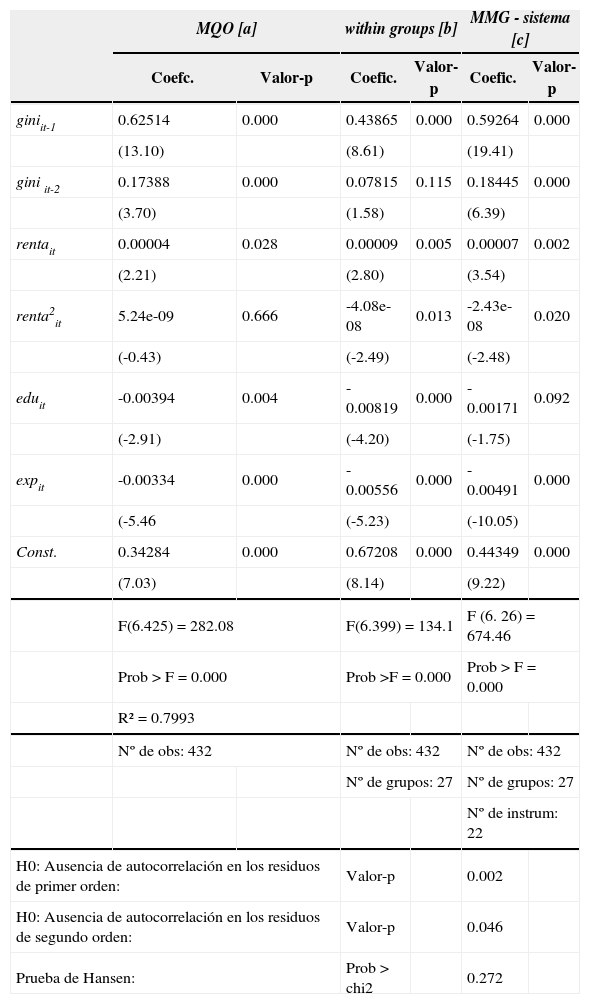
Se observa que en la columna [a], del cuadro 1, los valores de los coeficien-tes estimados de la variable giniit-1 y giniit-1 por mqo son, de hecho, mayores que los valores estimados en la columna [b] para esa misma variable por within groups. Siendo así, si los instrumentos utilizados son adecuados, los valores de los coeficientes de esa variable estimados por mmg-sistema deben estar situados entre los límites de los coeficientes estimados por los dos métodos anteriores. Los valores logrados por mmg-sistema para esa variable en la columna [c], muestra que esa característica es satisfecha, indicando así que la distorsión causada por la presencia de variables endógenas en el lado derecho de la regresión y efectos fijos no observables fueron corregidos por mmg-sistema.
Resultados de los Modelos de Regresión para el Gini (1995-2012)
| MQO [a] | within groups [b] | MMG - sistema [c] | ||||
|---|---|---|---|---|---|---|
| Coefc. | Valor-p | Coefic. | Valor-p | Coefic. | Valor-p | |
| giniit-1 | 0.62514 | 0.000 | 0.43865 | 0.000 | 0.59264 | 0.000 |
| (13.10) | (8.61) | (19.41) | ||||
| gini it-2 | 0.17388 | 0.000 | 0.07815 | 0.115 | 0.18445 | 0.000 |
| (3.70) | (1.58) | (6.39) | ||||
| rentait | 0.00004 | 0.028 | 0.00009 | 0.005 | 0.00007 | 0.002 |
| (2.21) | (2.80) | (3.54) | ||||
| renta2it | 5.24e-09 | 0.666 | -4.08e-08 | 0.013 | -2.43e-08 | 0.020 |
| (-0.43) | (-2.49) | (-2.48) | ||||
| eduit | -0.00394 | 0.004 | -0.00819 | 0.000 | -0.00171 | 0.092 |
| (-2.91) | (-4.20) | (-1.75) | ||||
| expit | -0.00334 | 0.000 | -0.00556 | 0.000 | -0.00491 | 0.000 |
| (-5.46 | (-5.23) | (-10.05) | ||||
| Const. | 0.34284 | 0.000 | 0.67208 | 0.000 | 0.44349 | 0.000 |
| (7.03) | (8.14) | (9.22) | ||||
| F(6.425) = 282.08 | F(6.399) = 134.1 | F (6. 26) = 674.46 | ||||
| Prob > F = 0.000 | Prob >F = 0.000 | Prob > F = 0.000 | ||||
| R² = 0.7993 | ||||||
| Nº de obs: 432 | Nº de obs: 432 | Nº de obs: 432 | ||||
| Nº de grupos: 27 | Nº de grupos: 27 | |||||
| Nº de instrum: 22 | ||||||
| H0: Ausencia de autocorrelación en los residuos de primer orden: | Valor-p | 0.002 | ||||
| H0: Ausencia de autocorrelación en los residuos de segundo orden: | Valor-p | 0.046 | ||||
| Prueba de Hansen: | Prob > chi2 | 0.272 | ||||
Obs.: (i) Los valores en paréntesis son los desvíos modelos corregidos por el método de Windmeijer (2005); (ii) Los valores para la prueba de Hansen son los valores-p para la hipótesis nula de que los instrumentos son válidos. (iii) Utilizaron como instrumentos no mmg-sistema las variables explicativas en diferenciales desfasadas.
Los niveles de desfase para el ajuste del modelo son representados por los términos giniit-1 y giniit-2 en la primera y segunda línea del cuadro 1. Las variables desfasadas son significativas del punto de vista estadístico, siendo significa-tivos a 1% para los valores de la columna [a] e [c] que indica un ajuste correcto para el modelo de comportamiento dinámico de las variables estimadas.
Entre los varios modelos estimados, se optó por el modelo indicado en la columna [c] del cuadro 1, donde fue utilizada como variable endógena, la variable dependiente giniit desfasada en un período y la variable eduit. Ya las demás variables explicativas, fueron consideradas débilmente exógenas.
Las pruebas realizadas, en el modelo mmg-sistema, muestran que las propiedades estadísticas son aceptables. La prueba de Hansen, que verifica si los instrumentos utilizados requeridos por este modelo son válidos, es satisfactoria. Se incluyen, las pruebas estadísticas de Arellano y Bond (1991) para evaluar la existencia de autocorrelación de primer y segundo orden. Se nota, que la ausencia de autocorrelación de segundo orden es esencial para la consistencia del estimador mmg-sistema y la prueba confirma el no rechazo de autocorrelación de primer orden, aunque se rechace la hipótesis de auto correlación de segundo orden.
En la columna [a] del cuadro 1 todas las variables presentan señales significativas conforme esperado. El modelo fue estimado por mqo que, al desfasar la variable Gini en 2 periodos, pasó de un total de 486 para 432 observaciones, englobando todos los estados brasileños entre 1995 y 2012.
En la columna [c], del cuadro 1 del modelo mmg-sistema, el coeficiente de la variable dependiente desfasada en un periodo presentó un valor altamente significativo y, relativamente, más bajo que el estimador mqo, confirmando la expectativa de la persistencia de la desigualdad de la renta en Brasil para el periodo analizado.
Se verifica la existencia de una relación negativa entre la desigualdad y los años promedios de estudios, significativa en todos los modelos estimados, columnas [a], [b] y [c], con los respectivos valores: -0.00334, -0.00819 e -0.00171. De esta forma, aunque los valores no sean tan expresivos, corroboran con diversos autores como Shultz (1961), Enreberg y Smith (2000), que afirman que el aumento en el número de estudios de los individuos desarrolla habilidades y conocimientos, elevando la productividad. Esto permite a las personas adquirir salarios más elevados, disminuyendo las desigualdades de la renta y la pobreza.
Se observa aún en la columna [c] del cuadro 1, una relación negativa y significativa entre la expectativa de vida y la desigualdad de la renta, donde se presenta, aproximadamente, un valor estimado de -0.0049.
La renta domiciliar per cápita promedio de la población, bien como su forma cuadrática, en las regresiones estimadas, fue utilizada como medida del nivel de crecimiento económico. Los valores y señales encontradas -estadísticamente significantes para el within groups y mmg-sistema- para estas variables, indican que hay evidencias de la curva de Kuznets en Brasil dentro del periodo analizado, concordando con Bêrni, Marquetti y Kloeckner (2002), Bagolin, Gabe y Pontual (2003), Jacinto y Tejada (2004) y Salvato et al. (2006).
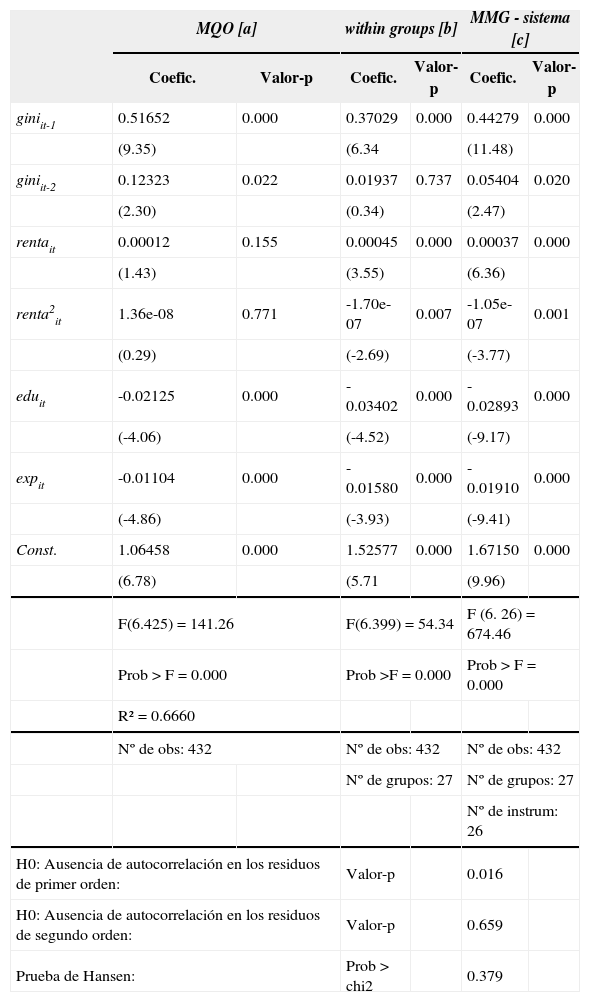
A fin de ratificar los resultados discutidos anteriormente, fue aplicada la misma metodología para el índice de Theil, en que el cuadro 2 revela que para el modelo mmg-sistema, columna [c], se percibe que hay una relación negativa, -0.02893, y significativa en un 1% entre la desigualdad y los años promedios de estudios. Validando, por tanto, el resultado encontrado para esta relación al hacer uso del índice de Gini en este trabajo y con la literatura ya mencionada en la sección 2.
Resultados de los Modelos de Regresión para Theil (1995-2012)
| MQO [a] | within groups [b] | MMG - sistema [c] | ||||
|---|---|---|---|---|---|---|
| Coefic. | Valor-p | Coefic. | Valor-p | Coefic. | Valor-p | |
| giniit-1 | 0.51652 | 0.000 | 0.37029 | 0.000 | 0.44279 | 0.000 |
| (9.35) | (6.34 | (11.48) | ||||
| giniit-2 | 0.12323 | 0.022 | 0.01937 | 0.737 | 0.05404 | 0.020 |
| (2.30) | (0.34) | (2.47) | ||||
| rentait | 0.00012 | 0.155 | 0.00045 | 0.000 | 0.00037 | 0.000 |
| (1.43) | (3.55) | (6.36) | ||||
| renta2it | 1.36e-08 | 0.771 | -1.70e-07 | 0.007 | -1.05e-07 | 0.001 |
| (0.29) | (-2.69) | (-3.77) | ||||
| eduit | -0.02125 | 0.000 | -0.03402 | 0.000 | -0.02893 | 0.000 |
| (-4.06) | (-4.52) | (-9.17) | ||||
| expit | -0.01104 | 0.000 | -0.01580 | 0.000 | -0.01910 | 0.000 |
| (-4.86) | (-3.93) | (-9.41) | ||||
| Const. | 1.06458 | 0.000 | 1.52577 | 0.000 | 1.67150 | 0.000 |
| (6.78) | (5.71 | (9.96) | ||||
| F(6.425) = 141.26 | F(6.399) = 54.34 | F (6. 26) = 674.46 | ||||
| Prob > F = 0.000 | Prob >F = 0.000 | Prob > F = 0.000 | ||||
| R² = 0.6660 | ||||||
| Nº de obs: 432 | Nº de obs: 432 | Nº de obs: 432 | ||||
| Nº de grupos: 27 | Nº de grupos: 27 | |||||
| Nº de instrum: 26 | ||||||
| H0: Ausencia de autocorrelación en los residuos de primer orden: | Valor-p | 0.016 | ||||
| H0: Ausencia de autocorrelación en los residuos de segundo orden: | Valor-p | 0.659 | ||||
| Prueba de Hansen: | Prob > chi2 | 0.379 | ||||
Obs.: (i) Los valores en paréntesis son los modelos deformados y corregidos por el método de Windmeijer (2005). (ii) Los valores para la prueba de Hansen son los valores-p para la hipótesis nula de que los instrumentos son válidos. (iii) Se utilizaron como instrumentos no mmg-sistema las variables explicativas en diferencias desfasadas.
Deteniéndose aún a la regresión hecha por mmg-sistema en el cuadro 2 que utiliza el índice de Theil como medida de desigualdad, se observa que, también, hay una relación significativa en 1% con valores y señales esperados para la expectativa de vida con relación la desigualdad de la renta en el país. Evidenciando una vez más que un aumento en la expectativa de los individuos reduce el cuadro de la desigualdad de la renta en Brasil.
La columna [c] del cuadro 2 muestra que la relación de la variable explicativa que representa una medida de crecimiento económico, la renta domiciliar per cápita en su forma cuadrática, posee su relación inversa con el índice de Theil, confirmando la misma inclinación encontrada en el modelo anterior en el cuadro 1. Se resalta que para Sen (2000), la medida del desarrollo económico debe llevar en cuenta las variables socioeconómicas como, el acceso a la educación, la disponibilidad de servicios de saneamiento, de salud y la expectativa de vida. Las variables únicamente relacionadas a la renta serían insuficientes para medir el nivel de desarrollo económico.
De esta forma, los resultados logrados en el cuadro 2 siguieron la misma inclinación del cuadro 1, en que para las regresiones con el coeficiente de Theil, el mmg-sistema presentan valores con señales esperadas y estadísticamente significantes para todas las variables. Luego, las condiciones de concavidad son atendidas para este índice de desigualdad e indican que no se puede rechazar la existencia de una curva en el formato de U invertida.
La elección de dos indicadores de desigualdad de la renta (índice de Gini y de Theil) y la linealidad de las variables tuvo como objetivo dar mayor robustez a los modelos estimados. Se puede decir que tal objetivo fue obtenido, visto que las estimativas realizadas, en su mayoría, convergieron para el resultado deseado.
En el abordaje estático del modelo mmg-sistema, columna [c] del cuadro 2, las señales de los coeficientes que fueron significantes son de acuerdo con lo esperado. En orden decreciente, la desigualdad medida por medio del índice de Theil es más sensible a la media de años de estudio (-0.02893), años promedio de la expectativa de vida (-0.01910) y de la renta (-1.05e-07).
Los resultados de los modelos estimados, tanto para el índice de Gini, como para el de Theil, apuntan que el crecimiento económico reduce la desigualdad de la renta. De esta forma, como ya se vio, se considera en el concepto menos restrictivo, que a corto plazo hay una conexión positiva entre la desigualdad de la renta y el nivel de renta per cápita. Ya a largo plazo, se percibe una relación de U invertida, pues hay una inversión de esta relación.
6Consideraciones finalesCon el fin de constatar la existencia de la relación de la U invertida entre la desigualdad de la renta y el crecimiento económico, propuesto por Simon Kuznets (1955), entre 1995 y 2012 en Brasil, este trabajo buscó mencionar estudios con las más diversas discusiones teóricas y econométricas pertinentes al objeto propuesto. Utilizando distintas estimativas, algunas de éstas corroboraron y otras rechazaron la hipótesis de Kuznets.
En la búsqueda por una respuesta para la indagación de la hipótesis de Kuznets, sobre el curso de la desigualdad de la renta en los países en desarrollo, en este estudio se propuso el uso de la metodología de datos de panel, empleando el método de los momentos generalizados en sistema (mmg-sistema) que lo diferencia de los demás trabajos antes publicados. Con este método fue posible amenizar problemas econométricos que afectan a la mayoría de los trabajos en esta área, como la endogeneidad de las variables explicativas.
Al analizar el comportamiento de la desigualdad, medidas por los coeficientes de Gini y de Theil, en todos los estados brasileños relacionados con la renta domiciliar per cápita promedio de la población y, también, en su forma cuadrática, las regresiones estimadas lograron valores y señales esperados y estadísticamente significantes para el mmg-sistema, ratificando que hay una conexión positiva entre la desigualdad de la renta y el nivel de la renta per cápita a corto plazo, sin embargo, a largo plazo acontece una inversión de esta relación.
No obstante, la expectativa de vida también presentó una relación inversa y significativa con relación al coeficiente de Gini y al de Theil. Siendo así que, habiendo un aumento en la expectativa de vida de los individuos, consecuentemente, habrá una baja de la desigualdad de la renta.
Tratándose de los años promedios de estudio, la educación, así como las demás variables analizadas, posee un efecto positivo en detrimento de la desigualdad de la renta, pues una elevación en el número de estudios de los individuos proporciona calificación, desarrolla habilidades y conocimientos que pueden aumentar la productividad y, por consiguiente, los salarios. Luego, se aumenta la renta y se disminuyen las desigualdades de la renta y la pobreza.
Las estimativas econométricas permitieron verificar que las series poseen un comportamiento autocorrelacionado, o sea, el resultado presente es dependiente de los resultados pasados. Los resultados evidenciaron, para todas las series, un comportamiento cíclico determinado por el periodo analizado, donde los aumentos de la renta, de la educación y de la expectativa de vida de los individuos influencian la desigualdad de la renta en sentido opuesto.
Las evidencias empíricas encontradas en ambos coeficientes de desigualdad utilizados, sugieren que la relación entre la desigualdad de la renta y el desarrollo económico para Brasil en el periodo analizado, sigue el modelo de la U invertida tal como fue propuesto por Kuznets en sus estudios. Luego, este trabajo, entra en consonancia con la literatura de los autores que corroboran con la hipótesis de Simon Kuznets (1955), donde la desigualdad de la renta en Brasil aumenta en los primeros periodos del desarrollo económico, y en las etapas más avanzadas del crecimiento la desigualdad tiende a caer.
Aunque la pesquisa haya cumplido con su objetivo, es conveniente acrecentar las características físicas y económicas del país, utilizando otras variables explicativas que tengan como objetivo probar la referida hipótesis de Kuznets en futuros estudios en los diferentes estados brasileños y regiones.