PROGRESOS
DE OBSTETRICIA
Y GINECOLOGÍA
Volumen 41
Número 2
Marzo 1998
A. Rodríguez-Oliver
J. Esquivias 1
A. Herruzo
S. Menjón
F. Montoya
M. P. Carrillo
F. Álamo
Aportación del análisis de imagen al diagnóstico mamográfico de nódulos circunscritos malignos y benignosDepartamento de Obstetricia y Ginecología.
1 Servicio de Anatomía Patológica.
Hospital Virgen de las Nieves. Granada
Correspondencia:
A. Rodríguez-Oliver
Departamento de Obstetricia y Ginecología.
Hospital «Virgen de las Nieves»
Avda. de las Fuerzas Armadas, 2
18014 Granada
Contribution of digital image analysis to mammographic diagnosis of circumscribed malignant and bening massesRodríguez-Oliver A, Esquivias J, Herruzo A, Menjón S, Montoya F, Carrillo MP, Álamo F. Aportación del análisis de imagen al diagnóstico mamográfico de nódulos circunscritos malignos y benignos. Prog Obstet Ginecol 1998;41:100-106Aceptado para publicación 17/10/97RESUMEN
Aunque la imagen típica del cáncer mamario sea la estrellada, una importante cantidad de nódulos mamarios malignos aparecen en la imagen mamográfica como masas circunscritas. Es difícil predecir por la imagen mamográfica si la naturaleza de un nódulo circunscrito es benigna o maligna.
Se han digitalizado y procesado 37 imágenes de nódulos mamarios malignos y 30 de benignos, analizando y comparando entre ellos diversos parámetros de forma (excentricidad, factor de forma, relación diámetro Feret y número de intercepción).
Se ha encontrado que los nódulos circunscritos malignos son significativamente más irregulares que los benignos si empleamos el factor de forma, aunque con los otros parámetros de forma los resultados son desiguales.
Se sugiere que la aplicación de técnicas de digitalización y análisis de imagen en nódulos circunscritos puede ayudar en la valoración de su naturaleza maligna o benigna.
PALABRAS CLAVE
Mamografía; Nódulos circunscritos; Digitalización; Análisis de imagen.
ABSTRACT
Although stellate shape is typical of breast cancer, there are many malignant tumors which appear as circumscribed masses. Based on such a view, it is difficult to decide whether they are benign or malignant.
37 malignant and 30 benign breast tumors have been digitalized and processed in order to analyze and compare several parameters between them (excentricity, form factor, Feret diameter and interception number).
If the form factor is considered, the malignant circumscribed masses are significantly more irregular than benigns one, although taking into account the other parameters related to shape there have been found uneven results.
We suggest that the use of digital image analysis of circumscribed masses might be of asset in differentiating the benign or malignant nature of lessions.
KEY WORDS
Mammograpy; Digital image analysis; Circumscribed masses.
INTRODUCCION
Aunque la imagen mamográfica característica del cáncer mamario sea el nódulo estrellado, una cantidad no despreciable de tumores malignos se presentan como nódulos circunscritos (1,2).
Estas lesiones pueden estar bien o mal delimitadas, ser circulares, ovaladas o lobuladas, y ser únicas o múltiples.
Las lesiones circunscritas más frecuentes son los quistes y los fibroadenomas. Un signo del halo evidente que rodee toda o gran parte de la lesión es característico de un quiste (1). Mientras los quistes suelen encontrarse en mujeres en edad próxima a la menopausia, los fibroadenomas aparecen en mujeres más jóvenes.
Es raro encontrar lesiones con todo su contorno bien delimitado, incluso lesiones benignas como fibroadenomas o quistes tienen alguna zona mas difusa en su periferia, generalmente debido a una reacción fibrosa del estroma cercano (3,4) y que puede traducirse en la mamografía como una ligera irregularidad de los bordes, el aplanamiento de uno de los lados o el signo de la «cola del cometa» (5).
Existen carcinomas, fundamentalmente el carcinoma medular (3 5-7), mucinoso (3, 5), papilar (8, 9), el carcinoma lobulillar infiltrante (1, 3, 10, 11) y el intraductal (12, 13) cuya imagen mamográfica simula en muchas ocasiones una lesión circunscrita redondeada, oval o lobulada y cuyo borde está en su mayor parte mal definido, sin que lleguen a formar una estructura radiada.
Teniendo en cuenta estos problemas diagnósticos, los resultados del análisis subjetivo de una imagen pueden ser muy diferentes; así, las discrepancias diagnósticas en mamografía pueden tomar valores importantes (14, 15).
Las técnicas de análisis de imagen y la informatización que conllevan facilitarían el estudio de un gran número de mamografías.
Con nuestro estudio pretendemos conocer si el análisis matemático de una imagen mamográfica digitalizada permite un mejor diagnóstico en cuanto a su naturaleza benigna o maligna.
MATERIAL Y MÉTODOS
Se han obtenido las mamografías de pacientes que acudieron a la Consulta de Patología Mamaria del Departamento de Obstetricia y Ginecología del Hospital Universitario Virgen de las Nieves de Granada. Se analizaron 37 casos de pacientes con nódulos circunscritos malignos y 30 mujeres con nódulos benignos circunscritos. En todos los casos existió confirmación histológica. Las historias clínicas fueron revisadas para verificar que la zona extirpada correspondía al área a estudiar en la mamografía.
Las mamografías de los casos con cáncer fueron tomadas entre los años 1984 y 1989 y las que corresponden a patología benigna entre 1988 y 1991 (antes de 1988 las intervenciones en enfermedades benignas de la mama eran muy escasas).
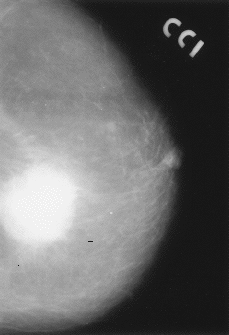
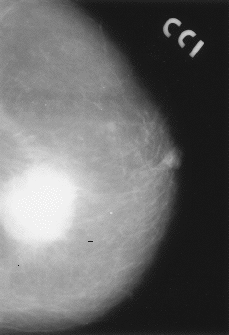
Las mamografías de los casos malignos fueron seleccionadas de entre todas las pacientes diagnosticadas en la unidad de cáncer de mama, y las de los casos benignos corresponden a mujeres operadas en el hospital entre 1988 y 1991. El único criterio de selección fue la exigencia de una calidad de imagen mínima (Figs. 1 y 2).
Se evaluaron ambas proyecciones mamográficas (craneocaudal y lateral) de forma independiente, su número no coincide ya que alguna de las proyecciones no tenía la calidad suficiente o el tumor no era visible en su totalidad en alguna de ellas.
Captación de las imágenes mamográficas
Una vez seleccionados los casos se realiza la conversión analógico-digital de la imagen, para lo cual se capta la imagen radiológica convencional expuesta en un negatoscopio con una cámara de vídeo Sony CCD conectada a un ordenador 486 ALR utilizando una tarjeta gráfica digitalizadora MATROX PIP 1024 y a través del programa de análisis de imagen VISILOG. De esta forma se almacenan las imágenes digitalizadas.
El tamaño de la matriz bidimensional que se obtiene (imagen digital) es de 256 x 256 píxels y las intensidades digitales (niveles de gris) van del 0 (negro) al 255 (blanco).
La delimitación de la zona tumoral se hizo mediante un sistema automático de umbralización (mediante esta función pueden separarse zonas de distinta densidad: a partir de una intensidad o nivel de gris en la imagen se seleccionan los puntos con mayor densidad). A veces, en la definición de la zona tumoral fue necesario señalar la zona de forma interactiva con el «ratón» del ordenador.
Una vez captadas las imágenes mamográficas se procedió a la cuantificación automática por parte del programa VISILOG del área, perímetro, excentricidad, diámetro Feret 0, diámetro Feret 90, número intercepción 0 y número de intercepción 90.
De la combinación de algunos de los anteriores surgen nuevos parámetros morfométricos:
-- Factor de forma (FF).
-- R1: n.° intercepción 90 / diámetro Feret 0.
-- R2: n.° intercepción 0 / diámetro Feret 90.
-- R: R1 x R2.
Definición de los parámetros anteriores
1) Área.
Su valor viene dado por el número de «pixels» que contiene la zona tumoral.
2) Perímetro.
Viene estimado por el número de puntos o «pixels» que están en el borde tumoral.
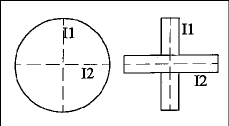
3) Excentricidad.
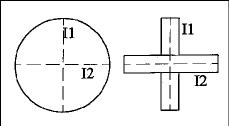
Es un parámetro que mide lo que un objeto se aleja de la simetría o de lo concéntrico. La excentricidad aumenta con la diferencia entre los valores de los ejes axiales y así mide la elongación de un objeto. Un disco o una cruz tienen una excentricidad nula (Fig. 3).
Ec (X) = (4 ¼)2 x (|1-|2)2 /A2(X)
donde A es el área y |2 y |1 los ejes axiales.
Si |1 = |2 la excentricidad es 0.
4) Diámetros Feret.
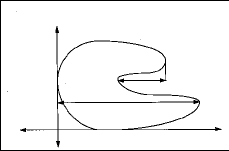
Miden un tamaño en direcciones específicas. Considerando una tangente a un objeto perpendicular a una dirección alfa en la que queremos medir el diámetro Feret, computamos la distancia de todos los puntos del objeto a esta línea. El diámetro Feret con respecto a alfa es el mayor valor de estas distancias (en la figura 4 estaría representado por la distancia a para el diámetro Feret 0).
5) Número de intercepción.
Se define como el número de entradas en un objeto a lo largo de una dirección dada. Este parámetro computa el número de intersecciones en una imagen binaria sobre la dirección principal de la malla.
En la figura 4 el número de intercepción 90 resultaría de la suma de a + b.
6) Factor de forma (FF).
Una forma no puede caracterizarse por una simple medida, ni siquiera por un conjunto de medidas. Varios parámetros han sido definidos para explicar caracteristicas de forma. La más común de tales medidas es el factor de forma, definido como:
Fc = L (X)2 / 4¼ x A(X)
donde L es el perímetro y A es el área
En el caso del círculo:
Fc = (2¼r)2 / 4¼ x ¼ r2 = 4¼2r2 / 4¼2r2 = 1
Esta fórmula clásica está basada en que el círculo define la regularidad absoluta.
Este cálculo no varía con la rotación, simetría o escala, no tiene dimensión. No es una medida local, pero sí una combinación de medidas locales.
7) Relación entre diámetros Feret y número de intercepción.
Se trata de un parámetro ideado por nosotros que relaciona variables definidas anteriormente:
R1 = N.° Intercep. 90 / Feret 0
R2 = N.° Intercep. 0 / Feret 90
R= R1 x R2
En un objeto sin entrantes a izquierda o derecha, el Feret 0 es igual que el número de intercepción 90. Si Feret 0 es distinto de Intercepción 90, el objeto tiene entrantes en la dirección de 0°.
En un objeto sin entrantes por arriba o por abajo, el Feret 90 es igual que el número de intercepción 0. Si Feret 90 es distinto de Intercepción 0, el objeto tiene entrantes en la dirección de 90°.
En un objeto regular sin ningún entrante por arriba ni por abajo, R1 estará cercano a 1, sin embargo, si el borde es irregular R1 > 1.
En un objeto que no presente entradas a derecha ni izquierda, R2 es parecido a 1, si por el contrario muestra irregularidades R2 > 1.
En objetos extremadamente irregulares los diámetros Feret y número de intercepción equivalentes se alejan mucho del valor 1. éste no es nuestro caso por lo que al obtener valores próximos a 1 nos pareció interesante utilizar ambas relaciones y hallar un nuevo parámetro morfométrico fruto de su multiplicación (R = R1 x R2).
Método estadístico
La finalidad más importante del trabajo consiste en la transformación de una variable cualitativa (forma) en cuantitativa y posteriormente proceder a su análisis para valorar posibles diferencias entre lesiones circunscritas benignas y malignas.
Se calculó la estadística básica para los distintos parámetros.
Se comprobó en primer lugar que las variables no seguían una distribución normal, para lo cual se utilizó el test de Kolmogorov-Smirnoff, por lo que en sus cálculos estadísticos se utilizó el test no paramétrico de Mann-Whitney para la comparación de dos muestras (lesiones benignas versus lesiones malignas). El análisis fue igualmente independiente para las proyecciones laterales y craneocaudales.
RESULTADOS
Se cuantificaron y analizaron los diferentes parámetros de forma atendiendo al origen benigno o maligno de la lesión, comparando las lesiones circunscritas benignas con las malignas.
En las tablas 1 y 2 se muestran los valores medios de las variables analizadas apreciando como en ambas proyecciones y con todos los parámetros, excepto la excentricidad, los nódulos circunscritos malignos muestran valores más altos y por tanto de mayor regularidad.
En las tablas 3 y 4 se presentan los resultados del análisis estadístico y, en su caso, el grado de significación.
En ambas proyecciones todos los parámetros muestran mayor irregularidad en los nódulos circunscritos malignos, aunque la significación estadística sólo se alcanza en proyección craneocaudal con el factor de forma (FF) y en proyección lateral el único que no obtiene significación es la excentricidad (Ex).
DISCUSIÓN
Aunque la imagen típica de un tumor maligno es la estrellada, una importante cantidad de lesiones malignas se presentan mamográficamente como nódulos circunscritos siendo estos casos los que realmente presentan grandes problemas diagnósticos (1).
Entre los tumores malignos que pueden adoptar imágenes de nódulos circunscritos están el carcinoma medular (3,6,7), papilar (8,9) mucinoso (3) e intraductal (12). Más raramente, los carcinomas infiltrantes tipo ductal (1,7,16) y lobulillar (1,3,10,11) pueden adoptar forma circunscrita. Este problema se ha querido solventar con el análisis de la regularidad del contorno sin resultados convincentes. Hoffken y Lanyi (3) y Paulus (4) comentan que es muy difícil encontrar lesiones con todo su contorno bien delimitado, ya que incluso lesiones benignas muestran una zona de su periferia mal delimitada debido a una reacción fibrosa del estroma que los rodea.
Para Gold y cols. (17) y Sickles (18) el análisis con magnificación de los nódulos mamográficos circunscritos revelaría posibles irregularidades en sus bordes que podrían darnos un diagnóstico sospechoso de carcinoma.
Para intentar aclarar estos problemas de forma y contornos y su repercusión clínica hemos utilizado diversos parámetros morfométricos tras la digitalización de la imagen mamográfica de pacientes con nódulos circunscritos benignos y malignos.
Al comparar los nódulos circunscritos malignos y benignos hemos encontrado que aquéllos son más irregulares. Este hecho alcanza significación estadística y ocurre en ambas proyecciones utilizando el parámetro FF. La excentricidad no muestra significación en ninguna de las proyecciones y los otros parámetros (R1, R2 y R) sólo son significativos en proyección lateral. Consideramos este hallazgo de especial interés ya que uno de los mayores problemas en el diagnóstico mamográfico lo constituyen las lesiones circunscritas.
Para Moskowitz (19), la existencia de un borde mal definido, aunque sea parcialmente, en una lesión circunscrita hace descender el valor predictivo positivo para benignidad en un 5-10%.
Se ha comprobado que uno de los mayores problemas diagnósticos en mamografía, tanto en su forma convencional como digital, es diferenciar las lesiones circunscritas malignas de las benignas.
Por consiguiente, es importante demostrar que existen parámetros de forma capaces de distinguir la naturaleza benigna o maligna de estas lesiones bien delimitadas. En nuestro estudio, el factor de forma (FF) ha mostrado ser el de mayor utilidad, hecho ya apreciado por Flageat y cols. (20).
Se podría incrementar la precisión diagnóstica utilizando una matriz de superior tamaño para aumentar el grado de resolución, idea compartida por Brzakovic y cols. (21).
Actualmente The National Cancer Institute ha reconocido en la mamografía digital y las técnicas desarrolladas en torno a ella una de las tecnologías de mayor impacto en el diagnóstico del cáncer de mama (22).
A nuestro juicio, el desarrollo de esta técnica u otras semejantes (más automatizadas), facilitaría la realización de un screening básico de un gran volumen de mamografías en estudios de poblaciones amplias o en grandes laboratorios radiológicos.
1 Marsteller LP, Shaw de Paredes E. Well defined masses in the breast. Radiographics 1989;9:13-37.
2 Tabár L, Dean PB. Teaching atlas of mammography. New York: Thieme-Straton; 1985.
3 Hoeffken W, Lanyi M, editores. Mamografía: Técnica. Diagnóstico. Diagnóstico diferencial. Resultados. Barcelona: Labor; 1978.
4 Paulus DD. Benign diseases of the breast. Radiol Clin North Am 1983;21:27-50.
5 Sadowsky N, Kopans DB. Breast cancer. Radiol Clin North Am 1983:21:51-80.
6 Meyer JE, Amin E, Lindfors KK, Lipman JC, Stomper PC, Genest D. Medullary carcinoma of the breast: mammographic and ultrasound appearance. Radiology 1989;170:79-82.
7 Sabaté Díaz J. Estado actual del diagnóstico por imagen en el cáncer de mama. Revisión de 1.000 casos. Radiología 1990;32: 545-62.
8 Schneider JA. Invasive papillary breast carcinoma: Mammographic and sonographic appearance. Radiology 1989;171:377-9.
9 Mitnick JS, Vázquez MF, Harris MN, Schechter S, Roses DF. Invasive papillary carcinoma of the breast: Mammographic appearance. Radiology 1990;177:803-6.
10 Mendelson EB, Harris KM, Doshi N, Tobon H. Infiltrating lobular carcinoma: Mammographic patterns with pathologic correlation. AJR 1989;153:265-71.
11 Hilleren DJ, Andersson IT, Lindholm K, Linnell FS. Invasive lobular carcinoma: Mammographic findings in a 10 year experience. Radiology 1991;178:149-54.
12 Ikeda DM, Andersson I. Ductal carcinoma in situ: Atypical mammographic appearances. Radiology 1989;172:661-6.
13 Stomper PC, Margolin FR. Ductal carcinoma in situ: the mammographers perspective. AJR 1994;162:585-91.
14 Swets JA, Getty DJ Pickett RM, D Orsi CJ, Seltzer SE, McNeil BJ. Enhancing and evaluating diagnostic accuracy. Med Decis Making 1991;11:9-18.
15 Ciccone G, Vineis P, Frigerio A, Segnan N. Inter-observer and intra-observer variability of mammogram interpretation: a field study. Eur J Cancer 1992;28A;6-7:1054-8.
16 Stomper PC, Leibowich S, Meyer JE. The prevalence and distribution of well circumscribed nódules on screening mammography: analysis of 1,500 mammograms. Breast Dis 1991;4:197-203.
17 Gold RH, Montgomery CK, Rambo ON. Significance of margination of benign and malignant infiltrative mammary lesions: roentgenographic-pathological correlation. AJR 1973;118:881-94.
18 Sickles EA. Breast masses: mammographic evaluation. Radiology 1989;173:297-303.
19 Moskowitz M. Follow-up of benign mammographic lesions. JAMA 1988;260:3669.
20 Flageat J, Schoenenberger P, Danguy des Deserts M. Techniques d''imagerie du sein en 1991. Deuxieme partie. J Radiol 1992;73:39-45.
21 Brzakovic D, Luo M, Brzakovic P. An approach to automated detection of tumors in mammograms. IEEE Trans Med Imaging 1990;9:233-41.
22 Shtern F. Digital mammography and related technologies: a perspective from the National Cancer Institute. Radiology 1992; 18:629-30.
| Figura 1.Mamografía con nódulo mamario circunscrito. |
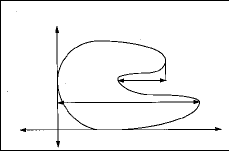
| Figura 2.Zona tumoral tras su procesamiento mediante análisis de imagen, lista para ser analizada matemáticamente. |
Diámetro Feret 0 = a
N.° intercepción 90 = a + b
Dirección 90°baDirección 0°
| Figura 3.La excentricidad es un parámetro morfométrico que mide lo que un objeto se aleja de la simetría o lo concéntrico, valorando la diferencia entre los dos ejes axiales. |
| Figura 4.El diámetro Feret es el mayor de los diámetros es una dirección dada. El número de intercepción viene dado por el número de entradas en un objeto a lo largo de una dirección. |
| Tabla 1 | Morfometría en las proyecciones laterales. Lesiones circunscritas | ||||||||||||||
| Valores medios | |||||||||||||||
| Tipo | N | Ex | R1 | R2 | R | FF | |||||||||
| Benigno | 26 | 0,331 | 1,041 | 1,037 | 1,081 | 32,25 | |||||||||
| Maligno | 33 | 0,435 | 1,113 | 1,091 | 1,218 | 46,85 | |||||||||
| N: Número de pacientes e imágenes; Ex: Excentricidad; | |||||||||||||||
| R1: Número de intercepción 90/diámetro Feret 0; R2: Número de intercepción 0/diámetro Feret 90; R: R1 x R2; FF: Factor de forma. | |||||||||||||||
| Tabla 2 | Morfometría en las proyecciones craneocaudales. Lesiones circunscritas | ||||||||||||||
| Valores medios | |||||||||||||||
| Tipo | N | Ex | R1 | R2 | R | FF | |||||||||
| Benigno | 29 | 0,489 | 1,048 | 1,057 | 1,108 | 37,72 | |||||||||
| Maligno | 31 | 0,346 | 1,113 | 1,155 | 1,287 | 44,12 | |||||||||
| N: Número de pacientes e imágenes; Ex: Excentricidad; | |||||||||||||||
| R1: Número de intercepción 90/diámetro Feret 0; R2: Número de intercepción 0/diámetro Feret 90; R: R1 x R2; FF: Factor de forma. | |||||||||||||||
| Tabla 4 | Morfometría en las proyecciones craneocaudales. Lesiones circunscritas | |||||||||
| Media rangos | ||||||||||
| Tipo | N | Ex | R1 | R2 | R | FF | ||||
| Benigno | 29 | 30,3 | 26,7 | 27,8 | 26,6 | 17,8 | ||||
| Maligno | 31 | 30,6 | 34,0 | 32,9 | 34,0 | 32,3* | ||||
| N: Número de pacientes e imágenes; Ex: Excentricidad; | ||||||||||
| R1: Número de intercepción 90/diámetro Feret 0; R2: Número de intercepción 0/diámetro Feret 90; R: R1 x R2; FF: Factor de forma. * p < 0,0001. | ||||||||||
| Tabla 3 | Morfometría en las proyecciones laterales. Lesiones circunscritas | |||||||||
| Media de rangos | ||||||||||
| Tipo | N | Ex | R1 | R2 | R | FF | ||||
| Benigno | 26 | 28,8 | 19,2 | 23,0 | 20,1 | 14,3 | ||||
| Maligno | 33 | 30,9 | 38,4* | 35,5* | 37,7* | 42,3* | ||||
| N: Número de pacientes e imágenes; Ex: Excentricidad; | ||||||||||
| R1: Número de intercepción 90/diámetro Feret 0; R2: Número de intercepción 0/diámetro Feret 90; R: R1 x R2; FF: Factor de forma. * p < 0,005. | ||||||||||
BIBLIOGRAFÍA