INTRODUCCIÓN
La biología ósea se desarrolla bajo la influencia de diversos factores, y del adecuado equilibrio entre ellos depende que se comporte adecuadamente frente a las cargas a las que está continuamente sometida. La resistencia mecánica del hueso depende tanto del contenido mineral óseo (cantidad), como de la arquitectura y características estructurales del hueso -con especial interés para el hueso trabecular-, lo que se ha llamado en los últimos años "calidad ósea"1-3.
Desde que Culmann y Meyer (1867), y posteriormente Wolf4, publicaran sus trabajos sobre las trayectorias de los haces trabeculares de la región proximal del fémur, el interés por conocer cómo se comporta esta región se basa en tres motivos principales: el uso de implantes protésicos ha aumentado considerablemente y es necesario entender la respuesta del hueso desde un punto de vista biomecánico; en segundo lugar, es necesaria una herramienta que mejore y complemente a la actual densitometría para el diagnóstico de la osteoporosis basándose en criterios no únicamente densitométricos, sino también estructurales, y por último, cuantificar la respuesta ósea a los tratamientos -farmacológicos o no- para la prevención de la pérdida de masa ósea5-7.
A través de la geometría fractal se puede realizar una aproximación al estudio de la arquitectura trabecular y obtener una serie de parámetros que nos aportan información sobre la complejidad de la estructura analizada. El término "fractal" fue acuñado por Benoît Mandelbrot en 1975 para referirse a una serie de objetos con una geometría que no podía ser explicada por la geometría clásica o euclídea, a través de triángulos, círculos, cuadrados, etc. Se define como un objeto matemático que se caracteriza por conservar su forma esencial, fragmentada o irregular, cuando varía la escala de observación8. Desde la década de los años ochenta, distintos investigadores están intentando describir el comportamiento de los sistemas biológicos con esta geometría9,10.
El hueso trabecular puede ser estudiado bajo las premisas de la geometría fractal y distintos autores lo han hecho en diferentes zonas del esqueleto y a partir de imágenes biomédicas11-16.
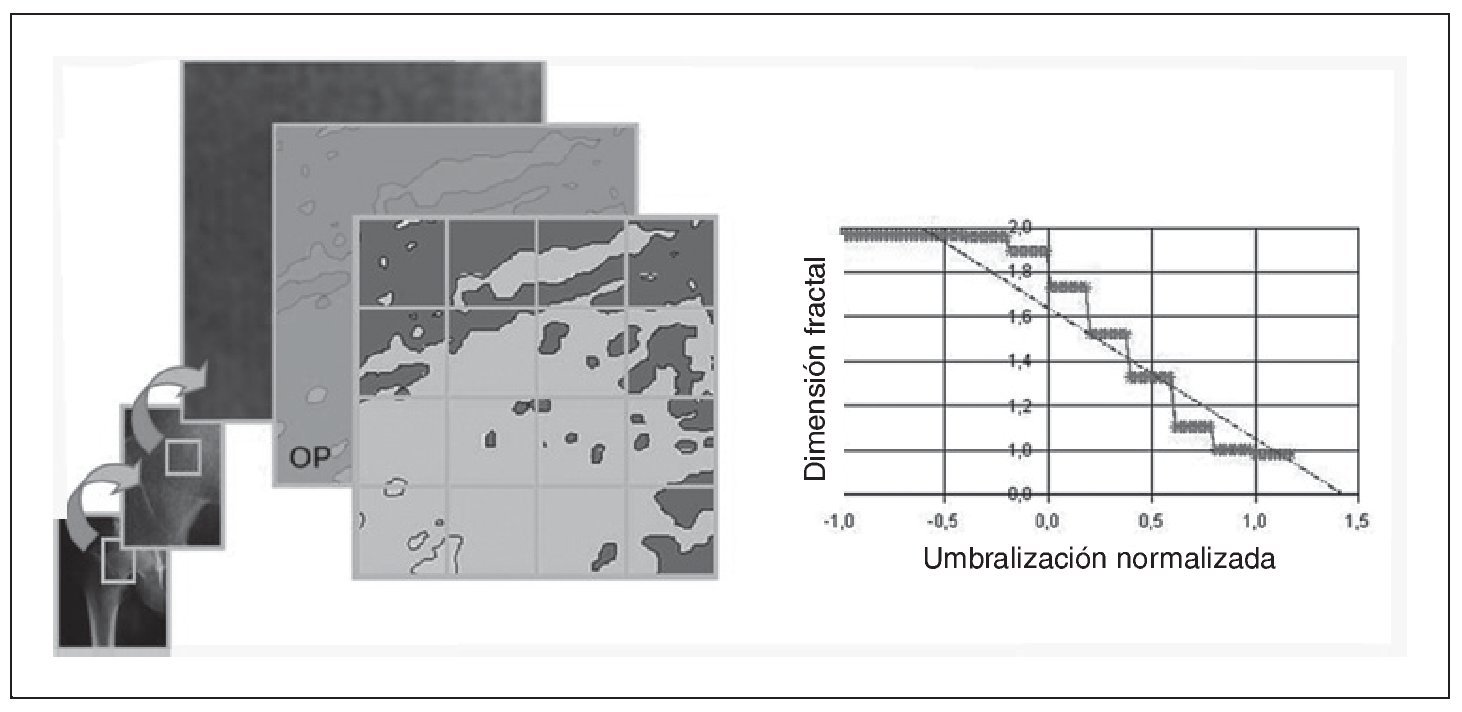
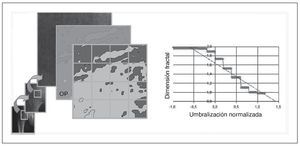
El parámetro que indica la complejidad de la estructura, o mejor aún, cuánto rellena el espacio, se conoce con el nombre de dimensión fractal y estará comprendida entre 1 (la dimensión topológica de una recta) y 2 (la dimensión topológica de un plano). Existen distintos métodos matemáticos para calcular la dimensión fractal, uno de los más utilizados es el box-counting method o método de conteo de celdas (fig. 1). Consiste en aplicar, sobre la imagen que se desea analizar, una cuadrícula con un determinado tamaño de celda. El algoritmo calcula cuántas de estas celdas son ocupadas por el contorno de la estructura analizada. Se realiza el mismo proceso con distintos tamaños de celda. La representación gráfica de estas dos variables en escala doblemente logarítmica da lugar a una recta cuya pendiente es precisamente la dimensión fractal17,18.
Fig. 1. Método de conteo de celdas. El algoritmo aplica una rejilla cuadriculada con un determinado tamaño de celda y registra cuántas de esas celdas son atravesadas por el contorno de la figura (es decir que posen píxeles blancos y negros) y repite el proceso para diferentes tamaños de celda. Se lleva a una escala doblemente logarítmica tanto el tamaño de celda como el número de celdas atravesadas en cada caso y se obtiene una recta cuya pendiente es la dimensión fractal del objeto.
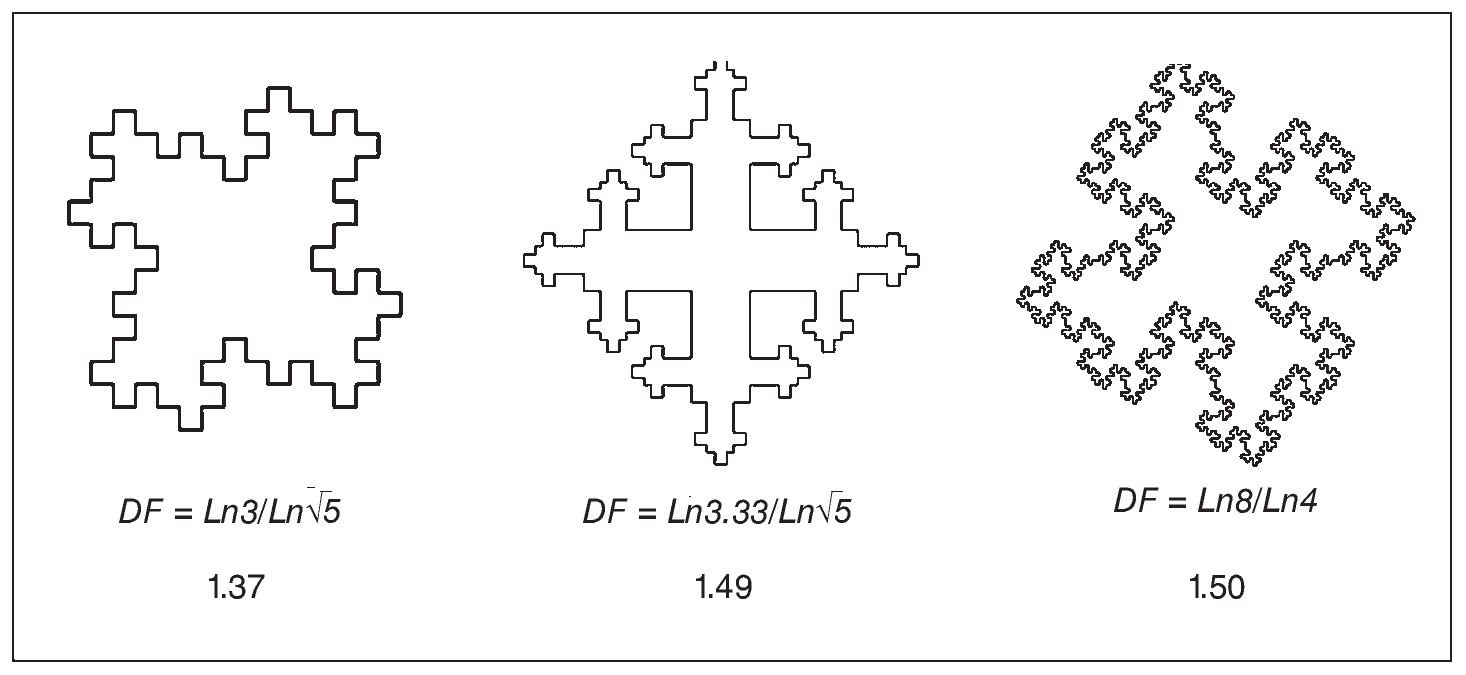
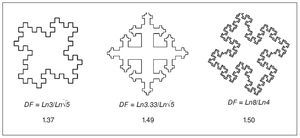
Aunque el valor de la dimensión fractal es útil para caracterizar el hueso trabecular, puede ocurrir que dos estructuras irregulares coincidan en su dimensión fractal aun teniendo una textura completamente distinta (fig. 2). Aparece así el concepto de "lacunaridad", que está relacionado con la distribución de los tamaños de las "lagunas" o huecos en la estructura y puede considerarse una medida de la textura o heterogeneidad8,19-21.
Fig. 2. Tres fractales generados por ordenador con un valor de la dimensión fractal (DF) similar pero con aspecto (textura) claramente distinto.
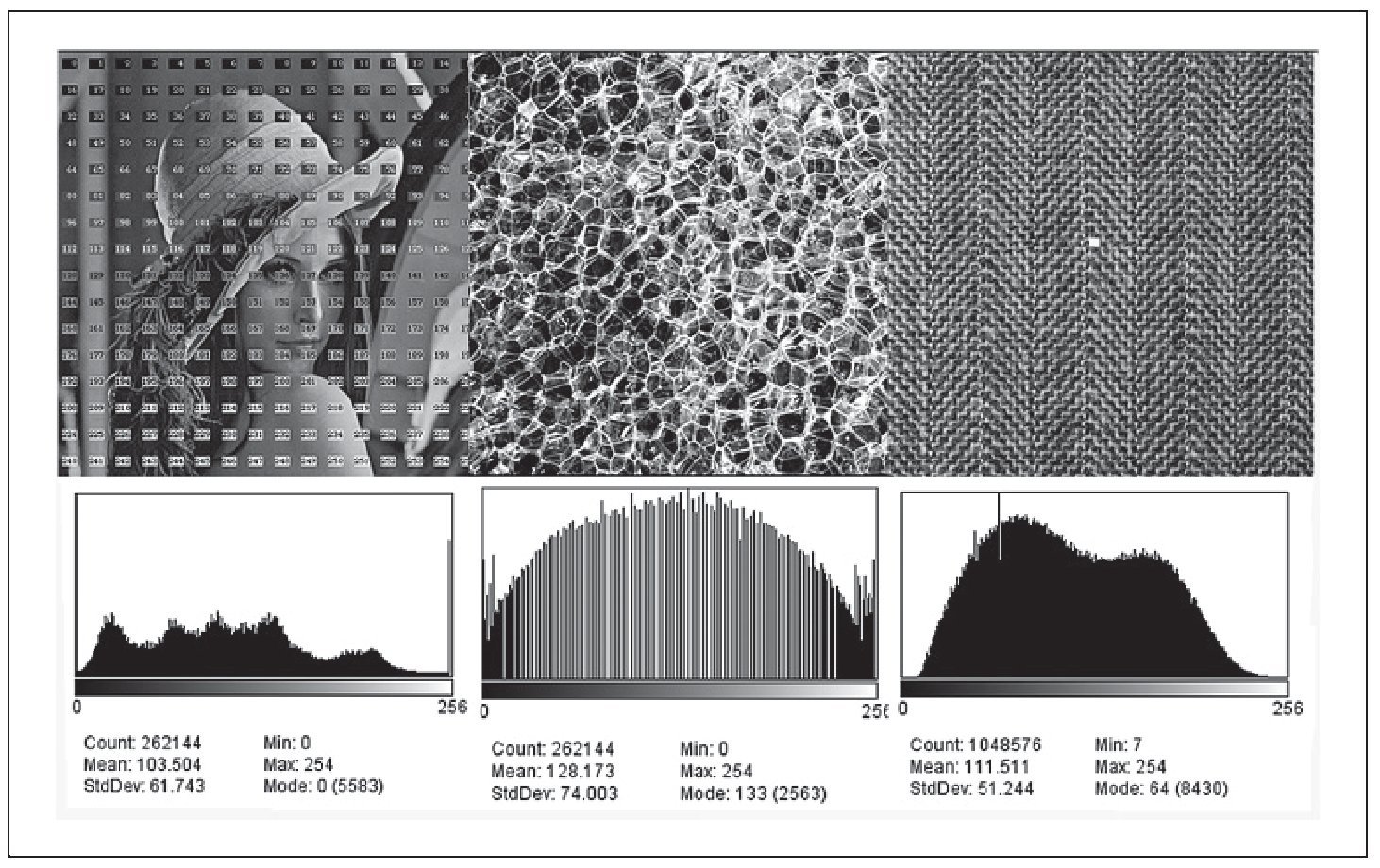
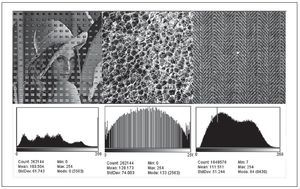
En el caso que nos ocupa, la lacunaridad se ha calculado mediante un algoritmo parecido al conteo de celdas -sliding-box method-, pero en esta ocasión la rejilla se va desplazando por toda la imagen. Desde otro enfoque completamente diferente, son muy conocidos en el ámbito del análisis de imagen, por su dificultad para ponerlos en práctica, los algoritmos que permiten discriminar texturas en las imágenes22. En este sentido, Haralick et al23 propusieron un método, el Grey Level Co-occurrence matrix -podría traducirse como "matriz de concurrencia del nivel de gris"- para diferenciar distintos tipos de terreno en las imágenes aéreas o por satélite. Desde ese momento este método se ha aplicado con más o menos éxito en aquellas situaciones en las que se plantea un problema de análisis de texturas (fig. 3). Uno de los parámetros que aporta este algoritmo es la entropía de la imagen, que se puede definir como la cantidad de información que contiene esta, entendida en términos de variabilidad y distribución de los niveles de gris de cada uno de los píxeles; a mayor entropía más heterogeneidad en la imagen.
Fig. 3. A cada píxel le corresponde un nivel de gris comprendido entre 0 y 255. Del análisis de la distribución de cada píxel con su vecino se puede obtener información sobre la textura de la imagen. En el caso de la entropía, esta está relacionada con la cantidad de información (en términos de variabilidad de niveles de gris) que contiene la imagen.
Aunque el hueso trabecular se ha analizado por varios investigadores mediante la geometría fractal, no ha sido así con la técnica del análisis de la matriz de grises. En nuestra opinión es interesante intentar determinar la posible relación que puede existir entre dos técnicas de análisis textural que parten desde unas premisas matemáticas radicalmente distintas.
Por tanto, los objetivos propuestos en este trabajo han sido:
1. Determinar los valores de la dimensión fractal, la lacunaridad y la entropía del hueso trabecular de la porción proximal del fémur.
2. Comparar estas variables en tres regiones con distinta distribución y orientación trabecular.
3. Determinar la posible correlación entre los distintos parámetros.
MATERIAL Y MÉTODO
MUESTRA
El estudio se realizó sobre una muestra de 20 fémures (10 derechos y 10 izquierdos) desecados, pertenecientes a una población mediterránea adulta de edad y sexo desconocidos, sobre cuyo tercio proximal se tomó una radiografía digital en proyección anteroposterior.
El sexo se estimó indirectamente a partir de las fórmulas discriminantes de Alemán et al24 creadas a partir de una población similar a la nuestra.
DIGITALIZACIÓN DE LA IMAGEN
Las radiografías se obtuvieron en el ámbito clínico por el mismo técnico de rayos y bajo las mismas condiciones (radiógrafo Siemens Siregraph CF a 63 Kv, 1,84 mAs; 6,8 s) con una bolsa de látex llena de agua interpuesta entre el foco y el hueso para simular los tejidos blandos. Las imágenes digitalizadas se exportaron desde el software incorporado al radiógrafo (Software Fluorospot Compact Siemens) con una matriz de 1.024 x 1.024 píxeles/10 bits, con una resolución de 72 píxeles por pulgada.
LOCALIZACIÓN DE LAS REGIONES DE INTERÉS
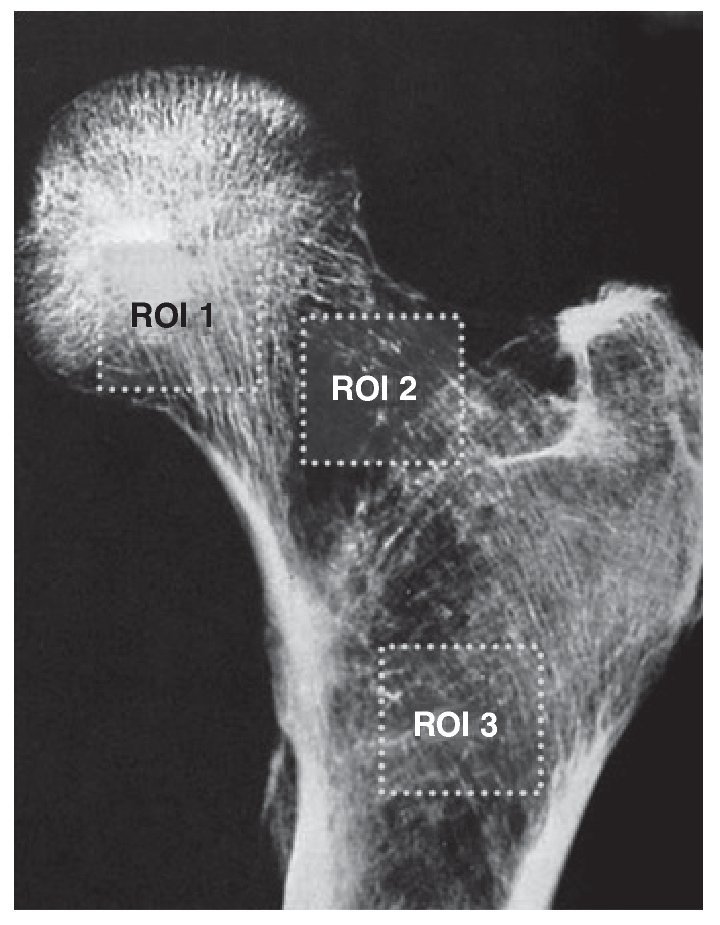
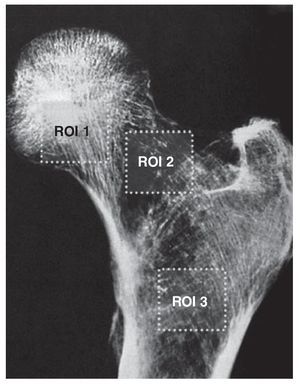
Se seleccionaron tres regiones de interés (ROI) de 100 x 100 píxeles (fig. 4) de forma que se relacionaran con el sistema ojival formado por el haz trabecular principal de compresión de la cabeza, y el haz principal de tensión (arciforme) que atraviesa el cuello, y con el sistema ojival resultante del cruce del haz arciforme y el haz trocantéreo.
Fig. 4. Las tres regiones de interés (ROI) se relacionan, respectivamente, con la cabeza, el cuello y el extremo distal de la metáfisis.
La ROI 1 se ubicó en la zona inferior de la cabeza femoral. La esquina inferomedial del cuadrado se hace coincidir con el resalte óseo inferior de la cabeza, en el límite de la línea del cartílago.
La ROI 2 se localizó en la parte superior del cuello femoral. La parte superior del cuadro de análisis contacta con la cortical superior del cuello.
La ROI 3 se situó en la región más distal de la metáfisis. Se toma como referencia inferior para la región de interés una proyección horizontal del vértice del trocánter menor hacia la metáfisis.
PREPROCESADO DE LA IMAGEN
Previamente al cálculo de la dimensión fractal y la lacunaridad es necesario preparar la imagen. En primer lugar se aplicó el filtro Unsharp Mask para mejorar el enfoque y eliminar regiones de incertidumbre. El filtro sustrae una copia desenfocada (desenfoque gausiano) de la imagen original. Se manejan dos parámetros: el radio de desenfoque, que es la desviación estándar (σ) del desenfoque gausiano (se utilizó σ= 2), y el peso de la máscara que determina la fuerza del filtrado, con posibles valores entre 0,1 y 0,9 (se tomó un valor de 0,6).
Posteriormente se aplicó un filtro para eliminar el ruido de fondo mediante el filtro Subtract Background basado en el algoritmo Rolling Ball25, que eliminará el fondo y resaltará la estructura ósea.
Por último, con la binarización se convirtió la imagen en binaria lista para calcular la dimensión fractal y la lacunaridad. El nivel de umbralizado se determinó automáticamente a partir del análisis del histograma (umbralizado = [nivel medio de gris del fondo + nivel medio de gris de los objetos]/2). La entropía se calculó según la describió Haralick23 y no fue necesario modificar la imagen de gris puesto que el algoritmo realiza los cálculos directamente sobre el histograma de los niveles de grises.
ANÁLISIS DE IMAGEN
El programa informático utilizado para el cálculo de la dimensión fractal, la lacunaridad y la entropía fue Image J 1.36b, de dominio público (Wayne Rasband, National Institute of Health, USA; http://rsb. info.nih.gob/ij/).
Para la determinación de la dimensión fractal y la lacunaridad se utilizaron los algoritmos box-counting method y sliding-box method respectivamente, disponibles en la aplicación FracLac 2.4d para Image J.
La entropía se calculó mediante el algoritmo Grey Level Co-occurrence Matrix, desarrollado también para Image J.
ANÁLISIS ESTADÍSTICO
El análisis estadístico se realizó con SPSS 13.0 (SPSS Inc. 2004).
Dado que algunas variables no cumplían los criterios de homogeneidad y homocedasticidad y que el tamaño muestral era relativamente pequeño, optamos por utilizar pruebas no paramétricas.
Utilizamos la prueba de Mann-Whitney para muestras independientes (intervalo de confianza [IC] del 95%) con el fin de comprobar si existían diferencias en cuanto al sexo y a la lateralidad. Como no se encontraron diferencias significativas ni en cuanto a sexo ni en cuanto a lateralidad, se empleó una muestra única para el resto de análisis. Aplicamos la prueba de Wilcoxon para muestras relacionadas (IC 95%) para comparar el valor de cada variable en cada región.
Por último, se calcularon los coeficientes de correlación lineal de Pearson (IC 95%) entre los pares de variables para determinar si existía alguna relación entre ellos.
RESULTADOS
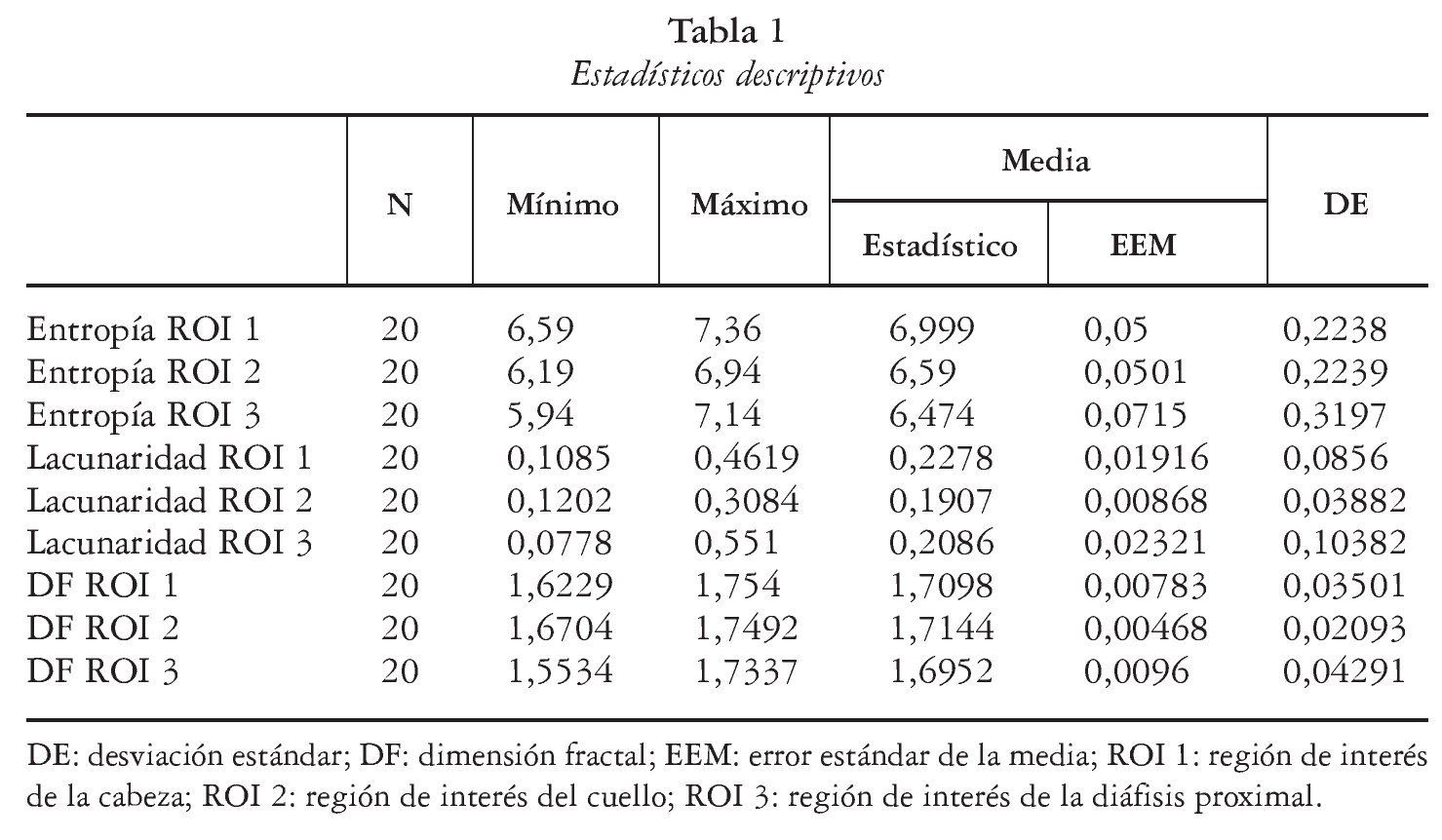
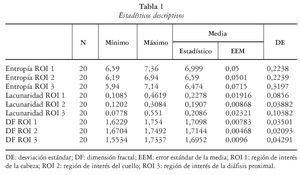
En la tabla 1 se muestran los estadísticos descriptivos para las variables analizadas en cada una de las regiones.
DIMENSIÓN FRACTAL
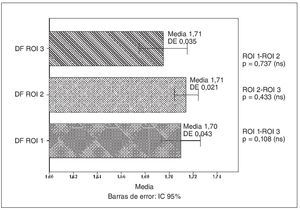
En la figura 5 se muestran las diferencias en la variable dimensión fractal en las tres regiones analizadas.
Fig. 5. Diagrama de barras con los intervalos de confianza (IC) para la variable dimensión fractal (DF) en las tres regiones de interés (ROI). DE: desviación estándar; ns: no significativo; p: valor de la significación estadística.
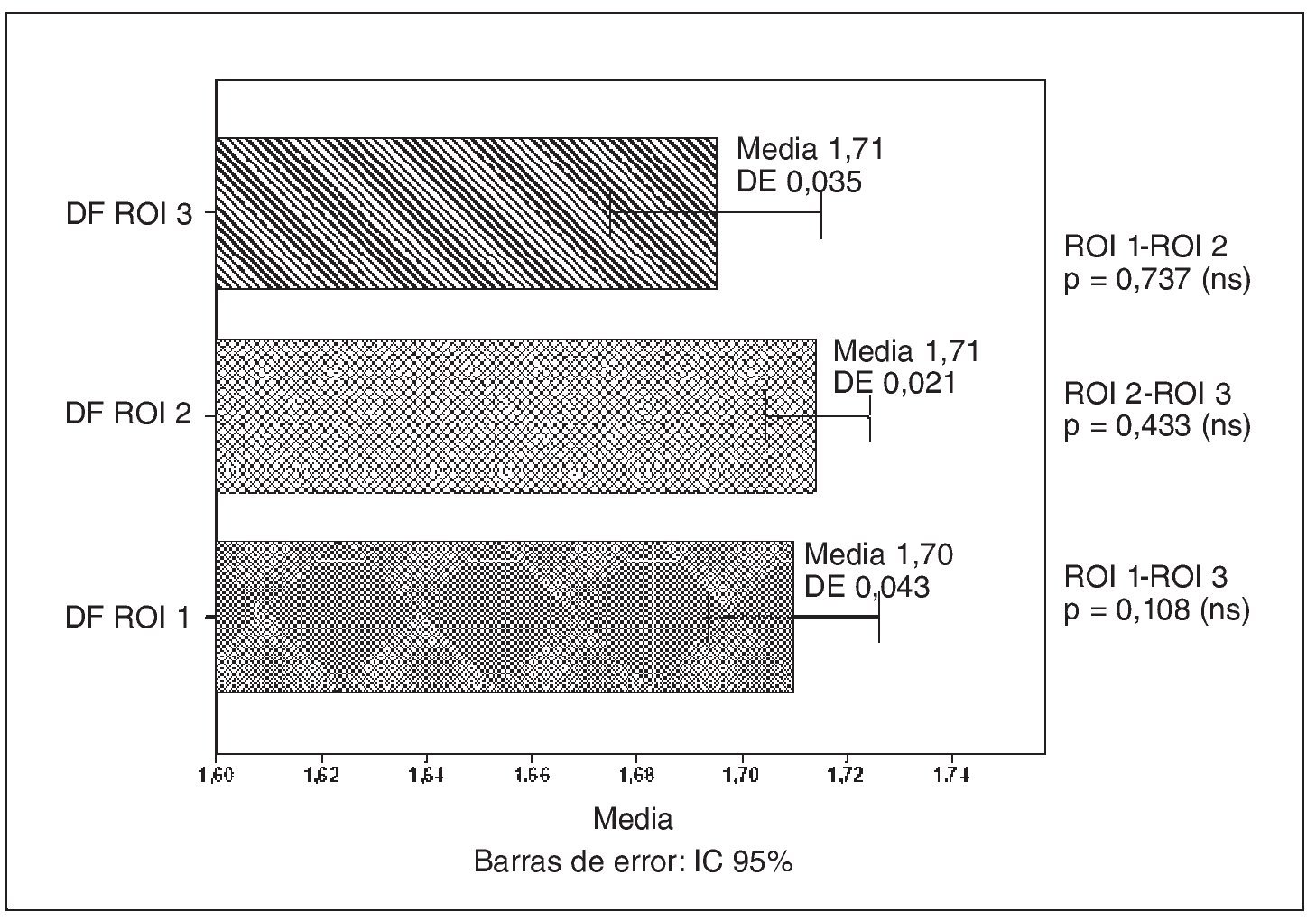
LACUNARIDAD
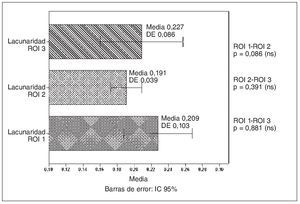
En la variable lacunaridad tampoco se encontraron diferencias significativas (fig. 6).
Fig. 6. Diagrama de barras con los intervalos de confianza (IC) para la variable lacunaridad en las tres regiones de interés (ROI). DE: desviación estándar; ns: no significativo; p: valor de la significación estadística.
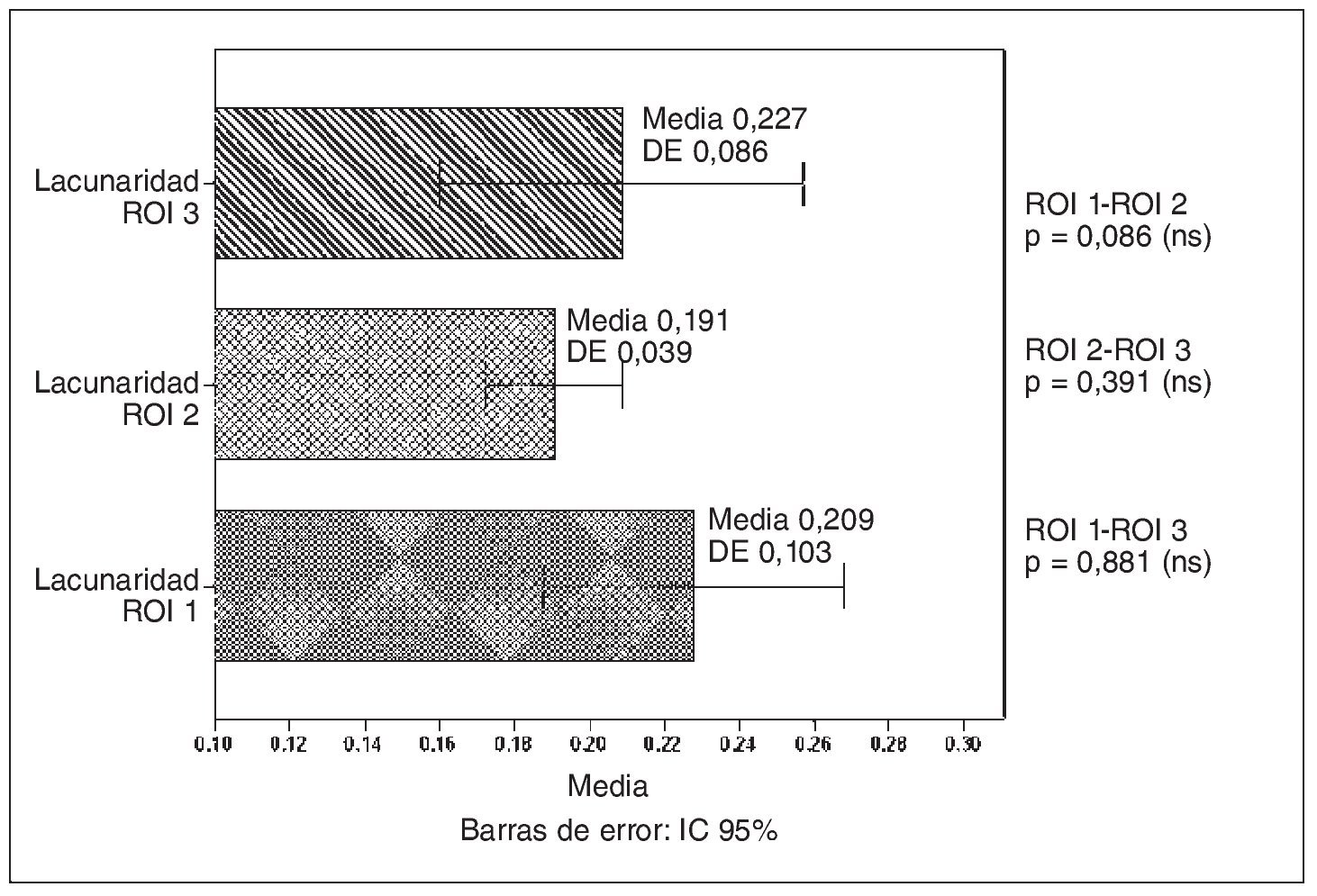
ENTROPÍA
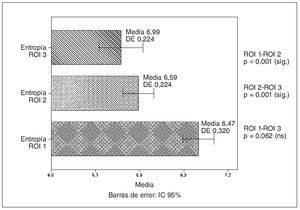
En la variable entropía se encontraron diferencias significativas para la ROI 1 respecto de ROI 2 y ROI 3, pero no en la pareja ROI 2 y ROI 3 (fig. 7).
Fig. 7. Diagrama de barras con los intervalos de confianza (IC) para la variable entropía en las tres regiones de interés (ROI). DE: desviación estándar; ns: no significativo; p: valor de la significación estadística; sig: significativo.
CORRELACIONES
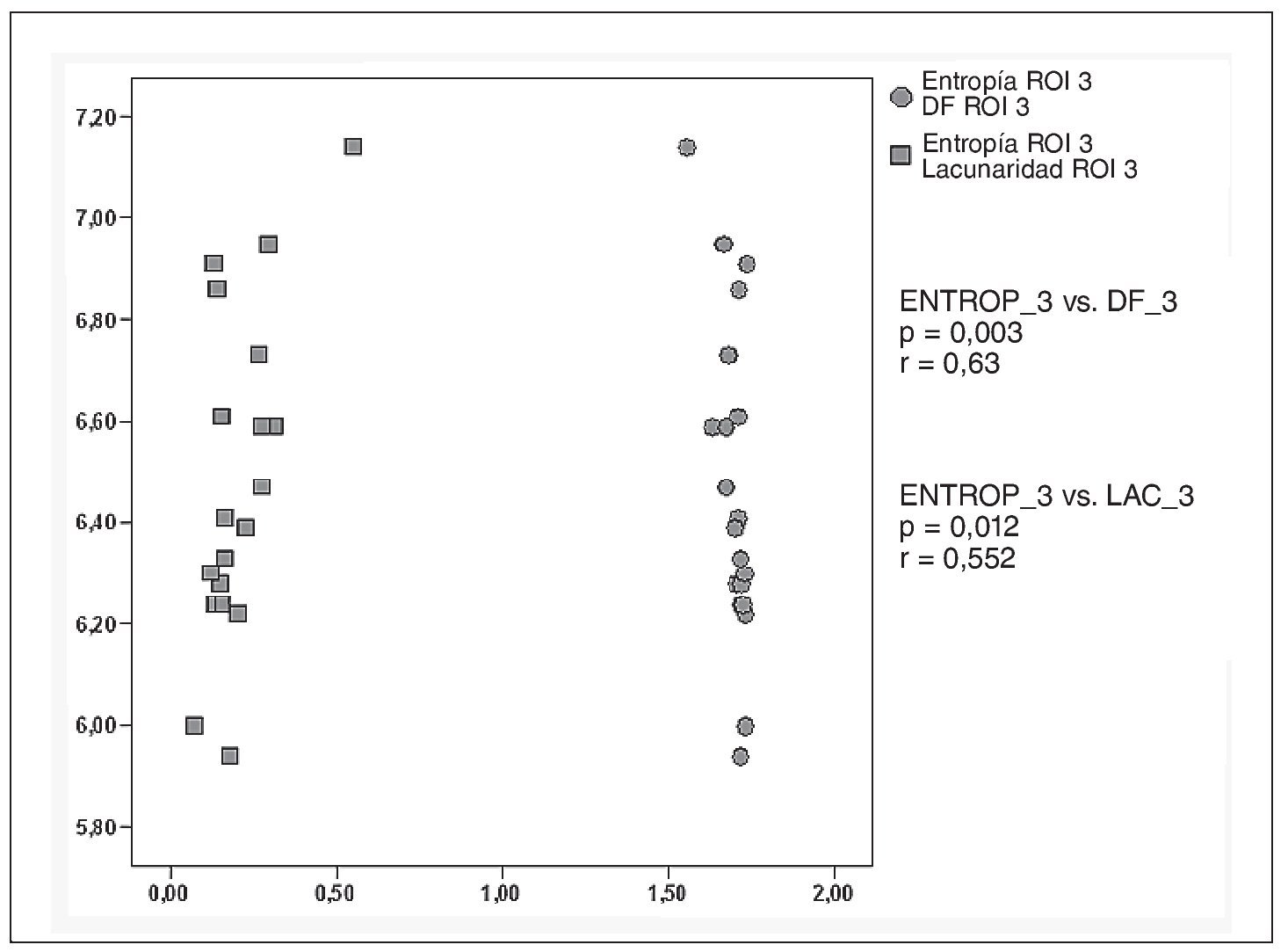
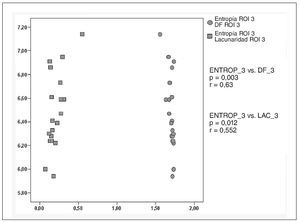
Solamente se encontraron correlaciones significativas entre la entropía, la dimensión fractal y la lacunaridad en ROI 3 -región distal de la metáfisis, a nivel del trocánter menor- (fig. 8).
Fig. 8. Gráfico de dispersión que muestra las correlaciones lineales bivariantes entre la entropía (ENTROP) y la dimensión fractal (DF) y lacunaridad (LAC). p: significación estadística; r: valor del coeficiente de correlación de Pearson; ROI: región de interés.
Nótese que la correlación entre la entropía y la dimensión fractal es inversa: cuanto mayor es el valor de la dimensión fractal, menor es el valor de la entropía, es decir más homogénea es la imagen.
Sin embargo, para la relación entropía/lacunaridad ocurre lo contrario, a mayor valor de la lacunaridad, mayor es la entropía. Cuanto más "lacunar" es la imagen, mayor es el grado de heterogeneidad.
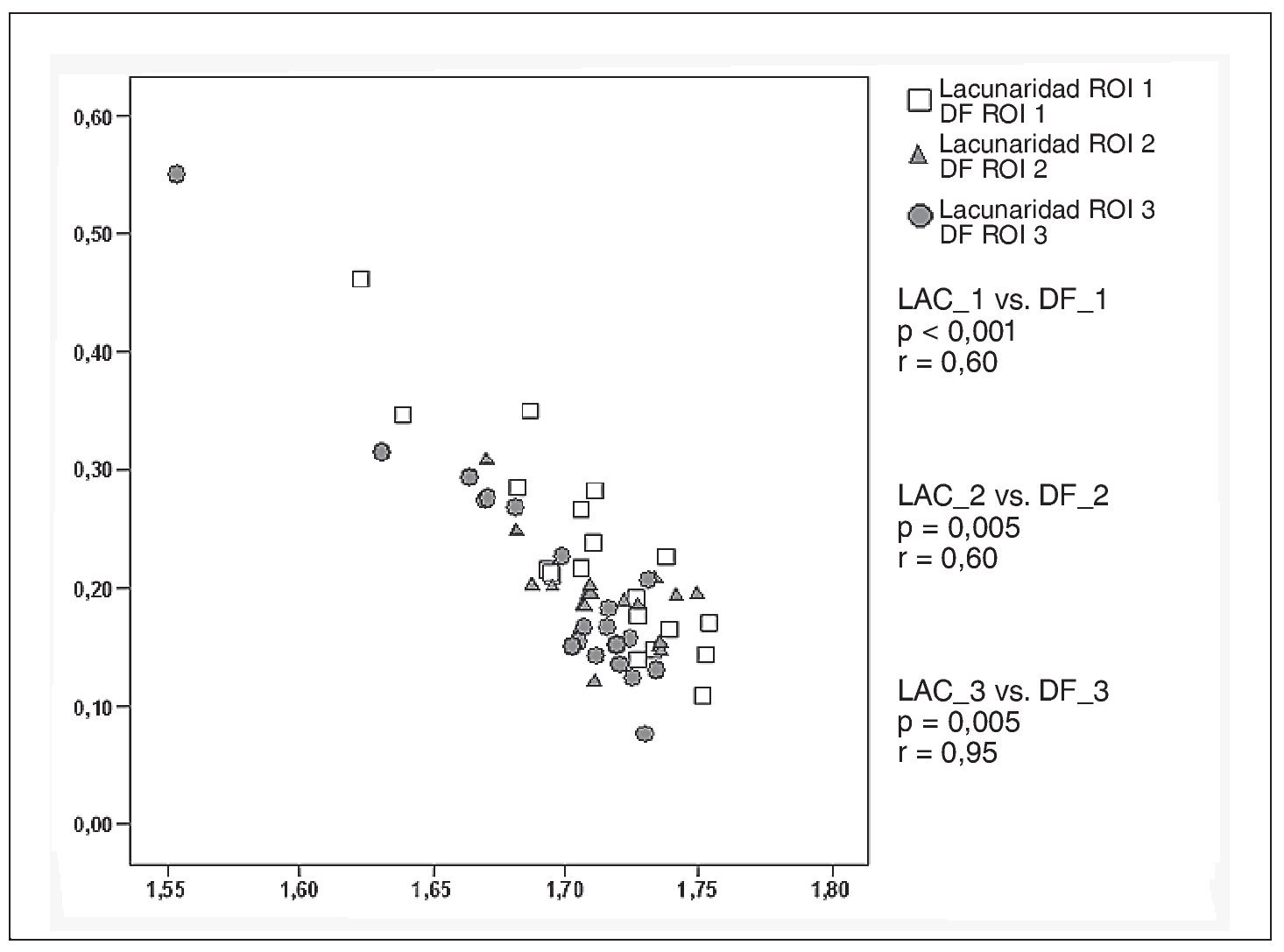
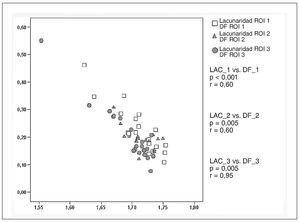
En la figura 9 se puede observar la fuerte correlación lineal inversa que hay entre los valores registrados en la dimensión fractal y la lacunaridad en las tres regiones analizadas.
DISCUSIÓN
Aunque el comportamiento y estructura óseas en principio son distintos en hombres que en mujeres, sobre todo en edades perimenopáusicas, no se encontraron diferencias significativas en cuanto al sexo para ninguna de las variables analizadas. Es posible que el rango de edad de la muestra sea muy amplio, y aunque todos los especímenes se corresponden con individuos adultos, desconocemos su edad. Por otra parte, recordemos que el sexo fue obtenido de forma indirecta a partir de las funciones discriminantes de Alemán et al24, que, aunque poseen una tasa de acierto entre el 80 y 90% para poblaciones similares (la nuestra no difiere significativamente de las que se calcularon; datos no publicados) no dejan de ser una estimación con un cierto margen de error. En este sentido sería deseable realizar un estudio con sujetos de sexo y edad conocida.
En cuanto al valor de la dimensión fractal en las tres regiones, no se encontraron diferencias significativas entre ninguno de los pares (fig. 5). Es evidente la diferencia estructural en las tres regiones analizadas, pero con el método utilizado no ha sido posible determinarlas. A la misma conclusión podemos llegar respecto de la variable lacunaridad (fig. 6).
Las transformaciones a las que se somete la imagen en la etapa de preproceso pueden influir notablemente en el cálculo de las variables de fractalidad y lacunaridad26.
Un ajuste más fino de los parámetros empleados en los filtros, así como la experimentación con distintas técnicas de mejora de la imagen y un estudio más minucioso de la influencia de los parámetros relativos al cálculo de la dimensión fractal y lacunaridad, podrían enriquecer los resultados hasta ahora obtenidos.
La determinación de la dimensión fractal -y por extensión de la lacunaridad- depende de varios factores, entre ellos las condiciones de la toma de la imagen, la resolución de la imagen analizada y del método empleado para el cálculo de dicha dimensión, aspectos que resaltan la mayoría de los autores que trabajan en esta línea13,18,27-29.
Como se puede observar en la figura 9, las variables dimensión fractal y lacunaridad están altamente correlacionadas. Esto era de esperar puesto que las bases teóricas para el cálculo de ambas variables es similar. No obstante, obsérvese que la correlación es de tipo inverso, es decir, que cuanto mayor es el valor de la dimensión fractal -es decir, cuanto más se acerca a 2, cuanto más rellena el plano- más bajo es el valor de la lacunaridad (o menos heterogénea es la imagen).
Fig. 9. Gráfico de dispersión que muestra las correlaciones lineales bivariantes entre la lacunaridad (LAC) y la dimensión fractal (DF) para las tres regiones de interés (ROI). p: significación estadística; r: valor del coeficiente de correlación de Pearson.
Son interesantes los resultados encontrados para la variable entropía, que se calcula de forma radicalmente distinta a las anteriores. De hecho, para esta variable se encontraron valores significativamente más altos (fig. 7) en la región de la cabeza respecto a la región del cuello y de la metáfisis distal, lo que indica que la región de la cabeza es más heterogénea, los niveles de gris son más variables. En esta región es donde se entrecruzan los dos haces principales de trabéculas (el haz de compresión y el haz arciforme o de tensión) (fig. 4). Pensamos que podría ser de interés ver qué tipo de relación existía entre la entropía y la dimensión fractal y la lacunaridad; las relaciones encontradas, aunque estadísticamente significativas y coherentes, tienen una fuerza media. Como la entropía y la lacunaridad son dos medidas de la heterogeneidad de la imagen (aunque desde enfoques completamente distintos), es de esperar que la relación entre ambas fuese de tipo directo, como así es (fig. 8). Según el razonamiento anteriormente expuesto, la correlación entre la entropía y la dimensión fractal debería ser inversa.
Aunque nuestros resultados son dudosos en el sentido de encontrar diferencias significativas en la arquitectura del hueso trabecular a través de la dimensión fractal, otros autores han obtenido resultados variados. Ruttimann et al27 observaron diferencias en la dimensión fractal en el hueso trabecular mandibular entre mujeres premenopáusicas y posmenopáusicas; Lynch et al30 usaron la dimensión fractal para determinar cambios osteoartríticos en la articulación de la rodilla usando imágenes radiográficas, y Majumdar et al28 encontraron dimensiones fractales más bajas en muestras de la cresta ilíaca de pacientes que habían sufrido fracturas por osteoporosis. Fazzalari y Parkinson31 también estudiaron la dimensión fractal en biopsias femorales de pacientes intervenidos con artroplastia total de cadera que poseían valores medios muy por debajo de los que hemos encontrado en nuestro estudio, aunque hay que anotar que la técnica de estudio fue diferente a la nuestra, y por tanto los valores no son comparables.Es, por tanto, importante dejar clara la metodología seguida en el proceso en cuanto a la toma de las imágenes, su digitalización, así como los algoritmos aplicados en la fase de preproceso de la imagen (realzado, filtros, umbralizado, etc.). Esta particularidad hace que los resultados obtenidos en los diferentes estudios sean difíciles de extrapolar y comparar.
Este tipo de análisis, aunque aún lejos de poder ser aplicado en la práctica clínica diaria, permite obtener de una forma relativamente sencilla y económica información sobre el entramado trabecular óseo.
CONCLUSIONES
Parece que la región de la cabeza es la que presenta diferencias más evidentes respecto del cuello y la región del trocánter menor.
La dimensión fractal, lacunaridad y variables texturales pueden ser buenas herramientas para la caracterización del hueso trabecular, aunque hemos encontrado variables desiguales. Es de resaltar la utilidad de la entropía para diferenciar y cuantificar zonas de hueso trabecular estructuralmente distintas.
Antes de poder utilizar estas herramientas de forma sistemática es necesario establecer previamente una gran cantidad de parámetros que pueden influir en el resultado final, desde la toma de las imágenes, pasando por su procesamiento, hasta su posterior análisis.
*Parte de los resultados de este trabajo fueron presentados en forma de Comunicación Póster en el XII Congreso de la SEIOMM, celebrado en Valencia del 16-19 de octubre de 2007.
Correspondencia: J. Ríos-Díaz.
Departamento de Ciencias de la Salud. Universidad Católica San Antonio de Murcia. Campus Los Jerónimos, s/n.
30107 Guadalupe. Murcia. España.
Correo electrónico: jrios@pdi.ucam.edu