Validación de los modelos de predicción de Framingham y PROCAM como estimadores del riesgo cardiovascular en una población colombiana

Resumen

Objetivo

Evaluar si las funciones de riesgo de Framingham y PROCAM son aplicables a la población colombiana.

Métodos

Se desarrolló un estudio de validación externa dentro de una cohorte histórica, en la que se incluyeron pacientes de la clínica de prevención primaria del Hospital Militar Central de Bogotá (Colombia). Se evaluaron 1.013 pacientes entre 30 y 74 años, libres de eventos cardiovasculares al ingreso a la cohorte (1984 a 1996) que recibieron seguimiento durante diez años en busca de eventos cardiovasculares (muerte coronaria, infarto del miocardio o angina de pecho). Se comparó el número de eventos cardiovasculares predichos y observados en esos diez años (calibración). Finalmente, se estimó la capacidad de las funciones de riesgo para separar los sujetos de alto y bajo riesgo (discriminación).

Resultados

En pacientes de riesgo bajo e intermedio, el número de eventos cardiovasculares predichos por la función de riesgo de Framingham sobrestimó los observados (relación entre eventos esperados y observados de 1,31), con baja capacidad para separar los pacientes de bajo riesgo de los de alto riesgo (AUC 0,65). La función de riesgo de PROCAM ajustada por sexo tuvo mejor capacidad de discriminación (AUC 0,74) con buena calibración (relación entre eventos esperados y observados de 1,07). No se contó con suficientes pacientes de alto riesgo para generalizar los resultados a esta población.

Conclusiones

La función de riesgo de Framingham debería usarse con precaución en población colombiana de riesgo bajo e intermedio sin historia previa de eventos cardiovasculares dado que sobrestima el riesgo y tiene baja capacidad de discriminación. La función de riesgo de PROCAM ajustada por sexo es una mejor opción para estimar el riesgo de enfermedad cardiovascular dura.

Abstract

Aims

To assess whether the Framingham and PROCAM risk functions were applicable to Colombian population.

Methods

We performed an external validation study within a historical cohort, including the patients of the primary prevention clinic from the Hospital Militar Central in Bogotá (Colombia). It comprised 1013 patients who were aged 30 to 74 years, free of cardiovascular disease at baseline (1984 to 1996) and followed over 10 years for cardiovascular disease events (coronary death, myocardial infarction, angina pectoris). We compared the number of predicted and observed 10-year cardiovascular disease events (calibration). Finally, we estimated the ability of the risk functions to separate high risk from low risk subjects (discrimination).

Results

In patients with low and intermediate risk, the number of cardiovascular disease events predicted by Framingham risk function overestimated those observed (predicted to observed ratio 1.31), with a low ability to separate high risk from low risk subjects (c-statistic 0.65). The PROCAM risk function adjusted by sex had better ability to separate high risk from low risk subjects (c-statistic 0.74) with good calibration (predicted to observed ratio 1.07). We do not have enough high risk patients to extrapolate our results in that population.

Conclusion

The Framingham risk function must be used with caution to estimate the absolute cardiovascular disease risk in Colombian low and intermediate risk population without any cardiovascular disease history because of its overestimation and low discrimination abilities. The PROCAM risk function adjusted by sex is a better option to estimate hard cardiovascular disease risk.

Introducción

Las enfermedades cardiovasculares (ECV) constituyen la principal causa de muerte en los países industrializados y en aquellos en vía de desarrollo¹. En Colombia son la principal causa de muerte, tanto en hombres como en mujeres mayores de 45 años, superando incluso las muertes violentas y las muertes asociadas a todos los cánceres combinados. Así mismo, la enfermedad isquémica cardiaca y la enfermedad cerebrovascular son las dos causas que producen las mayores tasas de discapacidad y mortalidad en dicho país².

Por tanto, resulta importante determinar la probabilidad de desarrollar enfermedad cardiovascular que cada paciente tiene si se pretende ofrecer un tratamiento acorde con el riesgo individual y eficiente desde la perspectiva administrativa de los sistemas de salud^3,4.

En la actualidad se dispone de múltiples sistemas de estimación de riesgo cardiovascular^5–13. Estos modelos matemáticos asignan diferentes pesos a cada uno de los factores de mayor riesgo (sexo, edad, tensión arterial, tabaquismo, diabetes, niveles de colesterol total, LDL y HDL, antecedentes familiares). En personas libres de enfermedad cardiovascular previa, generan un estimado del riesgo de desarrollar ECV dentro de un determinado lapso de tiempo.

Los modelos de predicción más conocidos y quizá los más utilizados en el mundo son la función de riesgo de Framingham y el modelo de PROCAM^5,6. El primero predice el riesgo de desarrollar muerte de origen coronario, infarto del miocardio (reconocido o no reconocido), angina de pecho o insuficiencia coronaria en un lapso de diez años⁵. La última actualización predice el riesgo de presentar eventos cardiovasculares duros como muerte o infarto agudo del miocardio sin tener en cuenta la angina⁶. Entre tanto, la función de riesgo de PROCAM⁹ estima la probabilidad de desarrollar muerte coronaria o un primer infarto del miocardio en los siguientes diez años.

Si bien las ecuaciones de predicción de riesgo derivadas de estos estudios gozan de gran aceptación y se usan ampliamente en Colombia, existen múltiples evidencias que demuestran que no se pueden aplicar directamente en todas las poblaciones^14–18.

Se han descrito diversas causas por las cuales un modelo no funciona de forma adecuada en todas las poblaciones, entre ellas, diferencias en la carga genética, nivel socioeconómico y hábitos dietéticos o variaciones en los sistemas de salud. Esto trae consigo la necesidad de realizar una validación de todos los modelos de predicción en una población diferente a aquella en la que se desarrollaron inicialmente (validación externa)^4,19,20, que a vez evalúe el comportamiento del modelo de predicción en una nueva población, mediante la valoración de la calibración y la capacidad de discriminación del mismo²¹.

Hasta el momento no se han realizado estudios para validar los modelos de Framingham y PROCAM como estimadores de riesgo de enfermedad cardiovascular en la población colombiana, y en general en poblaciones suramericanas. Existen razones para pensar que el riesgo de ECV es sistemáticamente diferente en nuestro medio si se tienen en cuenta las marcadas diferencias demográficas de nuestra población, al compararla con las poblaciones totalmente caucásicas y urbanas en las que se desarrollaron los modelos.

Métodos

Se desarrolló un estudio de validación externa basado en una cohorte histórica, en el que se incluyeron, como población de validación, los pacientes que ingresaron en la Clínica de Prevención Primaria del Hospital Militar Central (Bogotá, Colombia).

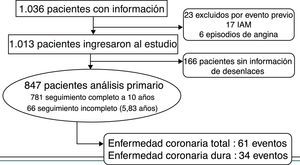
Inicialmente se evaluaron las historias clínicas de 1.036 pacientes, entre 30 y 74 años que correspondieron al total de pacientes que ingresaron en la Clínica de prevención primaria en el período comprendido entre 1984 y 1996. Para el análisis, sin embargo, solo se tuvieron en cuenta 1.013 pacientes que estuvieron libres de enfermedad coronaria cuando ingresaron en el programa. Se consideraron libres de enfermedad coronaria si a su ingreso en la clínica de prevención primaria no reportaban: infarto del miocardio o angina de pecho diagnosticada por un médico y evidencia de infarto agudo del miocardio en electrocardiograma de 12 derivaciones de ingreso, definido como presencia de onda Q significativa (mayor del 30% de la amplitud total del QRS).

Un primer evaluador extrajo los datos relativos a las variables de exposición registradas al ingreso de los pacientes en la clínica de prevención primaria, incluyendo la información de edad, sexo, índice de masa corporal, glucemia en ayunas y uso de hipoglucemiantes; tensión arterial sistólica, diastólica y uso de antihipertensivos; colesterol total, colesterol-LDL, colesterol-HDL y triglicéridos; así como tabaquismo y antecedentes familiares.

Con base en estos datos se calculó el riesgo de presentar enfermedad coronaria total (muerte de origen coronario, infarto del miocardio, angina de pecho o insuficiencia coronaria) o enfermedad coronaria dura (muerte de origen coronario, infarto del miocardio) de acuerdo con las escalas de predicción de riesgo de Framingham y PROCAM respectivamente, mediante el uso de las definiciones operativas y categorías que cada uno de esos estudios empleó en el estudio original.

Como variable de desenlace se evaluó la presencia de evento cardiovascular total o duro durante los diez años siguientes al ingreso al estudio. Con el fin de disminuir el riesgo de sesgo, asociado a una búsqueda más exhaustiva de desenlaces en pacientes con mayor cantidad de factores de riesgo, la recolección de los datos de la variable de desenlace fue diligenciada por un segundo evaluador que desconocía la estratificación de riesgo inicial. Las historias en las que este segundo evaluador evidenció posibles eventos coronarios fueron reevaluadas por un experto (Especialista en Medicina Interna), quien verificó la presencia del evento y definió si correspondía a enfermedad coronaria dura o total.

Cuando no se disponía de datos del total de tiempo de seguimiento del paciente, se consignó el tiempo durante el cual se disponía de información completa. En caso de fallecimiento se determinó la causa con base en el diagnóstico consignado en el certificado de defunción y en la epicrisis.

Análisis estadístico

Inicialmente se realizó un análisis descriptivo de la población y se calcularon los riesgos relativos de enfermedad coronaria total y enfermedad coronaria dura. Para ello se diseñó un modelo de regresión logística multivariada con ayuda del programa estadístico STATA 10.

De acuerdo con los datos obtenidos al ingreso en la cohorte se generaron las estimaciones de riesgo de cada paciente según los modelos de Framingham y PROCAM. Ya que para generar estos cálculos es indispensable disponer de resultados para todas las variables, se decidió imputar valores para los datos faltantes, mediante método hot deck, teniendo una tasa de datos faltantes inferior al 3% para cada una de las variables.

Con esta información se procedió a realizar la validación de los modelos teniendo en cuenta para el análisis la calibración y la capacidad de discriminación de los mismos en la población colombiana.

Para evaluar la calibración se generaron cinco subgrupos de riesgo y en el interior de cada uno se compararon los eventos esperados con los eventos realmente observados. Esta información se presenta adicionalmente de forma gráfica incluyendo la proporción de eventos esperados en el eje X y la proporción de eventos observados en el eje Y; en dicha gráfica un modelo bien calibrado debería tener idealmente una pendiente de uno y un intercepto de 0. Para evaluar esta hipótesis se realizó el test de Hosmer-Lemeshow²². Si bien el estadístico de resumen puede ser de utilidad, la decisión de si el modelo está calibrado de manera correcta se basó en una decisión clínica, teniendo en cuenta si el error de calibración puede cambiar las conductas a tomar en el interior de cada uno de los subgrupos de riesgo.

Para evaluar la capacidad de discriminación de cada uno de los modelos (Framingham y PROCAM) en la población se generó una curva ROC. Dado que la capacidad de discriminación de los modelos iniciales no es óptima (Framingham 0,77 y PROCAM 0,82) se consideró el modelo con adecuada capacidad de discriminación, si presentaba un valor C en la población estudio cercano al valor C del modelo en la población en la que se generó. Es decir, se consideraron adecuados los modelos que presentaron un área bajo la curva ROC en la población estudio mayor a 0,7.

Cuando los modelos no presentaron adecuada calibración y capacidad de discriminación, se evaluó en qué medida los ajustes hechos por los mismos grupos que desarrollaron el modelo mejoraron las características operativas del modelo en la población estudio.

En vista de la presencia de un grupo de pacientes con pérdidas al seguimiento en cuyos casos no se conocieron los desenlaces, se decidió realizar un análisis de sensibilidad para evaluar el impacto de la pérdida de información en los resultados obtenidos. Se evaluaron, por tanto, las características demográficas y la frecuencia de los factores de riesgo cardiovascular en la población de pacientes en quienes no se conocieron desenlaces y se compararon con el grupo que contaba con la información completa. Los resultados se cotejaron mediante una prueba z de diferencia de proporciones para dos muestras.

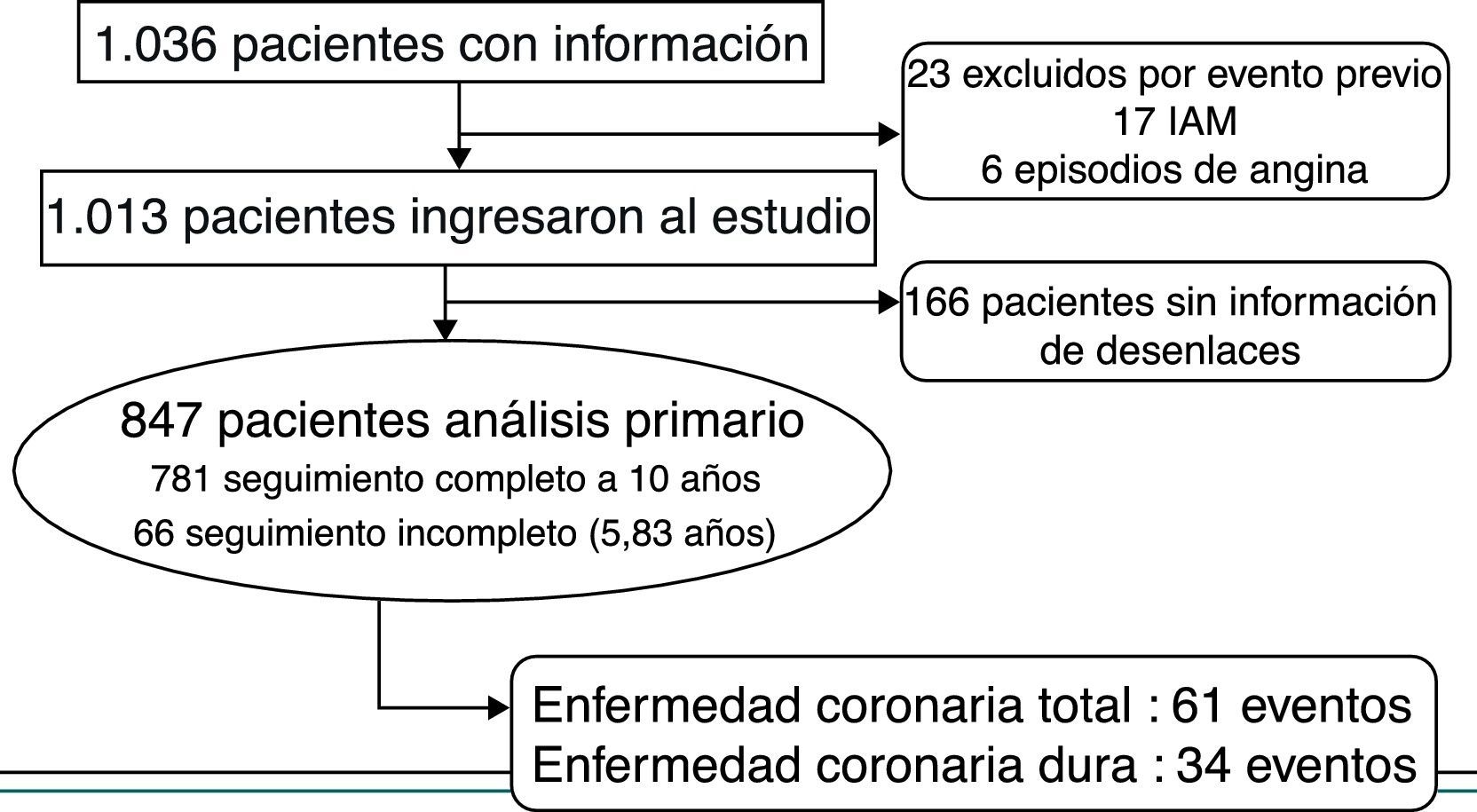
Resultados

Población de estudio

Como se indicó antes, para el estudio se obtuvo información de 1.036 pacientes, de los cuales se excluyeron 23 por evento coronario previo al ingreso (17 pacientes con infarto agudo del miocardio y 6 con episodios de angina previos al inicio del seguimiento). En total se analizaron 1.013 pacientes, de quienes se obtuvo información de desenlaces en 847 (83,6%); 781 pacientes (77,2%) tuvieron seguimiento completo hasta completar diez años o hasta la muerte; 66 (6,4%) tuvieron seguimiento incompleto. De ellos 7 ya habían presentado eventos para el momento en que se perdió el seguimiento (3 infarto agudo del miocardio y 4 angina inestable). El tiempo que estos 66 pacientes permanecieron en la cohorte fue en promedio 5,83 años (DE 2,49 años). En los 166 pacientes restantes (16,4%) no se logró obtener información de desenlaces (fig. 1). Durante el seguimiento se documentaron en total 61 (6,1%) eventos de enfermedad coronaria total y 34 (3,4%) eventos de enfermedad coronaria dura.

Figura 1.

Causas de exclusión, seguimiento y desenlaces.

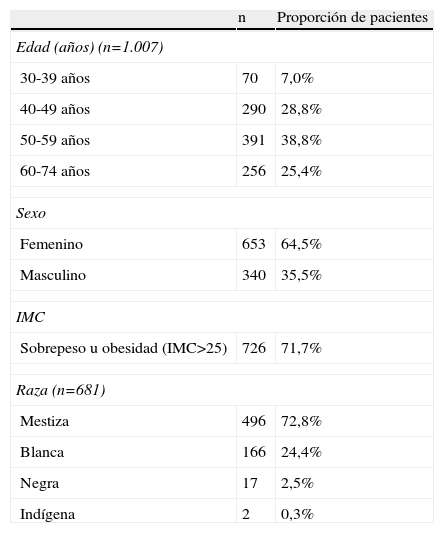
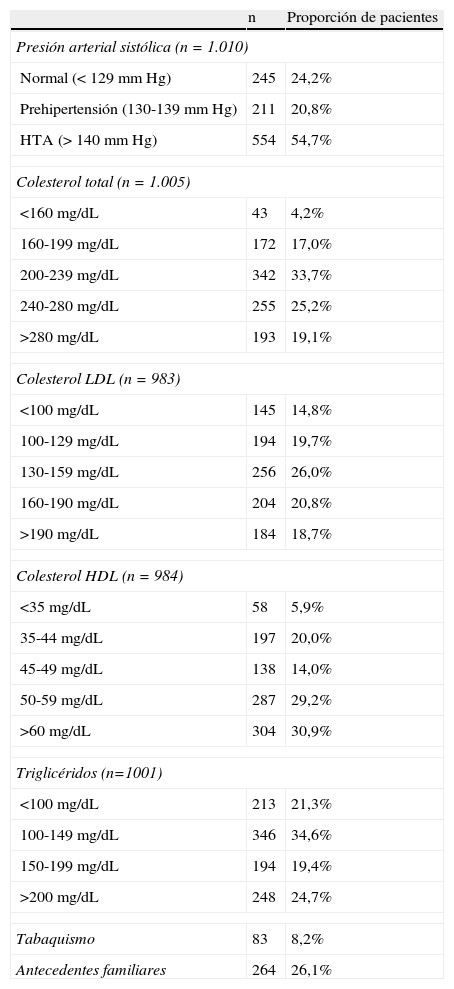
Las características demográficas de la población (1.013 pacientes) incluyendo edad, sexo, índice de masa corporal y raza, se muestran en la tabla 1. La distribución según categorías para cada factor de riesgo se describe en la tabla 2.

Tabla 1.

Características demográficas de la población

	n	Proporción de pacientes
Edad (años) (n=1.007)
30-39 años	70	7,0%
40-49 años	290	28,8%
50-59 años	391	38,8%
60-74 años	256	25,4%
Sexo
Femenino	653	64,5%
Masculino	340	35,5%
IMC
Sobrepeso u obesidad (IMC>25)	726	71,7%
Raza (n=681)
Mestiza	496	72,8%
Blanca	166	24,4%
Negra	17	2,5%
Indígena	2	0,3%

Tabla 2.

Distribución según categorías para cada factor de riesgo

	n	Proporción de pacientes
Presión arterial sistólica (n = 1.010)
Normal (< 129 mm Hg)	245	24,2%
Prehipertensión (130-139 mm Hg)	211	20,8%
HTA (> 140 mm Hg)	554	54,7%
Colesterol total (n = 1.005)
<160 mg/dL	43	4,2%
160-199 mg/dL	172	17,0%
200-239 mg/dL	342	33,7%
240-280 mg/dL	255	25,2%
>280 mg/dL	193	19,1%
Colesterol LDL (n = 983)
<100 mg/dL	145	14,8%
100-129 mg/dL	194	19,7%
130-159 mg/dL	256	26,0%
160-190 mg/dL	204	20,8%
>190 mg/dL	184	18,7%
Colesterol HDL (n = 984)
<35 mg/dL	58	5,9%
35-44 mg/dL	197	20,0%
45-49 mg/dL	138	14,0%
50-59 mg/dL	287	29,2%
>60 mg/dL	304	30,9%
Triglicéridos (n=1001)
<100 mg/dL	213	21,3%
100-149 mg/dL	346	34,6%
150-199 mg/dL	194	19,4%
>200 mg/dL	248	24,7%
Tabaquismo	83	8,2%
Antecedentes familiares	264	26,1%

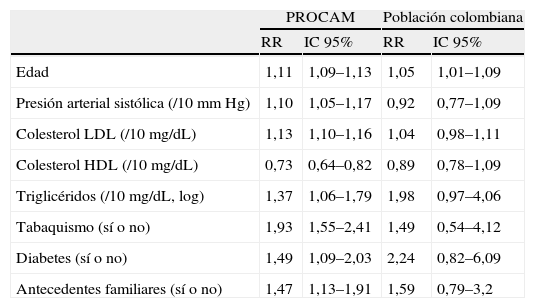
Los riesgos relativos de enfermedad coronaria dura de acuerdo con el modelo de PROCAM, para la población de estudio y para la población en la que se desarrolló el estudio original, se observan en la tabla 3. Al comparar las dos poblaciones se hallaron valores muy similares para todas las variables con intervalos de confianza que se superpusieron, haciéndolas más fácilmente comparables.

Tabla 3.

Riesgos relativos de enfermedad coronaria dura en el estudio de PROCAM vs. población colombiana. Análisis de regresión logística multivariado

	PROCAM		Población colombiana
	RR	IC 95%	RR	IC 95%
Edad	1,11	1,09–1,13	1,05	1,01–1,09
Presión arterial sistólica (/10 mm Hg)	1,10	1,05–1,17	0,92	0,77–1,09
Colesterol LDL (/10 mg/dL)	1,13	1,10–1,16	1,04	0,98–1,11
Colesterol HDL (/10 mg/dL)	0,73	0,64–0,82	0,89	0,78–1,09
Triglicéridos (/10 mg/dL, log)	1,37	1,06–1,79	1,98	0,97–4,06
Tabaquismo (sí o no)	1,93	1,55–2,41	1,49	0,54–4,12
Diabetes (sí o no)	1,49	1,09–2,03	2,24	0,82–6,09
Antecedentes familiares (sí o no)	1,47	1,13–1,91	1,59	0,79–3,2

Validación de los modelos

Modelo de Framingham

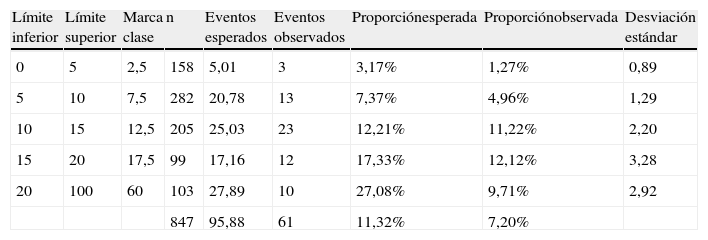
La tabla 4 evalúa la calibración del modelo de Framingham en la población de estudio comparando al interior de cada uno de los cinco subgrupos de riesgo los eventos de enfermedad coronaria total esperados con los eventos realmente observados. Para este análisis se tuvieron en cuenta solo los 847 pacientes de los que se conocía el desenlace.

Tabla 4.

Calibración del modelo de Framingham. Eventos esperados vs. eventos observados

Límite inferior	Límite superior	Marca clase	n	Eventos esperados	Eventos observados	Proporciónesperada	Proporciónobservada	Desviación estándar
0	5	2,5	158	5,01	3	3,17%	1,27%	0,89
5	10	7,5	282	20,78	13	7,37%	4,96%	1,29
10	15	12,5	205	25,03	23	12,21%	11,22%	2,20
15	20	17,5	99	17,16	12	17,33%	12,12%	3,28
20	100	60	103	27,89	10	27,08%	9,71%	2,92
			847	95,88	61	11,32%	7,20%

Se presentan las siguientes columnas: límite inferior del subgrupo de riesgo, límite superior del subgrupo de riesgo, marca de clase, número de pacientes en cada subgrupo, número de eventos esperados en cada subgrupo, número de eventos observados en cada subgrupo, proporción esperada, proporción observada en cada subgrupo y desviación estándar de la misma. Los eventos para esta tabla son enfermedad coronaria total (61 eventos). Para el análisis solo se tuvieron en cuenta 847 pacientes de quienes se conocieron desenlaces.

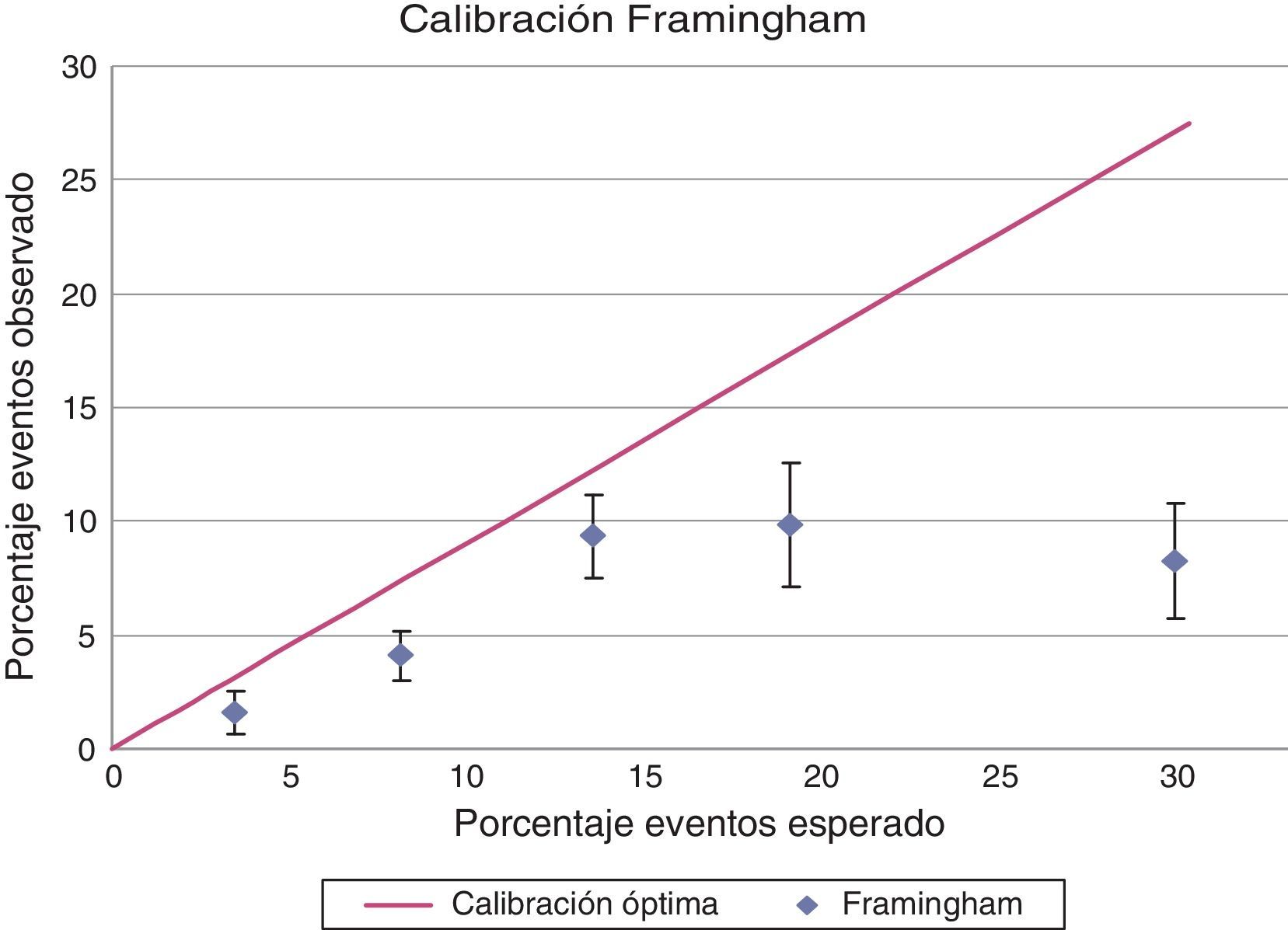
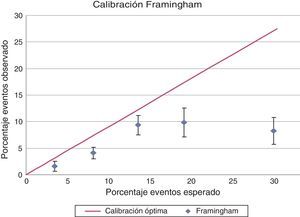
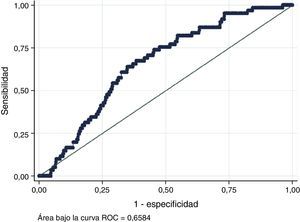
La figura 2 muestra la relación entre la proporción de eventos esperada y la proporción de eventos realmente observada. El modelo sobrestima el riesgo de presentar enfermedad coronaria total en todas las categorías de riesgo. Sin embargo, esta sobrestimación es mínima en las categorías de riesgo bajo y moderado (diferencia absoluta entre proporción de eventos esperados y observados 2,26 y 2,3% respectivamente) por lo que se considera que el modelo está calibrado para estos subgrupos de riesgo. La prueba de Hosmer-Lemeshow fue de 7,83 con un valor de p de 0,3476. La relación entre los eventos esperados y los eventos observados para los pacientes de riesgo bajo e intermedio fue de 1,31 (68 eventos esperados/51 eventos observados).

Figura 2.

Calibración del modelo de Framingham. Porcentaje de eventos esperados vs. porcentaje de eventos observados.

El gráfico muestra la relación entre la proporción de eventos esperada (eje X) y la proporción de eventos realmente observada (eje Y). La línea recta indica cómo debería comportarse la curva si se tuviera una calibración perfecta del modelo.

El comportamiento en la categoría de alto riesgo es diferente, lo que evidenció que el modelo no está calibrado. En este caso la diferencia absoluta entre proporción de eventos esperados y observados fue de 17,4; HL mayor a 20. Cabe resaltar la baja cantidad de pacientes en esta categoría de riesgo.

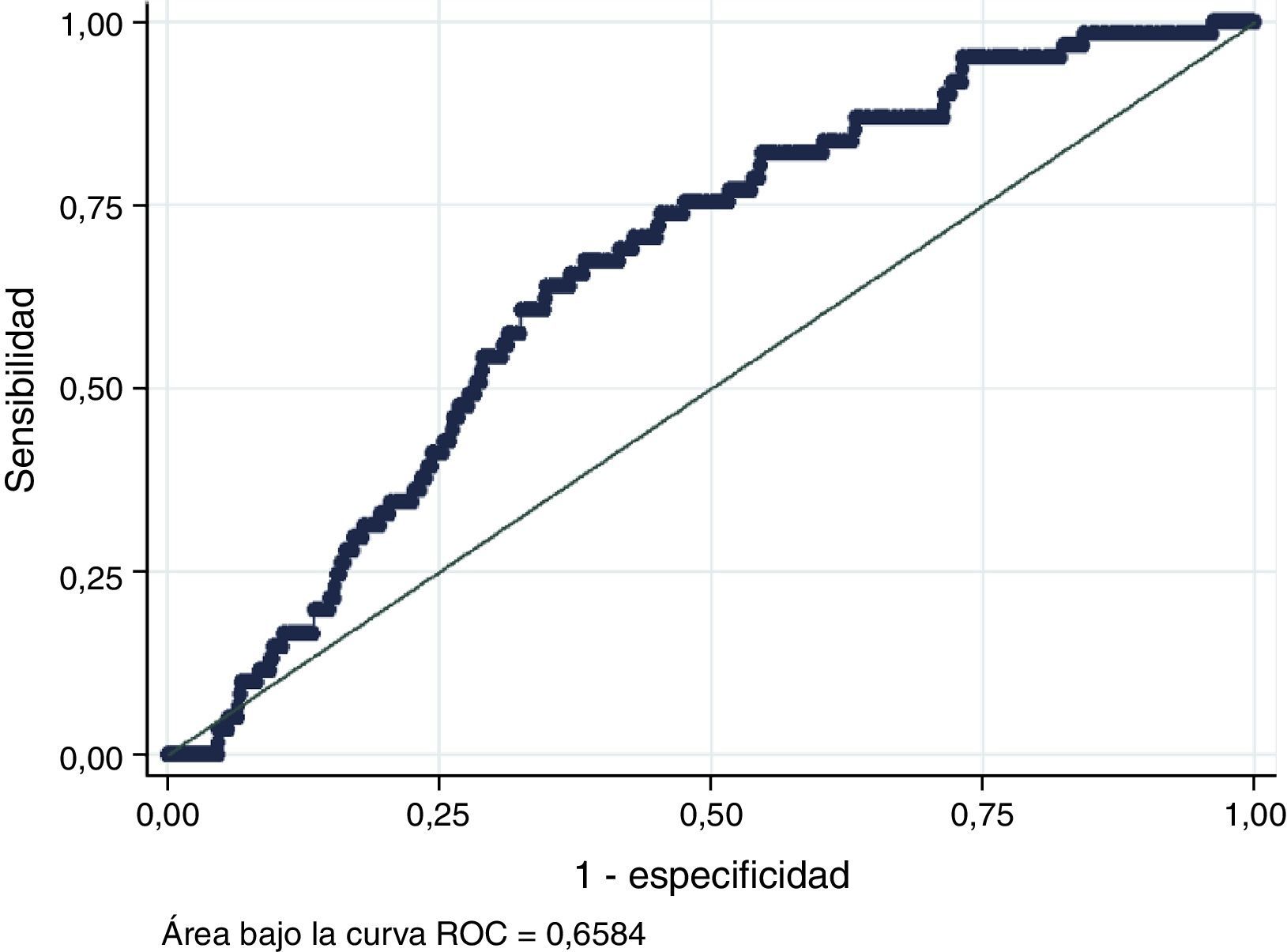
Por otra parte, se evaluó la capacidad de discriminación del modelo que generó un gráfico de características operativas del receptor (fig. 3). El área bajo la curva fue de 0,6584 (IC 0,62577-0,69072), muy por debajo de la capacidad de discriminación del modelo en la población en la que se desarrolló inicialmente (0,77) y menor a la que se consideró a priori como aceptable de 0,7.

Figura 3.

Discriminación del modelo de Framingham. Curva de características operativas del receptor.

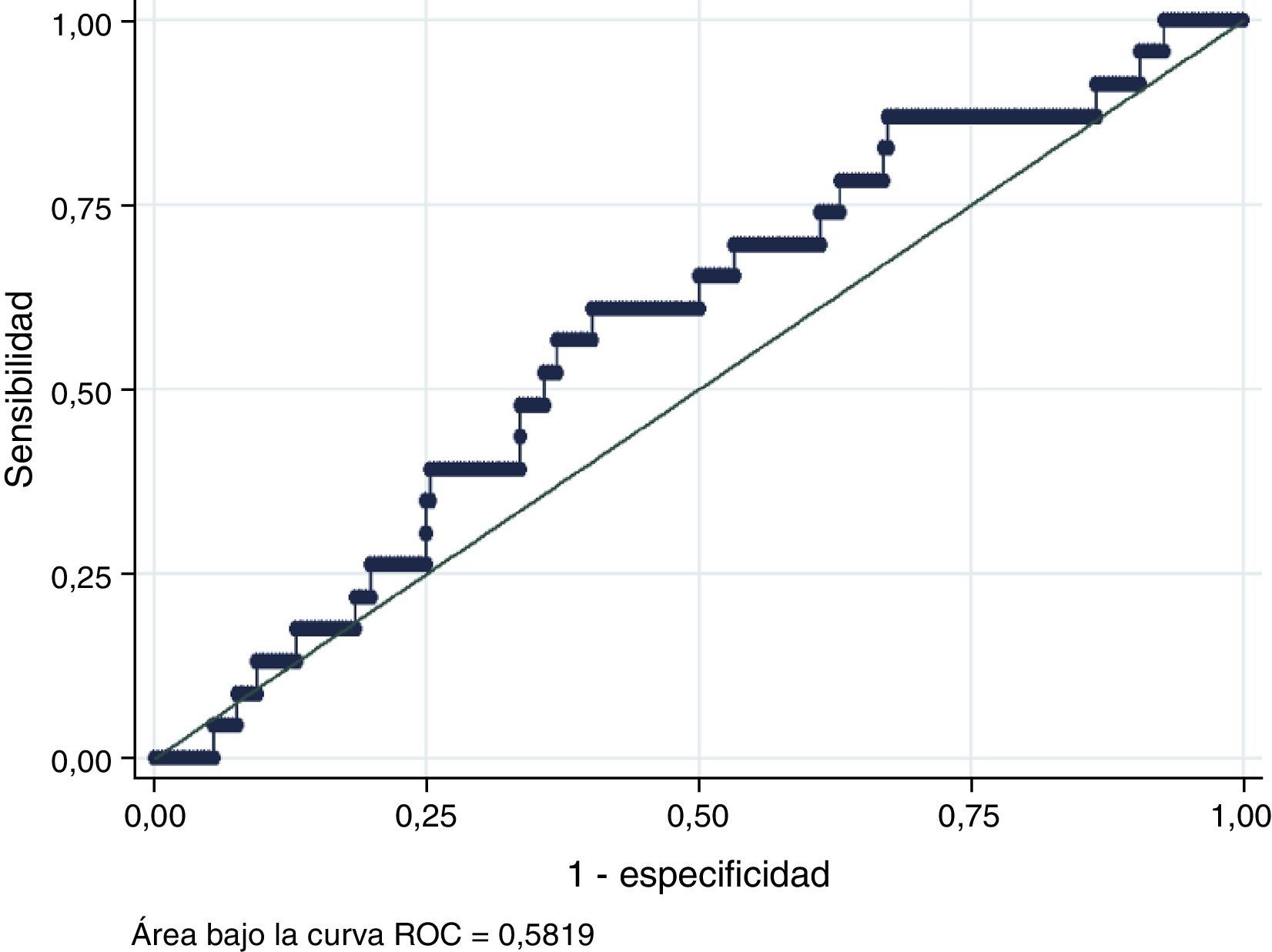
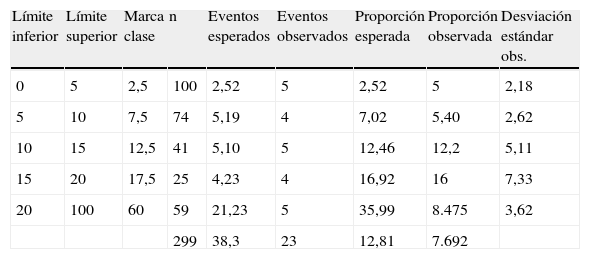
Modelo de PROCAM

La tabla 5 evalúa la calibración del modelo comparando al interior de cada uno de los subgrupos los eventos de ECV esperados con los eventos realmente observados para el modelo de PROCAM. Considerando que el modelo de PROCAM se basó en una población exclusivamente masculina, en principio se realizó un análisis teniendo en cuenta solo los 299 pacientes de género masculino en quienes se conocieron desenlaces.

Tabla 5.

Calibración del modelo de PROCAM en hombres. Eventos esperados vs. eventos observados

Límite inferior	Límite superior	Marca clase	n	Eventos esperados	Eventos observados	Proporción esperada	Proporción observada	Desviación estándar obs.
0	5	2,5	100	2,52	5	2,52	5	2,18
5	10	7,5	74	5,19	4	7,02	5,40	2,62
10	15	12,5	41	5,10	5	12,46	12,2	5,11
15	20	17,5	25	4,23	4	16,92	16	7,33
20	100	60	59	21,23	5	35,99	8.475	3,62
			299	38,3	23	12,81	7.692

Se presentan las siguientes columnas: límite inferior del subgrupo de riesgo, límite superior del subgrupo de riesgo, marca de clase, número de pacientes en cada subgrupo, número de eventos esperados en cada subgrupo, número de eventos observados en cada subgrupo, proporción esperada, proporción observada en cada subgrupo y desviación estándar de la misma.

Los eventos para esta tabla son enfermedad coronaria dura (23 eventos). Se tuvieron en cuenta para el análisis solo los 299 pacientes masculinos en los que se conocieron desenlaces.

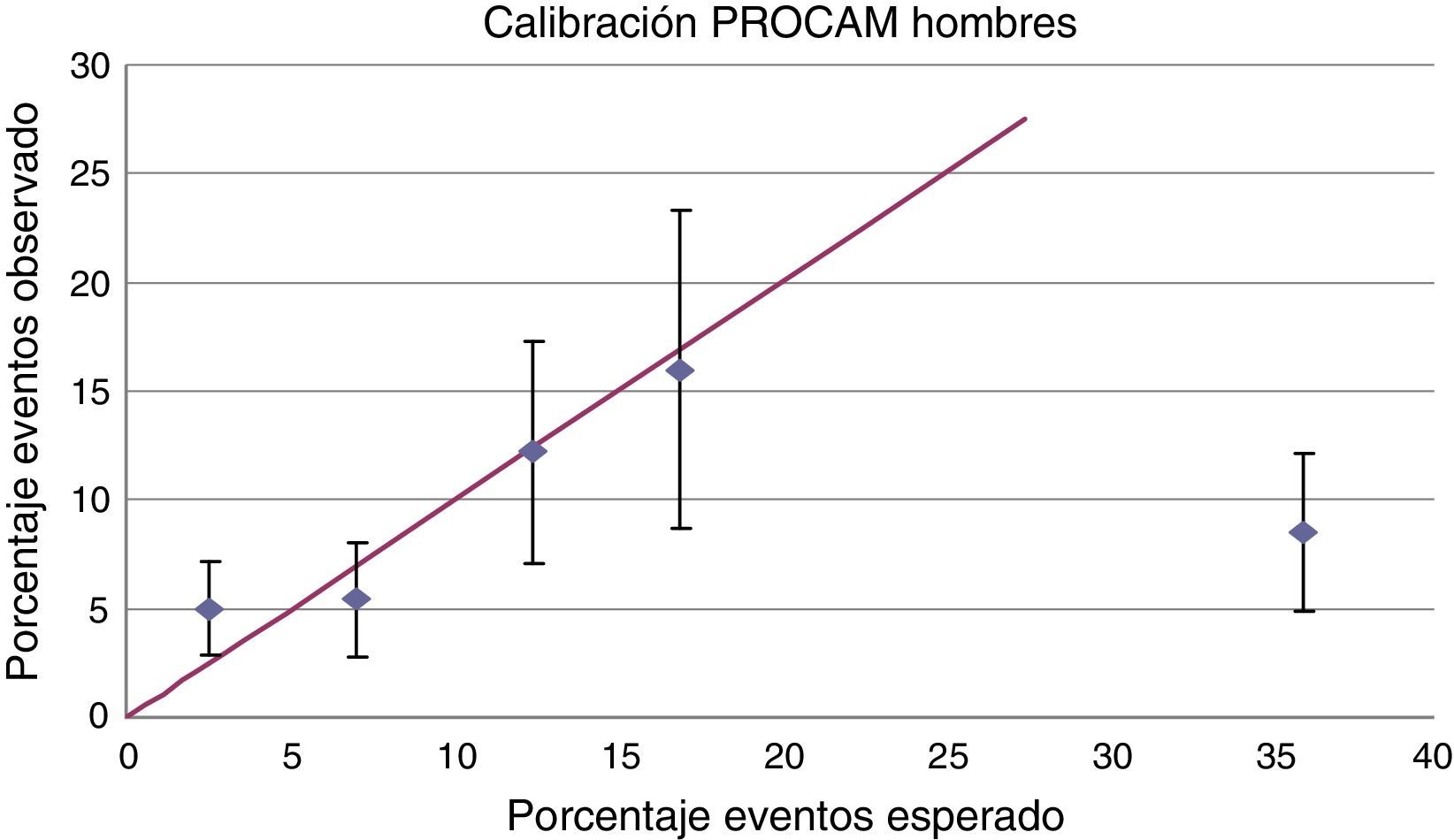
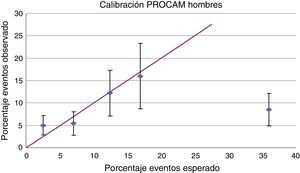
La figura 4 muestra la relación entre el porcentaje de eventos esperado y el porcentaje de eventos realmente observado. Al igual que lo observado para el modelo de Framingham, el de PROCAM está adecuadamente calibrado para las categorías de riesgo bajo e intermedio con diferencias absolutas entre el porcentaje de eventos esperado y observado menores al 3%; sin embargo, se hallaron intervalos de confianza muy amplios debidos especialmente al bajo tamaño de la muestra analizada y la escasa cantidad de eventos (HL = 18). En el caso de los pacientes de alto riesgo nuevamente se encontró una diferencia muy amplia entre el porcentaje de eventos esperado y el observado (27%), a partir de lo cual se concluyó que el modelo no está calibrado para este grupo.

Figura 4.

Calibración del modelo de PROCAM en hombres. Porcentaje de eventos esperados vs. porcentaje de eventos observados.

El gráfico muestra la relación entre la proporción de eventos esperada (eje X) y la proporción de eventos realmente observada (eje Y). La línea recta muestra cómo debería comportarse la curva si se tuviera una calibración perfecta del modelo.

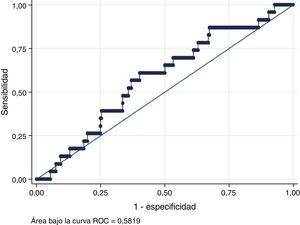
Pese a la calibración correcta del modelo en la población colombiana se halló una baja capacidad de discriminación del mismo con área bajo la curva ROC de 0,5819 (IC 95%: 0,52378-0,63846), muy por debajo del valor observado en la población en la que se desarrolló el modelo original (0,8) (fig. 5).

Figura 5.

Discriminación del modelo de PROCAM en hombres. Curva de características operativas del receptor.

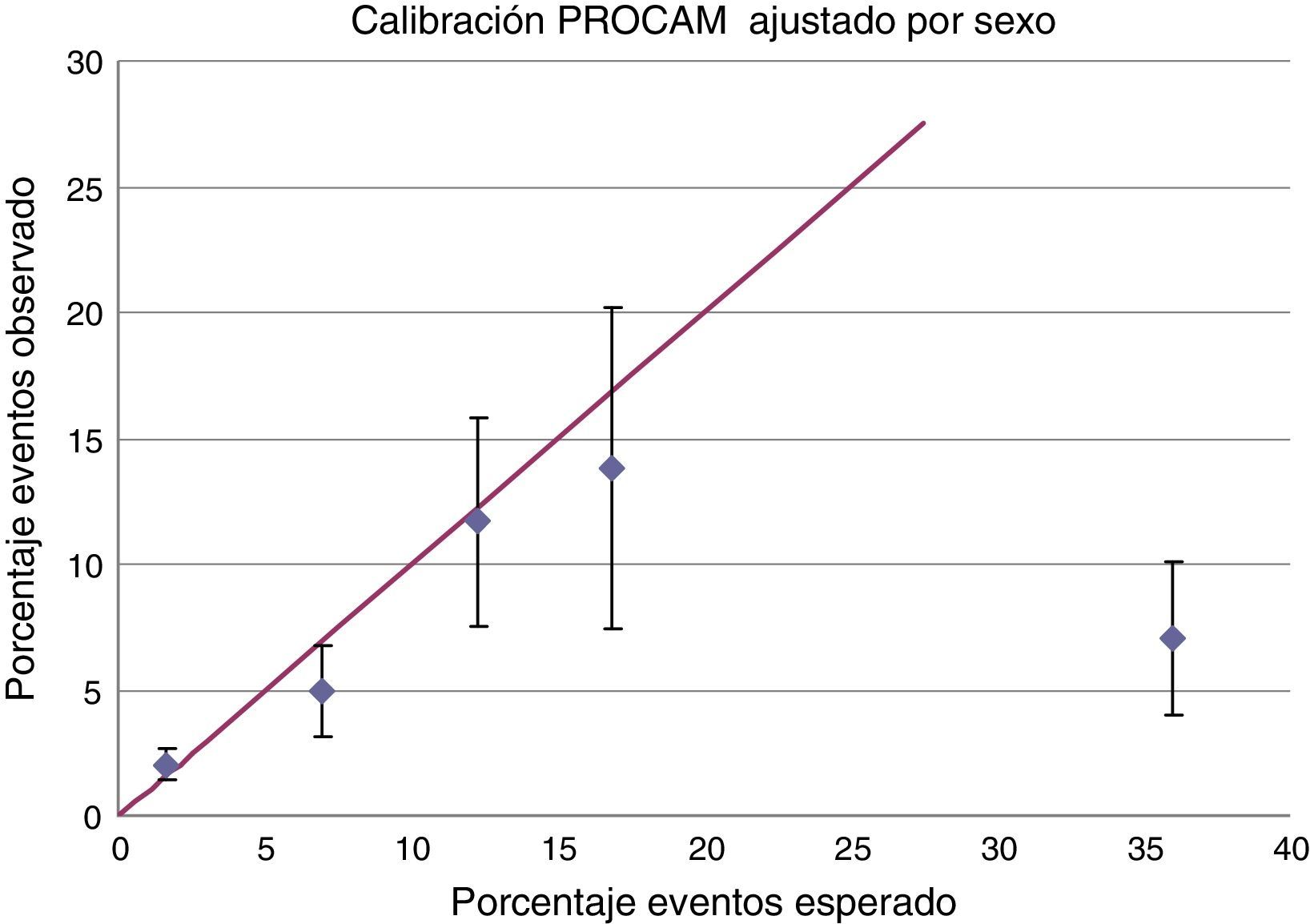
Modelo de PROCAM para hombres y mujeres ajustado

Con miras a hacer el análisis más robusto con un mayor tamaño de muestra y considerando que en la práctica con frecuencia el médico utiliza la escala de riesgo de PROCAM también en mujeres, el modelo no fue elaborado inicialmente en población femenina, se decidió analizar la validez del mismo incluyendo mujeres, pero realizando el ajuste recomendado por el grupo de estudio de PROCAM. De acuerdo con esta publicación se recomienda ajustar el riesgo en el sexo femenino multiplicando por 0,25 en pacientes no diabéticas.

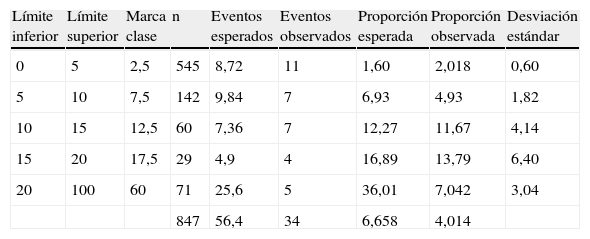
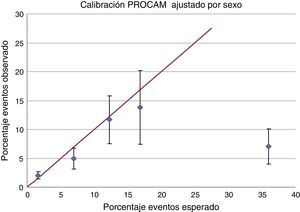
La tabla 6 evalúa la calibración del modelo PROCAM ajustado por sexo. La figura 6 representa la relación entre el porcentaje de eventos esperado y el realmente observado. En este caso se encontraron resultados similares a los vistos en la validación del modelo de PROCAM para la población masculina con una adecuada calibración en las poblaciones de riesgo bajo e intermedio, con mejores intervalos de confianza. Para la población de bajo riesgo la diferencia absoluta entre el porcentaje esperado y el observado fue menor al 0,1%, y para el riesgo intermedio fue de 1,3%. El estadístico de Hosmer-Lemeshow (HL = 9,2, p = 0,2379) es compatible con una adecuada calibración del modelo en poblaciones de riesgo bajo e intermedio. Nuevamente se halló una amplia diferencia entre los eventos observados y esperados en la población de alto riesgo, población donde el modelo no está calibrado; Hosmer-Lemeshow (35, p < 0,0001).

Tabla 6.

Calibración del modelo de PROCAM para hombres y mujeres ajustado por sexo. Eventos esperados vs. eventos observados

Límite inferior	Límite superior	Marca clase	n	Eventos esperados	Eventos observados	Proporción esperada	Proporción observada	Desviación estándar
0	5	2,5	545	8,72	11	1,60	2,018	0,60
5	10	7,5	142	9,84	7	6,93	4,93	1,82
10	15	12,5	60	7,36	7	12,27	11,67	4,14
15	20	17,5	29	4,9	4	16,89	13,79	6,40
20	100	60	71	25,6	5	36,01	7,042	3,04
			847	56,4	34	6,658	4,014

Se presentan las siguientes columnas: límite inferior del subgrupo de riesgo, límite superior del subgrupo de riesgo, marca de clase, número de pacientes en cada subgrupo, número de eventos esperados en cada subgrupo, número de eventos observados en cada subgrupo, proporción esperada, proporción observada en cada subgrupo y desviación estándar de la misma.

Los eventos para esta tabla son enfermedad coronaria dura (34 eventos). Se tuvieron en cuenta para el análisis los 847 pacientes en los que se conocieron desenlaces incluyendo hombres y mujeres.

Figura 6.

Calibración del modelo PROCAM para hombres y mujeres ajustado por sexo. Porcentaje de eventos esperado vs. porcentaje de eventos observado.

El gráfico muestra la relación entre la proporción de eventos esperada (eje X) y la proporción de eventos realmente observada (eje Y). La línea recta muestra cómo debería comportarse la curva si se tuviera una calibración perfecta del modelo.

De nuevo cabe resaltar que solo una cantidad muy pequeña de pacientes (8,4%) corresponde a riesgo alto, lo que podría explicar al menos en parte la calibración inadecuada del modelo en esa población.

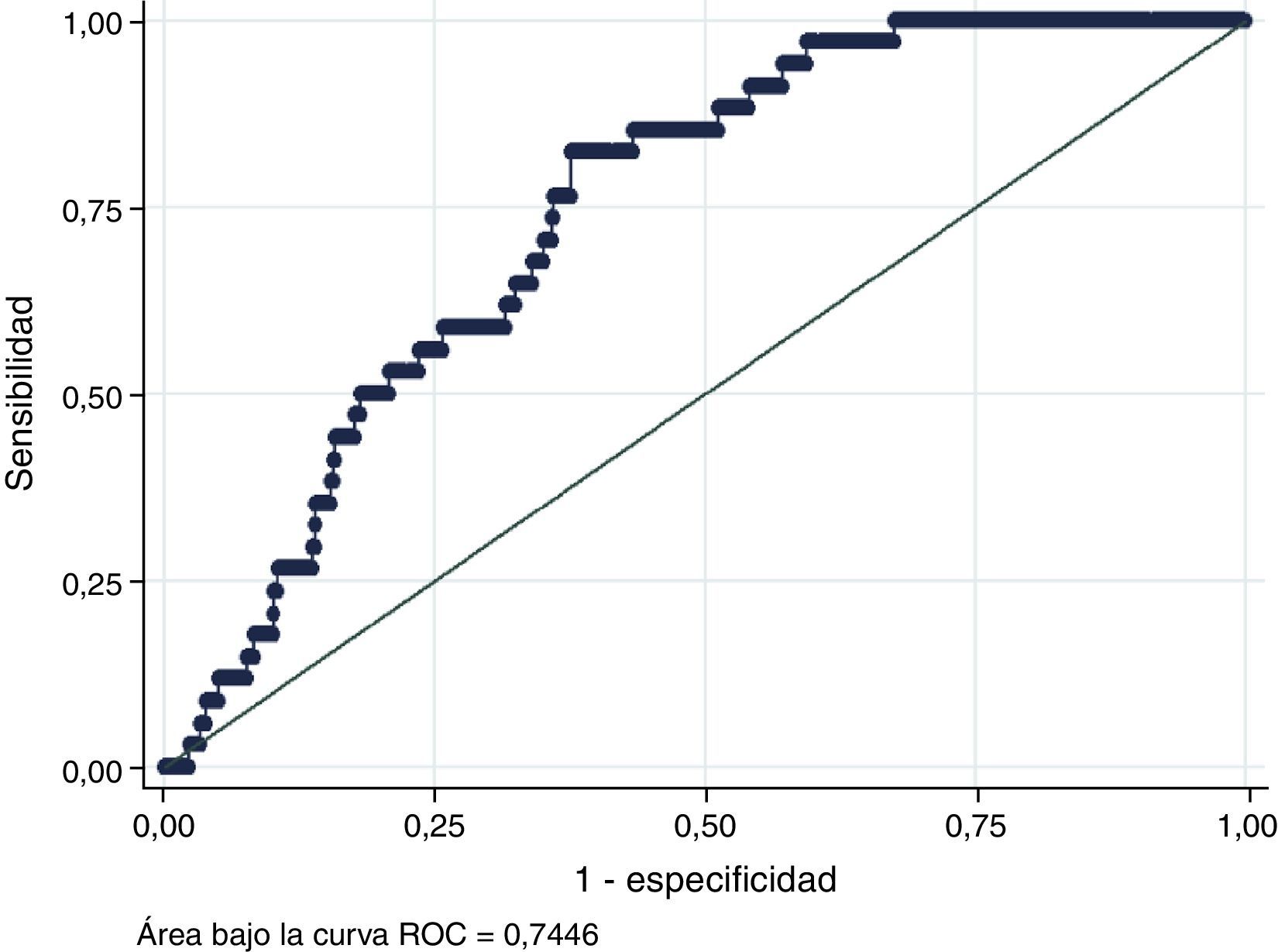
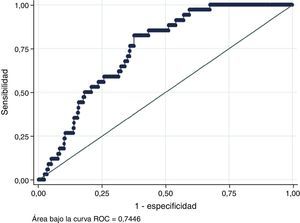
Al evaluar la capacidad de discriminación del modelo de PROCAM ajustado por el sexo se evidenció una mejoría significativa respecto al modelo aplicado solo a hombres. En este caso encontró un área bajo la curva de 0,7446 (IC 95%: 0,71422 - 0,77403), similar a la que se observó en la población en la que se desarrolló, cumpliendo la condición definida a priori para el análisis (AUC > 0,7) (fig. 7).

Figura 7.

Discriminación del modelo de PROCAM para hombres y mujeres ajustado. Curva de características operativas del receptor.

Análisis de sensibilidad

Dada la importante cantidad de pacientes de quienes no se conocía el desenlace (16,5%), se decidió realizar un análisis de sensibilidad para evaluar el impacto de esa pérdida de información en los resultados obtenidos.

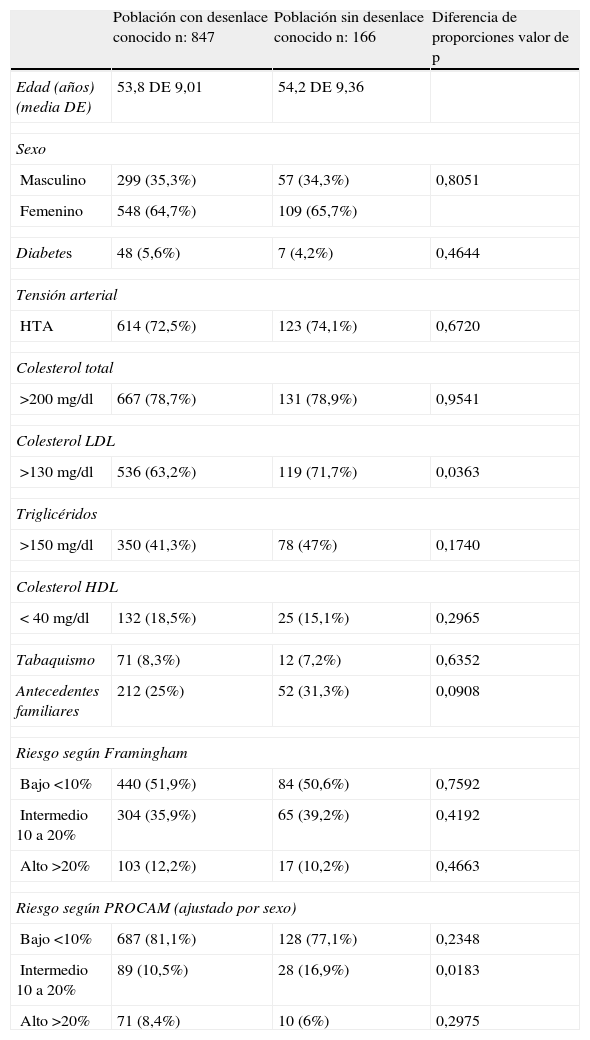
La tabla 7 muestra que la población en la que no se obtuvieron desenlaces es en general muy similar a la población con desenlaces conocidos. No se encontró diferencia clínica ni estadísticamente significativa en cuanto a las características demográficas y los factores de riesgo presentados; solo se observó una proporción discretamente mayor de pacientes con niveles por fuera de las metas de colesterol LDL en la población en la que no se disponía de datos de desenlace.

Tabla 7.

Características de las poblaciones con y sin desenlaces conocidos

	Población con desenlace conocido n: 847	Población sin desenlace conocido n: 166	Diferencia de proporciones valor de p
Edad (años)(media DE)	53,8 DE 9,01	54,2 DE 9,36
Sexo
Masculino	299 (35,3%)	57 (34,3%)	0,8051
Femenino	548 (64,7%)	109 (65,7%)
Diabetes	48 (5,6%)	7 (4,2%)	0,4644
Tensión arterial
HTA	614 (72,5%)	123 (74,1%)	0,6720
Colesterol total
>200 mg/dl	667 (78,7%)	131 (78,9%)	0,9541
Colesterol LDL
>130 mg/dl	536 (63,2%)	119 (71,7%)	0,0363
Triglicéridos
>150 mg/dl	350 (41,3%)	78 (47%)	0,1740
Colesterol HDL
< 40 mg/dl	132 (18,5%)	25 (15,1%)	0,2965
Tabaquismo	71 (8,3%)	12 (7,2%)	0,6352
Antecedentes familiares	212 (25%)	52 (31,3%)	0,0908
Riesgo según Framingham
Bajo <10%	440 (51,9%)	84 (50,6%)	0,7592
Intermedio 10 a 20%	304 (35,9%)	65 (39,2%)	0,4192
Alto >20%	103 (12,2%)	17 (10,2%)	0,4663
Riesgo según PROCAM (ajustado por sexo)
Bajo <10%	687 (81,1%)	128 (77,1%)	0,2348
Intermedio 10 a 20%	89 (10,5%)	28 (16,9%)	0,0183
Alto >20%	71 (8,4%)	10 (6%)	0,2975

De igual forma, no hubo diferencias significativas en la distribución de los pacientes en categorías de riesgo bajo, intermedio o alto según los modelos de Framingham y PROCAM ajustado por sexo, para cada una de esas poblaciones.

Discusión

Pocos tópicos han recibido tanta atención en la literatura médica durante los últimos cinco años como la estimación de riesgo cardiovascular²³. La utilización de escalas para determinar el riesgo, como los modelos de Framingham y PROCAM, entre otros, no solo permiten detectar pacientes de alto riesgo, sino guiar las recomendaciones de tratamiento. Las guías de manejo de la OMS²⁴ y de múltiples sociedades científicas^25–27 se basan actualmente en el riesgo absoluto que tiene cada paciente de presentar un evento coronario a diez años, para establecer acciones clínicas en aquellos individuos que tienen mayor probabilidad de ser beneficiados con las intervenciones tempranas. El fundamento de que esta aproximación médica sea costo-efectiva es de especial importancia en los países en vía de desarrollo, donde la carga de enfermedad de las afecciones cardiovasculares viene en franco aumento durante las últimas décadas²⁸.

La población objeto de estudio proviene de un sistema de salud con características de excepción, en razón a la naturaleza primordial de la actividad de sus miembros, en particular, personal activo o retirado de las fuerzas militares y sus beneficiarios, quienes son atendidos de forma permanente dentro de las instituciones de salud pertenecientes al sistema, con un plan de beneficios más amplio, lo que conlleva mínima movilidad hacia otros aseguradores de servicios de salud y en cierta forma provee largos periodos de seguimiento. Sin embargo, el comportamiento de su perfil epidemiológico no tiene diferencias significativas en las primeras causas de mortalidad y morbilidad identificadas por el Ministerio de la Protección Social²⁹ para Colombia, a excepción de otras patologías más relacionadas con la actividad específica, como los componentes de trauma de guerra y las enfermedades infecciosas propias de áreas del país en donde se realizan las operaciones militares.

Llama la atención que la población de estudio tiene una prevalencia relativamente baja de diabetes mellitus (5,4%) comparada con las poblaciones en las que se desarrollaron los modelos (entre 6 y 7%) o con el valor encontrado para la población de Bogotá (Colombia) en el estudio CARMELA, el cual informó un 8,1%³⁰ e incluso comparada con la frecuencia de esta enfermedad reportada por la OPS para la población colombiana (7%)²⁹. De igual forma es llamativa la menor prevalencia de tabaquismo (8,2%), comparada con la encontrada en los estudios en los que se desarrollaron los modelos (alrededor del 35%) y con la prevalencia reportada en otros estudios colombianos, la cual se sitúa alrededor del 15 al 18%³¹; por el contrario, es de destacar el alto predominio de dislipidemia, hipertensión y obesidad. La explicación para estos resultados puede fundamentarse en que se trata de una población involucrada en una clínica de prevención primaria. A pesar de ello dicha población tiene una adecuada representación de población de bajo riesgo, hecho que hace que las conclusiones del estudio sean aplicables a pacientes que asisten a clínicas de prevención primaria, que son finalmente en quienes realmente se utilizan las escalas en la práctica médica, y en general a la población colombiana.

El estudio evalúa las características operativas de las escalas más utilizadas para estimar el riesgo cardiovascular en Colombia. Pese a que se han desarrollado nuevos modelos predictivos de riesgo cardiovascular en los últimos años y en diferentes países del mundo, algunos que incluyen nuevos marcadores bioquímicos de riesgo (QRISK, Reynolds risk score –mujeres–, Reynolds risk score –hombres–, SCORE y otras calibraciones basadas en modelos tradicionales), en el estudio la intención fue validar los dos modelos más utilizados en nuestro medio: Framingham y PROCAM en una población definida perteneciente a una Clínica de Prevención Primaria y que por las condiciones propias de pertenecer a un sistema de salud especial podía garantizar cierta continuidad en el seguimiento a largo plazo.

Se halló que la capacidad del modelo de Framingham para separar los pacientes de bajo y alto riesgo (discriminación) es relativamente baja en nuestra población, similar a lo observado en poblaciones de Francia e Irlanda¹⁴ e inferior a la reportada en otras poblaciones de Europa¹⁶, China¹⁷ e incluso en una población argentina³² (valores entre 0,75 y 0,78), hallazgo posiblemente asociado a la baja cantidad de eventos encontrados en la población estudiada.

Al evaluar la calibración del modelo se definió que sobreevalúa el riesgo de presentar enfermedad coronaria global (muerte cardiovascular, infarto agudo de miocardio o angina inestable); sin embargo, esta sobrestimación es relativamente estrecha con una relación entre los eventos esperados y observados de 1,31, inferior a la observada en estudios realizados en China¹⁷ y en múltiples países europeos^14,16. Posiblemente la explicación esté dada por la disminución en la incidencia de enfermedad coronaria y las tasas de mortalidad en la población occidental desde 1980. El momento en que los pacientes se incluyeron en la cohorte (1985 a 1996) fue mucho más reciente al estudio de Framingham que se inició entre 1971 y 1972.

Así, pues, este constituye el primer estudio que evalúa la calibración del modelo de Framingham en una población suramericana basado en la comparación directa de los eventos esperados y observados en una cohorte seguida durante diez años. Una de las bondades de este estudio es el hecho de tratarse de la evaluación de una cohorte iniciada desde 1984 donde se hizo el registro sistemático, no automatizado, de una serie de factores de riesgo y variables clínicas y paraclínicas de pacientes incorporados en una clínica de prevención primaria, incluyendo la medición de factores no usuales para esa época, como el perfil lipídico completo. Así mismo, se recuperó la información después de una búsqueda exhaustiva y se generó la necesidad institucional de optimización de los registros históricos y hacia el futuro.

Los resultados demuestran que la sobrestimación del riesgo es mucho menor a la calculada en un estudio previo realizado en Chile el cual consideró la prevalencia local de factores de riesgo de ECV y la incidencia de acontecimientos coronarios para adaptar la función de Framingham, al no existir estudios poblacionales de cohorte para generar estimaciones de riesgo coronario local, con la conclusión de que el modelo sobreevaluaría en casi cuatro veces el riesgo cardiovascular³³.

Al evaluar el modelo de PROCAM ajustado por sexo, en la población de estudio se observaron muy buenas características operativas. La capacidad de discriminación de este modelo (AUC 0,74) resultó mejor que la encontrada en las demás poblaciones en que se ha validado¹⁴ y similar a la encontrada en la población en la que se desarrolló el modelo a pesar de la baja cantidad de eventos en población de estudio. De forma similar se halló una excelente calibración del modelo en poblaciones de riesgo bajo e intermedio, con una relación entre eventos esperados y observados de 1,07. Estas características operativas hacen del modelo de PROCAM ajustado por sexo, un mejor estimador de riesgo cardiovascular en nuestra población que el modelo de Framingham, más aún si se considera que el primero evalúa como desenlace enfermedad coronaria dura (muerte de origen coronario más infarto agudo del miocardio), que constituye una forma más confiable de medir el riesgo cardiovascular, ya que elimina el sesgo asociado a desenlaces blandos y menos repetibles como lo es la angina inestable.

La mayor limitación del estudio está dada por la baja cantidad de pacientes de alto riesgo que entraron a la cohorte, lo que imposibilita generalizar los resultados a esa población. Se requieren, por tanto, nuevos estudios en población colombiana y suramericana de alto riesgo para evaluar la validez de estos y otros modelos para predecir riesgo cardiovascular.

Adicionalmente, otra limitación del estudio es el alto porcentaje de pacientes con pérdidas al seguimiento (16,6%); no obstante, al evaluar la población en la que se conocieron los desenlaces y al compararla con la población en la que se perdió el seguimiento se encontraron similitudes en cuanto a los factores de riesgo y la estimación global de riesgo cardiovascular, lo que sugiere que estas pérdidas no indujeron un sesgo relevante en los resultados.

Conclusiones

Los resultados de la validación sugieren que la escala de Framingham debería usarse con precaución en población colombiana de riesgo bajo e intermedio sin historia previa de ECV, en razón a que sobrestimó el riesgo y demostró una baja capacidad de discriminación. La utilización de las ecuaciones de PROCAM ajustada por sexo mostró ser una mejor opción para estimar el riesgo de enfermedad cardiovascular dura en la población de estudio, por lo cual debería aplicarse en la población colombiana.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.