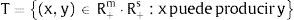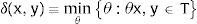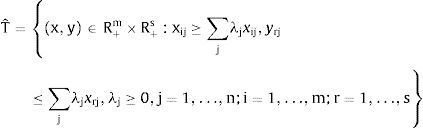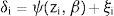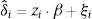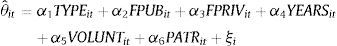El papel que las fundaciones desempeñan actualmente en la sociedad justifica el análisis de su eficiencia, resultando imprescindible conocer si los recursos de los que disponen son convenientemente destinados a su finalidad. En este sentido, el trabajo que presentamos propone un enfoque actual y sin precedentes para el análisis de los determinantes de la eficiencia de las fundaciones de España durante el período 2008-2010.
Método y datosNuestro análisis se basa en la elección de aquellos factores exógenos que resumen y describen de una forma óptima la situación de estas organizaciones, así como en la elección de la metodología de la técnica no paramétrica DEA y, más concretamente, el procedimiento bietápico de doble bootstrap de Simar y Wilson.
Como inputs discrecionales se proponen la dotación fundacional, el total de activos, el total de gastos y el número de empleados. Los outputs considerados son el nivel de los ingresos obtenidos y el número de usuarios atendidos.
ResultadosLos resultados del modelo indican una ineficiencia técnica pura (supuesto CRS) del 27,7%. Relajando la hipótesis CRS por la VRS, la ineficiencia en el empleo de los inputs alcanza el 31,92%. Adicionalmente, y utilizando el procedimiento bootstrap de Simar y Wilson, se obtiene una ineficiencia técnica del 28,70%.
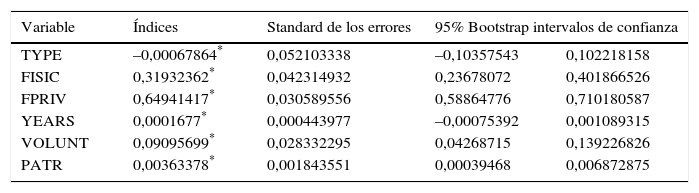
ConclusionesEl análisis DEA de dos etapas revela que las fundaciones más eficientes se caracterizan por su naturaleza privada. Así mismo, las fundaciones con mayor antigüedad, las que cuentan con voluntarios entre sus colaboradores y las que poseen un número amplio de patronos son igualmente más eficientes.
The role that foundations play in society today justifies the analysis of their efficiency, resulting essential to know if the resources available are conveniently designed for their purpose. In this sense, the work presented proposes an unprecedented and current approach for the analysis of the determinants of the efficiency of the Spanish foundations during the 2008-2010 period.
Method and dataOur analysis is based on the choice of exogenous factors that summarize and describe in an optimal way the situation of these organizations, as well as the choice of the nonparametric technique DEA, and more specifically, the nonparametric double bootstrap Simar and Wilson model based on a truncated-regression to estimate the effect of a group of relevant factors.
As inputs, total assets, total expenditure and the number of employees are proposed. The outputs considered are the level of income obtained and the number of users that were attended.
ResultsThe model results indicate a pure technical inefficiency (CRS assumption) of 27.7%. Relaxing the CRS hypothesis by the VRS, the inefficient use of inputs reaches 31.92%. Additionally, and using the bootstrap procedure Simar and Wilson, a technical inefficiency of 28.70% is obtained.
ConclusionsThe two-stage DEA analysis reveals that the most efficient foundations are characterized by their private nature. Likewise, the longest-serving foundations, those that have volunteers among their employees and those with a large number of patrons, are also more efficient.
En la sociedad se generan una serie de demandas que ni el sector público ni el sector privado atienden, ya sea por razones económicas o por falta de capacidad de gestión. Las fundaciones, junto a otras instituciones del tercer sector, desarrollan un importante papel en este sentido, dando respuesta a ciertas necesidades sociales y proporcionando por tanto un ahorro al sector público. Adicionalmente, teniendo en cuenta un contexto como el actual y el papel que las fundaciones ocupan en la sociedad, se justifica el análisis de su eficiencia, resultando imprescindible conocer si los recursos disponibles son convenientemente destinados a su finalidad. De acuerdo con Dorta y León (2008), la información económico-financiera y la divulgación de la misma tiene un papel legitimador ante la sociedad para las fundaciones, junto al impacto social y económico que estas producen. Por tanto, la medida del rendimiento de una fundación mediante la determinación de si la aplicación de sus recursos económicos es la adecuada para conseguir su objetivo productivo resulta más que necesaria. Asimismo, puede resultar de gran utilidad determinar cuáles son los factores que contribuyen favorablemente a la eficiencia en este tipo de organizaciones.
En el ámbito internacional se están produciendo importantes avances en la medición del impacto conseguido por las actividades realizadas desde las entidades sin fines lucrativos (ESFL). Con el objetivo de que tanto financiadores como beneficiarios puedan ser conscientes de dichos resultados, se han realizado investigaciones en múltiples organizaciones para desarrollar enfoques comunes de análisis de resultados y medición del impacto, como por ejemplo Kramer, Parkhurst y Vaidyanathan (2009), con el propósito de cambiar la visión y eficiencia en el sector de las ESFL. También se pueden encontrar en la literatura amplios debates sobre los conceptos y la medición de la eficiencia y la eficacia en las ESFL, así como importantes iniciativas que pretenden guiar a estas entidades en las prácticas más habituales con las que los propios financiadores miden los impactos y retornos producidos por los fondos aportados.
En el ámbito nacional, la Asociación Española de Contabilidad y Administración de Empresas (AECA, 2010) indica que la información económico-financiera de las ESFL debe permitir a sus usuarios apreciar la eficacia y la eficiencia en la gestión de la entidad, definiendo ambos términos como la culminación de proyectos y programas en función de las fuentes de financiación obtenidas, quedando por tanto latente la importancia que la eficiencia tiene para estas entidades.
Las fundaciones españolas hacen pública su información económico-financiera mediante un modelo contable muy cercano, en líneas generales, al utilizado en el mundo empresarial, a excepción del plan de actuación, con el que se incrementa el nivel de exigencia para estas organizaciones y las deja más cerca, si cabe, de las administraciones públicas y del control de gestión. La adaptación sectorial del Plan General de Contabilidad español a las ESFL se compone de dos partes perfectamente diferenciadas: en el anexoi se encuentran las normas contables propias para las ESFL, y en el anexoii se contiene el modelo para el plan de actuación.
La información básica que contiene este plan de actuación consiste en una descripción de las actividades a realizar, una cuantificación de los recursos humanos a emplear, el número de beneficiarios esperados, los objetivos y los indicadores, el detalle de gastos previstos (recursos económicos a emplear) y los ingresos previstos (recursos económicos a obtener). Esta información, junto con la contenida en el apartado correspondiente a la actividad de la entidad, aporta cuantificación de determinadas variables que abren grandes posibilidades en el ámbito de las medidas de eficiencia en las fundaciones españolas.
Partiendo de las reflexiones anteriores, en este estudio se pretende evaluar el nivel de eficiencia de las fundaciones españolas en el periodo 2008-2010, así como la identificación de un grupo de determinantes de la misma seleccionado siguiendo la literatura.
El periodo objeto de estudio coincide con los años de mayor intensidad de la crisis en España, a la que no han resultado ajenas las propias fundaciones y cuyas consecuencias comienzan a ser visibles en 2012. Así, según Rubio, Sosvilla y Méndez (2014), se estima que hasta 2012 desaparecieron en torno a 1.000 fundaciones con algún tipo de actividad, lo que significa que han desaparecido más de un 10% del universo fundacional en España. Los autores atribuyen tal reducción a dos hechos significativos: el proceso de consolidación de las administraciones públicas, que provocó una extinción o reagrupación de fundaciones públicas y, en segundo lugar, el impacto directo de la crisis en el sector fundacional.
Las fundaciones españolas se han visto obligadas en los últimos años a atender un mayor número de beneficiarios con menores recursos tanto públicos como privados. Así, el número de beneficiarios directos netos de las fundaciones españolas ha aumentado en un 60%, pasando de 17,8 millones en 2008 a 28,62 millones en 2010, lo que indica la relevancia de su impacto social y el esfuerzo realizado durante el periodo objeto de estudio. Sin embargo, en 2012 el número de beneficiarios comienza a decaer, vislumbrándose el agotamiento del sector fundacional. Sin embargo, esta tendencia no se muestra para los ingresos en la misma proporción (Rubio et al., 2014).
El escenario descrito, junto al papel crítico que las fundaciones juegan en la sociedad, motivan la necesidad y la importancia de una gestión óptima para alcanzar sus objetivos, o incluso para mantener su propia viabilidad, lo que refuerza el interés del presente estudio sobre la eficiencia de este tipo de organizaciones así como del análisis de determinantes de la misma.
Este trabajo se ha estructurado en 4 secciones principales. En la siguiente sección se desarrolla el estado actual de la literatura sobre eficiencia en las fundaciones. La tercera sección continúa con el estudio empírico dirigido al análisis de la eficiencia de las fundaciones mediante la técnica DEA y la determinación de la significatividad de cierto grupo de factores explicativos de la misma. El trabajo concluye con la sección dedicada a conclusiones.
Análisis de la eficiencia en las fundaciones. Revisión de la literaturaAl contrario que el sector empresarial, el sector no lucrativo cuenta con escasos estudios que centren su atención en el análisis de la eficiencia: Callen, Klein y Tinkelman (2003); Herranz (2005); González y Cañadas (2005); Steingrüber y Larsson (2006) o Kramer et al. (2009), entre otros. Esta situación puede estar motivada por la falta de datos disponibles y por las propias características del sector, en el que la medición del desempeño a través del resultado económico carece de sentido por su carácter no lucrativo. Este escenario pone de relieve la necesidad de estudios que faciliten métodos alternativos orientados hacia la medición y el análisis de la eficiencia.
Adicionalmente, son todavía más inusuales los estudios empíricos que apliquen la metodología DEA al análisis de la eficiencia de ESFL, destacando los trabajos de Fuentelsaz, Marcuello y Urbina (1998), García-Cebrián y Marcuello (2007), Golden, Brockett, Betak, Smith y Cooper (2012) y Guzmán, Hurtado y Ramos (2013). Si observamos únicamente los estudios sobre eficiencia exclusivos para fundaciones, la escasez es todavía mayor. A este respecto se ha de mencionar que en González y Rúa (2007), Rey (2007) y De Andrés, Azofra y Romero (2009) se realiza un análisis de la eficiencia en la gestión de las fundaciones centrándose fundamentalmente en el uso de indicadores.
Más concretamente, González y Rúa (2007) elaboran un estudio empírico utilizando información contable externa, balance y cuenta de resultados de fundaciones culturales y docentes aplicando la metodología de datos de panel. Los resultados obtenidos no presentan la suficiente significación estadística, concluyendo la necesidad de utilizar indicadores de gestión —cuantitativos— y sociales —es decir, información extracontable—. Asimismo, ponen de manifiesto que los ingresos lucrativos ayudan a mejorar la eficiencia de las fundaciones, ya que, al prescindir de ellos, la gestión se vuelve menos eficiente o más volátil su resultado. Además, si la entidad obtiene un excedente positivo y no lo destina en el ejercicio siguiente a inversiones de su actividad, tanto dicho excedente como los incrementos en dotación y pasivo fijo son destinados a activos financieros, por lo que proponen al legislador limitar el volumen de inversiones financieras de estas entidades, evitando así que puedan convertirse en gestoras de fondos «encubiertas».
En Rey (2007) se realiza un análisis del debate que se mantiene desde hace bastantes años en foros profesionales y académicos sobre la conveniencia de medir el desempeño organizativo y el impacto social de las fundaciones y las fórmulas alternativas para conseguirlo. Para ello, el autor recopila y analiza desde una perspectiva teórica un amplio repertorio de alternativas evaluadoras para las fundaciones, poniendo finalmente de manifiesto que no se ha llegado a ninguna metodología y práctica de gestión sistemática para la mayor parte de estas organizaciones.
Finalmente De Andrés et al. (2009) realizan un estudio empírico bajo el modelo Tobit, con una muestra de fundaciones españolas, al objeto de identificar aquellas características de la composición del patronato de una fundación determinantes para su nivel de eficiencia. Los autores concluyen que son similares en la mayoría de aspectos a las del consejo de administración de las organizaciones mercantiles.
Si nos centramos exclusivamente en la metodología DEA, hasta la fecha de redacción de este artículo (octubre de 2016) solo hemos encontrado publicados dos estudios sobre la eficiencia de las fundaciones españolas, desarrollados por los mismos autores y centrados en las fundaciones de tipo asistencial: Martínez y Guzmán (2010, 2014). En el primer estudio se realiza un análisis de eficiencia y productividad de las fundaciones de tipo asistencial con domicilio social en la Región de Murcia para el periodo 2000-2004. Para ello aplican un modelo DEA básico de tipo radial, el conocido como modelo CCR de orientación input, así como los índices de productividad total de Malmquist según la propuesta de Färe, Grosskopf, Norris y Zhang (1994).
Posteriormente, en el trabajo del año 2014 los autores evalúan de nuevo el rendimiento para las fundaciones de tipo asistencial, pero de ámbito estatal, para el período 2008-2009. Como principal novedad analizan mediante una regresión la posible asociación de la eficiencia alcanzada con covariables tales como tamaño, liquidez, endeudamiento y antigüedad. Como principal limitación se señala el reducido espacio temporal examinado así como la limitación de la propia muestra, por lo que los resultados obtenidos requieren ser validados en pro de su representatividad para el sector fundacional en su conjunto.
Metodológicamente, por tanto, ninguno de los trabajos precedentes ha aplicado una propuesta análoga a la del presente trabajo. El carácter determinista de los modelos DEA de tipo radial plantea diversos problemas, como, por ejemplo, un sesgo inherente en los coeficientes de eficiencia estimados. Por otro lado, el análisis de determinantes de eficiencia resulta también crucial para la inclusión de variables no discrecionales que pueden afectar a la eficiencia de cierta fundación. En consecuencia, consideramos de gran interés seguir abriendo camino en la línea de investigación relativa al estudio de la eficiencia de las fundaciones en su conjunto, y sus determinantes, mediante el uso de la metodología DEA, constituyendo nuestro trabajo un avance más en este sentido.
Estudio empíricoMuestras y variablesSon escasas las fuentes directas de información sobre fundaciones en España, y la mayoría consisten en estudios de carácter puntual, lo que dificulta el seguimiento del sector. Sin embargo, en los últimos años se aprecia un mayor interés por mejorar las fuentes de información del sector no lucrativo en general. Así, a título de ejemplo, podemos citar los grupos de trabajo de la Comisión de Entidades Sin Fines Lucrativos (ESFL) de la Asociación Española de Contabilidad y Administración de Empresas (AECA), el Grupo de Estudios Sociales y Económicos del Tercer Sector GESES), el Instituto de Innovación Social de ESADE y el Instituto de Análisis Estratégico de Fundaciones (INAEF).
En la actualidad resulta inviable recurrir a información pública centralizada sobre el sector fundacional en España, ya que debido a la estructura que hasta hace bien poco han tenido los registros de fundaciones, la información se encontraba dispersa por toda la geografía nacional y no existía ningún sistema mediante el cual se centralizase la información pública y fuese fácilmente accesible. Es por ello que resulta muy complejo poder agregar esta información.
No obstante, interesa destacar la reciente aprobación de la entrada en funcionamiento del protectorado único de fundaciones de competencia estatal, y la puesta en marcha del registro único también para fundaciones de competencia estatal, previsto por la Ley 50/2002, que ha entrado en funcionamiento a finales de 2015. Se da respuesta así a una de las principales demandas del propio sector fundacional. De acuerdo con Benito-López e Ibáñez-Carpena (2013), entre otras ventajas podría contribuir a la producción de información agregada del sector fundacional, ayudando a incrementar el conocimiento del sector fundacional y a mejorar su difusión y utilidad, si bien es cierto que con esta medida tan solo se consigue centralizar parte de la información (alrededor de un tercio de fundaciones activas, según Rubio et al., 2014).
Ante la ausencia de información pública centralizada, las estadísticas e informaciones más representativas y actuales, en estos momentos, se elaboran por el INAEF, perteneciente a la Asociación Española de Fundaciones (AEF), que recopila y posee la mayor base de datos sobre fundaciones con información para cada una de las registradas, tal como año de constitución, patronato, actividades, información económico-financiera, número de usuarios, etc. Partiendo de dichos datos, el último estudio publicado relativo a los atributos fundamentales del sector fundacional en España abarca el periodo 2008-2012 (Rubio et al., 2014).
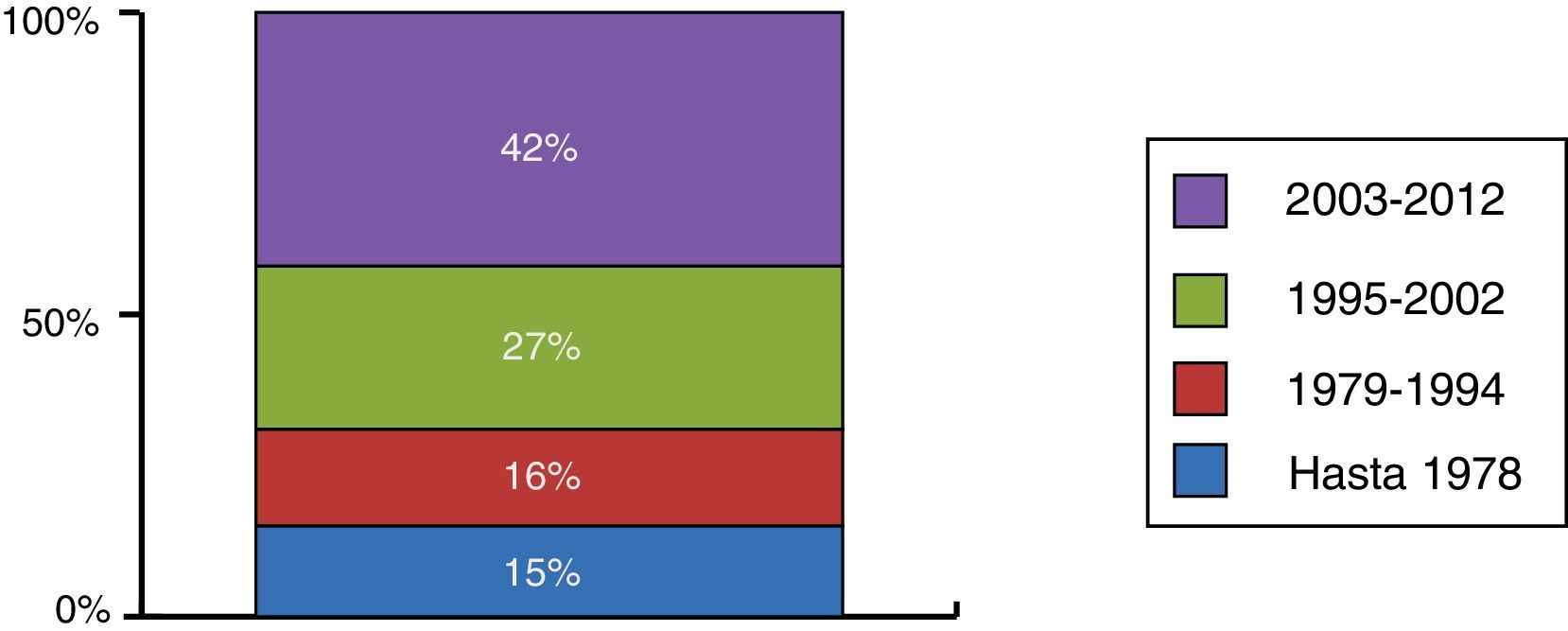
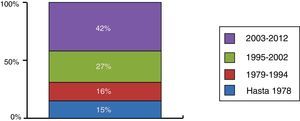
El sector de las fundaciones españolas lo componen más de 13.000 fundaciones registradas y no extinguidas, de las que se clasifican activas en el mencionado periodo 2008-2012 una media de 9.500 fundaciones. De ellas, el 69,3% tenían en el año 2012 una antigüedad inferior a 18años, tal y como se deduce de la figura 1, es decir, se habían constituido con posterioridad a la primera Ley de Fundaciones del año 1994.
Antigüedad de las fundaciones españolas (porcentaje de fundaciones).
Fuente: Rubio et al. (2014).
En cuanto al nivel de ingresos que presentan, casi 2 de cada 3 fundaciones son de reducido tamaño, con ingresos inferiores a 500.000euros. Las que superan los 2.400.000 euros de ingresos se sitúan en torno al 12% del total, y las que cuentan con ingresos por encima de 10 millones de euros oscilan en torno al 3%. Entre los fundadores personas jurídicas, la tipología más habitual consiste en las de carácter privado (65% del total).
El impacto social de las fundaciones está cifrado por la magnitud agregada de los beneficiarios directos de sus servicios y actividades, que en 2012 se han cuantificado en casi 30millones de usuarios, según Rubio et al. (2014).
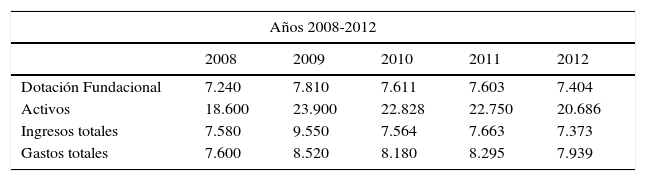
Desde la perspectiva del empleo directo que se genera, encontramos que el sector fundacional supuso en 2012 el 1,14% del empleo total generado en la economía española, suponiendo más de 200.000 empleos directos. Los empleos generados junto a los principales datos económicos agregados de las fundaciones activas nos pueden dar una idea de su impacto económico (tabla 1).
Datos económicos agregados del sector fundacional (millones de euros)
| Años 2008-2012 | |||||
|---|---|---|---|---|---|
| 2008 | 2009 | 2010 | 2011 | 2012 | |
| Dotación Fundacional | 7.240 | 7.810 | 7.611 | 7.603 | 7.404 |
| Activos | 18.600 | 23.900 | 22.828 | 22.750 | 20.686 |
| Ingresos totales | 7.580 | 9.550 | 7.564 | 7.663 | 7.373 |
| Gastos totales | 7.600 | 8.520 | 8.180 | 8.295 | 7.939 |
Fuente: Rubio et al. (2014)
La obtención de datos para la realización de nuestro estudio empírico ha sido posible gracias a la colaboración de la AEF, que facilitó la información disponible en sus bases de datos para los ejercicios 2008, 2009 y 2010, compuesta por una población de 13.962 fundaciones. Dicha información proviene tanto de las cuentas anuales como del plan de actuación. La fase de recopilación resultó compleja y dilatada; algunas fundaciones facilitaron la información a la AEF mediante el uso de formularios web; en otros casos los datos fueron completados por la propia AEF con la información aportada desde los diferentes registros nacionales y autonómicos. En cualquier caso, resulta importante aclarar que la información tratada corresponde a datos efectivamente realizados por cada una de las fundaciones, y no los previstos.
Se procedió a depurar dicha información, en primer lugar seleccionando los siguientes registros por cada una de las fundaciones y año: fecha de constitución, voluntariado, número de patronos, número de patronos por razón del cargo, dotación fundacional, total de activo, total de gastos, número de empleados, remuneración de los asalariados, número de beneficiarios, total de ingresos, y excedente. A continuación se descartaron aquellas fundaciones de las que no se disponía de alguno de los citados datos para los tres ejercicios objeto de estudio, resultando finalmente y de forma sorprendente, por lo reducido del número, un total de 98 fundaciones.
Una de las dificultades más importantes a la hora de desarrollar este tipo de estudios consiste en la determinación y cuantificación de los inputs y outputs. A este respecto, uno de los criterios que se tuvieron en cuenta para la selección, además de su idoneidad, consistió en el hecho de que se tratase de variables cuya información fuera pública mediante las cuentas anuales y el plan de actuación que presentan las fundaciones, al objeto de facilitar su cuantificación y las posibilidades de acceso para futuros estudios.
Se optó por considerar como input la dotación fundacional, que tiene como cometido aportar viabilidad económica a un determinado proyecto de interés general. Los fundadores renuncian totalmente al patrimonio que aportan a la fundación para que contribuya a la realización de actividades de interés general, frente al llamado capital propiedad de las sociedades mercantiles, cuyo propósito consiste en preservar las aportaciones y obtener una rentabilidad adicional mediante dividendos. Por tanto, la dotación fundacional se diferencia del capital de las entidades mercantiles principalmente en la ausencia de títulos de propiedad-control que puedan ser enajenados, cedidos o intercambiados, o de los que se espera algún tipo de contraprestación económica en el caso de que la entidad cesara en sus actividades y fuese objeto de liquidación.
Igualmente, se consideró indispensable incluir como input el activo, que actúa de soporte para la generación futura en la producción de rentas e ingresos que aseguran el cumplimiento de los fines fundacionales. Por lo que respecta a los gastos, resulta innegable que son un input básico para el desarrollo de los diferentes proyectos de cualquier entidad. A pesar de que es una variable habitualmente utilizada, nos encontramos con el inconveniente de que las fundaciones no tengan una valoración real y total de la misma en la cuenta de resultados. Como ejemplo cabe mencionar los trabajos prestados por los voluntarios.
También se ha incluido como input el número de empleados. Dado que la gran mayoría de fundaciones pertenecen al sector servicios, los recursos humanos se presentan como un input básico para el sector. A este respecto, y de acuerdo con Herranz (2005), se ha considerado el número de empleados y no el gasto de personal; con ello, además de eliminar el sesgo causado por la estructura salarial de cada fundación, se trata el factor desde un punto de vista técnico o de productividad, y no desde un punto de vista económico.
Por el lado de los outputs, el número de beneficiarios finales de los servicios de las fundaciones es uno de los indicadores clave del impacto social del sector, hasta el punto de que la ley de fundaciones exige la publicación del número de beneficiarios de las diferentes actuaciones en la correspondiente memoria anual, constituyendo un indicador crítico para evaluar la evolución y mejora continua de sus actividades.
Se incluyen también como output los ingresos, una variable habitual en los estudios de eficiencia; de forma análoga a lo mencionado para los gastos, nos encontramos con el inconveniente de que las fundaciones pueden no tener su valoración real, puesto que en ocasiones no perciben contraprestación económica por su actividad. En Martínez y Guzmán (2014) dicha variable se introduce como input porque estos autores determinan el número de servicios que se pueden prestar. Sin embargo, en nuestro trabajo se contempla como output en coherencia con el tratamiento dado por el plan de actuación. Efectivamente, en dicho plan los gastos se recogen como los recursos a aplicar y los ingresos como los recursos a obtener, es decir, la consecuencia de los recursos aplicados serán los recursos obtenidos o ingresos; por tanto, se han considerado los gastos como un input y los ingresos como un output. Esta orientación de los ingresos responde a la forma tradicional de medir la eficiencia mediante la proporción de producción obtenida sobre los costes empleados, orientación empleada por otros autores en estudios de fundaciones (González y Rúa, 2007; Benito-López e Ibáñez-Carpena, 2013). Ambos outputs —ingresos y número de usuarios— evidencian pros y contras, pero al tratarlos conjuntamente se complementan y aumentan la probabilidad de que la medida de eficiencia ofrezca resultados más objetivos.
Se han descartado dos variables incluidas en la muestra seleccionada. No se ha considerado la remuneración de los asalariados como input, ya que, como se ha expuesto, introduce el sesgo de la estructura salarial de cada fundación. Igualmente se ha excluido el excedente debido a que medir el desempeño de las fundaciones a través del resultado económico de su cuenta de resultados, como sucede en el sector empresarial, no es la forma más adecuada: el objetivo no es la maximización del beneficio sino acometer fines de interés general. Así, en ICAC (2002), el libro Blanco de la Contabilidad indica que la finalidad más importante que debe atender la contabilidad de este tipo de entidades no consiste en cuantificar el resultado económico obtenido, por ser este ajeno a su finalidad, sino reflejar la financiación conseguida en un periodo económico y el empleo que se ha realizado de la misma en la consecución de sus finalidades programadas, así como reflejar que la entidad se encuentra en condiciones de responder de todos los compromisos que haya asumido, bien sean estos de carácter económico o de carácter social.
Tras el análisis de las diferentes ventajas e inconvenientes que presentan las variables relacionadas y partiendo de la información disponible en las cuentas anuales y en el plan de actuación de una fundación, así como de estudios anteriores sobre eficiencia en fundaciones, procedemos a enumerar los inputs y outputs que hemos considerado más adecuados entre las diferentes variables disponibles para la muestra seleccionada.
Inputs:
Dotación = Dotación fundacional.
Activo = Total de active.
Gasto = Total de gasto.
Empleados = Número de empleados.
Outputs:
Beneficiarios = Número de beneficiarios o destinatarios directos atendidos.
Ingresos = Total de ingresos.
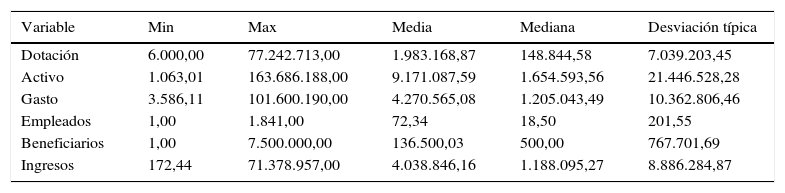
La tabla 2 proporciona algunos estadísticos descriptivos de las variables inputs y outputs empleadas en el análisis del periodo 2008-2010, con el fin de conocer el comportamiento de las diferentes variables dentro de la muestra.
Estadísticos descriptivos inputs-output 2008-2010
| Variable | Min | Max | Media | Mediana | Desviación típica |
|---|---|---|---|---|---|
| Dotación | 6.000,00 | 77.242.713,00 | 1.983.168,87 | 148.844,58 | 7.039.203,45 |
| Activo | 1.063,01 | 163.686.188,00 | 9.171.087,59 | 1.654.593,56 | 21.446.528,28 |
| Gasto | 3.586,11 | 101.600.190,00 | 4.270.565,08 | 1.205.043,49 | 10.362.806,46 |
| Empleados | 1,00 | 1.841,00 | 72,34 | 18,50 | 201,55 |
| Beneficiarios | 1,00 | 7.500.000,00 | 136.500,03 | 500,00 | 767.701,69 |
| Ingresos | 172,44 | 71.378.957,00 | 4.038.846,16 | 1.188.095,27 | 8.886.284,87 |
Fuente: elaboración propia
Los valores de la columna desviación típica indican que los datos están distribuidos en un rango amplio, evidenciando la enorme heterogeneidad que presentan entre sí las unidades que conforman este estudio empírico, en consonancia con la realidad del sector fundacional.
MetodologíaLa elección de la técnica no paramétrica DEA como metodología para el análisis de eficiencia de las fundaciones españolas es especialmente adecuada y utilizada para el estudio de organizaciones cuyo objetivo no es la maximización del beneficio, lo que permite la evaluación de la eficiencia con diferentes inputs y outputs, tanto cuantitativos como cualitativos. En efecto, se trata de uno de los métodos más populares para estimar la eficiencia. Su objetivo es definir una frontera, obtenida a partir de los datos, y representada por las unidades de decisión (decision making units [DMU]) que muestran una mejor práctica observada. Las DMU que no se encuentran en dicha frontera son consideradas ineficientes. La gran virtud inicial de este enfoque estriba en la no imposición de hipótesis restrictivas sobre el proceso generador de datos. En consecuencia, desde las definiciones iniciales de Debreu (1951), Shephard (1953, 1970) y Farrell (1957), una buena parte de la literatura ha seguido esta ruta basada en el empleo de técnicas de programación lineal para obtener estimadores de la eficiencia, principalmente a partir de la propuesta DEA.
Supongamos un grupo de n DMU, DMUj, j = 1,2,…,n, para las que consideramos un conjunto común de m inputs, xiji=1i=m, y s outputs, yrjr=1r=s. El conjunto de posibilidades de producción, T, y el conjunto de todos los posibles vectores de input y de output, se define como sigue:
El índice DEA se puede calcular bajo varias orientaciones. Los trabajos precedentes sobre fundaciones ya referidos anteriormente que han utilizado la técnica DEA, como Martínez y Guzmán (2010, 2014), asumen que las fundaciones persiguen minimizar sus inputs dados los outputs. Al igual que en estos trabajos precedentes, asumiremos una orientación hacia la minimización input.
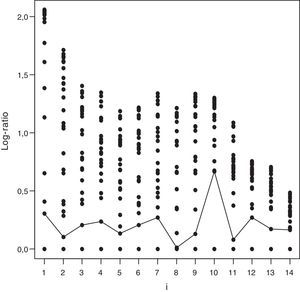
La medida de eficiencia técnica, llamada Debreu-Farrell, se define como:
Para δ(x,y) = 1, la DMU es eficiente, e ineficiente cuando δ(x,y)<, asumimos que la caracterización tecnológica sigue las condiciones1 de regularidad, pero la verdadera tecnología es desconocida, por lo que tenemos que estimar las medidas de ineficiencia a partir de los datos observados. Concretamente, la estimación DEA de T para la hipótesis de rendimientos constantes a escala (CRS) se define como2:
Los λj son las variables de intensidad sobre las que se lleva a cabo la optimización (2), y Tˆ es el cono convexo de libre disposición más pequeño en el espacio (x, y). Sustituyendo T con Tˆ, las estimaciones de los índices de eficiencia, δˆ (x, y), son consistentes para los verdaderos índices de eficiencia, δ(x, y).
Los modelos DEA básicos, como los desarrollados por Charnes, Cooper y Rhodes (1978) y Banker, Charnes y Cooper (1984), fueron etiquetados como deterministas y la metodología se ha aplicado ampliamente en la evaluación de la eficiencia de las unidades productivas; una colección de estas aplicaciones se puede encontrar en Seiford (1996), Tavares (2002), Emrouznejad, Parker y Tavares (2008) o Cook y Seiford (2009).
Este carácter inicialmente no paramétrico de la metodología presentaba algunos inconvenientes; en especial, la imposibilidad de realizar inferencia estadística. No obstante, las propiedades estadísticas de los estimadores DEA comenzaron a analizarse mediante el empleo de resultados asintóticos (Kneip, Park y Simar, 1998; Park, Simar y Weiner, 2000; Kneip, Simar y Wilson, 2008), o mediante el procedimiento bootstrap (Simar y Wilson, 1998, 1999, 2000, 2004, 2007, 2011a, 2011b, 2015).
En resumen, los estimadores no paramétricos presentaban el denominado problema de la dimensionalidad3, siendo además sesgados. Abordar la incertidumbre en los datos implicaba seguir una nueva rama de la literatura que permitiera estimar desviaciones estándar y obtener intervalos de confianza. El trabajo de Simar y Wilson (1998) fue el primero en introducir el procedimiento bootstrap, propuesto inicialmente por Efron (1979), para llevar a cabo inferencia estadística; proporcionaba una estimación del sesgo así como la varianza y, a partir de ahí, intervalos de confianza. Más tarde, el procedimiento se hizo más flexible en Simar y Wilson (2000), y en Wilson (2008) el algoritmo fue computacionalmente implementado mediante el software estadístico FEAR.
Las peculiaridades del proceso de producción, o las condiciones económicas, pueden ser responsables de parte de la ineficiencia detectada. Resulta así crucial introducir en escena el papel de variables exógenas, también llamadas ambientales, que aunque quedan fuera del control de las unidades evaluadas pueden afectar a su eficiencia. Las causas de la ineficiencia se analizan, por tanto, teniendo en cuenta un conjunto de factores externos que caractericen adecuadamente el entorno objetivo.
Para medir el impacto de las variables ambientales en la eficiencia se han desarrollado en la literatura diversos procedimientos, ampliamente presentados y descritos en el reciente artículo de Simar y Wilson (2015). Basándonos en este trabajo seguiremos el procedimiento bietápico según la propuesta de Simar y Wilson (2007), que supuso un punto de inflexión en el tratamiento de los factores exógenos, y del que los autores ofrecen una discusión actualizada en Simar y Wilson (2011b). En la primera etapa se estima la eficiencia técnica mediante el DEA, y en una segunda etapa las estimaciones resultantes se regresan sobre las variables ambientales4. El objetivo de esta segunda etapa es descubrir los factores que afectan significativamente a la eficiencia; se trata de la etapa más polémica de este tipo de procedimientos, y se han probado varias técnicas econométricas.
En Simar y Wilson (2011b, 2015) los autores aclaran algunos aspectos críticos de un área de investigación en la que muchos estudios han seguido en ocasiones un curso errático y confuso. Concretamente señalan que dentro de las asunciones del modelo, la regresión Tobit constituye una mala especificación.
De acuerdo con Simar y Wilson (2007), los coeficientes de eficiencia para cada DMU se obtienen en una primera fase a partir de la consideración de las variables discrecionales. El modelo adopta la forma siguiente:
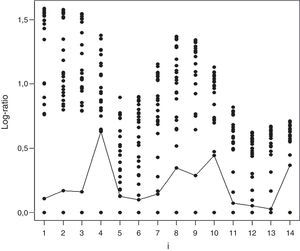
Se asume que δi es una función, ψ, de covariables ambientales, zi, que se espera que tengan influencia en la eficiencia de la DMUi, donde β denota un vector de parámetros, a estimar junto con una variable aleatoria distribuida de forma independiente, ξi, que representa la parte de la ineficiencia no explicada por zi5. Como en la práctica no es posible observar δi, Simar y Wilson (2007) proponen dos formas de abordar la situación. En la primera, las estimaciones DEA de la primera etapa, δˆi, reemplazan a los coeficientes no observados, δi en (4), con6 ψ(zi,β)= zi·β. Dado que las estimaciones de DEA son consistentes bajo los supuestos del modelo de Simar y Wilson (2007), la estimación de máxima verosimilitud de la siguiente regresión truncada produce estimaciones consistentes:
Sin embargo, como señalan Simar y Wilson (2011b, p. 209), aunque los δˆi son estimadores consistentes para δi, convergen lentamente y están sesgados, y el procedimiento bootstrap presentado en el algoritmo1 de Simar y Wilson (2007) es, según los autores, el único método válido para hacer inferencia sobre β cuando (5) se estima por máxima verosimilitud.
En la segunda forma de abordar el problema, es el estimador insesgado, δˆˆi, quien reemplaza a los coeficientes δi en (4), con ψ(zi,β) = zi·β, y produce otro modelo de regresión truncada en el que la estimación máximo verosímil produce estimaciones consistentes de β. De nuevo, este procedimiento bootstrap alternativo, el algoritmo2 de Simar y Wilson (2007), es el único método conocido para hacer inferencia válida sobre β. Simar y Wilson (2007) demuestran que cuando el número de unidades es bajo, el uso del algoritmo2 empeora el error de estimación comparado con el algoritmo1. En consecuencia, proponemos aplicar el algoritmo1 en nuestra aplicación7.
Análisis de eficienciaA continuación se va a acometer el estudio de eficiencia para la muestra seleccionada. De manera previa a los cálculos de los coeficientes de eficiencia se realiza un análisis de outliers con el objetivo de depurar los datos sobre los que plantear el estudio empírico, y así garantizar la idoneidad de la muestra.
Posteriormente se procede a obtener los coeficientes de eficiencia bajo varios supuestos y para cada una de las fundaciones que componen la muestra, según el modelo DEA con orientación input, es decir, se pone el énfasis en la minimización del input dado el nivel de outputs alcanzado por una fundación; se preguntará en cuánto podría reducirse el empleo de inputs. Los cálculos han sido realizados con FEAR 2.01 desarrollado por Wilson (2008) con el paquete estadístico R8.
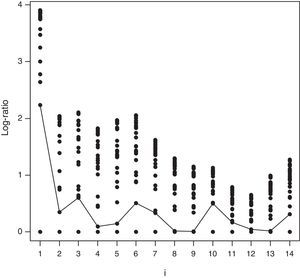
Análisis de outliersComo señala Wilson (1993), la metodología DEA es especialmente sensible a la presencia de observaciones extremas (outliers), por lo que se recomienda desarrollar una depuración previa de los datos sobre los que se vaya a plantear el estudio empírico. De esta forma se garantiza la idoneidad de la muestra, al eliminarse todos aquellos casos con un volumen inasumible de valores perdidos o con mediciones de la eficiencia que puedan considerarse atípicas. Para ello existen diversos métodos, como Wilson (1993, 1995), Simar (2003) o Porembski, Breitenstein y Alpar (2005). El primer autor propone hacer uso de funciones de influencia para detectar posibles puntos atípicos. Haciendo uso del concepto de frontera esperada de orden-m de Cazals, Florens y Simar (2002), la propuesta de Simar (2003) se basa en un análisis de sensibilidad relativo a varios valores del parámetro m. Ambos métodos son los más empleados en la literatura y se hallan implementados en el softwareR. En este trabajo emplearemos la rutina descrita por Wilson (1993).
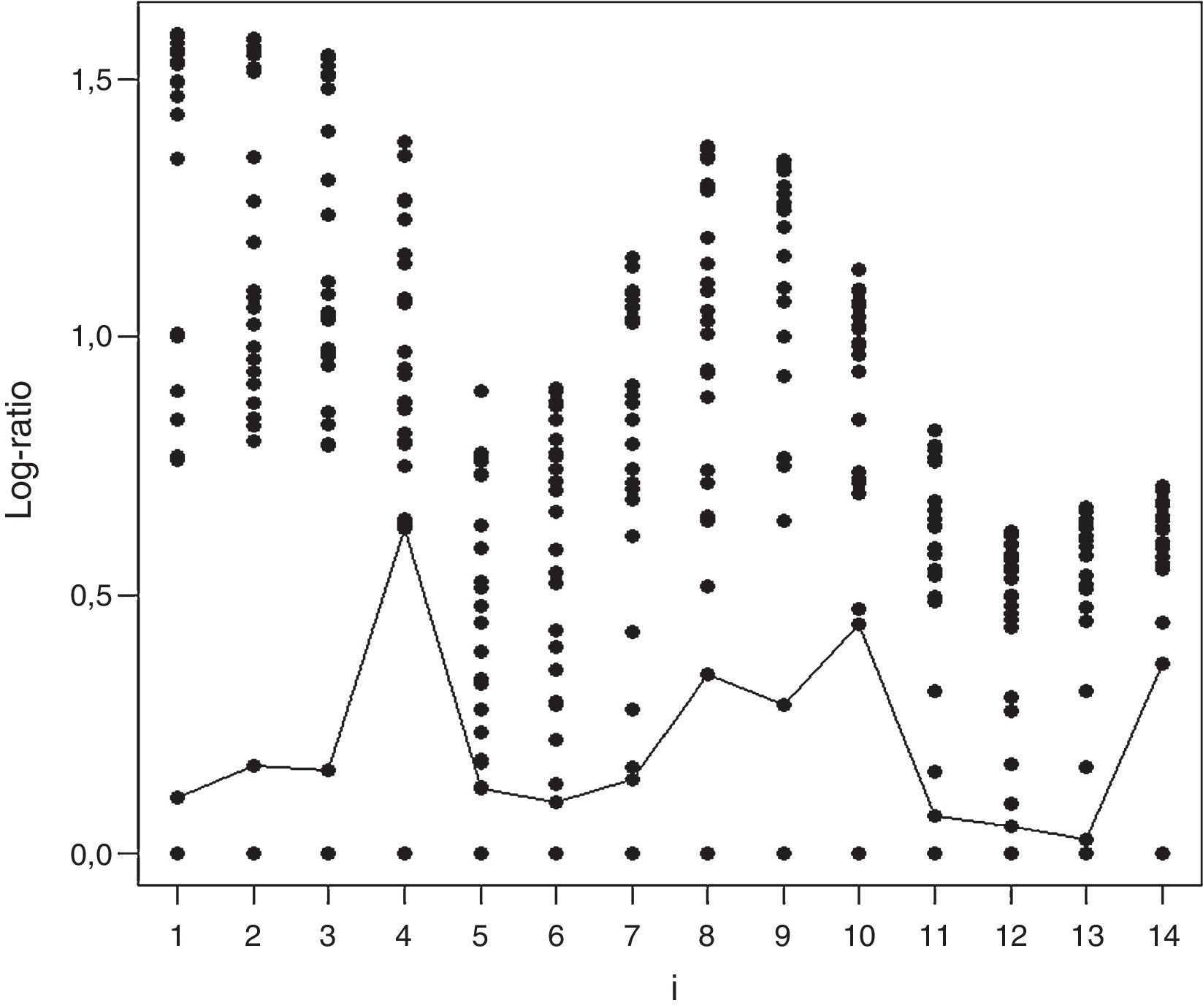
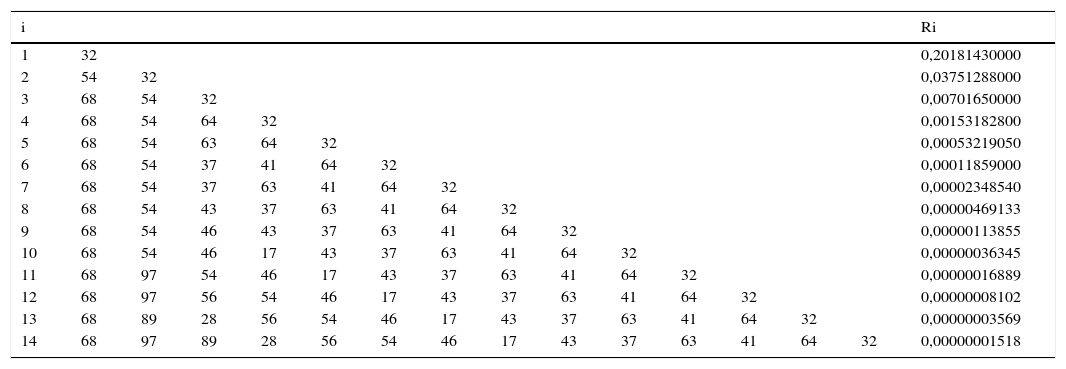
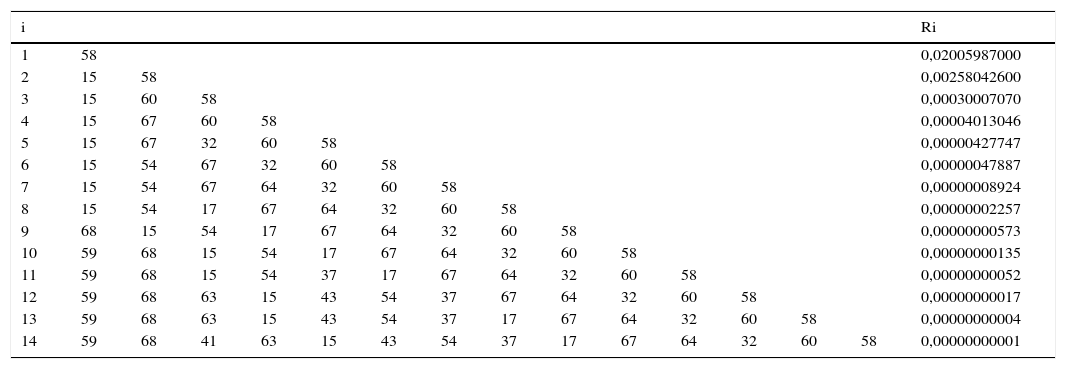
Partiendo de la definición de función de influencia geométrica de Andrews y Pregibon (1978), el método construye y analiza el gráfico del logaritmo de ratios. El análisis de la separación entre los menores valores de dicho ratio indica la posible presencia de un outlier. Dicho cociente se calcula para cada uno de los posibles subconjuntos, L, de tamaño i, donde la elección del valor de i es arbitraria. Así, el análisis se ilustra gráficamente y se calculan los valores del estadístico Ri de Wilson (1993). La figura 2 y la tabla 3, obtenidas mediante el software FEAR 2.01, ofrecen el resultado para el año 2008.
Log-ratio Plot Wilson (1993). Año 2008.
Valores de Ri. Wilson, 1993. Año 2008
| i | Ri | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 32 | 0,20181430000 | |||||||||||||
| 2 | 54 | 32 | 0,03751288000 | ||||||||||||
| 3 | 68 | 54 | 32 | 0,00701650000 | |||||||||||
| 4 | 68 | 54 | 64 | 32 | 0,00153182800 | ||||||||||
| 5 | 68 | 54 | 63 | 64 | 32 | 0,00053219050 | |||||||||
| 6 | 68 | 54 | 37 | 41 | 64 | 32 | 0,00011859000 | ||||||||
| 7 | 68 | 54 | 37 | 63 | 41 | 64 | 32 | 0,00002348540 | |||||||
| 8 | 68 | 54 | 43 | 37 | 63 | 41 | 64 | 32 | 0,00000469133 | ||||||
| 9 | 68 | 54 | 46 | 43 | 37 | 63 | 41 | 64 | 32 | 0,00000113855 | |||||
| 10 | 68 | 54 | 46 | 17 | 43 | 37 | 63 | 41 | 64 | 32 | 0,00000036345 | ||||
| 11 | 68 | 97 | 54 | 46 | 17 | 43 | 37 | 63 | 41 | 64 | 32 | 0,00000016889 | |||
| 12 | 68 | 97 | 56 | 54 | 46 | 17 | 43 | 37 | 63 | 41 | 64 | 32 | 0,00000008102 | ||
| 13 | 68 | 89 | 28 | 56 | 54 | 46 | 17 | 43 | 37 | 63 | 41 | 64 | 32 | 0,00000003569 | |
| 14 | 68 | 97 | 89 | 28 | 56 | 54 | 46 | 17 | 43 | 37 | 63 | 41 | 64 | 32 | 0,00000001518 |
En la figura 2, una línea recta conecta los segundos menores valores para cada i, ilustrando la separación entre las menores ratios para cada valor de i, desde i=1 hasta i=14. Así, por ejemplo, para i=4 se obtiene un salto relativamente mayor que el resto. La tabla 3 muestra los valores de R(i)Min en el espectro desde i=1 hasta i=14. En consonancia con la figura 2, el salto producido en i=4 se corresponde con las fundaciones que recoge la tabla 3.
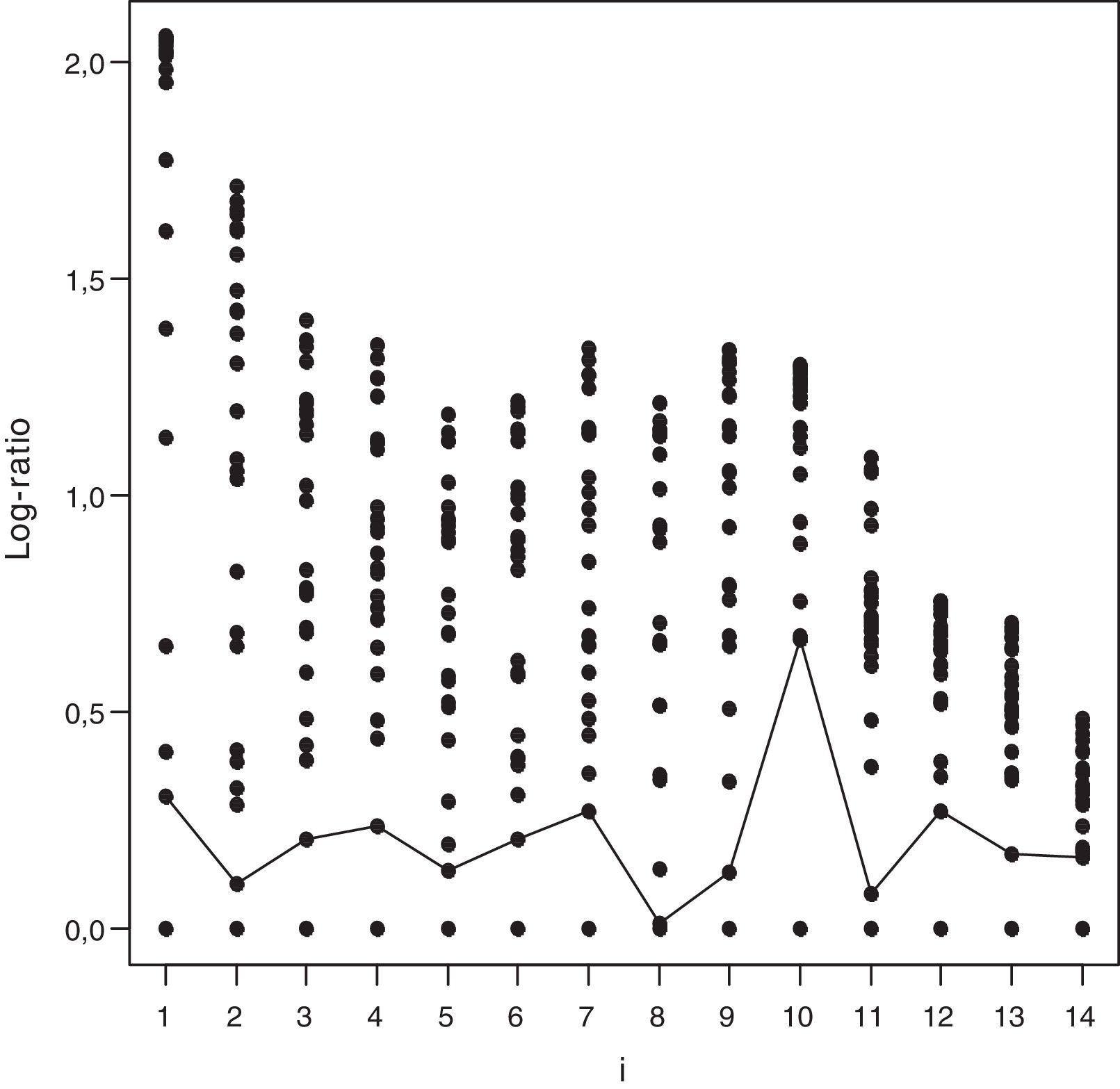
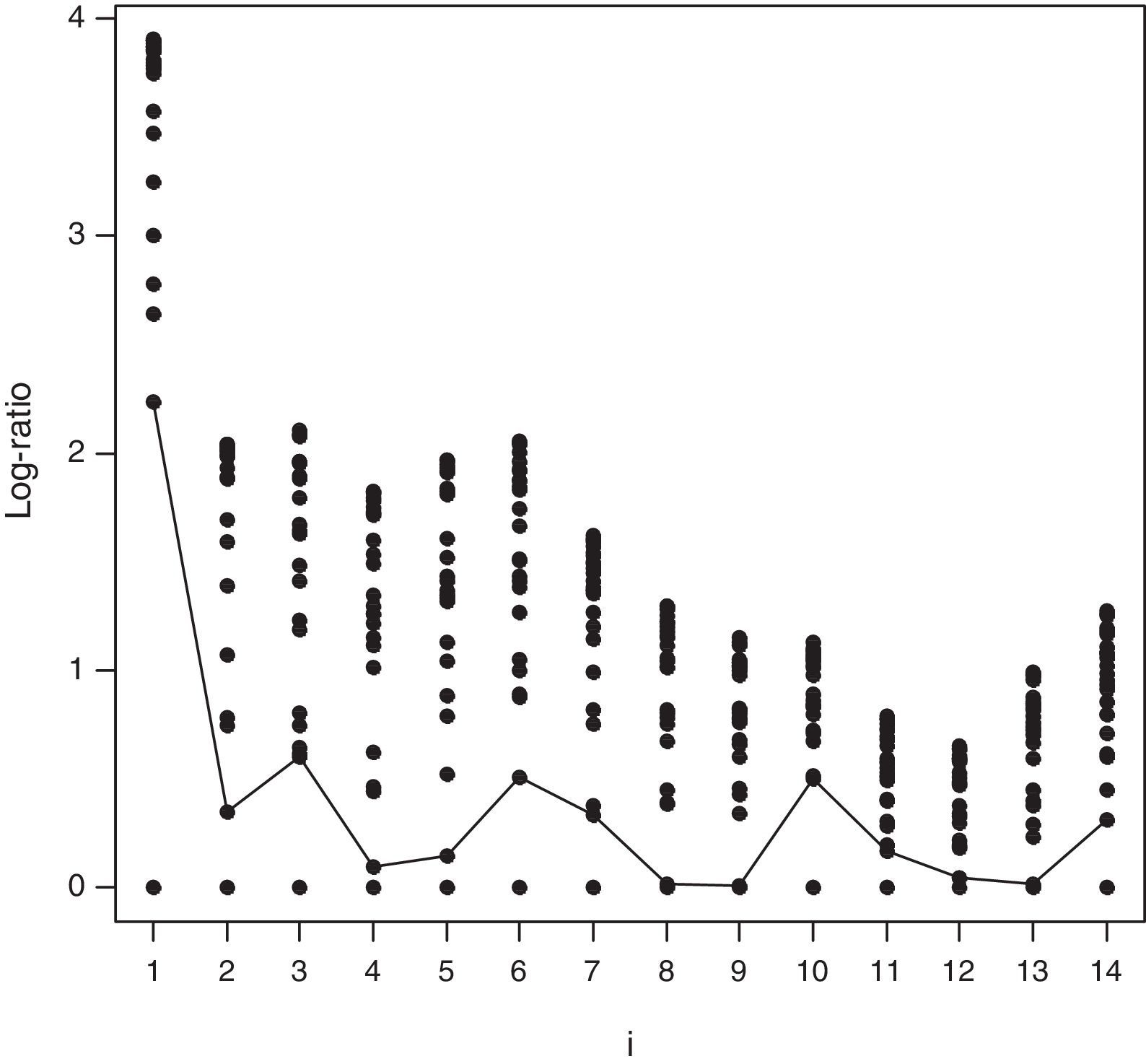
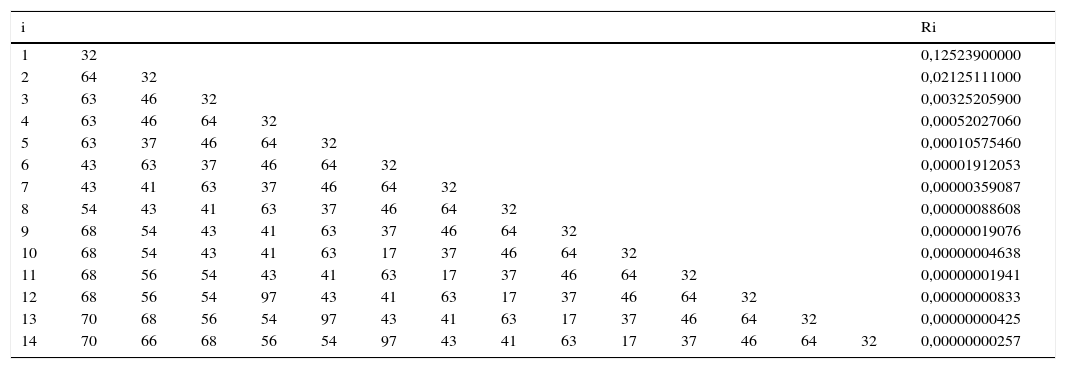
Para el año considerado (2008), los valores del estadístico no señalan la necesidad de eliminar ninguna DMU. Además, como señalan Wheelock y Wilson, 2008, p. 212), «siempre es complicado en aplicaciones empíricas determinar por qué una observación es atípica. Si tiene una baja probabilidad de que se produzca, el dato puede ser de interés para el análisis. Si ocasiona distorsión en los resultados, entonces debe ser solucionada o retirada». En la misma línea y más recientemente, Simar y Wilson (2015, p. 91) indican que «determinar qué constituye un outlier implica necesariamente cierta subjetividad por parte del investigador». Los resultados y análisis para los años 2009 y 2010 son análogos y se ofrecen en las figuras 3 y 4 y en las tablas 4 y 5.
Log-ratio Plot Wilson (1993). Año 2009.
Log-ratio Plot Wilson (1993). Año 2010.
Valores de Ri. Wilson, 1993. Año 2009
| i | Ri | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 32 | 0,12523900000 | |||||||||||||
| 2 | 64 | 32 | 0,02125111000 | ||||||||||||
| 3 | 63 | 46 | 32 | 0,00325205900 | |||||||||||
| 4 | 63 | 46 | 64 | 32 | 0,00052027060 | ||||||||||
| 5 | 63 | 37 | 46 | 64 | 32 | 0,00010575460 | |||||||||
| 6 | 43 | 63 | 37 | 46 | 64 | 32 | 0,00001912053 | ||||||||
| 7 | 43 | 41 | 63 | 37 | 46 | 64 | 32 | 0,00000359087 | |||||||
| 8 | 54 | 43 | 41 | 63 | 37 | 46 | 64 | 32 | 0,00000088608 | ||||||
| 9 | 68 | 54 | 43 | 41 | 63 | 37 | 46 | 64 | 32 | 0,00000019076 | |||||
| 10 | 68 | 54 | 43 | 41 | 63 | 17 | 37 | 46 | 64 | 32 | 0,00000004638 | ||||
| 11 | 68 | 56 | 54 | 43 | 41 | 63 | 17 | 37 | 46 | 64 | 32 | 0,00000001941 | |||
| 12 | 68 | 56 | 54 | 97 | 43 | 41 | 63 | 17 | 37 | 46 | 64 | 32 | 0,00000000833 | ||
| 13 | 70 | 68 | 56 | 54 | 97 | 43 | 41 | 63 | 17 | 37 | 46 | 64 | 32 | 0,00000000425 | |
| 14 | 70 | 66 | 68 | 56 | 54 | 97 | 43 | 41 | 63 | 17 | 37 | 46 | 64 | 32 | 0,00000000257 |
Valores de Ri. Wilson, 1993. Año 2010
| i | Ri | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 58 | 0,02005987000 | |||||||||||||
| 2 | 15 | 58 | 0,00258042600 | ||||||||||||
| 3 | 15 | 60 | 58 | 0,00030007070 | |||||||||||
| 4 | 15 | 67 | 60 | 58 | 0,00004013046 | ||||||||||
| 5 | 15 | 67 | 32 | 60 | 58 | 0,00000427747 | |||||||||
| 6 | 15 | 54 | 67 | 32 | 60 | 58 | 0,00000047887 | ||||||||
| 7 | 15 | 54 | 67 | 64 | 32 | 60 | 58 | 0,00000008924 | |||||||
| 8 | 15 | 54 | 17 | 67 | 64 | 32 | 60 | 58 | 0,00000002257 | ||||||
| 9 | 68 | 15 | 54 | 17 | 67 | 64 | 32 | 60 | 58 | 0,00000000573 | |||||
| 10 | 59 | 68 | 15 | 54 | 17 | 67 | 64 | 32 | 60 | 58 | 0,00000000135 | ||||
| 11 | 59 | 68 | 15 | 54 | 37 | 17 | 67 | 64 | 32 | 60 | 58 | 0,00000000052 | |||
| 12 | 59 | 68 | 63 | 15 | 43 | 54 | 37 | 67 | 64 | 32 | 60 | 58 | 0,00000000017 | ||
| 13 | 59 | 68 | 63 | 15 | 43 | 54 | 37 | 17 | 67 | 64 | 32 | 60 | 58 | 0,00000000004 | |
| 14 | 59 | 68 | 41 | 63 | 15 | 43 | 54 | 37 | 17 | 67 | 64 | 32 | 60 | 58 | 0,00000000001 |
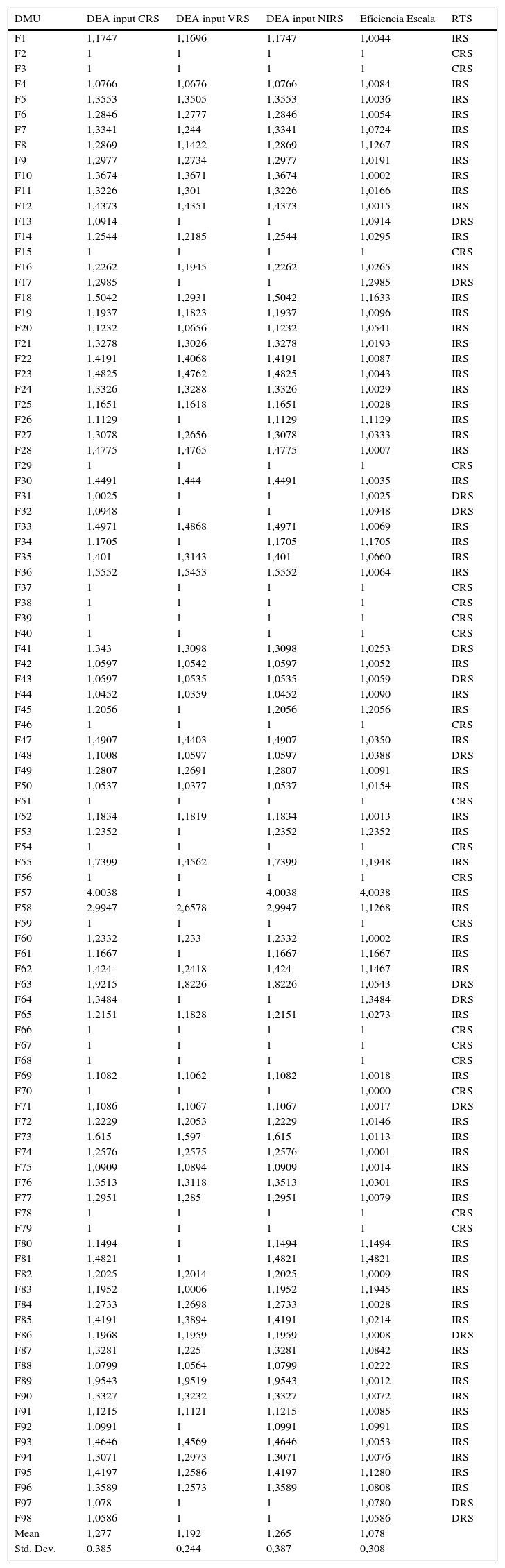
La tabla 6 contiene los coeficientes de eficiencia para los datos medios del período, según el modelo DEA de orientación input bajo los supuestos CRS (rendimientos a escala constante), VRS (rendimientos a escala variable) y NIRS (rendimientos no crecientes a escala).
Coeficientes de eficiencia y rendimientos a escala. 2008-2010
| DMU | DEA input CRS | DEA input VRS | DEA input NIRS | Eficiencia Escala | RTS |
|---|---|---|---|---|---|
| F1 | 1,1747 | 1,1696 | 1,1747 | 1,0044 | IRS |
| F2 | 1 | 1 | 1 | 1 | CRS |
| F3 | 1 | 1 | 1 | 1 | CRS |
| F4 | 1,0766 | 1,0676 | 1,0766 | 1,0084 | IRS |
| F5 | 1,3553 | 1,3505 | 1,3553 | 1,0036 | IRS |
| F6 | 1,2846 | 1,2777 | 1,2846 | 1,0054 | IRS |
| F7 | 1,3341 | 1,244 | 1,3341 | 1,0724 | IRS |
| F8 | 1,2869 | 1,1422 | 1,2869 | 1,1267 | IRS |
| F9 | 1,2977 | 1,2734 | 1,2977 | 1,0191 | IRS |
| F10 | 1,3674 | 1,3671 | 1,3674 | 1,0002 | IRS |
| F11 | 1,3226 | 1,301 | 1,3226 | 1,0166 | IRS |
| F12 | 1,4373 | 1,4351 | 1,4373 | 1,0015 | IRS |
| F13 | 1,0914 | 1 | 1 | 1,0914 | DRS |
| F14 | 1,2544 | 1,2185 | 1,2544 | 1,0295 | IRS |
| F15 | 1 | 1 | 1 | 1 | CRS |
| F16 | 1,2262 | 1,1945 | 1,2262 | 1,0265 | IRS |
| F17 | 1,2985 | 1 | 1 | 1,2985 | DRS |
| F18 | 1,5042 | 1,2931 | 1,5042 | 1,1633 | IRS |
| F19 | 1,1937 | 1,1823 | 1,1937 | 1,0096 | IRS |
| F20 | 1,1232 | 1,0656 | 1,1232 | 1,0541 | IRS |
| F21 | 1,3278 | 1,3026 | 1,3278 | 1,0193 | IRS |
| F22 | 1,4191 | 1,4068 | 1,4191 | 1,0087 | IRS |
| F23 | 1,4825 | 1,4762 | 1,4825 | 1,0043 | IRS |
| F24 | 1,3326 | 1,3288 | 1,3326 | 1,0029 | IRS |
| F25 | 1,1651 | 1,1618 | 1,1651 | 1,0028 | IRS |
| F26 | 1,1129 | 1 | 1,1129 | 1,1129 | IRS |
| F27 | 1,3078 | 1,2656 | 1,3078 | 1,0333 | IRS |
| F28 | 1,4775 | 1,4765 | 1,4775 | 1,0007 | IRS |
| F29 | 1 | 1 | 1 | 1 | CRS |
| F30 | 1,4491 | 1,444 | 1,4491 | 1,0035 | IRS |
| F31 | 1,0025 | 1 | 1 | 1,0025 | DRS |
| F32 | 1,0948 | 1 | 1 | 1,0948 | DRS |
| F33 | 1,4971 | 1,4868 | 1,4971 | 1,0069 | IRS |
| F34 | 1,1705 | 1 | 1,1705 | 1,1705 | IRS |
| F35 | 1,401 | 1,3143 | 1,401 | 1,0660 | IRS |
| F36 | 1,5552 | 1,5453 | 1,5552 | 1,0064 | IRS |
| F37 | 1 | 1 | 1 | 1 | CRS |
| F38 | 1 | 1 | 1 | 1 | CRS |
| F39 | 1 | 1 | 1 | 1 | CRS |
| F40 | 1 | 1 | 1 | 1 | CRS |
| F41 | 1,343 | 1,3098 | 1,3098 | 1,0253 | DRS |
| F42 | 1,0597 | 1,0542 | 1,0597 | 1,0052 | IRS |
| F43 | 1,0597 | 1,0535 | 1,0535 | 1,0059 | DRS |
| F44 | 1,0452 | 1,0359 | 1,0452 | 1,0090 | IRS |
| F45 | 1,2056 | 1 | 1,2056 | 1,2056 | IRS |
| F46 | 1 | 1 | 1 | 1 | CRS |
| F47 | 1,4907 | 1,4403 | 1,4907 | 1,0350 | IRS |
| F48 | 1,1008 | 1,0597 | 1,0597 | 1,0388 | DRS |
| F49 | 1,2807 | 1,2691 | 1,2807 | 1,0091 | IRS |
| F50 | 1,0537 | 1,0377 | 1,0537 | 1,0154 | IRS |
| F51 | 1 | 1 | 1 | 1 | CRS |
| F52 | 1,1834 | 1,1819 | 1,1834 | 1,0013 | IRS |
| F53 | 1,2352 | 1 | 1,2352 | 1,2352 | IRS |
| F54 | 1 | 1 | 1 | 1 | CRS |
| F55 | 1,7399 | 1,4562 | 1,7399 | 1,1948 | IRS |
| F56 | 1 | 1 | 1 | 1 | CRS |
| F57 | 4,0038 | 1 | 4,0038 | 4,0038 | IRS |
| F58 | 2,9947 | 2,6578 | 2,9947 | 1,1268 | IRS |
| F59 | 1 | 1 | 1 | 1 | CRS |
| F60 | 1,2332 | 1,233 | 1,2332 | 1,0002 | IRS |
| F61 | 1,1667 | 1 | 1,1667 | 1,1667 | IRS |
| F62 | 1,424 | 1,2418 | 1,424 | 1,1467 | IRS |
| F63 | 1,9215 | 1,8226 | 1,8226 | 1,0543 | DRS |
| F64 | 1,3484 | 1 | 1 | 1,3484 | DRS |
| F65 | 1,2151 | 1,1828 | 1,2151 | 1,0273 | IRS |
| F66 | 1 | 1 | 1 | 1 | CRS |
| F67 | 1 | 1 | 1 | 1 | CRS |
| F68 | 1 | 1 | 1 | 1 | CRS |
| F69 | 1,1082 | 1,1062 | 1,1082 | 1,0018 | IRS |
| F70 | 1 | 1 | 1 | 1,0000 | CRS |
| F71 | 1,1086 | 1,1067 | 1,1067 | 1,0017 | DRS |
| F72 | 1,2229 | 1,2053 | 1,2229 | 1,0146 | IRS |
| F73 | 1,615 | 1,597 | 1,615 | 1,0113 | IRS |
| F74 | 1,2576 | 1,2575 | 1,2576 | 1,0001 | IRS |
| F75 | 1,0909 | 1,0894 | 1,0909 | 1,0014 | IRS |
| F76 | 1,3513 | 1,3118 | 1,3513 | 1,0301 | IRS |
| F77 | 1,2951 | 1,285 | 1,2951 | 1,0079 | IRS |
| F78 | 1 | 1 | 1 | 1 | CRS |
| F79 | 1 | 1 | 1 | 1 | CRS |
| F80 | 1,1494 | 1 | 1,1494 | 1,1494 | IRS |
| F81 | 1,4821 | 1 | 1,4821 | 1,4821 | IRS |
| F82 | 1,2025 | 1,2014 | 1,2025 | 1,0009 | IRS |
| F83 | 1,1952 | 1,0006 | 1,1952 | 1,1945 | IRS |
| F84 | 1,2733 | 1,2698 | 1,2733 | 1,0028 | IRS |
| F85 | 1,4191 | 1,3894 | 1,4191 | 1,0214 | IRS |
| F86 | 1,1968 | 1,1959 | 1,1959 | 1,0008 | DRS |
| F87 | 1,3281 | 1,225 | 1,3281 | 1,0842 | IRS |
| F88 | 1,0799 | 1,0564 | 1,0799 | 1,0222 | IRS |
| F89 | 1,9543 | 1,9519 | 1,9543 | 1,0012 | IRS |
| F90 | 1,3327 | 1,3232 | 1,3327 | 1,0072 | IRS |
| F91 | 1,1215 | 1,1121 | 1,1215 | 1,0085 | IRS |
| F92 | 1,0991 | 1 | 1,0991 | 1,0991 | IRS |
| F93 | 1,4646 | 1,4569 | 1,4646 | 1,0053 | IRS |
| F94 | 1,3071 | 1,2973 | 1,3071 | 1,0076 | IRS |
| F95 | 1,4197 | 1,2586 | 1,4197 | 1,1280 | IRS |
| F96 | 1,3589 | 1,2573 | 1,3589 | 1,0808 | IRS |
| F97 | 1,078 | 1 | 1 | 1,0780 | DRS |
| F98 | 1,0586 | 1 | 1 | 1,0586 | DRS |
| Mean | 1,277 | 1,192 | 1,265 | 1,078 | |
| Std. Dev. | 0,385 | 0,244 | 0,387 | 0,308 |
CRS: constante; DRS: descensos; IRS: incrementos; RTS: rendimientos a escala.
Las fundaciones con puntuaciones iguales a 1 son eficientes. De acuerdo con la función de distancia Shephard, cuando el coeficiente es superior a la unidad, la DMU es ineficiente. El índice CRS mide la eficiencia global para cada fundación y se compone de una combinación de la eficiencia técnica pura (índice VRS) y de la eficiencia de escala. Las puntuaciones de eficiencia técnica global y eficiencia técnica pura proporcionan una medición de la eficiencia de escala y las puntuaciones NIRS ayudan a medir los rendimientos a escala9.
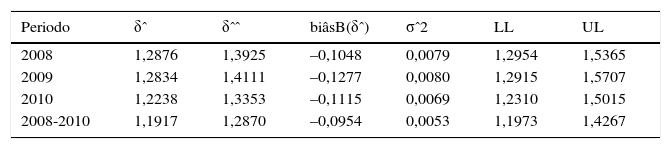
La ineficiencia técnica pura se corresponde con la parte de ineficiencia debida a la gestión; en consecuencia, los índices VRS (o BCC) pueden interpretarse como una medida de la capacidad de gestión; otra parte de la ineficiencia viene provocada porque la unidad opera en una escala desfavorable y se trata de la ineficiencia de escala. Bajo el supuesto de CRS, el conjunto de referencia puede estar formada por DMU eficientes de cualquier tamaño. El índice medio de eficiencia bajo CRS es 1,277, es decir, cuando son consideradas todas las fuentes de ineficiencia, en promedio, y teniendo en cuenta los niveles de outputs, las fundaciones podrían reducir sus inputs el 27,7%.
Sin embargo, a la hora de valorar la eficiencia técnica pura, parece más sensato que las comparaciones se establezcan con unidades de similar comportamiento a la evaluada, aspecto que se consigue relajando la hipótesis de CRS por la de VRS. La puntuación promedio de eficiencia bajo VRS es 1,3192.
Siguiendo a Färe y Grosskopf (1985), la eficiencia de escala se obtiene dividiendo la eficiencia CRS entre la VRS. Bajo una escala decreciente, DRS, dada una disminución en el valor de sus inputs, la disminución en el output es proporcionalmente inferior.
No obstante, dado el caso analizado (fundaciones), resulta más interesante abordar el problema de cómo mejorar la eficiencia, lo que conduce al análisis de sus determinantes que abordaremos más adelante.
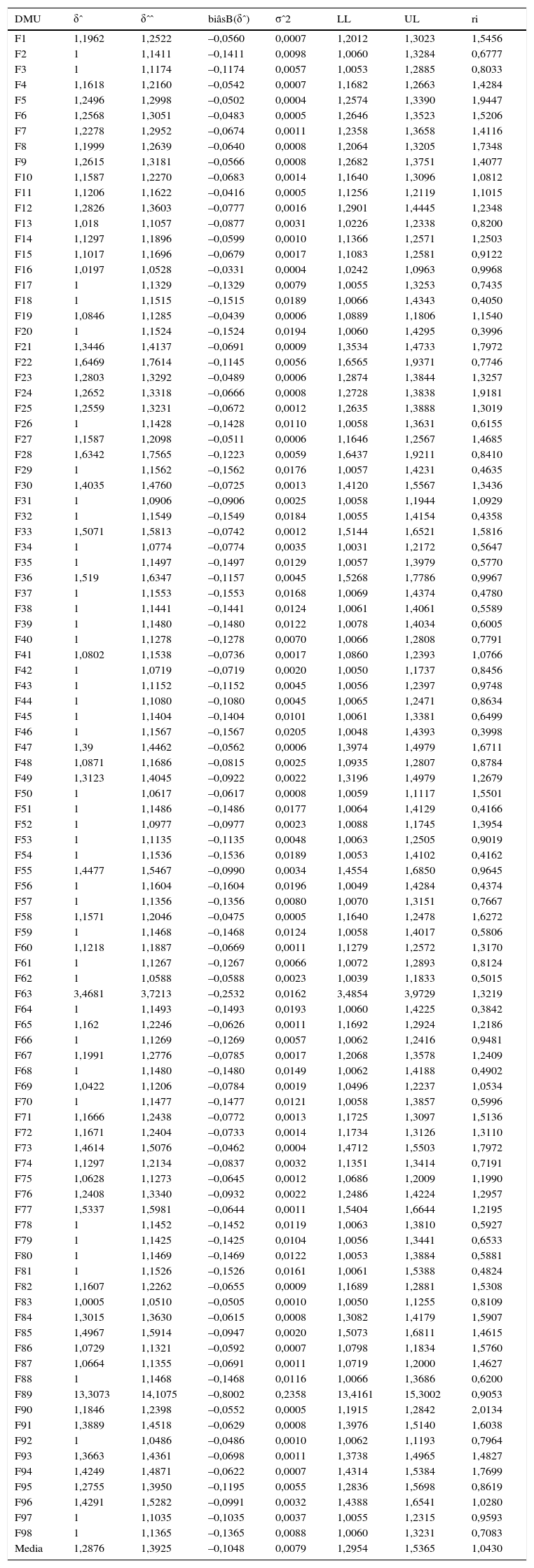
Procedimiento bootstrap de corrección del sesgoEl modelo DEA es relativamente sencillo de estimar pero tiene diversas limitaciones. Con independencia del objetivo perseguido en trabajos que utilizan este tipo de medidas básicas, como la simple búsqueda de las unidades más eficientes, o de las proyecciones hacia la frontera, resulta de gran importancia poner de relieve que el estimador de la medida de eficiencia está sesgado desde su propia construcción10; de hecho, Simar y Wilson (2007, p. 40) señalan que en todas las aplicaciones recopiladas el sesgo inherente de los coeficientes de eficiencia había sido ignorado. Con el fin de considerar la naturaleza estocástica del problema de estimación utilizamos el procedimiento de Simar y Wilson (2000) para corregir el sesgo en las estimaciones de los índices de eficiencia VRS, estimando al mismo tiempo los intervalos de confianza.
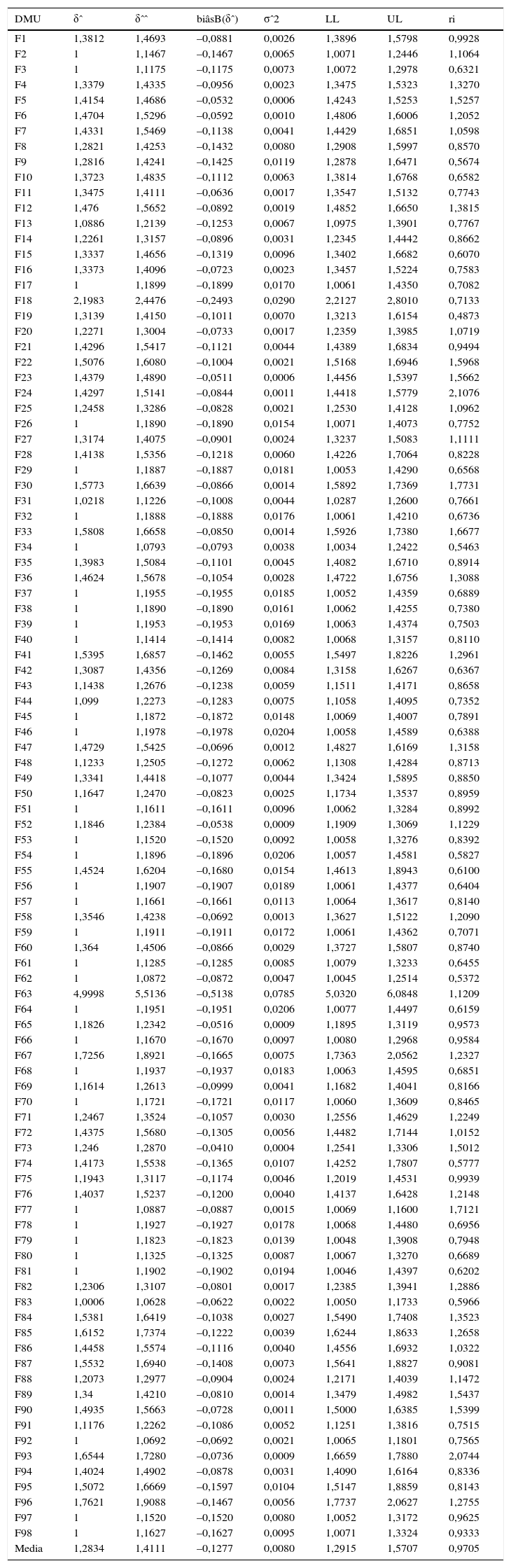
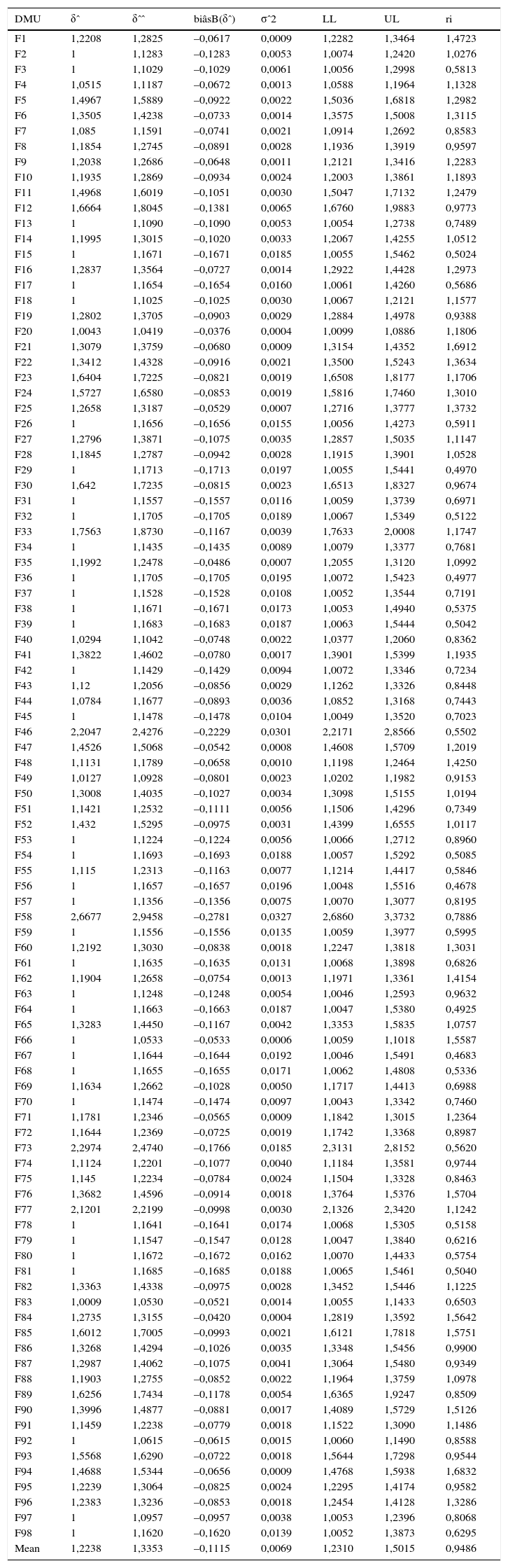
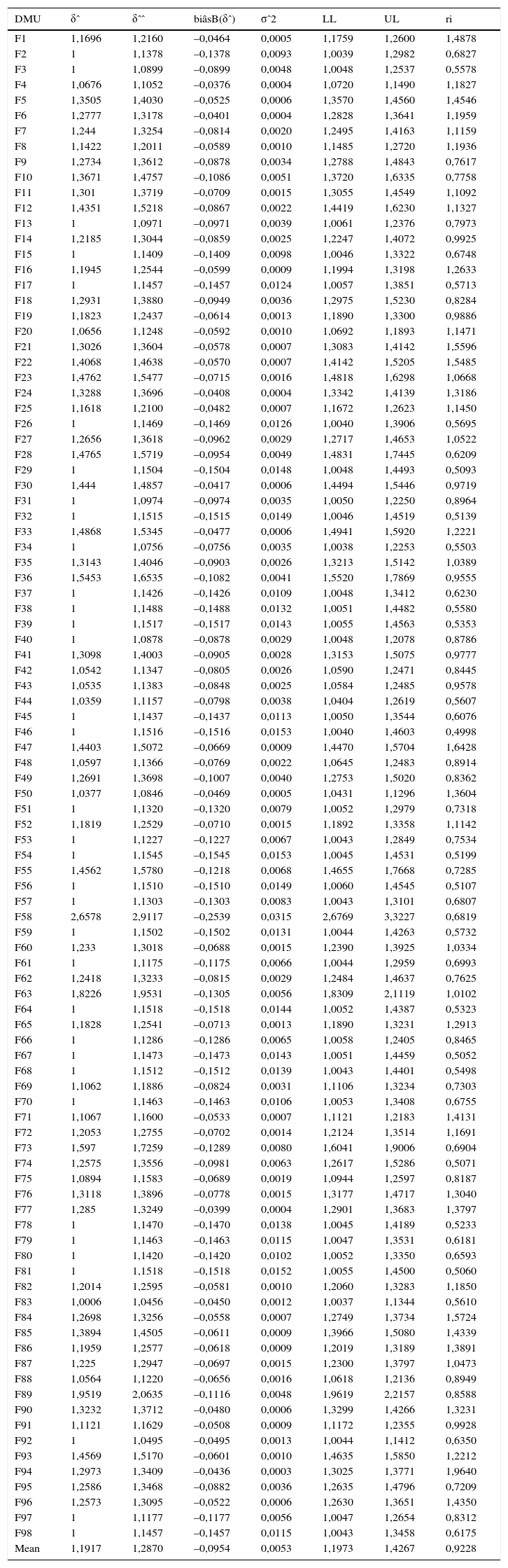
Las tablas 7-10 muestran los detalles para 2008, 2009 y 2010 individualmente y el periodo 2008-2010 considerado en su conjunto, con información sobre las estimaciones de eficiencia de los resultados de DEA con el procedimiento bootstrap.
Año 2008. Coeficientes de eficiencia VRS de orientación input. Simar y Wilson (2000)
| DMU | δˆ | δˆˆ | biâsB(δˆ) | σˆ2 | LL | UL | ri |
|---|---|---|---|---|---|---|---|
| F1 | 1,1962 | 1,2522 | –0,0560 | 0,0007 | 1,2012 | 1,3023 | 1,5456 |
| F2 | 1 | 1,1411 | –0,1411 | 0,0098 | 1,0060 | 1,3284 | 0,6777 |
| F3 | 1 | 1,1174 | –0,1174 | 0,0057 | 1,0053 | 1,2885 | 0,8033 |
| F4 | 1,1618 | 1,2160 | –0,0542 | 0,0007 | 1,1682 | 1,2663 | 1,4284 |
| F5 | 1,2496 | 1,2998 | –0,0502 | 0,0004 | 1,2574 | 1,3390 | 1,9447 |
| F6 | 1,2568 | 1,3051 | –0,0483 | 0,0005 | 1,2646 | 1,3523 | 1,5206 |
| F7 | 1,2278 | 1,2952 | –0,0674 | 0,0011 | 1,2358 | 1,3658 | 1,4116 |
| F8 | 1,1999 | 1,2639 | –0,0640 | 0,0008 | 1,2064 | 1,3205 | 1,7348 |
| F9 | 1,2615 | 1,3181 | –0,0566 | 0,0008 | 1,2682 | 1,3751 | 1,4077 |
| F10 | 1,1587 | 1,2270 | –0,0683 | 0,0014 | 1,1640 | 1,3096 | 1,0812 |
| F11 | 1,1206 | 1,1622 | –0,0416 | 0,0005 | 1,1256 | 1,2119 | 1,1015 |
| F12 | 1,2826 | 1,3603 | –0,0777 | 0,0016 | 1,2901 | 1,4445 | 1,2348 |
| F13 | 1,018 | 1,1057 | –0,0877 | 0,0031 | 1,0226 | 1,2338 | 0,8200 |
| F14 | 1,1297 | 1,1896 | –0,0599 | 0,0010 | 1,1366 | 1,2571 | 1,2503 |
| F15 | 1,1017 | 1,1696 | –0,0679 | 0,0017 | 1,1083 | 1,2581 | 0,9122 |
| F16 | 1,0197 | 1,0528 | –0,0331 | 0,0004 | 1,0242 | 1,0963 | 0,9968 |
| F17 | 1 | 1,1329 | –0,1329 | 0,0079 | 1,0055 | 1,3253 | 0,7435 |
| F18 | 1 | 1,1515 | –0,1515 | 0,0189 | 1,0066 | 1,4343 | 0,4050 |
| F19 | 1,0846 | 1,1285 | –0,0439 | 0,0006 | 1,0889 | 1,1806 | 1,1540 |
| F20 | 1 | 1,1524 | –0,1524 | 0,0194 | 1,0060 | 1,4295 | 0,3996 |
| F21 | 1,3446 | 1,4137 | –0,0691 | 0,0009 | 1,3534 | 1,4733 | 1,7972 |
| F22 | 1,6469 | 1,7614 | –0,1145 | 0,0056 | 1,6565 | 1,9371 | 0,7746 |
| F23 | 1,2803 | 1,3292 | –0,0489 | 0,0006 | 1,2874 | 1,3844 | 1,3257 |
| F24 | 1,2652 | 1,3318 | –0,0666 | 0,0008 | 1,2728 | 1,3838 | 1,9181 |
| F25 | 1,2559 | 1,3231 | –0,0672 | 0,0012 | 1,2635 | 1,3888 | 1,3019 |
| F26 | 1 | 1,1428 | –0,1428 | 0,0110 | 1,0058 | 1,3631 | 0,6155 |
| F27 | 1,1587 | 1,2098 | –0,0511 | 0,0006 | 1,1646 | 1,2567 | 1,4685 |
| F28 | 1,6342 | 1,7565 | –0,1223 | 0,0059 | 1,6437 | 1,9211 | 0,8410 |
| F29 | 1 | 1,1562 | –0,1562 | 0,0176 | 1,0057 | 1,4231 | 0,4635 |
| F30 | 1,4035 | 1,4760 | –0,0725 | 0,0013 | 1,4120 | 1,5567 | 1,3436 |
| F31 | 1 | 1,0906 | –0,0906 | 0,0025 | 1,0058 | 1,1944 | 1,0929 |
| F32 | 1 | 1,1549 | –0,1549 | 0,0184 | 1,0055 | 1,4154 | 0,4358 |
| F33 | 1,5071 | 1,5813 | –0,0742 | 0,0012 | 1,5144 | 1,6521 | 1,5816 |
| F34 | 1 | 1,0774 | –0,0774 | 0,0035 | 1,0031 | 1,2172 | 0,5647 |
| F35 | 1 | 1,1497 | –0,1497 | 0,0129 | 1,0057 | 1,3979 | 0,5770 |
| F36 | 1,519 | 1,6347 | –0,1157 | 0,0045 | 1,5268 | 1,7786 | 0,9967 |
| F37 | 1 | 1,1553 | –0,1553 | 0,0168 | 1,0069 | 1,4374 | 0,4780 |
| F38 | 1 | 1,1441 | –0,1441 | 0,0124 | 1,0061 | 1,4061 | 0,5589 |
| F39 | 1 | 1,1480 | –0,1480 | 0,0122 | 1,0078 | 1,4034 | 0,6005 |
| F40 | 1 | 1,1278 | –0,1278 | 0,0070 | 1,0066 | 1,2808 | 0,7791 |
| F41 | 1,0802 | 1,1538 | –0,0736 | 0,0017 | 1,0860 | 1,2393 | 1,0766 |
| F42 | 1 | 1,0719 | –0,0719 | 0,0020 | 1,0050 | 1,1737 | 0,8456 |
| F43 | 1 | 1,1152 | –0,1152 | 0,0045 | 1,0056 | 1,2397 | 0,9748 |
| F44 | 1 | 1,1080 | –0,1080 | 0,0045 | 1,0065 | 1,2471 | 0,8634 |
| F45 | 1 | 1,1404 | –0,1404 | 0,0101 | 1,0061 | 1,3381 | 0,6499 |
| F46 | 1 | 1,1567 | –0,1567 | 0,0205 | 1,0048 | 1,4393 | 0,3998 |
| F47 | 1,39 | 1,4462 | –0,0562 | 0,0006 | 1,3974 | 1,4979 | 1,6711 |
| F48 | 1,0871 | 1,1686 | –0,0815 | 0,0025 | 1,0935 | 1,2807 | 0,8784 |
| F49 | 1,3123 | 1,4045 | –0,0922 | 0,0022 | 1,3196 | 1,4979 | 1,2679 |
| F50 | 1 | 1,0617 | –0,0617 | 0,0008 | 1,0059 | 1,1117 | 1,5501 |
| F51 | 1 | 1,1486 | –0,1486 | 0,0177 | 1,0064 | 1,4129 | 0,4166 |
| F52 | 1 | 1,0977 | –0,0977 | 0,0023 | 1,0088 | 1,1745 | 1,3954 |
| F53 | 1 | 1,1135 | –0,1135 | 0,0048 | 1,0063 | 1,2505 | 0,9019 |
| F54 | 1 | 1,1536 | –0,1536 | 0,0189 | 1,0053 | 1,4102 | 0,4162 |
| F55 | 1,4477 | 1,5467 | –0,0990 | 0,0034 | 1,4554 | 1,6850 | 0,9645 |
| F56 | 1 | 1,1604 | –0,1604 | 0,0196 | 1,0049 | 1,4284 | 0,4374 |
| F57 | 1 | 1,1356 | –0,1356 | 0,0080 | 1,0070 | 1,3151 | 0,7667 |
| F58 | 1,1571 | 1,2046 | –0,0475 | 0,0005 | 1,1640 | 1,2478 | 1,6272 |
| F59 | 1 | 1,1468 | –0,1468 | 0,0124 | 1,0058 | 1,4017 | 0,5806 |
| F60 | 1,1218 | 1,1887 | –0,0669 | 0,0011 | 1,1279 | 1,2572 | 1,3170 |
| F61 | 1 | 1,1267 | –0,1267 | 0,0066 | 1,0072 | 1,2893 | 0,8124 |
| F62 | 1 | 1,0588 | –0,0588 | 0,0023 | 1,0039 | 1,1833 | 0,5015 |
| F63 | 3,4681 | 3,7213 | –0,2532 | 0,0162 | 3,4854 | 3,9729 | 1,3219 |
| F64 | 1 | 1,1493 | –0,1493 | 0,0193 | 1,0060 | 1,4225 | 0,3842 |
| F65 | 1,162 | 1,2246 | –0,0626 | 0,0011 | 1,1692 | 1,2924 | 1,2186 |
| F66 | 1 | 1,1269 | –0,1269 | 0,0057 | 1,0062 | 1,2416 | 0,9481 |
| F67 | 1,1991 | 1,2776 | –0,0785 | 0,0017 | 1,2068 | 1,3578 | 1,2409 |
| F68 | 1 | 1,1480 | –0,1480 | 0,0149 | 1,0062 | 1,4188 | 0,4902 |
| F69 | 1,0422 | 1,1206 | –0,0784 | 0,0019 | 1,0496 | 1,2237 | 1,0534 |
| F70 | 1 | 1,1477 | –0,1477 | 0,0121 | 1,0058 | 1,3857 | 0,5996 |
| F71 | 1,1666 | 1,2438 | –0,0772 | 0,0013 | 1,1725 | 1,3097 | 1,5136 |
| F72 | 1,1671 | 1,2404 | –0,0733 | 0,0014 | 1,1734 | 1,3126 | 1,3110 |
| F73 | 1,4614 | 1,5076 | –0,0462 | 0,0004 | 1,4712 | 1,5503 | 1,7972 |
| F74 | 1,1297 | 1,2134 | –0,0837 | 0,0032 | 1,1351 | 1,3414 | 0,7191 |
| F75 | 1,0628 | 1,1273 | –0,0645 | 0,0012 | 1,0686 | 1,2009 | 1,1990 |
| F76 | 1,2408 | 1,3340 | –0,0932 | 0,0022 | 1,2486 | 1,4224 | 1,2957 |
| F77 | 1,5337 | 1,5981 | –0,0644 | 0,0011 | 1,5404 | 1,6644 | 1,2195 |
| F78 | 1 | 1,1452 | –0,1452 | 0,0119 | 1,0063 | 1,3810 | 0,5927 |
| F79 | 1 | 1,1425 | –0,1425 | 0,0104 | 1,0056 | 1,3441 | 0,6533 |
| F80 | 1 | 1,1469 | –0,1469 | 0,0122 | 1,0053 | 1,3884 | 0,5881 |
| F81 | 1 | 1,1526 | –0,1526 | 0,0161 | 1,0061 | 1,5388 | 0,4824 |
| F82 | 1,1607 | 1,2262 | –0,0655 | 0,0009 | 1,1689 | 1,2881 | 1,5308 |
| F83 | 1,0005 | 1,0510 | –0,0505 | 0,0010 | 1,0050 | 1,1255 | 0,8109 |
| F84 | 1,3015 | 1,3630 | –0,0615 | 0,0008 | 1,3082 | 1,4179 | 1,5907 |
| F85 | 1,4967 | 1,5914 | –0,0947 | 0,0020 | 1,5073 | 1,6811 | 1,4615 |
| F86 | 1,0729 | 1,1321 | –0,0592 | 0,0007 | 1,0798 | 1,1834 | 1,5760 |
| F87 | 1,0664 | 1,1355 | –0,0691 | 0,0011 | 1,0719 | 1,2000 | 1,4627 |
| F88 | 1 | 1,1468 | –0,1468 | 0,0116 | 1,0066 | 1,3686 | 0,6200 |
| F89 | 13,3073 | 14,1075 | –0,8002 | 0,2358 | 13,4161 | 15,3002 | 0,9053 |
| F90 | 1,1846 | 1,2398 | –0,0552 | 0,0005 | 1,1915 | 1,2842 | 2,0134 |
| F91 | 1,3889 | 1,4518 | –0,0629 | 0,0008 | 1,3976 | 1,5140 | 1,6038 |
| F92 | 1 | 1,0486 | –0,0486 | 0,0010 | 1,0062 | 1,1193 | 0,7964 |
| F93 | 1,3663 | 1,4361 | –0,0698 | 0,0011 | 1,3738 | 1,4965 | 1,4827 |
| F94 | 1,4249 | 1,4871 | –0,0622 | 0,0007 | 1,4314 | 1,5384 | 1,7699 |
| F95 | 1,2755 | 1,3950 | –0,1195 | 0,0055 | 1,2836 | 1,5698 | 0,8619 |
| F96 | 1,4291 | 1,5282 | –0,0991 | 0,0032 | 1,4388 | 1,6541 | 1,0280 |
| F97 | 1 | 1,1035 | –0,1035 | 0,0037 | 1,0055 | 1,2315 | 0,9593 |
| F98 | 1 | 1,1365 | –0,1365 | 0,0088 | 1,0060 | 1,3231 | 0,7083 |
| Media | 1,2876 | 1,3925 | –0,1048 | 0,0079 | 1,2954 | 1,5365 | 1,0430 |
Año 2009. Coeficientes de eficiencia VRS de orientación input. Simar y Wilson (2000)
| DMU | δˆ | δˆˆ | biâsB(δˆ) | σˆ2 | LL | UL | ri |
|---|---|---|---|---|---|---|---|
| F1 | 1,3812 | 1,4693 | –0,0881 | 0,0026 | 1,3896 | 1,5798 | 0,9928 |
| F2 | 1 | 1,1467 | –0,1467 | 0,0065 | 1,0071 | 1,2446 | 1,1064 |
| F3 | 1 | 1,1175 | –0,1175 | 0,0073 | 1,0072 | 1,2978 | 0,6321 |
| F4 | 1,3379 | 1,4335 | –0,0956 | 0,0023 | 1,3475 | 1,5323 | 1,3270 |
| F5 | 1,4154 | 1,4686 | –0,0532 | 0,0006 | 1,4243 | 1,5253 | 1,5257 |
| F6 | 1,4704 | 1,5296 | –0,0592 | 0,0010 | 1,4806 | 1,6006 | 1,2052 |
| F7 | 1,4331 | 1,5469 | –0,1138 | 0,0041 | 1,4429 | 1,6851 | 1,0598 |
| F8 | 1,2821 | 1,4253 | –0,1432 | 0,0080 | 1,2908 | 1,5997 | 0,8570 |
| F9 | 1,2816 | 1,4241 | –0,1425 | 0,0119 | 1,2878 | 1,6471 | 0,5674 |
| F10 | 1,3723 | 1,4835 | –0,1112 | 0,0063 | 1,3814 | 1,6768 | 0,6582 |
| F11 | 1,3475 | 1,4111 | –0,0636 | 0,0017 | 1,3547 | 1,5132 | 0,7743 |
| F12 | 1,476 | 1,5652 | –0,0892 | 0,0019 | 1,4852 | 1,6650 | 1,3815 |
| F13 | 1,0886 | 1,2139 | –0,1253 | 0,0067 | 1,0975 | 1,3901 | 0,7767 |
| F14 | 1,2261 | 1,3157 | –0,0896 | 0,0031 | 1,2345 | 1,4442 | 0,8662 |
| F15 | 1,3337 | 1,4656 | –0,1319 | 0,0096 | 1,3402 | 1,6682 | 0,6070 |
| F16 | 1,3373 | 1,4096 | –0,0723 | 0,0023 | 1,3457 | 1,5224 | 0,7583 |
| F17 | 1 | 1,1899 | –0,1899 | 0,0170 | 1,0061 | 1,4350 | 0,7082 |
| F18 | 2,1983 | 2,4476 | –0,2493 | 0,0290 | 2,2127 | 2,8010 | 0,7133 |
| F19 | 1,3139 | 1,4150 | –0,1011 | 0,0070 | 1,3213 | 1,6154 | 0,4873 |
| F20 | 1,2271 | 1,3004 | –0,0733 | 0,0017 | 1,2359 | 1,3985 | 1,0719 |
| F21 | 1,4296 | 1,5417 | –0,1121 | 0,0044 | 1,4389 | 1,6834 | 0,9494 |
| F22 | 1,5076 | 1,6080 | –0,1004 | 0,0021 | 1,5168 | 1,6946 | 1,5968 |
| F23 | 1,4379 | 1,4890 | –0,0511 | 0,0006 | 1,4456 | 1,5397 | 1,5662 |
| F24 | 1,4297 | 1,5141 | –0,0844 | 0,0011 | 1,4418 | 1,5779 | 2,1076 |
| F25 | 1,2458 | 1,3286 | –0,0828 | 0,0021 | 1,2530 | 1,4128 | 1,0962 |
| F26 | 1 | 1,1890 | –0,1890 | 0,0154 | 1,0071 | 1,4073 | 0,7752 |
| F27 | 1,3174 | 1,4075 | –0,0901 | 0,0024 | 1,3237 | 1,5083 | 1,1111 |
| F28 | 1,4138 | 1,5356 | –0,1218 | 0,0060 | 1,4226 | 1,7064 | 0,8228 |
| F29 | 1 | 1,1887 | –0,1887 | 0,0181 | 1,0053 | 1,4290 | 0,6568 |
| F30 | 1,5773 | 1,6639 | –0,0866 | 0,0014 | 1,5892 | 1,7369 | 1,7731 |
| F31 | 1,0218 | 1,1226 | –0,1008 | 0,0044 | 1,0287 | 1,2600 | 0,7661 |
| F32 | 1 | 1,1888 | –0,1888 | 0,0176 | 1,0061 | 1,4210 | 0,6736 |
| F33 | 1,5808 | 1,6658 | –0,0850 | 0,0014 | 1,5926 | 1,7380 | 1,6677 |
| F34 | 1 | 1,0793 | –0,0793 | 0,0038 | 1,0034 | 1,2422 | 0,5463 |
| F35 | 1,3983 | 1,5084 | –0,1101 | 0,0045 | 1,4082 | 1,6710 | 0,8914 |
| F36 | 1,4624 | 1,5678 | –0,1054 | 0,0028 | 1,4722 | 1,6756 | 1,3088 |
| F37 | 1 | 1,1955 | –0,1955 | 0,0185 | 1,0052 | 1,4359 | 0,6889 |
| F38 | 1 | 1,1890 | –0,1890 | 0,0161 | 1,0062 | 1,4255 | 0,7380 |
| F39 | 1 | 1,1953 | –0,1953 | 0,0169 | 1,0063 | 1,4374 | 0,7503 |
| F40 | 1 | 1,1414 | –0,1414 | 0,0082 | 1,0068 | 1,3157 | 0,8110 |
| F41 | 1,5395 | 1,6857 | –0,1462 | 0,0055 | 1,5497 | 1,8226 | 1,2961 |
| F42 | 1,3087 | 1,4356 | –0,1269 | 0,0084 | 1,3158 | 1,6267 | 0,6367 |
| F43 | 1,1438 | 1,2676 | –0,1238 | 0,0059 | 1,1511 | 1,4171 | 0,8658 |
| F44 | 1,099 | 1,2273 | –0,1283 | 0,0075 | 1,1058 | 1,4095 | 0,7352 |
| F45 | 1 | 1,1872 | –0,1872 | 0,0148 | 1,0069 | 1,4007 | 0,7891 |
| F46 | 1 | 1,1978 | –0,1978 | 0,0204 | 1,0058 | 1,4589 | 0,6388 |
| F47 | 1,4729 | 1,5425 | –0,0696 | 0,0012 | 1,4827 | 1,6169 | 1,3158 |
| F48 | 1,1233 | 1,2505 | –0,1272 | 0,0062 | 1,1308 | 1,4284 | 0,8713 |
| F49 | 1,3341 | 1,4418 | –0,1077 | 0,0044 | 1,3424 | 1,5895 | 0,8850 |
| F50 | 1,1647 | 1,2470 | –0,0823 | 0,0025 | 1,1734 | 1,3537 | 0,8959 |
| F51 | 1 | 1,1611 | –0,1611 | 0,0096 | 1,0062 | 1,3284 | 0,8992 |
| F52 | 1,1846 | 1,2384 | –0,0538 | 0,0009 | 1,1909 | 1,3069 | 1,1229 |
| F53 | 1 | 1,1520 | –0,1520 | 0,0092 | 1,0058 | 1,3276 | 0,8392 |
| F54 | 1 | 1,1896 | –0,1896 | 0,0206 | 1,0057 | 1,4581 | 0,5827 |
| F55 | 1,4524 | 1,6204 | –0,1680 | 0,0154 | 1,4613 | 1,8943 | 0,6100 |
| F56 | 1 | 1,1907 | –0,1907 | 0,0189 | 1,0061 | 1,4377 | 0,6404 |
| F57 | 1 | 1,1661 | –0,1661 | 0,0113 | 1,0064 | 1,3617 | 0,8140 |
| F58 | 1,3546 | 1,4238 | –0,0692 | 0,0013 | 1,3627 | 1,5122 | 1,2090 |
| F59 | 1 | 1,1911 | –0,1911 | 0,0172 | 1,0061 | 1,4362 | 0,7071 |
| F60 | 1,364 | 1,4506 | –0,0866 | 0,0029 | 1,3727 | 1,5807 | 0,8740 |
| F61 | 1 | 1,1285 | –0,1285 | 0,0085 | 1,0079 | 1,3233 | 0,6455 |
| F62 | 1 | 1,0872 | –0,0872 | 0,0047 | 1,0045 | 1,2514 | 0,5372 |
| F63 | 4,9998 | 5,5136 | –0,5138 | 0,0785 | 5,0320 | 6,0848 | 1,1209 |
| F64 | 1 | 1,1951 | –0,1951 | 0,0206 | 1,0077 | 1,4497 | 0,6159 |
| F65 | 1,1826 | 1,2342 | –0,0516 | 0,0009 | 1,1895 | 1,3119 | 0,9573 |
| F66 | 1 | 1,1670 | –0,1670 | 0,0097 | 1,0080 | 1,2968 | 0,9584 |
| F67 | 1,7256 | 1,8921 | –0,1665 | 0,0075 | 1,7363 | 2,0562 | 1,2327 |
| F68 | 1 | 1,1937 | –0,1937 | 0,0183 | 1,0063 | 1,4595 | 0,6851 |
| F69 | 1,1614 | 1,2613 | –0,0999 | 0,0041 | 1,1682 | 1,4041 | 0,8166 |
| F70 | 1 | 1,1721 | –0,1721 | 0,0117 | 1,0060 | 1,3609 | 0,8465 |
| F71 | 1,2467 | 1,3524 | –0,1057 | 0,0030 | 1,2556 | 1,4629 | 1,2249 |
| F72 | 1,4375 | 1,5680 | –0,1305 | 0,0056 | 1,4482 | 1,7144 | 1,0152 |
| F73 | 1,246 | 1,2870 | –0,0410 | 0,0004 | 1,2541 | 1,3306 | 1,5012 |
| F74 | 1,4173 | 1,5538 | –0,1365 | 0,0107 | 1,4252 | 1,7807 | 0,5777 |
| F75 | 1,1943 | 1,3117 | –0,1174 | 0,0046 | 1,2019 | 1,4531 | 0,9939 |
| F76 | 1,4037 | 1,5237 | –0,1200 | 0,0040 | 1,4137 | 1,6428 | 1,2148 |
| F77 | 1 | 1,0887 | –0,0887 | 0,0015 | 1,0069 | 1,1600 | 1,7121 |
| F78 | 1 | 1,1927 | –0,1927 | 0,0178 | 1,0068 | 1,4480 | 0,6956 |
| F79 | 1 | 1,1823 | –0,1823 | 0,0139 | 1,0048 | 1,3908 | 0,7948 |
| F80 | 1 | 1,1325 | –0,1325 | 0,0087 | 1,0067 | 1,3270 | 0,6689 |
| F81 | 1 | 1,1902 | –0,1902 | 0,0194 | 1,0046 | 1,4397 | 0,6202 |
| F82 | 1,2306 | 1,3107 | –0,0801 | 0,0017 | 1,2385 | 1,3941 | 1,2886 |
| F83 | 1,0006 | 1,0628 | –0,0622 | 0,0022 | 1,0050 | 1,1733 | 0,5966 |
| F84 | 1,5381 | 1,6419 | –0,1038 | 0,0027 | 1,5490 | 1,7408 | 1,3523 |
| F85 | 1,6152 | 1,7374 | –0,1222 | 0,0039 | 1,6244 | 1,8633 | 1,2658 |
| F86 | 1,4458 | 1,5574 | –0,1116 | 0,0040 | 1,4556 | 1,6932 | 1,0322 |
| F87 | 1,5532 | 1,6940 | –0,1408 | 0,0073 | 1,5641 | 1,8827 | 0,9081 |
| F88 | 1,2073 | 1,2977 | –0,0904 | 0,0024 | 1,2171 | 1,4039 | 1,1472 |
| F89 | 1,34 | 1,4210 | –0,0810 | 0,0014 | 1,3479 | 1,4982 | 1,5437 |
| F90 | 1,4935 | 1,5663 | –0,0728 | 0,0011 | 1,5000 | 1,6385 | 1,5399 |
| F91 | 1,1176 | 1,2262 | –0,1086 | 0,0052 | 1,1251 | 1,3816 | 0,7515 |
| F92 | 1 | 1,0692 | –0,0692 | 0,0021 | 1,0065 | 1,1801 | 0,7565 |
| F93 | 1,6544 | 1,7280 | –0,0736 | 0,0009 | 1,6659 | 1,7880 | 2,0744 |
| F94 | 1,4024 | 1,4902 | –0,0878 | 0,0031 | 1,4090 | 1,6164 | 0,8336 |
| F95 | 1,5072 | 1,6669 | –0,1597 | 0,0104 | 1,5147 | 1,8859 | 0,8143 |
| F96 | 1,7621 | 1,9088 | –0,1467 | 0,0056 | 1,7737 | 2,0627 | 1,2755 |
| F97 | 1 | 1,1520 | –0,1520 | 0,0080 | 1,0052 | 1,3172 | 0,9625 |
| F98 | 1 | 1,1627 | –0,1627 | 0,0095 | 1,0071 | 1,3324 | 0,9333 |
| Media | 1,2834 | 1,4111 | –0,1277 | 0,0080 | 1,2915 | 1,5707 | 0,9705 |
Año 2010. Coeficientes de eficiencia VRS de orientación input. Simar y Wilson (2000)
| DMU | δˆ | δˆˆ | biâsB(δˆ) | σˆ2 | LL | UL | ri |
|---|---|---|---|---|---|---|---|
| F1 | 1,2208 | 1,2825 | –0,0617 | 0,0009 | 1,2282 | 1,3464 | 1,4723 |
| F2 | 1 | 1,1283 | –0,1283 | 0,0053 | 1,0074 | 1,2420 | 1,0276 |
| F3 | 1 | 1,1029 | –0,1029 | 0,0061 | 1,0056 | 1,2998 | 0,5813 |
| F4 | 1,0515 | 1,1187 | –0,0672 | 0,0013 | 1,0588 | 1,1964 | 1,1328 |
| F5 | 1,4967 | 1,5889 | –0,0922 | 0,0022 | 1,5036 | 1,6818 | 1,2982 |
| F6 | 1,3505 | 1,4238 | –0,0733 | 0,0014 | 1,3575 | 1,5008 | 1,3115 |
| F7 | 1,085 | 1,1591 | –0,0741 | 0,0021 | 1,0914 | 1,2692 | 0,8583 |
| F8 | 1,1854 | 1,2745 | –0,0891 | 0,0028 | 1,1936 | 1,3919 | 0,9597 |
| F9 | 1,2038 | 1,2686 | –0,0648 | 0,0011 | 1,2121 | 1,3416 | 1,2283 |
| F10 | 1,1935 | 1,2869 | –0,0934 | 0,0024 | 1,2003 | 1,3861 | 1,1893 |
| F11 | 1,4968 | 1,6019 | –0,1051 | 0,0030 | 1,5047 | 1,7132 | 1,2479 |
| F12 | 1,6664 | 1,8045 | –0,1381 | 0,0065 | 1,6760 | 1,9883 | 0,9773 |
| F13 | 1 | 1,1090 | –0,1090 | 0,0053 | 1,0054 | 1,2738 | 0,7489 |
| F14 | 1,1995 | 1,3015 | –0,1020 | 0,0033 | 1,2067 | 1,4255 | 1,0512 |
| F15 | 1 | 1,1671 | –0,1671 | 0,0185 | 1,0055 | 1,5462 | 0,5024 |
| F16 | 1,2837 | 1,3564 | –0,0727 | 0,0014 | 1,2922 | 1,4428 | 1,2973 |
| F17 | 1 | 1,1654 | –0,1654 | 0,0160 | 1,0061 | 1,4260 | 0,5686 |
| F18 | 1 | 1,1025 | –0,1025 | 0,0030 | 1,0067 | 1,2121 | 1,1577 |
| F19 | 1,2802 | 1,3705 | –0,0903 | 0,0029 | 1,2884 | 1,4978 | 0,9388 |
| F20 | 1,0043 | 1,0419 | –0,0376 | 0,0004 | 1,0099 | 1,0886 | 1,1806 |
| F21 | 1,3079 | 1,3759 | –0,0680 | 0,0009 | 1,3154 | 1,4352 | 1,6912 |
| F22 | 1,3412 | 1,4328 | –0,0916 | 0,0021 | 1,3500 | 1,5243 | 1,3634 |
| F23 | 1,6404 | 1,7225 | –0,0821 | 0,0019 | 1,6508 | 1,8177 | 1,1706 |
| F24 | 1,5727 | 1,6580 | –0,0853 | 0,0019 | 1,5816 | 1,7460 | 1,3010 |
| F25 | 1,2658 | 1,3187 | –0,0529 | 0,0007 | 1,2716 | 1,3777 | 1,3732 |
| F26 | 1 | 1,1656 | –0,1656 | 0,0155 | 1,0056 | 1,4273 | 0,5911 |
| F27 | 1,2796 | 1,3871 | –0,1075 | 0,0035 | 1,2857 | 1,5035 | 1,1147 |
| F28 | 1,1845 | 1,2787 | –0,0942 | 0,0028 | 1,1915 | 1,3901 | 1,0528 |
| F29 | 1 | 1,1713 | –0,1713 | 0,0197 | 1,0055 | 1,5441 | 0,4970 |
| F30 | 1,642 | 1,7235 | –0,0815 | 0,0023 | 1,6513 | 1,8327 | 0,9674 |
| F31 | 1 | 1,1557 | –0,1557 | 0,0116 | 1,0059 | 1,3739 | 0,6971 |
| F32 | 1 | 1,1705 | –0,1705 | 0,0189 | 1,0067 | 1,5349 | 0,5122 |
| F33 | 1,7563 | 1,8730 | –0,1167 | 0,0039 | 1,7633 | 2,0008 | 1,1747 |
| F34 | 1 | 1,1435 | –0,1435 | 0,0089 | 1,0079 | 1,3377 | 0,7681 |
| F35 | 1,1992 | 1,2478 | –0,0486 | 0,0007 | 1,2055 | 1,3120 | 1,0992 |
| F36 | 1 | 1,1705 | –0,1705 | 0,0195 | 1,0072 | 1,5423 | 0,4977 |
| F37 | 1 | 1,1528 | –0,1528 | 0,0108 | 1,0052 | 1,3544 | 0,7191 |
| F38 | 1 | 1,1671 | –0,1671 | 0,0173 | 1,0053 | 1,4940 | 0,5375 |
| F39 | 1 | 1,1683 | –0,1683 | 0,0187 | 1,0063 | 1,5444 | 0,5042 |
| F40 | 1,0294 | 1,1042 | –0,0748 | 0,0022 | 1,0377 | 1,2060 | 0,8362 |
| F41 | 1,3822 | 1,4602 | –0,0780 | 0,0017 | 1,3901 | 1,5399 | 1,1935 |
| F42 | 1 | 1,1429 | –0,1429 | 0,0094 | 1,0072 | 1,3346 | 0,7234 |
| F43 | 1,12 | 1,2056 | –0,0856 | 0,0029 | 1,1262 | 1,3326 | 0,8448 |
| F44 | 1,0784 | 1,1677 | –0,0893 | 0,0036 | 1,0852 | 1,3168 | 0,7443 |
| F45 | 1 | 1,1478 | –0,1478 | 0,0104 | 1,0049 | 1,3520 | 0,7023 |
| F46 | 2,2047 | 2,4276 | –0,2229 | 0,0301 | 2,2171 | 2,8566 | 0,5502 |
| F47 | 1,4526 | 1,5068 | –0,0542 | 0,0008 | 1,4608 | 1,5709 | 1,2019 |
| F48 | 1,1131 | 1,1789 | –0,0658 | 0,0010 | 1,1198 | 1,2464 | 1,4250 |
| F49 | 1,0127 | 1,0928 | –0,0801 | 0,0023 | 1,0202 | 1,1982 | 0,9153 |
| F50 | 1,3008 | 1,4035 | –0,1027 | 0,0034 | 1,3098 | 1,5155 | 1,0194 |
| F51 | 1,1421 | 1,2532 | –0,1111 | 0,0056 | 1,1506 | 1,4296 | 0,7349 |
| F52 | 1,432 | 1,5295 | –0,0975 | 0,0031 | 1,4399 | 1,6555 | 1,0117 |
| F53 | 1 | 1,1224 | –0,1224 | 0,0056 | 1,0066 | 1,2712 | 0,8960 |
| F54 | 1 | 1,1693 | –0,1693 | 0,0188 | 1,0057 | 1,5292 | 0,5085 |
| F55 | 1,115 | 1,2313 | –0,1163 | 0,0077 | 1,1214 | 1,4417 | 0,5846 |
| F56 | 1 | 1,1657 | –0,1657 | 0,0196 | 1,0048 | 1,5516 | 0,4678 |
| F57 | 1 | 1,1356 | –0,1356 | 0,0075 | 1,0070 | 1,3077 | 0,8195 |
| F58 | 2,6677 | 2,9458 | –0,2781 | 0,0327 | 2,6860 | 3,3732 | 0,7886 |
| F59 | 1 | 1,1556 | –0,1556 | 0,0135 | 1,0059 | 1,3977 | 0,5995 |
| F60 | 1,2192 | 1,3030 | –0,0838 | 0,0018 | 1,2247 | 1,3818 | 1,3031 |
| F61 | 1 | 1,1635 | –0,1635 | 0,0131 | 1,0068 | 1,3898 | 0,6826 |
| F62 | 1,1904 | 1,2658 | –0,0754 | 0,0013 | 1,1971 | 1,3361 | 1,4154 |
| F63 | 1 | 1,1248 | –0,1248 | 0,0054 | 1,0046 | 1,2593 | 0,9632 |
| F64 | 1 | 1,1663 | –0,1663 | 0,0187 | 1,0047 | 1,5380 | 0,4925 |
| F65 | 1,3283 | 1,4450 | –0,1167 | 0,0042 | 1,3353 | 1,5835 | 1,0757 |
| F66 | 1 | 1,0533 | –0,0533 | 0,0006 | 1,0059 | 1,1018 | 1,5587 |
| F67 | 1 | 1,1644 | –0,1644 | 0,0192 | 1,0046 | 1,5491 | 0,4683 |
| F68 | 1 | 1,1655 | –0,1655 | 0,0171 | 1,0062 | 1,4808 | 0,5336 |
| F69 | 1,1634 | 1,2662 | –0,1028 | 0,0050 | 1,1717 | 1,4413 | 0,6988 |
| F70 | 1 | 1,1474 | –0,1474 | 0,0097 | 1,0043 | 1,3342 | 0,7460 |
| F71 | 1,1781 | 1,2346 | –0,0565 | 0,0009 | 1,1842 | 1,3015 | 1,2364 |
| F72 | 1,1644 | 1,2369 | –0,0725 | 0,0019 | 1,1742 | 1,3368 | 0,8987 |
| F73 | 2,2974 | 2,4740 | –0,1766 | 0,0185 | 2,3131 | 2,8152 | 0,5620 |
| F74 | 1,1124 | 1,2201 | –0,1077 | 0,0040 | 1,1184 | 1,3581 | 0,9744 |
| F75 | 1,145 | 1,2234 | –0,0784 | 0,0024 | 1,1504 | 1,3328 | 0,8463 |
| F76 | 1,3682 | 1,4596 | –0,0914 | 0,0018 | 1,3764 | 1,5376 | 1,5704 |
| F77 | 2,1201 | 2,2199 | –0,0998 | 0,0030 | 2,1326 | 2,3420 | 1,1242 |
| F78 | 1 | 1,1641 | –0,1641 | 0,0174 | 1,0068 | 1,5305 | 0,5158 |
| F79 | 1 | 1,1547 | –0,1547 | 0,0128 | 1,0047 | 1,3840 | 0,6216 |
| F80 | 1 | 1,1672 | –0,1672 | 0,0162 | 1,0070 | 1,4433 | 0,5754 |
| F81 | 1 | 1,1685 | –0,1685 | 0,0188 | 1,0065 | 1,5461 | 0,5040 |
| F82 | 1,3363 | 1,4338 | –0,0975 | 0,0028 | 1,3452 | 1,5446 | 1,1225 |
| F83 | 1,0009 | 1,0530 | –0,0521 | 0,0014 | 1,0055 | 1,1433 | 0,6503 |
| F84 | 1,2735 | 1,3155 | –0,0420 | 0,0004 | 1,2819 | 1,3592 | 1,5642 |
| F85 | 1,6012 | 1,7005 | –0,0993 | 0,0021 | 1,6121 | 1,7818 | 1,5751 |
| F86 | 1,3268 | 1,4294 | –0,1026 | 0,0035 | 1,3348 | 1,5456 | 0,9900 |
| F87 | 1,2987 | 1,4062 | –0,1075 | 0,0041 | 1,3064 | 1,5480 | 0,9349 |
| F88 | 1,1903 | 1,2755 | –0,0852 | 0,0022 | 1,1964 | 1,3759 | 1,0978 |
| F89 | 1,6256 | 1,7434 | –0,1178 | 0,0054 | 1,6365 | 1,9247 | 0,8509 |
| F90 | 1,3996 | 1,4877 | –0,0881 | 0,0017 | 1,4089 | 1,5729 | 1,5126 |
| F91 | 1,1459 | 1,2238 | –0,0779 | 0,0018 | 1,1522 | 1,3090 | 1,1486 |
| F92 | 1 | 1,0615 | –0,0615 | 0,0015 | 1,0060 | 1,1490 | 0,8588 |
| F93 | 1,5568 | 1,6290 | –0,0722 | 0,0018 | 1,5644 | 1,7298 | 0,9544 |
| F94 | 1,4688 | 1,5344 | –0,0656 | 0,0009 | 1,4768 | 1,5938 | 1,6832 |
| F95 | 1,2239 | 1,3064 | –0,0825 | 0,0024 | 1,2295 | 1,4174 | 0,9582 |
| F96 | 1,2383 | 1,3236 | –0,0853 | 0,0018 | 1,2454 | 1,4128 | 1,3286 |
| F97 | 1 | 1,0957 | –0,0957 | 0,0038 | 1,0053 | 1,2396 | 0,8068 |
| F98 | 1 | 1,1620 | –0,1620 | 0,0139 | 1,0052 | 1,3873 | 0,6295 |
| Mean | 1,2238 | 1,3353 | –0,1115 | 0,0069 | 1,2310 | 1,5015 | 0,9486 |
Periodo 2008-2010. Coeficientes de eficiencia VRS de orientación input. Simar y Wilson (2000)
| DMU | δˆ | δˆˆ | biâsB(δˆ) | σˆ2 | LL | UL | ri |
|---|---|---|---|---|---|---|---|
| F1 | 1,1696 | 1,2160 | –0,0464 | 0,0005 | 1,1759 | 1,2600 | 1,4878 |
| F2 | 1 | 1,1378 | –0,1378 | 0,0093 | 1,0039 | 1,2982 | 0,6827 |
| F3 | 1 | 1,0899 | –0,0899 | 0,0048 | 1,0048 | 1,2537 | 0,5578 |
| F4 | 1,0676 | 1,1052 | –0,0376 | 0,0004 | 1,0720 | 1,1490 | 1,1827 |
| F5 | 1,3505 | 1,4030 | –0,0525 | 0,0006 | 1,3570 | 1,4560 | 1,4546 |
| F6 | 1,2777 | 1,3178 | –0,0401 | 0,0004 | 1,2828 | 1,3641 | 1,1959 |
| F7 | 1,244 | 1,3254 | –0,0814 | 0,0020 | 1,2495 | 1,4163 | 1,1159 |
| F8 | 1,1422 | 1,2011 | –0,0589 | 0,0010 | 1,1485 | 1,2720 | 1,1936 |
| F9 | 1,2734 | 1,3612 | –0,0878 | 0,0034 | 1,2788 | 1,4843 | 0,7617 |
| F10 | 1,3671 | 1,4757 | –0,1086 | 0,0051 | 1,3720 | 1,6335 | 0,7758 |
| F11 | 1,301 | 1,3719 | –0,0709 | 0,0015 | 1,3055 | 1,4549 | 1,1092 |
| F12 | 1,4351 | 1,5218 | –0,0867 | 0,0022 | 1,4419 | 1,6230 | 1,1327 |
| F13 | 1 | 1,0971 | –0,0971 | 0,0039 | 1,0061 | 1,2376 | 0,7973 |
| F14 | 1,2185 | 1,3044 | –0,0859 | 0,0025 | 1,2247 | 1,4072 | 0,9925 |
| F15 | 1 | 1,1409 | –0,1409 | 0,0098 | 1,0046 | 1,3322 | 0,6748 |
| F16 | 1,1945 | 1,2544 | –0,0599 | 0,0009 | 1,1994 | 1,3198 | 1,2633 |
| F17 | 1 | 1,1457 | –0,1457 | 0,0124 | 1,0057 | 1,3851 | 0,5713 |
| F18 | 1,2931 | 1,3880 | –0,0949 | 0,0036 | 1,2975 | 1,5230 | 0,8284 |
| F19 | 1,1823 | 1,2437 | –0,0614 | 0,0013 | 1,1890 | 1,3300 | 0,9886 |
| F20 | 1,0656 | 1,1248 | –0,0592 | 0,0010 | 1,0692 | 1,1893 | 1,1471 |
| F21 | 1,3026 | 1,3604 | –0,0578 | 0,0007 | 1,3083 | 1,4142 | 1,5596 |
| F22 | 1,4068 | 1,4638 | –0,0570 | 0,0007 | 1,4142 | 1,5205 | 1,5485 |
| F23 | 1,4762 | 1,5477 | –0,0715 | 0,0016 | 1,4818 | 1,6298 | 1,0668 |
| F24 | 1,3288 | 1,3696 | –0,0408 | 0,0004 | 1,3342 | 1,4139 | 1,3186 |
| F25 | 1,1618 | 1,2100 | –0,0482 | 0,0007 | 1,1672 | 1,2623 | 1,1450 |
| F26 | 1 | 1,1469 | –0,1469 | 0,0126 | 1,0040 | 1,3906 | 0,5695 |
| F27 | 1,2656 | 1,3618 | –0,0962 | 0,0029 | 1,2717 | 1,4653 | 1,0522 |
| F28 | 1,4765 | 1,5719 | –0,0954 | 0,0049 | 1,4831 | 1,7445 | 0,6209 |
| F29 | 1 | 1,1504 | –0,1504 | 0,0148 | 1,0048 | 1,4493 | 0,5093 |
| F30 | 1,444 | 1,4857 | –0,0417 | 0,0006 | 1,4494 | 1,5446 | 0,9719 |
| F31 | 1 | 1,0974 | –0,0974 | 0,0035 | 1,0050 | 1,2250 | 0,8964 |
| F32 | 1 | 1,1515 | –0,1515 | 0,0149 | 1,0046 | 1,4519 | 0,5139 |
| F33 | 1,4868 | 1,5345 | –0,0477 | 0,0006 | 1,4941 | 1,5920 | 1,2221 |
| F34 | 1 | 1,0756 | –0,0756 | 0,0035 | 1,0038 | 1,2253 | 0,5503 |
| F35 | 1,3143 | 1,4046 | –0,0903 | 0,0026 | 1,3213 | 1,5142 | 1,0389 |
| F36 | 1,5453 | 1,6535 | –0,1082 | 0,0041 | 1,5520 | 1,7869 | 0,9555 |
| F37 | 1 | 1,1426 | –0,1426 | 0,0109 | 1,0048 | 1,3412 | 0,6230 |
| F38 | 1 | 1,1488 | –0,1488 | 0,0132 | 1,0051 | 1,4482 | 0,5580 |
| F39 | 1 | 1,1517 | –0,1517 | 0,0143 | 1,0055 | 1,4563 | 0,5353 |
| F40 | 1 | 1,0878 | –0,0878 | 0,0029 | 1,0048 | 1,2078 | 0,8786 |
| F41 | 1,3098 | 1,4003 | –0,0905 | 0,0028 | 1,3153 | 1,5075 | 0,9777 |
| F42 | 1,0542 | 1,1347 | –0,0805 | 0,0026 | 1,0590 | 1,2471 | 0,8445 |
| F43 | 1,0535 | 1,1383 | –0,0848 | 0,0025 | 1,0584 | 1,2485 | 0,9578 |
| F44 | 1,0359 | 1,1157 | –0,0798 | 0,0038 | 1,0404 | 1,2619 | 0,5607 |
| F45 | 1 | 1,1437 | –0,1437 | 0,0113 | 1,0050 | 1,3544 | 0,6076 |
| F46 | 1 | 1,1516 | –0,1516 | 0,0153 | 1,0040 | 1,4603 | 0,4998 |
| F47 | 1,4403 | 1,5072 | –0,0669 | 0,0009 | 1,4470 | 1,5704 | 1,6428 |
| F48 | 1,0597 | 1,1366 | –0,0769 | 0,0022 | 1,0645 | 1,2483 | 0,8914 |
| F49 | 1,2691 | 1,3698 | –0,1007 | 0,0040 | 1,2753 | 1,5020 | 0,8362 |
| F50 | 1,0377 | 1,0846 | –0,0469 | 0,0005 | 1,0431 | 1,1296 | 1,3604 |
| F51 | 1 | 1,1320 | –0,1320 | 0,0079 | 1,0052 | 1,2979 | 0,7318 |
| F52 | 1,1819 | 1,2529 | –0,0710 | 0,0015 | 1,1892 | 1,3358 | 1,1142 |
| F53 | 1 | 1,1227 | –0,1227 | 0,0067 | 1,0043 | 1,2849 | 0,7534 |
| F54 | 1 | 1,1545 | –0,1545 | 0,0153 | 1,0045 | 1,4531 | 0,5199 |
| F55 | 1,4562 | 1,5780 | –0,1218 | 0,0068 | 1,4655 | 1,7668 | 0,7285 |
| F56 | 1 | 1,1510 | –0,1510 | 0,0149 | 1,0060 | 1,4545 | 0,5107 |
| F57 | 1 | 1,1303 | –0,1303 | 0,0083 | 1,0043 | 1,3101 | 0,6807 |
| F58 | 2,6578 | 2,9117 | –0,2539 | 0,0315 | 2,6769 | 3,3227 | 0,6819 |
| F59 | 1 | 1,1502 | –0,1502 | 0,0131 | 1,0044 | 1,4263 | 0,5732 |
| F60 | 1,233 | 1,3018 | –0,0688 | 0,0015 | 1,2390 | 1,3925 | 1,0334 |
| F61 | 1 | 1,1175 | –0,1175 | 0,0066 | 1,0044 | 1,2959 | 0,6993 |
| F62 | 1,2418 | 1,3233 | –0,0815 | 0,0029 | 1,2484 | 1,4637 | 0,7625 |
| F63 | 1,8226 | 1,9531 | –0,1305 | 0,0056 | 1,8309 | 2,1119 | 1,0102 |
| F64 | 1 | 1,1518 | –0,1518 | 0,0144 | 1,0052 | 1,4387 | 0,5323 |
| F65 | 1,1828 | 1,2541 | –0,0713 | 0,0013 | 1,1890 | 1,3231 | 1,2913 |
| F66 | 1 | 1,1286 | –0,1286 | 0,0065 | 1,0058 | 1,2405 | 0,8465 |
| F67 | 1 | 1,1473 | –0,1473 | 0,0143 | 1,0051 | 1,4459 | 0,5052 |
| F68 | 1 | 1,1512 | –0,1512 | 0,0139 | 1,0043 | 1,4401 | 0,5498 |
| F69 | 1,1062 | 1,1886 | –0,0824 | 0,0031 | 1,1106 | 1,3234 | 0,7303 |
| F70 | 1 | 1,1463 | –0,1463 | 0,0106 | 1,0053 | 1,3408 | 0,6755 |
| F71 | 1,1067 | 1,1600 | –0,0533 | 0,0007 | 1,1121 | 1,2183 | 1,4131 |
| F72 | 1,2053 | 1,2755 | –0,0702 | 0,0014 | 1,2124 | 1,3514 | 1,1691 |
| F73 | 1,597 | 1,7259 | –0,1289 | 0,0080 | 1,6041 | 1,9006 | 0,6904 |
| F74 | 1,2575 | 1,3556 | –0,0981 | 0,0063 | 1,2617 | 1,5286 | 0,5071 |
| F75 | 1,0894 | 1,1583 | –0,0689 | 0,0019 | 1,0944 | 1,2597 | 0,8187 |
| F76 | 1,3118 | 1,3896 | –0,0778 | 0,0015 | 1,3177 | 1,4717 | 1,3040 |
| F77 | 1,285 | 1,3249 | –0,0399 | 0,0004 | 1,2901 | 1,3683 | 1,3797 |
| F78 | 1 | 1,1470 | –0,1470 | 0,0138 | 1,0045 | 1,4189 | 0,5233 |
| F79 | 1 | 1,1463 | –0,1463 | 0,0115 | 1,0047 | 1,3531 | 0,6181 |
| F80 | 1 | 1,1420 | –0,1420 | 0,0102 | 1,0052 | 1,3350 | 0,6593 |
| F81 | 1 | 1,1518 | –0,1518 | 0,0152 | 1,0055 | 1,4500 | 0,5060 |
| F82 | 1,2014 | 1,2595 | –0,0581 | 0,0010 | 1,2060 | 1,3283 | 1,1850 |
| F83 | 1,0006 | 1,0456 | –0,0450 | 0,0012 | 1,0037 | 1,1344 | 0,5610 |
| F84 | 1,2698 | 1,3256 | –0,0558 | 0,0007 | 1,2749 | 1,3734 | 1,5724 |
| F85 | 1,3894 | 1,4505 | –0,0611 | 0,0009 | 1,3966 | 1,5080 | 1,4339 |
| F86 | 1,1959 | 1,2577 | –0,0618 | 0,0009 | 1,2019 | 1,3189 | 1,3891 |
| F87 | 1,225 | 1,2947 | –0,0697 | 0,0015 | 1,2300 | 1,3797 | 1,0473 |
| F88 | 1,0564 | 1,1220 | –0,0656 | 0,0016 | 1,0618 | 1,2136 | 0,8949 |
| F89 | 1,9519 | 2,0635 | –0,1116 | 0,0048 | 1,9619 | 2,2157 | 0,8588 |
| F90 | 1,3232 | 1,3712 | –0,0480 | 0,0006 | 1,3299 | 1,4266 | 1,3231 |
| F91 | 1,1121 | 1,1629 | –0,0508 | 0,0009 | 1,1172 | 1,2355 | 0,9928 |
| F92 | 1 | 1,0495 | –0,0495 | 0,0013 | 1,0044 | 1,1412 | 0,6350 |
| F93 | 1,4569 | 1,5170 | –0,0601 | 0,0010 | 1,4635 | 1,5850 | 1,2212 |
| F94 | 1,2973 | 1,3409 | –0,0436 | 0,0003 | 1,3025 | 1,3771 | 1,9640 |
| F95 | 1,2586 | 1,3468 | –0,0882 | 0,0036 | 1,2635 | 1,4796 | 0,7209 |
| F96 | 1,2573 | 1,3095 | –0,0522 | 0,0006 | 1,2630 | 1,3651 | 1,4350 |
| F97 | 1 | 1,1177 | –0,1177 | 0,0056 | 1,0047 | 1,2654 | 0,8312 |
| F98 | 1 | 1,1457 | –0,1457 | 0,0115 | 1,0043 | 1,3458 | 0,6175 |
| Mean | 1,1917 | 1,2870 | –0,0954 | 0,0053 | 1,1973 | 1,4267 | 0,9228 |
Las columnas δˆ y δˆˆ proporcionan respectivamente los coeficientes VRS originales y los coeficientes insesgados11. La columna biâsB(δˆ) contiene el sesgo estimado mediante bootstrap, considerando a tal efecto un valor B=2.000 replicaciones. Las tres últimas columnas muestran los datos de inferencia estadística, la varianza estimada y los límites inferiores (LL) y superiores (UL) de los intervalos de confianza al 95%. Los índices de eficiencia obtenidos mediante el modelo bootstrap se encuentran dentro de los límites inferiores y superiores; se trata de una estimación más robusta de la eficiencia técnica pura que la ofrecida por los modelos DEA básicos, como el VRS.
En la tabla 11 se resumen de manera comparada los resultados para cada uno de los tres años y para el periodo total. El promedio para 2008 del índice insesgado de eficiencia técnica pura es 1,3925, lo que sugiere que, en promedio, las fundaciones podrían haber reducido sus inputs en un 39,25%. En 2009 el valor promedio es algo superior (1,4111), y 2010 resulta ser el mejor ejercicio, con 1,3353. El periodo 2008-2010 en su conjunto presenta un valor promedio de 1,2870.
Coeficientes medios de eficiencia. VRS–Insesgados. Orientación Input. Simar y Wilson (2000)
| Periodo | δˆ | δˆˆ | biâsB(δˆ) | σˆ2 | LL | UL |
|---|---|---|---|---|---|---|
| 2008 | 1,2876 | 1,3925 | –0,1048 | 0,0079 | 1,2954 | 1,5365 |
| 2009 | 1,2834 | 1,4111 | –0,1277 | 0,0080 | 1,2915 | 1,5707 |
| 2010 | 1,2238 | 1,3353 | –0,1115 | 0,0069 | 1,2310 | 1,5015 |
| 2008-2010 | 1,1917 | 1,2870 | –0,0954 | 0,0053 | 1,1973 | 1,4267 |
Una vez determinado el nivel de eficiencia de las fundaciones españolas para el periodo objeto de estudio, se procede a abordar el problema de cómo mejorar dicho nivel, planteando unas hipótesis de partida a contrastar. La metodología de apoyo se basa en el análisis de determinantes de la eficiencia de las fundaciones durante el periodo 2008-2010 mediante el procedimiento bietápico de Simar y Wilson (2007).
La tabla 12 contiene la selección y descripción de las variables seleccionadas para esta fase del análisis, basándonos en la información de la que disponemos y en la literatura existente.
Análisis de determinantes de eficiencia. Factores ambientales
| Nombre | Descripción |
|---|---|
| TYPE | Variable Dummy. Privada / Pública. 0 = Privada, 1 = Pública |
| FISIC | Variable Dummy. Fundadores Personas Físicas. 0 = No, 1 = Sí |
| FPRIV | Variable Dummy. Fundadores Personas Jurídicas Privadas. 0 = No, 1 = Sí |
| YEARS | Antigüedad en años (esta variable toma valores diferentes para cada año) |
| VOLUNT | Variable Dummy. Existencia de voluntarios. 0 = No, 1 = Sí (esta variable toma valores diferentes para cada año) |
| PATR | Número de patronos (esta variable toma valores diferentes para cada año) |
A continuación planteamos las hipótesis a contrastar:Hipótesis 1 Las fundaciones de naturaleza privada son más eficientes al ser más ágiles en su gestión, debido a que cuentan con menos trabas burocráticas. En este sentido, no hemos encontrado ningún trabajo que considere la naturaleza pública o privada de las fundaciones como determinante de su eficiencia. Existen otros trabajos previos en los que de alguna manera se trata de contrastar si las organizaciones privadas son más o menos eficientes que organizaciones de otro tipo; así, y relacionado con el sector de la economía social (Guzmán et al., 2013), se evidencia en un primer momento que los niveles de eficiencia de las sociedades cooperativas son superiores a los presentados por las sociedades laborales, si bien en pruebas posteriores el resultado es el opuesto. El patronato se define como el órgano colegiado que gobierna una fundación y debe estar integrado por un mínimo de tres patronos12; estos pueden ser tanto personas físicas como personas jurídicas, y en este último caso pueden ser tanto públicas como privadas. Se plantea la hipótesis de que la naturaleza de sus fundadores, pública o privada, no debe condicionar la eficiencia de una fundación, no existiendo literatura previa al respecto. Con esta hipótesis, al igual que en la hipótesis anterior, se trata de averiguar si la iniciativa privada puede resultar más o menos eficiente que la iniciativa pública, pero a diferencia de la anterior se enfoca desde el punto de vista de la composición del patronato de una fundación. La antigüedad de una fundación supone una mayor experiencia y posicionamiento, lo cual puede contribuir a alcanzar mayores niveles de eficiencia. En este sentido, Golden et al. (2012) corroboran esta hipótesis; sin embargo, Martínez y Guzmán (2014) concluyen lo contrario, es decir, que las fundaciones más jóvenes son más eficientes. La colaboración de voluntarios determina un efecto negativo en la eficiencia. Las fundaciones emplean tanto personal remunerado como voluntario para realizar sus actuaciones, lo que queda recogido en el plan de actuación, que contempla este hecho al diferenciar entre personal asalariado, personal con contrato de servicios y personal voluntario. Pese a que una estructura de personal compuesta en parte por voluntarios puede resultar muy interesante para una fundación al suponer una opción muy económica y generadora de una buena imagen social, como contrapartida puede provocar situaciones de incertidumbre al no estar garantizada su continuidad, pudiéndose llegar incluso a tener rupturas de actividad. Es por ello que de partida planteamos como hipótesis a contrastar un efecto negativo del personal voluntario sobre la eficiencia de una fundación, pese a que instituciones tales como la Fundación Lealtad considera a esta figura como uno de los principales indicadores de su impacto social. A pesar de su relevancia en el sector, es un factor cuya influencia en la eficiencia no se ha estudiado en trabajos de investigación previos. En estudios relativos a otro tipo de entidades, como Marcuello (1999), se ha considerado la figura del voluntario tanto como input como output, sin llegar a concluir cómo determina la eficiencia. Siguiendo a Callen et al. (2003), la dimensión del patronato no será un condicionante para la eficiencia.
Para validar las hipótesis anteriores el modelo utilizado, se puede representar mediante:
El término θˆit en (6) representa los coeficientes de eficiencia CRS13 de cada fundación para t=2008, 2009, 2010. La elección se debe a que los índices con orientación CCR identifican la ineficiencia total, mientras que el índice con orientación VRS solo contempla la eficiencia técnica pura, perdiendo la eficiencia de escala. De acuerdo con lo señalado, aplicaremos el algoritmo1 de Simar y Wilson (2007) y se construyen intervalos de confianza al 95% para cada parámetro estimado14. Los resultados obtenidos se muestran en la tabla 13.
Determinantes de la eficiencia de las fundaciones españolas 2008–2010, Simar y Wilson (2007)
| Variable | Índices | Standard de los errores | 95% Bootstrap intervalos de confianza | |
|---|---|---|---|---|
| TYPE | –0,00067864* | 0,052103338 | –0,10357543 | 0,102218158 |
| FISIC | 0,31932362* | 0,042314932 | 0,23678072 | 0,401866526 |
| FPRIV | 0,64941417* | 0,030589556 | 0,58864776 | 0,710180587 |
| YEARS | 0,0001677* | 0,000443977 | –0,00075392 | 0,001089315 |
| VOLUNT | 0,09095699* | 0,028332295 | 0,04268715 | 0,139226826 |
| PATR | 0,00363378* | 0,001843551 | 0,00039468 | 0,006872875 |
* Significación al 5%.
El modelo se ajusta bien a los datos, con todos los coeficientes estadísticamente significativos al nivel del 5%. Los resultados por variables se resumen a continuación:
- -
TYPE: el signo estimado es negativo. La base de asignación de valores de esta variable (0=privada, 1=pública) supone que las fundaciones de tipo privado son más eficientes.
- -
FISIC: el signo estimado es positivo, lo que implica que con los valores asignados a esta variable las fundaciones con fundadores personas físicas son más eficientes.
- -
FPRIV: el signo estimado es también positivo, lo que significa que las fundaciones con fundadores personas jurídicas privadas son más eficientes que cuando se trata de personas jurídicas públicas.
- -
YEARS: el signo estimado es positivo. En consecuencia, la antigüedad de la fundación tiene un efecto positivo sobre la eficiencia.
- -
VOLUNT: el signo estimado es positivo, lo que implica que las fundaciones con voluntarios son más eficientes.
- -
PATR: el signo estimado también es positivo, es decir, el número de patronos tiene un efecto positivo sobre la eficiencia.
Este trabajo realiza un análisis de los determinantes de la eficiencia de las fundaciones españolas durante el período 2008-2010, partiendo del hecho de que el análisis sobre la eficiencia de las entidades sin fin de lucro en general, y de las fundaciones en particular, no es abundante en la literatura disponible. Nuestro trabajo se basa en la elección de aquellos factores exógenos que, dadas las peculiares características del sector, resumen y describen de una forma óptima la situación de tales organizaciones, así como en la elección de la metodología de análisis, es decir, la técnica no paramétrica DEA y, más concretamente, el procedimiento bietápico de doble bootstrap de Simar y Wilson (2007). Dada la naturaleza no paramétrica de esta metodología, resulta preceptivo realizar una depuración de datos; para ello se utiliza el procedimiento de detección de outliers de Wilson (1993), resultando que la muestra es idónea y no procede eliminar ninguna de las unidades económicas de decisión.
Como inputs discrecionales se proponen la dotación fundacional, el total de activos, el total de gastos y el número de empleados. Los resultados del modelo indican una ineficiencia técnica pura (supuesto CRS) del 27,7%. Por tanto, las fundaciones españolas podrían obtener para el periodo 2008-2010 por término medio un ahorro en sus inputs hasta dicho porcentaje, sin alterar el nivel de los ingresos obtenidos y el número de usuarios atendidos (outputs). Relajando la hipótesis CRS por la VRS, la ineficiencia en el empleo de los inputs alcanza el 31,92%. Adicionalmente, y utilizando el procedimiento bootstrap de Simar y Wilson (2000), se obtiene una ineficiencia técnica del 28,70%. Concluimos, por tanto, que durante el periodo 2008-2010 las fundaciones españolas en conjunto no alcanzan unos niveles de productividad deseables, conformando la frontera eficiente tan solo una de cada cinco de estas fundaciones.
Los resultados conducen a que los administradores de este tipo de organizaciones deberían poner énfasis en la gestión de su dotación fundacional, activos, gastos y número de empleados para mejorar su eficiencia. De lo anterior se deriva la necesidad de abordar el problema de cómo mejorar el nivel de eficiencia de las fundaciones españolas. El análisis de dos etapas revela que las fundaciones más eficientes se caracterizan por su naturaleza privada. Asimismo, las fundaciones con mayor antigüedad, las que cuentan con voluntarios entre sus colaboradores y las que poseen un número amplio de patronos son igualmente más eficientes.
Estos resultados nos llevan a interpretar que las fundaciones cuya administración está más cerca de las prácticas empresariales son más productivas, quizás debido a la ausencia de trabas burocráticas que las dotan de una mayor agilidad en su gestión. En cuanto a la antigüedad, puede decirse que la experiencia adquirida a lo largo del tiempo les permite una mayor capacidad en el desarrollo de su fin fundacional, además del prestigio que aporta una organización reconocida y asentada en su entorno. La relación positiva presentada por la colaboración de los voluntarios y el número de patronos con la eficiencia supone una conclusión opuesta a las hipótesis de partida que tal vez podría explicarse por el hecho de que ambas figuras carecen de una contraprestación económica y, por tanto, realizan aportaciones altruistas, tal y como afirma la Fundación Lealtad en su web, que considera a esta figura como uno de los principales indicadores del impacto social, contando desde nuestro punto de vista con una identificación profesional y personal con los fines fundacionales que potencia la generación de una imagen social beneficiosa.
Con los resultados de este trabajo consideramos que se contribuye a orientar principalmente a los gestores de las fundaciones para que implanten mecanismos de planificación y control que les orienten en la asignación de recursos hacia las actividades que contribuyan en mayor medida al cumplimiento de sus fines. Para ello, resulta indispensable contar con gestores y procedimientos que aseguren un desarrollo y control adecuado. Además, se contribuye a que las administraciones públicas tengan propuestas de mejora para apoyar al sector fundacional desde una doble vertiente: por un lado guiándolas en su gestión y, por otro, asignando los recursos públicos hacia las acciones más eficientes.
Resulta evidente que este estudio es sumamente novedoso en este campo de investigación por la escasez de trabajos previos y por la profundidad del mismo respecto a los ya existentes. Contempla además una muestra amplia en cuanto al número de años y al número de fundaciones. Se considera también que realiza una contribución importante al sector fundacional y abre numerosas vías para futuros trabajos de investigación que, por un lado, contrasten los resultados obtenidos y, por otro, los desarrollen y complementen.
Pese al desfase temporal del periodo 2008-2010, objeto de este estudio, respecto a la fecha actual, la muestra estudiada pone de manifiesto como las fundaciones en un contexto de crisis económica deben mejorar su eficiencia. Es por ello que el planteamiento de futuras líneas de trabajo en este sentido con datos más actuales y una muestra más amplia contribuirán a contrastar los resultados obtenidos. Se insiste en la necesidad de seguir centralizando la información pública relativa a fundaciones; pese a que recientemente se ha dado un paso importante en dicho sentido con la creación del registro de fundaciones de competencia estatal, creado en virtud de la Orden PRE/2537/2015, de 26 de noviembre, ello no es suficiente, ya que sigue quedando dispersa la información de las fundaciones con competencia autonómica, que son mayoría en el conjunto nacional.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Ver Färe y Lovell (1978), Färe y Primont (1995), Charnes, Cooper, Lewin y Seiford (1994) o Thanassoulis (2001).
CRS mide la eficiencia global de cada unidad (eficiencia técnica pura y eficiencia de escala). La variable vuelve a escala, VRS (modelo de eficiencia, por Banker et al., 1984), y se estima mediante la restricción de ∑λj=1; proporciona medidas de eficiencia técnica pura. La puntuación de eficiencia de escala se obtiene dividiendo la puntuación CRS por la puntuación de VRS (Färe y Grosskopf, 1985).
Lo que significa que la tasa de convergencia disminuye cuando la dimensión del conjunto alcanzable aumenta. La ratio de convergencia del estimador FDH es n1/p+q, mientras que para el DEA con la asunción adicional de convexidad, la tasa lograda es n2/p+q+1 (ver Simar y Zelenyuk, 2011).
El procedimiento de estimación bietápico no es la única forma de medir el impacto de las variables ambientales en la eficiencia. Una revisión detallada puede obtenerse en trabajos como Benito-López, Moreno-Enguix y Solana-Ibáñez (2011). Más recientemente, Simar y Wilson (2015) realizan una puesta al día actualizada de las diversas propuestas. En resumen, las principales se resumen en tres tipos: unietápico, el arriba señalado de dos etapas, y el enfoque denominado probabilístico, basado en las fronteras condicionadas según la propuesta de Cazals et al. (2002) o Daraio y Simar (2007). En nuestra aplicación, dada la congruencia existente entre los coeficientes estimados según Simar y Wilson (2007) y los coeficientes según Daraio y Simar (2005), el uso de fronteras condicionales no resultó necesario.
Para más detalles, ver Simar y Wilson (2007 y 2011b).
Daraio, Simar y Wilson (2010, p. 4): «En la literatura empírica, los investigadores han asumido tradicionalmente ψ(zi,β) = zi·β, donde β es un vector de parámetros. Además de las hipótesis 2.1-2-3, Simar y Wilson (2007) asumen que el error, ¿, está distribuido (truncado) de forma normal con el fin reflejar la literatura empírica. Alternativamente, ψ(zi), y se puede asumir que la distribución de ¿ es no paramétrica».
Para los pasos y detalles del algoritmo hay que hacer referencia a Simar y Wilson (2007); también a los trabajos aplicados, como Benito-López et al. (2011) y Benito-López, Solana-Ibáñez y Moreno-Enguix (2012). Con este objetivo, FEAR 2.01 incluye DEA, boot.sw98, rnorm.trunc y t.reg entre sus rutinas.
En consecuencia, la eficiencia se mide en términos de la función de distancia Shephard, recíproco de las medidas de eficiencia (Farrell, 1957).
Se ha añadido en la columna final el valor del estadístico ri=13biâsB(δˆ)/σˆ2. Sus valores pueden ser utilizados para evaluar si la aplicación de la corrección puede aumentar el error cuadrático medio. En Simar y Wilson (2000, p. 790) los autores aconsejan que la corrección solo se debe utilizar cuando la relación está muy por encima de la unidad.
Ley 50/2002, de 26 de diciembre, de Fundaciones. Artículo 15.1, Patronos. El Patronato estará constituido por un mínimo de tres miembros, que elegirán entre ellos un Presidente, si no estuviera prevista de otro modo la designación del mismo en la escritura de constitución o en los Estatutos. Asimismo, el Patronato deberá nombrar un Secretario, cargo que podrá recaer en una persona ajena a aquel, en cuyo caso tendrá voz pero no voto, y a quien corresponderá la certificación de los acuerdos del Patronato.
Empleamos los coeficientes tipo Farrell al objeto de que el signo del coeficiente estimado para cada variable ambiental coincida con el sentido de su aportación.
Para mayor detalle, ver Zelenyuk y Zheka (2006) o el apéndice1 de Latruffe, Davidova y Balcombe (2008). Además, según Alexander, Haug y Jaforullah (2010, p. 108), los intervalos de confianza convencionales basados en una aproximación normal son menos precisos que los basados en intervalos de confianza bootstrap, y, lo que es más importante, conducen a conclusiones diferentes.