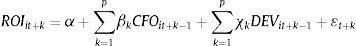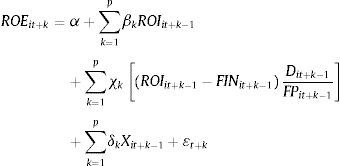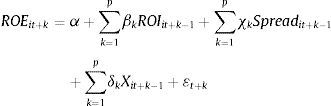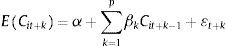Una evaluación empírica de los métodos de predicción de la rentabilidad y su relación con las características corporativas

Resumen

En el presente trabajo llevamos a cabo una evaluación crítica de los métodos de predicción de la rentabilidad basados en el concepto de persistencia, probando su eficacia sobre una amplia muestra de empresas españolas. Nuestros resultados ponen de manifiesto cómo 2 de las técnicas analizadas, la autorregresiva y la de separación de componentes, aportan las estimaciones de mayor calidad en la mayoría de las ocasiones y exhiben, en líneas generales, el mayor contenido predictivo incremental para diferentes especificaciones de la rentabilidad y para horizontes temporales a uno y 5 años. Además, la evidencia obtenida también revela que la calidad de las predicciones no depende solamente de la elección del método de estimación, sino que también guarda una importante relación con las propias características corporativas de las compañías, tales como el tamaño, las tasas de crecimiento o los niveles actuales de rentabilidad.

Abstract

This paper presents a critical evaluation of profitability prediction models based on the concept of persistence, based on a wide sample of Spanish companies. Our results indicate that 2 of functional specifications tested —the autoregressive and the separation of profitability components— yield the highest quality estimates in most cases for different measures of profitability and prediction horizons to one and five years. Moreover, the evidence found also demonstrates that the quality of predictions does not only depend on the estimation method chosen, but also on the corporate characteristics such as size, growth rates, and levels of current profitability.

Introducción

Una de las ideas más firmemente compartidas en el ámbito del análisis financiero y de la valoración de empresas, tanto en la investigación académica como en la práctica profesional, es que ambas disciplinas son marcadamente prospectivas y, por ello, uno de sus cometidos fundamentales consiste en realizar predicciones de variables y ratios susceptibles de ser empleados en modelos de valoración, en la evaluación de la capacidad financiera de las compañías o en el análisis del riesgo crediticio, entre otras utilidades. Pero como el futuro es incierto, los pronósticos son siempre subjetivos, imprecisos y sujetos a error, lo que ha impulsado el desarrollo de técnicas, métodos y modelos para refinarlos, sin que hasta la fecha hayamos podido encontrar un procedimiento que sea suficientemente convincente y consistente para gozar de general aceptación.

Pero, sorprendentemente, este lugar central que se le adjudica a la capacidad predictiva de la información financiera no se ha visto correspondido en el ámbito de la investigación, que a nuestro juicio aún es insuficiente e incompleta, y queda, por tanto, un largo camino por recorrer. A nuestro entender, solamente podemos identificar un subconjunto reducido de trabajos dedicados al análisis de la capacidad predictiva, en los que existe un cierto grado de acuerdo en considerar que la desagregación del resultado, o de la rentabilidad, en sus componentes mejora la calidad de los pronósticos (Fairfield, Sweeney y Yohn, 1996; Richardson, Sloan, Soliman y Tuna, 2005; Esplin, Hewitt, Plumlee y Yohn, 2014).

El presente trabajo pretende contribuir a la evidencia disponible con una evaluación crítica de los métodos de predicción de la rentabilidad, probando su eficacia en horizontes temporales a corto y largo plazo y tomando como base una amplia muestra de empresas españolas. La más reciente literatura ha acogido 3 métodos de predicción; el primero de ellos, que denominaremos autorregresivo, consiste en pronosticar su comportamiento futuro mediante un modelo en el que la o las variables independientes son las rentabilidades de la firma en el ejercicio o ejercicios precedentes. El segundo, que designaremos como separación de componentes, estima la rentabilidad mediante la descomposición de la rentabilidad actual en los diferentes elementos que la integran, y en el que cada uno de sus componentes es representado por una variable independiente en un modelo de regresión multivariante. El tercer procedimiento, que llamaremos método de integración de componentes, aborda la estimación de la rentabilidad en 2 etapas; en la primera se estima el valor futuro de cada componente de la rentabilidad empleando un modelo en el que la o las variables independientes son el valor actual de dicho componente en el ejercicios o ejercicios anteriores y, en la segunda etapa, la rentabilidad futura se pronostica por agregación de los pronósticos individuales de cada elemento integrante de la rentabilidad que han sido estimados en la etapa previa.

Como hemos indicado, nuestro trabajo pone a prueba las 3 técnicas de pronóstico y evalúa la calidad de las estimaciones por ellos proporcionadas para 2 medidas de rentabilidad, ROI y ROE, tanto a corto plazo (un año) como a largo plazo (5 años). Hasta la fecha, los estudios empíricos más cercanos al nuestro, los de Fairfield et al. (1996) y Esplin et al. (2014), solamente habían analizado la capacidad predictiva del ROE a corto plazo, a un año, sin considerar ni horizontes temporales más dilatados ni las posibilidades de predicción del ROI. En este sentido, entendemos que nuestra aportación incorpora una visión más completa de los pronósticos de las rentabilidades que los estudios precedentes, por abarcar 2 medidas alternativas de rentabilidad en 2 contextos temporales diferentes.

Podemos anticipar que los hallazgos que documentamos se sitúan en una línea similar a las de estudios previos llevados a cabo en la década de los setenta y ochenta (Mueller, 1977; Cubbin y Geroski, 1987; Geroski y Jacquemin, 1988; Jacobson, 1988), que muestran que el modelo univariante autorregresivo de primer orden AR1 es superior a otras especificaciones alternativas; pero nuestros resultados son también notablemente diferentes a los de la más reciente literatura específica sobre predicción de resultados y rentabilidades. Así, Fairfield et al. (1996) y Esplin et al. (2014) alcanzan conclusiones bien distintas, pues sus mejores estimaciones de la rentabilidad futura son las obtenidas con el enfoque de separación de componentes, los primeros, y empleando el método de integración de componentes del resultado, los segundos.

A nuestro modo de ver, nuestro estudio aporta a la literatura sobre predicción de la rentabilidad una evidencia empírica adicional con datos españoles y aporta un análisis de la relación existente entre los errores de predicción y las características corporativas que la investigación ha venido asociando con la calidad de las predicciones, cuestión que juzgamos de interés y que hasta donde nuestro conocimiento alcanza no había sido abordada hasta la fecha.

Revisión de la literatura

En general, la investigación contable sobre predicción de la rentabilidad parece dar por hecho que el modelo autorregresivo es inferior en calidad predictiva a los modelos de separación y de integración de componentes. No obstante, la literatura económica viene reiterando que no existe superioridad teórica de unos procedimientos de estimación sobre otros, y que ni siquiera se han aportado argumentos concluyentes para explicar la evidencia empírica disponible, debido, como sostienen Bermingham y D’Agostino (2011), a que el proceso de generación de los resultados y sus componentes es desconocido. Frente a esta posición, Pivetta y Reis (2007) advierten que la persistencia es una propiedad univariante, y esta característica lo convierte en el mejor de los métodos disponibles para pronosticar la evolución de las variables económicas. Esta debilidad teórica podría explicar la falta de consenso existente, y es la que ha llevado a Dangerfield y Morris (1992) a afirmar que la utilidad de cada procedimiento es una cuestión de hecho, lo que necesariamente requiere ser empíricamente contrastado y evaluado en cada concreto contexto de predicción, sin que a priori pueda afirmarse qué método es el más apropiado para cada conjunto de información.

Como escriben Fama y French (2000), la primitiva literatura sobre predicción de rentabilidades y resultados se basaba en el empleo de series temporales, hoy relegadas a un segundo plano, lo que creaba la necesidad de contar con compañías de largas trayectorias históricas, lo que inducía notables sesgos de supervivencia y, sobre todo, estimaciones muy imprecisas. Esta metodología fue superada gracias al empleo de regresiones anuales de corte transversal que, al no requerir el empleo de prolongadas series temporales, permitieron estudiar la capacidad predictiva sobre amplias muestras de empresas, dando lugar a una mejora muy significativa de la calidad de las estimaciones.

Los antecedentes de la actual línea de investigación sobre predicción de rentabilidades, cimentada, como hemos visto, en estudios de corte transversal, podemos situarlos a partir de los estudios sobre persistencia publicados en los años setenta y ochenta¹. Mueller (1977) vinculó la persistencia de la rentabilidad al grado de competencia existente en los mercados y documentó cómo en los sectores con mayor presión competitiva las rentabilidades anormalmente elevadas eran menos persistentes, y cómo se desvanecían y revertían con rapidez a la rentabilidad media o normal de cada sector. Su aportación estimuló el estudio de la persistencia y, así, Cubbin y Geroski (1987), Geroski y Jacquemin (1988) y Jacobson (1988), con muestras de empresas británicas, europeas y estadounidenses, respectivamente, mostraron cómo la persistencia no solamente guardaba relación con el nivel competitivo de cada sector, sino que, además, firmas con la misma filiación sectorial obtenían rentabilidades muy distintas, por lo que podía afirmarse, en consecuencia, que la persistencia no solamente viene condicionada por elementos exógenos como las circunstancias de los mercados, sino que es, también, una característica individual o endógena de cada compañía. Subrayemos, por la relevancia que supone para nuestro trabajo, que estos primeros hallazgos compartieron una metodología común e identificaron el univariante como el enfoque que mejor caracterizaba el comportamiento de las empresas y el que mejor sustentaba su evidencia empírica.

Tras esta primera etapa, las investigaciones sobre predicción de resultados y rentabilidades con base en el concepto de persistencia podemos situarlas al final de la década de los años ochenta, cuando Ou (1990) y Ou y Penman (1989), en 2 trabajos muy celebrados en su día, examinaron la capacidad de los diferentes componentes del resultado para pronosticar el signo positivo o negativo de los cambios futuros en los resultados. Algunos años más tarde, Finger (1994) analizó la magnitud de los errores de pronóstico cometidos en las predicciones de flujos de efectivo a uno, 4 y 8 años generadas por el resultado y los flujos de efectivo de operaciones, y alcanzó como conclusión que estos últimos cometen menores errores en predicciones a un ejercicio y que son similares a las obtenidas con un horizonte temporal mayor. Dechow, Kothari y Watts (1998), con datos de un amplio horizonte temporal, 1963–1992, documentaron, de modo contrario a Finger (1994), que el resultado contable es más eficaz que los flujos de tesorería en pronósticos a largo plazo, superioridad que era especialmente patente en compañías con ciclo de operaciones dilatado.

La literatura más cercana en tiempo y contenido a nuestro estudio, orientada a la predicción de la rentabilidad con base en la separación de esta en sus componentes, cabe situarla a partir del trabajo de Fairfield et al. (1996), quienes, asumiendo que resultados más persistentes son también mejor pronosticables, documentaron cómo dicha desagregación proporciona mejores predicciones del ROE que los modelos univariantes. Para llegar a esta conclusión, los autores emplearon un modelo multivariante en el que las variables independientes eran los diferentes componentes del resultado, tanto los de carácter transitorio (operaciones discontinuas o resultados extraordinarios) como los generados por las operaciones ordinarias. Sobre estos últimos —margen bruto, gastos generales y de administración, amortizaciones y gastos financieros— es sobre los que realmente descansaba la calidad de las predicciones, a diferencia de los resultados extraordinarios o los discontinuos, cuyo poder predictivo era muy escaso y que, en opinión de los autores, tenían que ser descartados en la predicción de la rentabilidad futura debido a su naturaleza marcadamente transitoria.

Otros estudios posteriores avanzaron en la senda trazada por Fairfield et al. (1996) y, así, Fairfield y Yohn (2001) estudiaron en qué medida la desagregación del ROI en sus componentes clásicos de Du Pont, margen y rotación, predecían sus cambios futuros con mayor acierto que empleando un modelo univariante. Tomando una muestra de firmas con margen positivo, no encontraron una capacidad predictiva significativamente mayor en el enfoque de separación de componentes que en el univariante, pero sí obtuvieron evidencia de cómo los cambios presentes en margen y rotación pronosticaban los cambios futuros en ROI mejor que con metodología univariante. Barth, Cram y Nelson (2001), a partir del trabajo de Dechow et al. (1998), investigaron las implicaciones de los ajustes por devengo en la predicción de los flujos de efectivo, mostrando cómo cada componente de aquellos refleja una información diferente y, por tanto, una capacidad predictiva también diferente, de manera que su desagregación mejoraba significativamente la capacidad predictiva de los flujos de tesorería.

Como en los estudios anteriores, Nissim y Penman (2003) también emplearon una aproximación de separación de elementos para evaluar la utilidad del endeudamiento en la predicción del ROE, poniendo de manifiesto cómo las deudas asociadas con actividades operativas tenían una mayor aportación en la predicción que las vinculadas a actividades financieras. Richardson et al. (2005) desagregaron los ajustes por devengo totales en 3 componentes: activos circulantes de operaciones, pasivos circulantes de operaciones y variación de activos financieros netos: mostraron una mayor capacidad predictiva los componentes cuya valoración contable está basada en transacciones, frente a los elementos cuya valoración está soportada en juicios y estimaciones.

Frente a estos trabajos basados en modelos de separación de componentes, Nissim y Penman (2001) y Esplin et al. (2014) han sido los primeros en aplicar a la investigación contable el método de integración de componentes. El trabajo de los primeros no tenía por objeto evaluar la mayor o menor calidad de las predicciones, sino que realizaron las estimaciones contenidas en su estudio siguiendo un enfoque de integración. Por el contrario, Esplin et al. (2014) sí han comparado la capacidad predictiva de los métodos de separación e integración de componentes distinguiendo entre resultados operativos y financieros de las empresas de su muestra, y han obtenido mejores pronósticos mediante el empleo del método de integración.

En España, los trabajos de Reverte (2002), Giner y Reverte (2003) y Giner e Íñiguez (2006) han aportado evidencias adicionales. Así, con una muestra de empresas españolas, Reverte (2002) analiza la capacidad de la información financiera para predecir los resultados futuros, en un horizonte de temporal entre uno y 3 años, e incorporando a su análisis diferentes variables fundamentales adicionales que mejoran las predicciones a 3 años. Giner y Reverte (2003), tomando una muestra de empresas de 4 países europeos, analizan en qué medida las diferencias normativas e institucionales explican la distinta capacidad predictiva de la información financiera en cada país, obteniendo resultados que ponen de manifiesto el impacto de las diferencias en la regulación contable en la calidad de las predicciones. Giner e Íñiguez (2006) contrastan la validez de 2 modelos teóricos de valoración para la predicción de resultados anormales, y empleando una muestra de empresas españolas no financieras concluyen que la inclusión de variables representativas del contexto económico mejora significativamente la calidad de los pronósticos. Finalmente, Reverte y Guzmán (2010), con base en una muestra de pequeñas y medianas empresas españolas, dejan constancia del poder predictivo de los niveles de eficiencia y productividad, variables no consideradas en estudios previos y que mejoran la capacidad de predicción del resultado y del valor contable de los recursos propios.

En suma, de nuestra revisión de la literatura sobre predicción de la rentabilidad podemos deducir que los estudios iniciales, basados en el empleo de series temporales, dieron paso a metodologías de corte transversal, apoyadas en el concepto de persistencia como soporte de la capacidad predictiva. Los trabajos adheridos a este enfoque han aportado resultados muy dispares, lo que viene a confirmar la creencia, reiterada y mantenida en el tiempo, de que no puede designarse a priori la superioridad de un método de estimación sobre los restantes, y que se trata, en definitiva y como antes hemos afirmado, de una cuestión fáctica que requiere enjuiciar cada caso concreto y en función de su contexto particular.

Diseño de la investigación

Evaluación de los métodos de predicción de la rentabilidad

Como hemos indicado, nuestra tarea consistirá en analizar, para cada uno de los métodos de predicción de rentabilidad —autorregresivo, de separación y de integración de componentes—, la propiedad que Fairfield et al. (1996) han denominado contenido predictivo incremental, entendiendo por tal la mejora operada en los pronósticos generados por cada método con relación a un modelo de referencia o modelo base. Para ello operaremos con arreglo a la metodología que es habitual en la literatura, y que consiste en una aproximación en 2 etapas, En la primera, estimaremos los parámetros de cada uno de los modelos a partir de una muestra de empresas (in-sample), y en la segunda, los parámetros estimados en la primera etapa servirán como inputs para obtener los pronósticos de ROI y ROE fuera de muestra (out-of-sample), tanto a corto plazo (un año) como a largo plazo (5 años). Las predicciones proporcionadas por cada método serán comparadas con las rentabilidades realmente alcanzadas, y la diferencia entre las pronosticadas y las conseguidas, es decir, el error de pronóstico cometido, nos permitirá evaluar el contenido predictivo incremental de cada método, que será mayor cuanto más reducido sea el error. La descripción detallada de las predicciones y de los errores generados la abordaremos en una de las secciones siguientes.

Como hemos comentado con anterioridad, no existe ningún método de predicción que sea teóricamente superior a los restantes, por lo que su análisis comparativo es una cuestión empírica. Así, Hendry y Hubrich (2011) —que descartan a priori la posible eficacia del enfoque univariante— consideran que los pronósticos obtenidos por separación de componentes son tan válidos y certeros como los proporcionados por los modelos de integración en los casos en los que el proceso de generación de los datos es conocido. No obstante, cuando dicho proceso no puede ser identificado, sostienen que no es posible concluir con cuál de los enfoques es superior, de modo que las propiedades no observables de los datos serán las que determinen qué procedimiento es el que posee mayor contenido predictivo². Por esta razón, la primera de nuestras hipótesis nulas que será objeto de contraste se enuncia del modo siguiente.H₀₁

Los métodos de predicción de la rentabilidad no poseen contenido predictivo incremental sobre los pronósticos basados en el paseo aleatorio.

Por tanto, no planteamos ninguna hipótesis adicional acerca de cuál de los 3 métodos a examen es superior, habida cuenta de la incapacidad teórica reconocida en la literatura para argumentar ex ante la supremacía de unos sobre otros.

Para contrastar la primera de las hipótesis, analizaremos el contenido predictivo incremental de cada método, comparando, como en Fairfield et al. (2009), los errores de pronóstico incurridos por cada uno de estos con los cometidos por el método basado en el paseo aleatorio (random walk), que tomaremos como referencia, y que, en síntesis, asume el azar y considera que el pronóstico menos erróneo es el comportamiento de la misma variable en el pasado reciente³. Desde el trabajo seminal de Stigler (1963) sabemos que existen razones económicas que dan soporte a la hipótesis de reversión a la media de la rentabilidad, y estudios como los llevados a cabo por Watts (1970) y Watts y Leftwich (1977) documentan que algunos modelos de predicción del resultado no ajustan mucho mejor que las más simples de las estimaciones, basadas en esta hipótesis del paseo aleatorio. De hecho, la primera literatura contable empírica sobre predicción, iniciada con Ball y Watts (1972) y Brooks y Buckmaster (1976), se debatía entre considerar que los resultados son en alguna medida predecibles y la hipótesis del paseo aleatorio. Por tanto, la asunción básica del paseo aleatorio es:

Donde X_it es una medida de la rentabilidad obtenida por la empresa i en el periodo t, y k es el número de periodos posteriores a t. Según cuál sea la medida de rentabilidad que hay que pronosticar, ROI o ROE, la expresión [1] podrá ser:

Nuestro análisis empírico consistirá en realizar predicciones a uno y 5 años, es decir, tomando k los valores 1 y 5, respectivamente. Los pronósticos generados por el método de paseo aleatorio serán empleados para compararlos, en primer lugar, con los obtenidos con un modelo autorregresivo ARIMA (p,0,0) de orden uno y 5, y de aquí que su estimación se efectúe con base en la siguiente especificación:

Que dará lugar a los modelos autorregresivos:

Los 2 métodos siguientes, que denominaremos de separación de componentes y de integración de componentes, asumen que cada componente de la rentabilidad posee un grado de persistencia diferente y, por tanto, una contribución también distinta a su pronóstico. Así, el modelo de separación estima la rentabilidad futura efectuando una regresión de esta sobre los distintos componentes del resultado del ejercicio corriente. Con relación al ROI, procederemos como Sloan (1996) y lo desagregaremos en sus elementos caja y devengo, al objeto de analizar la diferente persistencia y capacidad predictiva de ambos, también a uno y 5 ejercicios.

Donde CFO_it+k-1 es el cash flow generado por las operaciones y DEV_it+k-1 son los ajustes por devengo totales, ambos deflactados por el activo total. En cuanto al ROE, efectuaremos la descomposición que proponen Healy y Palepu (2007) en rentabilidad económica, apalancamiento financiero y efecto impositivo, y que hasta donde nuestro conocimiento alcanza no ha sido abordado en estudios previos.

Siendo D_it+k-1 el importe de la deuda total, FP_it+k-1 el valor contable de los fondos propios, FIN_it+k-1 el cociente entre el resultado financiero del ejercicio y la deuda total y T_it+k-1 el gasto devengado por impuesto sobre sociedades⁴. Para simplificar las notaciones de la ecuación anterior, denominaremos Spread_t+k a la expresión, ROIit+k−1−FINit+k−1Dit+k−1FPit+k−1que pasará a ser:

Por último, el método de integración de componentes genera sus pronósticos mediante una aproximación en 2 etapas. En la primera se estima cada componente C_it+k de la rentabilidad de un modo individual, empleando un modelo como el [2] anterior:

En la segunda etapa, una vez estimados los valores futuros de cada componente, E(C_it), y obtenidos los parámetros αˆ y βˆ de la ecuación genérica [5], las predicciones de rentabilidad se obtienen por agregación de los diferentes elementos que la integran, de manera que:

Y que aplicaremos como:

Del mismo modo que hicieron Lev y Thiagarajan (1993), Abarbanell y Bushee (1997), Reverte (2002) y Giner e Íñiguez (2006), todos los modelos incluirán variables representativas del contexto económico, que, como han documentado los citados trabajos, mejoran la capacidad predictiva. Así, incorporaremos el control del ciclo económico, que será representado por el producto interior bruto (PIB) de cada ejercicio; también añadiremos las expectativas macroeconómicas, aproximadas mediante las estimaciones del Banco de España de las variaciones anuales esperadas del PIB; un subrogado del ciclo de negocio de las empresas, que pretendemos captar a través de la edad de las compañías, y, por último, controlaremos la filiación sectorial de cada firma, agregando variables dicotómicas que caracterizarán los 7 grandes sectores económicos que hemos considerado: agrario, minería, manufactura, energía, construcción, comercio y servicios.

Finalmente, una vez generados los pronósticos de rentabilidad por cada uno de los procedimientos anteriores, evaluaremos y compararemos la calidad de estos a través de los errores de pronóstico cometidos por cada método, que serán la diferencia entre las rentabilidades reales y las pronosticadas, tomadas tanto en valores directos como en valores absolutos. Será mejor aquel que posea un mayor contenido predictivo incremental, es decir, el que incurra en menores errores de pronóstico y, por consiguiente, arroje las estimaciones que mayores mejoras representen con respecto al método de paseo aleatorio que vamos a tomar como referencia básica.

Los efectos de las características corporativas sobre los errores de predicción

La segunda de las hipótesis que serán objeto de contraste tiene por objeto profundizar en nuestro análisis y refinar la evidencia obtenida tras el contraste de la primera. Los errores de predicción podrían estar ocasionados no solo por el método elegido, sino que también podrían guardar relación con algunos atributos o características corporativas que afectarían a la calidad de los pronósticos, de manera que dichas características afectasen a los errores de predicción cometidos por cada método. Aunque una parte de la literatura, entre la que cabe destacar a Baginski, Lorek, Willinger y Branson (1999), Fama y French (2000), Nissim y Penman (2003) y Soliman (2004, 2008), considera que dichas características son un elemento determinante del proceso de predicción, hasta donde sabemos esta cuestión no ha sido expresamente abordada hasta la fecha en la literatura sobre la materia. Por ello la segunda de las hipótesis que contrastar es la que sigue:H₀₂

La calidad de las predicciones proporcionadas por cada método no guarda relación con las características corporativas de las compañías cuya rentabilidad se pronostica.

Con tal finalidad, emplearemos un modelo de regresión en el que la variable dependiente serán los errores de predicción en valores absolutos y relativos de cada método, y tomaremos como variables independientes aquellas características que por ser las que la investigación ha asociado a la capacidad predictiva hemos seleccionado como candidatas para explicar los errores: el tamaño, el nivel de endeudamiento, el crecimiento y la obtención de rentabilidades anormalmente elevadas o reducidas. Su especificación econométrica es la siguiente:

Siendo ErrROI_it+k y ErrROE_it+k los errores cometidos por cada uno de los métodos de predicción, tomados tanto en valores directos como absolutos. En cuanto a las variables explicativas, todas ellas referidas al ejercicio t en el que se realizan las predicciones, la presencia del tamaño, TAM_it, obedece a que las compañías de mayor dimensión, como se deduce de los resultados de Fama y French (2000), Frankel y Litov (2008), Baginski et al. (1999) y Watts y Zimmerman (1978), podrían exhibir resultados más pronosticables y, por tanto, su relación con la variable dependiente sería negativa. Por el contrario, el endeudamiento, END_it, guardaría una relación inversa si, como sostienen Fama y French (2000), Nissim y Penman (2003) y Frankel y Litov (2008), la volatilidad inducida por los costes financieros generara perturbaciones en la serie temporal de los resultados, de modo que su asociación con los errores sería positiva.

El crecimiento, CREC_it, podría mostrar una relación negativa con la capacidad predictiva (Fama y French, 2000; Fairfield y Yohn, 2001; Soliman, 2004), pues mientras las firmas con menores tasas de crecimiento suelen mostrar rentabilidades estabilizadas, las de mayor crecimiento propenden a una mayor inestabilidad temporal, y de aquí que su relación con los errores podría ser positiva. Finalmente, las rentabilidades anormalmente elevadas, DEC_10_it, o anormalmente reducidas, DEC_1_it, tienden, como está documentado desde el trabajo de Freeman, Ohlson y Penman (1982), a revertir a valores medios por mostrar una débil persistencia, y esta característica podría hacerlas menos pronosticables e inducir mayores errores, guardando una relación positiva con la variable dependiente.

Especificación de variables y procedimiento de estimación de modelos

Las variables que vamos a incorporar a los modelos sobre los que descansa nuestro análisis empírico se describen del modo que sigue. ROI se define como el cociente entre resultado antes de intereses e impuestos y el activo total al cierre del ejercicio. ROE, que expresa el retorno que la compañía proporciona a sus propietarios por los recursos que estos aportan, es el cociente entre el resultado neto después de impuestos y los fondos propios medios al cierre del ejercicio. Como en los trabajos españoles antes citados de Reverte (2002), Giner y Reverte (2003) y Giner e Íñiguez (2006), nuestras medidas de rentabilidad incluyen todo tipo de resultados, incluidos los extraordinarios.

Para las predicciones de los modelos de separación e integración de componentes, las variables se definen como sigue: DEV_it+k-1 y CFO_it+k-1, presentes en los modelos [3] y [6a], son, respectivamente, los ajustes por devengo y los cash flows procedentes de las operaciones, y han sido tomadas del estado de flujos de efectivo de las cuentas anuales. Para los ejercicios anteriores a 2008, en los que dicho estado no era obligatorio, ambas variables han sido calculadas a partir de los datos disponibles en los balances y cuentas de pérdidas y ganancias; una y otra están deflactadas por el activo medio total del ejercicio. Con respecto a las variables de los modelos [4] y [6b], D_it+k-1 es el importe de la deuda total al cierre del ejercicio, FP_it+k-1 el valor contable de los fondos propios al cierre del ejercicio, FIN_it+k-1 el cociente entre el resultado financiero del ejercicio y la deuda total y T_it+k-1 el gasto total devengado por impuesto sobre sociedades.

Por último, las variables independientes de los modelos [7a] y [7b], diseñados para analizar el vínculo existente entre los errores de predicción de cada método y las características corporativas que hemos seleccionado, se definen del modo que sigue: TAM_it es el activo total al cierre del ejercicio, esta variable se expresa en forma logarítmica, como es habitual en la literatura, para mitigar el efecto de las observaciones influyentes; END_it es el cociente entre la deuda total y el activo total al cierre del ejercicio; CREC_it es la tasa de crecimiento anual de la cifra de negocios; DECIL_1_it es una variable binaria que toma el valor 1 cuando la observación se encuentra localizada en el decil de ROI_it o ROE_it más elevado y 0 en caso contrario, y DECIL_10_it es una variable dicotómica a la que se le asigna el valor 1 cuando la observación está situada en el decil de ROI_it o ROE_it más reducido, y 0 en otro caso.

La estimación de los parámetros de todos los modelos de regresión la llevaremos a cabo empleando el procedimiento de Huber-White para obtener los estadísticos t basados en errores estándares robustos, opción que estima los mismos valores de los coeficientes, pero que corrige posibles problemas de heterogeneidad y normalidad.

Muestra, estadísticos descriptivos y correlaciones entre variables

Criterios de formación de la muestra

La muestra de empresas se ha obtenido de la base de datos SABI^® en el mes de septiembre de 2014, a la que se solicitó información de sociedades mercantiles independientes para el periodo 2004-2008, activas, auditadas, que presentaran sus cuentas en formato normal, no pertenecientes a los sectores financiero, seguros y sin ánimo de lucro (grupos 65, 66, 67, 73, 74, 75, 91, 92 y 95 de CNAE-2009) y con observaciones disponibles en el ejercicio precedente y en cada uno de los 5 siguientes. Así, por ejemplo, para que una empresa esté incluida en el ejercicio 2004 debe contar con datos disponibles desde 2003 a 2009, ambos inclusive, y para estar incluida en 2006, sus datos deben abarcar el periodo comprendido entre 2005 y 2011; es decir, se requieren 7 ejercicios consecutivos.

Aunque la longitud de la serie temporal requerida no es excesiva, podría ocasionarse un posible sesgo de supervivencia, y con la finalidad de mitigar su impacto en nuestros resultados empíricos hemos permitido que las empresas puedan entrar y salir de la muestra, al objeto de formar una muestra variable y replicar en alguna medida las circunstancias reales de los mercados, Por ello, la muestra está integrada por todas las empresas presentes en SABI^® que en un determinado ejercicio tienen suficientes datos para configurar las variables requeridas.

Adicionalmente, las empresas de la muestra han de contar con fondos propios superiores a 100.000 euros en todos los ejercicios y con activos y cifra de negocios mayores de 1.000.000 euros, con la finalidad, por un lado, de evitar el efecto adverso ocasionado por denominadores reducidos (Esplin et al., 2014) y, por otro, de excluir compañías de tamaño muy reducido (Dichev y Tang, 2008; Fairfield et al., 2009). También hemos eliminado de la muestra, como Esplin et al. (2014), todas las observaciones con un valor absoluto de ROI_it superior a 50% y de ROE_it superior a 100%, como es habitual en la literatura (Fairfield et al., 1996; Fairfield y Yohn, 2001), así como las ilegibles o con datos incompletos. Finalmente, hemos descartado las observaciones localizadas en los percentiles 1% y 99% de las variables dependientes, lo que ha dado lugar a una muestra final de trabajo de 19.839 observaciones empresa-año.

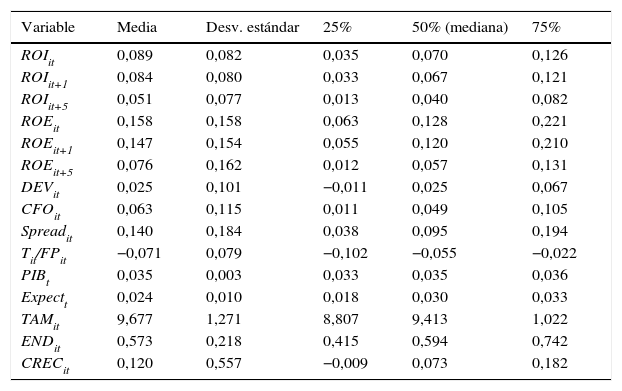
Estadísticos descriptivos de la muestra y correlaciones entre variables

La tabla 1 recoge los principales estadísticos descriptivos de la muestra. Una primera lectura pone de relieve cómo los valores medios de las medidas de rentabilidad son, en todas las variables, sistemáticamente mayores que las medianas, lo que indica una distribución estadística asimétrica y con mayor carga en la cola de la derecha, debido al impacto de las observaciones con mayor valor numérico. Esta circunstancia podría estar explicada por la opción de liquidación o abandono documentada por Hayn (1995) para el caso de empresas con resultados negativos o deprimidos.

Tabla 1.

Estadísticos descriptivos de la muestra

Variable	Media	Desv. estándar	25%	50% (mediana)	75%
ROIit	0,089	0,082	0,035	0,070	0,126
ROIit+1	0,084	0,080	0,033	0,067	0,121
ROIit+5	0,051	0,077	0,013	0,040	0,082
ROEit	0,158	0,158	0,063	0,128	0,221
ROEit+1	0,147	0,154	0,055	0,120	0,210
ROEit+5	0,076	0,162	0,012	0,057	0,131
DEVit	0,025	0,101	−0,011	0,025	0,067
CFOit	0,063	0,115	0,011	0,049	0,105
Spreadit	0,140	0,184	0,038	0,095	0,194
Tit/FPit	−0,071	0,079	−0,102	−0,055	−0,022
PIBt	0,035	0,003	0,033	0,035	0,036
Expectt	0,024	0,010	0,018	0,030	0,033
TAMit	9,677	1,271	8,807	9,413	1,022
ENDit	0,573	0,218	0,415	0,594	0,742
CRECit	0,120	0,557	−0,009	0,073	0,182

La muestra, tras la eliminación de las observaciones extremas, comprende 19.839 observaciones empresa-año de sociedades mercantiles independientes para el periodo 2004-2008, activas, auditadas, que presentan sus cuentas en formato normal, no pertenecientes a los sectores financiero, seguros y sin ánimo de lucro y con observaciones disponibles en el ejercicio precedente y en cada uno de los 5 siguientes.

Para cada firma i, ejercicio t y periodo posterior k:

CFO_+t son los flujos de efectivo generados por las operaciones; CREC_it es la tasa de crecimiento anual de la cifra de negocios; DEV_it+k son los ajustes por devengo; END_it es el cociente entre la deuda total y al activo total del ejercicio; Expect_t es la predicción sobre la variación del producto interior bruto; FIN_it+k es el cociente entre el resultado financiero del ejercicio y la deuda total al cierre de ejercicio; FP_it+k es el valor contable de los fondos propios al cierre del ejercicio; PIB_t es el producto interior bruto; ROE_it+k es el cociente entre resultado neto y los fondos propios medios al cierre del ejercicio; ROI_it+k es el cociente entre el resultado antes de intereses e impuestos y el activo medio total al cierre del ejercicio; Spread_it es el efecto del apalancamiento financiero sobre el ROE, [(ROI_it+k-FIN_it+k)]*(D_it+k/FP_it+k), siendo D_it+k el importe de la deuda total al cierre del ejercicio; TAM_it es el logaritmo neperiano del activo total al cierre del ejercicio; T_it+k es el gasto devengado por impuesto sobre sociedades.

También es interesante destacar la fuerte dispersión existente en la mayoría de las variables, hecho que es aún más evidente en el caso del ROE, con desviaciones estándares muy elevadas con relación a sus valores medios, lo que pone de relieve la gran diversidad inducida por el impacto de estructuras de capital muy diferentes y de los costes financieros a ellas asociados.

Con respecto a las correlaciones existentes entre las variables que vamos a emplear en nuestro análisis empírico, y según datos que no mostramos aquí, los valores alcanzados tanto en términos de valores directos de Pearson como de rangos de Spearman nos permiten descartar cualquier sospecha de multicolinealidad.

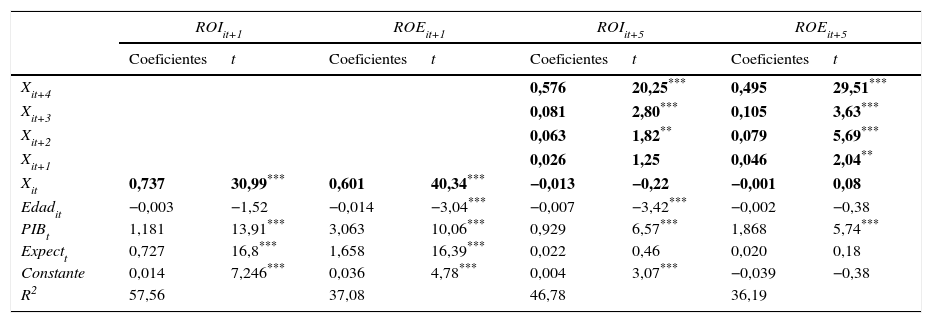
Resultados empíricos

Estimación de parámetros para su empleo en los métodos de predicción

La tabla 2 muestra los resultados obtenidos de la regresión de los modelos [2a] y [2b], cuyos parámetros —a los que, como hemos comentados, hemos añadido determinadas variables de contexto y la edad de la empresa, expresada en forma logarítmica para moderar el impacto de posibles observaciones extremas— emplearemos para llevar a cabo las predicciones de las rentabilidades a corto y a largo plazo. En primer lugar, las estimaciones a un año de ROI_it+1 y ROE_it+1 aportan unos coeficientes de las variables independientes, ROI_it y ROE_it, positivos y muy significativos, con valores de 0,737 y 0,601, respectivamente, que indican una persistencia similar a la documentada en la literatura empírica, que es superior en el caso de ROI_it. Esta menor persistencia del ROE_it con relación al ROI_it, que como veremos será una constante a lo largo de todo nuestro análisis empírico, puede ser la consecuencia de la notable influencia que la volatilidad ejerce sobre la persistencia, como han demostrado Dichev y Tang (2008) y Frankel y Litov (2008). Este hallazgo es también coherente con los documentados por Nissim y Penman (2003), que muestran cómo el endeudamiento, que es un determinante del ROE, afecta negativamente a su persistencia y a la predicción de sus valores futuros.

Tabla 2.

Resultados de la regresión del modelo: Xit+k=α+∑k=1pβkXit+k−1+εt+k

	ROIit+1		ROEit+1		ROIit+5		ROEit+5
	Coeficientes	t	Coeficientes	t	Coeficientes	t	Coeficientes	t
Xit+4					0,576	20,25^***	0,495	29,51^***
Xit+3					0,081	2,80^***	0,105	3,63^***
Xit+2					0,063	1,82^**	0,079	5,69^***
Xit+1					0,026	1,25	0,046	2,04^**
Xit	0,737	30,99^***	0,601	40,34^***	−0,013	−0,22	−0,001	0,08
Edadit	−0,003	−1,52	−0,014	−3,04^***	−0,007	−3,42^***	−0,002	−0,38
PIBt	1,181	13,91^***	3,063	10,06^***	0,929	6,57^***	1,868	5,74^***
Expectt	0,727	16,8^***	1,658	16,39^***	0,022	0,46	0,020	0,18
Constante	0,014	7,246^***	0,036	4,78^***	0,004	3,07^***	−0,039	−0,38
R^2	57,56		37,08		46,78		36,19

Las características de la muestra y la definición de las variables están descritas en la tabla 1. Errores estándares y covarianzas calculados robustos, empleando la propuesta de Huber-White.

^* Significación estadística > 90%.

**

Significación estadística > 95%.

***

Significación estadística > 99%.

Todas las regresiones de los modelos incluyen controles sectoriales.

En negrita, variables experimentales.

También merecen ser comentados los valores estacionarios obtenidos en las regresiones de ROI_it+1 y ROE_it+1, definidos como α/(1–β). En el caso de ROI_it+1, este valor asciende a 0,0532, lo que significa que cuando el ROI es superior al 5,32% existe una elevada probabilidad de reversión para descender por debajo del indicado 5,32% en el periodo siguiente, y a la inversa, valores por debajo del 5,32% tenderán a superar este valor estacionario en el siguiente ejercicio. Para ROE_it+1, su valor estacionario es 0,0902 (9,02%), sujeto a idéntica interpretación.

En segundo lugar, la tabla 2 también recoge las predicciones a 5 años, ROI_it+5 y ROE_it+5. Con relación a ROI_it+5, es interesante comprobar cómo los coeficientes asociados a las variables representativas de la rentabilidad van reduciendo paulatinamente tanto su valor numérico como su significación estadística, desvaneciéndose esta a partir del cuarto año. Idéntica pauta es la seguida por las predicciones de ROE_it+5, con coeficientes y significaciones decrecientes.

En cuanto a las variables de control, el ciclo económico, subrogado a través de PIB_t, es positivo y estadísticamente significativo en todos los casos, mientras que las expectativas, aproximadas mediante Expect_t, solamente son significativas en las estimaciones a un año, también con signo positivo. Por último, los coeficientes de determinación indican una notable calidad de ajuste, superiores en las predicciones de ROI.

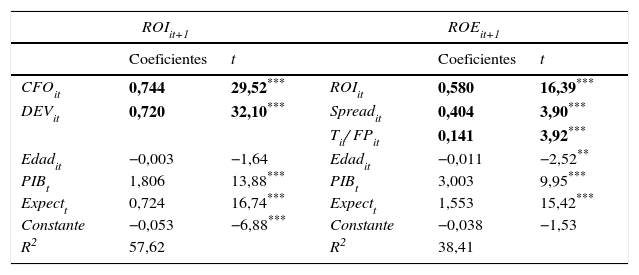
La tabla 3 muestra los resultados obtenidos en la estimación de los parámetros de los modelos genéricos [3] y [4] de separación de componentes de ROI y ROE, respectivamente, a un año. En la predicción de ROI_it+1 hemos obtenido coeficientes similares para ambos componentes, CFO_it y DEV_it, 0,74 y 0,72, respectivamente, lo que indica una persistencia muy parecida, si bien la evidencia disponible en la literatura documenta una persistencia generalmente mayor del componente caja al componente devengo de la rentabilidad. En cuanto a las estimaciones de los componentes de ROE_it+1, es ROI_it el que mayor persistencia aporta, seguido de Spread_it y en último lugar el componente fiscal, T_it/FP_it, debido, muy posiblemente, a la inestabilidad que ocasionan los impuestos diferidos en el gasto total devengado por impuestos sobre beneficios. De nuevo es positivo y significativo el control del ciclo económico, así como las expectativas macroeconómicas, mientras que los coeficientes de determinación arrojan unos valores numéricos prácticamente idénticos a los mostrados en la tabla 4 anterior, lo que indica que la desagregación de la rentabilidad en sus componentes no mejora significativamente la calidad del ajuste.

Tabla 3.

Resultados de la regresión de los modelos:

ROIit+1			ROEit+1
	Coeficientes	t		Coeficientes	t
CFOit	0,744	29,52^***	ROIit	0,580	16,39^***
DEVit	0,720	32,10^***	Spreadit	0,404	3,90^***
			Tit/ FPit	0,141	3,92^***
Edadit	−0,003	−1,64	Edadit	−0,011	−2,52^**
PIBt	1,806	13,88^***	PIBt	3,003	9,95^***
Expectt	0,724	16,74^***	Expectt	1,553	15,42^***
Constante	−0,053	−6,88^***	Constante	−0,038	−1,53
R^2	57,62		R^2	38,41

ROI_it+1 = α + βCFO_it + χDEV_it + ¿

ROE_it+1 = α + βROI_it + χSpread_it + δX_it + ¿

Las características de la muestra y la definición de las variables están descritas en la tabla 1. Errores estándares y covarianzas calculados robustos, empleando la propuesta de Huber-White.

^* Significación estadística > 90%.

**

Significación estadística > 95%.

***

Significación estadística > 99%.

Todas las regresiones de los modelos incluyen controles sectoriales.

En negrita, variables experimentales.

Tabla 4.

Resultados de la regresión de los modelos:

ROIit+5			ROEit+5
	Coeficientes	t		Coeficientes	t
CFOit+4	0,576	17,99^***	ROIit+4	0,585	16,28^***
CFOit+3	0,087	10,03^***	ROIit+3	0,043	1,73^*
CFOit+2	0,060	6,85^***	ROIit+2	0,082	3,21^***
CFOit+1	0,028	3,05^***	ROIit+1	0,012	0,48
CFOit	−0,015	−1,97^**	ROIit	0,026	1,15
DEVit+4	0,558	15,47^***	Spreadit+4	0,368	18,99^***
DEVit+3	0,072	8,38^***	Spreadit+3	0,128	9,47^***
DEVit+2	0,043	4,90^***	Spreadit+2	0,102	7,52^***
DEVit+1	0,018	1,96^*	Spreadit+1	0,057	4,43^***
DEVit	−0,029	−3,68^***	Spreadit	0,006	0,52
			Tit/ FPit+4	0,220	6,00^***
Edadit	−0,007	−3,29^***	Tit/ FPit+3	0,137	3,62^***
PIBt	0,992	7,03^***	Tit/ FPit+2	0,153	4,05^***
Expectt	0,035	0,75	Tit/ FPit+1	0,054	1,49
			Tit/ FPit	0,032	0,94
Constante	−0,007	−0,57
			Edadit	−0,001	−0,19
			PIBt	2,025	6,15^***
			Expectt	0,062	0,57
			Constante	−0,0475	−1,78^*
R^2	47,16		R^2	36,62

ROIit+5=α+∑k=1pβkCFOit+k−1+∑k=1pχkDEVit+k−1+εt+5

ROEit+5=α+∑k=1pβkROIit+k−1+∑k=1pχkSpreadit+k−1+∑k=1pδkXit+k−1+εt+5

Las características de la muestra y la definición de las variables están descritas en la tabla 1. Errores estándares y covarianzas calculados robustos, empleando la propuesta de Huber-White.

*

Significación estadística > 90%.

**

Significación estadística > 95%.

***

Significación estadística > 99%.

Todas las regresiones de los modelos incluyen controles sectoriales.

En negrita, variables experimentales.

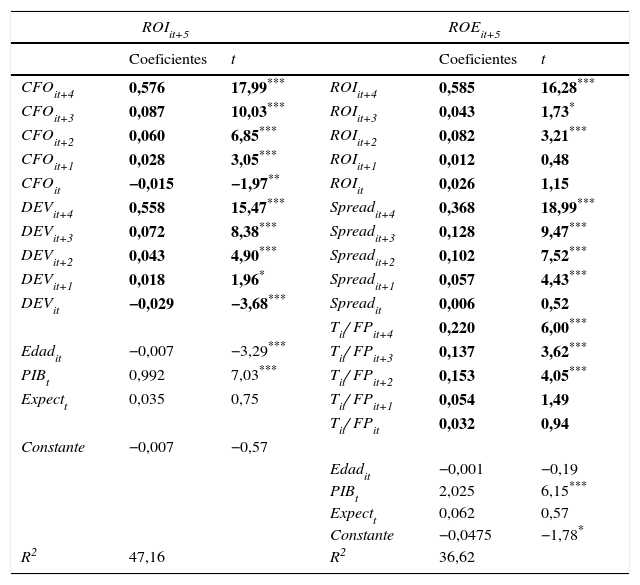
La tabla 4 recoge los resultados de las regresiones de los modelos de separación de componentes a 5 años. Con relación a las predicciones de ROI_it+5, podemos comprobar cómo los coeficientes vinculados a las variables independientes CFO_it+k y DEV_it+k van descendiendo en la misma medida en que se distancian del quinto ejercicio, y son estadísticamente significativos y positivos, a excepción de los coeficientes asociados al ejercicio base de las predicciones, CFO_it y DEV_it, que tienen signo negativo, lo que es coherente con el fenómeno de reversión a la media de la rentabilidad documentado por Freeman et al. (1982). Con respecto a ROE_it+5, sus componentes muestran un comportamiento similar en los coeficientes asociados a los 3 ejercicios más próximos al quinto, perdiéndose la significación estadística a partir del cuarto. El control del ciclo es una vez más positivo y significativo, pero no así las expectativas, y los coeficientes de determinación son, también en este caso, muy similares a los obtenidos con los modelos autorregresivos.

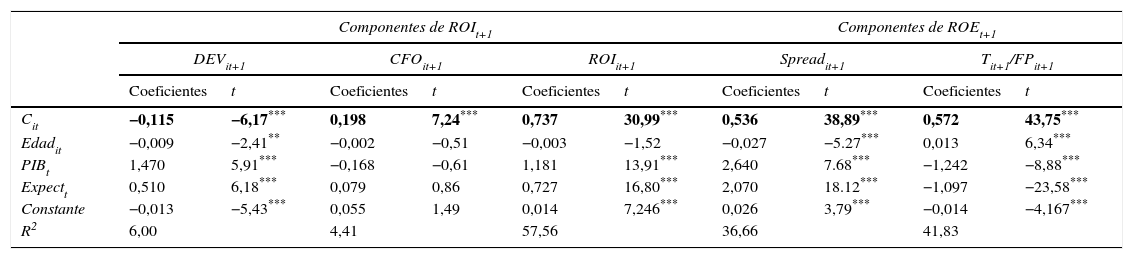
La tabla 5 recoge los resultados obtenidos de la regresión de los modelos de integración de componentes -[6a] y [6b]— a un año. En el primero, la estimación de ROI_it+1 por adición de los parámetros estimados de DEV_it+1 y CFO_it+1 aporta unos coeficientes significativos, pero de muy baja persistencia: negativo el asociado a los ajustes por devengo y positivo el vinculado al cash flow de operaciones, que vienen a confirmar, en el primer caso, la correlación negativa entre los ajustes por devengo de ejercicios adyacentes documentada por Dechow (1994) y, en el segundo, su elevada volatilidad e inestabilidad temporal (Dechow y Ge, 2006). Con respecto al ROE_it+1, sin embargo, la persistencia que muestran sus 3 componentes es muy superior, en especial la de ROI_it+1. Podemos comprobar cómo los coeficientes de determinación de los modelos de los componentes de ROI_it+1 son notoriamente reducidos, mientras que los de ROI_it+1 arrojan valores en la línea de los documentados en las regresiones anteriores.

Tabla 5.

Resultados de la regresión del modelo: C_it+1 = α + β · C_it + ¿_it+1

	Componentes de ROIt+1						Componentes de ROEt+1
	DEVit+1		CFOit+1		ROIit+1		Spreadit+1		Tit+1/FPit+1
	Coeficientes	t	Coeficientes	t	Coeficientes	t	Coeficientes	t	Coeficientes	t
Cit	−0,115	−6,17^***	0,198	7,24^***	0,737	30,99^***	0,536	38,89^***	0,572	43,75^***
Edadit	−0,009	−2,41^**	−0,002	−0,51	−0,003	−1,52	−0,027	−5.27^***	0,013	6,34^***
PIBt	1,470	5,91^***	−0,168	−0,61	1,181	13,91^***	2,640	7.68^***	−1,242	−8,88^***
Expectt	0,510	6,18^***	0,079	0,86	0,727	16,80^***	2,070	18.12^***	−1,097	−23,58^***
Constante	−0,013	−5,43^***	0,055	1,49	0,014	7,246^***	0,026	3,79^***	−0,014	−4,167^***
R^2	6,00		4,41		57,56		36,66		41,83

Las características de la muestra y la definición de las variables están descritas en la tabla 1. Para cada firma i y ejercicio t, C_it representa cada uno de los componentes del ROI_it y del ROE_it. Errores estándar y covarianzas calculados robustos, empleando la propuesta de Huber-White.

^* Significación estadística > 90%.

**

Significación estadística > 95%.

***

Significación estadística > 99%.

En negrita, variables experimentales.

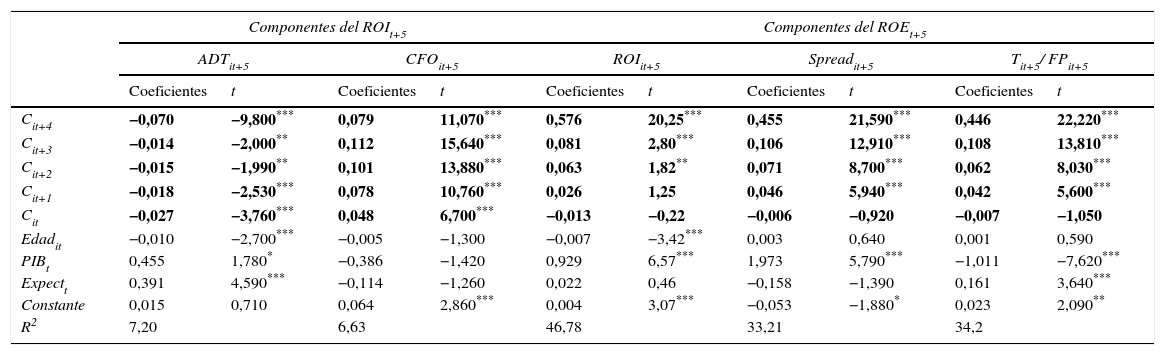
Finalmente, la tabla 6 detalla los resultados de la regresión a 5 años de los modelos [6a] y [6b]. Como en las estimaciones de ROI_it+1, los coeficientes obtenidos para ROI_it+5 indican una débil persistencia, negativa en el caso de los ajustes por devengo, DEV_it+5, y positiva en el del cash flow, CFO_it+5, siendo estadísticamente significativas las variables de los 5 ejercicios y, de nuevo, con una calidad de ajuste también reducida, a tenor de los valores del coeficiente de determinación, en línea con los resultados del modelo a un año. Con respecto a los coeficientes generados para ROE_it+5, su persistencia es muy superior a la de ROI_it+5, a tenor de los valores numéricos alcanzados por sus 3 componentes, si bien en el ejercicio más distante en el horizonte de predicción desaparece la significación estadística. Como ya sucediera en el modelo de predicción a un año, los coeficientes de determinación indican una razonable calidad del ajuste, en línea con las estimaciones que venimos mostrando.

Tabla 6.

Resultados de la regresión del modelo: Cit+5=α+∑k=1pβkCit+k−1+εt+5

	Componentes del ROIt+5				Componentes del ROEt+5
	ADTit+5		CFOit+5		ROIit+5		Spreadit+5		Tit+5/ FPit+5
	Coeficientes	t	Coeficientes	t	Coeficientes	t	Coeficientes	t	Coeficientes	t
Cit+4	−0,070	−9,800^***	0,079	11,070^***	0,576	20,25^***	0,455	21,590^***	0,446	22,220^***
Cit+3	−0,014	−2,000^**	0,112	15,640^***	0,081	2,80^***	0,106	12,910^***	0,108	13,810^***
Cit+2	−0,015	−1,990^**	0,101	13,880^***	0,063	1,82^**	0,071	8,700^***	0,062	8,030^***
Cit+1	−0,018	−2,530^***	0,078	10,760^***	0,026	1,25	0,046	5,940^***	0,042	5,600^***
Cit	−0,027	−3,760^***	0,048	6,700^***	−0,013	−0,22	−0,006	−0,920	−0,007	−1,050
Edadit	−0,010	−2,700^***	−0,005	−1,300	−0,007	−3,42^***	0,003	0,640	0,001	0,590
PIBt	0,455	1,780^*	−0,386	−1,420	0,929	6,57^***	1,973	5,790^***	−1,011	−7,620^***
Expectt	0,391	4,590^***	−0,114	−1,260	0,022	0,46	−0,158	−1,390	0,161	3,640^***
Constante	0,015	0,710	0,064	2,860^***	0,004	3,07^***	−0,053	−1,880^*	0,023	2,090^**
R^2	7,20		6,63		46,78		33,21		34,2

Las características de la muestra y la definición de las variables están descritas en la tabla 1. Para cada firma i y ejercicio t, C_it representa cada uno de los componentes del ROI_it y del ROE_it. Errores estándar y covarianzas calculados robustos, empleando la propuesta de Huber-White.

*

Significación estadística > 90%.

**

Significación estadística > 95%.

***

Significación estadística > 99%.

Todas las regresiones de los modelos incluyen controles sectoriales.

En negrita, variables experimentales.

Predicciones generadas por cada método. Resultados y análisis comparado

Los coeficientes obtenidos de la regresiones mostradas en las tablas 2–6 nos servirán como instrumentos para abordar la fase de predicción fuera de la muestra (out-of-sample) de ROI_it+k y ROE_it+k. Para llevar a cabo dichas predicciones existen diferentes aproximaciones, si bien cuando se dispone de una serie temporal suficientemente larga el procedimiento más habitual consiste en dividir la muestra en 2 periodos, denominados periodo de estimación y de predicción, se obtienen los parámetros de las observaciones correspondientes al periodo de estimación y se aplican a las que integran el periodo de predicción, con lo que se obtienen los errores de pronóstico.

Con el objetivo de mitigar el problema generado por cortas series temporales recurriremos a la solución empleada por Ferson, Nallareddy y Xie (2013), quienes emplean un procedimiento que maximiza el volumen de datos disponibles para la estimación de los parámetros, Así, la estimación utiliza la muestra completa, y deja fuera de ella el ejercicio para el que se van a obtener los parámetros. Por ejemplo, para predecir la rentabilidad del ejercicio 2006 a un año se estiman los coeficientes de una muestra configurada por las observaciones de los ejercicios de 2003 a 2005 y de 2007 a 2012, y para pronosticar la rentabilidad del ejercicio 2010 a 5 años se estiman los coeficientes de una muestra formada por los ejercicios 2003 y 2004 y 2006 y 2007. Este será el modo de obtener las predicciones fuera de muestra, que es denominado por Ferson et al. (2013) como step around (en contraste con el tradicional step ahead antes mencionado),

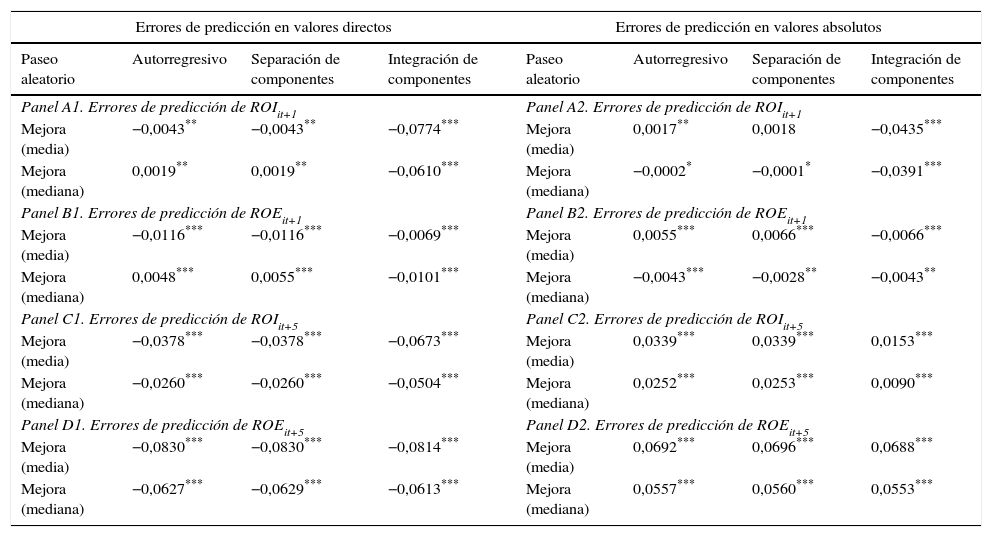
La tabla 7 recoge los errores de predicción en los que cada método ha incurrido, tanto en valores directos o con signos como en valores absolutos, lo que nos permite anticipar que los resultados obtenidos nos llevan a rechazar la hipótesis nula planteada y a aceptar la alternativa, es decir, que los métodos de predicción de la rentabilidad poseen contenido predictivo incremental sobre los pronósticos basados en el paseo aleatorio.

Tabla 7.

Errores cometidos por los métodos de predicción

Errores de predicción en valores directos				Errores de predicción en valores absolutos
Paseo aleatorio	Autorregresivo	Separación de componentes	Integración de componentes	Paseo aleatorio	Autorregresivo	Separación de componentes	Integración de componentes
Panel A1. Errores de predicción de ROIit+1				Panel A2. Errores de predicción de ROIit+1
Mejora (media)	−0,0043^**	−0,0043^**	−0,0774^***	Mejora (media)	0,0017^**	0,0018	−0,0435^***
Mejora (mediana)	0,0019^**	0,0019^**	−0,0610^***	Mejora (mediana)	−0,0002^*	−0,0001^*	−0,0391^***
Panel B1. Errores de predicción de ROEit+1				Panel B2. Errores de predicción de ROEit+1
Mejora (media)	−0,0116^***	−0,0116^***	−0,0069^***	Mejora (media)	0,0055^***	0,0066^***	−0,0066^***
Mejora (mediana)	0,0048^***	0,0055^***	−0,0101^***	Mejora (mediana)	−0,0043^***	−0,0028^**	−0,0043^**
Panel C1. Errores de predicción de ROIit+5				Panel C2. Errores de predicción de ROIit+5
Mejora (media)	−0,0378^***	−0,0378^***	−0,0673^***	Mejora (media)	0,0339^***	0,0339^***	0,0153^***
Mejora (mediana)	−0,0260^***	−0,0260^***	−0,0504^***	Mejora (mediana)	0,0252^***	0,0253^***	0,0090^***
Panel D1. Errores de predicción de ROEit+5				Panel D2. Errores de predicción de ROEit+5
Mejora (media)	−0,0830^***	−0,0830^***	−0,0814^***	Mejora (media)	0,0692^***	0,0696^***	0,0688^***
Mejora (mediana)	−0,0627^***	−0,0629^***	−0,0613^***	Mejora (mediana)	0,0557^***	0,0560^***	0,0553^***

Las características de la muestra están descritas en la tabla 1. Mejora es la diferencia entre los errores de predicción cometidos por cada método y el error de predicción cometido por el paseo aleatorio: es mejor el método que mayor mejora suponga. Tests de diferencias de medias basados en el estadístico t, y tests de diferencias de medianas basados en el test de rangos de Wilcoxon. La significación estadística de las diferencias de medias y de medianas se señala con asteriscos:

*

Significación estadística > 90% de probabilidad.

**

Significación estadística > 95% de probabilidad.

***

Significación estadística > 99% de probabilidad.

En negrita, variables experimentales.

Del análisis de los errores de predicción podemos extraer lecturas muy interesantes. En primer lugar, y con relación a los errores tomados en valores directos, las predicciones de ROI_it+1 a corto plazo (panel A1) hacen descartar el método de integración de componentes porque incurre en mayores errores de predicción que el paseo aleatorio, mientras que la calidad de los pronósticos, en promedio, es idéntica en los métodos autorregresivo y de separación de componentes y superior a la del paseo aleatorio; sin embargo, tomados en mediana, los métodos de predicción no consiguen batir al paseo aleatorio. Con respecto a ROE_it+1 (panel B1), los errores de pronóstico cometidos nos conducen a alcanzar la misma conclusión, es decir, mejores pronósticos de los métodos autorregresivo y de separación en términos de media, pero mayor calidad de las predicciones brindadas por el paseo aleatorio en términos de mediana.

El panel C1 recoge los errores de predicción de ROI_it+5, a largo plazo, también en valores directos. Es destacable, en primer lugar, que los 3 métodos poseen contenido predictivo incremental con respecto al paseo aleatorio, tanto en términos de media como de mediana. Sin embargo, la calidad de las predicciones de los métodos autorregresivo y de separación de componentes son casi idénticas y en todo caso superiores a las generadas por el método de agregación de componentes. Por último, el panel D1 ofrece los errores de predicción de ROE_it+5, y pone de nuevo de manifiesto la superioridad de los 3 métodos: son de mayor calidad el autorregresivo y el de separación.

En cuanto a los errores de predicción tomados en valores absolutos, el panel A2 muestra los errores de predicción de ROI_it+1 y el panel B2 los de ROE_it+1, revelándose en ambos casos la mayor capacidad predictiva del método de separación definida por la media de los errores; no obstante, en mediana ninguno de los 3 métodos mejora las predicciones del paseo aleatorio. Por último, los paneles C2 y D2 recogen los errores de predicción de ROI_it+5 y ROI_it+5, respectivamente, y en ellos se observan mejores pronósticos en los 3 métodos con relación al paseo aleatorio, tanto en media como en mediana: es el método de separación de componentes el que menores errores comete. No obstante, en términos de mediana, el modelo autorregresivo comete el mismo nivel de errores que el modelo de separación de componentes (0,0217), es decir, ninguno de ellos se presenta superior en el nivel de precisión de la predicción.

En síntesis, los resultados que acabamos de documentar en la tabla 7 revelan, en primer lugar, que las predicciones de ROI son ligeramente más acertadas que las de ROE, y que las realizadas a corto plazo son mejores que las obtenidas a largo plazo. En cuanto a la calidad predictiva de los procedimientos que hemos empleado, y desde una visión de conjunto de los errores de predicción cometidos, los métodos autorregresivo y de separación de componentes exhiben el mayor contenido predictivo incremental, tomando los errores tanto en valores directos como absolutos. Sin embargo, conviene tener presente que ninguno de los métodos ha mejorado al paseo aleatorio en predicciones de ROI y ROE a corto plazo con referencia a los valores de las medianas.

No obstante lo anterior, y aunque en líneas generales los métodos autorregresivos y de separación de componentes mejoran los pronósticos basados en el paseo aleatorio y han resultado ser más eficaces que el de integración de componentes, hemos de manifestar que otros criterios alternativos de desagregación de la rentabilidad —como por ejemplo, la clasificación de ingresos y gastos propuesta en el plan general de contabilidad— podrían conducirnos a obtener resultados diferentes.

Errores de predicción y características corporativas

Al objeto de verificar el posible influjo que algunas características corporativas podrían ejercer sobre la calidad de las predicciones generadas por cada método, hemos contrastado la segunda de las hipótesis formuladas llevando a cabo la regresión de los modelos [7a] y [7b]. La tabla 8 muestra, en 4 paneles, los resultados de las regresiones de los errores de pronóstico, tomados en valores absolutos, para cada uno de los métodos, de las medidas de rentabilidad ROI y ROE y de los horizontes temporales con los que venimos operando, uno y 5 ejercicios.

Tabla 8.

Resultados de la regresión de los modelos

	α	β1	β2	β3	β4	β5	R^2en %
Panel A. Errores de predicción de ROIit+1
Aleatorio	0,062^***	−0,002^***	−0,016^***	0,001^**	0,052^***	0,025^***	8,62
	6,21	−8,89	−11,81	2,07	15,18	18,27
Univariante	0,017^***	−0,002^***	−0,003^*	0,002^***	0,001	0,012^***	2,80
	5,82	−5,64	−1,76	3,73	0,35	7,25
Multivariante	0,018^***	−0,002^***	−0,004^**	0,003^***	0,000	0,012^***	5,00
	6,08	−5,71	−2,34	3,83	0,19	7,28
Agregación	0,137^***	−0,003^***	−0,058^***	0,001	0,138^***	0,061^***	22,62
	6,18	−9,34	−6,58	0,64	18,04	18,27
Panel B. Errores de predicción de ROEit+1
Aleatorio	−0,001	0,002^***	0,094^***	0,003^**	0,157^***	0,104^***	16,59
	−0,19	2,98	7,11	2,18	12,30	10,58
Univariante	−0,029	0,000	0,049	0,001	−0,002	0,026	1,01
	−4,13^***	−0,10	12,09^***	0,79	−0,39	6,53^***
Multivariante	−0,061^***	0,002^***	0,069^***	0,001	0,003	0,024^***	1,91
	−8,91	3,06	7,39	0,58	0,77	6,20
Agregación	0,043^***	0,002^***	0,002	−0,001	0,017^***	0,012^***	1,46
	10,59	3,81	0,89	−0,76	6,84	5,27
Panel C. Errores de predicción de ROIit+5
Aleatorio	0,11^***	−0,002^***	−0,053^***	0,003^***	0,143^***	0,015	21,08
	10,5	−5,20	−5,30	3,90	13,48	7,26
Univariante	−0,015^***	−0,001^***	0,009^***	−0,001	0,002	−0,006^***	2,10
	−4,59	−3,30	4,81	−1,27	0,78	−3,55
Multivariante	−0,013^***	−0,001^***	0,008^***	−0,001	−0,001	−0,006^***	1,70
	−4,10	−3,02	4,15	−1,17	−0,4	−3,56
Agregación	0,057^***	−0,004^***	−0,037^***	−0,003	−0,250^***	0,157^***	17,19
	7,10	−4,91	−7,89	−1,47	−10,10	34,35
Panel D. Errores de predicción de ROEit+5
Aleatorio	0,046^***	0,002^***	0,099^***	0,004^**	0,318^***	0,678^***	20,89
	5,76	2,95	11,27	2,54	13,47	15,00
Univariante	−0,024^***	0,003^***	−0,003	−0,002	−0,010^**	−0,017^***	1,50
	−3,20	3,82	−0,66	−1,49	−2,18	−4,03
Multivariante	−0,028^***	0,003^***	−0,001	−0,002	−0,009^**	−0,016^***	1,70
	−3,89	4,42	−0,34	−1,42	−2,03	−3,89
Agregación	−0,036^***	0,004^***	−0,002	−0,002	−0,005	−0,016^***	1,90
	−4,84	5,20	−0,35	−1,44	−1,04	−3,85

ErrROI_it+k = α + β₁ · TAM_it + β₂ · END_it + β₃ · CREC_it + β₄ · DEC _ 1_it + β₅ · DEC _ 10_it + ¿_it+k

ErrROE_it+k = α + β₁ · TAM_it + β₂ · END_it + β₃ · CREC_it + β₄ · DEC _ 1_it + β₅ · DEC _ 10_it + ¿_it+k

Las características de la muestra están descritas en la tabla 1. Para cada firma i, ejercicio t y periodo posterior k:

CREC_it es la tasa de crecimiento de la cifra de negocios; DECIL_10_it es una variable dicotómica a la que se le asigna el valor 1 cuando la observación está situada en el decil de ROI_it o ROE_it más reducido, y 0 en otro caso; DECIL_1_it es una variable binaria que toma el valor 1 cuando la observación se encuentra localizada en el decil de ROI_it o ROE_it más elevado y 0 en caso contrario; END_it es el cociente entre la deuda total y al activo medio del ejercicio; ErrROI_it+k y ErrROE_it+k son los errores de predicción cometidos por cada método, expresados en valores absolutos de ROI y ROE, respectivamente; TAM_it es el logaritmo neperiano del activo total al cierre del ejercicio.

Errores estándares y covarianzas calculados robustos, empleando la propuesta de Huber-White. La significación estadística se expresa en asteriscos:

*

Significación estadística > 90% de probabilidad.

**

Significación estadística > 95% de probabilidad.

***

Significación estadística > 99% de probabilidad.

De igual modo que en la sección anterior, podemos avanzar que los resultados nos llevan a rechazar la hipótesis nula y a aceptar la alternativa, es decir, que las características de las empresas afectan de manera significativa a la calidad de las predicciones proporcionadas por cada método. Podemos constatar, en primer lugar, cómo el coeficiente asociado a la primera de las variables independientes, el tamaño, TAM_it, muestra una relación casi siempre estadísticamente significativa con los errores de predicción; de signo negativo en los pronósticos de ROI y positivo en los de ROE, es decir, que los métodos cuya eficacia estamos analizando son más certeros cuando se emplean para pronosticar el ROI de las empresas más grandes, pero más ineficaces cuando se trata de establecer predicciones de ROE. Según nuestro parecer, esta aparente contradicción trae causa del hecho de que las empresas de mayor dimensión, dado su mayor poder de mercado, exhibirían unos niveles de rentabilidad económica más estables y por tanto más pronosticables, pero, al mismo tiempo, su mayor capacidad de negociación con sus acreedores financieros genera un mayor acceso a la financiación con deuda, y la incorporación de las cargas financieras, con su inevitable variabilidad en respuesta a los cambios en los tipos de interés, dificulta la predicción del ROE.

Con respecto al endeudamiento, END_it, los coeficientes a él asociados son negativos y significativos en las predicciones de ROI a corto plazo, pero positivos en ROE a un año, lo que indica mayor acierto en ROI y menor en ROE cuanto mayor es el nivel de endeudamiento de las empresas. Por el contrario, en pronósticos a largo no es posible identificar de manera clara su vinculación con los errores cometidos por los métodos.

Con relación al crecimiento, CREC_it, el signo y significación de sus coeficientes indica que esta característica de las empresas conduce —salvo en el caso del modelo de agregación— a la comisión de mayores errores de predicción en los pronósticos de ROI a corto plazo, sin mostrar significación estadística en los restantes errores. Finalmente, y en cuanto a las variables binarias representativas de niveles extremos de rentabilidad, DECIL_1_it, exhibe coeficientes en todo caso positivos y muy significativos, lo que viene a confirmar que la mayor reversión —debida a una menor persistencia— asociada a tasas de rentabilidad anormalmente reducidas, a diferencia de lo que sucede con las rentabilidades anormalmente elevadas, DECIL_10_it, ocasiona mayores dificultades de pronóstico y, por consiguiente, mayores errores en todos los métodos.

Tomada en su conjunto, esta evidencia indica que la comisión de errores de predicción no solamente depende del método elegido, sino también de las características de cada empresa, y así, por regla general las firmas de mayor dimensión, crecimiento moderado y niveles medios de rentabilidad pueden verse más favorecidas por mejores pronósticos que las más pequeñas, con mayores tasas de crecimiento o situadas en niveles de rentabilidad anormalmente elevados o reducidos. No obstante, nos parece particularmente interesante destacar que, aunque las características que hemos estudiado puedan afectar a la calidad de los pronósticos por inducir mayores o menores probabilidades de error, dichos atributos afectan por igual a todos los métodos, de manera que ninguno de ellos es especialmente sensible o singularmente inmune a alguna característica empresarial concreta.

Conclusiones

Nuestro trabajo ha tenido por objeto realizar una evaluación de los métodos de predicción de la rentabilidad basados en el concepto de persistencia, probando su eficacia sobre una amplia muestra de empresas españolas. Los resultados que hemos presentado y discutido han revelado cómo, de las técnicas analizadas, la autorregresiva y la de separación de componentes aportan las estimaciones de mayor calidad en la mayoría de las ocasiones y exhiben, en líneas generales, el mayor contenido predictivo incremental para diferentes especificaciones de la rentabilidad y para horizontes temporales a uno y 5 años. En cualquier caso, la eficacia de cada método es una cuestión de hecho, sin que a priori pueda defenderse con solidez argumental la mayor calidad de uno u otro, pues dependerá en gran medida del contexto en el que se realiza la predicción y de los criterios de desagregación de la rentabilidad en sus diferentes componentes.

Asimismo, la calidad de las predicciones logradas con los 3 métodos disponibles no depende solamente de la elección del instrumento de estimación elegido, sino que también guarda una importante relación con las propias características corporativas de las compañías, tales como el tamaño, las tasas de crecimiento y los niveles actuales de rentabilidad. En suma, la calidad predictiva es una cuestión de contexto que, además de la adecuada elección del método apropiado para cada caso, se ve condicionada por el tipo de empresa analizada.

En cualquier caso, nuestros hallazgos han de ser interpretados con cautela y han de quedar confinados al marco espacial y temporal de nuestra muestra, y, sobre todo, insistimos en la necesidad de tener muy en cuenta que el empleo de otros criterios alternativos de clasificación podrían aportarnos una evidencia empírica distinta a la documentada en este trabajo por estar basado en series temporales subyacentes muy diferentes. Además, nuestros resultados vienen a indicar que la calidad predictiva no solo depende de la adecuada selección del método de estimación, sino que existen determinados atributos de las empresas que ejercen una significativa influencia sobre aquellas, como el tamaño, el grado de endeudamiento, las tasas de crecimiento o los niveles actuales de rentabilidad, características que afectan por igual a los 3 métodos analizados.

Por último, consideramos que nuestro estudio contribuye a la literatura sobre la predicción de la rentabilidad al proporcionar una evidencia empírica adicional con datos españoles y aportar un análisis de la relación existente entre los errores de predicción y características corporativas resaltables. No obstante, nuestro trabajo también presenta inevitables limitaciones; así, en primer lugar, los resultados obtenidos podrían estar afectados en alguna medida por el impacto de operaciones corporativas como fusiones, adquisiciones o escisiones, que suponen una modificación estructural de las observaciones afectadas y dificulta la realización de pronósticos. En segundo lugar, y como ya hemos indicado, criterios diferentes de desagregación de la rentabilidad podrían inducir conclusiones también distintas, y, por último, nuestra muestra está integrada exclusivamente por empresas auditadas, circunstancia que supone un filtro de calidad, de modo que un criterio de selección muestral menos restrictivo, que hubiera permitido contar con empresas no auditadas, podría llevarnos a documentar una evidencia diferente.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.