Distintos trabajos apuntan al hecho de que la fase preanalítica es la que concentra la mayor parte de los errores que afectan al resultado final del análisis. El tiempo que transcurre entre la toma de una muestra y su llegada al laboratorio para su análisis es crucial para garantizar la calidad de los resultados. Si se considera además la tendencia general de concentración del proceso analítico en grandes laboratorios, toma especial relevancia el diseño y la planificación de las rutas de recogida de muestras que minimicen el tiempo de transporte.
Material y métodosEn primer lugar, se contextualiza el problema de la optimización de las rutas desde el punto de vista de la investigación operativa, presentando los dos modelos esenciales relacionados: el Vehicle Routing Problem y el Traveling Salesman Problem, introduciendo la representación de este último mediante grafos. Seguidamente, se describen dos estrategias básicas para obtener aproximaciones a las soluciones óptimas, que se aplicarán para resolver un caso sencillo y práctico con el fin de evaluar la calidad del servicio interno de transporte de muestras de un laboratorio clínico.
ResultadosSe presentan los resultados obtenidos y se valora la calidad de la ruta que sigue el coche valija (CV) del laboratorio, concluyendo que el servicio prestado es casi óptimo en relación con los posibles circuitos alternativos.
DiscusiónLa logística en el campo de la preanalítica es determinante en el buen funcionamiento de los laboratorios y un rasgo diferencial entre los que apuestan por la calidad y la innovación. Hemos creído conveniente redactar este artículo para que el personal sanitario encargado de la planificación y el seguimiento de las rutas de transporte de muestras sepa a qué tipo de problemas se enfrenta y cómo puede valorarlos. Consideramos que el ejemplo descrito, pese a su sencillez, puede despertar el interés del público al que va dirigido, y ayudar a la evaluación y mejora del proceso de recogida, traslado y análisis de las muestras.
Several studies point to the fact that the pre-analytical phase concentrates most of the errors affecting the outcome of the analysis. The time lag between taking a sample and its arrival to the laboratory for analysis is crucial to ensure the quality of results. If we consider the general trend of concentration of the analytical process in large laboratories, the design and planning of sample collection routes to minimise travel time becomes especially relevant.
Methods and materialsFirst of all, the authors contextualize the problem of route optimization from the viewpoint of Operational Research, presenting the two basic related models: the Vehicle Routing Problem (VRP) and the Travelling Salesman Problem (TSP), introducing the representation of the latter through graphs. Afterwards, they describe two basic strategies for obtaining approximations to the optimal solutions, applying them to solve a simple and practical case to evaluate the quality of an internal transport service from a clinical laboratory.
ResultsThe authors present the results and evaluate the quality of the route held by the lab′s car bag, concluding that the service is nearly optimal in relation to possible alternative circuits.
DiscussionLogistics in the field of pre-analytical processes is closely related to success in the daily operation of laboratories, and a distinguishing feature between those who are committed to quality and innovation. We thought it advisable to write this article so that the health personnel responsible for planning and monitoring sample transportation routes should know what problems there are and how to assess them. We consider that the example described here, despite its simplicity, can stimulate the interest of the audience it is directed to and can help to assess and improve the processes that include, collection, transport and analysis of clinical samples.
Los laboratorios clínicos del sistema público nacional español están involucrados, desde hace mucho tiempo, en instaurar sistemas de control de calidad del proceso analítico en todas sus fases. El cumplimiento de la norma ISO 15189:2007, específica para la acreditación de laboratorios clínicos, es un ejemplo extendido del compromiso con la calidad, así como del esfuerzo y la voluntad colectiva de mejora continua en el servicio.
Distintos trabajos apuntan al hecho de que la fase preanalítica es la que concentra la mayor parte de los errores que afectan al resultado final del análisis1–3. Por este motivo, así como por nuestra formación, interés y experiencia profesional, este artículo pone atención en un aspecto muy concreto del control de la calidad en dicha fase.
Existe una tendencia general de concentración del proceso analítico en grandes laboratorios, encargados de analizar muestras procedentes de múltiples centros de extracción que pueden llegar a estar a distancias considerables del laboratorio. En esta situación, el adecuado transporte de los especímenes adquiere una especial relevancia: la calidad de las muestras depende tanto de las condiciones de su transporte como de que el tiempo que transcurre desde la toma de la muestra hasta su procesamiento en el laboratorio sea suficientemente reducido. Estas dos condiciones garantizan la estabilidad de la muestra y, por tanto, unos resultados analíticos de mayor fiabilidad.
En España, el estudio de la adecuada gestión de los recursos ha hecho que ciertas comunidades autónomas encarasen el problema de la gestión preanalítica creando una red de transporte de muestras interlaboratorios4. El establecimiento de protocolos y normativas referente a las condiciones de transporte de las muestras, con el fin de preservar su calidad, ha sido una de las preocupaciones principales de los organismos competentes5,6. Pero, como hemos señalado, existe otro factor a tener en consideración: debe gestionarse adecuadamente el tiempo de transporte de las muestras desde su lugar de origen hasta el laboratorio. De aquí en adelante nos centraremos en esbozar algunas ideas que, esperamos, sean de utilidad para quienes están involucrados en las tareas de planificación de la recogida de muestras o en las de auditoría interna del servicio de transporte.
Material y métodosLos Vehicle Routing Problem y Traveling Salesman ProblemLa planificación de tareas, horarios y rutas de transporte son ejemplos del área de estudio de la rama de las matemáticas conocida como investigación operativa. Es muy recomendable la lectura de los cuatro primeros capítulos (Parte I) de COMAP7 como introducción amena y bastante completa de las aplicaciones que tiene en la vida cotidiana la investigación operativa.
El problema general que debe intentar resolver el personal que planifica las rutas de transporte de las muestras es el siguiente: encontrar rutas que, iniciándose y terminándose en el laboratorio, cubran en el menor tiempo posible la visita y la recogida de muestras de todos los centros de extracción.
En caso de disponer de más de un vehículo para cubrir estas rutas de manera simultánea, el problema encajaría dentro de los conocidos como Vehicle Routing Problem (VRP), cuyo estudio introdujeron Dantzig y Ramser en 19598 y en el que no entraremos en detalle. Para disponer de un compendio de las distintas técnicas empleadas para intentar resolver los VRP es recomendable la lectura del libro de Toth y Vigo9.
En el caso de disponer de un único vehículo, el problema pasa a ser una colección de otro tipo de problemas relacionados: esta tipología recibe el nombre de Traveling Salesman Problem (TSP) debido a su equivalencia con los problemas que deben enfrentar los viajantes que tienen que realizar visitas comerciales a unas cuantas ciudades. El interés del viajante es pasar una sola vez por cada una de las ciudades que debe visitar, terminar el recorrido en el punto de partida y realizar este recorrido de la manera más corta posible. Una forma concisa y técnica de enunciar el TSP es la siguiente: encontrar circuitos hamiltonianos de coste mínimo.
Las técnicas clásicas para resolver los problemas VRP son técnicas de programación lineal que, en muchas ocasiones, presuponen que disponemos de soluciones de problemas del tipo TSP para subconjuntos de puntos por visitar. Por simplicidad en la exposición, y debido a la función divulgativa de este artículo, nos centraremos en describir dos de los métodos existentes para intentar resolver los problemas del tipo TSP: el método del «vecino más cercano» (VMC) y el de «aristas clasificadas» (AC), que a pesar de no ser de los métodos más punteros permiten poner en valor la aplicabilidad de las técnicas de la investigación operativa al control del error en la fase preanalítica. Una excelente referencia acerca del origen, los distintos puntos de vista desde los que se ha abordado el problema, las aplicaciones y algunos de los algoritmos de resolución es el primer capítulo de Applegate et al10. Otras referencias interesantes relacionadas con los intentos de resolución del TSP y los métodos asociados son los artículos de Rosenkrantz et al11, Padberg y Rinaldi12, Applegate et al13, y Dorigo y Gambardella14.
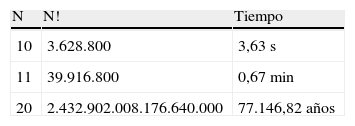
El enunciado del TSP es relativamente sencillo, pero su resolución entraña ciertas dificultades. Existe un método que sin duda nos permitiría obtener la solución exacta, que es el de calcular el tiempo de todas las rutas que puedan generarse a partir de los datos del problema y quedarse con la ruta con tiempo mínimo. En caso de querer minimizar distancia o coste, se sustituye «tiempo» por cualquiera de las dos variables. A este método se le puede denominar de «fuerza bruta» o de «pesquisa (o búsqueda) completa». Si N es el número de puntos por visitar, el problema reside en el número de posibles rutas, que viene dado por el factorial del número de puntos (N!): esto hace que la solución por fuerza bruta sea impracticable para valores de N incluso moderados con los medios computacionales actualmente a nuestro alcance (tabla 1).
En lenguaje técnico, el TSP se clasifica como un problema del tipo NP-completo, que son los que no pueden resolverse en tiempo polinomial en función de N (en el caso del TSP, N representa el número de puntos por visitar). Por tanto, el reto para la resolución de problemas TSP ha sido desarrollar métodos para conseguir, en un tiempo razonable, rutas óptimas o que estén suficientemente cerca de ser las óptimas. Como se ha comentado anteriormente, exponemos dos estrategias heurísticas (en función de algunos criterios razonables de selección de rutas se obtiene una aproximación a la ruta óptima) denominadas VMC y AC, aunque existen muchos más.
Descripción de las estrategiasVecino más cercano (VMC)Empezando por el punto de partida de la ruta, primero visitamos el punto más cercano y, a continuación, el punto más cercano todavía no visitado. Volvemos al punto de partida cuando ya no nos quedan puntos por visitar.
Aristas clasificadas (AC)Empezamos ordenando los caminos que unen cada par de puntos por visitar en orden creciente de tiempo (o en orden creciente de distancia o coste). En cada una de las etapas del proceso seleccionamos el camino que: a) nunca requiera que se junten tres caminos en el punto (puesto que, para tener una ruta que solo pase una vez por cada punto, únicamente podemos tener un camino de llegada y otro de salida relacionados con el punto); b) nunca cierre una ruta circular que no incluya todos los puntos que tenemos que visitar.
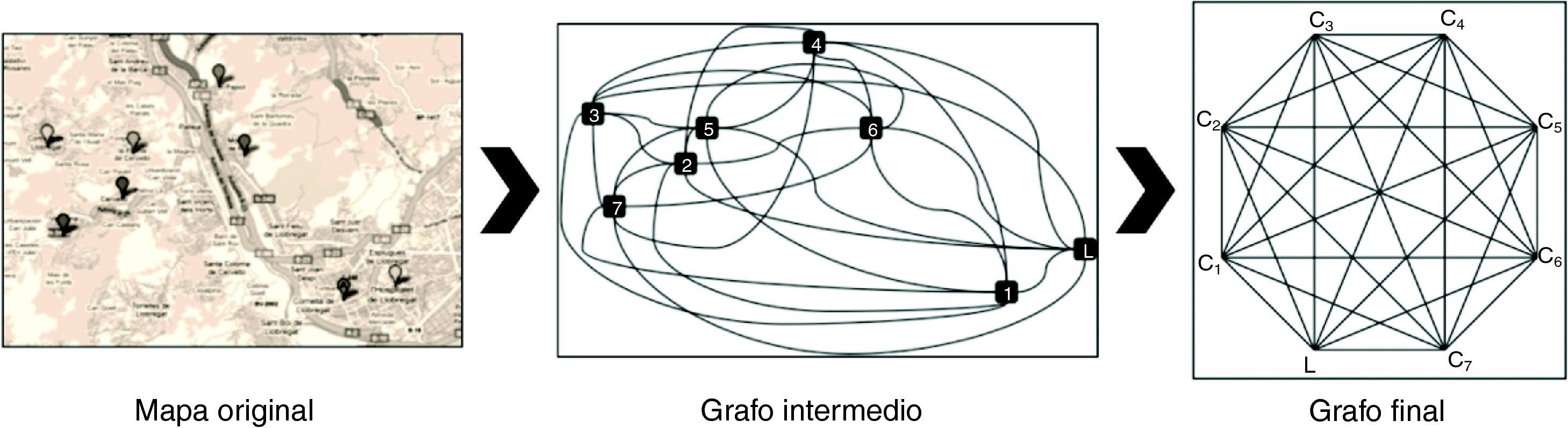
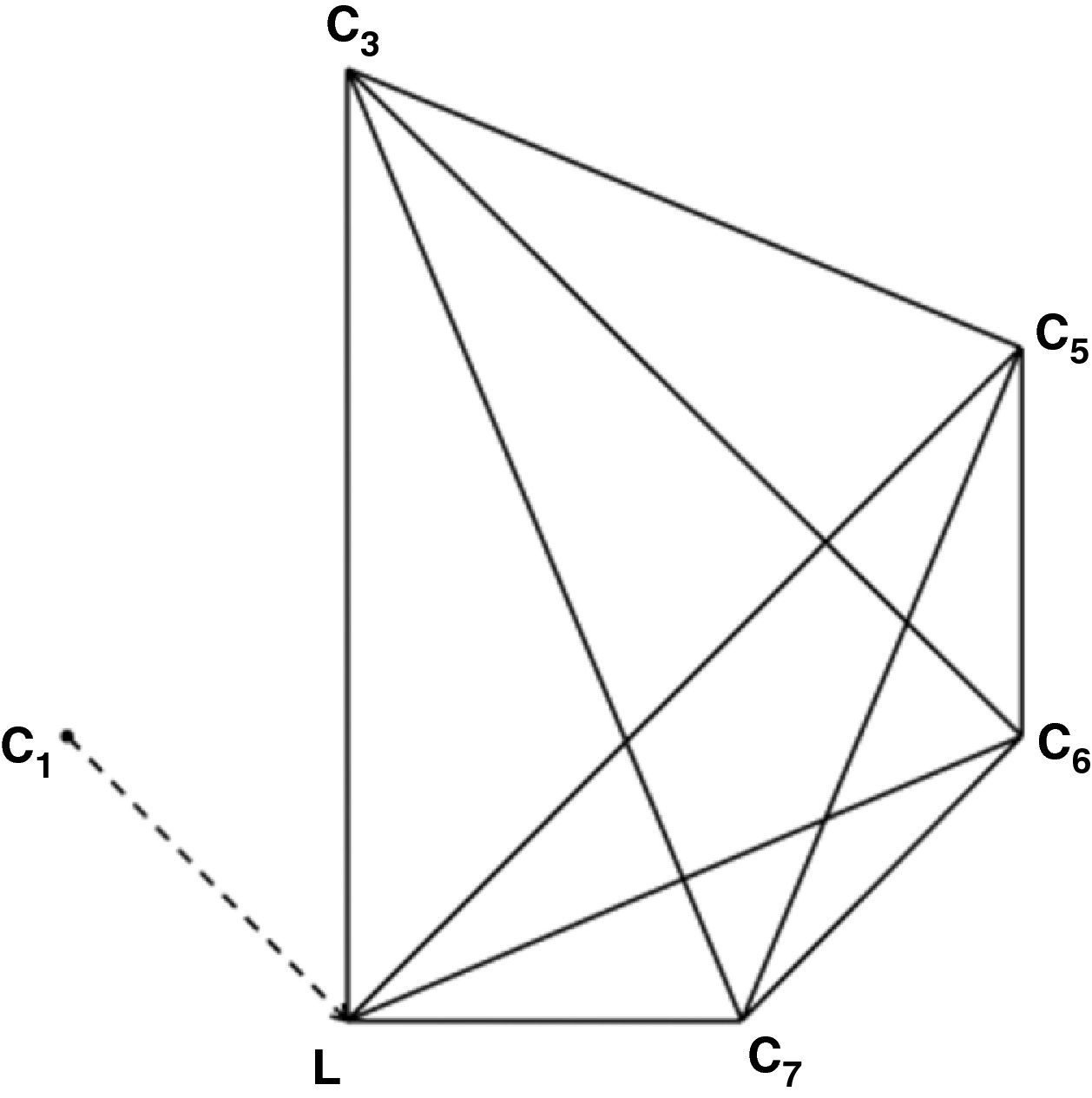
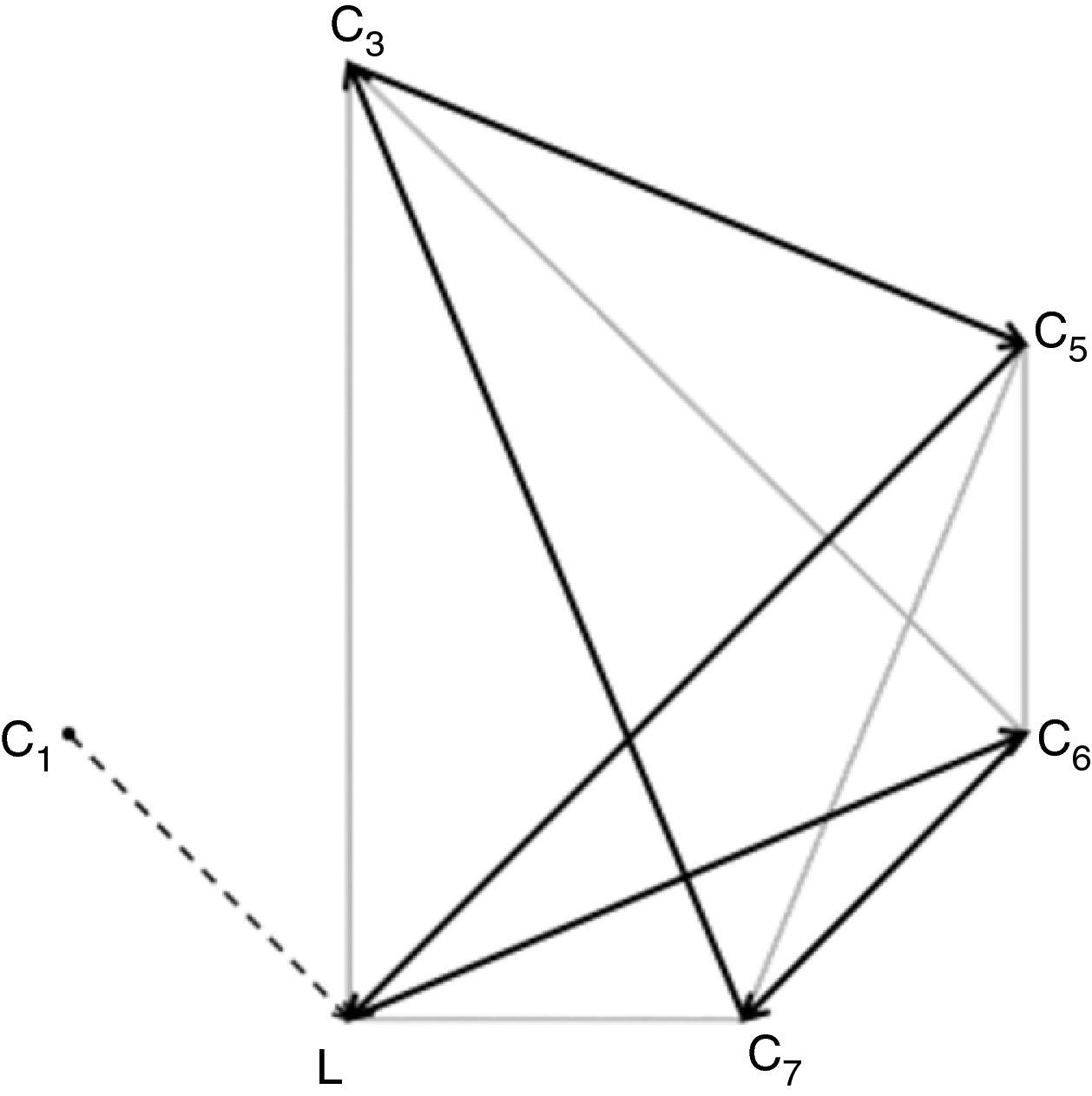
GrafosUna de las herramientas empleadas frecuentemente en la investigación operativa es la representación de los problemas de estudio mediante grafos (conjuntos de vértices y aristas). Por ejemplo, si estamos preocupados por encontrar una ruta de tiempo mínimo entre el laboratorio y siete puntos de extracción periféricos, podríamos representar todas las conexiones de la manera como se indica en la figura 1. En esta representación cada vértice Ci (i=1...7) es un centro de extracción, y el vértice L, el laboratorio. Las aristas representan los caminos que unen cada par de centros: sería interesante introducir los tiempos que se tarda en cubrir estos caminos, por lo que se introducen los grafos ponderados (pesos en las aristas, que representan en este caso los tiempos de recorrido).
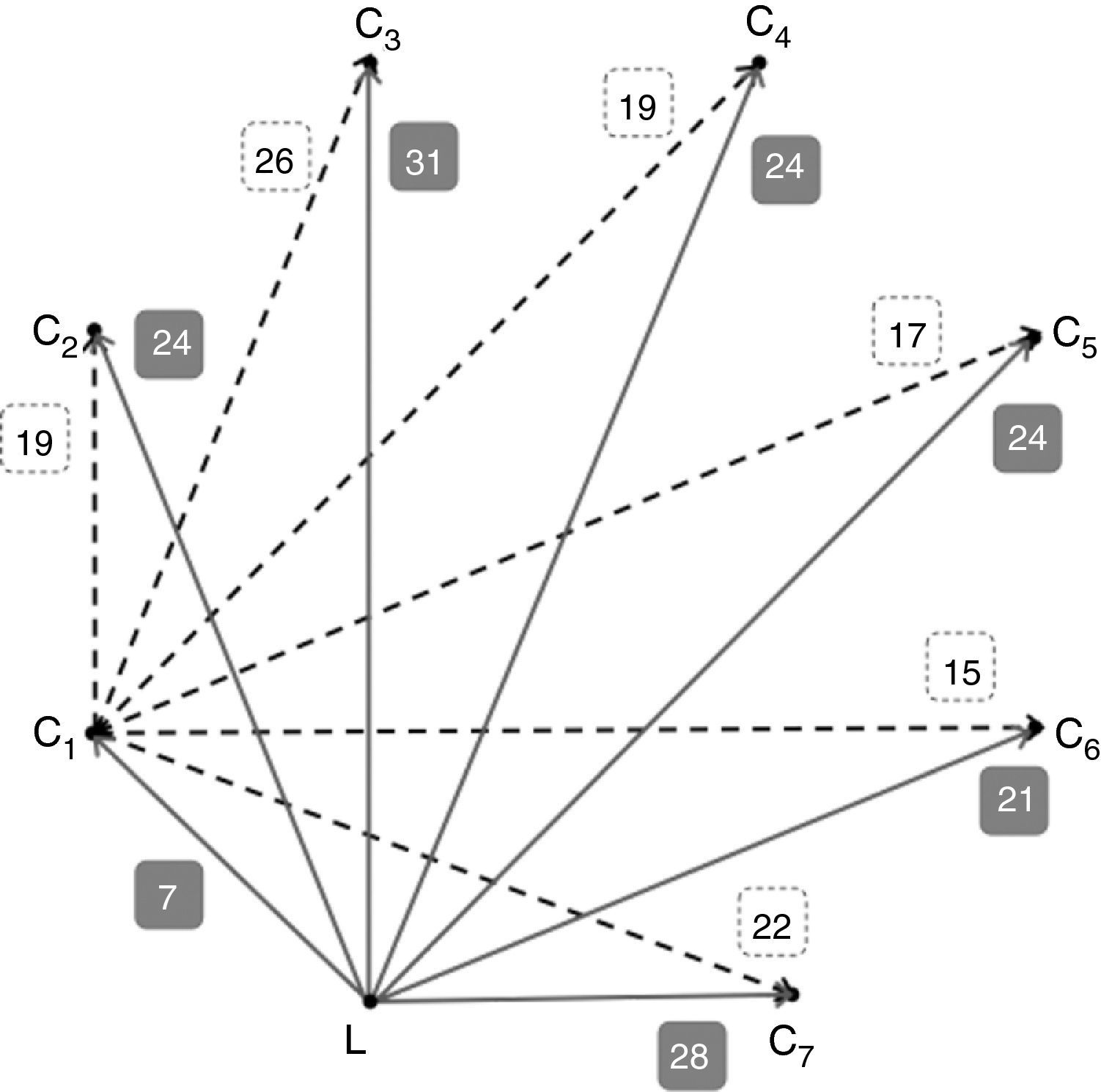
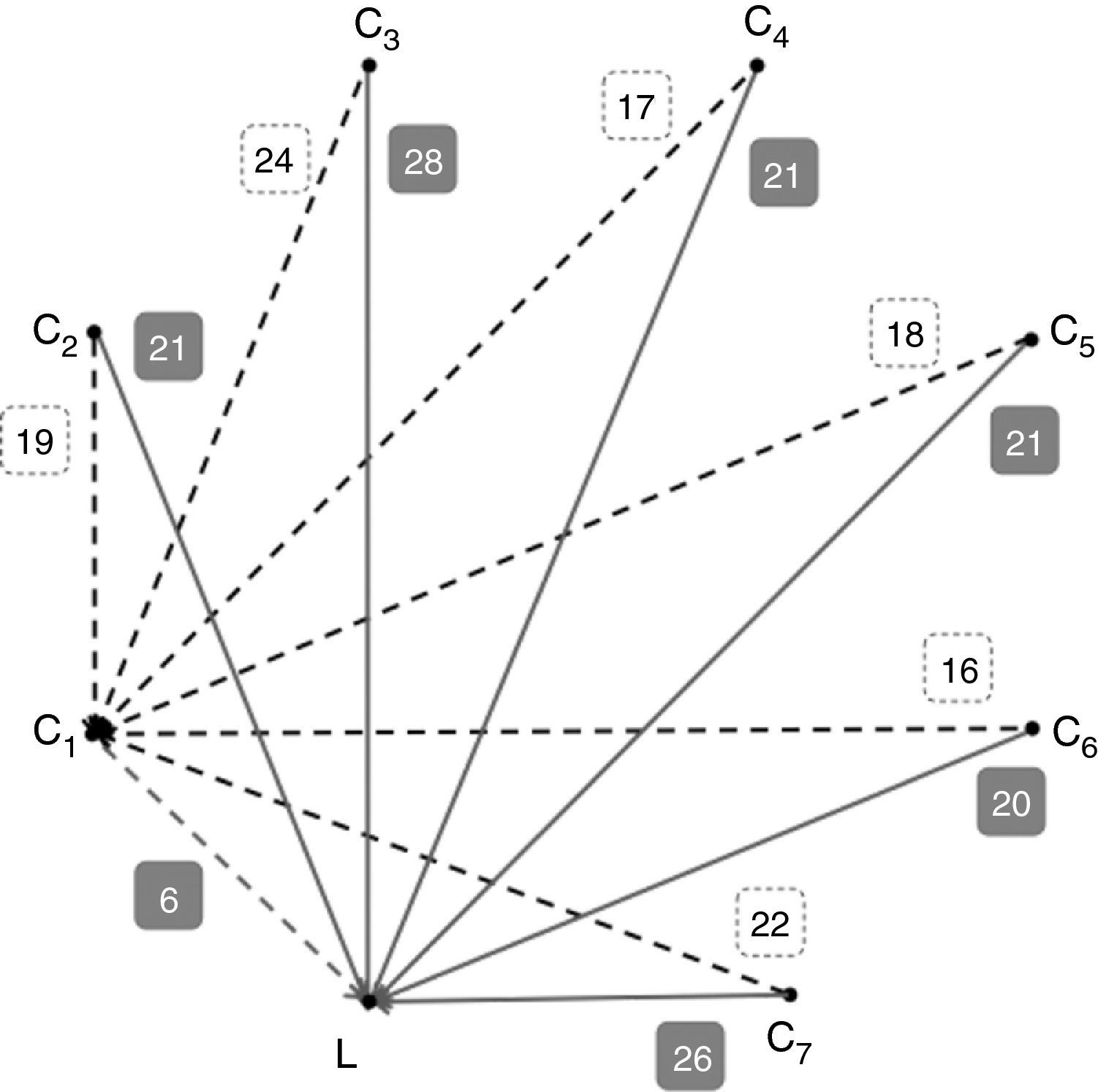
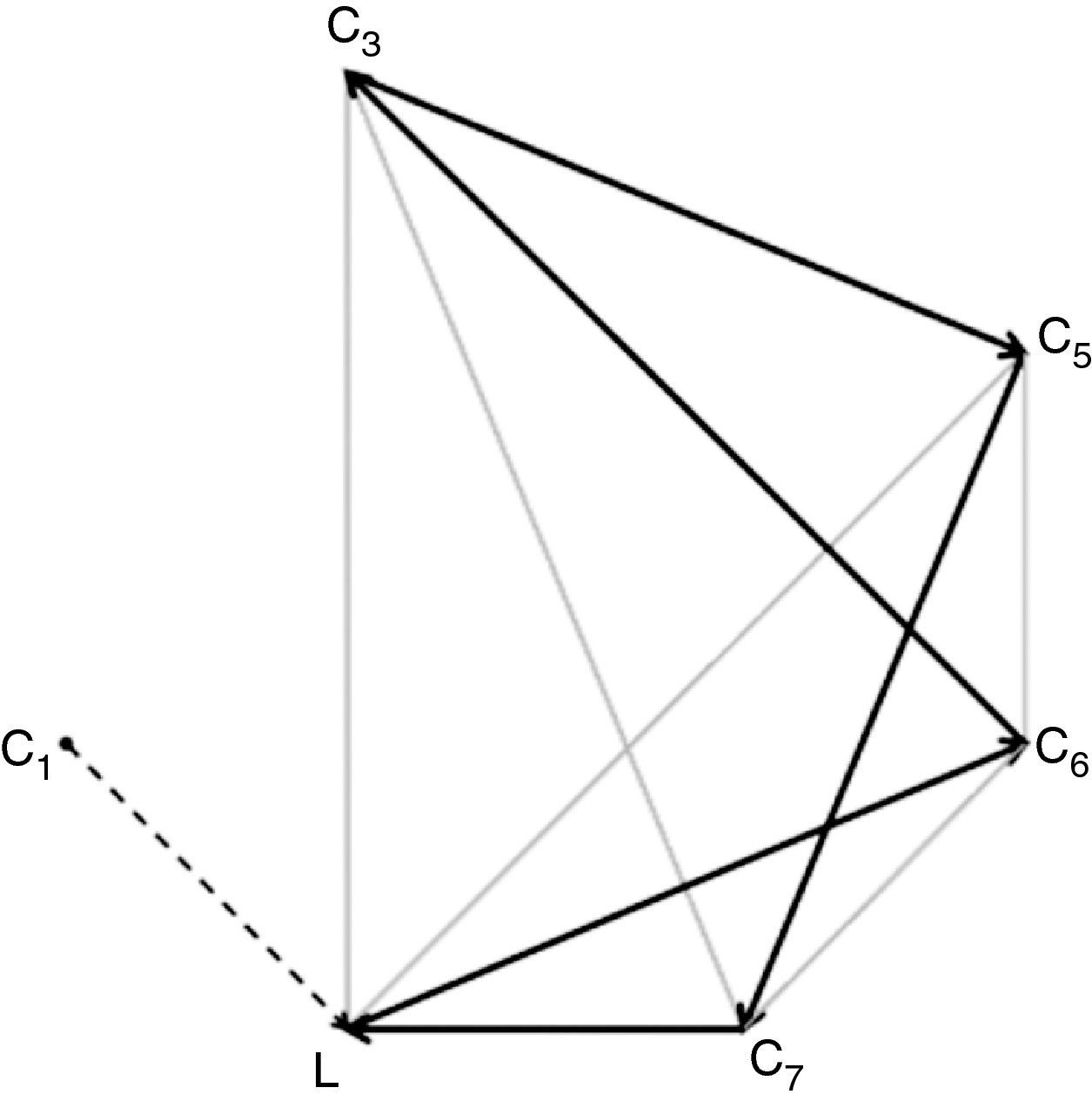
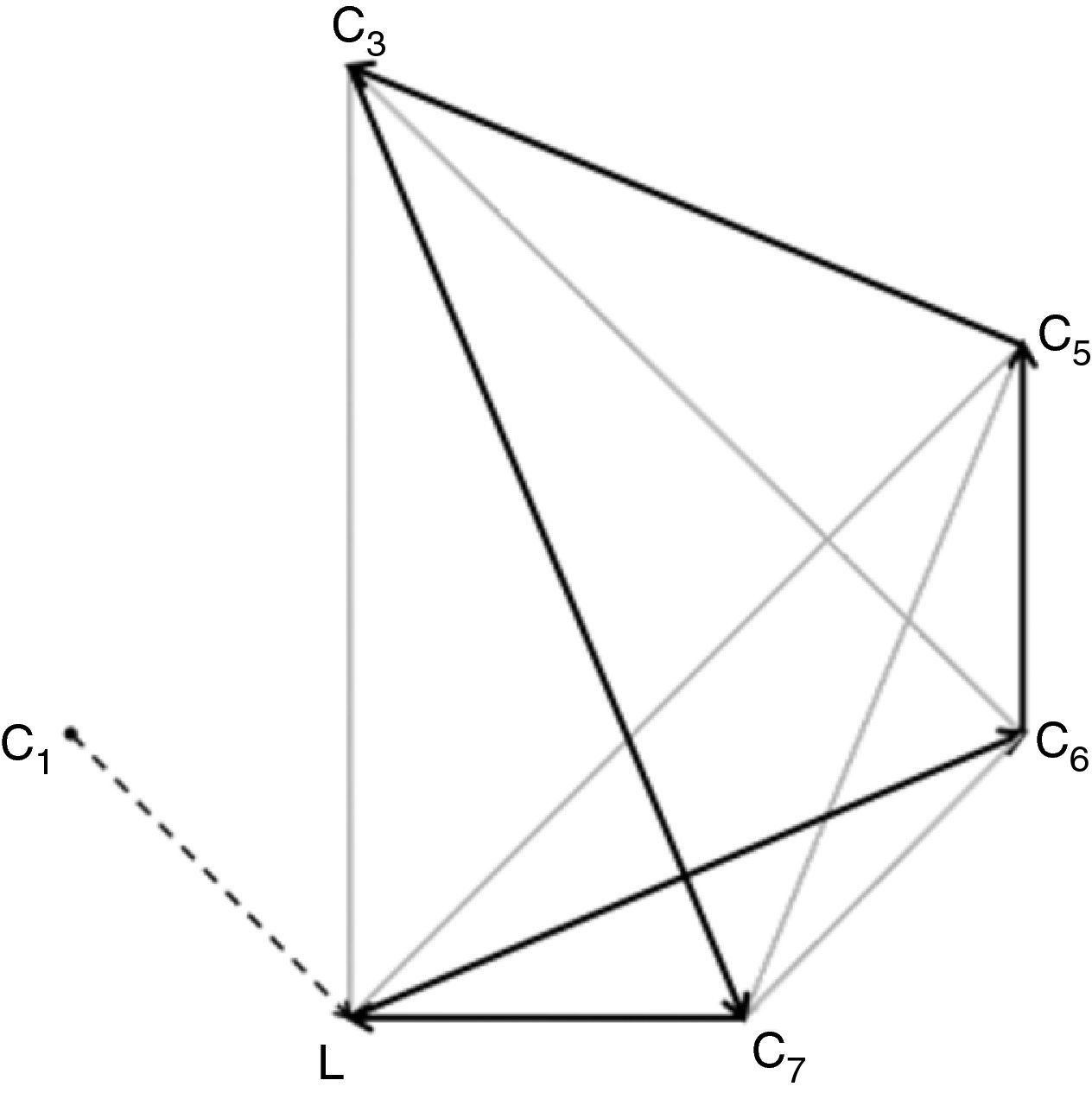
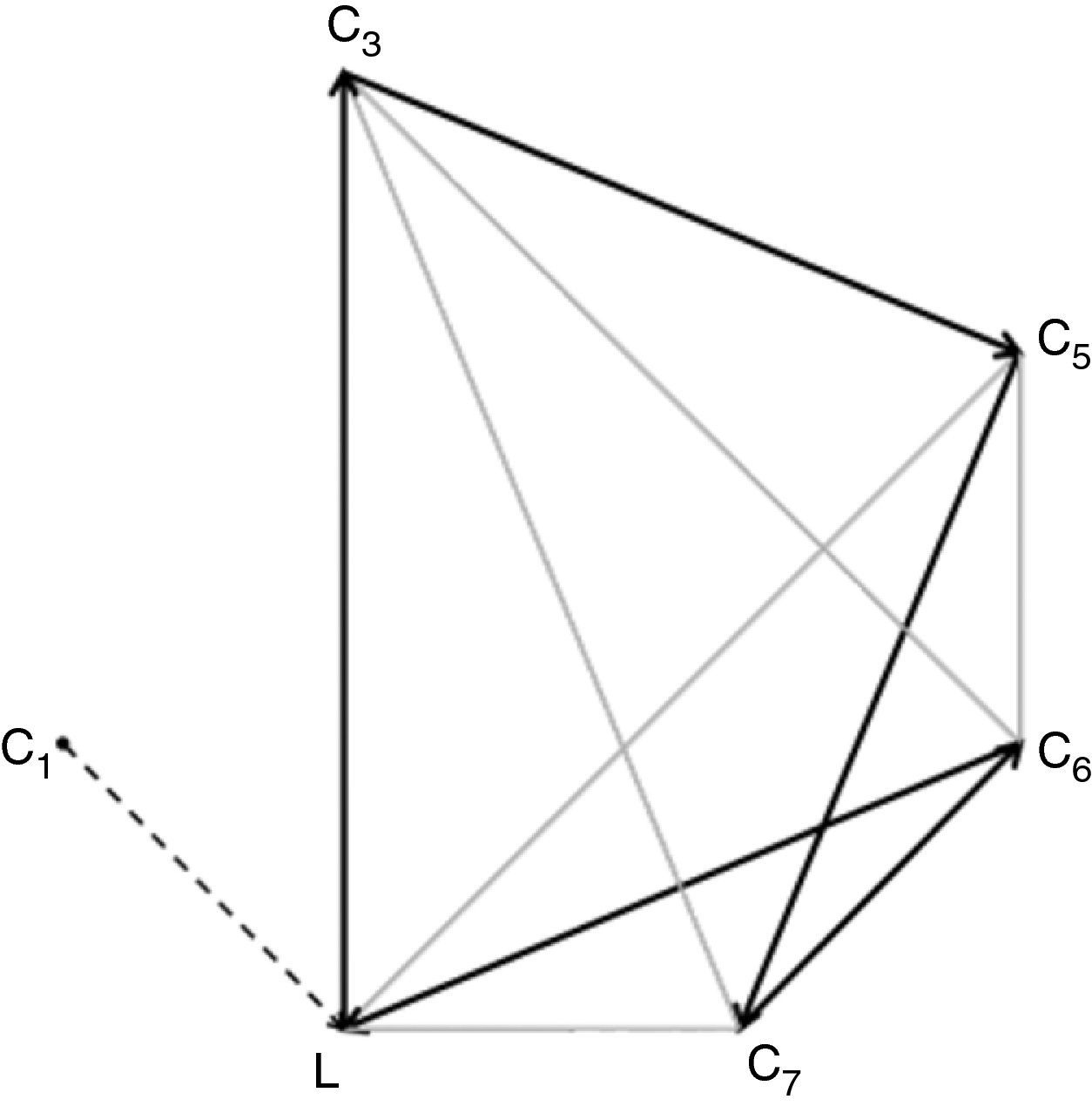
En la figura 2 se representa solo una parte del grafo ponderado asociado a la figura 1, para que la figura sea más comprensible: mostramos las aristas que, partiendo de L, conectan con todos los Ci (en líneas continuas y tiempos de llegada sobre fondo oscuro), y las aristas que, partiendo de C1, conectan con todos los demás vértices Ci (en líneas discontinuas y tiempos sobre fondo claro). Si los tiempos que se tarda en cubrir el camino entre Cj y Ck no dependen del punto de partida, entonces ya disponemos de toda la información en el grafo. De todas formas, es posible que el tiempo que necesitamos para ir de Cj a Ck sea distinto que el tiempo que necesitamos para ir de Ck a Cj (no todas las vías son de doble sentido, por ejemplo), por lo que deberíamos completar nuestro grafo con la información que presenta la figura 3, en la que se han representado las aristas que parten de cada Ci y se dirigen a L (en líneas continuas y tiempos de llegada sobre fondo oscuro) y las que parten de cada Ci y se dirigen a C1 (en líneas discontinuas y tiempos sobre fondo claro). Como puede observarse, el tiempo para ir de L a C1 son 7min (fig. 2), y el tiempo para ir de C1 a L, 6min (fig. 3). O, también, para ir de C1 a C4 tardamos 19min (fig. 2) y el tiempo necesario para ir de C4 a C1 son 17min (fig. 3).
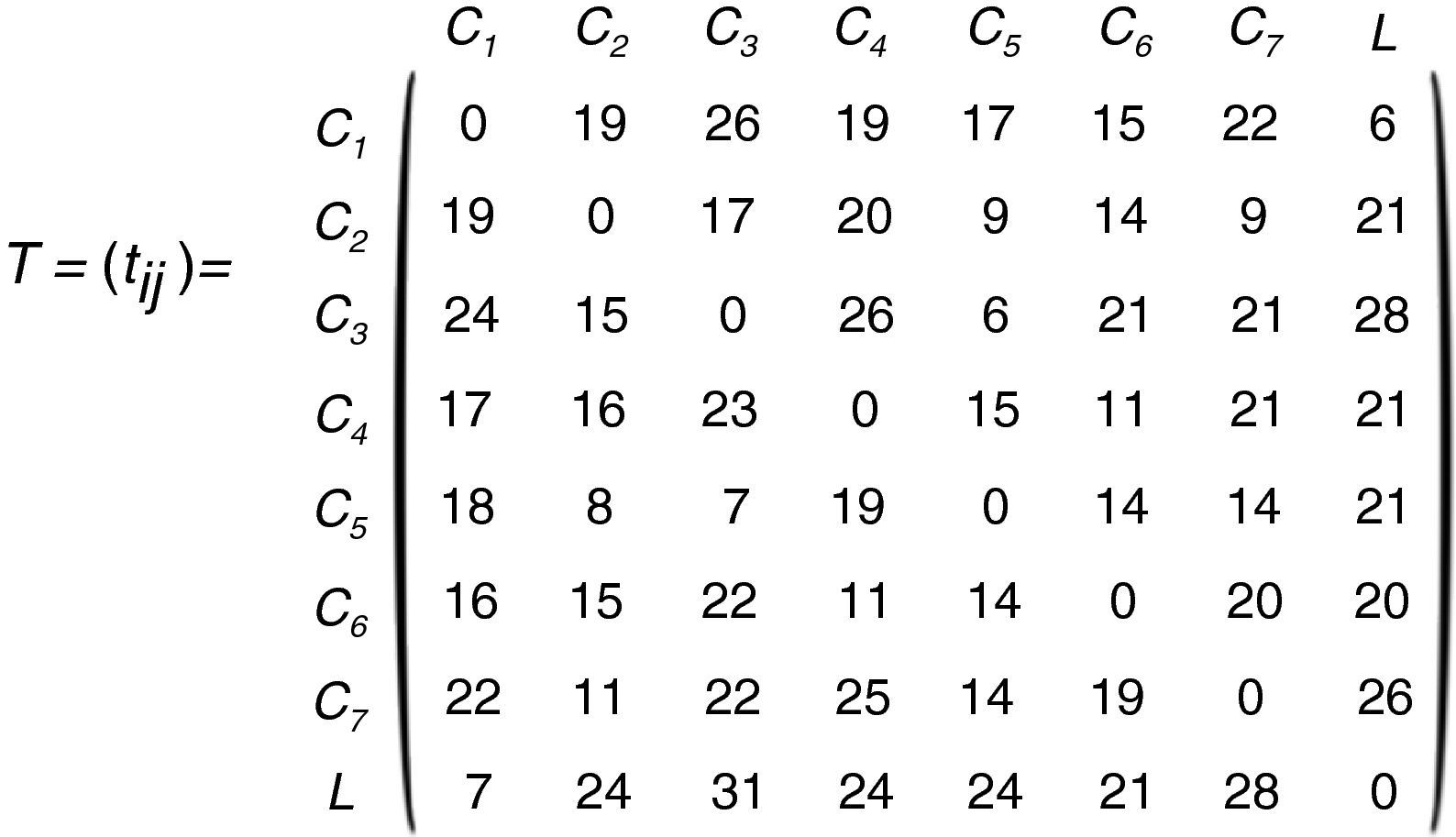
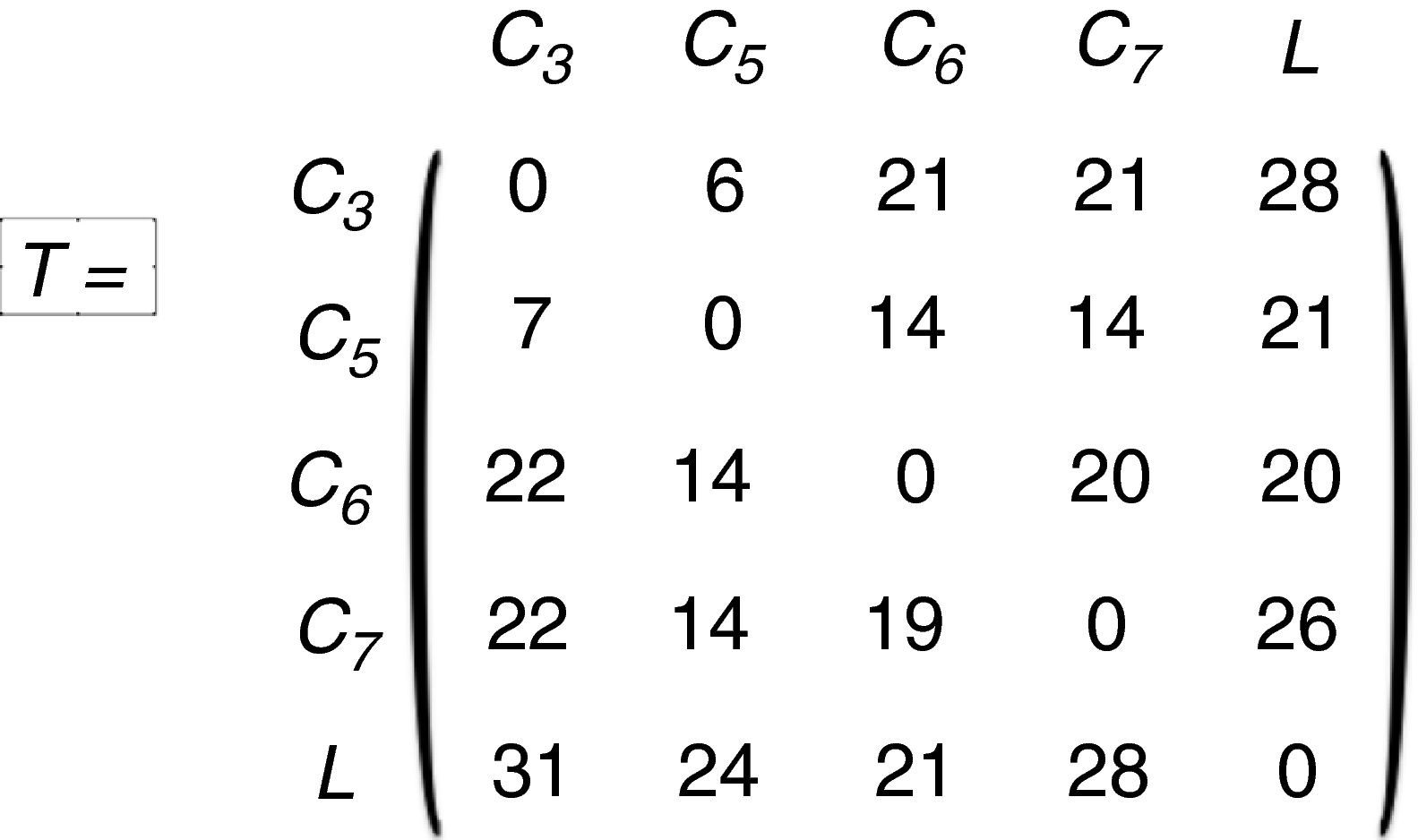
Una manera alternativa de representar los pesos de las aristas (los tiempos de recorrido) es mediante una matriz T=(tij), i,j=1,2,…,L… cuyos elementos tij corresponden a los tiempos que emplear para ir de Ci a Cj (fig. 4).
Ejercicio de ejemploPara este ejercicio hemos considerado una de las rutas de recogida de muestras que realiza el vehículo de recogida de muestras (CV) del Laboratori Clínic Territorial Metropolitana Sud (Hospitalet de Llobregat). Esta ruta cubre los centros de extracción C1, C3, C5, C6, C7 y L (donde L indica el laboratorio). Aunque cubre cinco centros y el laboratorio, en realidad, para el TSP asociado no hay que tener en cuenta en el análisis el vértice C1, puesto que se impone la restricción de que el CV parte de este centro de extracción y su siguiente parada es el laboratorio. Así pues, solo hay que intentar resolver el TSP para C3, C5, C6, C7 y L. El ejercicio ha consistido en buscar el valor óptimo para esta ruta mediante el método de la fuerza bruta (o pesquisa completa) (FB), calcular la solución empleando el método del VMC y, también, el de AC. Finalmente, se comparan las soluciones (rutas a seguir por el CV) obtenidas mediante los métodos VMC y AC con las rutas óptimas obtenidas por FB, así como con la ruta que efectúa en la práctica el CV.
Los tiempos necesarios para cubrir la distancia entre cada par de vértices se obtuvieron gracias a Google Maps. La matriz T contiene estos tiempos. Aunque somos conscientes de que no tienen por qué ser especialmente fiables, las posibles rutas se evalúan siempre con los tiempos en T, por lo que, como mínimo, establecemos un principio de coherencia en los cálculos.
En caso de tener que decidir entre dos o más caminos que unieran los vértices, se eligieron aquellos cuyo coste en tiempo fuera el mayor (este criterio se siguió para los dos sentidos de cada camino). Así pues, el grafo y la matriz de tiempos asociados al ejercicio que exponemos son los que se muestran en las figuras 5 y 6.
Los cálculos necesarios para obtener la ruta óptima por FB se han realizado en MS Excel.
En este ejemplo ilustrativo tan solo hay cuatro centros de extracción que no están sujetos a restricciones (C3, C5, C6 y C7), puesto que C1 y L tienen una posición fijada de antemano en la ruta (se parte del centro de extracción C1 y la siguiente visita es al laboratorio L). Por tanto, el número total de rutas posibles es 24 (4!) y podemos calcular el tiempo necesario para completar cada una de estas rutas por FB por tratarse de un número reducido de rutas. También interesa destacar que el número total de caminos o aristas entre las parejas de puntos por visitar en esta ruta (es decir, todos los caminos que podemos considerar eligiendo parejas de puntos en el conjunto formado por C3, C5, C6, C7 y L) es 10 (fig. 5, líneas continuas), pero como los tiempos para ir de Ci a Ck son, en general, distintos de los necesarios para ir de Ck a Ci, cada camino se desdobla en sus dos sentidos, resultando un total de 20 caminos. Por eso, debemos considerar los 20 elementos fuera de la diagonal de la matriz de la figura 6 o, también, por esa razón aparecen 20 caminos en la tabla 5.
ResultadosLos resultados obtenidos en el ejercicio de optimización de rutas realizado han sido los siguientes.
Método fuerza brutaExisten dos rutas de tiempo óptimo, que se presentan en la tabla 2 y en la figura 7, y en la tabla 3 y en la figura 8.
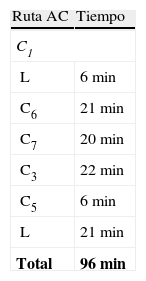
Mediante este método de aproximación a rutas óptimas obtenemos una de las dos soluciones óptimas existentes detectadas por FB (tabla 4). Como puede observarse, coincide con la presentada en la tabla 3 y la figura 8.
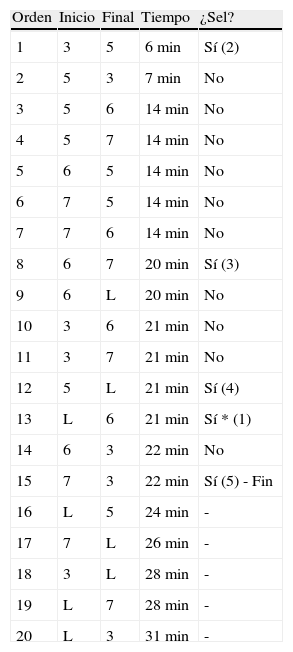
Método aristas clasificadasA partir de este algoritmo obtenemos una ruta que no se corresponde con ninguna de las dos rutas óptimas encontradas por FB (es 1min «más larga»). En la tabla 5, mostramos el proceso de selección de aristas (caminos) que nos conduce a esta aproximación (con la restricción de que debemos empezar en C1 e ir a L y, después de recorrer todos los puntos, terminar en L). En la tabla 6 y en la figura 9, presentamos la ruta encontrada mediante el método AC.
Esquema de aplicación del método AC
| Orden | Inicio | Final | Tiempo | ¿Sel? |
| 1 | 3 | 5 | 6min | Sí (2) |
| 2 | 5 | 3 | 7min | No |
| 3 | 5 | 6 | 14min | No |
| 4 | 5 | 7 | 14min | No |
| 5 | 6 | 5 | 14min | No |
| 6 | 7 | 5 | 14min | No |
| 7 | 7 | 6 | 14min | No |
| 8 | 6 | 7 | 20min | Sí (3) |
| 9 | 6 | L | 20min | No |
| 10 | 3 | 6 | 21min | No |
| 11 | 3 | 7 | 21min | No |
| 12 | 5 | L | 21min | Sí (4) |
| 13 | L | 6 | 21min | Sí * (1) |
| 14 | 6 | 3 | 22min | No |
| 15 | 7 | 3 | 22min | Sí (5) - Fin |
| 16 | L | 5 | 24min | - |
| 17 | 7 | L | 26min | - |
| 18 | 3 | L | 28min | - |
| 19 | L | 7 | 28min | - |
| 20 | L | 3 | 31min | - |
(*) Empezamos aquí y luego vamos al inicio de la tabla. La columna «Orden» indica el orden de clasificación de las aristas (de menor tiempo a mayor). Los números de las columnas «Inicio» y «Final» hacen referencia a los subíndices de los centros de extracción inicial y final asociados a cada arista, mientras que la columna «Tiempo» indica el tiempo necesario para cubrir el camino. Así, por ejemplo, el camino que consume menor tiempo («Orden»=1) es el que parte de C3 y llega a C5, para el que es necesario invertir 6min. La columna «¿Sel?» indica con un Sí o con un No si hemos seleccionado la arista en el proceso de obtención de la solución. Asimismo, el orden de selección de las aristas en el algoritmo AC está indicado entre paréntesis. Adicionalmente, marcamos con un asterisco * el primer camino seleccionado y con «Fin» el último. Al no haber empezado por el camino cuyo «Orden»=1 hablamos de método AC híbrido.
De hecho, el algoritmo que estamos aplicando puede considerarse un híbrido entre el de las AC y el del VMC, puesto que empezamos seleccionando el centro de extracción más próximo a L (es decir, el primer punto que visitamos se elige según VMC). El circuito que obtendríamos aplicando el algoritmo puro AC sería C1-L-C3-C5-C6-C7-L, de coste 103min (como puede observarse en la figura 10, es la undécima ruta, por tiempo, de las 24 posibles). El hecho de que el algoritmo puro proporcione una aproximación no demasiado buena ilustra uno de los problemas asociados a poder determinar a priori la calidad de las aproximaciones proporcionadas por los algoritmos heurísticos.
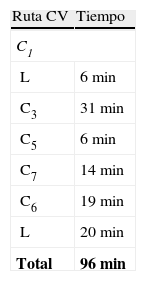
Ruta del coche valijaEn el momento previo a la realización del ejemplo propuesto, el CV hacía el recorrido (ruta real) que se presenta en la tabla 7 y en la figura 10. Como puede observarse, sin ser ninguno de los recorridos óptimos, el tiempo requerido para completar esta ruta era realmente muy ajustado (e idéntico al tiempo obtenido mediante el método de las AC, a pesar de ser una ruta distinta).
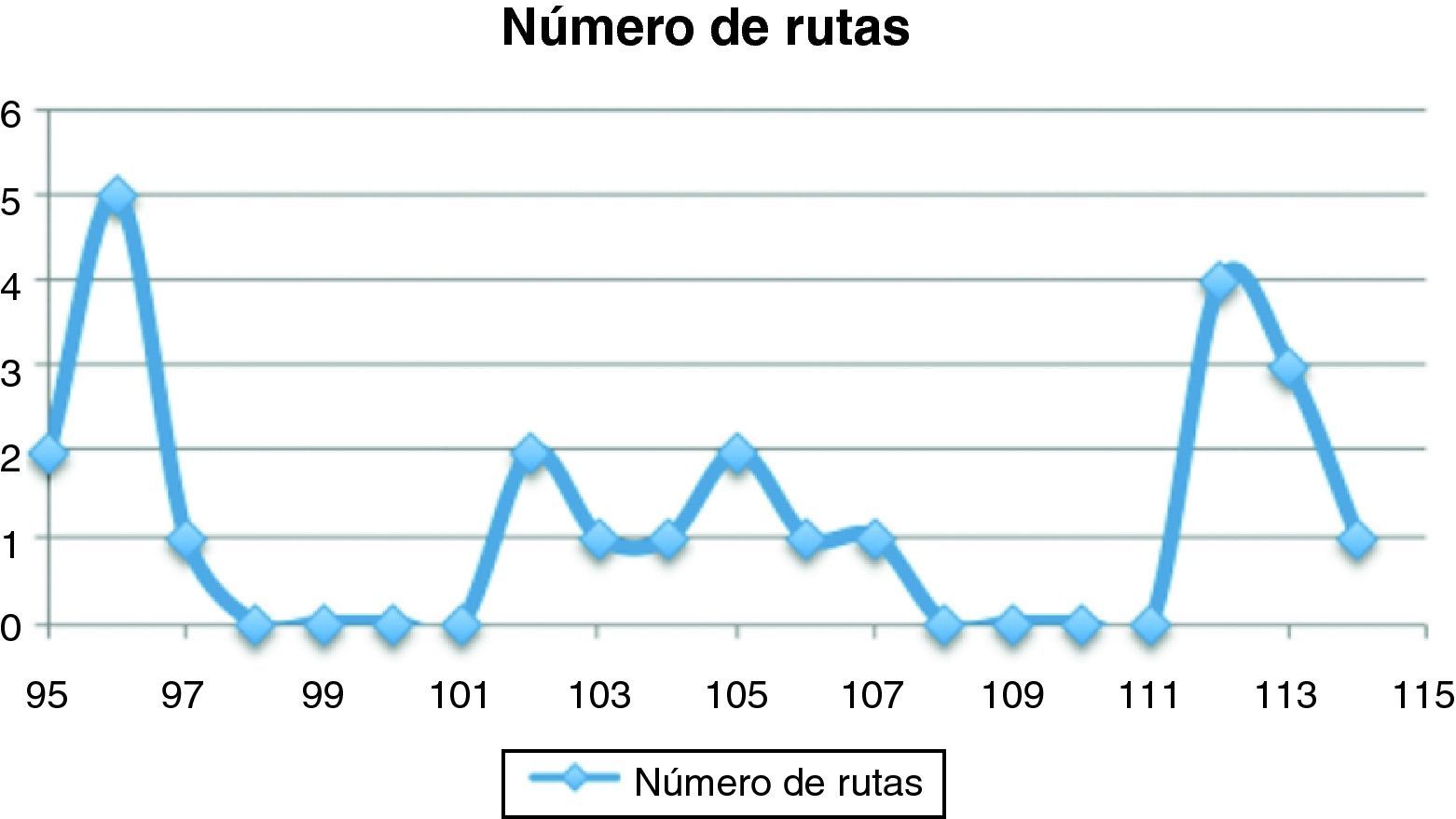
Al haber llevado a cabo la inspección completa de todos los recorridos posibles (FB), disponemos de todas las rutas y de los tiempos que consumen cada una de ellas. En la figura 11 se presenta un gráfico cuyo eje vertical indica el número de rutas que consumen el mismo tiempo (desde las 2 óptimas de 95min hasta la peor en tiempo, de 114min). Como se ha indicado con anterioridad, en nuestro ejemplo el número total de rutas posibles era solamente 24, por lo que hemos podido analizarlas todas (FB) y presentar, por ejemplo, la figura 11. En otros escenarios más complejos (rutas con un número mayor de centros de extracción por visitar), el tiempo necesario para analizar todas las rutas posibles por FB podría ser inasumible (tabla 1), con lo que las aproximaciones VMC y AC tomarían una especial relevancia. En este sentido, conviene remarcar que las rutas calculadas mediante los métodos VMC y AC han conducido a la obtención de soluciones óptimas o muy buenas aproximaciones para el ejemplo analizado, en el que intentábamos encontrar rutas que redujeran el tiempo transcurrido entre la recogida de las muestras y su llegada al laboratorio. Además, el ejercicio realizado ha permitido comprobar que la ruta que realiza el CV es una muy buena aproximación a las rutas óptimas en tiempo de recorrido.
DiscusiónLa logística en el campo de la preanalítica es determinante para el buen funcionamiento de los laboratorios y un rasgo diferencial entre los que apuestan por la calidad y la innovación.
Desde nuestro punto de vista, existen dos ámbitos independientes relacionados con el transporte de muestras en los que se pueden realizar mejoras: uno institucional y otro que afecta a la planificación de las rutas de transporte.
A nivel institucional debería realizarse un estudio sobre la viabilidad de incluir los vehículos de transporte de muestras en el grupo de vehículos con trato preferencial en caso de tráfico intenso. Esta medida permitiría reducir las incidencias actuales en estos servicios.
En relación con un incremento de los medios adjudicados al transporte, esta es una medida que compete a la empresa adjudicataria de la concesión y que, necesariamente, implicaría un incremento de los costes de subcontratación. Aquello que consideramos que sí puede demandarse es la inclusión, en los requisitos de las ofertas para la adjudicación de la subcontrata del transporte, de un informe detallado de la planificación logística que garantice (por parte de los concursantes) la llegada de todas las valijas al laboratorio desde los centros de extracción en un tiempo adecuado.
Por otra parte, consideramos que es importante evitar someter a presiones significativas por parte del laboratorio a los encargados del transporte, puesto que esto podría aumentar la precariedad de las condiciones de los conductores, incrementando las probabilidades de siniestralidad del vehículo. Además de los daños personales que podrían producirse, la pérdida de muestras o de gran parte de las mismas originaría una incidencia grave en la dinámica general del laboratorio.
Nuestra contribución, con este artículo, ha sido poner de manifiesto la importancia de una buena planificación logística de la recogida de muestras, así como dar algunas ideas sencillas para realizar una valoración de la calidad de los servicios de transporte. Evidentemente, los expertos de los departamentos de investigación operativa de universidades y empresas de logística deben ser los referentes si se precisan informes de evaluación certificados. No obstante, el personal sanitario encargado de la planificación y el seguimiento de las rutas de transporte no puede ser ajeno a esta metodología, puesto que parte de su responsabilidad es velar por una planificación óptima de las rutas de transporte de muestras para cumplir con el objetivo de mejorar el servicio y evitar los problemas derivados de una mala planificación.
En el sencillo ejemplo que hemos examinado, hemos comprobado que la ruta del CV era muy ajustada en tiempo a la ruta óptima: la sensación al iniciar la elaboración del artículo era que el servicio interno de transporte de muestras del laboratorio estaba realizando un gran trabajo. De este modo, a partir de estos sencillos cálculos, se ha podido justificar esta impresión preliminar.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Agradecemos personalmente a los señores Antonio Arañó y Sebastián Blasco, responsables de los vehículos internos de transporte de muestras del laboratorio, su gran profesionalidad y su compromiso con el trabajo que realizan: contribuyen decisivamente al buen funcionamiento del laboratorio.