Estudio biomecánico de cuatro sistemas de fijación y del uso de injerto anterior en un modelo de elementos finitos de la columna lumbar

Objetivos: Presentación de una nueva metodología para el modelado y validación del conjunto raquis-implante mediante el estudio biomecánico de cuatro sistemas de fijación y del uso de injerto anterior en un modelo basado en el método de elementos finitos de la columna lumbar L2-L5 en el que se simuló una corporectomía de L4. Material y método: Se ensayaron cuatro sistemas de fijación posterior basados en el uso de tornillos transpediculares anclados en bloques de polietileno, obteniendo su rigidez en los modos de carga de flexión, extensión, flexión lateral y torsión. Se realizaron modelos validados de los sistemas de fijación. Estos modelos se incorporaron al tramo de la columna lumbar L2-L5, en el cual se realizó una corporectomía de L4 estudiando la rigidez del conjunto, y las tensiones en los implantes. Se estudió en el modelo de la columna estabilizado con uno de los fijadores el efecto de la utilización de un injerto anterior entre L3 y L5. Resultados: El error medio cometido para todos los sistemas en la validación fue de un 3,7% y los errores medios por sistema inferiores al 6,5%. Se calcularon las tensiones máximas para todos los sistemas de fijación en los tornillos transpediculares, alcanzando sus valores máximos en los modos de carga de torsión y flexión. En los modos de carga de flexión y extensión los conectores transversales estuvieron sometidos a cargas prácticamente nulas, en flexión lateral las tensiones máximas fueron de 261,95 MPa y en torsión de 98,55 MPa. El uso del injerto anterior disminuye en un 80% las tensiones en el fijador en el modo de carga de flexión. Conclusiones: Se ha desarrollado una nueva metodología para el modelado y validación del conjunto raquis-implante que requiere no sólo la validación del modelo de la columna sino también el modelado y validación independiente de los sistemas de fijación. Ante una corporectomía de L4, en el caso de implantar un sistema de fijación posterior, la introducción de un injerto anterior puede evitar la rotura del implante por cargas cíclicas, ya que las tensiones que se alcanzan en los fijadores sin el soporte del injerto son cercanas al límite elástico de la aleación de titanio Ti6Al4V (795 MPa).

Objectives: A new method for modeling the spine-implant construct is presented. It was validated by a biomechanical study of four fixation systems and the use of an anterior graft based on a finite-element model of the L2-L5 lumbar spine in which an L4 corporectomy was performed. Experimental design: Four pedicle screw devices anchored in polyethylene blocks were tested. Their resistance was assessed in flexion, extension, lateral bending, and torsion loading models. Each device was modeled and validated. These models were incorporated into an L2-L5 lumbar spine segment model in which L4 corporectomy was performed to study the resistance of the construct and the forces in the fixation systems. In a spinal model stabilized with one of the devices, the effect of an anterior graft between L3 and L5 was studied. Results: The average validation error for all systems was 3.7%, with a maximum per-system error of less than 6.5%. The maximum stresses of all systems were found in the pedicle screws, reaching the highest values in the torsion and flexion modes. In the flexion and extension loading modes, the transversal connectors were exposed to practically no load. In the lateral bending mode, maximum stress was 261.96 MPa and in torsion, 98.55 MPa. Use of the anterior graft reduced stress by 80% in the flexion loading mode. Conclusions: A new method for modeling the spine-implant construct not only allows validation of the spinal model, but also independent modeling and validation of fixation systems. After L4 corpectomy, if a posterior fixation system is implanted, an anterior graft should be implanted to prevent implant rupture due to cyclical loading because the stress levels reached are close to the yield strength of Ti6AI4V titanium alloy (795 MPa).

Existe una gran cantidad de modelos para la columna basados en el método de elementos finitos^1-4, algunos de ellos han prestado mayor detalle a determinados aspectos como pueden ser el modelado de los discos^5,6, el modelado de las carillas articulares⁷ o a la realización de un modelado paramétrico de las vértebras que permita la incorporación de modificaciones al modelo de una forma más sencilla⁸. En algunos casos se realizan análisis del conjunto raquis-implante, simplificando de forma notable el modelo de la columna y de los implantes^9-12, mientras que en otros se llevaron a cabo modelos mucho más complejos tanto de la columna como de los implantes^13-16. Sin embargo, en ninguno de estos modelos se ha realizado un modelado previo e independiente de los sistemas de fijación que posteriormente incorporan, normalmente se simplificaban los fijadores a modelos de elementos barra dotándolos de las mismas características mecánicas que los materiales reales a los que representan. Al contar con modelos independientes de los fijadores se puede realizar un modelado teniendo en cuenta las características de todos los elementos: barras, tornillos y uniones entre tornillos y barras, que en ningún caso son perfectas¹⁷, para, a continuación, validar su comportamiento sometiéndolos a las mismas condiciones de carga y de contorno que en los ensayos que se realizan a los fijadores cuando son montados en bloques de polietileno.

Este trabajo tiene como primer objetivo presentar un método novedoso para el modelado y validación del conjunto raquis-implante, que requiere la validación independiente de los modelos de elementos finitos (MEF) de los cuatro sistemas de fijación, la validación del MEF del tramo de la columna lumbar L2-L5 y la incorporación al MEF de la columna lumbar L2-L5 del sistema de fijación. El segundo objetivo es el estudio del comportamiento de cuatro sistemas de fijación y del uso de injerto anterior en un modelo basado en el método de elementos finitos de la columna lumbar L2-L5 en el que se simuló una corporectomía de L4.

MATERIAL Y MÉTODO

Estudio experimental

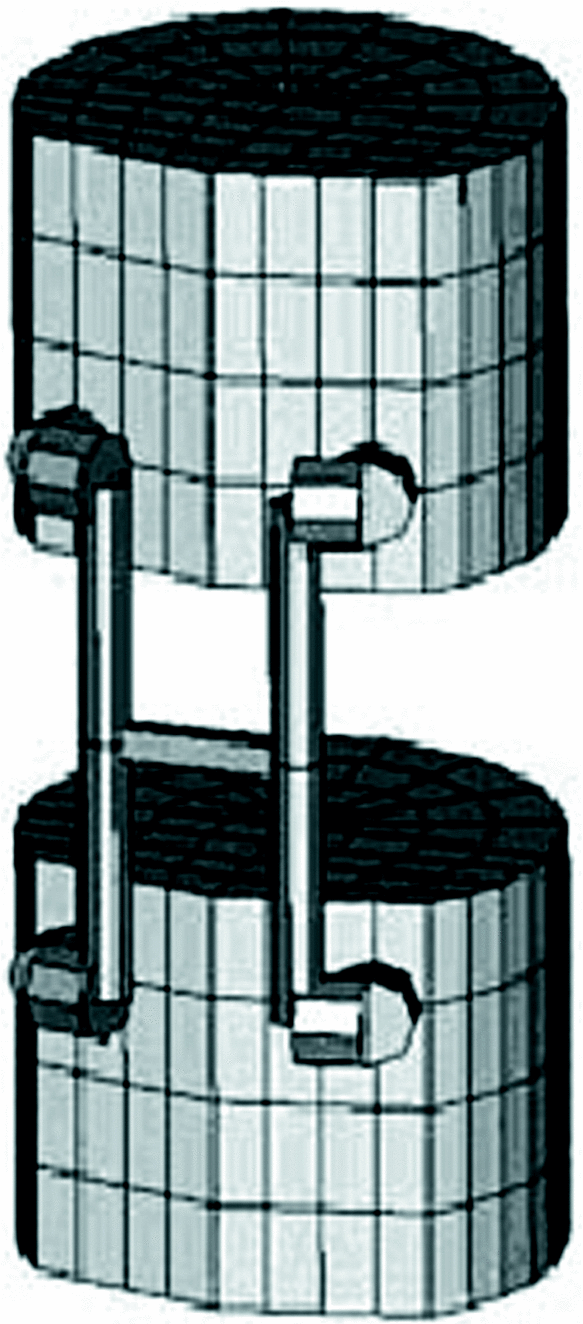
Los sistemas de fijación ensayados fueron (Fig. 1): el POLIAXIS^® (CD-Pharma). El sistema CD-Horizon^® (Medtronic Ibérica). El sistema PERFIL^® (Lafitt, S.A.). El sistema ISOLA^® (Depuy-Acromed, Johnson & Johnson), todos ellos de aleación de titanio (Ti6Al4V).

Figura 1. A) Sistema de fijación de raquis POLIAXIS^®. B) Sistema de fijación de raquis CD-Horizon^®(CDH). C) Sistema de fijación de raquis PERFIL^®. D) Sistema de fijación de raquis ISOLA^®.

Para realizar los ensayos, los sistemas se anclaron sobre bloques de polietileno de ultra alto peso molecular (UHMWPE)¹⁸. Todos los sistemas fueron ensayados en los modos de carga de flexión, extensión, torsión y flexión lateral en una máquina de tracción-compresión-torsión (SERVOSIS, ME-402/1, España), obteniéndose los valores de rigidez de los sistemas ante cada modo de carga. Se realizaron 5 repeticiones para cada ensayo sobre la misma muestra, al no ser destructivos. Las condiciones del ensayo se mantuvieron constantes para todos los sistemas: a) en flexión y extensión, control por fuerza, velocidad de aplicación de carga 250 N/s y fin del ensayo al aplicar 300 N; b) en torsión, control por fuerza, velocidad de aplicación de carga 0,01 Nm/s y fin del ensayo al aplicar 1 Nm, y c) flexión lateral: control por fuerza, velocidad de aplicación de carga 250 N/s y fin del ensayo al aplicar 100 N.

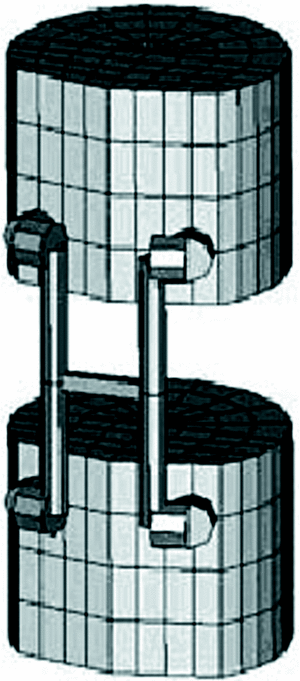
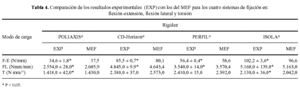
Los sistemas modelados fueron los mismos que los ensayados experimentalmente en bloques de polietileno. El modelado de cada uno de ellos consistió en reproducir de forma simplificada la geometría de los elementos reales (Fig. 2) mediante elementos barra dotándolos de las características mecánicas de los elementos reales: módulo elástico del material (E), módulo a cortantes (G) y coeficiente Poisson (ν). Para modelar la unión entre los tornillos y las barras o entre barras se usaron elementos muelle para disminuir la rigidez del grado o grados de libertad que caracterizan las conexiones (Tabla 1). Para ajustar la rigidez del muelle se recurrió a los datos experimentales de rigidez obtenidos de los ensayos de los sistemas de fijación montados sobre bloques de polietileno. Para modelar la unión tornillo-polietileno o tornillo-vértebra se embebieron los elementos barra que simulan los tornillos en los bloques de polietileno o en las vértebras¹⁵. Las uniones definidas de la forma anterior dejaron completamente liberada la rotación del tornillo dentro de la vértebra o de los bloques de polietileno con respecto a su eje longitudinal, siendo la orientación de los tornillos y la configuración de los sistemas los que la limitaron, pero dieron un anclaje total a los tornillos ante cargas de extracción.

Figura 2. MEF del sistema PERFIL^®.

Las cargas y condiciones de contorno aplicadas a los distintos modelos de los sistemas de fijación en cada uno de los modos de carga estudiados fueron las mismas que las consideradas en los ensayos. Dada la complejidad del raquis lumbar, se realizaron una serie de simplificaciones que permitieron un modelado y mallado más sencillo del modelo del tramo de raquis lumbar L2-L5.

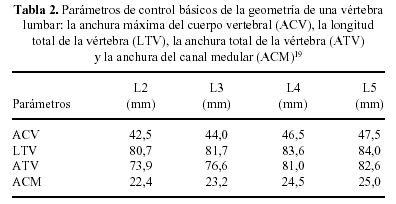
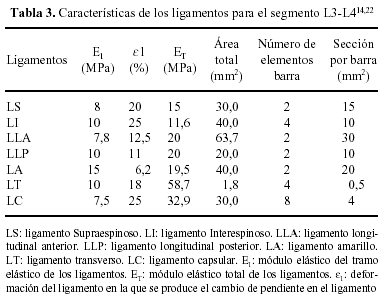
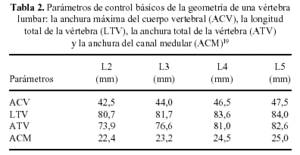
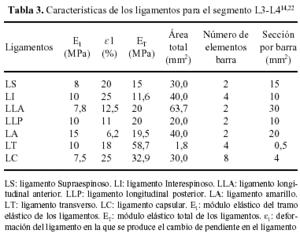
Como primera simplificación se procedió a definir una vértebra lumbar paramétrica controlada por cuatro parámetros básicos: la anchura máxima del cuerpo vertebral (ACV), la longitud anteroposterior de la vértebra (LTV), la anchura total de la vértebra (ATV) y la anchura del canal medular (ACM)^5,7,8,19,20 (Tabla 2). Las ATV, ACU y ACM se obtuvieron a partir de los estudios realizados por Panjabi et al (1992). La longitud total de la vértebra se tomó como valor de partida 84 mm para L5 y se modificó mínimamente para el resto de vértebras^7,8. Para el modelado de las carillas articulares sólo se consideró su angulación con respecto al plano sagital. Las superficies articulares de las carillas se modelaron planas, paralelas y separadas en reposo una distancia de 0,1 mm^7,21. Para simular el contacto entre superficies articulares se introdujeron elementos de contacto tipo nodo-superficie. Los ligamentos se modelaron como elementos cable; para simular el comportamiento no lineal de los ligamentos se recurrió a utilizar dos elementos cable en paralelo¹⁵ y con las características de los ligamentos tomadas de trabajos previos^14,22 para la unidad vertebral funcional (UVF) L3-L4 (Tabla 3).

Las vértebras se dividieron en el modelo en cuatro zonas con características mecánicas diferenciadas: a) hueso trabecular con un módulo elástico (E) de 100 MPa y coeficiente de Poisson (ν) de 0,2, b) huesocortical (E = 12 GPa, ν = 0,3), c) carillas articulares (E = 12 GPa, ν = 0,3) y trabecular posterior (E = 3,5 GPa, ν = 0,25)¹⁴. El disco intervertebral se dividió en tres zonas: el núcleo pulposo, los cartílagos de unión y el anillo fibroso, con características mecánicas obtenidas a partir de trabajos previos^{3,7,8,14,15,21,23-25}. El anillo fibroso se modeló con un módulo elástico de 2 MPa y un coeficiente de Poisson 0,45; el módulo elástico del núcleo fue de 0,25 MPa y su coeficiente de Poisson 0,499 y los cartílagos de unión se modelaron con características mecánicas de hueso cortical. Las fibras de colágeno se modelaron como elementos cable de dos nodos situados en el contorno exterior e interior del anillo fibroso con una inclinación aproximada de 30° con respecto a los cartílagos de unión, con un módulo elástico de 650 MPa y una sección de 1 mm².

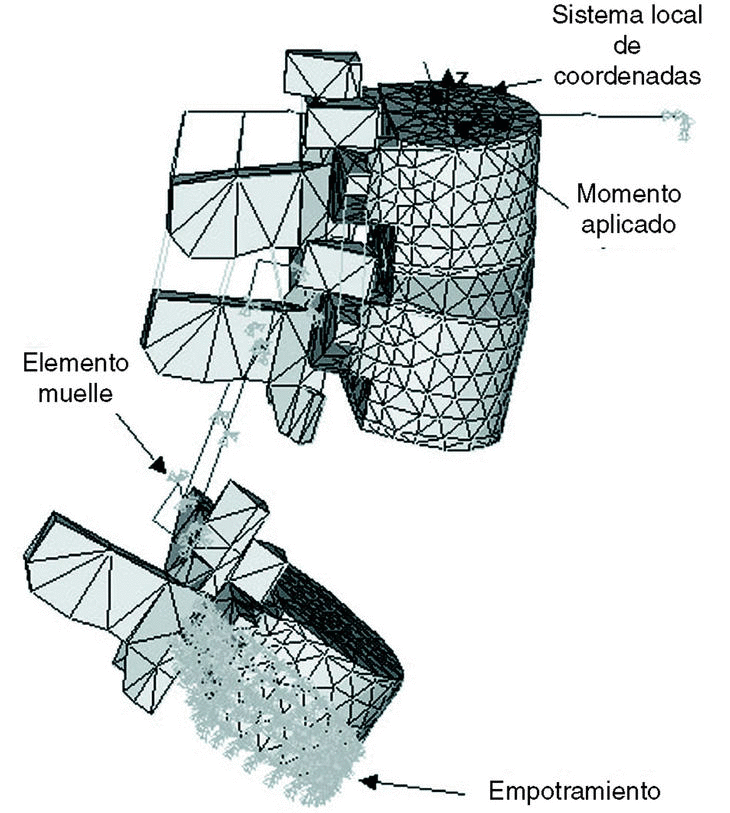
Sobre la columna se aplicaron momentos puros en todos los modelos y modos carga considerados (flexión, extensión, flexión lateral y torsión) sobre el nodo central del entramado de barras rígidas del cuerpo vertebral proximal (L2), la magnitud de la carga fue de 8 Nm en todos los casos^7,8,12,26. Se registraron los giros de L2 para obtener la rigidez de la columna intacta e instrumentada en cada modo de carga. Para el análisis no lineal, se realizó un control por momentos y se utilizó el método de Newton-Raphson para el cálculo iterativo de las soluciones²⁷.

Una vez modelados los sistemas de fijación los parámetros que se ajustaron para validar el sistema de fijación fueron las constantes de los muelles de las uniones. El parámetro global seleccionado para la validación de los sistemas de fijación ante todos los modos de carga fue la rigidez global del sistema (K = C/d), donde C es la fuerza o momento aplicado y d el desplazamiento vertical o giro del punto de aplicación de la misma. Los modelos de los sistemas de fijación se consideraron validados cuando la diferencia entre la rigidez experimental, obtenida mediante los ensayos propios, y la rigidez analítica fuera menor de un 10% ante cada modo de carga.

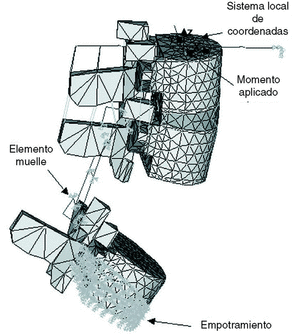
Una vez modelados y validados los modelos de los sistemas de fijación y de la columna intacta se procedió a introducir en el modelo de la columna los sistemas de fijación, estudiando la rigidez del conjunto raquis-implante y las tensiones en el fijador, ante una lesión muy grave de la columna como es una corporectomía de L4, que fue simulada mediante la eliminación de la vértebra L4 y sus ligamentos adyacentes (Fig. 3). En los modelos realizados se analizó la situación que se produce en el postoperatorio inmediato, en el cual la artrodesis no tiene capacidad para asumir carga²⁸.

Figura 3. Condiciones de contorno para la columna instrumentada con el sistema POLIAXIS^®, ante el momento de extensión.

Sobre el modelo del conjunto raquis-implante con el sistema POLIAXIS^® se modeló el estado de la columna en el postoperatorio inmediato, en la que se había realizado una artrodesis posterolateral y otra anterior. La masa de injerto posterolateral, al realizarse mediante fragmentos de hueso trabecular, sin función mecánica en el postoperatorio inmediato, no se modeló. La artrodesis anterior, en cambio, al realizarse con un injerto estructural más resistente que trabaja desde el primer momento, sí que se modeló, considerándose dos casos: a) utilización de injerto de hueso esponjoso tricortical, como el procedente del hueso ilíaco (E = 12 MPa, ν = 0,3) y b) utilización de injerto de peroné, muy resistente a compresión por su alto porcentaje de hueso cortical (E = 100 MPa, ν = 0,2).

Al estudiarse la acción de este injerto en el postoperatorio inmediato se modeló el injerto unido a la vértebra inferior y en contacto con la superior. El modelado se realizó de esta forma al considerar que el injerto en el postoperatorio inmediato no está fusionado con las vértebras, pero sí que se encuentra suficientemente bien encajado como para no poder desplazarse de su posición. Los modos de carga y la magnitud del momento fueron los mismos que en los casos anteriores, añadiendo una precarga de compresión de 150 N.

RESULTADOS

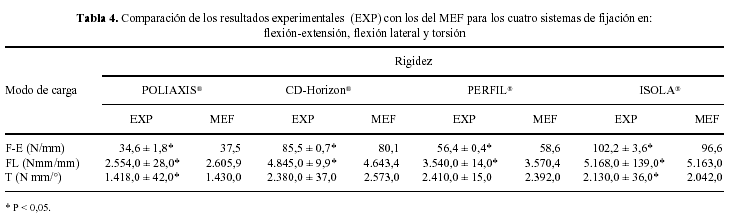
Los cuatro sistemas de fijación mostraron comportamientos diferenciados debido a su diferente geometría y rigidez de sus uniones con diferencias estadísticamente significativas (p < 0,05) en todos los modos de carga, con la excepción de los sistemas CDH^® y PERFIL^® en torsión. El error medio cometido al comparar los valores de rigidez obtenidos a partir de los modelos por elementos finitos y los estudios experimentales para todos los fijadores y en todos los modos de carga estuvo por debajo del 4% en todos los casos y los errores medios por sistema fueron iguales o inferiores al 6,5% (Tabla 4).

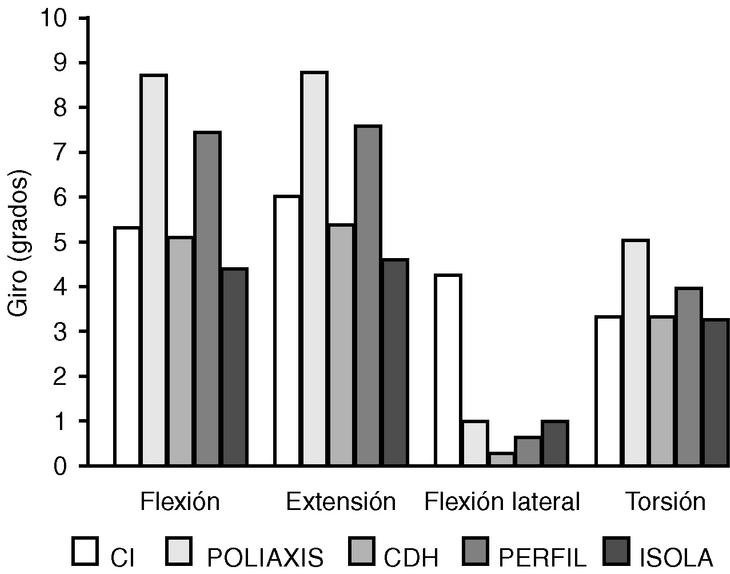
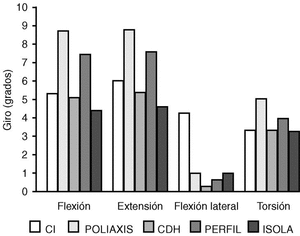
Los valores de rigidez del modelo MEF para el tramo de la columna L2-L5 fueron de 3 Nm/° en flexión, de 2,8 Nm/° en extensión, de 3,8 Nm/° en flexión lateral y de 4,7 Nm/° en torsión. La implantación de los cuatro sistemas de fijación en el modelo de la columna supuso comportamientos diferentes del conjunto raquis-implante en cada caso (Fig. 4).

Figura 4. Giros para el MEF del tramo de la columna L3-L5. Cargas aplicadas de 8 Nm en todos los modos de carga para la columna intacta (CI), e instrumentada con los sistemas de fijación POLIAXIS^®, CD-Horizon^® (CDH), PERFIL^® e ISOLA^®.

A partir de los modelos se estudiaron las tensiones máximas de Navier debidas a la flexión compuesta que se producen en las barras, conector transversal y en los tornillos de los sistemas de fijación. La tensión en las barras alcanzó su valor máximo en los modos de carga de flexión (306,11 MPa) y extensión (305,41 MPa) para el sistema POLIAXIS^® mientras que en los restantes sistemas fueron de menor magnitud. Las tensiones en los tornillos en la zona anatómica de los pedículos en esta zona alcanzaron los valores máximos en el modo de carga de flexión (638,83 MPa) y extensión (639,61 MPa) para el sistema ISOLA^®, siendo también elevadas las tensiones en los tornillos en el modo de carga de torsión para todos los sistemas, superando para el POLIAXIS^® y CDH^® a las debidas a cargas de flexión y extensión. Las tensiones máximas en el conector transversal se produjeron en los modos de carga de flexión lateral con un máximo para el sistema POLIAXIS^® (261,95 MPa) y en torsión (98,55 MPa) para el sistema PERFIL^®, en los modos de carga de flexión y extensión son despreciables en todos los sistemas. Destacaron los valores muy bajos de tensiones en el conector transversal para el sistema ISOLA^® en torsión y flexión lateral.

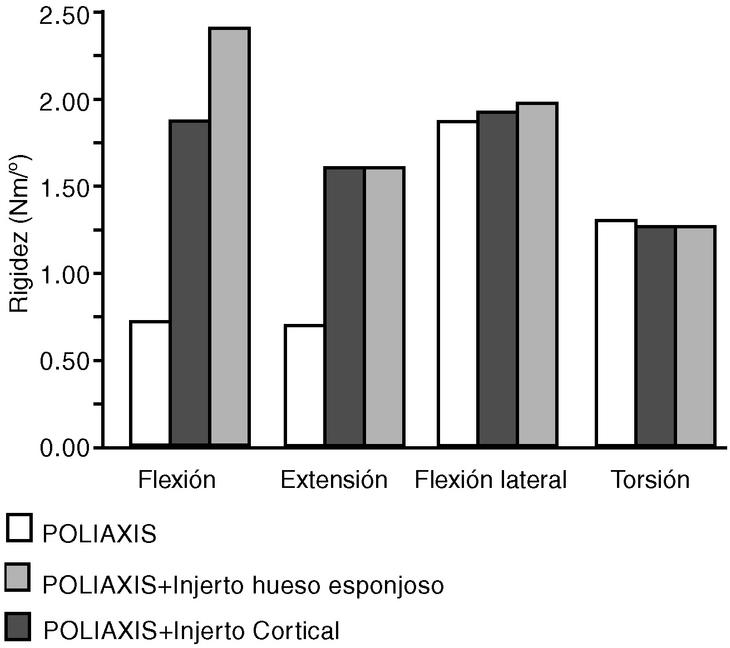
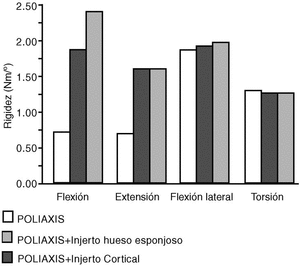
El efecto más significativo sobre la rigidez de la utilización del injerto fue un incremento en la rigidez a flexión de un 162% con injerto de hueso esponjoso y de un 234% al usar injerto de hueso de peroné. Los incrementos de rigidez fueron mínimos en flexión lateral, al incrementarse en un 4% y un 6% respectivamente y nulos en los restantes modos de carga (Fig. 5).

Figura 5. Valores de rigidez de la columna L2-L5 instrumentada con el sistema POLIAXIS^® antes y después de introducir injerto anterior en puntal entre L3 y L5.

Utilizando injerto procedente de hueso esponjoso las disminuciones de tensiones en las barras en los modos de carga de flexión fueron de un 76% y en flexión lateral del 0,5%, siendo también importantes las reducciones de tensiones en la parte posterior de los tornillos transpediculares en estos dos modos de carga, con un 62% en flexión y 23% en flexión lateral. Al utilizar injerto procedente de peroné las disminuciones de tensiones fueron más importantes en las barras en los modos de carga de flexión (82%) y flexión lateral (20%), siendo también importantes las reducciones de tensiones en los tornillos transpediculares en estos dos modos de carga flexión (78%) y flexión lateral (22%).

DISCUSIÓN

Los modelos existentes del conjunto raquis implante^9-16 incorporan los sistemas de fijación a los modelos MEF de la columna sin antes modelarlos de forma independiente. En este trabajo se ha realizado una validación independiente de los sistemas de fijación y del modelo de la columna lumbar, por tanto al unirlos en un único modelo raquis-implante los resultados serán correctos si las uniones entre los bloques de polietileno-tornillos transpediculares y vértebras-tornillos transpediculares se comportan de forma similar. Esta condición se ha verificado al comprobar que los pares necesarios para la inserción de los tornillos en los bloques de polietileno pretaladrados es de 1,75 ± 0,12 Nm, similar al par de inserción de los tornillos transpediculares medido intraoperatoriamente en pacientes sin osteoporosis (1,72 ± 0,23 Nm)²⁹.

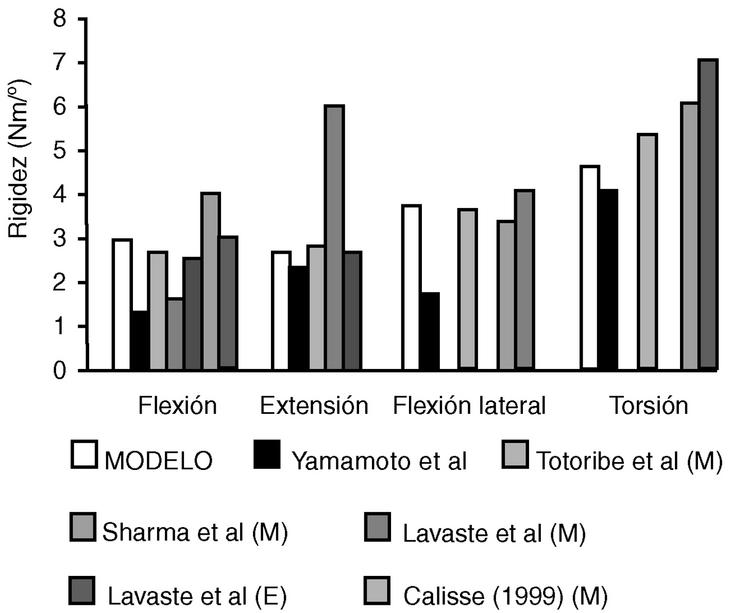
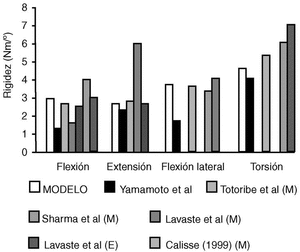
Para asegurar la validez del modelo MEF del tramo de la columna L2-L5, los valores de rigidez del modelo se han comparado con los obtenidos por Lavaste et al⁸ y Yamamoto et al³⁰ en sus respectivos estudios experimentales in vitro de la columna lumbar (Fig. 6). El modelo planteado se ha ajustado mucho mejor con los valores in vitro de Lavaste et al⁸ en flexión y flexión lateral, mientras que en los otros modos de carga se ha asemejado su comportamiento a los ensayos in vitro de Yamamoto et al³⁰. Al comparar el modelo propio con otros modelos de la columna lumbar^3,7,8,24,31, su comportamiento ha sido cercano al de los restantes modelos excepto al de Calisse²⁴ a extensión, que modela las carillas articulares mediante elementos cable¹².

Figura 6. Rigidez media de una unidad vertebral funcional. Comparación de los resultados del modelo propio (MODELO) ante cargas de 8 Nm con los obtenidos por otros trabajos experimentales (E) (Lavaste et al (1992) aplicando momentos de 8 Nm y Yamamoto et al (1989) aplicando 10 Nm) y los valores obtenidos a partir de otros modelos (M) (Lavaste et al (1992) y Totoribe et al (1999) aplicando 8 Nm y Sharma et al (1995) y Calisse (1999), aplicando 10 Nm).  

Los sistemas de fijación implantados en el modelo de la columna han presentado distintos comportamientos debido a sus diferentes geometrías y rigideces. El sistema POLIAXIS^® ha sido el menos rígido en todos los modos de carga debido a que sus barras son las de menor diámetro (5,5 mm), mientras que el ISOLA^® ha sido el más rígido en todos los modos de carga debido a que sus barras son de mayor diámetro (6,35 mm), excepto en flexión lateral debido a la proximidad de las barras longitudinales en el modelo. Por el contrario, el sistema CDH^® ha sido el más rígido en flexión lateral debido a la mayor separación de las barras al carecer de conectores laterales. Para los sistemas con características geométricas semejantes en tornillos y barras, como han sido los sistemas CDH^® y PERFIL^®, las diferencias de rigidez que han aparecido en los modos de carga de flexión y extensión se han debido a las distintas características de las uniones tornillo barra. En los modos de carga de torsión y flexión lateral también se ha apreciado que aquellos sistemas con uniones en el conector transversal de menor rigidez (POLIAXIS^® y PERFIL^®) los giros han sido mayores, a excepción del ISOLA^® en flexión lateral en el que los mayores giros han sido debidos a que el conector transversal en el modelo ha sido el de menor longitud como consecuencia de la proximidad de las barras longitudinales.

Las diferencias en magnitud de las tensiones se han debido al diferente diámetro de las barras, las de menor diámetro (5,5 mm en el POLIAXIS^®) han presentado mayores tensiones, mientras que en los restantes sistemas han sido de menor magnitud por ser las barras de diámetro 6 mm (CDH^® y PERFIL^®) y de 6,35 mm (ISOLA^®). Las tensiones en los tornillos transpediculares también han dependido del diámetro de los mismos, siendo máximas para el sistema ISOLA^® debido a que de los cuatro sistemas modelados es el que cuenta con elementos barra para simular los tornillos de menor diámetro (4 mm).

Las tensiones máximas en el conector transversal se han producido en los modos de carga de flexión lateral para el sistema POLIAXIS^® y en torsión para el sistema PERFIL^®. En los modos de carga de flexión y extensión han sido despreciables las tensiones en todos los sistemas, lo cual indica que el conector transversal no trabajaba en estos modos de carga. Estos resultados han sido similares a los presentados en los estudios de Lim et al¹¹ y Prat et al¹⁷. Han destacado los valores muy bajos de tensiones en el conector transversal para el sistema ISOLA^® en torsión y flexión lateral, en ambos casos se ha debido a las diferencias de configuración de este sistema en el que se encuentran más juntas las barras longitudinales y por tanto el conector es muy corto.

El importante incremento de rigidez que se ha producido en el modo de carga de flexión en el modelo en el que se estudia la influencia del injerto en puntal anterior entre L3 y L5, ha sido debido a que el injerto de peroné tiene un módulo elástico muy superior al del hueso trabecular (12 GPa frente a 100 MPa). Estos resultados se han aproximado a los obtenidos experimentalmente por Gurr et al³², que conseguían incrementos de rigidez de un 200% al usar una instrumentación con injerto anterior de hueso ilíaco ante una lesión similar, en la que existía una desestabilización total por lesión de las tres columnas (anterior, media y posterior). Los resultados obtenidos en torsión y flexión lateral se han mantenido en la línea de los obtenidos por Whitecloud y Larocca (1976). Por último, en el modo de carga de extensión el incremento de rigidez que se ha producido es debido a la precarga, no a la utilización del injerto.

Las tensiones en el sistema de fijación presentaron una importante disminución, debido exclusivamente al uso del injerto. La reducción de tensiones en las barras y tornillos en el modo de carga de flexión hubiera sido mayor si no se hubiera aplicado la precarga de compresión. La reducción de tensiones en el conector transversal no ha sido significativa en ninguno de los dos casos.

Los incrementos de rigidez y disminución de tensiones han aumentado al usar hueso cortical en el injerto en lugar de hueso trabecular, pero han sido de pequeña magnitud si se considera que el hueso trabecular del modelo tiene un módulo elástico de 100 MPa y el de cortical de 12 GPa. Por tanto, sería justificable la utilización de injertos de hueso trabecular, ya que son los que proporcionan la mayor estimulación para la formación ósea³³ y consiguen disminuir suficientemente las cargas que debe soportar el implante. No obstante, el problema que presenta el uso de hueso trabecular es que tiene una carga de rotura muy baja, entre

0,2 MPa y 10,5 MPa, que es muy inferior a la del hueso cortical, que se sitúa según el estudio entre 121 MPa y 200 MPa^34-37. En el modelo propio con injerto trabecular las tensiones de Von Mises en el injerto han alcanzado valores de 1,7 MPa, cercanas a la tensión de rotura del hueso trabecular. Por tanto, para un correcto funcionamiento mecánico del injerto a largo plazo lo más indicado es que el injerto utilizado contenga porcentajes similares de hueso trabecular y cortical; un hueso que posee estas características sería el de la cresta ilíaca.

CONCLUSIONES

1. Se presenta una metodología novedosa para el modelado y validación mediante el método de elementos finitos del conjunto raquis-implante, validado no sólo un modelo de la columna, sino también un modelado y validación de forma independiente de los sistemas de fijación.

2. En el modelado de los fijadores se ha aportado una novedosa caracterización de las conexiones entre elementos, que permite reproducir los grados de libertad de las conexiones, dotándolas de la misma rigidez que las conexiones reales.

3. Este método de caracterizar los sistemas de fijación queda perfectamente reflejado cuando se estudia el comportamiento de los distintos sistemas de fijación implantados en el modelo de la columna, ya que la rigidez de los montajes se modifica por las dimensiones de los distintos componentes de los implantes y por la rigidez de las uniones entre tornillo-barra y barra-conector transversal.

4. En caso de corporectomía el fijador implantado deberá tener un diámetro de barras y tornillos lo mayor posible o incorporar un injerto anterior, ya que las tensiones que se alcanzan en los tornillos y barras de los sistemas de fijación son cercanas al límite elástico de la aleación de titanio Ti6Al4V (795 MPa).

AGRADECIMIENTOS

Financiado parcialmente por la Generalitat Valenciana, Plan Tecnológico Valenciano dentro del programa para la Promoción de la I+D Precompetitiva (1995-1997) y el Ministerio de Industria y Energía (MINER), dentro del programa ATYCA (L 282/98; L46/1999).

A las empresas Lafitt, S.A. y CD-Pharma, S.A. por la cesión de los sistemas para la realización de los ensayos y por permitir la utilización del nombre comercial del sistema e imágenes del mismo en el artículo.

A las empresas Medtronic Iberia, S.A. y Depuy-Acromed (Grupo Johnson & Johnson) por permitir la utilización del nombre comercial del sistema e imágenes del mismo en el artículo.