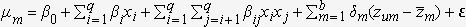El análisis conjunto es una técnica utilizada para estudiar las preferencias de los consumidores en estudios de mercado. Uno de los aspectos más importantes relacionados con el desarrollo de dicha técnica, se centra en fijar el conjunto de elección que deben evaluar los entrevistados. De forma tradicional, se utilizan diseños factoriales para estimar los valores parciales de los factores. Sin embargo, si el investigador, además, está interesado en estimar las interacciones entre dos o más factores, estos diseños requieren un número tan elevado de alternativas que se hace difícil su evaluación, provocando que los entrevistados no utilicen criterios compensatorios. La utilización de diseños Box-Behnken agrupados en bloques permite reducir el esfuerzo cognitivo de los entrevistados y, a la vez, ajustar un modelo de segundo grado. Este trabajo ilustra, mediante un experimento, el uso y las ventajas de utilizar diseños Box-Behnken en estudios de mercado. Los resultados obtenidos muestran el mayor rendimiento de estos modelos en comparación con los diseños factoriales habituales.
Conjoint analysis is a technique used to study consumer preferences in market research. One of the most important issues is to determine the choice set which respondents must assess; usually factorial designs to estimate part-worth factors have been used. But, if the researcher is also interested in estimating two or more factor interactions, factorial designs require such a large number of alternatives that makes their evaluation very difficult, leading respondents to not use compensatory criteria. Using Box-Behnken designs in blocks reduce the cognitive effort made by respondents and, at the same time, it allows fitting a quadratic model. This paper illustrates, through an experiment, the properties and how to use Box-Behnken designs in market research. Results showed a better performance of these models when compared with standard factorial designs.
El análisis conjunto (AC) es una técnica de investigación utilizada tanto en el ámbito académico como empresarial para analizar las preferencias declaradas de los consumidores sobre nuevos productos y servicios que se prevé lanzar al mercado (Gustafsson, Herrmann y Huber, 2007). Si bien en la primera etapa de desarrollo de esta técnica –hace más de cuarenta años– el análisis se solía centrar en las preferencias individuales de cada entrevistado, la aparición de los modelos de elección discreta ha permitido el desarrollo de análisis agregados de población o de segmentos de mercado. En estos estudios agregados es importante, no solo las estimaciones de los valores parciales de los factores principales, sino también los de los efectos que generan las interacciones entre dos o más factores; esto es especialmente relevante cuando el objeto de estudio son productos o servicios con atributos sensoriales (Green y Srinivasan, 1990).
Sin embargo, para poder estimar las interacciones entre dos o más factores se requieren diseños con un número muy elevado de alternativas. Esto implica que en los estudios de mercado los entrevistados deben realizar un enorme esfuerzo para clasificar y valorar todos los perfiles propuestos (Huber, Wittink, Fiedler y Miller, 1993). Esta carga cognitiva puede generar efectos negativos en la estimación del modelo, pues induce a los entrevistados a no utilizar el criterio compensatorio durante el proceso de elección y a recurrir a cualquier heurístico simplificador (Payne, Bettman y Johnson, 1988). Este efecto no deseado se traduce, a su vez, en un mayor volumen de error en los datos recogidos, lo que distorsiona el diagnóstico y perjudica la toma de decisiones en la política comercial de la empresa (Hauser y Rao, 2004; Salisbury y Feinberg, 2010).
La literatura considera que el error que se comete al cumplimentar los experimentos de elección discreta procede mayoritariamente de dos fuentes. Por un lado, los errores derivados de las características personales de los encuestados (e.g., la capacidad cognitiva y los diferentes grados de comprensión [Jaffe, Jamieson y Berger, 1992], los diferentes grados de implicación y de participación [Homer y Kahle, 1990] o, incluso, el tipo de enfoque regulador del entrevistado [Som y Lee, 2012]). Por otro lado, los errores derivados de las características del diseño experimental (e.g., el número de alternativas que debe evaluar cada entrevistado [Huffman y Kahn, 1998; Iyengar y Lepper, 2000], o, incluso, las características de los factores que forman el conjunto de elección [Som y Lee, 2012]).
Este estudio se centra en la segunda fuente de error y, en particular, en cómo se configura el conjunto de elección y las consecuencias que tiene este diseño en la generación de error en los estudios de AC. En particular, se analiza el papel que juegan el número de perfiles y la composición de factores que debe evaluar cada entrevistado. Además, y como una de las contribuciones originales de este trabajo, se propone un diseño alternativo, novedoso en la investigación de mercados, que puede mejorar el rendimiento del AC agregado: el diseño de Box-Behnken (DBB). El DBB es un diseño de estructura ingeniosa basado en la creación de diseños de bloques incompletos balanceados con un número suficiente de combinaciones que permiten su ajuste mediante modelos cuadráticos (Myers, Montgomery y Anderson-Cook, 2009). Este diseño permite reducir tanto el número de perfiles como el de factores que se considera en cada conjunto de elección. Esto contribuye a disminuir el esfuerzo cognitivo que requiere la evaluación de cada perfil, facilita el auto equilibrado de los factores, y permite estimar un modelo con una estructura de alias1, donde las interacciones entre dos factores no se confundan entre ellas.
El objetivo de este trabajo es, por tanto, doble. El primero, revisar los aspectos del diseño experimental que contribuyen a la generación de error en el AC. El segundo de los objetivos es ilustrar el uso de los DBB en el estudio del comportamiento del consumidor, mostrando su mayor rendimiento mediante un experimento comparativo con un diseño factorial fraccionado habitual en la mayoría de aplicaciones empíricas (Hauser y Rao, 2004).
Elementos del diseño experimental que pueden generar error en el análisis conjuntoEfectos del tamaño del conjunto de elecciónEl AC es una técnica que permite a los investigadores estimar las preferencias declaradas, de una muestra de consumidores, recogidas mediante un proceso de elección en el cual se evalúan diferentes conjuntos de perfiles de productos hipotéticos descritos por sus marcas, sus precios, y otros atributos (Louviere, Street y Burgess, 2003). Cada grupo de perfiles, denominado conjunto de elección, se configura mediante la combinación de atributos siguiendo un patrón denominado diseño experimental. Este diseño depende del número de atributos (factores) que se quieran considerar y del número de variaciones (niveles) incluidas en cada atributo. Por consiguiente, cuanto mayor sea el número de factores y niveles mayor será el número de perfiles que deberán evaluar los consumidores. Aquí surge la pregunta sobre el efecto que tendrá este hecho en la conducta de los consumidores que participan en el experimento.
La literatura, sin embargo, no ofrece una respuesta clara a esta cuestión. Por un lado, la teoría económica considera que un amplio número de alternativas favorece al individuo, dado que ofrece una mayor probabilidad de encontrar la opción que mejor se ajusta a sus propias preferencias (Lancaster, 1990). En este contexto, se entiende que el individuo se enfrenta a un proceso de elección donde cada una de las opciones, por sí misma, genera un grado de utilidad que la convierte en más o menos preferida; también se considera que el individuo tiene la habilidad o la capacidad operativa para calcular la opción que maximiza su utilidad. A este enfoque se le denomina teoría de la elección racional del individuo (Frank, 2005). Por tanto, dada la heterogeneidad en gustos de los consumidores, se asume que un conjunto de elección más amplio cuenta con una mayor capacidad para lograr que alguna de las alternativas existentes satisfaga, en mayor medida, sus necesidades (Anderson, 2006; Iyengar y Lepper, 2000). Además, la literatura señala que una amplia gama de opciones puede reducir el grado de vacilación en la elección (Ariely y Levav, 2000). En definitiva, si asumimos que en el diseño de un experimento de elección discreta la conducta del consumidor queda representada por el modelo de utilidad aleatoria, la inclusión de toda la información disponible sobre las marcas y los atributos que compiten en el mercado equivale a proporcionarle la mayor información posible sobre la oferta existente. Por ello, excluir opciones dentro del conjunto de alternativas sería equivalente a descartar datos que pueden ser relevantes en el proceso de elección (Zeithammer y Lenk, 2009).
Sin embargo, existen trabajos que destacan los efectos negativos que se derivan de ofrecer un elevado número de opciones a los individuos. Estos efectos han sido analizados tanto desde una perspectiva cuantitativa como desde un enfoque cualitativo. Cuantitativamente, la presencia de muchos atributos, ya sean perfiles o niveles, reduce la cantidad de información disponible para cada atributo, lo que implica reducir su potencia y la precisión en las estimaciones (Deshazo y Fermo, 2002). Mediante una aproximación cualitativa, la teoría del procesamiento de la información considera que los individuos disponen de una racionalidad limitada, por lo que no pueden abarcar, procesar mediante cálculos y retener toda la información disponible o necesaria en un proceso de toma de decisiones conforme el número de alternativas se va incrementando (Simon, 1990). Cada diseño experimental determina el número de perfiles que debe evaluar cada sujeto y, por tanto, el grado de complejidad del proceso de elección y la mayor o menor probabilidad de generar error (Louviere, Islam, Wasi, Street y Burgess, 2008). La complejidad normativa viene determinada por el número de pasos cognitivos que debe realizar cada entrevistado tanto para comprender el proceso de evaluación como para tomar una decisión2 (Johnson y Meyer, 1984). Así, a medida que el número de alternativas se incrementa y el número de variables también, el esfuerzo cognitivo crece de manera exponencial (Shugan, 1980).
A partir de todo lo anterior, parece evidente que el tamaño del conjunto de elección es determinante en la generación de error puesto que cualquier proceso de elección que realiza un entrevistado es el resultado de un equilibrio entre el coste generado por el esfuerzo mental de tomar la decisión y el beneficio que le reporta tomar la decisión correcta.
Efectos del número de factores que configuran el perfilExisten, habitualmente, dos maneras de presentar los estímulos a los individuos (Wittink, Vriens y Burhenne, 1992): (1) los diseños de perfil completo, y (2) los diseños de perfil parcial. En el primer enfoque, cada alternativa viene determinada por la combinación de todos los factores o variables incluidos en el experimento. Por el contrario, en el perfil parcial solo algunos factores participan en la formación de los perfiles. Generalmente, se suelen utilizar los estímulos de perfil completo debido a que proporcionan descripciones más realistas de los productos hipotéticos al incluir todos los atributos que se desean analizar. Además, se puede hacer un uso directo de los constructos habituales para evaluar el comportamiento del consumidor (e.g., la intención de compra, la probabilidad de elección, la posibilidad de cambiar a una nueva marca, etc. [Green y Srinivasan, 1990; Hauser y Rao, 2004]). No obstante, los estímulos de perfil completo presentan el inconveniente de hacer más compleja la evaluación, ya que deben considerar varios factores al mismo tiempo, y esto puede desembocar en el uso de heurísticos diferentes del modelo compensatorio (Payne et al., 1988). Por otro lado, los modelos que ajustan los resultados de estos experimentos tienden a minusvalorar los factores menos sustanciales y a sobrevalorar los más relevantes, siendo poco representativos de la vida real. De hecho, debido a los problemas de saturación informativa en los procesos de elección el perfil completo suele estar restringido a cinco o seis factores. A pesar de sus limitaciones, cuando existe un número limitado de factores y un entorno en el que la correlación es importante, el perfil completo es generalmente mejor en términos de validez predictiva (Green y Srinivasan, 1990).
No obstante, es posible obtener resultados igualmente eficaces utilizando diseños con perfiles parciales (Kuhfeld, Tobias y Garratt, 1994). La utilización de estos diseños se ha incrementado de forma importante desde la aparición del análisis conjunto adaptativo3 (ACA) (Johnson, 1987). En los diseños basados en perfiles parciales la carga cognitiva es mucho menor que en los diseños de perfil completo, dado el menor número de factores que aquellos incluyen. Además, la literatura considera que la utilización de experimentos con perfiles parciales puede mejorar la identificación y la estimación de los parámetros frente a los modelos de perfil completo. En esta línea, Zeithammer y Lenk (2009) sugieren que en términos de análisis de la varianza y la covarianza, excluir algunos atributos del conjunto de elección puede permitir evaluar mejor el resto de los atributos. Esto es especialmente relevante cuando alguno de los atributos destaca sobre los demás. Así por ejemplo, si un experimento considera tres atributos y se realiza una evaluación de perfil completo en la que se comparan productos que incluyen todos estos atributos, en modelos de elección discreta existe una tendencia a sobredimensionar el atributo dominante frente a los otros dos. Por el contrario, si se utiliza un modelo de perfil parcial (e.g., de dos en dos), en algunos casos la comparación se realizará entre los dos atributos menos destacados y los resultados tenderán a un mayor equilibrio, mejorando la estimación de los atributos menos relevantes (Kuhfeld et al., 1994; Sandor y Wedel, 2001).
También, la utilización de diseños basados en perfiles parciales es especialmente recomendable en aquellas situaciones en las que el individuo se enfrenta a conjuntos de elección en los que los perfiles están formados por variaciones de factores más que por variaciones de niveles4, situación muy habitual en la toma de decisiones diaria (Som y Lee, 2012). De hecho, son necesarios muchos más pasos mentales para comparar dos atributos diferentes dentro de un conjunto de elección (e.g., en el caso de un automóvil, comparar entre la potencia del motor y el interior de piel), que para comparar dos niveles de un mismo atributo (e.g., entre la capacidad de un motor de 1,5 litros y otro de 2,2 litros) (Gourville y Soman, 2005). Esta diferencia entre el esfuerzo cognitivo para elegir entre un conjunto alineado y otro no alineado se incrementa a medida que lo hace el conjunto de elección (Som y Lee, 2012).
Diseños organizados en bloques y diseños Box-BehnkenDiseños organizados en bloques con estructura estadísticaEl principal argumento para la utilización de diseños organizados en bloques está en su propia definición. El bloqueo, según la definición tradicional fisheriana, es una restricción a la aleatorización del diseño (Gilmour y Trinca, 2006). Consiste en separar el conjunto de elección en subconjuntos de menor tamaño siguiendo algún criterio para su separación. En los diseños estadísticos se suele utilizar como criterio la confusión, aunque también se utilizan otros como la aleatoriedad. Por lo tanto, el uso de bloques contribuye a reducir la variabilidad de respuestas que pueden generar los entrevistados debido a diferentes circunstancias; e.g., la existencia de un intervalo de tiempo o espacio entre un subconjunto de elección y otro, o las propias circunstancias personales como estados de ánimo, grado de distracción, etc. (Rosenbaum, 1999). Por otro lado, también cabe señalar que cuando los investigadores usan bloques, se asume que los efectos del bloque son aditivos, generando un único cambio en la variable dependiente, así como que no hay interacción entre la variable de bloqueo y ninguno de los factores (Yang y Draper, 2003). Además, la organización de los perfiles en bloques puede generar información estadística más relevante, mejorando la varianza y la covarianza de las estimaciones, debido a las restricciones que incorpora la exclusión de algunas alternativas (Keane, 1992). Por otro lado, la evaluación de bloques es más fácil y rápida, por lo que en los estudios donde se utilizan subconjuntos de elección más pequeños se puede realizar un mayor número de tareas de elección.
Uno de los aspectos más relevantes en este tipo de diseños es cómo organizar los perfiles en bloques. En los experimentos desarrollados en disciplinas como la química o la ingeniería, en las que el número de perfiles es reducido, se suelen utilizar los diseños estadísticos basados en la estructura de alias para formar los bloques (Box, Hunter y Hunter, 2005). Por el contrario, en investigación de mercados los perfiles que configuran los bloques se suelen asignar de forma aleatoria, ya que el número de perfiles suele ser mucho más elevado (Zeithammer y Lenk, 2009).
No obstante, aunque la utilización de perfiles parciales agrupados en bloques de forma aleatoria puede mejorar el rendimiento frente al uso de conjuntos de elección con perfiles completos, en ningún caso garantiza que el diseño resultante tenga una capacidad de resolución que permita estimar los factores principales y las interacciones sin un elevado grado de confusión. En particular, en este trabajo se considera que el uso de bloques estadísticos puede mejorar el resultado que se obtiene con la utilización de subconjuntos aleatorios, puesto que permite conocer de antemano tanto su grado de resolución como los factores e interacciones que es posible estimar sin confusión5.
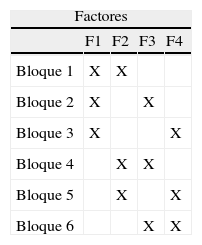
El diseño Box-BehnkenBox y Behnken (1960) desarrollaron una familia de diseños eficientes para factores con dos o tres niveles que permiten, además, un ajuste con modelos cuadráticos. Se trata de un diseño creativo basado en la construcción de bloques incompletos balanceados. Un ejemplo con cuatro factores y seis bloques vendría determinado por la matriz que se muestra en la tabla 1.
Como se puede observar en la tabla 1, se trata de una estructura de diseño basada en perfiles parciales organizados en bloques. Cada bloque está formado por combinaciones de perfiles en los que intervienen solo dos de los cuatro factores. Así, en el bloque 1 –incluye los factores 1 y 2– el diseño es un factorial completo 22 = 4 perfiles resultado de combinar dos de los niveles de F1 y F2 (cada factor tiene dos niveles, −1 y+1) y los factores no señalados, F3 y F4 se fijan en el centro (F3 = 0, F4 = 0). El mismo procedimiento se seguiría con cada uno de los bloques 2 a 6, con un factorial 22 completo para cada par de factores señalados mientras que el tercero y el cuarto se fijan en 0. En resumen, cada bloque estaría formado por cuatro perfiles resultado de combinar dos factores y el experimento total estaría formado por 24 perfiles. Para su evaluación, tanto en AC clásico como en modelos de elección discreta donde cada sujeto evalúa bien el conjunto de elección o varios bloques, se requiere que cada grupo de consumidores evalúe al menos dos bloques, de tal manera que en los dos bloques estén comprendidos los cuatro factores que se quieren estimar.
En la mayoría de estudios de mercado donde se utiliza el AC los diseños habituales para configurar el conjunto de elección son los factoriales fraccionados, a menudo con dos a tres niveles y con el mismo intervalo en cada factor (Green, Helsen y Shandler, 1988). En ese tipo de estudios los DBB pueden ser utilizados como unas herramientas eficientes y alternativas a los diseños factoriales fraccionados sobre todo cuando la carga informativa que contiene cada factor es elevada. Además, también se pueden utilizar estos diseños en los modelos de elección discreta, donde el entrevistado elige la mejor opción entre las alternativas contenidas en cada bloque; en este caso, no obstante, es importante considerar la carga de trabajo que supone la evaluación del experimento completo.
El DBB tiene una serie de características relevantes. La primera es que proporciona un número de perfiles suficiente para testar la bondad del ajuste. Además, este tipo de diseño no se desvía de un diseño rotativo hasta los siete factores. Verificar la rotación del diseño es muy sencillo, ya que basta comparar dos momentos impares y verificar que son cero. En tercer lugar, los DBB tienen una estructura de diseño esférica. Eso quiere decir que todos los puntos límites están a la distancia de la raíz cuadrada de 2 desde el centro del diseño; por tanto, no hay puntos a evaluar en las posiciones más extremas, a una distancia raíz cuadrada de 3 desde el centro de diseño. Esto limita su uso a situaciones en las que el investigador no está interesado en hacer predicciones acerca de las opciones más extremas. Sin embargo, esta limitación no es tan importante; tanto en el AC como en los modelos de elección discreta el análisis está mucho más enfocado en considerar variaciones de los valores a lo largo del rango que en la consideración de las posiciones más extremas (Train, 2009).
A partir de los argumentos teóricos desarrollados, en este trabajo se compara el rendimiento de los diseños factoriales fraccionados y el DBB. En particular, y dado que los DBB proporcionan un conjunto de elección en el que existe una menor variación de alternativas no asignables, en este trabajo se asume que estos diseños suponen una menor carga de trabajo, un menor esfuerzo, favorecen el auto equilibrado del diseño y, por tanto, presentan un rendimiento superior al que tienen los diseños factoriales fraccionados; estos últimos tienen una variación mayor en las alternativas no asignables y, por tanto, requieren mayor esfuerzo cognitivo. En definitiva, el propósito principal de esta investigación es comprobar que el DBB tiene un rendimiento superior y una distribución más equilibrada en el peso de los factores que el diseño factorial fraccionado, dada la menor carga de trabajo y el menor esfuerzo cognitivo a realizar por el entrevistado.
Metodología: estudio comparativo entre un diseño factorial fraccionado y un DBBCon objeto de acometer el objetivo de la investigación, en este trabajo se propone un experimento entre sujetos en el que dos grupos de individuos evalúan, cada uno de ellos, un conjunto de elección de ambos diseños. El proceso de recogida de datos ha seguido la lógica del análisis de subconjuntos, que es habitual en los modelos de elección discreta y en el análisis conjunto adaptativo, y que difiere del AC clásico en que cada grupo de individuos analiza un subconjunto de perfiles en lugar de que cada sujeto deba evaluar todos los perfiles como sucede en el AC clásico (Chrzan y Orme, 2000). En particular, se comparan los resultados de dos diseños: un diseño factorial fraccionado y un DBB mixto, en términos del coeficiente de determinación ajustado (R2adj) y en términos del rango y la varianza del peso de los factores, como medida de concentración, que obtiene cada uno de los modelos que utiliza cada diseño.
Para el desarrollo del experimento se toman datos sobre la evaluación de diseños de sitios web hipotéticos para un hotel (se pueden ver ejemplos en http://www.ub.edu/mkt/marketing_bali/). Los individuos utilizados en el experimento fueron estudiantes de grado de la Universidad de Barcelona. Los individuos fueron invitados a participar en el experimento y asignados, de manera aleatoria, a dos salas de informática donde, siguiendo las instrucciones de los investigadores, estuvieron visitando diferentes sitios webs simulados de un hotel (se puede ver un ejemplo en el anexo). Además se les suministró un cuestionario para que evaluaran cada una de las webs visitadas en una escala de 1 a 10 dependiendo del grado de preferencia (donde 1 indica el grado de preferencia menor y 10 un grado máximo de preferencia). El conjunto de elección estaba formado por 8 perfiles que configuraban un bloque y, de manera aleatoria, cada entrevistado tenía acceso a un solo bloque.
El estudio incluía cinco factores (de dos niveles cada uno) relacionados tanto con las características del establecimiento hotelero (contenido) como sobre la forma de presentar la información en la web (continente) y codificados de manera vectorial: (F1) espacio donde se recogen las opiniones de otros clientes (−1 = ausencia, 1 = presencia), (F2) número de habitaciones (−1 = 20 habitaciones, 1 = 800 habitaciones), (F3) Precio cinco noches (−1 = 230 euros, 1 = 1.200 euros), (F4) Tipo de ilustración utilizada (−1 = imagen estática, 1 = vídeo) y (F5) Número de actividades que organiza el establecimiento (−1 = 4 actividades, 1 = 40 actividades). Tanto los factores como los niveles se obtuvieron después de analizar varios folletos de los hoteles de un destino turístico real. En un principio, se diseñaron los escenarios teniendo en cuenta que en el DBB los espacios vacíos indicaban ausencia del atributo en la página web.
No obstante, tras aplicar un pre-test con veintitrés estudiantes de doctorado en investigación de empresas, los encuestados manifestaron que la evaluación de sitios webs en los que faltaba información esencial constituía un ejercicio excesivamente artificial, restando validez al esfuerzo realizado en el diseño de las webs. Por lo tanto, se decidió sustituir la ausencia del factor en el diseño web por el valor cero, definido como el valor actual de los factores del hotel sin manipular. Así, para el factor «número de habitaciones» 0 = 350 habitaciones, para el factor «precio» 0 = 650 euros, para el factor «tipo de ilustración» 0 = imágenes dinámicas, y para el factor «número de actividades» 0 = 20 actividades. En el caso del primer factor, «la presencia de opiniones de otros clientes», dada su naturaleza, no se ha considerado la opción cero. Esto no modifica, en ningún caso, la capacidad resolutiva del experimento puesto que esta se genera por la variación de los factores y no por los que permanecen fijos (Huertas-Garcia et al., 2012).
Los diseños utilizados fueron los siguientes. Para la primera opción, media fracción de un diseño 25 que representan 16 sitios web, y cuenta con una capacidad de resolución V6 lo que permite estimar los factores principales y las interacciones de dos factores sin confusión. Para la segunda opción se optó por un DBB mixto, con el primer factor fijado en dos niveles y los otros cuatro factores organizados en bloques incompletos de dos factores cada uno, lo que representa un total de 24 diseños web. Para no interferir en el experimento con un número diferente de perfiles para cada entrevistado, se organizaron en una estructura de bloques en los que cada uno de ellos incluyera el mismo número de alternativas, de modo que cada individuo tuviera el mismo conjunto de elección. Con este objetivo, el medio factorial fue dividido en dos bloques de 8 perfiles cada uno y el DBB en tres bloques de 8 perfiles, de tal modo que los criterios de bloqueo no se confundieran con los factores principales ni con las interacciones de dos factores.
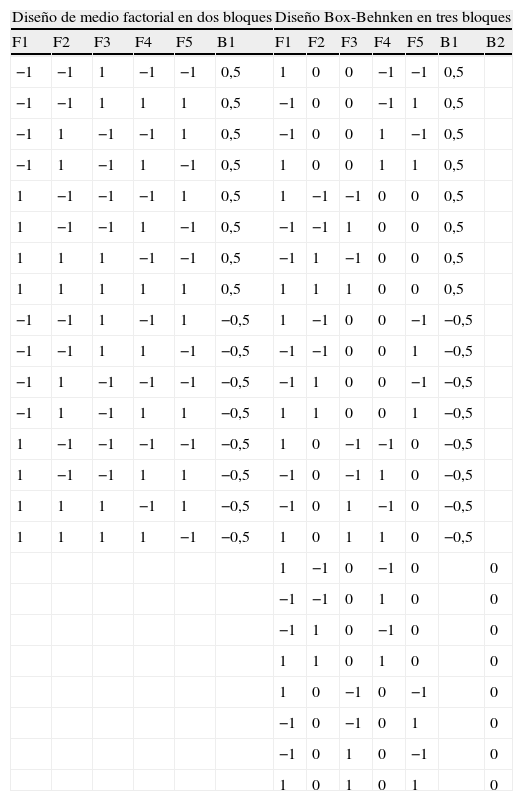
La tabla 2 muestra el diseño resultante con las dos alternativas de diseño, así como la codificación de cada uno de los cinco factores. Como hemos comentado con anterioridad, la muestra la componen estudiantes universitarios de grado de una universidad española. En total, 300 estudiantes que utilizan de forma habitual Internet, con experiencia en realizar compras online y que manifestaron no conocer el destino evaluado. Poco más de la mitad de la muestra eran mujeres (58%), la mayoría en torno a 23 años (49%), y el 93% españoles. Los experimentos se llevaron a cabo en la sala de informática durante el período de clase en octubre de 2011. 150 estudiantes evaluaron el diseño factorial fraccionado en dos grupos de 75 para cada bloque y los otros 150 respondieron el diseño DBB, 50 encuestados al azar de cada uno de los tres bloques. De cada experimento se recogieron 1.200 datos (tabla 2).
Diseño experimental utilizado
| Diseño de medio factorial en dos bloques | Diseño Box-Behnken en tres bloques | |||||||||||
| F1 | F2 | F3 | F4 | F5 | B1 | F1 | F2 | F3 | F4 | F5 | B1 | B2 |
| −1 | −1 | 1 | −1 | −1 | 0,5 | 1 | 0 | 0 | −1 | −1 | 0,5 | |
| −1 | −1 | 1 | 1 | 1 | 0,5 | −1 | 0 | 0 | −1 | 1 | 0,5 | |
| −1 | 1 | −1 | −1 | 1 | 0,5 | −1 | 0 | 0 | 1 | −1 | 0,5 | |
| −1 | 1 | −1 | 1 | −1 | 0,5 | 1 | 0 | 0 | 1 | 1 | 0,5 | |
| 1 | −1 | −1 | −1 | 1 | 0,5 | 1 | −1 | −1 | 0 | 0 | 0,5 | |
| 1 | −1 | −1 | 1 | −1 | 0,5 | −1 | −1 | 1 | 0 | 0 | 0,5 | |
| 1 | 1 | 1 | −1 | −1 | 0,5 | −1 | 1 | −1 | 0 | 0 | 0,5 | |
| 1 | 1 | 1 | 1 | 1 | 0,5 | 1 | 1 | 1 | 0 | 0 | 0,5 | |
| −1 | −1 | 1 | −1 | 1 | −0,5 | 1 | −1 | 0 | 0 | −1 | −0,5 | |
| −1 | −1 | 1 | 1 | −1 | −0,5 | −1 | −1 | 0 | 0 | 1 | −0,5 | |
| −1 | 1 | −1 | −1 | −1 | −0,5 | −1 | 1 | 0 | 0 | −1 | −0,5 | |
| −1 | 1 | −1 | 1 | 1 | −0,5 | 1 | 1 | 0 | 0 | 1 | −0,5 | |
| 1 | −1 | −1 | −1 | −1 | −0,5 | 1 | 0 | −1 | −1 | 0 | −0,5 | |
| 1 | −1 | −1 | 1 | 1 | −0,5 | −1 | 0 | −1 | 1 | 0 | −0,5 | |
| 1 | 1 | 1 | −1 | 1 | −0,5 | −1 | 0 | 1 | −1 | 0 | −0,5 | |
| 1 | 1 | 1 | 1 | −1 | −0,5 | 1 | 0 | 1 | 1 | 0 | −0,5 | |
| 1 | −1 | 0 | −1 | 0 | 0 | |||||||
| −1 | −1 | 0 | 1 | 0 | 0 | |||||||
| −1 | 1 | 0 | −1 | 0 | 0 | |||||||
| 1 | 1 | 0 | 1 | 0 | 0 | |||||||
| 1 | 0 | −1 | 0 | −1 | 0 | |||||||
| −1 | 0 | −1 | 0 | 1 | 0 | |||||||
| −1 | 0 | 1 | 0 | −1 | 0 | |||||||
| 1 | 0 | 1 | 0 | 1 | 0 | |||||||
La función de utilidad que se trata de ajustar en este estudio es un modelo polinomio de segundo orden:
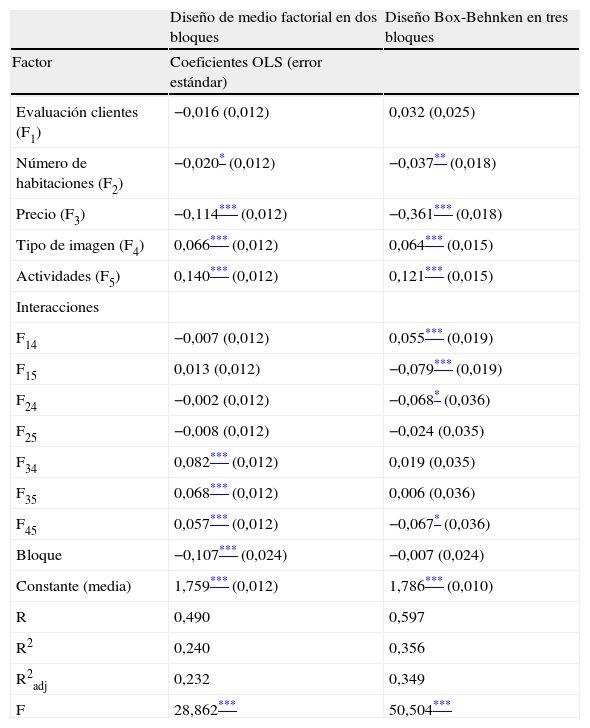
donde μ mide la utilidad total de cada perfil m, bi son los valores de la pendiente del vector de cada factor principal i, bij los efectos de la interacción de dos factores i y j, y bii los efectos de los factores cuadrados, δm es el coeficiente que refleja el efecto de bloque m, zum es una variable dicotómica, cuyos valores son zum = 1 si la observación uth está en el bloque mth, z–m es el promedio de las variables ficticias utilizadas para eliminar una de ellas y no hacer a la matriz de coeficientes singular, y e es el término de error. Finalmente, se transformó la variable dependiente en logaritmo y se ajustó el modelo por MCO utilizando PASW 18.ResultadosEl resultado obtenido (tabla 3) muestra que la bondad del ajuste es superior en el experimento que utiliza un DBB para todas las variables de control (R2adj = 0,353, frente a 0,232 para el diseño fraccional). Igualmente, los signos son similares y los pesos parecidos en los cuatro factores principales de ambos experimentos, lo que es un señal de la validez interna. No obstante, las principales diferencias entre ambos modelos se encuentran en la significatividad, los signos y los pesos de las interacciones entre pares de factores. En el diseño factorial las interacciones F34 (interacción entre precio y tipo de imagen; 0,082, p < 0,01), F35 (interacción entre precio y número de actividades; 0,068, p < 0,01) y F45 (interacción entre tipo de imagen y número de actividades; 0,057, p < 0,01) son significativas y presentan signo positivo. Por su parte, en el experimento diseñado con un DBB existen cuatro interacciones de dos niveles significativas; tres de ellas (F14 [interacción entre evaluación del cliente y tipo de imagen; 0,055, p < 0,01], F15 [interacción entre evaluación del cliente y número de actividades; −0,079, p < 0,01], F24 [interacción entre número de habitaciones y tipo de imagen; −0,068, p < 0,1]) no son significativas en el modelo de diseño factorial; la cuarta (F45 [interacción entre tipo de imagen y número de actividades; −0,067, p < 0,1]) también es significativa en el diseño factorial pero con signo contrario.
Estimación de los modelos
| Diseño de medio factorial en dos bloques | Diseño Box-Behnken en tres bloques | |
| Factor | Coeficientes OLS (error estándar) | |
| Evaluación clientes (F1) | −0,016 (0,012) | 0,032 (0,025) |
| Número de habitaciones (F2) | −0,020* (0,012) | −0,037** (0,018) |
| Precio (F3) | −0,114*** (0,012) | −0,361*** (0,018) |
| Tipo de imagen (F4) | 0,066*** (0,012) | 0,064*** (0,015) |
| Actividades (F5) | 0,140*** (0,012) | 0,121*** (0,015) |
| Interacciones | ||
| F14 | −0,007 (0,012) | 0,055*** (0,019) |
| F15 | 0,013 (0,012) | −0,079*** (0,019) |
| F24 | −0,002 (0,012) | −0,068* (0,036) |
| F25 | −0,008 (0,012) | −0,024 (0,035) |
| F34 | 0,082*** (0,012) | 0,019 (0,035) |
| F35 | 0,068*** (0,012) | 0,006 (0,036) |
| F45 | 0,057*** (0,012) | −0,067* (0,036) |
| Bloque | −0,107*** (0,024) | −0,007 (0,024) |
| Constante (media) | 1,759*** (0,012) | 1,786*** (0,010) |
| R | 0,490 | 0,597 |
| R2 | 0,240 | 0,356 |
| R2adj | 0,232 | 0,349 |
| F | 28,862*** | 50,504*** |
Respecto a la concentración del peso de los factores, el rango en el diseño factorial fraccionado es de 0,254 frente al DBB cuyo recorrido es de 0,482, y en el caso de la varianza es de 0,005 en el diseño factorial fraccionado mientras en el DBB la varianza es de 0,013. Esto indica una mayor concentración de los resultados en el diseño factorial fraccionado de perfil completo y una mayor dispersión en el DBB de perfil parcial.
También se recoge una diferencia importante entre ambos tipos de diseños respecto a la variable de bloqueo. Como se puede observar en la tabla 3, en el diseño factorial dicha variable es significativa (−0,107; p < 0,01), por lo que pierde el carácter neutral; esto no sucede en el DBB, donde la variable de bloqueo no es significativa. Este resultado refleja la dificultad práctica que tiene separar un grupo de individuos en dos bloques completamente aleatorios mientras que es mucho más fácil si se reparten en tres o cuatro bloques. Lo anterior es indicativo de la tendencia de los individuos que han contestado el segundo bloque del diseño factorial a valorar en mayor medida los resultados que aquellos que han respondido al primer bloque.
Por otro lado, aunque ambos diseños generan resultados similares en los factores principales, en las interacciones significativas de dos factores parecen mostrar patrones de conductas diferentes entre ellos.
En definitiva, el DBB genera un mayor rendimiento con una muestra del mismo tamaño, ya que consigue un mejor ajuste del modelo y un mayor rango en las respuestas, aunque el número de variables significativas es similar. Por lo tanto, se confirmaría de manera relevante la propuesta de investigación definida en el marco teórico de este trabajo (tabla 3).
Conclusiones e implicaciones para la investigación de mercadosNumerosos trabajos han estudiado como afecta el diseño experimental en el proceso de evaluación de los entrevistados y, por extensión, en la variabilidad y fiabilidad de los resultados obtenidos (Johnson y Orme, 1996; Wittink, Krishnamurthi y Nutter, 1982; Zeithammer y Lenk, 2009). El presente estudio supone una contribución en esta línea de investigación, al proponer la adaptación de los DBB organizados en bloques al desarrollo de la investigación de mercados. Este diseño permite reducir el tamaño del conjunto de elección, mediante el uso de bloques, y el número de factores no alineados que debe evaluar cada sujeto (consumidor) entrevistado, gracias a la estructura de perfiles parciales balanceados. De este modo, al reducir el esfuerzo cognitivo que deben realizar los entrevistados al evaluar el conjunto de elección, se esperaba que el rendimiento fuera mayor al de los diseños factoriales fraccionados de perfil completo. Los resultados obtenidos confirman esta suposición, sugiriendo un rendimiento superior en el DBB. Así, el test F, que evalúa la variación explicada, y los otros estadísticos de control son bastante superiores en el DBB que en el diseño factorial fraccionado.
Además, la organización de los perfiles en una estructura de bloques incompletos balanceados permite que todos los atributos sean evaluados el mismo número de veces, pero dentro de un rango comparativo menor que contribuye al auto equilibrio del experimento. Por consiguiente, un menor esfuerzo cognitivo junto a un mejor equilibrio comparativo se traduce en una menor variación en las respuestas de los consumidores, reduciéndose así el riesgo de sobrestimación de alguno de los factores más relevantes dentro del conjunto de elección. Las medidas de control, tanto el rango como la varianza de los resultados, muestran valores más pequeños en el diseño factorial fraccionado frente al DBB. Esto indica una mayor concentración de los resultados, hecho que va en la línea señalada por Zeithammer y Lenk (2009) y, en consonancia con Johnson y Meyer (1984); estos autores sugieren que al aumentar la complejidad de los experimentos el peso de los factores tiende a concentrarse, moviéndose desde los atributos menos importantes hacia los más importantes.
Otro de los resultados que presenta el análisis comparativo es un incremento en el coeficiente de determinación del 50% del DBB frente al diseño factorial fraccionado. Teniendo en cuenta que cada individuo que ha participado en el experimento ha evaluado el mismo número de opciones (ocho websites), esta mejora del rendimiento solo puede ser atribuida a la utilización de diseños de perfil parcial. Es decir, el rendimiento mejora cuando se reduce el número de factores no alineados y se concentra el esfuerzo en valorar unos pocos factores con variaciones alineadas, lo que confirma el resultado obtenido por Gourville y Soman (2005). Además, a este incremento en el rendimiento, ha podido contribuir la característica del servicio evaluado y la forma en que se han presentado los perfiles a los entrevistados. En este sentido, cabe recordar que se han utilizado ocho webs simuladas que combinaban los niveles de cinco factores, de contenido y de continente, sobre un establecimiento turístico en un destino poco conocido. Se trata de un conjunto de elección cuya evaluación requiere cierto grado de atención para apreciar las diferencias entre los perfiles, así como un esfuerzo cognitivo para su comparación que no precisan algunos experimentos en los cuales solo se nombran los atributos (Holbrook y Moore, 1981). Por tanto, se puede concluir que en contextos en los que el conjunto de elección representa un esfuerzo cognitivo importante, e.g., cuando se comparan imágenes o frases, los DBB pueden alcanzar un mayor rendimiento.
Por consiguiente, los investigadores de mercados que deseen utilizar la técnica experimental o el análisis conjunto para recoger los datos deben tener en cuenta que la organización de los perfiles en bloques, así como la utilización de estímulos de perfil parcial, mejora el rendimiento en los experimentos que requieren un esfuerzo cognitivo elevado. Es decir, establecer el conjunto de elección dependerá del grado de dificultad de la elección, del número de factores considerados y, seguramente, de las habilidades cognitivas del público objetivo. Se podría considerar que una forma de reducir el grado de dificultad del conjunto de elección sería utilizar presentaciones más sencillas, citando simplemente los atributos, en lugar de describirlos con frases o representarlos mediante imágenes. Sin embargo, esto incrementaría el grado de artificialidad de la prueba de laboratorio que iría en contra de la validez predictiva. Otra alternativa podría ser utilizar diseños ACA, que combinan en un solo test preguntas para determinar la importancia de los atributos y experimentos en bloques de perfiles formados por los atributos valorados en la primera fase. Sin embargo, la alternativa DBB permite, en un solo experimento, evaluar perfiles con un esfuerzo cognitivo moderado y obtener resultados equilibrados para un conjunto de elección de hasta siete factores.
Por otro lado, esta investigación ha abierto un interrogante. Los resultados obtenidos muestran una distribución diferente de las interacciones de dos factores significativas entre ambos experimentos, lo que apunta a la presencia de estrategias de decisión distintas en función de la estructura del diseño. Esto nos hace suponer que los individuos participantes han sustituido el criterio compensatorio por algún heurístico simplificador (Payne et al., 1988). No obstante, en el contexto de este estudio no parece que esta haya sido la explicación. El número de perfiles que contenía cada conjunto de elección ha sido de ocho, muy por debajo de los límites señalados por la literatura en torno a los veinte (Johnson y Orme, 1996); además, cabría esperar que la utilización de heurísticos simplificadores pudiera generar interacciones totalmente ilógicas. Al contrario, la mayoría de interacciones estimadas en ambos diseños, que podrían leerse como elasticidades cruzadas, son totalmente racionales y ajustadas a los preceptos de la literatura. Parte de esta variación podría venir explicada por el auto balanceado que generan los bloques de experimentos de perfil parcial. Sin embargo, con los datos de los que se dispone, no es posible tener la certeza sobre si esta diferencia en la distribución de las interacciones obedece a esta razón. En futuras investigaciones, por tanto, sería interesante analizar la naturaleza que subyace en las diferentes conductas observadas.
También se podría reflexionar sobre las ventajas de los DBB en diferentes categorías de productos. Ya se ha apuntado que la comparación de webs, donde variaban características del servicio ofrecido junto a atributos del continente, suponía un esfuerzo cognitivo importante. Por ello, se deduce que en productos más sencillos de evaluar estas diferencias serían menores. Esto indicaría que los DBB alcanzarían el mayor rendimiento en estudios de mercado donde se comparen productos sofisticados, como e.g., ordenadores personales, electrodomésticos, etc.
Por último, una de las principales limitaciones del trabajo se basa en el hecho de que el experimento solo se ha probado con una sola muestra y en un estudio concreto. Además, también se debe considerar el reducido tamaño de la muestra que ha impedido que algunos factores se hayan acabado de definir. Sería interesante replicar el DBB en experimentos adicionales, de productos diferentes y con varios formatos de presentación de los factores, que permitan confirmar la bondad del diseño propuesto. Adicionalmente, es importante tener en cuenta las propias limitaciones del DBB, que no considera las posiciones más extremas (este hecho es poco frecuente en los estudios de elección discreta), y que a partir de siete factores se desvía del diseño rotativo. Ahora bien, de acuerdo con los resultados del meta análisis de Wittink y Cattin (1989), la consideración de hasta siete factores supone casi la mitad de los experimentos empíricos desarrollados en la investigación de mercados. No obstante, siempre sería posible acoplar un diseño plegado con los que poder analizar hasta catorce factores. Un diseño plegado es una réplica invertida del diseño original, en el sentido de que los niveles +1 y −1 del primer experimento están totalmente invertidos en el segundo (Box et al., 2005).
FinanciaciónLos autores desean reconocer el apoyo financiero de la Dirección general de Investigación Científica y Técnica del Ministerio de Economía y Competitividad (proyecto n.º ECO2012-31712).
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Autor para correspondencia: Facultad de Economía y Empresa, Universidad de Barcelona, Avda. Diagonal 690, 08034 Barcelona, España.
La estructura de alias de un diseño de experimentos define los factores e interacciones que están confundidos unos con otros, determinando la capacidad interpretativa de los mismos en los diseños factoriales fraccionados.
Por ejemplo, si un individuo debe elegir entre dos perfiles donde uno es un concepto de coche con techo solar y en el otro con el interior de piel debe realizar, al menos, tres pasos cognitivos: efectuar una valoración del techo solar, una valoración del interior en piel, y comparar entre ambos atributos.
El ACA es un modelo flexible que combina diferentes procedimientos de investigación de mercados en un solo estudio (e.g., cuestionarios de autoevaluación junto con diseños experimentales ortogonales), y que va adaptando de forma secuencial el diseño experimental, basado en perfiles parciales, en función de las preferencias declaradas en las etapas previas (Green, Krieger y Agarwal, 1991).
Som y Lee (2012) denominan «surtido alineado» y «surtido no alineado» a la variación de niveles y factores, respectivamente.
Un ejemplo de diseño estadístico de perfiles parciales organizado en bloques de dos y el cálculo de su capacidad de resolución se puede encontrar en Huertas-Garcia, Forgas-Coll y Gazquez-Abad (2012).
La capacidad resolutiva de los experimentos se clasifica con números romanos; los de resolución V indican que los factores principales y las interacciones de dos factores no están confundidos entre ellos y, por consiguiente, tiene sentido su estimación.