Se conoce que la red de puntos y meridianos de acupuntura es una red compleja que incluye los llamados microsistemas. Esto permite atribuirle la propiedad fractal de autosimilitud, pero no se sabe si es un fractal. Se determina la dimensión fractal de la red compleja de puntos y meridianos de acupuntura por medio de 2 métodos independientes: el primero estima la dimensión fractal a través de los algoritmos de recuento de cajas (box counting) y radio de masa (radius mass) y el segundo realiza un cálculo directo de la dimensión mediante la aplicación de la definición de volumen de la dimensión fractal al gráfico. La dimensión fractal estimada varió entre 1,28 y 1,91, con razones de correlación de 0,999 en todos los casos. No fue posible calcular la dimensión fractal por el método de volumen, ya que el volumen gráfico no varió en una relación de ley de potencia con la distancia. Por lo tanto, se estableció que la red de puntos y meridianos de acupuntura no es un fractal. En comparación con otros sistemas complejos, la red compleja de puntos de acupuntura tiene una complejidad que es similar a la red metabólica de Caenorhabditis elegans y a la red del linaje de células embrionarias, aunque menor que otras redes biológicas.
Acupoints and meridians are known to form a complex network that includes the so-called microsystems, something that signals the presence of the self-similar fractal property, but whether the network is a fractal or not remains unknown. The fractal dimension of the acupoints and meridians complex network is determined by means of two independent methods: the first estimates the fractal dimension by means of the box counting and radius mass algorithms, the second performs a straightforward calculation of the dimension from applying the volume definition of fractal dimension to the graph. The estimated fractal dimension varied between 1.28 and 1.91, with correlation ratios of 0.999 in all cases. It was not possible to calculate the fractal dimension by the volume method since the graph volume did not vary in a power law relation to the distance. Therefore it is established that the acupoints and meridians network is not a fractal one. In comparison to other complex systems, the acupoints complex network has a complexity that is similar to the Caenorhabditis elegans metabolic one and to the embryonic cell lineage network, although lower than other biological networks.
La acupuntura y la totalidad de las llamadas medicinas tradicionales asiáticas han sido generalmente consideradas como no científicas o una mera curiosidad étnica por la comunidad científica. Esta investigación es parte de un proyecto que tiene como objetivo la integración de los principios y conceptos de la medicina moderna y la tradicional mediante la aplicación de la investigación de la red compleja al modelo fisiológico Jing-Luo de la medicina tradicional asiática. En la visión tradicional, el hombre es un ser originado desde el cosmos, y penetrado por varios sistemas de Qi que viajan a través de los meridianos o canales (Jing-Luo) y emergen en los puntos de acupuntura de la superficie. Este sistema de circulación de Qi asegura y apoya todas las funciones vitales. El primero se asemeja notablemente al concepto moderno de la red y, como se ha demostrado, los puntos de acupuntura y los meridianos de hecho conforman una red compleja que muestra ambas propiedades: “mundo pequeño” y “libre de escala”1.
Después de considerar lo anterior, surge una pregunta: ¿cuán compleja es la red de los puntos y los meridianos de acupuntura en comparación con otras redes biológicas o humanas ya conocidas?
La complejidad de una red dada se determina por su dimensión fractal2, y este artículo trata sobre la determinación de la dimensión fractal de la red de puntos y meridianos de acupuntura. La dimensión fractal de la red de puntos y meridianos de acupuntura se puede determinar porque esta se puede representar en el plano como una colección de nodos (puntos de acupuntura, órganos) y aristas (trazado de los meridianos), tal como el resto de las redes, en lo que se llama un gráfico. Como ya se ha mencionado, la propiedad libre de escala de los puntos de acupuntura y de la red de meridianos no garantiza que la red sea una estructura fractal; las redes libres de escala pueden ser autosimilares, aunque no fractales1,3. También la red puede tener una dimensión fractal y no ser una red con estructura fractal en absoluto. La presencia de la llamada acupuntura de “microsistemas”, que representa todo el organismo en un área reducida de la superficie del cuerpo, ciertamente sugiere que está presente la propiedad atribuida a los fractales llamada “autosimilitud”.
Independientemente de si se consideran o no los planteamientos de la medicina tradicional asiática como no científicos, varias otras preguntas pueden surgir. Una que resulta de suma importancia es la siguiente: ¿Cómo puede ser posible que los antiguos chinos hayan elaborado un modelo de red compleja de la fisiología humana al menos en el año 100 antes de nuestra era, la fecha aceptada para el clásico de la medicina china Nei Jing?
Los fractales son formas geométricas con varias propiedades interesantes —entre ellas, la autosimilitud en varias escalas de medida— y que tienen una dimensión fractal o fraccionada. Una diferencia notable con formas no fractales es que una figura geométrica en el plano euclidiano tiene una dimensión topológica de número entero igual a 2, pero los fractales tienen una dimensión fraccionaria tal como la curva del copo de nieve, que tiene una dimensión de 1,264.
MétodosSe utilizó la red de puntos y meridianos de acupuntura previamente creada con 718 nodos y 1.107 aristas1. En esta estructura, los nodos se corresponden con los puntos de acupuntura, los órganos Zang-Fu y algunos puntos de bifurcación necesarios para asegurar una representación lo más exacta posible; también se incluyen las aristas que corresponden a las vías internas y externas (superficie).
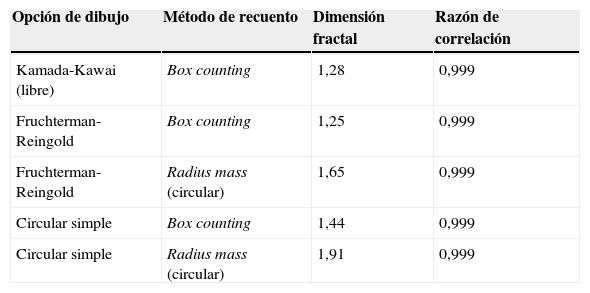
La dimensión fractal de una red se puede hallar fundamentalmente de dos maneras. El primer procedimiento consiste en dibujar la gráfica de la red en el plano y a continuación estimar la dimensión fractal en un segundo paso por medio de un software que la obtiene a partir del gráfico. Con el segundo método se calcula directamente la dimensión fractal a partir de la lista de conexiones sin tener que representarla gráficamente. Aquí se utilizaron ambos métodos debido a que el segundo permite determinar si la red es un fractal o no. La gráfica de la red se obtuvo mediante el software gratuito de análisis de redes Pajek5. Se dibujó con las opciones “circular simple”, “Fruchterman-Reingold” y “Kamada-Kawai” y se guardó en formato BMP. La estimación de la dimensión fractal se realizó en un segundo paso mediante la aplicación del software libre Fractalyse6 a cada una de las imágenes obtenidas anteriormente, seleccionando las opciones: recuento por cajas (box counting) y radio de masa (radius mass). En la tabla 1 se muestran las dimensiones fractales y los resultados de la razón de correlación.
Estimación de la dimensión fractal de la red de puntos y meridianos de acupuntura
| Opción de dibujo | Método de recuento | Dimensión fractal | Razón de correlación |
|---|---|---|---|
| Kamada-Kawai (libre) | Box counting | 1,28 | 0,999 |
| Fruchterman-Reingold | Box counting | 1,25 | 0,999 |
| Fruchterman-Reingold | Radius mass (circular) | 1,65 | 0,999 |
| Circular simple | Box counting | 1,44 | 0,999 |
| Circular simple | Radius mass (circular) | 1,91 | 0,999 |
El segundo método utiliza la conceptualización desarrollada por Shanker7, donde la dimensión fractal se calcula directamente a partir de los datos de conexión de la red utilizando la definición de volumen para la dimensión fractal, siendo esta la más apropiada para evaluaciones numéricas8. La definición de volumen indica que la dimensión fractal es el exponente de escala de la variación del volumen de red con la distancia8. En el presente trabajo, la dimensión fractal se calculó por medio de una secuencia de comandos codificados en lenguaje M mediante el software Matlab R2008. A partir de la matriz de adyacencia del gráfico de la red de puntos y meridianos de acupuntura, el código (script) devuelve los valores de volumen por cada unidad de aumento en la distancia (el número de caminos más cortos en el gráfico). Lo anterior permite realizar una representación gráfica de la variación de volumen frente a distancia, y evaluar si el volumen varía en una ley de potencia con respecto a la distancia; si esto es así, entonces la red es fractal. Se provee el código (script) en idioma M y la matriz de adyacencia de la red.
ResultadosLa dimensión fractal según se estimó por medio del software Fractalyse utilizando las opciones box counting y radius mass; estuvo entre 1,25 y 1,91, dependiendo del algoritmo de dibujo y la calidad de la estimación. Esta última, medida por la razón de correlación, fue de 0,999 en todos los casos (tabla 1).
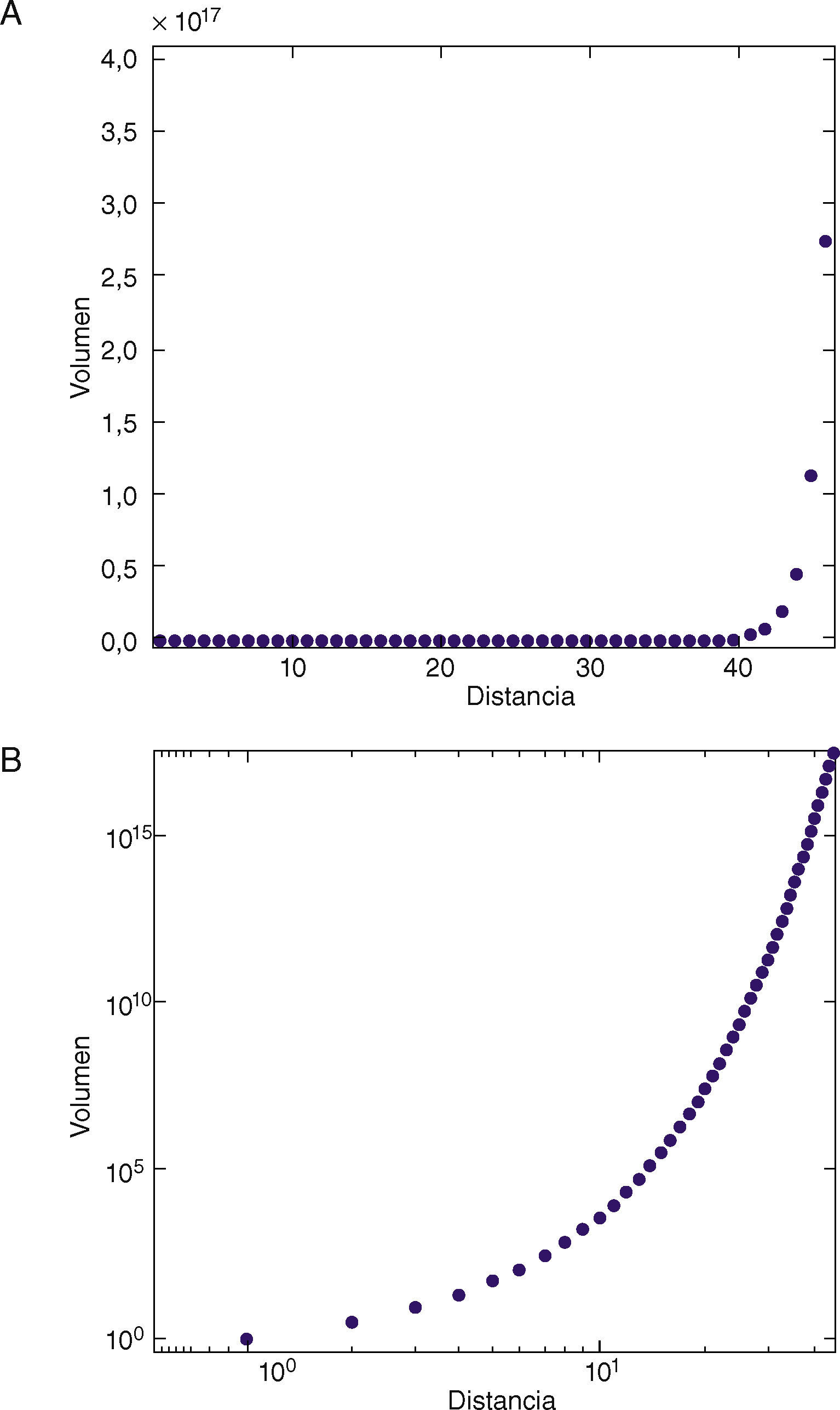
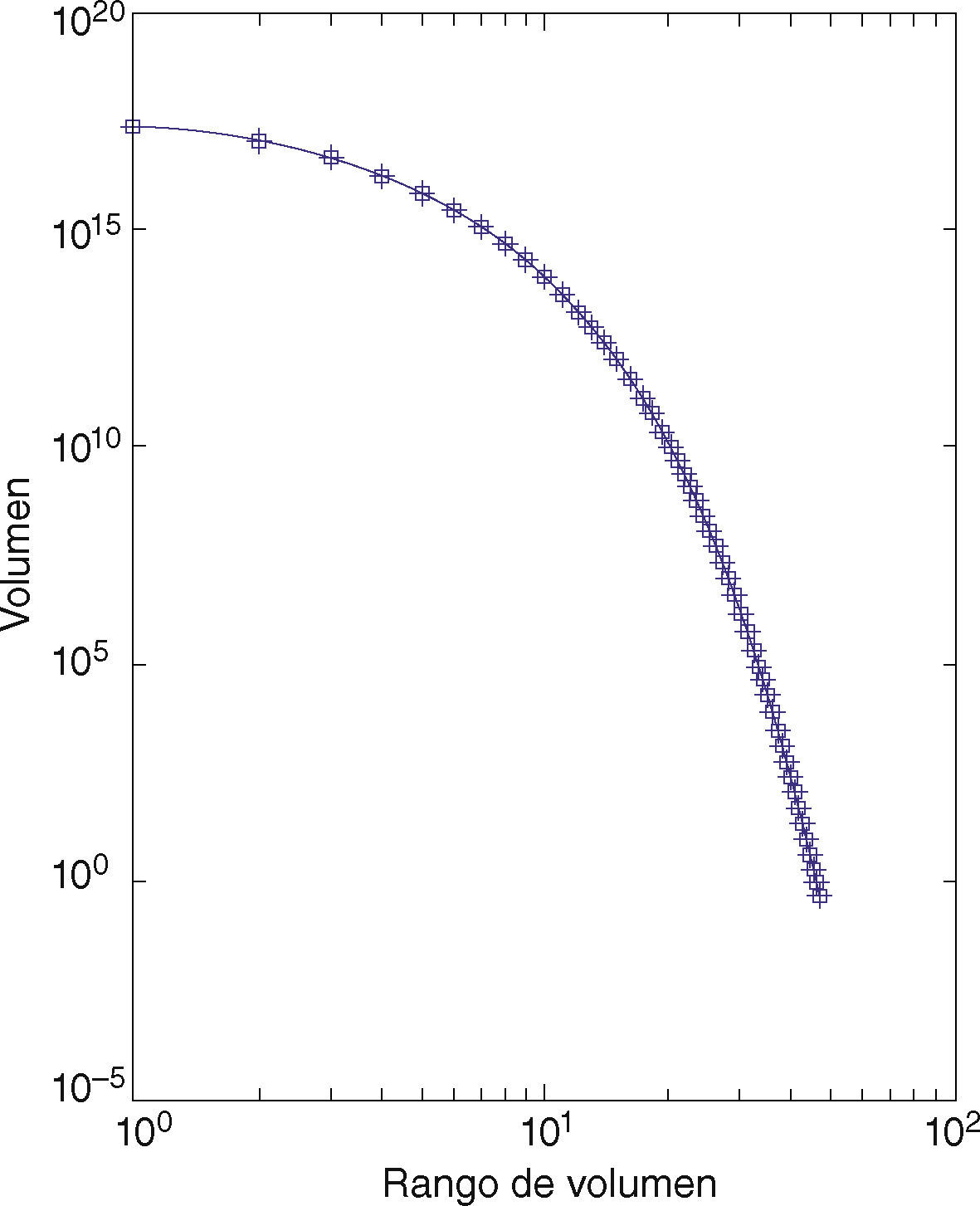
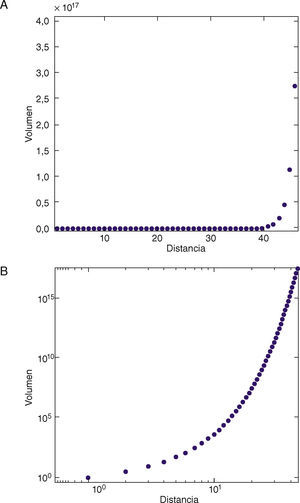
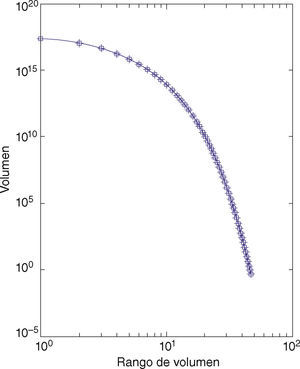
Con este trabajo también se pretende determinar si la red de puntos y meridianos de acupuntura es un fractal o no. Se obtuvo el gráfico volumen frente a distancia y, como se puede apreciar en la figura 1A, el volumen aumenta aparentemente en una relación de ley de potencia a la distancia; pero la respuesta se encuentra precisamente en el gráfico de escala logarítmica doble (fig. 1B). En este debería aparecer como una línea recta, pero no lo hace. La conclusión es que la variación del volumen con la distancia no está libre de escala y, por tanto, la red no se parece a sí misma a diferentes distancias o radios, ergo la red de puntos y meridianos de acupuntura no es un fractal. Tampoco el gráfico de rango-volumen muestra la recta característica de las distribuciones libres de escala (fig. 2). Esta es la razón por la que no se puede calcular también la dimensión fractal por el método del volumen para esta red, no hay una sola escala para la distribución de volumen con la distancia.
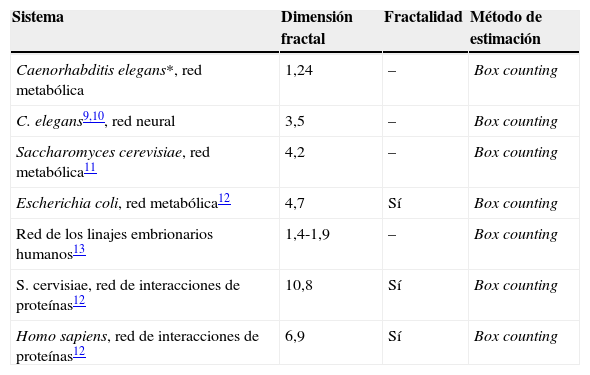
Se presentaron 2 métodos para determinar la dimensión fractal de la red de puntos y meridianos de acupuntura: el primero lleva a cabo la estimación de la dimensión fractal y el segundo un cálculo sencillo. Sin embargo, este segundo no se pudo completar debido a que el volumen no varía con la distancia en una ley de potencia. Como se puede apreciar de la tabla 1, la dimensión fractal así obtenida también varía de acuerdo con el algoritmo gráfico elegido para dibujar la red. La dimensión fractal se ha estimado para varias redes biológicas complejas (tabla 2). En la tabla 2 se puede observar que la red de puntos y meridianos de acupuntura es de una complejidad comparable a la red metabólica de Caenorhabditis elegans, y a la red celular de los linajes embrionarios humanos, y de una complejidad inferior a la red neural de C. elegans: un hecho que podría estar en relación con la cantidad más baja de aristas en la red de puntos de acupuntura en relación con estas otras.
La dimensión fractal de varias redes biológicas complejas
| Sistema | Dimensión fractal | Fractalidad | Método de estimación |
|---|---|---|---|
| Caenorhabditis elegans*, red metabólica | 1,24 | – | Box counting |
| C. elegans9,10, red neural | 3,5 | – | Box counting |
| Saccharomyces cerevisiae, red metabólica11 | 4,2 | – | Box counting |
| Escherichia coli, red metabólica12 | 4,7 | Sí | Box counting |
| Red de los linajes embrionarios humanos13 | 1,4-1,9 | – | Box counting |
| S. cervisiae, red de interacciones de proteínas12 | 10,8 | Sí | Box counting |
| Homo sapiens, red de interacciones de proteínas12 | 6,9 | Sí | Box counting |
*Calculada por medio del software Fractalyse.
El segundo objetivo de este trabajo fue determinar si la red de puntos de acupuntura tiene un carácter fractal, como se muestra en el gráfico de la figura 1A se puede apreciar que aparentemente el volumen aumenta en una ley de potencia con respecto a la distancia a la que se calculó; pero si se observa este mismo gráfico en una escala logarítmica doble, se puede ver que este ajuste no es tan bueno como parecía; lo que niega que haya una ley de potencia en la distribución volumen frente a distancia y, en consecuencia, la red no es fractal. Lo anterior no se contradice con el hecho de que estructuras autosimilares como los microsistemas de acupuntura estén presentes en el modelo más general de la circulación del Qi: una red no fractal puede ser autosimilar3. También el carácter no fractal de la red de puntos y meridianos de acupuntura se puede deducir de una propiedad denominada concordancia de redes (assortativity)14. Se ha establecido que las redes en las que los nodos ricos en conexiones tienden a enlazar preferentemente con otros nodos ricos no son fractales y esto es lo que ocurre precisamente con la red de puntos de acupuntura y meridianos: esta red tiene un coeficiente positivo de concordancia1. Estos argumentos anteriores empiezan a tener sentido para el conocedor del sistema Jing-Luo. Si se observa cuidadosamente los meridianos y puntos de acupuntura se puede notar que la estructura de conexión de los meridianos es diferente de la de los órganos. Los meridianos tienden a conectarse en una secuencia de puntos de acupuntura que tienen una entrada y una salida, mientras que los Zanf-Fu tienen múltiples entradas y salidas. Un ejemplo conocido de red compleja no biológica y no fractal es internet a nivel del sistema autónomo. Asimismo, hay otros tipos de redes libres de escala no fractales más autosimilares3.
ConclusionesLa red de acupuntura y meridianos tiene una complejidad comparable a la metabólica de C. elegans y a la red de los linajes celulares embrionarios humanos, pero significativamente más bajo que otras redes biológicas.
La red de puntos y meridianos de acupuntura no es un fractal.
El carácter autosimilar de la red queda por estudiar más en detalle.
Conflicto de interesesEl autor declara no tener ningún conflicto de intereses.