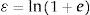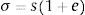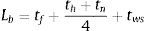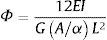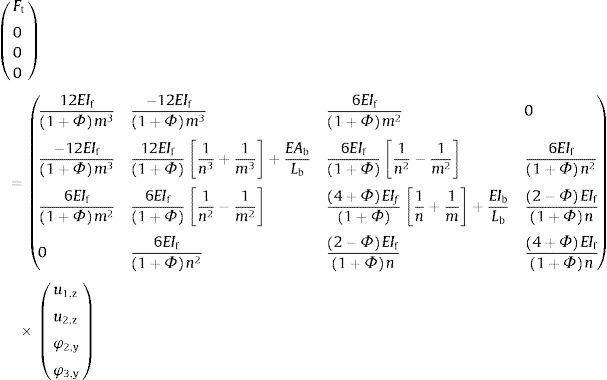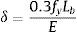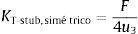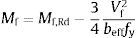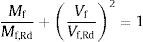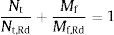Este artículo presenta el análisis mediante técnicas numéricas y experimentales de componentes T-equivalente asimétricas, refiriéndose ésta al posicionamiento de los pernos respecto al alma del perfil. El objetivo principal de realizar este análisis es el de evaluar la influencia de dicha asimetría en la rigidez y sobre todo en la resistencia final, y compararlas a las de componentes simétricas. Se definen dos modelos numéricos para analizar el comportamiento: uno matricial de barras rígidas y otro con elementos finitos sólidos. Los resultados obtenidos con ambos modelos se comparan con ensayos experimentales, tanto para para una componente simétrica como una asimétrica, obteniéndose un error menor del 10 % para el cálculo de la rigidez e inferior al 20% para la resistencia final. Se comprueba que, como cabía esperar, la asimetría repercute en una redistribución de la carga en los pernos, produciéndose un fallo prematuro del conjunto con respecto a la configuración simétrica. Por tanto, puede deducirse que los análisis numéricos realizados son capaces de cuantificar dicha redistribución.
The analysis of asymmetric T-stub components by the position of bolts respect to the web, has been carried out using numerical and experimental approaches. The main objective of this analysis is to evaluate the influence of such asymmetry on the stiffness and strength. A matrix frame model with beam-column elements and rigid connections has been developed as well as with solid elements. Results obtained with these numerical models have been compared with those obtained from experimental tests carried out, for both symmetrical and asymmetrical components, obtaining errors below 10% for stiffness and lower than 20% for the final strength. It was found, as expected, that the asymmetry leads to a redistribution of the load on the bolts, causing premature failure of the assembly. Therefore the numerical analysis performed is capable of quantifying such redistribution.
Los Eurocódigos estructurales [1] establecen el método de las componentes como una metodología general para el análisis de la unión entre diferentes miembros que constituyen una estructura metálica, sea cuales sean las características de las partes que conforman dicha unión. Según esta metodología la conexión es desglosada en partes más simples, cuyo comportamiento es analizado separadamente. Las propiedades de la conexión completa, en términos de resistencia y rigidez, se determinan ensamblándolas a través de un modelo analítico equivalente de resortes en serie y en paralelo.
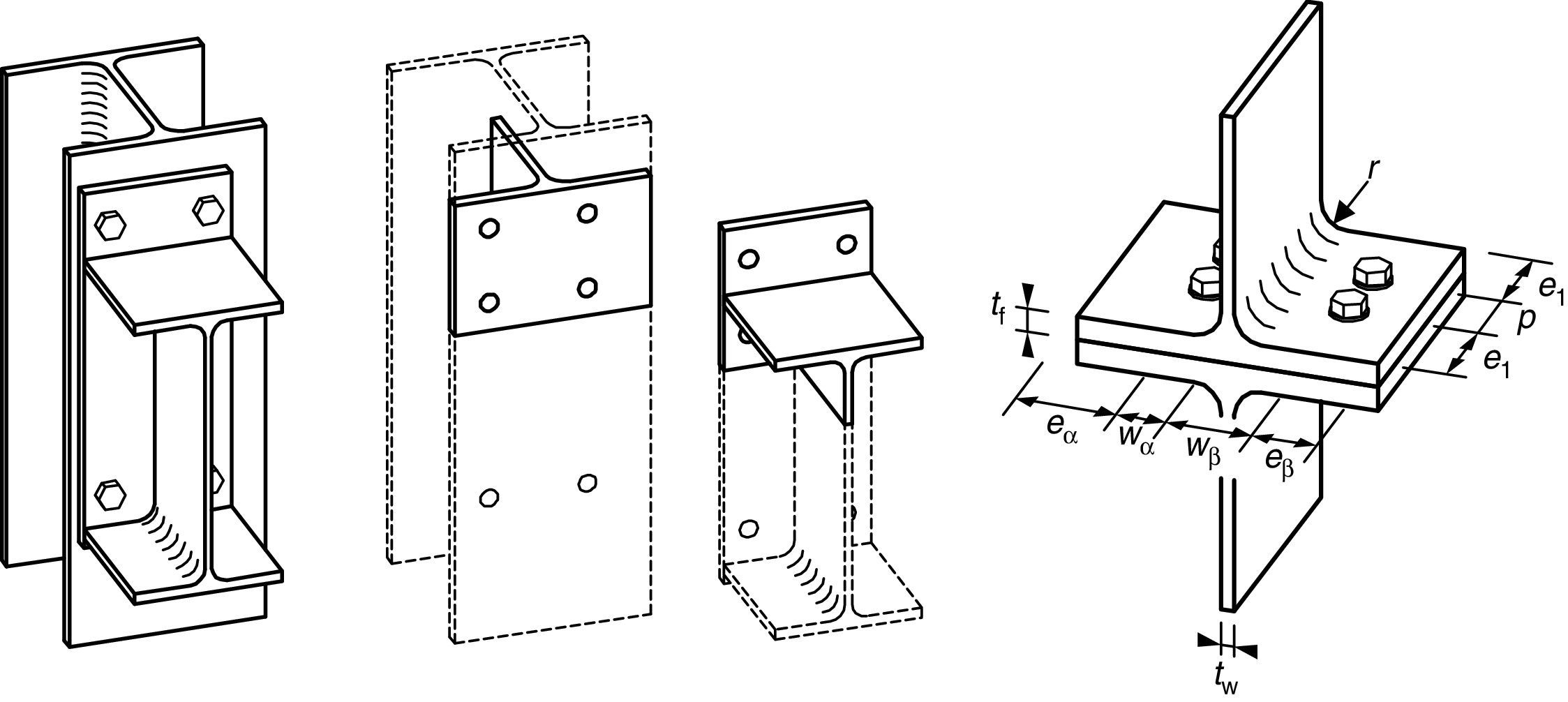
En el caso de conexiones rígidas o semirrígidas con capacidad de transmitir giro, el comportamiento de la zona traccionada de la conexión, que se corresponde con la flexión de la chapa de tope, puede asimilarse mediante la componente T-equivalente («T-stub»). Ésta consiste en dos perfiles en T, laminados o soldados, conectados mediante pernos a través de las alas y sometidos a una fuerza de tracción en las almas. El comportamiento de esta componente, en términos de resistencia, rigidez y ductilidad, dependerá principalmente de las características mecánicas de los materiales y de las propiedades geométricas de los perfiles y de los pernos. Así pues se pueden distinguir tres modos de fallo diferentes: el correspondiente a la plastificación del ala del perfil, conocido también como flexible (modo 1); el modo semirrígido que es considerado por el colapso simultáneo del ala del perfil y de los pernos (modo 2) y finalmente el producido por el fallo de los pernos, definido como rígido (modo 3). El que uno u otro modo de fallo tenga lugar dependerá básicamente de la relación entre la resistencia a flexión del ala del perfil y la resistencia a tracción de los pernos.
La necesidad de acometer el estudio particular de componentes T-equivalente asimétricas surge de la necesidad de tener que desarrollar en determinados diseños conexiones de forma que la posición de los pernos no se encuentra centrada respecto al alma del perfil (ver fig. 1), atendiendo generalmente a un criterio constructivo.
1.1Estado de la investigaciónEl estudio del comportamiento de un elemento estructural, como es el caso de las componentes asociadas a una conexión, puede abordarse a través de tres diferentes metodologías. La analítica, por medio de expresiones teóricas según modelos de comportamiento. La experimental, costosa y difícil de implementar. Y la numérica donde la más extendida es la de los elementos finitos, y que tienen la ventaja de poder considerar una gran cantidad de fenómenos físicos (tanto lineales como no lineales) y de estudiar diferentes geometrías a un costo relativamente bajo.
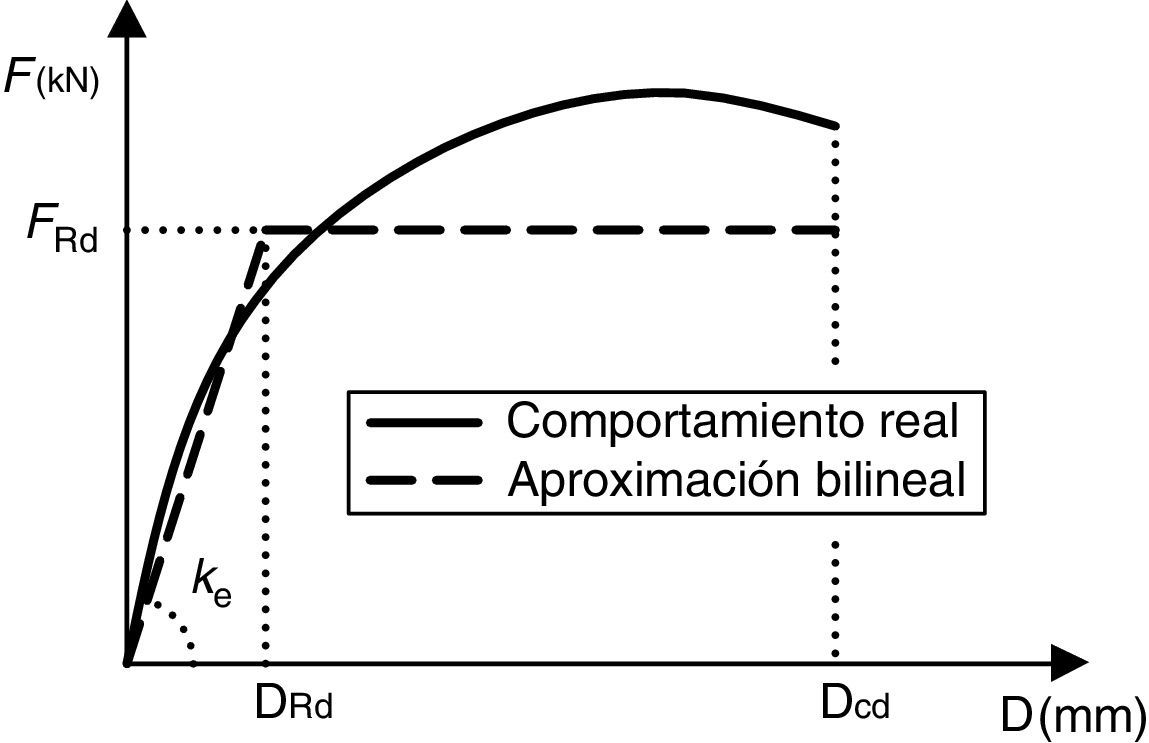
Los parámetros principales a determinar en el estudio de una conexión o una componente son tres (fig. 2):
- 1.
Rigidez inicial ke: establece la rigidez de la componente en régimen elástico lineal (es decir, para esfuerzos inferiores al esfuerzo de fluencia del material considerado).
- 2.
Fuerza máxima resistente FRd: fuerza máxima admisible que puede aplicarse en el elemento,
- 3.
Ductilidad Δcd-ΔRd: capacidad de deformación máxima en condiciones de plastificación, desde el inicio de la fluencia hasta la rotura de la componente.
El estudio de componentes T-equivalente ha sido abordado por numerosos autores; caracterizar su comportamiento permite evaluar las propiedades de conexiones empernadas con chapa extendida, ampliamente utilizadas.
Douty y McGuire [2] propusieron un modelo clásico de viga tipo Navier/Bernoulli para evaluar la resistencia de las componentes. Asimilaron la componente al comportamiento de una viga sometida a una carga puntual intermedia, y simuló las fuerzas de contacto como unos apoyos simples en los extremos. Respecto al modelamiento con elementos finitos, R.S. Nair et al.[3] desarrollaron un modelo elástico-plástico incremental, y realizaron un análisis con elementos en dos dimensiones. Considerando la doble simetría, desarrollaron solamente un cuarto de modelo apoyado sobre una base rígida; el ala del perfil se modelizó con elementos superficiales y el perno como un conjunto de resortes en paralelo de igual rigidez. El fallo de la T-equivalente podía producirse en dos circunstancias: cuando la deformación media de los resortes que simulan al perno superaba la máxima obtenida por el ensayo al material de los pernos, o cuando se desarrolla un mecanismo plástico en el ala del perfil. Más tarde Yee y Melchers [4] consideraron un modelo similar para obtener el desplazamiento máximo, considerando las fuerzas de palanca originadas por el contacto entre las alas de los perfiles y estableciendo condiciones de compatibilidad de deformaciones en los pernos. Fue Agerskov [5] quien propuso considerar la reducción de la resistencia debido al esfuerzo cortante, y definió una nueva longitud equivalente del perno para evaluar la rigidez, basada en la asimetría de éste respecto al plano de contacto entre alas de los perfiles. Zoetmeijer [6] definió una metodología para el análisis de la zona traccionada de conexiones viga-pilar y estableció los diferentes modos de fallo según el elemento en el que se produjera el colapso; también estableció las longitudes eficaces para el análisis resistente. Incluyó la consideración del ancho equivalente calculado según el patrón de plastificación, obteniendo resultados cotejados con ensayos experimentales. Con objeto de establecer una formulación fácil de implementar en normativa, Jaspart [7] sugirió una serie de simplificaciones, basadas en valores comúnmente adoptados y propuso una modificación de la fórmula de la rigidez basada en una redistribución de las fuerzas de palanca. Posteriormente Faella et al.[8] definieron una nueva formulación para evaluar la rigidez a través de los límites en modelos viga, considerando también el efecto del pretensado de los pernos, y definió un nuevo ancho equivalente no basado en el cálculo de la resistencia. A su vez Swanson [9] desarrolló un esquema de decisión para evaluar la curva fuerza-desplazamiento, y propuso una modificación de la posición del perno respecto al alma del perfil, cotejándola con los resultados experimentales del programa de ensayos desarrollado; adicionalmente formuló un modelo basado en sus ensayos experimentales mediante elementos sólidos. Girão [10] estableció un modelo analítico y de elementos finitos de componente T-equivalente que recoge todas las consideraciones definidas por autores previamente.
Recientemente Loureiro [11] y Reinosa [12] definieron un modelo matricial con elementos tipo barra para analizar la rigidez en componentes T-equivalente con pernos pretensados y no pretensados respectivamente. El parámetro correspondiente al ancho equivalente del ala fue calibrado mediante simulaciones numéricas, con elementos finitos superficiales, ajustando los parámetros con los resultados experimentales publicados por Jaspart [7] y Faella et al.[8].
2Programa experimental2.1Descripción de los ensayos de laboratorioPara abordar la calibración del modelo analítico, se desarrolló un programa de ensayos realizados en el Departamento de Ingeniería Civil de la Universidade de Coimbra (Portugal). Estos ensayos consistieron en un total de 2 probetas obtenidas de perfiles laminados en caliente HEB400 de acero S275 y pernos pavonados de 20mm de diámetro y calidad 8.8. Se ensayaron configuraciones tanto simétrica como asimétrica. Las características geométricas de las probetas (tabla 1) fueron estimadas previamente para que se produjera la rotura principalmente en el modo 3 de colapso por plastificación del perno, ya que una de las principales características que se pretendía observar era la asimetría en la distribución de las cargas en los pernos y el fallo prematuro originado por dicha asimetría.
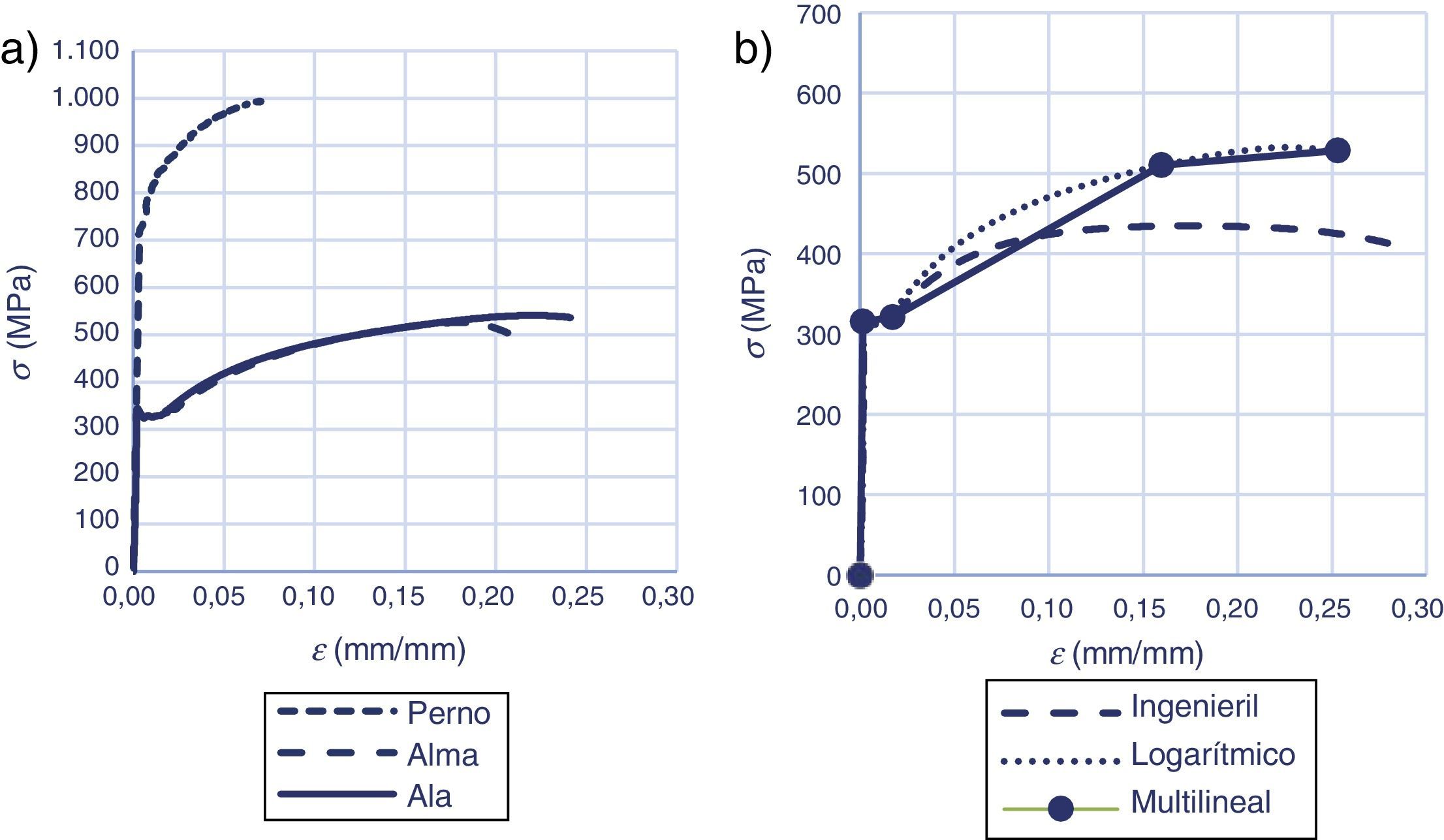
Para la caracterización de los materiales, se obtuvieron muestras en el sentido longitudinal en varias zonas del perfil, con objeto de considerar la diferencia de propiedades como consecuencia de la laminación del perfil. Se realizaron ensayos de tracción del acero del alma y del ala de los perfiles de los que fueron fabricadas las probetas, así como de los pernos, según norma Rilem [13]. De las curvas tensión-deformación (Fig. 3a y 3b) se calcularon los puntos más representativos, obteniendo un diagrama multilineal de cada material.
Los datos registrados experimentalmente se corresponden con los relativos a la curva tensión-deformación nominal. Los referentes a las propiedades reales del material se obtienen considerando la reducción de sección en la zona de estricción, debiéndose por tanto multiplicar los primeros por los coeficientes definidos en las ecuaciones (1) y (2) respectivamente:
donde e es la deformación registrada directamente por la máquina de ensayos, s es la tensión calculada con el área inicial de la probeta (obteniendo la conocida curva tensión-deformación ingenieril del material), y ¿ y σ son la deformación unitaria y la tensión real del material contemplando la reducción de sección por efecto Poisson.3Modelo teórico numéricoBasado en las propuestas de A. Louireiro [11] y de J.M. Reinosa [12], se han construido dos modelos matriciales, constituidos por elementos barra con conexiones rígidas. El ala del perfil es considerada como una barra de sección rectangular de espesor igual al espesor del ala tf y ancho igual al ancho del ala. La longitud total considerada en el ala es de 2m+2n, siendo m la distancia equivalente del perno hasta el alma y n la distancia equivalente del perno al punto de aplicación de la resultante de presiones de contacto entre las dos alas, igual consideración que definido en [1]. El perno es considerado como una barra de longitud total igual a la longitud efectiva según la ecuación (3) y de sección circular según el diámetro efectivo.
donde Lb es la longitud equivalente del perno, tf es el espesor del ala del perfil, th es la longitud de la cabeza del perno, tn es la altura de la tuerca y tws es el espesor de las arandelas.Considerando las deformaciones producidas por cortante, el comportamiento del material como lineal y los efectos de esfuerzos axiles y flectores desacoplados, la matriz de rigidez elemental en coordenadas locales puede expresarse como la ecuación (4):
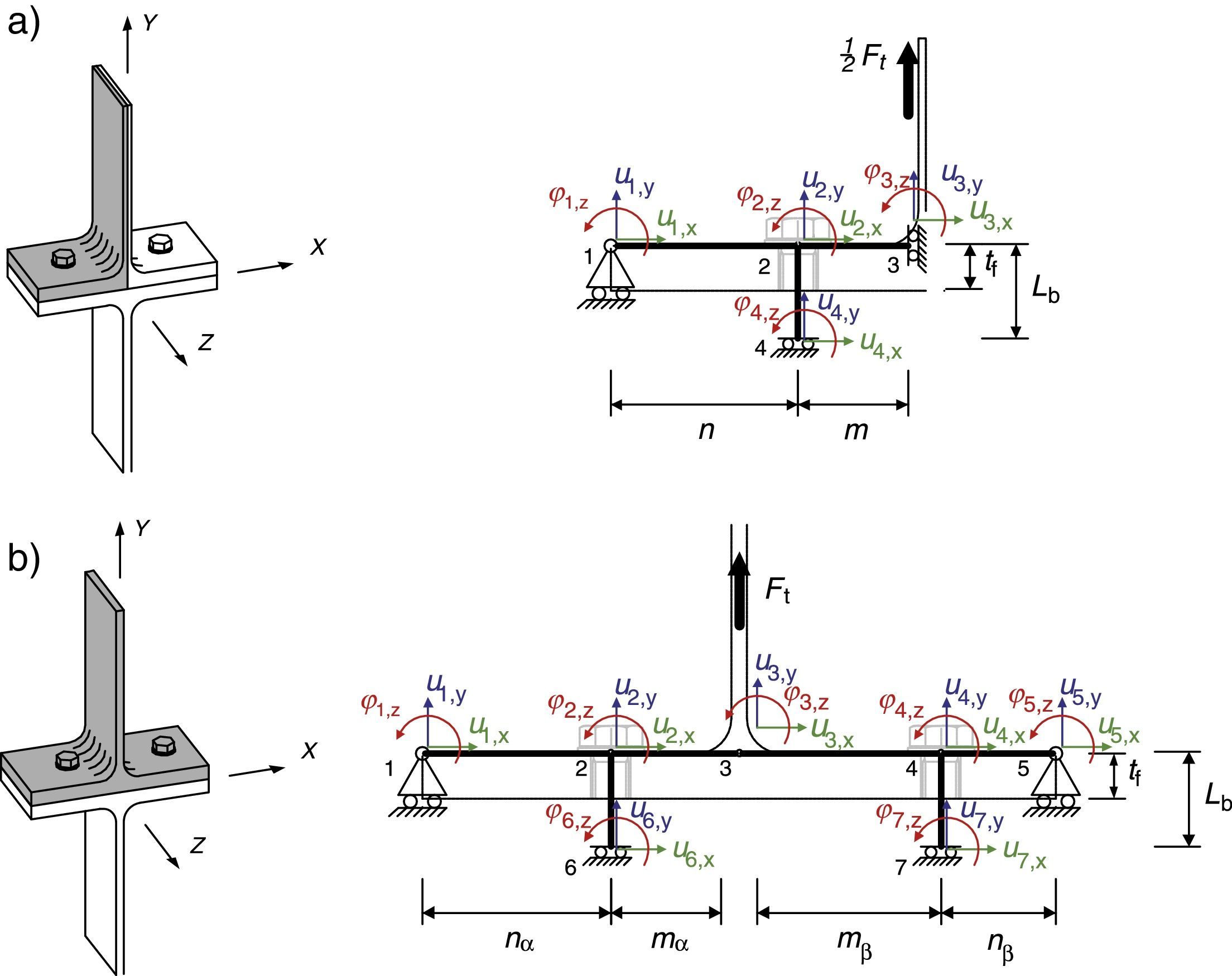
donde kie es la matriz de rigidez del elemento i en coordenadas locales, Ei su módulo de elasticidad, Li la longitud, Ai es el área de la sección, Ii es el momento de inercia de la sección, E es el módulo de Young del material, G es el módulo transversal del material, α es el factor de forma de la sección y Φ es el coeficiente que considera la deformación por esfuerzo cortante, evaluado según la ecuación (5).El modelo simétrico puede simplificarse a un cuarto del real debido a la simetría que existe respecto a los planos XY e YZ (fig. 4a), quedando un modelo de 4 nodos y 3 elementos. En el caso asimétrico (fig. 4b) sólo se puede establecer la condición de asimetría respecto al plano YZ, por lo que el modelo definitivo de análisis consta de 7 nodos y 6 barras.
Referente a las condiciones de contorno, éstas son compatibles con los efectos y las simetrías consideradas. El efecto palanca es reproducido en el modelo como una restricción del movimiento en la dirección Y, ubicada en el extremo del ala. La simetría en el perno es reproducida mediante una condición que restringe el desplazamiento longitudinal del perno y el giro, pero no así el transversal en la dirección X. La condición de simetría respecto al plano YZ correspondiente a las componentes simétricas ha sido modelizada de forma análoga a la del perno.
donde If es la inercia del ala del perfil y Ab e Ib son el área y la inercia del perno respectivamente, asociadas al diámetro equivalente y nα, mα, nβ, mβ, definen la posición de los pernos en el modelo simétrico y en el asimétrico respectivamente.Se ha programado un modelo no lineal que considera la posibilidad de que no se desarrollen las fuerzas de palanca mencionadas previamente. Para los modos de fallo tipo 3, la rigidez del ala del perfil es suficientemente elevada como para producir que la reacción en el apoyo extremos sea negativa; este efecto no es posible, por lo que en caso de existir dicha condición se recalcula el sistemas eliminando dicho apoyo extremo.
Se empleó el software Wolfram Mathematica [14] para la resolución de los sistemas de ecuaciones resultantes obtenidos con las matrices de rigidez dadas en las ecuaciones (6) y (7).
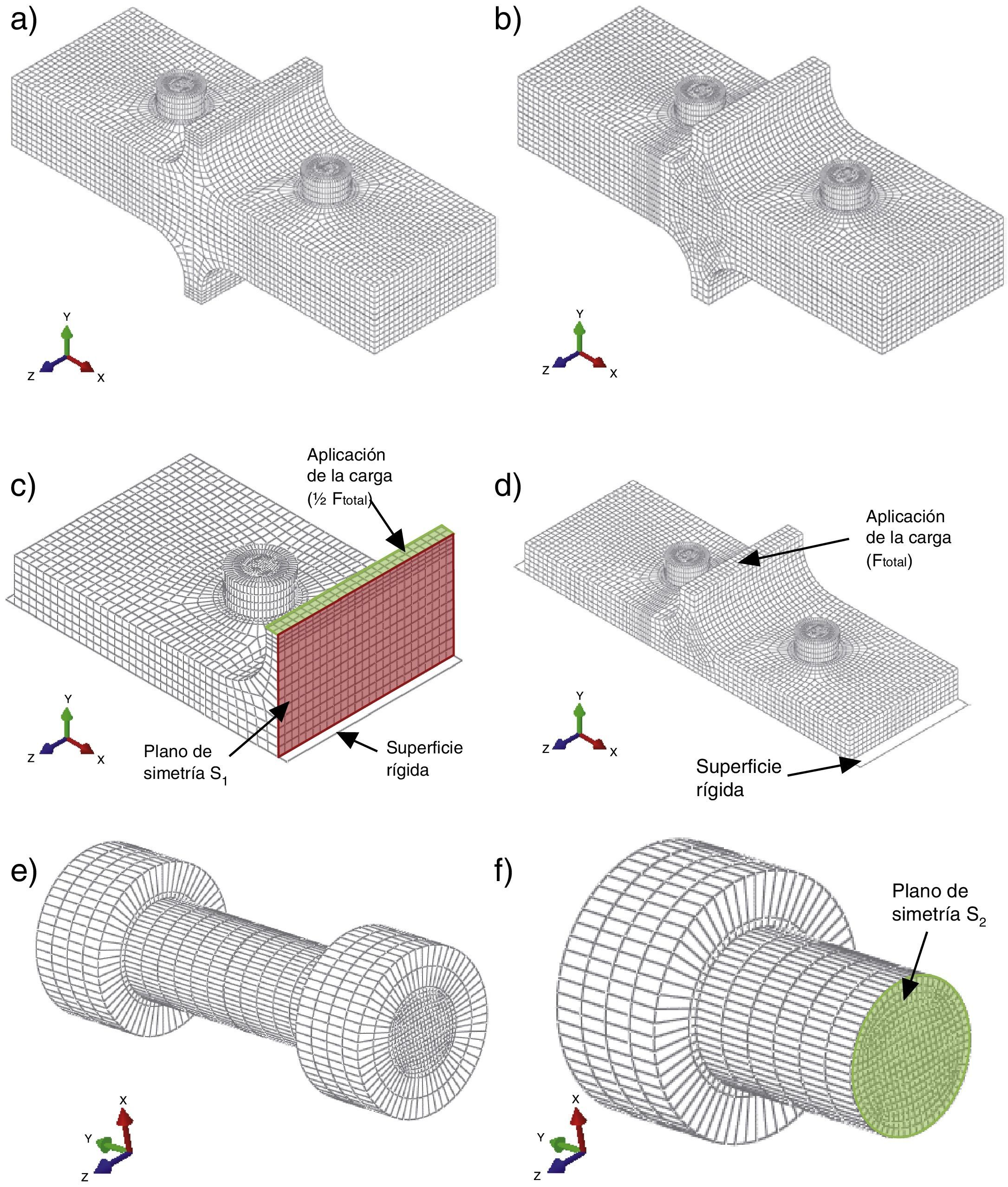
4Modelo de elementos finitosEl análisis mediante elementos finitos ha sido abordado con el software comercial Abaqus® [15,16]. Se ha considerado el efecto de la no linealidad geométrica y del material, así como la interacción entre los elementos, realizando el análisis hasta la rotura. En ambos casos se considera la simetría respecto al plano de contacto entre las alas de los perfiles T en contacto (Fig. 5a y Fig. 5b). En el espécimen simétrico se pueden identificar dos condiciones de simetría (fig. 5c): una primera respecto al plano medio del alma y la segunda respecto a la cara inferior del ala, por lo que solamente es necesario modelar un cuarto de la geometría. El espécimen del caso asimétrico sólo tiene un plano de simetría y es necesario modelar la mitad de la geometría (fig. 5d). Para implementar en el modelo estas condiciones, en la primera se considera la cara modelada contenida en el plano S1 con el desplazamiento perpendicular a dicho plano restringido. La segunda condición se implementa mediante la incorporación de la superficie rígida, sobre la que hay definido un contacto de la cara inferior del ala del perfil. La consideración de simetría en el perno (fig. 5e) se consigue restringiéndose el desplazamiento vertical en la zona contenida en el plano S2 (fig. 5f).
Para considerar la condición de simetría es preciso definir una superficie rígida sobre la que apoye el ala del perfil (posicionado en el plano XZ). Adicionalmente es necesario establecer las condiciones de contorno correspondientes en el perno, que se corresponde con restricción del desplazamiento vertical (dirección Y).
Para el mallado del elemento finito se han utilizado elementos hexaédricos C3D8R de la librería de Abaqus, que se corresponden con sólidos tridimensionales de ocho nodos con integración reducida incompatibles y control de bloqueo por cortante. El modelo simétrico consta de 14161 nodos y 11356 elementos; el modelo asimétrico es mayor, al no disponer de la condición de asimetría respecto al alma como en el simétrico, siendo un total de 30447 nodos y 25068 elementos.
Referente a la preparación del modelo para el mallado automático, las partes fueron subdivididas convenientemente, con objeto de obtener una malla coherente y no distorsionada. Se utilizó un mallado con un tamaño de elemento aproximado de 4mm, distorsión máxima de 0.2 y ángulo máximo de las caras del nodo de 160°. En las zonas de contacto (perímetro de los agujeros y cabeza del perno) se contemplaron tamaños más pequeños con objeto de poder caracterizar correctamente este fenómeno.
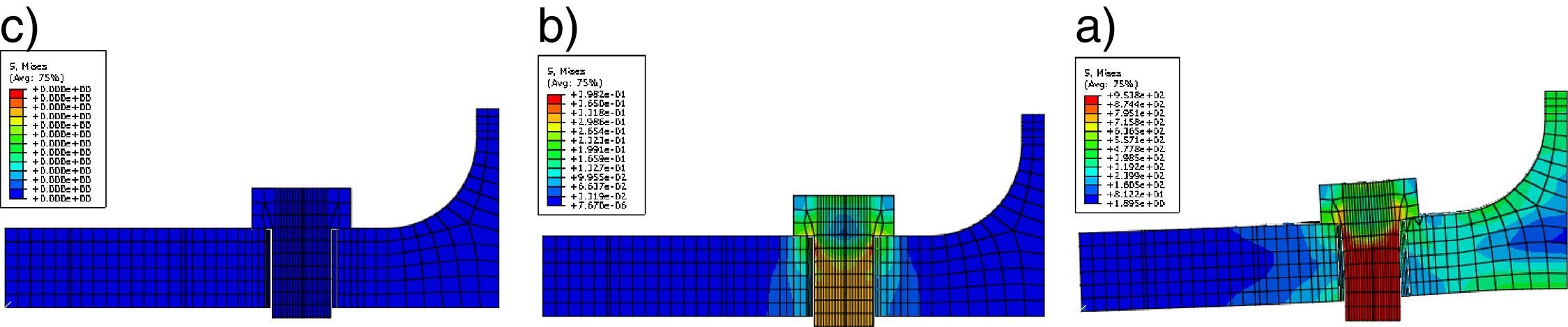
El efecto del pretensado de los pernos también fue considerado en los análisis. Éste se contempló en el modelo mediante un desplazamiento longitudinal impuesto en el vástago del perno, que origine tensiones iguales del 30% del límite de fluencia del material, valor con el que fueron apretados los pernos. Se han programado tres pasos principales de análisis. En el primero, en el que las partes del se definen las superficies de contacto, así como las condiciones de simetría a excepción de la correspondiente al perno (fig. 6a). El segundo paso se corresponde con la simulación del pretensado, desarrollado a través del desplazamiento del perno la distancia correspondiente: al existir una condición de contacto entre la parte inferior de la cabeza y la parte superior del ala del perfil, se produce la tracción en el perno como se aprecia en fig. 6b. El cálculo de la distancia de desplazamiento se efectúa según la ecuación:
donde fy es la tensión de fluencia del material del perno, Lb es la longitud equivalente del perno y E es el módulo de elasticidad del perno.Sustituyendo estos datos por los equivalentes del ensayo, se obtiene que el desplazamiento prescrito en la parte inferior del medio perno modelado es igual a 0,0312mm. En el tercer paso (fig. 6c) se incorpora la condición de contorno correspondiente a la simetría del perno y la aplicación de la carga en la superficie correspondiente al alma del perfil. Al tratarse de un análisis no lineal, el análisis se desarrolla incrementando la carga y evaluando las condiciones para cada paso de carga. Se consideró un contacto tangencial isótropo con un coeficiente de rozamiento de 0.3, y un contacto normal sin cohesión con control mediante el método del penalti [7].
La calibración del modelo de elementos finitos se llevó a cabo mediante comparación con los resultados experimentales. El primer estudio desarrollado en la calibración es la convergencia de malla, donde se trata de encontrar la malla que minimice el número de elementos consiguiendo un suficiente grado de aproximación, con objeto de reducir en lo posible el tiempo de cómputo teniendo siempre y cuando los resultados obtenidos sean fiables. Se desarrollaron varios análisis con diferentes tamaños de malla y diferentes condiciones. Finalmente se optó por emplear un tamaño máximo del elemento de 4mm, debiendo ser el mínimo número de elementos en el espesor del ala del perfil de 4 (Bursi & Jaspart [7]).
Como criterio de parada se adoptó lo establecido previamente por otros autores [17], se considera un criterio de parada simplificado. Dicho criterio consiste en establecer el fin del cálculo cuando se alcanza la deformación correspondiente a la resistencia a la rotura en alguno de los elementos, en el perfil o en los pernos, comparando este valor máximo con la deformación principal media máxima en cada nodo, obtenida del cálculo de elementos finitos.
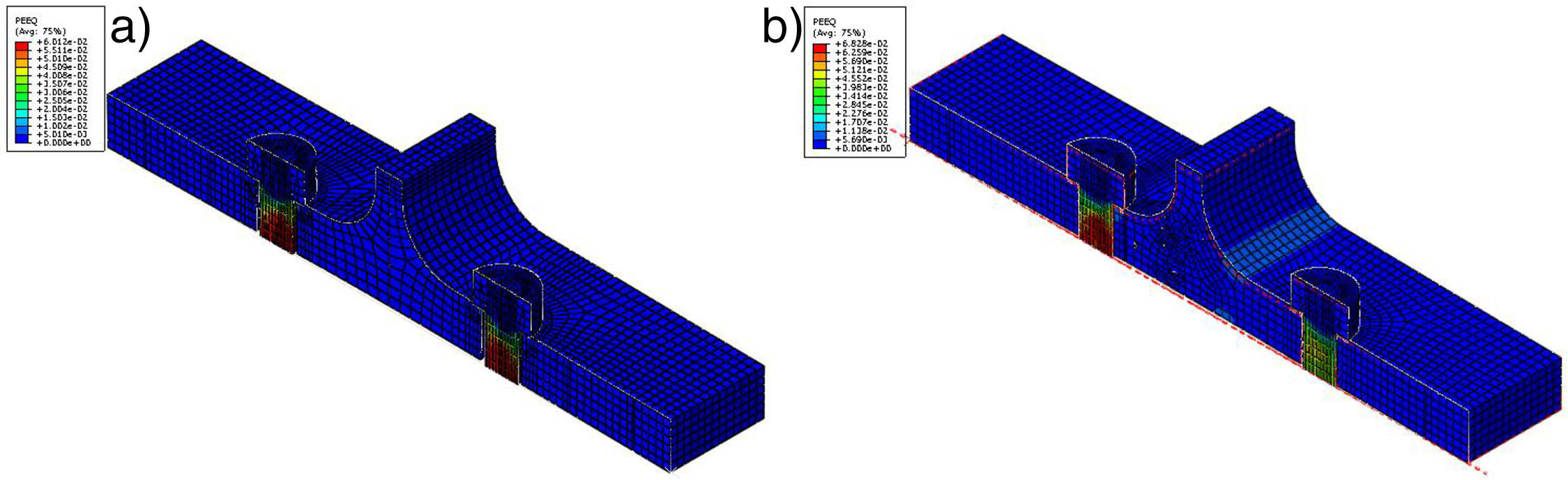
Como puede observarse del modelo asimétrico (fig. 7b), tal y como cabría esperar, el perno que se encuentra más próximo al alma del perfil es el que se sobrecarga más, por lo que se produce un fallo prematuro de la conexión por deformación excesiva de este perno. Mientras tanto, en la conexión simétrica (fig. 7a) el colapso se produce simultáneamente en ambos pernos.
5Discusión de resultadosPara la obtención de la curva Fuerza-desplazamiento correspondiente al comportamiento de la componente, se evaluaron la rigidez inicial y la resistencia. La rigidez elástica se evalúa según la relación entre la fuerza aplicada F y el desplazamiento del punto de aplicación. Según las nomenclatura adoptada y acorde a los modelos definidos, para el caso simétrico se determina según ecuación (8), ya que al considerarse en el modelo la simetría sólo actúa la mitad de la carga. Para el sistema asimétrico según la ecuación (9).
donde F es la fuerza aplicada, u3 es el desplazamiento del alma y KT-stub,simétrico y KT-stub,asimétrico son las rigideces de los modelos simétrico y asimétrico respectivamente.El cálculo de la resistencia máxima se realiza a través del análisis de las tensiones a partir de los resultados de esfuerzos axil, cortante y flector obtenidos según el análisis matricial y considerando el criterio de plastificación de Von Misses. Para la comprobación en la sección del ala se tiene en cuenta la reducción de la capacidad por la fuerza cortante actuante según ecuación (10), conforme a lo definido por C. Faella et al.[8], pudiéndose evaluar la capacidad última según la ecuación (11).
donde Mf y Vf son el momento flector y el esfuerzo cortante respectivamente en la sección de estudio, Mf,Rd es el momento flector resistente de la sección del ala, y Vf,Rd es el cortante resistente de dicha sección y beff es el ancho eficaz definido según [1].En el caso del perno, el análisis de tensiones se desarrolla considerando el efecto combinado de la tracción y la flexión según la ecuación (12).
donde Nt y Mf son el esfuerzo axial y el momento flector en la sección de estudio, y Nt,Rd y Mf,Rd son el axil y el momento resistente de la sección.Respecto a la rigidez inicial y la resistencia máxima fueron calculadas mediante tratamiento de los datos obtenidos. Los resultados se muestran en la tabla 2. La comparación de las curvas experimentales con los resultados numéricos obtenidos se muestra gráficamente en la fig. 8 para ambos ensayos.
Características mecánicas calculadas, experimentales y según modelos numéricos
| Ensayo ID | Resultados experimentales / Resultados analíticos / Resultados numéricos | |||||
|---|---|---|---|---|---|---|
| kEXP (kN/mm) | kANA (kN/mm) | kFEM (kN/mm) | Pu,EXP (kN) | Pu,ANA (kN) | Pu,FEM (kN) | |
| 04a | 735.01 | 814.72 | 725.92 | 485.76 | 413.39 | 460.13 |
| 04b | 642.24 | 830.65 | 770.25 | 419.38 | 353.36 | 412.01 |
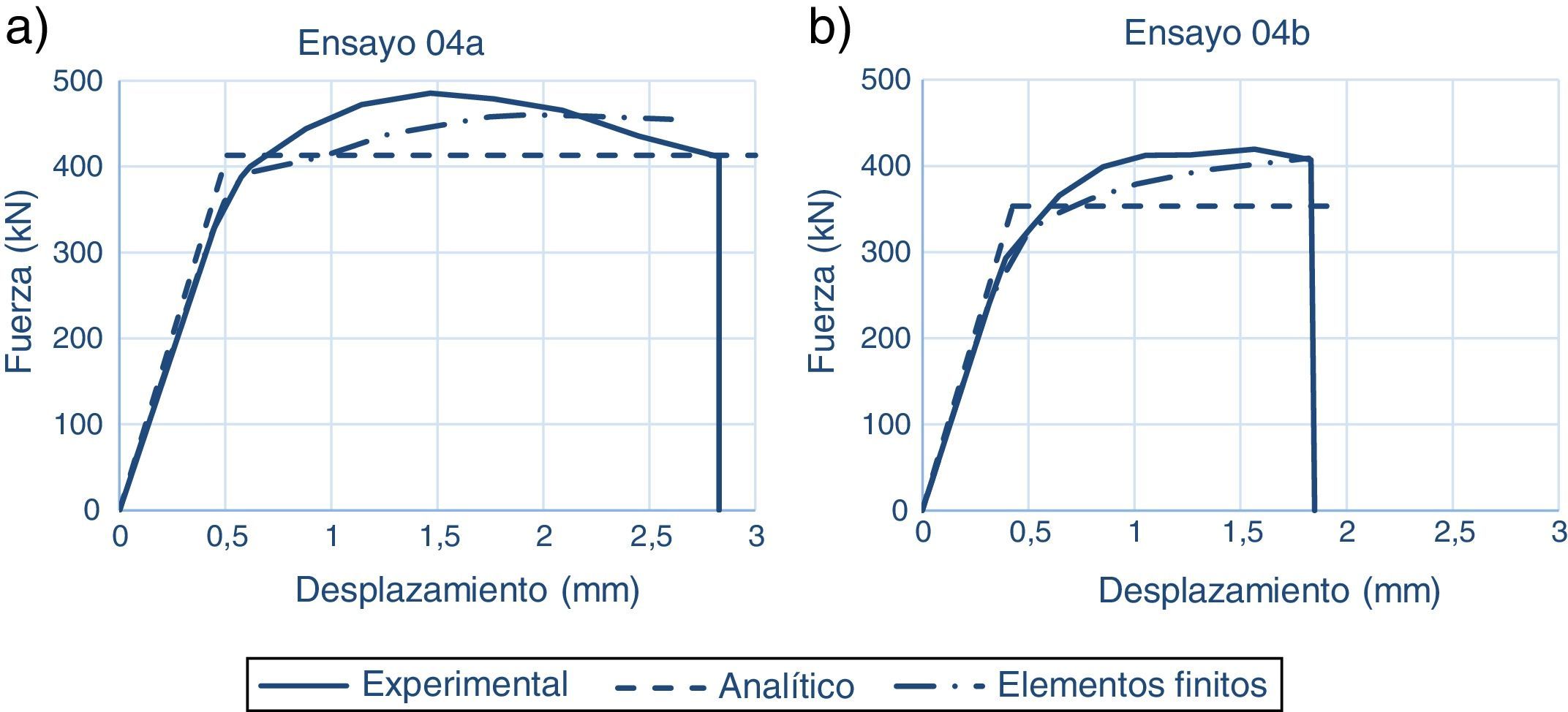
Referente al modelo de elementos finitos, se seleccionaron los datos precisos procedentes del análisis. La carga total aplicada fue analizada a través de la reacción total sobre los elementos de la superficie frontal del alma del perfil (multiplicada por cuatro a analizar el modelo simétrico). El desplazamiento es obtenido igualmente de la misma posición, obteniéndose como el doble del valor medio de los desplazamientos de los elementos. Estos datos fueron obtenidos para cada paso de análisis, pudiéndose por tanto graficar la curva fuerza-desplazamiento total (Fig. 8a y 8b).
Se observa en los resultados experimentales, que el error cometido en el cálculo de la carga última está por debajo del 20%, produciéndose el fallo por plastificación del perno como se esperaba por las características geométricas y mecánicas de los componentes que conforman el ensamblaje. Además la carga última es mayor en el modelo simétrico que en el asimétrico, por el efecto ya comentado de distribución no simétrica de la misma en los pernos. Respecto a la rigidez se obtienen diferencias de los modelos numéricos respecto a los reales inferiores al 10%. La diferencia de rigidez obtenida entre el modelo simétrico respecto al modelo asimétrico no es significativa, como puede apreciarse. Puede deducirse que las diferencias obtenidas son originadas como consecuencia de la no consideración en el modelo teórico de determinados parámetros, tales como tolerancias dimensionales y no homogeneidad en los materiales, lo que repercutiría en una flexibilidad mayor. Adicionalmente cabe destacar que los pernos se han modelado como conectados rígidamente al ala del perfil, situación que no ocurre en la realidad, existiendo un determinado giro relativo entre las dos partes. Los errores obtenidos en los resultados son menores que los obtenidos por otros autores [7,9,10], donde llegan a obtenerse diferencias de hasta el 50% entre el modelo teórico y los resultados experimentales, Así mismo, se confirma que la asimetría produce una redistribución de la carga en los pernos, produciendo el fallo de la unión a valores menores de la carga aplicada que cuando la distribución de los pernos es simétrica.
6ConclusionesEl presente artículo supone la primera publicación que, a conocimiento de los autores, se ha realizado sobre el estudio de T-equivalentes asimétricas, que aparecen frecuentemente por necesidades constructivas en estructuras metálicas.
El estudio realizado propone un modelo analítico con elementos tipo barra en el que se fijan las condiciones de simetría y se determinan los parámetros característicos.
Los resultados obtenidos utilizando el modelo teórico numérico propuesto se aproximan más a los resultados experimentales que los publicados previamente en la bibliografía.
Así mismo se confirma que la asimetría produce una redistribución de la carga en los pernos, produciendo el fallo de la conexión a valores menores de la carga aplicada que cuando la distribución de los pernos es simétrica.
Los resultados fueron analizados también con simulaciones mediante elementos finitos. Se observó la buena correlación entre el modelo propuesto y los resultados analíticos y experimental.
La presente investigación supone la apertura de una línea de trabajo extensa, al tratarse de una componente no estudiada hasta el momento y que sería preciso caracterizar completamente, con el fin de establecer sus condiciones de seguridad. Un modelo en elementos finitos fiable para definir el comportamiento de componentes T-equivalente asimétricas, cmo el que se presenta en la segunda parte de este artículo, es el siguiente paso lógico de este estudio.
El presente trabajo se desarrolla gracias al respaldo económico por parte de la Universidad de Jaén y de la Universidade de Coimbra por la disposición de los laboratorios y de los equipos de ensayos, todo ello dentro del proyecto 3DJOINTS - Comportamento tridimensional de ligações metálicas” - FCT Fundação para a Ciência e a Tecnologia, Ministério da Ciência, Tecnología e Ensino Superior de Portugal - Cod. PTDC/ECM/116904/2010. Así mismo se agradece a la empresa FATOR Tornillería Industrial por la donación del material.