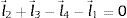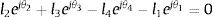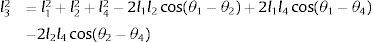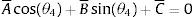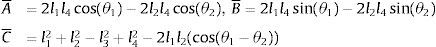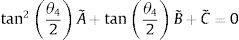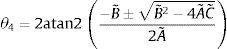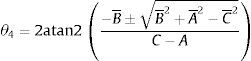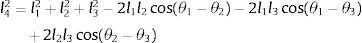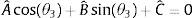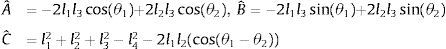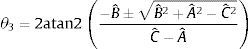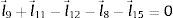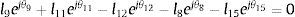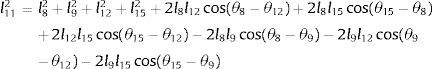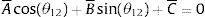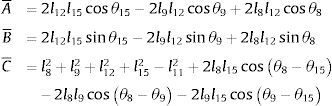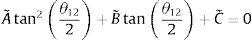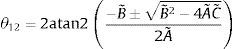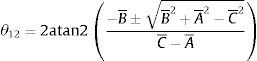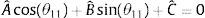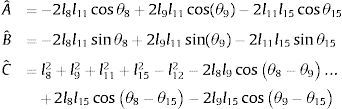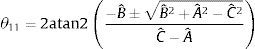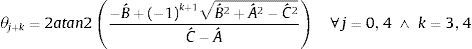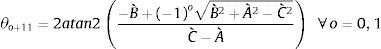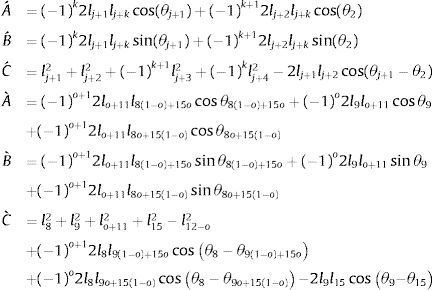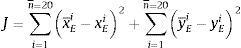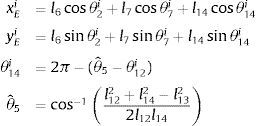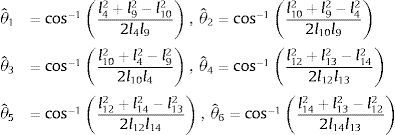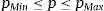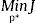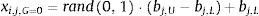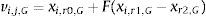El diseño de la extremidad de un robot bípedo es un punto clave para mejorar la locomoción y el desempeño de robots bípedos. El empleo de mecanismos que reproduzcan la marcha no es una tarea sencilla ya que se requiere generar un movimiento en el espacio Cartesiano con más grados de libertad que los considerados en un mecanismo. En este trabajo se propone un mecanismo planar de ocho eslabones con un grado de libertad como extremidad bípeda y se analiza su comportamiento en el seguimiento de una trayectoria similar a la marcha. Para el diseño del mecanismo propuesto se establece formalmente la síntesis dimensional como un problema de optimización numérica. Con el propósito de obtener diseños viables dentro del espacio de las soluciones reales en el problema de optimización, se incorpora un mecanismo de manejo de restricciones en el algoritmo de evolución diferencial (ED) y se analiza el comportamiento del algoritmo bajo diferentes parámetros de cruza. Resultados experimentales comprueban el enfoque de diseño en un prototipo de laboratorio.
The limb design for a biped robot is a key issue to improve the locomotion and the performance of biped robots. The use of mechanism for tracking the gait is not an easy task because the degree of freedom (d.g.f) of the Cartesian space movement does not correspond to the d.g.f of the mechanism. Hence in this paper, an eight-bar planar mechanism with a one d.o.f is proposed as biped limb and the biped gait tracking behavior in the mechanism is analyzed. A numeric optimization problem is formally stated to design the proposed mechanism based on dimensional synthesis. A constraint handling mechanism is included into the differential evolution algorithm (DE) algorithm in order to obtain mechanism design with real solutions in the optimization problem and the behavior of the algorithm with different crossover parameters is analyzed. Experimental results verify the design approach in a laboratory prototype.
Durante los últimos años, la investigación en la locomoción de robots bípedos se ha incrementado debido a que su estudio puede ayudar a la detección de trastornos de la marcha, identificación de factores de equilibrio, evaluación clínica de la marcha en los programas de rehabilitación [1] así como al diseño de exoesqueletos y prótesis robóticas. Sin embargo, el modelado exacto de la marcha de robots bípedos es una tarea compleja porque existe un gran número de variables involucradas, tales como las variables antropométricas que incluyen la altura, el peso, y la longitud de las extremidades; datos espacio temporales que comprenden las variables como la velocidad al caminar, longitud de paso o tiempo de fase; variables cinemáticas que involucra los ángulos de unión, desplazamiento o aceleraciones a través de los ejes; variables cinéticas que incluyen fuerza y par en el pie. Los resultados presentados en [2], con máquinas de caminado dinámico pasivo, establece que los parámetros mecánicos de un robot bípedo (variables antropométricas, espacio-temporales, cinemáticas y cinéticas) tienen gran impacto en la existencia y calidad de la marcha, es decir, no sólo se requiere entender desde un punto de vista de sistemas de control la marcha bípeda, sino también se necesita estudiar el mecanismo de locomoción desde un punto de vista mecánico.
Mientras más grados de libertad (g.d.l.) se presenten en un robot bípedo, más suave es su movimiento. Sin embargo, resulta en un sistema más complejo de controlar por lo que se requerirá de un análisis de movimiento humano para optimizar la marcha del robot bípedo [3]. Varios estudios han reducido la complejidad del caminar bípedo implementando uniones no actuadas [4], resortes en el pie, eslabones flexibles [5] o incluso mecanismos en algunas partes del robot bípedo como por ejemplo en las rodillas [6]. En este artículo se está interesado en el diseño de un mecanismo para la extremidad inferior de un robot bípedo, que reproduzca el movimiento de marcha en el plano sagital. Para este propósito, se diseña un mecanismo de ocho eslabones con un grado de libertad para reproducir la marcha bípeda. La obtención de las dimensiones cinemáticas de mecanismos que satisfacen un movimiento deseado está con base en la síntesis dimensional [7]. Los métodos gráficos y analíticos no son apropiados para resolver varios puntos de precisión en la síntesis dimensional, por lo que se ha optado por el uso de métodos numéricos los cuales están comúnmente combinadas con técnicas de optimización y el establecimiento de problemas de optimización. Sin embargo, no resulta conveniente utilizar técnicas de optimización basados en el gradiente [8,9] debido a que convergen a soluciones cercanas al punto inicial, i.e., no presenta buen desempeño en problemas altamente no lineales, divergen en problemas discontinuos, entre otros. Por tal motivo se necesitan otro tipo de técnicas para resolver problemas complejos (de ingeniería) como es el caso de las técnicas meta-heurísticas [10,11]. Es así que en la última década se ha optado por utilizar algoritmos evolutivos para realizar la síntesis de mecanismos [12–15]. En [13] se utiliza el algoritmo de búsqueda de Cuckoo para resolver el problema de síntesis dimensional de mecanismo de seis barras Stephenson III. Se observó que el algoritmo puede aproximar el ángulo de rotación deseado con el actual con una desviación máxima de 1.77% considerando dos casos de estudio. Así mismo, se han estado comparando el desempeño de algoritmos meta-heurísticos en la síntesis de mecanismos, como en [14] en donde se propone un enfoque dinámico para la síntesis de un mecanismo de cuatro eslabones y se utiliza el algoritmo de evolución diferencial, algoritmo de forrajeo de bacterias modificado y el algoritmo de tormenta de ideas para resolverlo. Los resultados muestran que el algoritmo de evolución diferencial presenta una mejor búsqueda de la solución óptima a pesar de que los otros dos algoritmos presentan resultados competitivos. Debido a la complejidad de encontrar soluciones dentro del espacio de búsqueda en la síntesis dimensional de mecanismos, se han propuesto enfoques nuevos de algoritmos heurísticos para resolver dichos problemas como en [15], en donde se implementa el algoritmo competitivo imperialista para la síntesis dimensional de generación de trayectoria de un mecanismo de cuatro barras, así como se han propuesto esquemas auto-adaptables para la sintonización de los parámetros de control del algoritmo de evolución diferencial [16].
En este trabajo se propone el diseño óptimo de un mecanismo de ocho eslabones con un grado de libertad para ser considerado como extremidad inferior de un robot bípedo en donde se consideren variables antropométricas y cinemáticas para su diseño. Dichas variables se obtienen a través de la propuesta de un problema de optimización que involucra variables espacio-temporales de la marcha del robot bípedo así como un mecanismo de manejo de restricciones en el algoritmo de ED que guía la búsqueda hacia regiones en donde es factible el diseño. El análisis del factor de cruza en el algoritmo de ED indica que se requiere de a lo más un 45% de información de los parámetros del vector hijo para dirigir la búsqueda hacia regiones con mejores soluciones, en donde el diseño obtenido aproxime su movimiento al de la marcha bípeda.
La estructura del artículo es la siguiente: en la Sección 2 se muestra y explica el mecanismo a utilizar para la locomoción bípeda así como su cinemática. La función objetivo, las variables de diseño y las restricciones en el problema de optimización para la síntesis dimensional se establecen formalmente en la Sección 3. En la sección 4 se detalla el algoritmo de evolución diferencial, así como el mecanismo de manejo de restricciones propuesto. El análisis de los resultados obtenidos por el algoritmo, así como los resultados experimentales, se discuten en la sección 5. Finalmente, en la sección 6 se proporcionan las conclusiones pertinentes y trabajo a futuro.
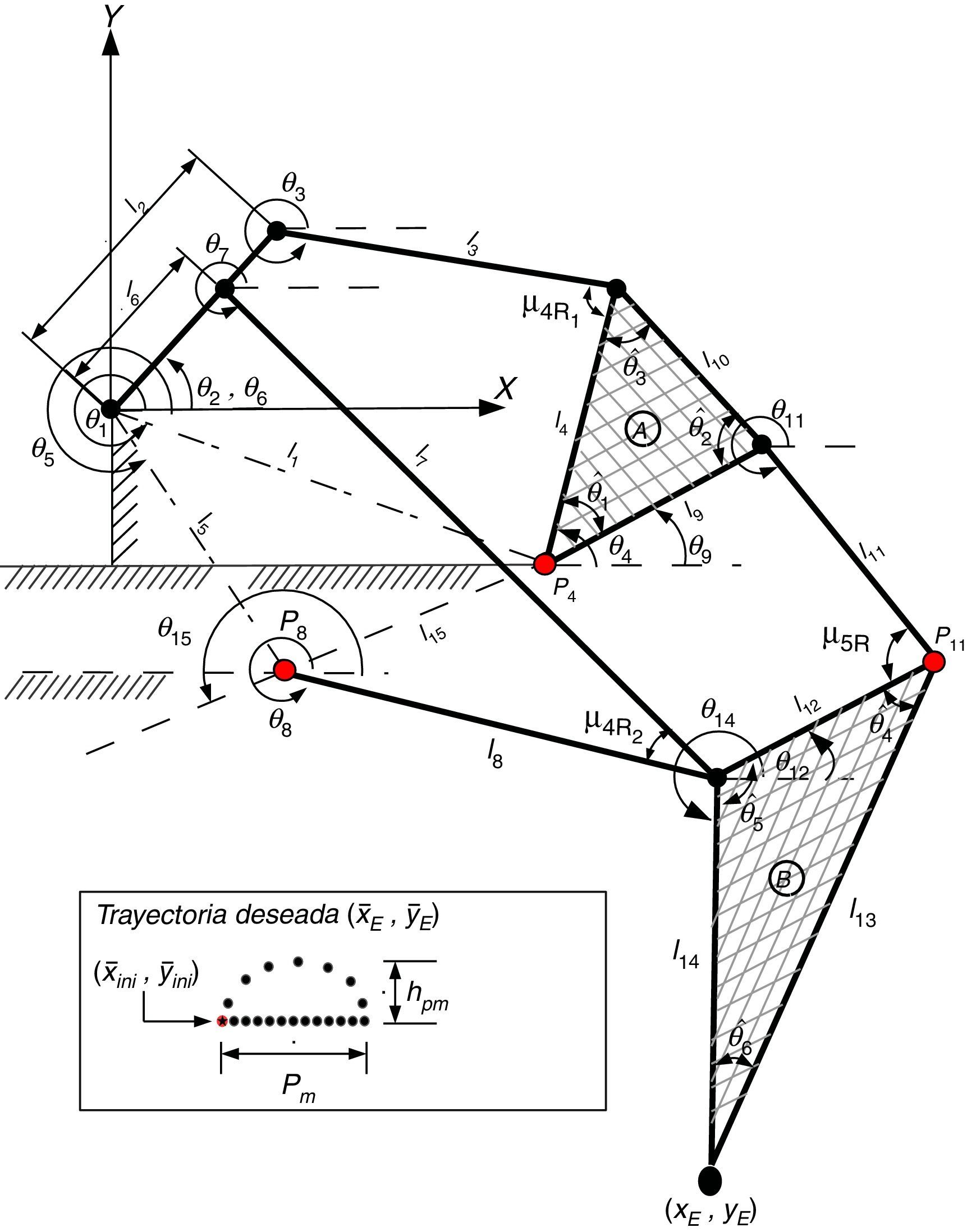
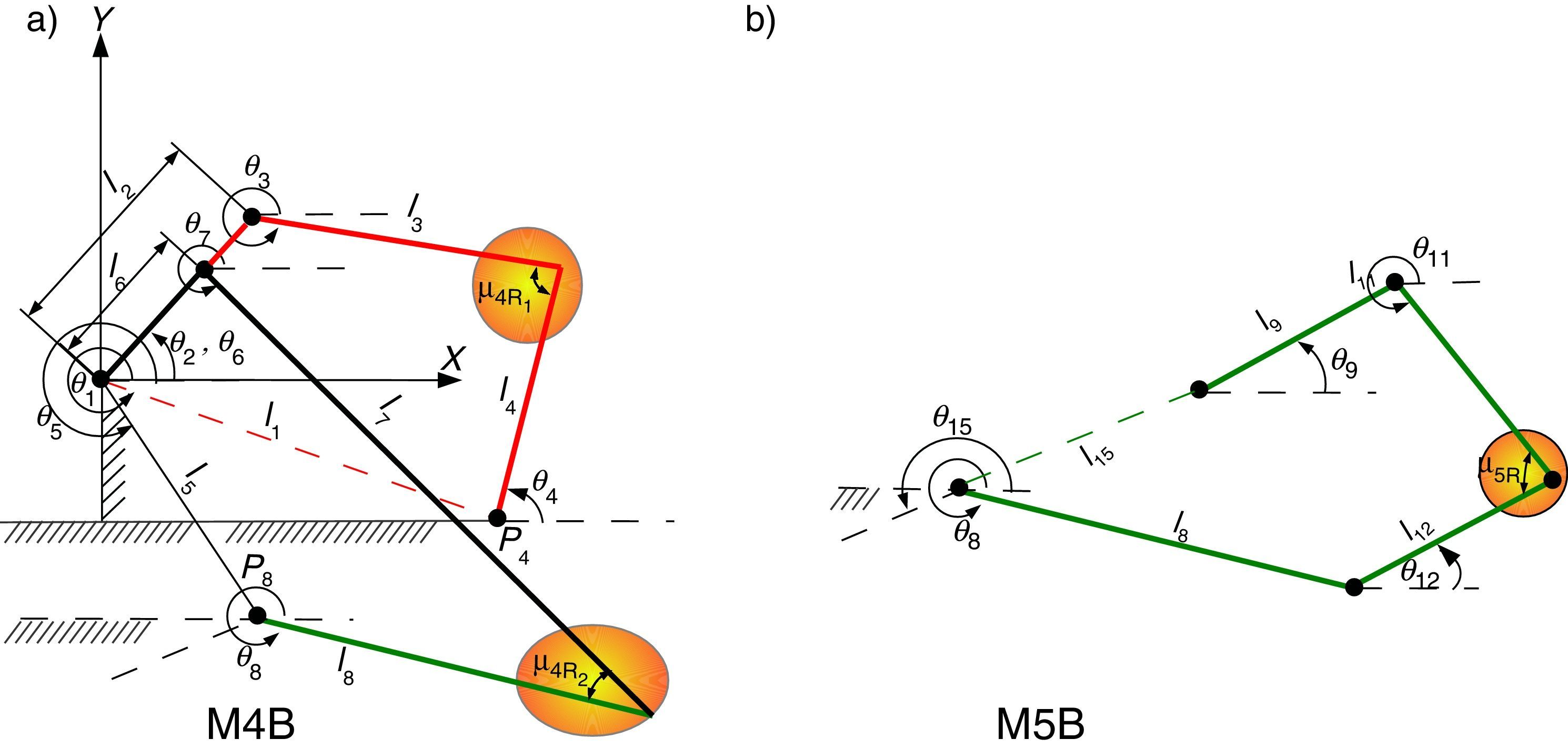
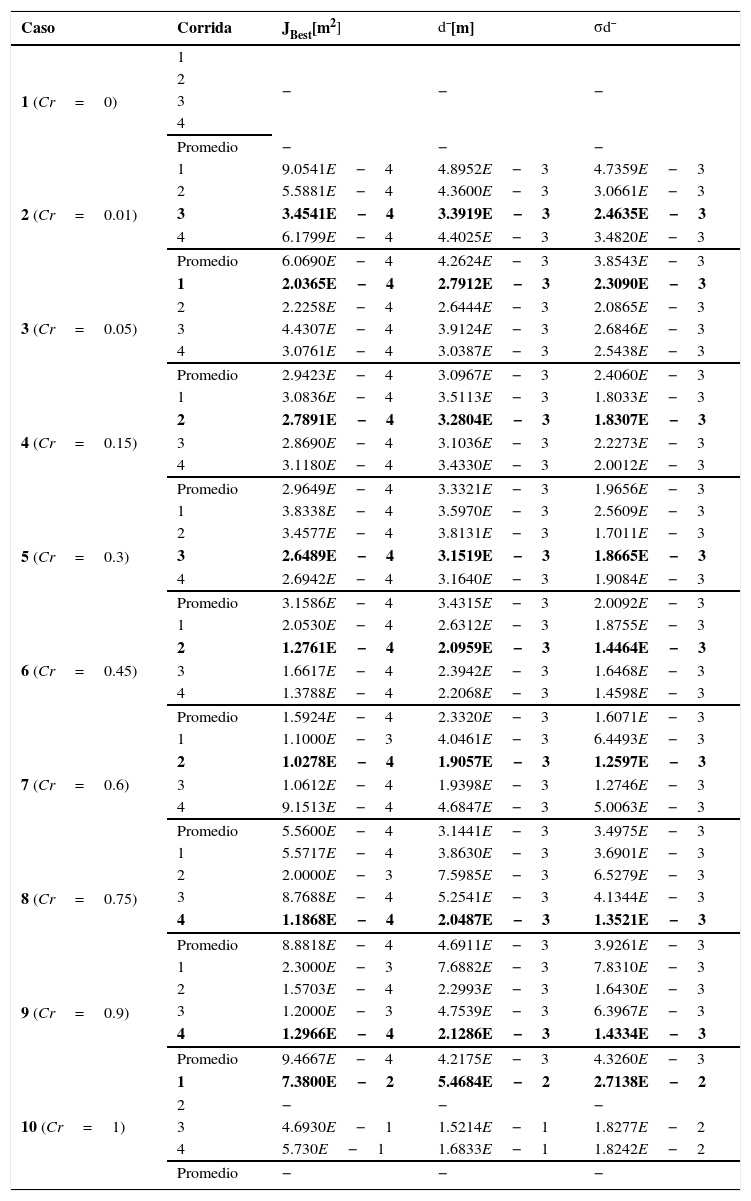
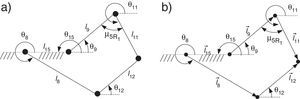
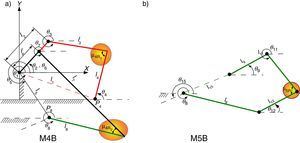
2Análisis del mecanismo de marcha en el plano sagitalEl mecanismo para realizar un movimiento similar a la marcha humana en el plano sagital se muestra en la figura 1. Este mecanismo se propone como extremidad del robot bípedo y contempla un grado de libertad y diez uniones. Los parámetros cinemáticos del mecanismo están dados por las longitudes li ∀i=1, 2, .., 14, por los ángulos internos de los dos eslabones con forma triangular θˆj, ∀ j=1, 2, ..., 6 y por el desplazamiento angular θi de las longitudes li con respecto al sistema de coordenada inercial X−Y.
Con el propósito de parametrizar el comportamiento cinemático del mecanismo, se asume que el mecanismo de marcha cuenta con dos mecanismos de cuatro barras y uno de cinco barras en su configuración. Cada mecanismo de cuatro barras está formado por un eslabón de entrada, un eslabón de salida, un eslabón acoplador y un eslabón fijo. Las longitudes de cada eslabón está dado por l2 y l6 para los eslabones de entrada, l4 y l8 para los eslabones de salida, l3 y l7 para los eslabones del acoplador y l1 y l5 para los eslabones fijos. Se considera que el desplazamiento angular de los eslabones de entrada es el mismo para los dos mecanismos de cuatro barras y se representa como θ2. Por otro lado, el mecanismo de cinco barras está formado por dos eslabones de entrada con longitudes l8 y l9, dos eslabones del acoplador l11 y l12 y un eslabón fijo con longitud l15. A continuación se describe el modelo cinemático del mecanismo de marcha representado en la figura 1.
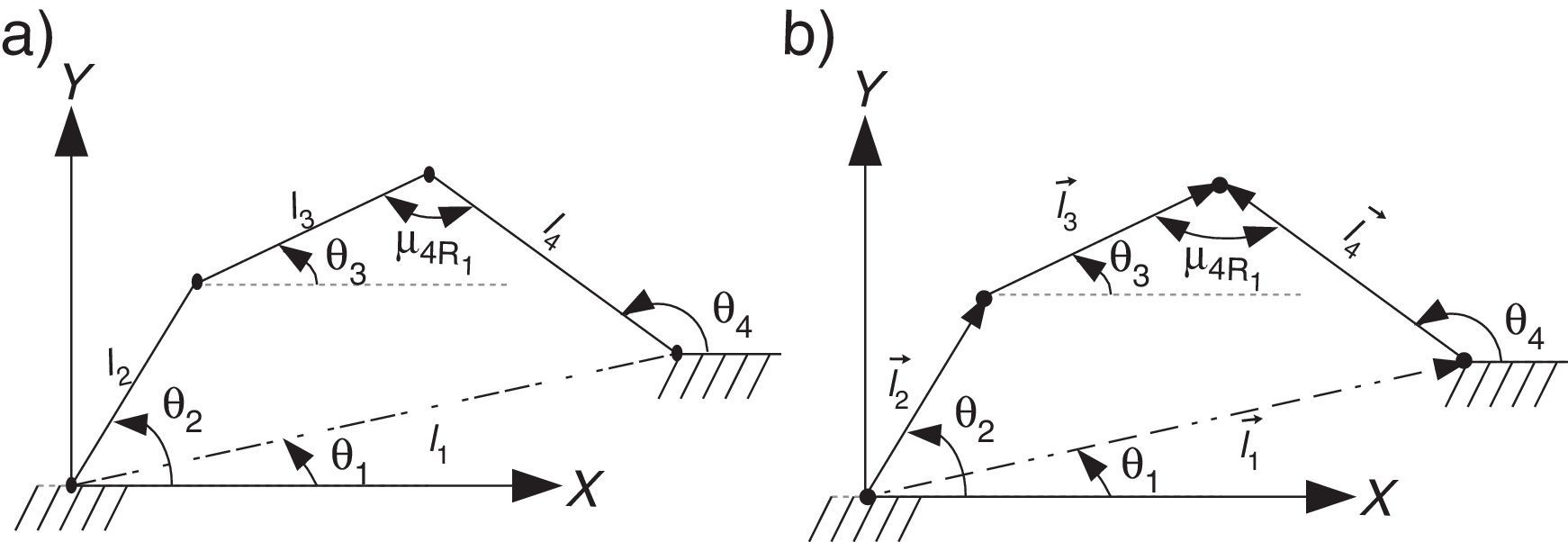
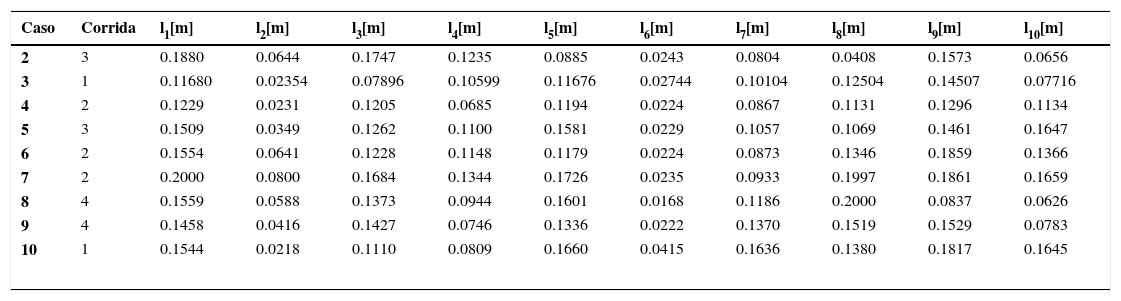
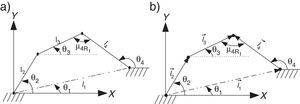
2.1Cinemática del mecanismo de cuatro barrasPara realizar el análisis cinemático de los dos mecanismos de cuatro barras (M4B) que considera el mecanismo de marcha de la figura 1, se procederá por el M4B formado por los eslabones l1 - l4. En la figura 2a, se observa el M4B y en la figura 2b se muestra su diagrama de vectores, donde θi es el ángulo que forma el i-ésimo eslabón con respecto al eje X del sistema de coordenadas inercial, li es la longitud del i-ésimo eslabón y μ4Ri es el ángulo de transmisión del i−e´simo mecanismo de cuatro barras.
La ecuación de lazo cerrado [17] del M4B está dado por la ecuación (1), donde l→i es el vector que se forma del i-ésimo eslabón
Representando (1) en notación de números complejos resulta (2)
Utilizando la fórmula de Euler en (2) y separando la parte real e imaginaria se obtiene (3) y (4)
Para obtener el ángulo θ4 se agrupan los términos en (3) y (4) y elevamos al cuadrado, resultando en (5), (6)
Resolviendo el sistema de ecuaciones (5), (6) y agrupando términos, resulta en (7)
Se agrupan términos en (7) y hacemos uso de la identidad cos(θ1−θ2)=cosθ1cosθ2+sinθ1sinθ2, por lo que resulta en la ecuación de Freudenstein [18,19] mostrado en (8)
donde:Sustituyendo la identidad trigonométrica sin(θ4)=2tan(θ42)/(1+tan2(θ42)), cos(θ4)=(1−tan2(θ42))/(1+tan2(θ42)) en la ecuación (8) resulta en (9), donde A˜=(−A¯+C¯),B˜=2B¯, C˜=(A¯+C¯)
Por lo tanto, el ángulo θ4 se obtiene de (9) al resolver la ecuación cuadrática, resultando en (10), donde atan2 es la función arco tangente dos [20]
Simplificando (10), resulta en (11)
Con el propósito de obtner el ángulo θ3, se agrupan los términos en (3) y (4) y elevamos al cuadrado, resultando en (12), (13)
Resolviendo el sistema de ecuaciones (12), (13) y agrupando términos, resulta en (14)
Se agrupan términos en (14) y hacemos uso de la siguiente identidad cos(θ1−θ2)=cosθ1cosθ2+sinθ1sinθ2, por lo que resulta la ecuación de Freudenstein [18,19] mostrado en (15)
donde:Realizando un procedimiento similar al mostrado previamente para encontrar θ4, se obtiene θ3(16)
Para encontrar los ángulos θ7 y θ8 del otro M4B, se realiza un procedimiento similar al que se utilizó previamente para encontrar θ3 y θ4.
Finalmente en la tabla 1 se muestra las dos posibles configuraciones que puede tener el mecanismo de cuatro barras, las cuales dependen del signo de la raíz cuadrada.
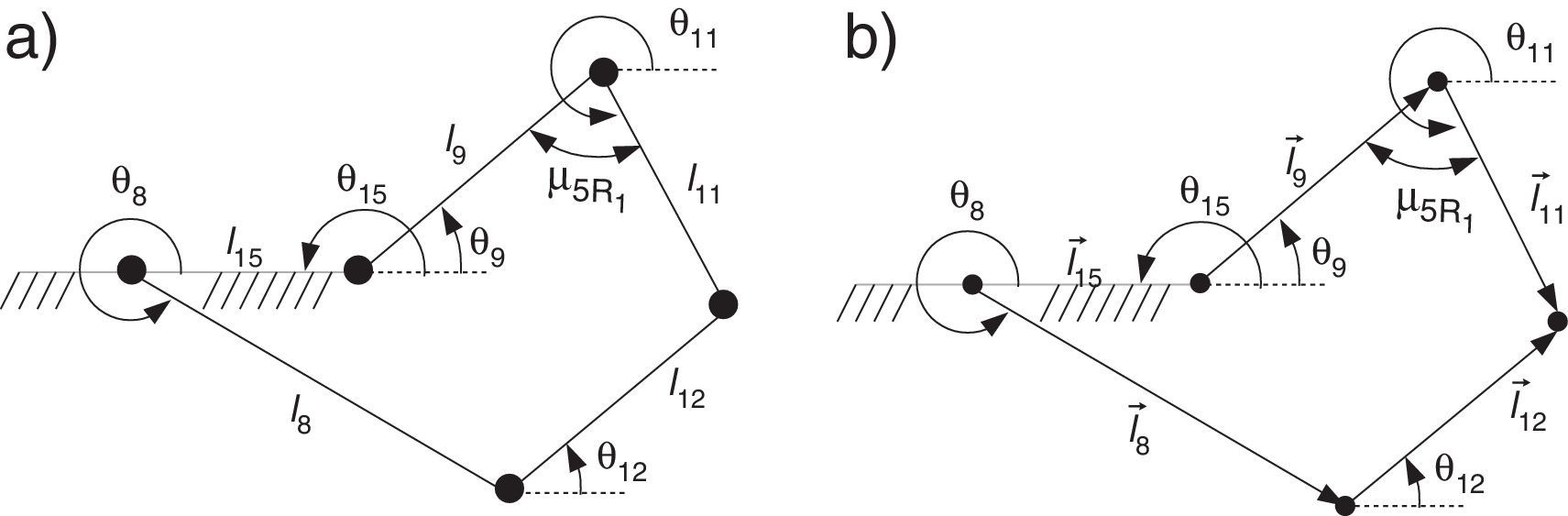
2.2Cinemática del mecanismo de cinco barrasEn la figura 3a, se observa el mecanismo de 5 barras y en la figura 3b se muestra un diagrama de vectores, donde θi es el ángulo del i-ésimo eslabón con respecto al sistema de coordenadas inercial X−Y, li es la longitud del i-ésimo eslabón y μ5R1 es el ángulo de transmisión del mecanismo de cinco barras (M5B).
La ecuación de lazo cerrado del mecanismo de 5 barras está dado por la ecuación (17), donde l→i es el vector que se forma del i-ésimo eslabón
Representando (17) en notación de números complejos resulta en (18):
Utilizando la identidad de Euler en (18), separando la parte real e imaginaria y elevando al cuadrado cada una de ellas, se obtiene (19), (20)
Resolviendo el sistema de ecuaciones (19), (20) y agrupando términos, resulta en (21)
Se agrupan términos en (21) y hacemos uso de la siguiente identidad cos(θϱ−θϰ)=cosθϱcosθϰ+sinθϱsinθϰ, ∀ [ϱ, ϰ]∈{[8, 15], [8, 9], [9, 15]}, por lo que resulta la ecuación de Freudenstein [18,19] mostrado en (22)
donde:Sustituyendo la identidad trigonométrica sin(θ12)=2tan(θ122)/(1+tan2(θ122)), cos(θ12)=(1−tan2(θ122))/(1+tan2(θ122)) en la ecuación (22) resulta en (23), donde A˜=(−A¯+C¯),B˜=2B¯, C˜=(A¯+C¯)
Por lo tanto, el ángulo θ12 se obtiene de (23) al resolver la ecuación cuadrática, resultando en (24), donde atan2 es la función arco tangente dos [20]
Simplificando (24), resulta en (25)
Con el propósito de obtener el ángulo θ11, se utiliza la identidad de Euler en (18), se separa la parte real e imaginaria y se elevan al cuadrado cada una de ellas, lo que resulta en (26), (27)
Resolviendo el sistema de ecuaciones (26), (27), agrupando términos y con el uso de la identidad cos(θϱ−θϰ)=cosθϱcosθϰ+sinθϱsinθϰ, ∀ [ϱ, ϰ]∈{[8, 15], [8, 9], [9, 15]}, resulta en la ecuación de Freudenstein [18,19] mostrada en (28)
donde:Realizando un procedimiento similar al que se realizó cuando se obtuvo θ12, se puede obtener θ11 de (29)
Finalmente en la tabla 2 se muestra las dos posibles configuraciones que puede tener el mecanismo de cinco barras, las cuales dependen del signo de la raíz cuadrada.
2.3Parametrización de la cinemática del mecanismo de marchaDel análisis anterior, se puede definir de forma concreta, en las ecuaciones (30) y en (31), la parametrización de la cinemática completa del mecanismo de marcha representado en la figura 1
donde:3Síntesis dimensional del mecanismo de marchaSe establece la síntesis dimensional de generación de trayectoria [21] que consistirá en obtener las dimensiones características del mecanismo de marcha para cumplir una trayectoria preestablecida en el punto (xE, yE) de la figura 1. Para tal fin, se establece un problema de optimización numérica en donde la función objetivo, variables de diseño y restricciones se detallan a continuación.
3.1Función objetivoDebido a que se requiere realizar con un buen desempeño la generación de una trayectoria en el punto (xE, yE) del mecanismo de marcha mostrado en la figura 1, se establece como función objetivo J el cuadrado del error entre las n¯ coordenadas de la trayectoria deseada (x¯E,y¯E) y las n¯ coordenadas generadas por el mecanismo (xE, yE). La función objetivo se representa en (32), donde para el caso particular el total de coordenadas a satisfacer es n¯=20
donde:3.2Variables de diseñoSe considera que las variables de diseño del mecanismo de marcha sean sus parámetros antropométricos y los parámetros cinemáticos [22]. Los parámetros antropométricos están dados por las longitudes li ∀ i=1, 2, ..., 14, los parámetros cinemáticos dados por los ángulos de los eslabones base de los dos mecanismos de cuatro barras θ1, θ5 y los n¯ desplazamientos angulares de la manivela para producir las n¯ coordenadas en (xE, yE), i.e., θ2={θ2i | i=1,2,...,n¯}. Además se establece como variable de diseño la coordenada inicial x¯ini de la trayectoria deseada en el eje X (ver fig. 1) con el propósito de promover la reconfigurabilidad del mecanismo de marcha en diferentes posiciones de la trayectoria deseada. En consecuencia de lo antes mencionado, las variables de diseño se agrupan en el vector p∈R17+n¯(33)
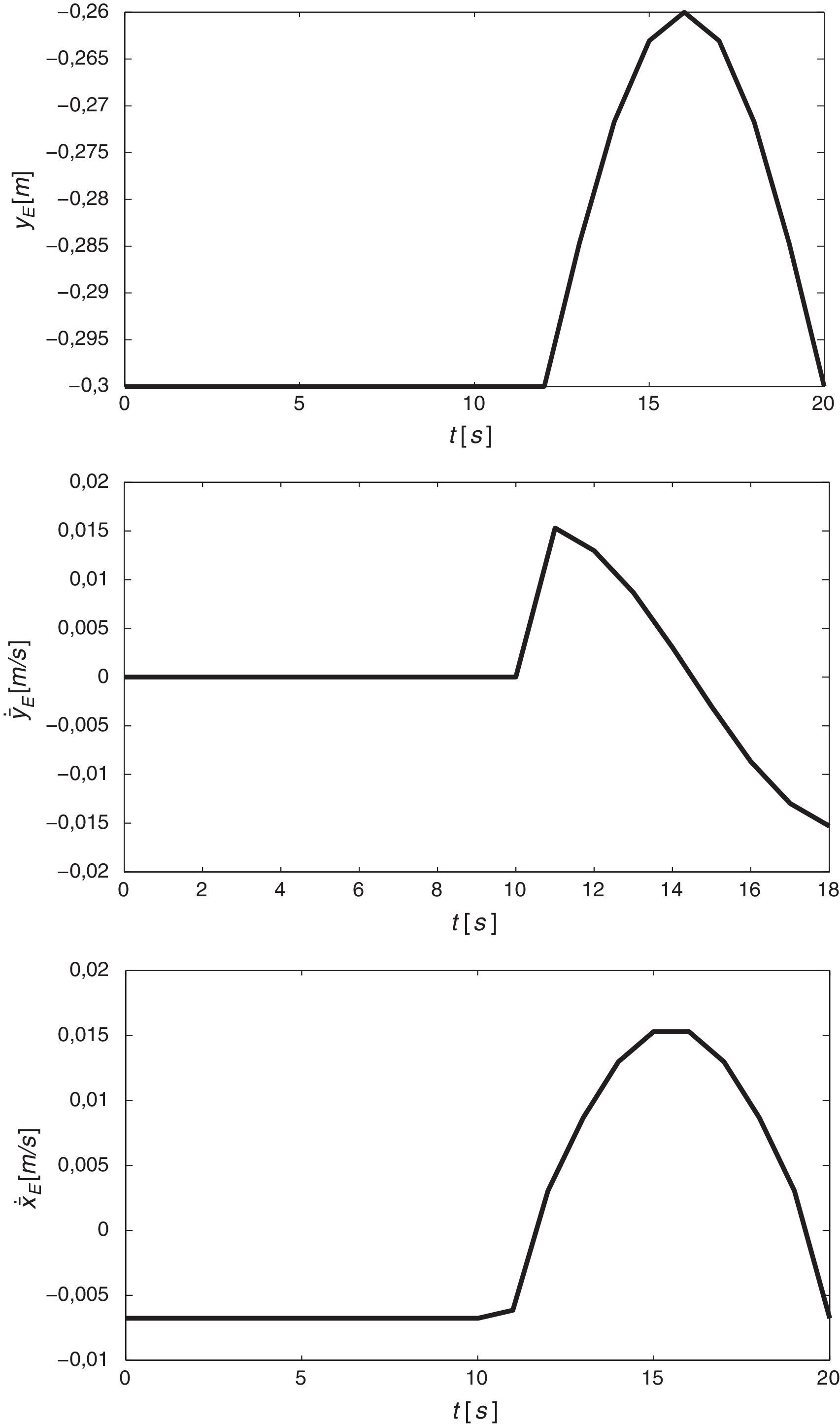
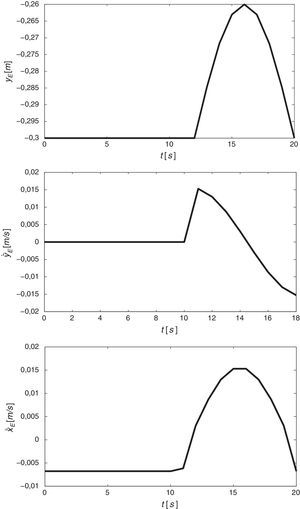
3.3Restricciones3.3.1Movimiento de marcha deseadoLa trayectoria deseada que se establece para el movimiento de marcha de la extremidad del robot bípedo se obtiene a partir de un estudio biomecánico del tobillo durante la fase de balanceo del caminar humano en adultos jóvenes [23]. Debido a que se requiere obtener el mecanismo de la extremidad del robot bípedo en una escala menor, se propone una trayectoria similar en forma a la reportada en la figura 5 en [23]. La representación gráfica de la trayectoria deseada en el plano X-Y se muestra en la figura 1, y en la figura 4 se muestra el desplazamiento vertical y¯E, la velocidad vertical y¯E· y la velocidad horizontal x¯E· de la trayectoria deseada y que puede ser comparada con los resultados reportados en la figura 5 de [23], los cuales son similares.
Con el propósito de satisfacer que el punto (xE, yE) del mecanismo presente el movimiento de marcha mencionado previamente, se incorpora como restricción de igualdad la trayectoria deseada mostrada en la figura 1 y la cual se representa analíticamente en (34) y (35). Esta trayectoria tiene una forma semi-elíptica unida en su eje mayor por una recta de longitud pm=0.08m, cuya longitud corresponde al parámetro espacio temporal de longitud de paso de la marcha del mecanismo. El eje menor de la trayectoria semi-elíptica es el parámetro espacio temporal de altura máxima del tobillo en la fase de balanceo y la cual está dada por hpm=0.04m. Se asume que la trayectoria está formada por n¯=n¯a+n¯b=20 coordenadas cartesianas, donde n¯a=13 y n¯b=7 son las coordenadas correspondientes a la fase de apoyo y a la fase de balanceo, respectivamente. Para el caso particular, se considera que los parámetros espacio temporales de la fase de apoyo y fase de balanceo sean del 65% y del 35% del total del ciclo de marcha [24], respectivamente. Por otra parte, el parámetro antropométrico de la longitud total de la extremidad del robot bípedo se establece de 0.3m y se incorpora en la coordenada y¯ini=−0.3m en el movimiento generado en el eje Y de la trayectoria deseada en la fase de apoyo (observar (35))
3.3.2Criterio de GrashofPara realizar un movimiento continuo en el mecanismo de marcha de la extremidad del robot bípedo cuando se considera una velocidad constante en los eslabones de entrada, se requiere garantizar que al menos un eslabón pueda girar libremente. El criterio de Grashof [25] para mecanismos de cuatro eslabones establece que si la suma de las longitudes del eslabón más corto y más largo es menor o igual a la suma de los dos eslabones restantes, entonces al menos un eslabón puede rotar completamente. Por tal motivo se incluye el criterio de Grashof como restricciones del diseño para ambos mecanismos de cuatro barras. Esta restricción se muestra en (36)–(37)
Además, para permitir que los mecanismos de cuatro barras presenten configuraciones manivela-balancín en los eslabones de entrada y salida, respectivamente (i.e., (l2, l6) y (l4, l8)), y a su vez garantizar un movimiento continuo en el mecanismo de marcha del robot bípedo, se establecen las restricciones mostradas en (38)–(41)
3.3.3Estructura triangularEl mecanismo de marcha presenta dos eslabones con estructuras triangulares marcadas en la figura 1 con las letras A y B. Con el propósito de preservar dicha estructura en el proceso de optimización, se requiere satisfacer la propiedad geométrica de los ángulos interiores de un triángulo, la cual establece que en el espacio Euclideano, la suma de los ángulos interiores de un triángulo es igual a π radianes. Es así que se incluyen las restricciones (42)–(45) con el propósito de preservar las dos estructuras triangulares en el mecanismo de marcha, donde los ángulos interiores de la estructura triangular se obtienen haciendo uso de la ley de cosenos
donde:Cabe mencionar que las restricciones de igualdad (42) y (43) se transforman en dos restricciones de desigualdad cada una, con el propósito de que no sea estricta y que no se afecte en gran medida por las aproximaciones decimales. Así, las restricciones (42) y (43) resultan en las restricciones de desigualdad dadas por (46)-(49), donde Tolh=1E−10 es el valor de tolerancia de la restricción de igualdad (42) y (43)
3.3.4Calidad de transmisión de movimientoUna medida que nos indica la efectividad con la cual el movimiento del eslabón de entrada del mecanismo se transmite hacia el eslabón de salida es el ángulo de transmisión [26]. En un mecanismo de cuatro eslabones, el ángulo de transmisión μϱ ∀ ϱ∈{4R1, 4R2} es el ángulo formado entre el eslabón acoplador y el eslabón balancín, como se observa en la figura 5a y en la figura 1. Cuando el ángulo de transmisión tiene el valor ideal de μϱ=π2rad, se efectúa la mejor transmisión de fuerza y la exactitud del movimiento del eslabón de salida es menos sensible a errores de manufactura (tolerancia) y a cambios de dimensiones debido a una dilatación/contracción térmica del material. Se recomienda que el ángulo de transmisión se encuentre en el intervalo [π4,3π4]rad[26]. Por lo tanto se propone como restricción que el valor mínimo y máximo del ángulo de transmisión (μmin, μmax) de los mecanismos de cuatro barras en el mecanismo de marcha se encuentren en el intervalo [π4,3π4]rad. Las restriciones relacionadas al ángulo de transmisión de los M4B se muestran en las ecuaciones (50)–(53)
Para el mecanismo de cinco eslabones, el ángulo de transmisión μ5R es el ángulo formado entre el eslabón l11 y el eslabón l12, como se observa en la figura 5b, y en la figura 1. Se desea que la fuerza ejercida por los eslabones de entrada del mecanismo de cinco barras se transmitan efectivamente al punto (xE, yE) únicamente en la fase de apoyo, ya que es la fase en donde se requiere soportar el peso de la extremidad. Por tal motivo, se establece de igual manera que el ángulo de transmisión μ5R del mecanismo de cinco eslabones se encuentre en el intervalo [π4,3π4]rad en la fase de apoyo por lo que resulta en las restricciones mostradas en (54)–(55)
3.3.5Morfología funcional de la extremidad bípedaOtra restricción importante a considerar es que la morfología del mecanismo cumpla la función de locomoción del robot bípedo, es decir, que pueda realizar la marcha. Para llevar a cabo la función de locomoción se considera que las uniones P4=[P4x, P4y], P8=[P8x, P8y] y P11=[P11x, P11y], los cuales se observan en la figura 1, deben estar por encima de la trayectoria que se desea, lo que indicará que no pueden estar por debajo del suelo. Dicha restricción se muestra en (56)–(58)
3.3.6Movimiento cinemático válidoLa restricción de movimiento cinemático válido involucra que los n¯ desplazamientos angulares de la manivela θ2, los cuales producen las n¯ coordenadas Cartesianas (xE, yE) en el mecanismo de marcha, presenten un movimiento cinemático real o válido, i.e., que el radicando de las expresiones (30) y (31) resulten en un valor positivo. Esta restricción se muestra en (59)–(60)
3.3.7Límites en las variables de diseñoLos límites en las variables de diseño se eligen teniendo en cuenta lo siguiente: Longitudes reales i.e., longitudes no negativas y de tamaño apropiado de acuerdo a las especificaciones del prototipo; desplazamiento angular que contemple el intervalo [0, 2π]rad y posición inicial de la trayectoria deseada en el eje X en el intervalo [−0.5, 0.5]m. Los límites en las variables de diseño se establecen como restricciones de desigualdad dadas en (61), considerando como las cotas mínimas pMin ∈ R17+n¯ y las máximas pMax ∈ R17+n¯ las proporcionadas en la tabla 3
Una vez que se definen las variables de diseño, función objetivo y restricciones del diseño del mecanismo de marcha para la extremidad de un robot bípedo, se puede formular el problema de optimización que consiste en encontrar los parámetros antropométricos, cinemáticos y de coordenada inicial dados por el vector p*(33) de tal manera que se minimize el cuadrado del error J(32) generado entre el punto (xE, yE) del mecanismo y el movimiento de marcha pre-establecido, sujeto al comportamiento cinemático del mecanismo (30)–(31) representado en forma compacta como θi=f(θ2i,p), al movimiento de marcha deseado (34)–(35), al criterio de Grashof (36)–(41), a la estructura triangular de los eslabones A y B(42)–(45), a la calidad de transmisión de movimiento (50)–(55), a la morfología funcional (56)–(58), al movimiento cinemático válido (59)–(60) y a las cotas en las variables de diseño (61). Formalmente el problema de optimización se puede establecer como (62)–(66)
Sujeto a:
4Evolución diferencialEvolución diferencial (ED) es un método de búsqueda directa estocástica basada en población dentro de la clase de algoritmos evolutivos. El primer artículo escrito sobre el algoritmo de evolución diferencial apareció como un informe técnico por R. Storn y K.V. Price en 1995 [27]. Desde entonces, evolución diferencial ha sido utilizado en una variedad de problemas de optimización en ingeniería, debido principalmente a que ED presenta una buena aproximación a la solución en un tiempo razonable, es simple, sencillo de entender e implementar así como presenta pocos parámetros a sintonizar.
El esquema de ED que se utilizó para resolver el problema mostrado en la sección 3.4 fué el ED/RAND/1/BIN, en donde el término RAND indica que la forma como se selecciona el individuo base es aleatoria y que a su vez el número 1 indica que es una sola diferencia de un par de individuos el que modifica el individuo base en el proceso de mutación, y el término BIN indica que se realiza una cruza binomial.
El algoritmo de ED como la mayoría de los algoritmos evolutivos consta de los siguientes procesos: inicialización, mutación, cruza y selección. A continuación se realizará una descripción de los procesos del algoritmo de ED [28].
4.1Proceso de inicializaciónEn esta etapa se inicializa a la población de NP individuos, la cual representa a las posibles soluciones de dimensión D del problema de optimización. Con el propósito de cubrir, en la población inicial, el mayor espacio de búsqueda en el proceso de optimización, se establece que se genere cada individuo en forma pseudo-aleatoria, dentro del intervalo establecido por su valor límite inferior bj,L y superior bj,U del j−e´simo parámetro de diseño de cada individuo. Por lo tanto, el j−e´simo parámetro del i−e´simo individuo de la población inicial G=0 descrito por xi,j,G=0, se inicializa de acuerdo a lo descrito en (67), donde i=1, ..., NP, j=1..., D, G=1, ..., Gmax y rand(0, 1) es un número pseudo-aleatorio en el intervalo (0, 1)
4.2Proceso de mutaciónEl algoritmo de ED muta a la población para producir una población de NP vectores mutantes v→G∈RNP×D. La ecuación (68), muestra el proceso de mutación, donde el factor de escala F∈(0, 1) es el que controla la velocidad en la que la población evoluciona y es un factor importante para prevenir el estancamiento en el proceso de búsqueda [29]. Además los individuos r0, r1yr2 son elegidos de una manera pseudo-aleatoria de tal forma que se cumpla que r0≠r1≠r2≠i
4.3Proceso de cruzaEl proceso de cruza consiste en transmitir la información de los parámetros de diseño (combinar la información genética) entre los individuos padres (objetivo) xj,i,G y el vector mutante vj,i,G a un vector llamado hijo o de prueba uj,i,G con una factor de recombinación (factor de cruza) establecido con el parámetro CR∈(0, 1). En el caso particular del presente trabajo se utiliza la cruza uniforme o binomial, descrito en (69), debido a que por su desempeño, es el que más se ha utilizado en la literatura [29]. Un factor de cruza CR<0.5 indica que tiene mayor probabilidad de ser seleccionados los parámetros del vector padre que del vector hijo y viceversa
4.4Proceso de selecciónEn esta etapa, se compara el desempeño del vector hijo u→i,G con el vector padre x→i,G con el propósito de mantener el individuo más apto a la siguiente generación. Debido a que el esquema original de evolución diferencial no incluye un manejo de las soluciones en un espacio de búsqueda restringido, se incluye un enfoque similar al método de manejo de restricciones propuesta por Deb [30] para algoritmos genéticos.
Con el propósito de explicar el criterio de selección propuesto, a continuación se establecerán algunas definiciones particulares de este trabajo de los individuos cuando violan restricciones:
Definición 1 Un individuo se considera imaginario si su solución de diseño no es posible de realizar debido a que no cumple con las restricciones de estructura triangular y las de movimiento cinemático válido. Estos individuos no promueven la diversidad de los individuos ya que se encuentra en el espacio de búsqueda restringido imaginario.
Definición 2 Un individuo se considera no factible si cumple con las restricciones de estructura triangular y las de movimiento cinemático válido, pero no cumple con al menos una de las otras restricciones impuestas en el problema de optimización en cuestión. Estos individuos podrían promover la diversidad de los individuos en el espacio de búsqueda restringido real.
A partir de las definiciones previamente mencionadas, se puede expresar el mecanismo de manejo de restricciones (MMR) propuesta en este trabajo, el cual guía al algoritmo de ED hacia regiones factibles en el espacio de búsqueda de una manera más eficiente. Establece que de dos individuos (soluciones), el individuo que presenta mejor desempeño y que se prefiere que continúe a la siguiente generación, es aquel que cumple con alguno de los siguientes criterios:
- •
Si los dos individuos son factibles, pasa a la siguiente generación la que tiene mejor valor de aptitud.
- •
Un individuo factible o uno no factible pasa a la siguiente generación si compite con un individuo imaginario.
- •
Si los dos individuos son imaginarios, pasa a la siguiente generación el individuo hijo.
- •
Entre dos individuos no factibles, el que presenta un menor número de restricciones violadas pasa a la siguiente generación.
El MMR propuesto en este trabajo descarta las regiones de búsqueda en donde la solución no es posible de realizar (presentan valores imaginarios) y favorece a aquellas en donde se violan menos restricciones.
El pseudo-código del algoritmo ED/RAND/1/BIN con el manejo de restricciones propuesta en este trabajo se muestra en el algoritmo 1.
Algoritmo 1 Pseudo-código del algoritmo de evolución diferencial ED/RAND/1/BIN con el manejo de restricciones propuesto.1:
Begin
2:
G←0
3:
Crear una población aleatoria x→i,G,∀i=1,…,NP
4:
Evaluar Jx→i,G,gx→i,G,∀i=1,…,NP
5:
whileG<=Gmaxdo
6:
fori←1toNPdo
7:
Seleccionar aleatoriamente r0≠r1≠r2∈x→G.
8:
jrand←randint1,D
9:
forj←1toDdo
10:
Proceso de mutación y cruza
11:
end for
12:
Evaluar Ju→i,G+1,gu→i,G+1
13:
ifu→i,G+1 es mejor que x→i,Gthen(conbaseenelMMRpropuesto)
14:
x→i,G+1←u→i,G+1
15:
else
16:
x→i,G+1←xi,G
17:
end if
18:
end for
19:
G←G+1
20:
end while
21:
end
Para resolver el problema de síntesis dimensional con base en un problema de optimización descrito en la sección 3, se utilizó el algoritmo ED/RAND/1/BIN con el manejo de restricciones detallado en la sección 4. Se realizaron diez casos de estudio, en donde en cada caso de estudio se modificó el factor de cruza con los siguientes valores CR∈{0, 0.01, 0.05, 0.15, 0.3, 0.45, 0.6, 0.75, 0.9, 1}. Por cada caso de estudio se realizaron cuatro corridas. Los parámetros del algoritmo que permanecen constantes para todos los casos de estudio son el tamaño de población de veinte individuos NP=20 y el máximo número de generaciones de Gmax=500E3, además el factor de escala se selecciona de manera aleatoria en el intervalo F∈(0.3, 0.9) para cada generación.
Se utilizó el programa de Matlab® para implementar el algoritmo y resolver el problema de optimización en una computadora de escritorio con un procesador Intel Core i7 @3.50 GHz con 16GB en RAM. El tiempo de convergencia promedio de las cuarenta corridas es de 2h.
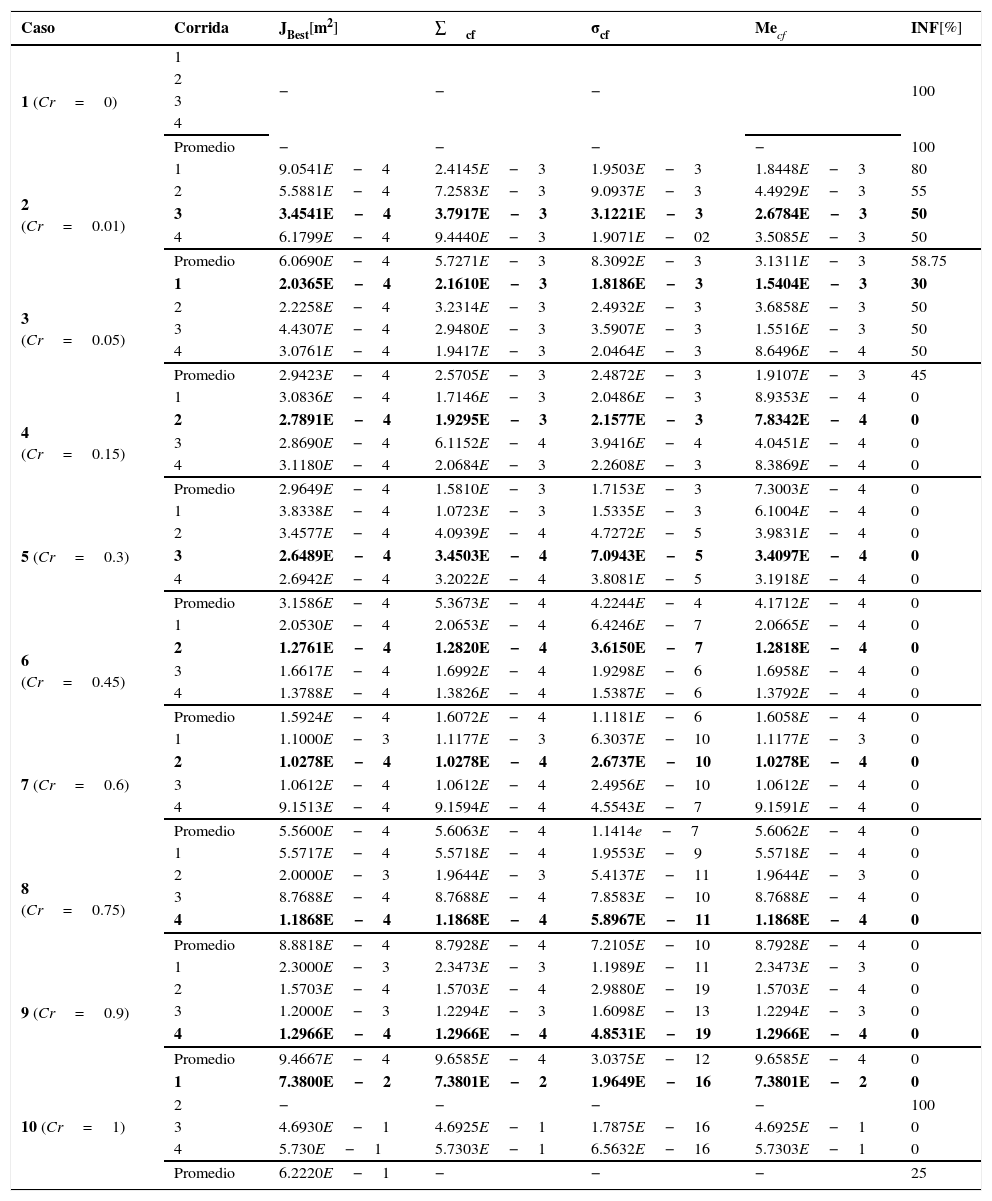
El concentrado de los resultados obtenidos con el algoritmo de ED se muestra en la tabla 4, cuya distribución es la siguiente: en la primer columna nombrada Caso se observan los diferentes casos de estudio; en la segunda columna nombrada Corrida se muestran las cuatro diferentes corridas para cada caso de estudio; en la tercer columna representada por JBest se muestra el valor de la función objetivo del mejor individuo factible en la última generación para cada corrida; en la cuarta, quinta y sexta columna se muestra el promedio, la desviación estándar y la mediana del valor de la función objetivo de los individuos factibles en la última generación para cada caso de análisis, y se denota por el símbolo ∑cf, Mecf y σcf, respectivamente. Por último, en la séptima columna representada por INF se obtiene el porcentaje de individuos no factibles en la última generación del total de la población NP para cada corrida.
Resultados obtenidos con el algoritmo ED/RAND/1/BIN con el manejo de restricciones propuesto al considerar los diferentes casos de estudio
| Caso | Corrida | JBest[m2] | ∑cf | σcf | Mecf | INF[%] |
|---|---|---|---|---|---|---|
| 1 (Cr=0) | 1 | − | − | − | 100 | |
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| Promedio | − | − | − | − | 100 | |
| 2 (Cr=0.01) | 1 | 9.0541E−4 | 2.4145E−3 | 1.9503E−3 | 1.8448E−3 | 80 |
| 2 | 5.5881E−4 | 7.2583E−3 | 9.0937E−3 | 4.4929E−3 | 55 | |
| 3 | 3.4541E−4 | 3.7917E−3 | 3.1221E−3 | 2.6784E−3 | 50 | |
| 4 | 6.1799E−4 | 9.4440E−3 | 1.9071E−02 | 3.5085E−3 | 50 | |
| Promedio | 6.0690E−4 | 5.7271E−3 | 8.3092E−3 | 3.1311E−3 | 58.75 | |
| 3 (Cr=0.05) | 1 | 2.0365E−4 | 2.1610E−3 | 1.8186E−3 | 1.5404E−3 | 30 |
| 2 | 2.2258E−4 | 3.2314E−3 | 2.4932E−3 | 3.6858E−3 | 50 | |
| 3 | 4.4307E−4 | 2.9480E−3 | 3.5907E−3 | 1.5516E−3 | 50 | |
| 4 | 3.0761E−4 | 1.9417E−3 | 2.0464E−3 | 8.6496E−4 | 50 | |
| Promedio | 2.9423E−4 | 2.5705E−3 | 2.4872E−3 | 1.9107E−3 | 45 | |
| 4 (Cr=0.15) | 1 | 3.0836E−4 | 1.7146E−3 | 2.0486E−3 | 8.9353E−4 | 0 |
| 2 | 2.7891E−4 | 1.9295E−3 | 2.1577E−3 | 7.8342E−4 | 0 | |
| 3 | 2.8690E−4 | 6.1152E−4 | 3.9416E−4 | 4.0451E−4 | 0 | |
| 4 | 3.1180E−4 | 2.0684E−3 | 2.2608E−3 | 8.3869E−4 | 0 | |
| Promedio | 2.9649E−4 | 1.5810E−3 | 1.7153E−3 | 7.3003E−4 | 0 | |
| 5 (Cr=0.3) | 1 | 3.8338E−4 | 1.0723E−3 | 1.5335E−3 | 6.1004E−4 | 0 |
| 2 | 3.4577E−4 | 4.0939E−4 | 4.7272E−5 | 3.9831E−4 | 0 | |
| 3 | 2.6489E−4 | 3.4503E−4 | 7.0943E−5 | 3.4097E−4 | 0 | |
| 4 | 2.6942E−4 | 3.2022E−4 | 3.8081E−5 | 3.1918E−4 | 0 | |
| Promedio | 3.1586E−4 | 5.3673E−4 | 4.2244E−4 | 4.1712E−4 | 0 | |
| 6 (Cr=0.45) | 1 | 2.0530E−4 | 2.0653E−4 | 6.4246E−7 | 2.0665E−4 | 0 |
| 2 | 1.2761E−4 | 1.2820E−4 | 3.6150E−7 | 1.2818E−4 | 0 | |
| 3 | 1.6617E−4 | 1.6992E−4 | 1.9298E−6 | 1.6958E−4 | 0 | |
| 4 | 1.3788E−4 | 1.3826E−4 | 1.5387E−6 | 1.3792E−4 | 0 | |
| Promedio | 1.5924E−4 | 1.6072E−4 | 1.1181E−6 | 1.6058E−4 | 0 | |
| 7 (Cr=0.6) | 1 | 1.1000E−3 | 1.1177E−3 | 6.3037E−10 | 1.1177E−3 | 0 |
| 2 | 1.0278E−4 | 1.0278E−4 | 2.6737E−10 | 1.0278E−4 | 0 | |
| 3 | 1.0612E−4 | 1.0612E−4 | 2.4956E−10 | 1.0612E−4 | 0 | |
| 4 | 9.1513E−4 | 9.1594E−4 | 4.5543E−7 | 9.1591E−4 | 0 | |
| Promedio | 5.5600E−4 | 5.6063E−4 | 1.1414e−7 | 5.6062E−4 | 0 | |
| 8 (Cr=0.75) | 1 | 5.5717E−4 | 5.5718E−4 | 1.9553E−9 | 5.5718E−4 | 0 |
| 2 | 2.0000E−3 | 1.9644E−3 | 5.4137E−11 | 1.9644E−3 | 0 | |
| 3 | 8.7688E−4 | 8.7688E−4 | 7.8583E−10 | 8.7688E−4 | 0 | |
| 4 | 1.1868E−4 | 1.1868E−4 | 5.8967E−11 | 1.1868E−4 | 0 | |
| Promedio | 8.8818E−4 | 8.7928E−4 | 7.2105E−10 | 8.7928E−4 | 0 | |
| 9 (Cr=0.9) | 1 | 2.3000E−3 | 2.3473E−3 | 1.1989E−11 | 2.3473E−3 | 0 |
| 2 | 1.5703E−4 | 1.5703E−4 | 2.9880E−19 | 1.5703E−4 | 0 | |
| 3 | 1.2000E−3 | 1.2294E−3 | 1.6098E−13 | 1.2294E−3 | 0 | |
| 4 | 1.2966E−4 | 1.2966E−4 | 4.8531E−19 | 1.2966E−4 | 0 | |
| Promedio | 9.4667E−4 | 9.6585E−4 | 3.0375E−12 | 9.6585E−4 | 0 | |
| 10 (Cr=1) | 1 | 7.3800E−2 | 7.3801E−2 | 1.9649E−16 | 7.3801E−2 | 0 |
| 2 | − | − | − | − | 100 | |
| 3 | 4.6930E−1 | 4.6925E−1 | 1.7875E−16 | 4.6925E−1 | 0 | |
| 4 | 5.730E−1 | 5.7303E−1 | 6.5632E−16 | 5.7303E−1 | 0 | |
| Promedio | 6.2220E−1 | − | − | − | 25 |
De acuerdo a los resultados mostrados en la tabla 4, se puede observar lo siguiente:
- •
En letra negrita se muestran las mejores corridas i.e., aquellas cuyos individuos son factibles y encuentran una mejor aptitud, para cada caso de estudio. Se observa en la columna JBest que en promedio el caso 6 (CR=0.45) presenta una mejor convergencia hacia mejores soluciones en las diferentes corridas y que a partir de un cambio del factor de cruza CR=0.45, la convergencia del algoritmo de ED tiende hacia peores resultados. Los resultados indican que existe una relación entre el factor de cruza (eje de abscisas) y la obtención de mejores soluciones (eje de la ordenadas). Esta relación presenta un comportamiento con concavidad negativa en el punto CR=0.45 por lo que los mejores resultados se encuentran alrededor del valor de factor de cruza CR=0.45.
- •
Con excepción del caso 1 y del 10, todos los restantes casos de estudio proporcionan un resultado aceptable i.e., JBest<9.5E−4. De los mejores casos de estudio (JBest<4E−4) se encuentran los casos 3−6, en los cuales se escoge un factor de cruza en el intervalo CR∈[0.05, 0.45]. Por lo que para obtener mejores resultados, se requiere de un máximo de alrededor del 45% de la información de los parámetros del vector hijo para dirigir la búsqueda hacia regiones con mejores soluciones.
- •
Para uno de los mejores casos de estudio (caso 3), se observa la presencia de individuos no factibles en la población de la última generación (ver columna INF). Conforme disminuye el valor del factor de cruza se aumenta en promedio la generación de individuos no factibles.
- •
Cuando al problema de la síntesis dimensional del mecanismo de marcha no se le incluye el proceso de cruza en el algoritmo de ED, el proceso de búsqueda únicamente encuentra individuos imaginarios como se observa en el caso 1 marcado con un guión, por tal motivo la importancia de la selección adecuada del factor de cruza en la solución del problema.
- •
Los individuos factibles generados en la última generación para los casos de estudio 2−4, no presentan en promedio, una convergencia hacia el mejor individuo JBest (ver columna 4 de la tabla 4) por lo que en la población en la última generación existe diversidad en las soluciones (exploración del espacio de búsqueda), como lo indica la desviación estándar de la columna 5 de la tabla 4. Además, la mediana se encuentra con un valor mayor al mejor individuo (ver columna 6 de la tabla 4), indicando que menos del 50% de los individuos se aproximan al mejor individuo. Lo descrito anteriormente no sucede para los casos 5−9 en donde se observa una convergencia hacia el mejor individuo JBest (explotación del espacio de búsqueda). Por lo tanto se atribuye que con el factor de cruza en el intervalo de CR∈[0.01, 0.15] se promueve la exploración del espacio de búsqueda y con CR∈[0.3, 0.9] se promueve la explotación de los individuos.
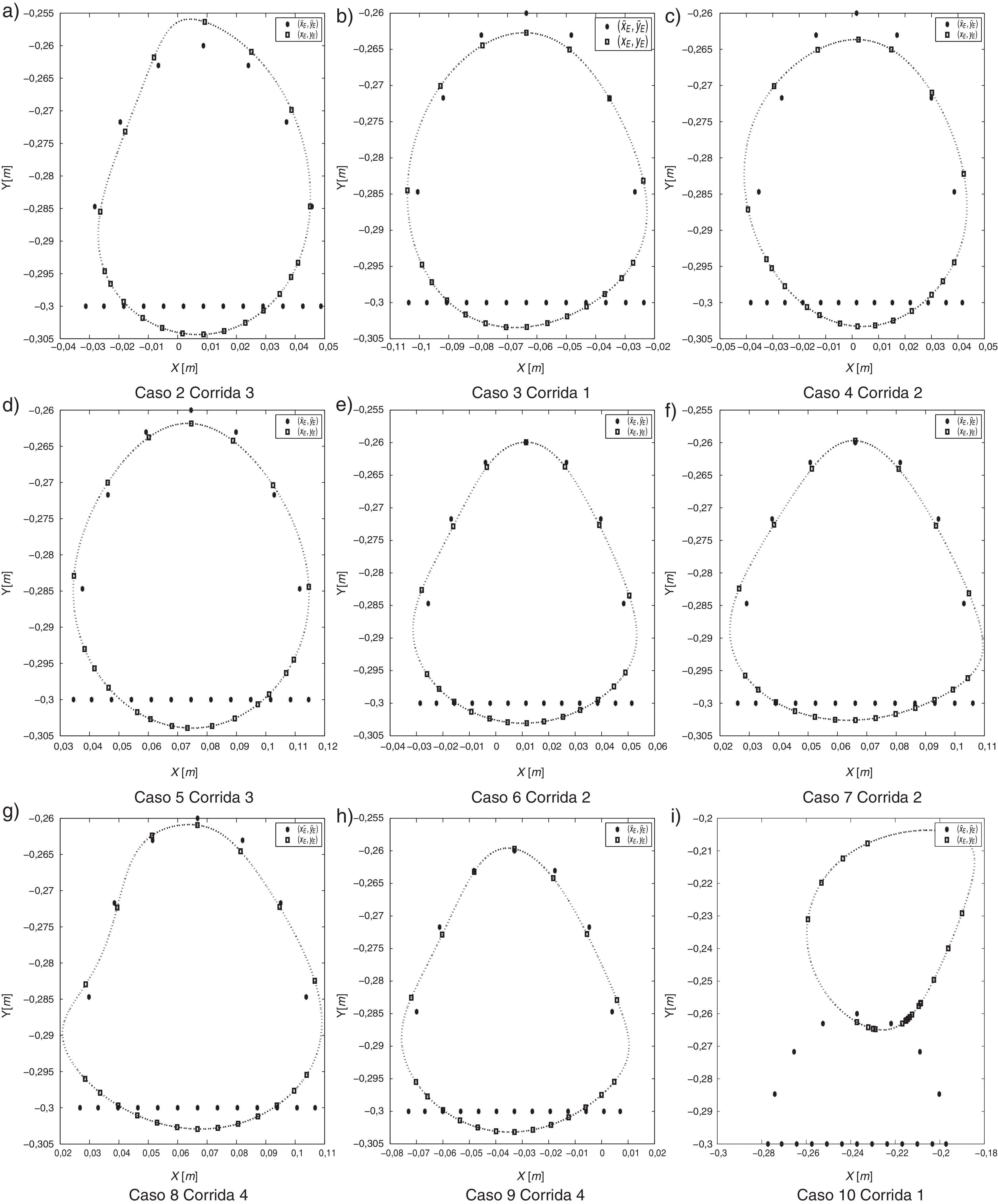
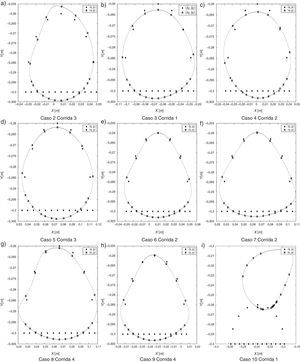
Con el propósito de analizar el desempeño del seguimiento de la trayectoria deseada en el mecanismo de marcha obtenido con las mejores corridas de cada caso de estudio, se incluye la tabla 5, en donde en la cuarta columna nombrada d¯ y la quinta nombrada σd¯, representan el promedio y la desviación estándar de la distancia Euclidiana que existe entre el vector de coordenadas Cartesianas deseadas (x¯E,y¯E) (trayectoria deseada) y el vector de coordenadas generadas por el mecanismo (xE, yE), respectivamente. Estas dos medidas nos indicarán que tan cerca se encuentra la trayectoria deseada de la trayectoria generada por el mecanismo. Mientras más se aproxime d¯ a cero, las coordenadas generadas por el mecanismo corresponderán de una manera más fiel al vector de coordenadas deseadas. Con base en estas dos medidas, se establece que el mejor diseño obtenido es generado por el caso 6, en donde en promedio, se presenta el menor error entre la trayectoria deseada y la generada por el mecanismo de 2.3320E−3m. Así mismo, el error entre los puntos es más uniforme que en los demás casos pudiéndose observar en la columna 5 de la tabla 5.
Resultados del desempeño en el seguimiento de la trayectoria deseada en los diseños de mecanismos de marcha obtenidos en los casos de estudio
| Caso | Corrida | JBest[m2] | d¯[m] | σd¯ |
|---|---|---|---|---|
| 1 (Cr=0) | 1 | − | − | − |
| 2 | ||||
| 3 | ||||
| 4 | ||||
| Promedio | − | − | − | |
| 2 (Cr=0.01) | 1 | 9.0541E−4 | 4.8952E−3 | 4.7359E−3 |
| 2 | 5.5881E−4 | 4.3600E−3 | 3.0661E−3 | |
| 3 | 3.4541E−4 | 3.3919E−3 | 2.4635E−3 | |
| 4 | 6.1799E−4 | 4.4025E−3 | 3.4820E−3 | |
| Promedio | 6.0690E−4 | 4.2624E−3 | 3.8543E−3 | |
| 3 (Cr=0.05) | 1 | 2.0365E−4 | 2.7912E−3 | 2.3090E−3 |
| 2 | 2.2258E−4 | 2.6444E−3 | 2.0865E−3 | |
| 3 | 4.4307E−4 | 3.9124E−3 | 2.6846E−3 | |
| 4 | 3.0761E−4 | 3.0387E−3 | 2.5438E−3 | |
| Promedio | 2.9423E−4 | 3.0967E−3 | 2.4060E−3 | |
| 4 (Cr=0.15) | 1 | 3.0836E−4 | 3.5113E−3 | 1.8033E−3 |
| 2 | 2.7891E−4 | 3.2804E−3 | 1.8307E−3 | |
| 3 | 2.8690E−4 | 3.1036E−3 | 2.2273E−3 | |
| 4 | 3.1180E−4 | 3.4330E−3 | 2.0012E−3 | |
| Promedio | 2.9649E−4 | 3.3321E−3 | 1.9656E−3 | |
| 5 (Cr=0.3) | 1 | 3.8338E−4 | 3.5970E−3 | 2.5609E−3 |
| 2 | 3.4577E−4 | 3.8131E−3 | 1.7011E−3 | |
| 3 | 2.6489E−4 | 3.1519E−3 | 1.8665E−3 | |
| 4 | 2.6942E−4 | 3.1640E−3 | 1.9084E−3 | |
| Promedio | 3.1586E−4 | 3.4315E−3 | 2.0092E−3 | |
| 6 (Cr=0.45) | 1 | 2.0530E−4 | 2.6312E−3 | 1.8755E−3 |
| 2 | 1.2761E−4 | 2.0959E−3 | 1.4464E−3 | |
| 3 | 1.6617E−4 | 2.3942E−3 | 1.6468E−3 | |
| 4 | 1.3788E−4 | 2.2068E−3 | 1.4598E−3 | |
| Promedio | 1.5924E−4 | 2.3320E−3 | 1.6071E−3 | |
| 7 (Cr=0.6) | 1 | 1.1000E−3 | 4.0461E−3 | 6.4493E−3 |
| 2 | 1.0278E−4 | 1.9057E−3 | 1.2597E−3 | |
| 3 | 1.0612E−4 | 1.9398E−3 | 1.2746E−3 | |
| 4 | 9.1513E−4 | 4.6847E−3 | 5.0063E−3 | |
| Promedio | 5.5600E−4 | 3.1441E−3 | 3.4975E−3 | |
| 8 (Cr=0.75) | 1 | 5.5717E−4 | 3.8630E−3 | 3.6901E−3 |
| 2 | 2.0000E−3 | 7.5985E−3 | 6.5279E−3 | |
| 3 | 8.7688E−4 | 5.2541E−3 | 4.1344E−3 | |
| 4 | 1.1868E−4 | 2.0487E−3 | 1.3521E−3 | |
| Promedio | 8.8818E−4 | 4.6911E−3 | 3.9261E−3 | |
| 9 (Cr=0.9) | 1 | 2.3000E−3 | 7.6882E−3 | 7.8310E−3 |
| 2 | 1.5703E−4 | 2.2993E−3 | 1.6430E−3 | |
| 3 | 1.2000E−3 | 4.7539E−3 | 6.3967E−3 | |
| 4 | 1.2966E−4 | 2.1286E−3 | 1.4334E−3 | |
| Promedio | 9.4667E−4 | 4.2175E−3 | 4.3260E−3 | |
| 10 (Cr=1) | 1 | 7.3800E−2 | 5.4684E−2 | 2.7138E−2 |
| 2 | − | − | − | |
| 3 | 4.6930E−1 | 1.5214E−1 | 1.8277E−2 | |
| 4 | 5.730E−1 | 1.6833E−1 | 1.8242E−2 | |
| Promedio | − | − | − |
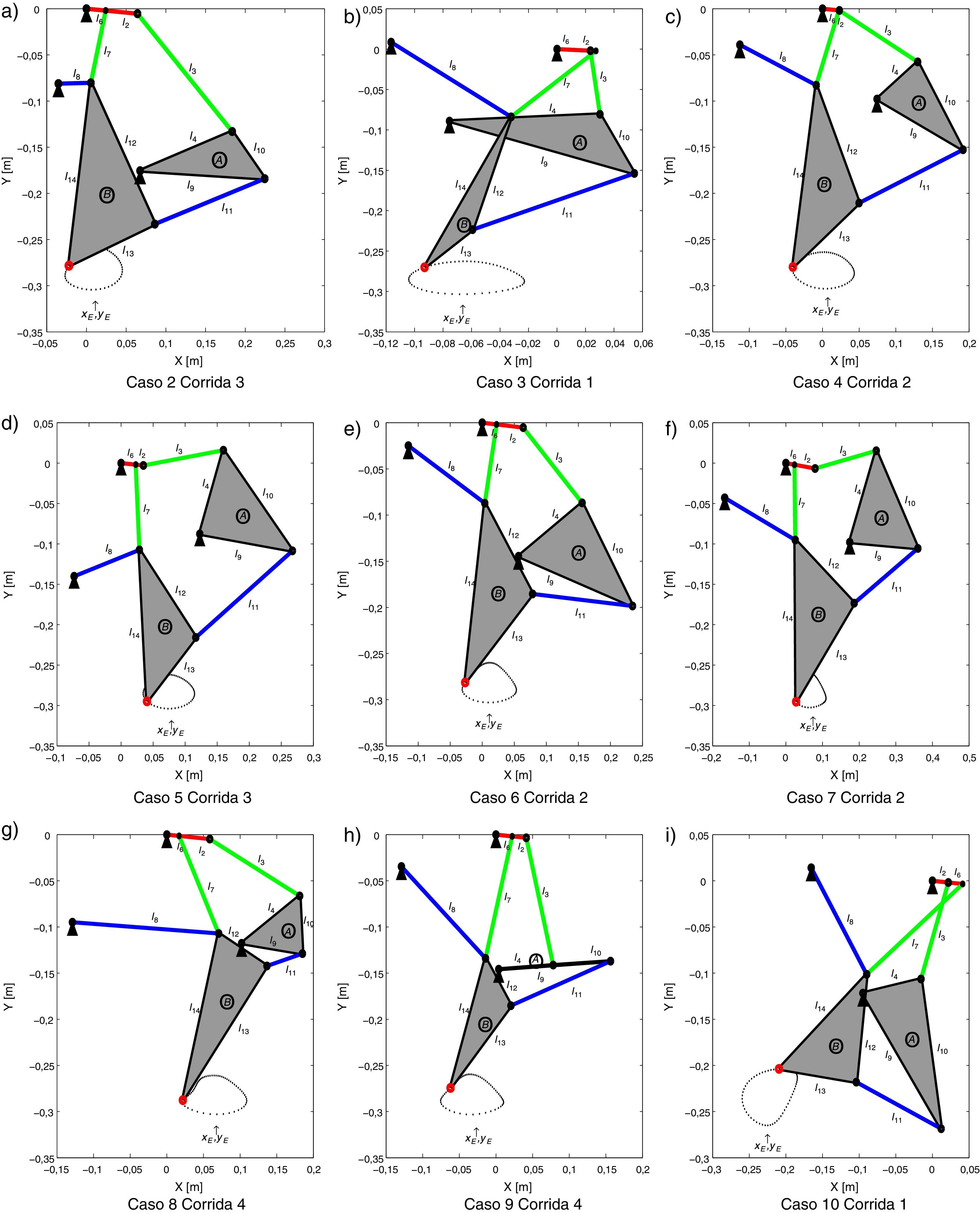
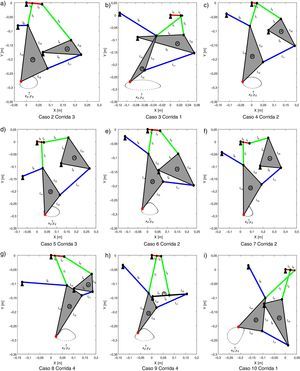
A continuación se procede a seleccionar la mejor solución de diseño de cada caso de estudio y se compara el error entre la trayectoria generada por el mecanismo y las coordenadas deseadas. En la tabla 6 se muestra las variables de diseño de cada una de las soluciones que se tomaron en consideración y en la figura 7 se puede observar el comportamiento del mecanismo de marcha a través de los diferentes diseños. La línea punteada representa el movimiento del mecanismo cuando la manivela gira completamente, i.e., θ2∈[0, 2π]. Mientras que el marcador cuadrado representa las coordenadas específicas (xE, yE) en el movimiento del mecanismo de marcha que se van a comparar con las coordenadas deseadas (x¯E,y¯E) marcadas con puntos grandes. Se puede observar que para el caso 10 el mecanismo de marcha no sigue a las coordenadas deseadas ya que tiene un error promedio mayor a 5.4684E−2 m como se muestra numéricamente en la distancia d¯ de la tabla 5. Se puede observar en la figura 6 y en la figura 7 así como verificarse numéricamente en la tabla 5 que los diseños de mecanismo de marcha que mejor sigue a las coordenadas deseadas son los obtenidos en los casos de estudio 3−7 ya que presentan un error promedio en el intervalo [2.3E−3, 3.5E−3] m y pueden reproducir, en gran medida, el movimiento de marcha pre-establecido considerando las restricciones impuestas en el diseño.
Variables de diseño p de una corrida en cada caso de estudio
| Caso | Corrida | l1[m] | l2[m] | l3[m] | l4[m] | l5[m] | l6[m] | l7[m] | l8[m] | l9[m] | l10[m] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 0.1880 | 0.0644 | 0.1747 | 0.1235 | 0.0885 | 0.0243 | 0.0804 | 0.0408 | 0.1573 | 0.0656 |
| 3 | 1 | 0.11680 | 0.02354 | 0.07896 | 0.10599 | 0.11676 | 0.02744 | 0.10104 | 0.12504 | 0.14507 | 0.07716 |
| 4 | 2 | 0.1229 | 0.0231 | 0.1205 | 0.0685 | 0.1194 | 0.0224 | 0.0867 | 0.1131 | 0.1296 | 0.1134 |
| 5 | 3 | 0.1509 | 0.0349 | 0.1262 | 0.1100 | 0.1581 | 0.0229 | 0.1057 | 0.1069 | 0.1461 | 0.1647 |
| 6 | 2 | 0.1554 | 0.0641 | 0.1228 | 0.1148 | 0.1179 | 0.0224 | 0.0873 | 0.1346 | 0.1859 | 0.1366 |
| 7 | 2 | 0.2000 | 0.0800 | 0.1684 | 0.1344 | 0.1726 | 0.0235 | 0.0933 | 0.1997 | 0.1861 | 0.1659 |
| 8 | 4 | 0.1559 | 0.0588 | 0.1373 | 0.0944 | 0.1601 | 0.0168 | 0.1186 | 0.2000 | 0.0837 | 0.0626 |
| 9 | 4 | 0.1458 | 0.0416 | 0.1427 | 0.0746 | 0.1336 | 0.0222 | 0.1370 | 0.1519 | 0.1529 | 0.0783 |
| 10 | 1 | 0.1544 | 0.0218 | 0.1110 | 0.0809 | 0.1660 | 0.0415 | 0.1636 | 0.1380 | 0.1817 | 0.1645 |
| Caso | Corrida | l11[m] | l12[m] | l13[m] | l14[m] | θ1[rad] | θ5[rad] | x¯ini | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 0.1470 | 0.1730 | 0.1171 | 0.2000 | 5.0798 | 4.3021 | −0.0312 | |||
| 3 | 1 | 0.13320 | 0.14216 | 0.05748 | 0.19582 | 4.00966 | 3.06881 | −0.10361 | |||
| 4 | 2 | 0.1532 | 0.1403 | 0.1139 | 0.1994 | 5.3625 | 3.4755 | −0.0383 | |||
| 5 | 3 | 0.1850 | 0.1396 | 0.1097 | 0.1878 | 5.6630 | 4.2310 | 0.0346 | |||
| 6 | 2 | 0.1565 | 0.1233 | 0.1423 | 0.1965 | 5.0853 | 3.3543 | −0.0286 | |||
| 7 | 2 | 0.1867 | 0.1788 | 0.2000 | 0.2000 | 5.7712 | 3.3936 | 0.0261 | |||
| 8 | 4 | 0.0502 | 0.0748 | 0.1852 | 0.1870 | 5.4266 | 3.7761 | 0.0268 | |||
| 9 | 4 | 0.1442 | 0.0618 | 0.1214 | 0.1482 | 4.7379 | 3.4032 | −0.0730 | |||
| 10 | 1 | 0.1265 | 0.1175 | 0.1064 | 0.1575 | 4.0496 | 3.0570 | −0.2772 | |||
| Caso | Corrida | θ21[rad] | θ22[rad] | θ23[rad] | θ24[rad] | θ25[rad] | θ26[rad] | θ27[rad] | θ28[rad] | θ29[rad] | θ210[rad] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 5.3962 | 5.2603 | 5.1150 | 4.9906 | 4.8715 | 4.7516 | 4.6313 | 4.4978 | 4.3689 | 4.2319 |
| 3 | 1 | 4.91129 | 4.78188 | 4.64298 | 4.50304 | 4.36735 | 4.23537 | 4.10417 | 3.96653 | 3.81810 | 3.63569 |
| 4 | 2 | 5.5159 | 5.3950 | 5.2230 | 5.1351 | 4.9973 | 4.8814 | 4.7633 | 4.6361 | 4.4924 | 4.3137 |
| 5 | 3 | 6.1597 | 6.0228 | 5.8078 | 5.7216 | 5.5893 | 5.4965 | 5.3478 | 5.2033 | 5.0383 | 4.9461 |
| 6 | 2 | 5.4254 | 5.3273 | 5.2332 | 5.1433 | 5.0585 | 4.9694 | 4.8862 | 4.7874 | 4.6866 | 4.5642 |
| 7 | 2 | 6.0796 | 5.9777 | 5.8853 | 5.7986 | 5.7149 | 5.6310 | 5.5448 | 5.4526 | 5.3504 | 5.2317 |
| 8 | 4 | 5.6133 | 5.5243 | 5.4434 | 5.3668 | 5.2921 | 5.2173 | 5.1403 | 5.0589 | 4.9704 | 4.8717 |
| 9 | 4 | 4.9453 | 4.8455 | 4.7554 | 4.6723 | 4.5934 | 4.5166 | 4.4398 | 4.3610 | 4.2771 | 4.1848 |
| 10 | 1 | 2.5346 | 4.9874 | 5.5911 | 5.2973 | 1.9328 | 2.7691 | 3.4190 | 2.9441 | 3.4451 | 2.9707 |
| Caso | Corrida | θ1111[rad] | θ212[rad] | θ213[rad] | θ214[rad] | θ215[rad] | θ216[rad] | θ217[rad] | θ218[rad] | θ219[rad] | θ220[rad] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4.1125 | 4.0202 | 3.6849 | 3.0474 | 2.4450 | 1.7956 | 0.7527 | 0.1494 | 5.8829 | 5.4840 |
| 3 | 1 | 3.40473 | 3.20009 | 2.50535 | 1.87675 | 1.30348 | 0.76677 | 0.26209 | 6.02176 | 5.33888 | 5.01058 |
| 4 | 2 | 4.1875 | 4.0254 | 3.3268 | 2.6398 | 2.0348 | 1.5937 | 1.0804 | 0.5174 | 5.8661 | 5.5719 |
| 5 | 3 | 4.7756 | 4.6779 | 4.1712 | 3.3552 | 2.8043 | 2.2555 | 1.7007 | 1.1544 | 0.4614 | 0.0026 |
| 6 | 2 | 4.4207 | 4.2743 | 3.5421 | 2.9951 | 2.4347 | 1.7711 | 1.0499 | 0.3915 | 6.1310 | 5.5286 |
| 7 | 2 | 5.0849 | 4.9163 | 3.9068 | 3.3822 | 2.8750 | 2.2369 | 1.5078 | 0.9490 | 0.4695 | 6.1784 |
| 8 | 4 | 4.7593 | 4.6483 | 4.0197 | 3.4936 | 2.9717 | 2.3803 | 1.7965 | 0.9470 | 0.2671 | 5.7049 |
| 9 | 4 | 4.0771 | 3.9588 | 3.1150 | 2.5708 | 2.0309 | 1.4121 | 0.6670 | 0.0032 | 5.7081 | 5.0442 |
| 10 | 1 | 2.9954 | 3.0573 | 2.9071 | 3.5033 | 4.6387 | 3.6319 | 2.7624 | 3.0065 | 2.7979 | 2.2580 |
Para validar los resultados numéricos obtenidos, se llevó a cabo la manufactura del mecanismo de marcha con el diseño obtenido en la corrida 1 del caso de estudio 3. El proceso de manufactura se llevó a cabo utilizando un programa de diseño asistido por computadora y una impresora 3D. En la figura 8 se muestra el prototipo experimental del diseño obtenido para el mecanismo de marcha del robot bípedo en el plano sagital.
Con el objetivo de mostrar la trayectoria que genera el prototipo experimental, se extrajo un conjunto de imágenes consecutivas obtenidas a partir del movimiento de marcha del mecanismo y se muestra en la figura 9. Se puede observar que la trayectoria que genera es similar a la obtenida en simulación, por lo que con el planteamiento del problema de optimización así como la técnica de optimización de evolución diferencial con el mecanismo de manejo de restricciones, permitió obtener, de manera satisfactoria, el diseño del mecanismo de tal forma que reproduzca el movimiento de marcha en el plano sagital y ésta puede ser utilizada como extremidad de un robot bípedo para una futura aplicación.
6ConclusionesEn este trabajo se propone un mecanismo de ocho eslabones con el propósito de reproducir una trayectoria de dos grados de libertad en el espacio Cartesiano (similar a la marcha en el plano sagital) con el mecanismo propuesto de un grado de libertad. El diseño del mecanismo propuesto se obtiene a través del establecimiento formal de un problema de optimización no lineal con restricciones y de la incorporación de un manejo de restricciones en el algoritmo de evolución diferencial que rechaza a las soluciones de diseño que no son físicamente realizables (imaginarías) y guía la búsqueda hacia regiones factibles con mejor desempeño en el diseño. Resultados experimentales comprueban el enfoque de diseño.
Del análisis del algoritmo de evolución diferencial con diferentes factores de cruza, se puede concluir que una baja probabilidad (menor al 45%) de recombinación con el vector hijo, promueve la búsqueda de regiones con mejores soluciones. Así mismo, mientras menos probabilidad de recombinación con el vector hijo exista, se generan más individuos no factibles. Por otro lado, se observa que con una alta probabilidad de recombinación del vector hijo, se presenta una convergencia prematura en el algoritmo, por lo que la búsqueda de soluciones de diseño se podría quedar estancado en mínimos locales.
El diseño obtenido con el enfoque de diseño propuesto a través de un problema de optimización numérica, indica que el mecanismo de un grado de libertad puede reproducir la marcha con una aproximación en el intervalo [2.3E−3, 3.5E−3] m (dependiendo del caso de estudio) a pesar de que la trayectoria sea de dos grados de libertad.
Dentro del trabajo futuro y con el propósito de promover la búsqueda de mejores soluciones en el seguimiento del mecanismo de los puntos deseados, se pretende analizar el desempeño de diferentes algoritmos evolutivos con diferentes mecanismos para explotar mejor las soluciones en el espacio de búsqueda así como incluir el ángulo de desfase entre las manivelas de los dos M4B como una variable de diseño adicional que permitirá un grado de movimiento adicional en el espacio de búsqueda.
Este trabajo fue apoyado en parte por la Secretaría de Investigación y Posgrado del Instituto Politécnico Nacional (SIP-IPN) bajo el proyecto SIP−20160826 y en parte por el Consejo Nacional de Ciencia y Tecnología (CONACYT) bajo el proyecto 182298.