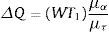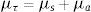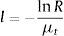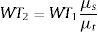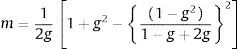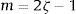Uno de los principales retos en óptica biomédica y en biofotónica es la simulación de la propagación de la luz en los tejidos biológicos. El método de Monte Carlo es la aproximación más empleada, y se puede afirmar que constituye un estándar por su flexibilidad y fiabilidad en modelar la geometría de un tejido heterogéneo.
Este trabajo muestra cómo analizar el comportamiento óptico de la piel y cómo algunas de las deducciones extraídas de este análisis pueden aportar información para el diagnóstico y el tratamiento de pieles. Se han aplicado las propiedades ópticas de pieles sanas de diferentes razas y, como alteración posible en la piel, se ha estudiado la presencia del basalioma. Los resultados nos ofrecen un método para distinguir entre piel «sana» y piel «enferma», lo que podría facilitar un procedimiento de identificación de pieles cancerígenas. Del estudio de los distintos tipos de pieles sanas se desprende, además, un ejemplo de aplicación inmediata que se beneficia del conocimiento adquirido por los valores obtenidos (fotodepilación).
En este trabajo se presentan los resultados más significativos de los programas de simulación basados en técnicas de Monte Carlo, que permiten estudiar el comportamiento de la piel frente a una radiación óptica. La aproximación a la trayectoria que sigue la luz en su interacción con el tejido se obtiene a partir de las propiedades ópticas conocidas a priori. Se realiza una aproximación general al tema, identificando los principales problemas que se plantean en este tipo de estudios y se emplea un programa comercial.
In both biomedical optics and biophotonics, one of the main challengers is the simulation of light spread in biological tissues. The approximation which is most used is Monte Carlo's method; it is a standard because of its flexibility and its reliability modeling heterogeneous tissues.
This paper shows how to analyse the optical behaviour of the skin, and how some of the deductions drawn from this analysis can add information for the diagnosis and treatment of skins. The optic qualities of healthy skins from different races have been applied; and as a possible alteration in the skin, basalioma presence has been studied. The results provide us with a method to distinguish between “healthy” and “ill” skin, which could make the procedure to identify cancer skins easier. From the study of the different healthy skins an example of immediate application also appears which benefits from the knowledge acquired from the values obtained (photodepilation).
In this work the most valued results of the simulation programs based in Monte Carlo's technics are presented, which allow studying the skin's behaviour facing an optical radiation; the approximation to the light trajectory interacting with the tissues is obtained from the optic qualities known before. First of all, a general approach to the theme is carried out, identifying the main problems that appear in this kind of studies and a commercial programme is used.
Los tejidos biológicos son medios de difícil estudio y caracterización ya que ante las radiaciones ópticas se comportan como medios no homogéneos y anisotrópicos, es decir, su estructura y composición no son uniformes y presentan distintas propiedades según la dirección del tejido [1].
Los tejidos biológicos son medios absorbentes cuyo índice de refracción medio es mayor que el del aire, siendo esta característica la responsable de la reflexión parcial de la radiación en la interfaz tejido-aire (reflexión de Fresnel), mientras que el resto penetra en el tejido.
El scattering y la absorción son los responsables, primero, del ensanchamiento del patrón de radiación del láser y de la disminución posterior a medida que viaja a través del tejido, mientras que el scattering a granel (bulk scattering) es la principal causa de la dispersión de una gran fracción de la radiación en la dirección opuesta a la propagación inicial. Por lo tanto, la propagación de luz dentro de un tejido depende de las propiedades de scattering y de la absorción de sus componentes: células, orgánulos celulares y diversos elementos de fibra [2]. El tamaño, la forma y la densidad de estas estructuras, su índice de refracción con respecto a la sustancia fundamental del tejido y los estados de polarización de la luz incidente juegan un papel importante en la propagación de la luz en los tejidos [3].
Los medios biológicos son a menudo modelados como conjuntos homogéneos de partículas esféricas, ya que muchas células y microorganismos, especialmente las células de la sangre, tienen forma de esferas o elipsoides. Un sistema sin interacción de partículas esféricas es el modelo más simple de tejido.
La teoría de Mie describe rigurosamente la difracción de la luz en una partícula esférica [4]. El desarrollo de este modelo consiste en trabajar con las estructuras de las partículas esféricas que se basa en la descomposición de ondas electromagnéticas incidentes dentro y fuera de la esfera dispersora en ondas esféricas en términos de funciones armónicas adaptadas a las condiciones de contorno de la partícula (mediante transformadas de Fourier)[5]. En la óptica de tejidos, debido a la complejidad de los sistemas, debemos añadir también a la teoría de Mie algunas complejidades como las esferas multicapa [6], en las que cada una presenta distintas capas con distintas propiedades o esferas monocapa, pero con homogeneidad no radial, anisotropía y/o actividad óptica en cada esfera.
A partir de que Wilson y Adam [7] incorporaran de forma innovadora las simulaciones de Monte Carlo (MC) en las interacciones de los tejidos biológicos con los láseres su uso ha ido aumentando, convirtiéndose en el método más utilizado y preferido por la comunidad científica [8] y llegando a proporcionar resultados comparables con los resultados experimentales [9,10]. Dicho método ofrece una solución rigurosa al problema del transporte de la luz por medios difusos y anisotrópicos, como el caso de un tejido biológico. Este método se utiliza para calcular numéricamente expresiones matemáticamente complejas y difíciles de evaluar con exactitud, o que no pueden resolverse analíticamente.
El simulador define los parámetros de propagación del fotón en forma de funciones de densidad de probabilidad, que describen la probabilidad de absorción o de una determinada dirección con el ángulo de scattering. Cada capa de tejido está descrita por los siguientes parámetros: el grosor, el índice de refracción, el coeficiente de absorción μa, el coeficiente de scattering μs y el factor de anisotropía g. También se tienen en cuenta los índices de refracción de los medios superiores e inferiores del tejido en estudio.
El coeficiente de absorción μa y el de scattering μs se definen como la probabilidad de la atenuación de la radiación incidente debido a la absorción o al scattering por la unidad incremental de la longitud del camino del fotón. Y g es la medida de la anisotropía de un medio que se puede caracterizar como el valor medio del coseno del ángulo de scattering[11].
El simulador de MC usado en este trabajo aborda el transporte de múltiples haces de un láser incidentes sobre distintos tipos de pieles, así como de una piel con basalioma, obteniendo un método para la caracterización y el diagnóstico de dicha enfermedad en las pieles.
Los parámetros ópticos introducidos en el simulador son los coeficientes de scattering, absorción y anisotropía de cada capa del objeto simulado, mientras que las propiedades ópticas que vamos a calcular serán la reflectancia, la transmitancia y la densidad de potencia en unidades de irradiancia, para comparar su valor en cada tipo de pieles y observar las diferencias que presentan.
En el siguiente apartado se describe la ecuación analítica que define la propagación de la luz en la piel; a continuación, en el apartado 3, se expone brevemente en qué consiste la simulación de MC y se presentan los parámetros más significativos. En el apartado 4 se indica el método de análisis empleado para realizar la simulación y obtener los resultados mostrados en el apartado 5 para los diferentes tipos de pieles. Por último, se resumen los datos relevantes del trabajo y los pasos que se deberían seguir para continuar con este tipo de estudios.
2Descripción de la interacción de la luz con los tejidos: ecuación de transporte radiativoLa propagación de la radiación luminosa a través de los sistemas biológicos se puede definir a partir de la teoría electromagnética fundamental, ya que el tejido biológico se puede considerar como un medio con una permitividad que varía espacialmente, y las variaciones del campo se podrían describir utilizando las ecuaciones de Maxwell [12].
Debido a la complejidad del problema por el desconocimiento de la permitividad variante del medio, la cantidad de procesos involucrados y la necesidad de mucho tiempo para poder llegar a la solución, el planteamiento con ecuaciones de Maxwell no es factible y necesitamos usar aproximaciones más o menos complejas, dependiendo del problema que queramos tratar para poder hallar soluciones satisfactorias.
La resolución de la ecuación analítica requiere por tanto de métodos numéricos. Recordemos la ecuación de transporte radiativo (ETR) de la propagación de la luz en medios no homogéneos, que se obtiene considerando cambios en el flujo de energía entrante, saliente, absorbida y emitida dentro de un volumen infinitesimal:
donde la variación del número de fotones que salen y entran del volumen por unidad de tiempo en la dirección de interés es: s→⋅∇L(r,s→,t)+1c∂L(r,s→,t)∂t; y debe ser igual a la atenuación de la intensidad lumínica por scattering y absorción, respectivamente, en la dirección de interés: (μa+μs)L(r,s→); más el incremento de la energía en la dirección debido al scattering de la luz entrante desde otras direcciones: μs∫4πL(r,s→,t)p(s→,s′→)dΩ′; más la fuente de fotones local que pudiera existir, en la posición r, y que se indica con: q(r,s→,t).Más en detalle podemos observar que según la teoría de transporte radiativo, la radiancia L(r,s→) de la luz en la posición r, que se propaga en la dirección descrita por el vector unitario s→ es disminuida debido a la absorción y al scattering, y aumentada por la luz que se propaga en dirección s′→ pero que ha sido dispersada en dirección s→.
En la ecuación (1), dΩ’ es el ángulo sólido diferencial en la dirección s→ y p(s→,s′→) es la función de fase, que es una función de densidad de probabilidad que describe los cambios en la dirección de los fotones entre s→ y s′→.
La ETR asume que las partículas (que causan la absorción y el scattering) están uniformemente distribuidas a través del medio y que no hay interacciones entre ellas.
Puesto que la integral de la función de fase es una función de densidad de probabilidad, está normalizada y se trata de la probabilidad de scattering de la dirección descrita por s→ a la dirección descrita por el vector s′→.
La función de fase no suele ser conocida. Dicha función se caracteriza por el parámetro g (factor de anisotropía):
3Descripción de la simulación de Monte CarloEl desarrollo de nuevos métodos iterativos para la solución de problemas de transferencia de la radiación directa e inversa en los medios con configuraciones arbitrarias y con condiciones de frontera o de contorno es crucial para las mediciones fiables capa por capa de radiación láser dentro de los tejidos y es necesaria para los fines prácticos, como la tomografía óptica difusa y la espectroscopia de los objetos biológicos.
El método de MC, que nace en la década de los treinta del siglo pasado, no encuentra su aplicación a los tejidos biológicos, como ya hemos dicho, hasta principios de los años ochenta y parece ser especialmente satisfactorio en este contexto; además, se está usando ampliamente para la solución numérica de la ETR en diferentes campos de conocimiento (como la astrofísica, la atmósfera y la óptica del océano, etc.). El método se basa en la simulación numérica de transporte de fotones en los medios de difusión. La posición del fotón depende exclusivamente de la posición anterior, y se generan caminos aleatorios que pueden describirse mediante cadenas de Marcov. Las migraciones aleatorias de los fotones dentro de una muestra pueden trazarse desde su entrada hasta que es absorbido o sale.
Los algoritmos conocidos permiten simular todas las capas de tejido con diferentes propiedades ópticas que se caracterizan junto con el tamaño final del haz incidente y la reflexión de la luz en las interfaces.
El fotón p se simula en paquetes de peso (w), posición actual (X), tiempo (t), longitud de onda (λ) y sistema de coordenadas local C’= (i’,j’,k’), donde k’ coincide por definición con la dirección de propagación U.
El tejido se discretiza en vóxeles, cada uno de los cuales está caracterizado por el vector (μa, μs, g, n), que representa el coeficiente de absorción lineal (cm–1), el coeficiente de scattering (cm–1), el factor de anisotropía y el índice de refracción.
En cada punto de interacción entre el fotón p y el material, este puede sufrir distintos procesos: absorción en el tejido, absorción-emisión o scattering en el tejido.
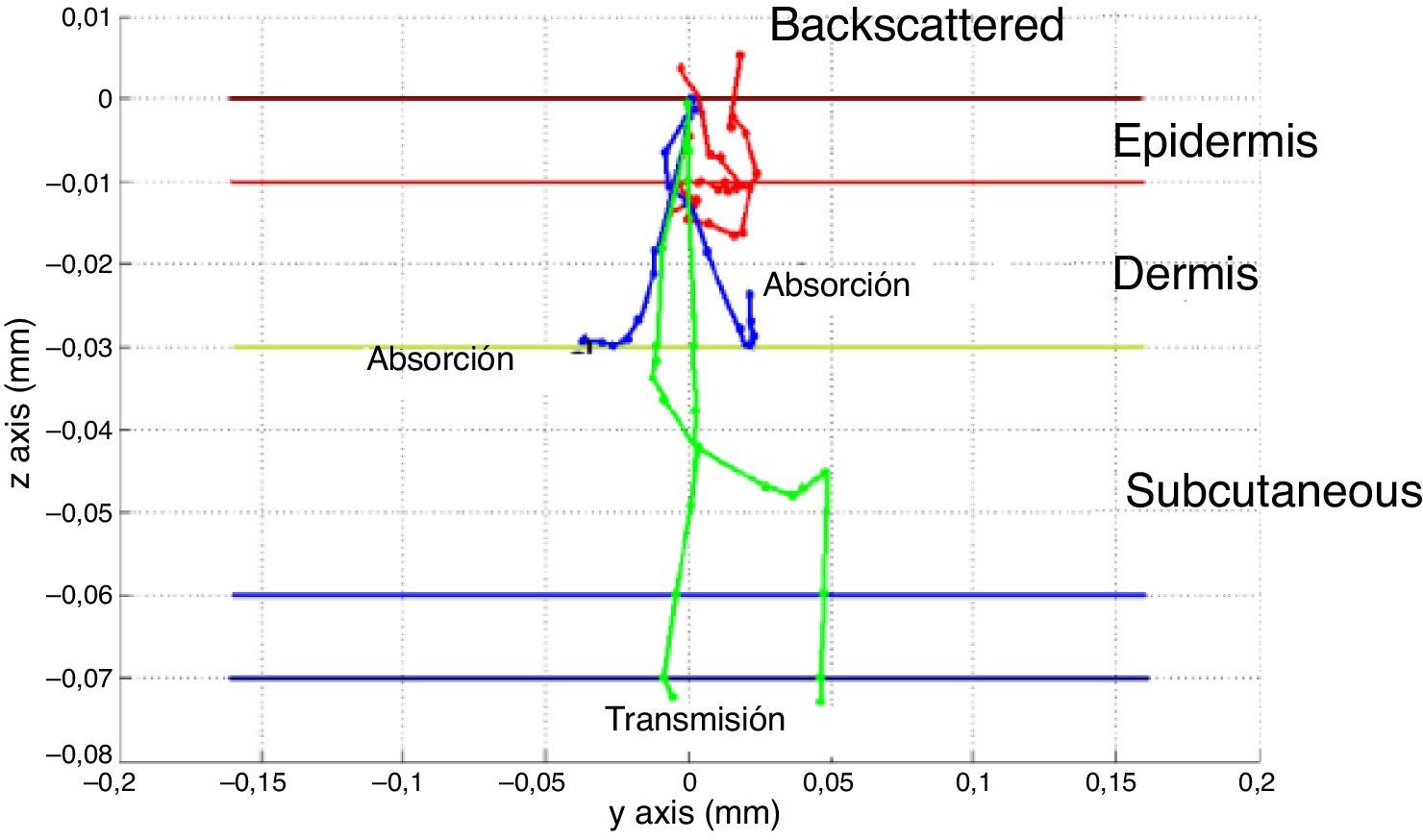
Un ejemplo de uso de MC es el de la figura 1, en el que podemos observar el camino que siguen varios fotones al atravesar la piel en estudio.
Trayectoria de varios fotones simulados por Monte Carlo en un tejido multicapa típica de piel de 0,07mm formado por epidermis, dermis, plexos e hipodermis [13].
A pesar de su alta precisión y de su aplicabilidad universal, el método de MC tiene un inconveniente importante: consume demasiado tiempo de cálculo. Para obtener una variación aceptable, debido a la naturaleza estadística de la modelización, necesita analizar un gran número de fotones. Por ejemplo, el código de MC en 3 dimensiones, diseñado para la interacción de fotones a través de complejos medios heterogéneos, permite obtener una relación señal-ruido superior a 100dB a distancias de 30mm con un detector de 1mm2 de superficie, pero requiere 108 fotones y se traduce en un tiempo de computación de en torno a 5-10 horas con un Pentium III 1.000MHz CPU.245 [14].
Las simulaciones MC son computacionalmente caras, especialmente cuando el coeficiente de absorción es mucho menor que el coeficiente de scattering del medio, en el cual los fotones pueden propagarse a larga distancia antes de ser absorbidos.
Dependiendo del problema por resolver, la técnica de MC se utiliza para simular tanto la reflectancia difusa o la transmitancia de una longitud de onda como de todo el espectro.
Con las técnicas de MC se pueden modelar otras características ópticas, en diferentes geometrías experimentales, como la técnica de captura de fotón en la que un paquete de fotones con un peso inicial se pone en marcha perpendicularmente a la superficie del tejido a lo largo de la dirección del haz de luz. No obstante, también son posibles otras geometrías.
En pocas palabras, el método de MC es un método para simular el transporte de la luz por el tejido por el envío de fotones o paquetes de fotones por un camino aleatorizado sobre una muestra virtual de tejido en un ordenador.
La fase y la polarización de los fotones no se toman en consideración debido a su comportamiento aleatorizado después de múltiples scatterings a través del tejido. El fenómeno aleatorizado del fotón también se ignora considerando al fotón exclusivamente como una partícula. El camino de cada paquete de fotones se simula sobre si emerge o se absorbe. En la figura 2 podemos observar el diagrama de flujo de dicho método aplicado a la interacción del láser con un tejido.
La simulación de MC cumple el siguiente algoritmo para cada paquete [15]:
- -
Seleccionar el siguiente fotón a simular que se puede obtener de un buffer en el que están almacenados los fotones pendientes o tratarse de un nuevo fotón que emite el láser.
- -
Actualizar las propiedades de los tejidos (scattering, absorción, anisotropía) a la longitud de onda del fotón actual.
- -
Calcular el siguiente punto de interacción con el sistema y desplazar el fotón allí, para lo cual puede que sea necesario atravesar varios vóxeles.
- -
Determinar el porcentaje del fotón que sufre absorción o scattering, resultando 2 fotones, uno que representa la fracción del paquete que sufre scattering y otro la que sufre absorción. Uno de los fotones se pone en buffer para la simulación posterior y se continúa la simulación con el otro.
- -
Si el peso w del fotón es inferior a un valor umbral, se considera que el fotón se absorbe totalmente.
- -
Repetir los primeros 5 pasos hasta que el fotón escape del volumen voxelizado (mallado) o sea totalmente absorbido.
- -
Se comprueba que el fotón impacte sobre los detectores externos.
Si el fotón cruza el límite de superficie en el medio ambiente, el peso del fotón contribuye a la reflectancia difusa o a la transmitancia. Si se produce una reflexión, el fotón cambia su movimiento en la dirección opuesta, desplazándose una distancia apropiada continuando con la ejecución.
Para obtener resultados estadísticamente significativos y aceptables se utilizan generalmente entre 1-10 millones de fotones.
En la simulación, el haz del láser entra en la superficie del tejido de forma ortogonal. La coordenada base del tejido y el centro del haz coinciden con las coordenadas (0,0,0). Inicialmente se calculan los coeficientes de absorción y de scattering reducido con anisotropía (g) igual a 0, es decir, suponiéndolo isotrópico. Parte de los fotones incidentes, después de múltiples scatterings dentro del medio, se emiten fuera de la superficie. Estas fracciones (dadas en términos de número de fotones) se determinan y se normalizan con respecto al número de fotones totales incidentes. Se toma en cuenta además el peso del fotón en el evento i de scattering (WTi). El camino de propagación del fotón simulado después de la incidencia normal es el que se muestra en la figura 1. Después de impactar se mueve a través de la dirección de incidencia, sin reflexión, y alcanza la posición 2 desde la posición 1, con una dosis de absorción de:
Al interactuar el fotón con el tejido se produce una disminución en el peso por absorción que viene dada por:
donde el coeficiente de transmisión (cm–1) es:La longitud del camino viene dada como ya vimos con anterioridad por:
El peso del nuevo fotón, del evento 2, WT2, es de
ya que después, en la posición 2, el fotón es dispersado y reflectado, con un ángulo de deflexión θ que viene dado porpara g distinto de 0,ζ es un valor aleatorizado de valores entre 0-1, para g=0El ángulo acimutal ψ, como densidad de probabilidad de que se disperse con ese ángulo azimutal, viene dado por
donde γ es un número aleatorizado entre 0-1.La propagación de fotones en los tejidos continúa hasta que la intensidad del fotón se reduzca al 5% de su intensidad incidente o hasta que el fotón es emitido por retroscattering hasta la superficie del tejido. Después, el siguiente fotón entra al tejido y describe el mismo proceso que el anunciado previamente. Este proceso continúa hasta que entra el último fotón.
4Material y métodoLa experimentación que presentamos está basada en la interacción de la radiación láser con varios tipos de pieles (piel caucásica, piel hispana, piel africana y piel con un elemento cancerígeno). Las propiedades ópticas de cada capa y de cada tipo de piel se han obtenido del análisis bibliográfico, así como en publicaciones y otros trabajos [16–18].
Como método de caracterización de dichas pieles se realiza el estudio diferenciador de parámetros como la transmitancia y la reflectancia, lo que nos permite clasificar e incluso diagnosticar el tipo de piel que se ha expuesto. No se aplican técnicas espectroscópicas, solo se mide la irradiancia de la señal reflejada y, dado que son simulaciones, estas nos permiten también conocer la señal transmitida.
Por un lado queremos, con orientación a la fotodepilación, conocer la longitud de onda a la que se produce la mayor irradiancia en la superficie donde se encuentra la raíz capilar, esgrimiendo que dicha longitud de onda sería la óptima para el tratamiento con el láser en cuestión. No entramos en efectos térmicos ni en posibles malos usos del láser por parte de quien lo esté radiando. Presentamos, pues, la longitud de onda óptima para cada tipo de piel, desprendiéndose el tipo de láser para la depilación del vello.
El programa utilizado para la simulación es el comercial TracePro® versión 7.0 en un ordenador portátil Intel® Pentium® Dual CPU 1,73Ghz y 2GB de RAM.
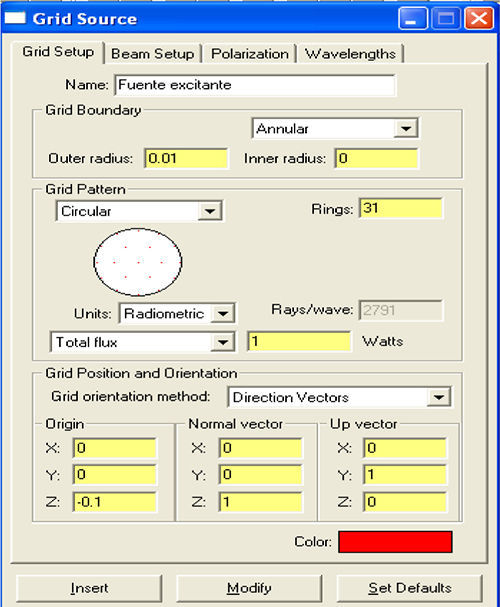
La fuente que hemos utilizado para todas las simulaciones ha sido una fuente circular de 0,01mm de radio, que va a radiar una potencia total de 1 vatio, y situada a 0,1mm de la piel que vamos a simular. Dado que el simulador no analiza problemas de calentamiento, ni efectos no lineales, aplicar mucha potencia solo facilita el disponer de un mayor número de fotones para el análisis numérico, como se ha indicado en el apartado 3.
Su patrón de retícula (grid-pattern) es circular, lo que determina un total de 2.791 rayos de luz en cada simulación. El ángulo medio de incidencia será de 5 grados y se ha ido variando la frecuencia de 50 en 50 nanómetros para observar las propiedades de irradiancia de cada uno de los tejidos expuestos. La elección de dichos parámetros y no de otros es debido a una búsqueda de un compromiso entre el tiempo de ejecución del programa informático (aproximadamente una hora de ejecución) y por ser valores validados, ya que han sido publicados por la comunidad científica [19]. La figura 3 muestra visualmente un menú del programa de simulación utilizada para la inserción de datos numéricos.
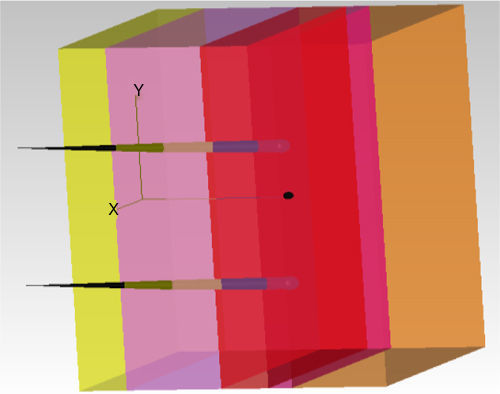
Las pieles a radiar van a tener la forma que se puede observar en la figura 4.
En ella se puede observar la distribución multicapa que presenta la piel formada por una epidermis, dermis, plexo superficial de la dermis, segunda dermis, hipodermis, folículos y fluidos en una piel de 1mm de altura por 0,5mm de profundidad. En la figura se considera la presencia de 2 folículos, pero el programa permite seleccionar la densidad de los mismos, tal y como veremos en el aparatado 5 de los resultados obtenidos.
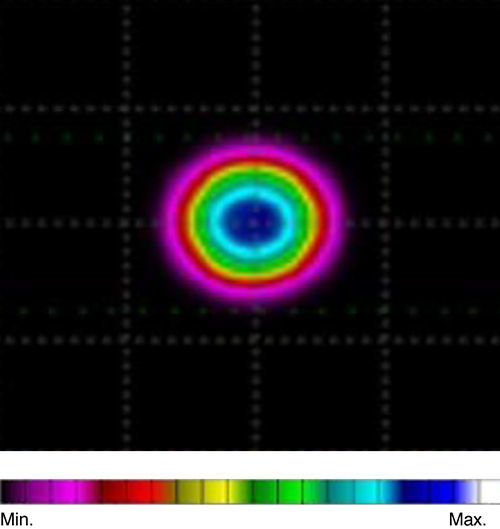
El patrón de radiación viene descrito en la figura 5, en la que la gama de colores va desde el azul hasta el fucsia, siendo el azul el que más densidad de potencia presenta y el fucsia el que menos. Se observa cómo el patrón de radiación va cambiando en la superficie de la raíz capilar para buscar la longitud de onda óptima.
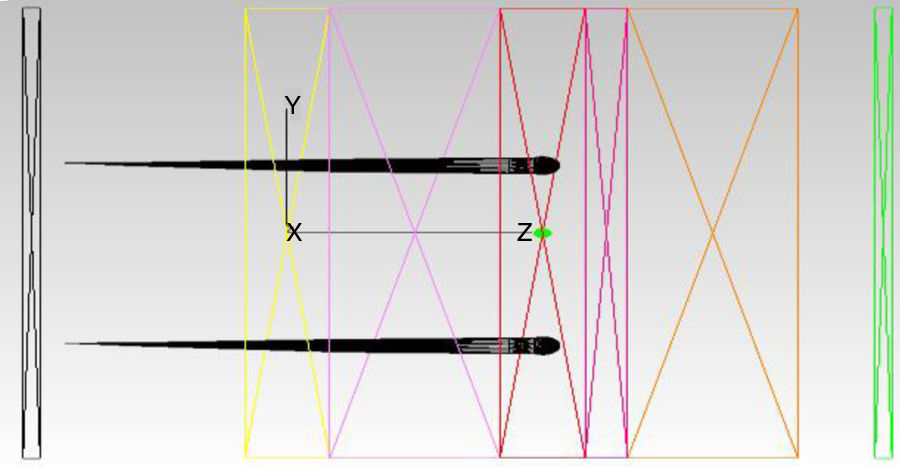
Para el estudio de diagnósticose emplean 2 detectores idénticos colocados a 0,3mm antes de la muestra para medir la reflectancia y a 0,1mm después de la muestra para medir su transmitancia a lo largo del tejido simulando el comportamiento del fotodetector de InGaAs tipo PT521. Los detectores se muestran en la figura 6, en la que el detector de reflectividad está a la izquierda (color negro) y el de transmitancia a la derecha (color verde):
5Resultados obtenidosSe han realizado simulaciones con distintos tipos de pieles, concretamente 5:
- -
Caucásica (tipo III).
- -
Africana (tipo VI).
- -
Caucásica con alta densidad capilar.
- -
Hispana (tipo V).
- -
Con basalioma.
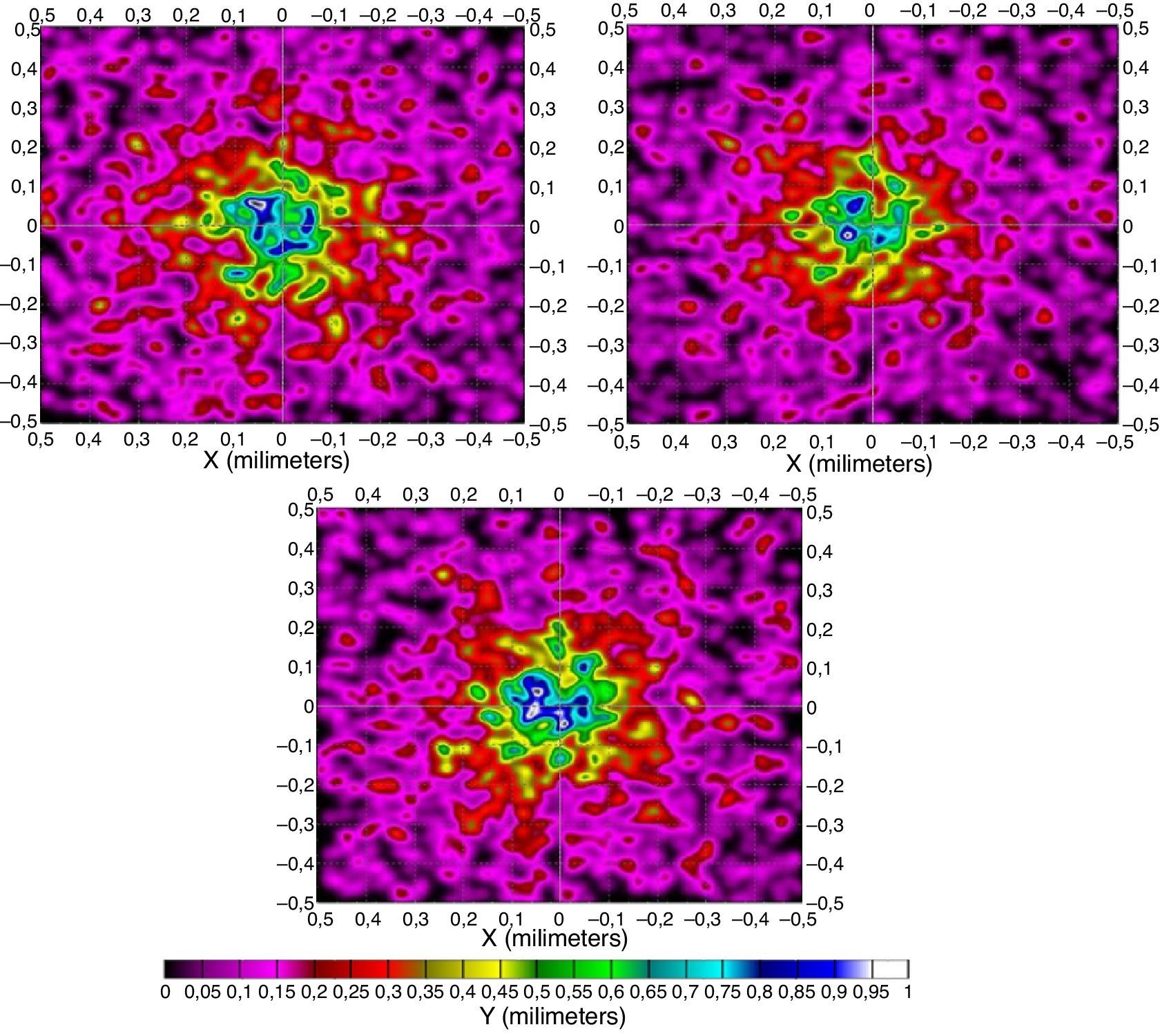
Las fuentes de luz empleadas en el estudio son monocromáticas, definidas con una anchura espectral 0; las simulaciones realizadas han requerido ir cambiando la fuente, aunque en todas con el patrón de radiación de la figura 5, con un rango analizado desde los 400nm hasta los 1.200nm (Δλ=50nm). Los resultados disponibles para cada simulación se corresponden con: el patrón de radiación en unidades de irradiancia en cada piel a cada longitud de onda en el plano de la raíz del folículo –solo se presentan 3 patrones a las longitudes de onda representativas de cada tipo de piel–; el valor de la irradiancia máxima y el de irradiancia media en todos los patrones; y los valores de la reflectancia y la transmitancia a cada longitud de onda obtenidos con los detectores.
A continuación se muestran los resultados representativos para cada tipo de piel. En el subapartado 5.6 se expone el análisis comparativo de todas las simulaciones realizadas y es de donde, principalmente, se pueden extraer las conclusiones más significativas del trabajo.
5.1Piel caucásicaLa piel caucásica es aquella que según la clasificación de Fitzpatrick [20] se quema moderadamente y se pigmenta correctamente, y se corresponde con las razas blancas europeas que no están expuestas habitualmente al sol.
El patrón de radiación del láser va cambiando al interceder con la materia a distintas longitudes de onda. En la figura 7 observamos el patrón de radiación en la superficie de la raíz del folículo.
Se observa, aunque no se muestren a todas las longitudes de onda, que el patrón de radiación va variando en λ del espectro visible (400-650nm). Esto es debido, principalmente, a que el espectro de la hemoglobina y de la melanina presenta actividad a estas longitudes de onda. Un dato importante que se debe tener en cuenta es que aunque la absorción sea mayor a longitudes de onda más bajas (por la hemoglobina y la melanina), esto no significa que tengamos mayor irradiancia a estas longitudes de onda en el folículo en cuestión, ya que cuanto menores sean las longitudes de onda mayor va a ser el scattering y todo será un compendio entre los 2 procesos.
5.2Piel africanaLa piel africana es aquella que según la clasificación de Fitzpatrick [20] no se quema nunca y se pigmenta intensivamente, y se corresponde con las razas negras.
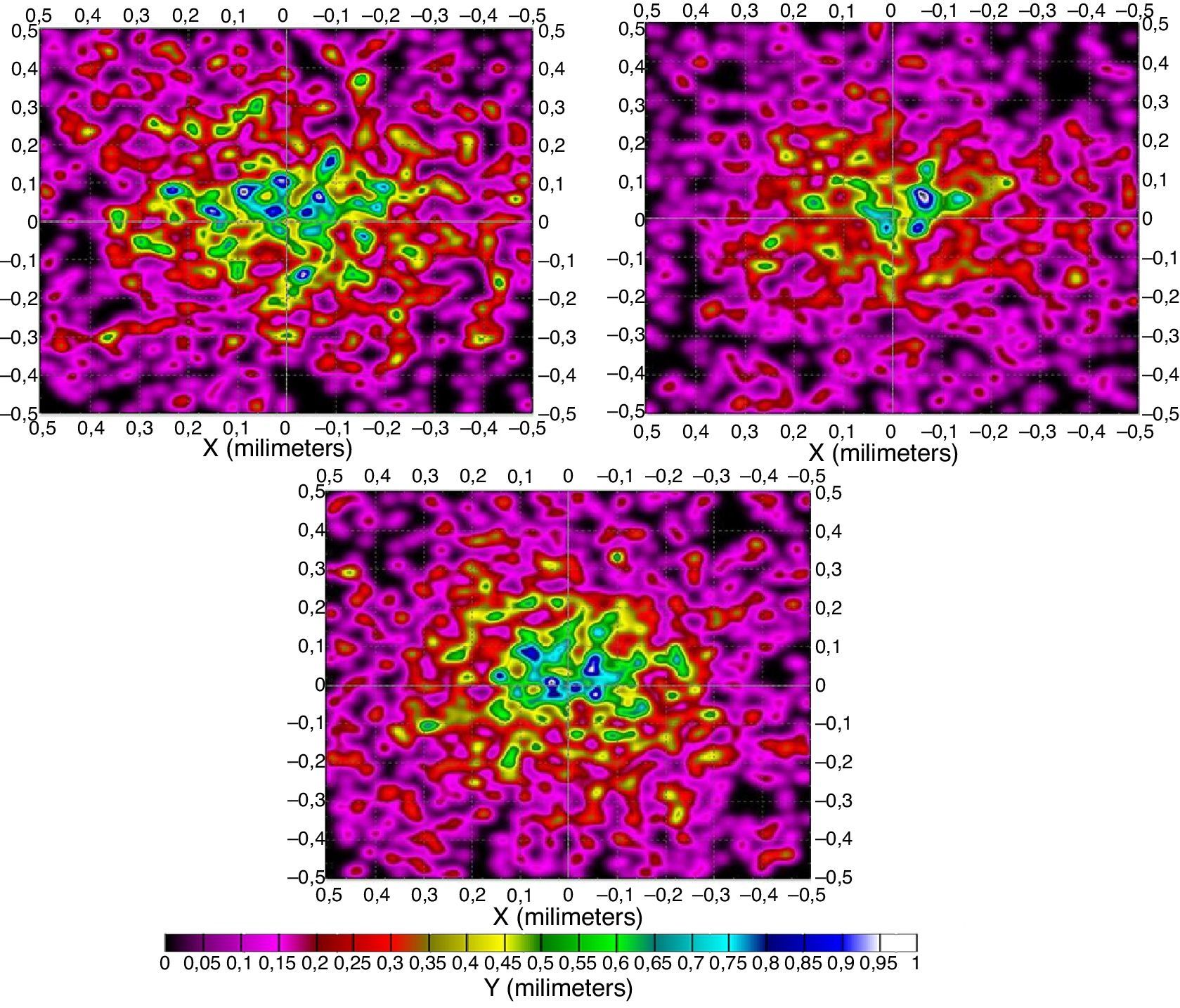
Como en el caso anterior, en la figura 8 presentamos la distintas formas que presenta el patrón de radiación en la superficie de la raíz del folículo. En ellas observamos importantes diferencias en cuanto a la forma y a la distribución de la irradiancia a lo largo de distintas longitudes de onda, debidas igualmente a las características ópticas de la piel y a la cantidad de hemoglobina y de melanina.
En la caracterización de su reflectancia y transmitancia se observa que a longitudes de onda más bajas predomina la reflexión sobre la transmisión, hecho que se invierte a la vez que subimos la longitud de onda (a partir de 1.000nm) tal como mostramos en las gráficas resumen (figs. 14 y 15) del apartado 5.6.
5.3Piel con alta densidad capilarSe radia sobre una piel caucásica con una concentración de 5 folículos por cada 400 micras de piel, en las mismas condiciones que el experimento 5.1 con piel caucásica. Debido a la alta densidad de materia anisotrópica, el patrón de radiación cambia más bruscamente que en los otros casos, como observamos en la figura 9.
El cambio en el patrón a longitudes de onda más bajas se debe, como en el caso anterior, a la ventana de absorción de la melanina y hemoglobina.
5.4Piel hispanaLa piel hispana es aquella que según la clasificación de Fitzpatrick [20] raramente se quema y se pigmenta con facilidad e intensidad (siempre presenta reacción de pigmentación inmediata), y se corresponde con las razas hispanas o árabes.
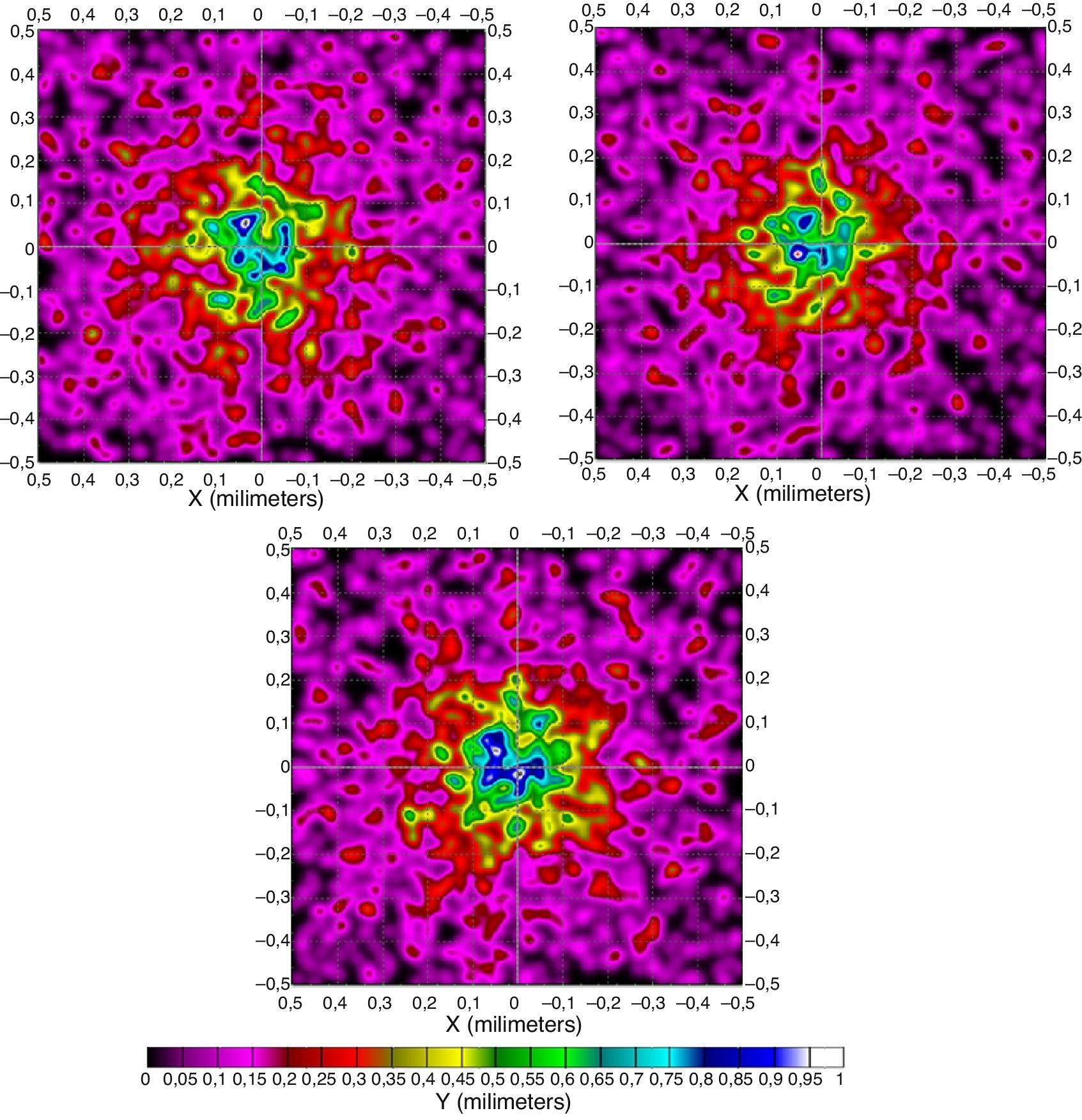
Como en el caso anterior presentamos, en la figura 10, las distintas formas que muestra el patrón de radiación en la superficie de la raíz del folículo. En ellas observamos importantes diferencias en cuanto a la forma y a la distribución de la irradiancia debido de nuevo, principalmente, a las características ópticas de la piel y a la cantidad de hemoglobina y melanina.
A diferencia de las otras, en este tipo de pieles cabe destacar que a longitudes de onda más bajas predomina la reflexión sobre la transmisión, hecho que se invierte a la vez que aumentamos la longitud de onda, en torno a los 800nm, tal como veremos en las gráficas resumen.
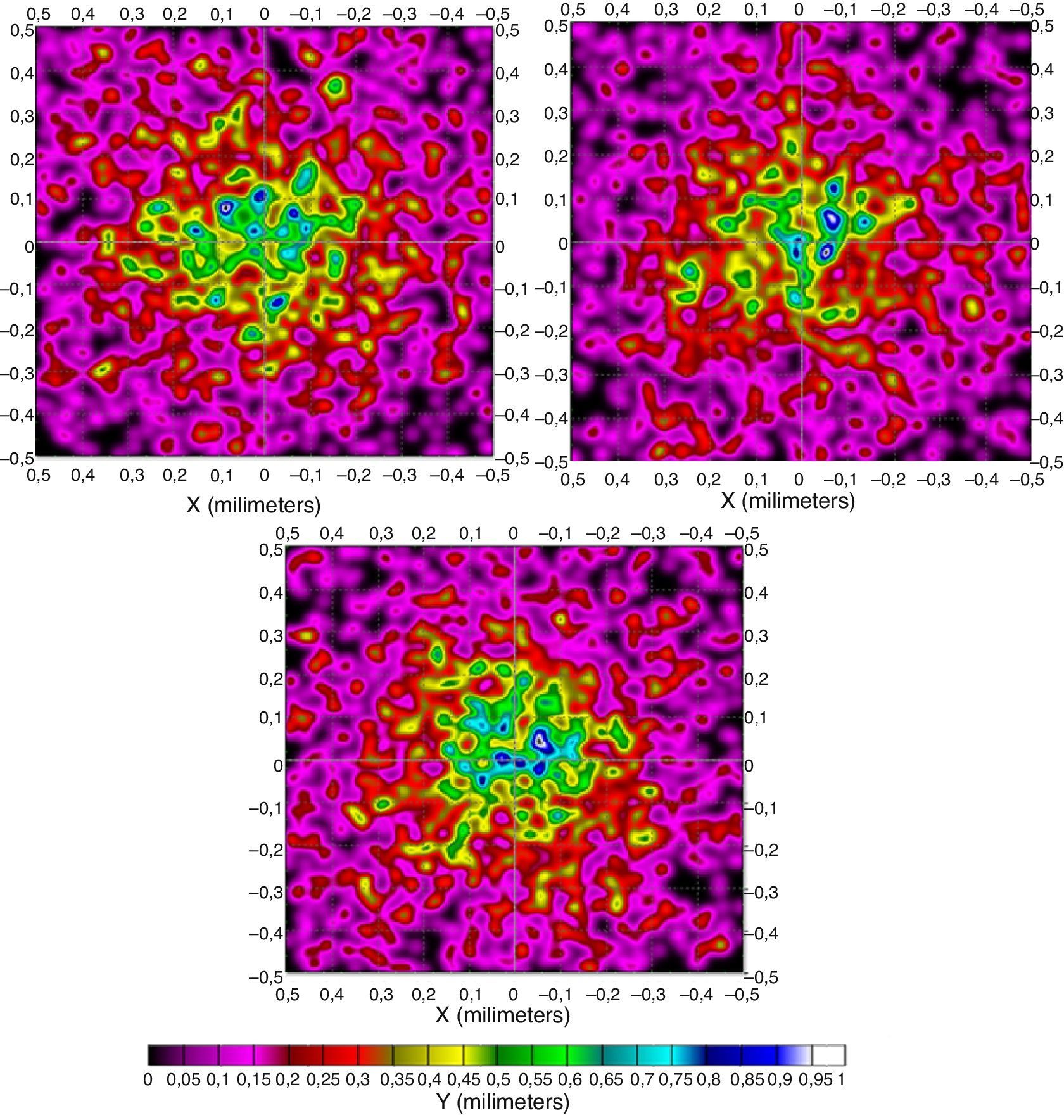
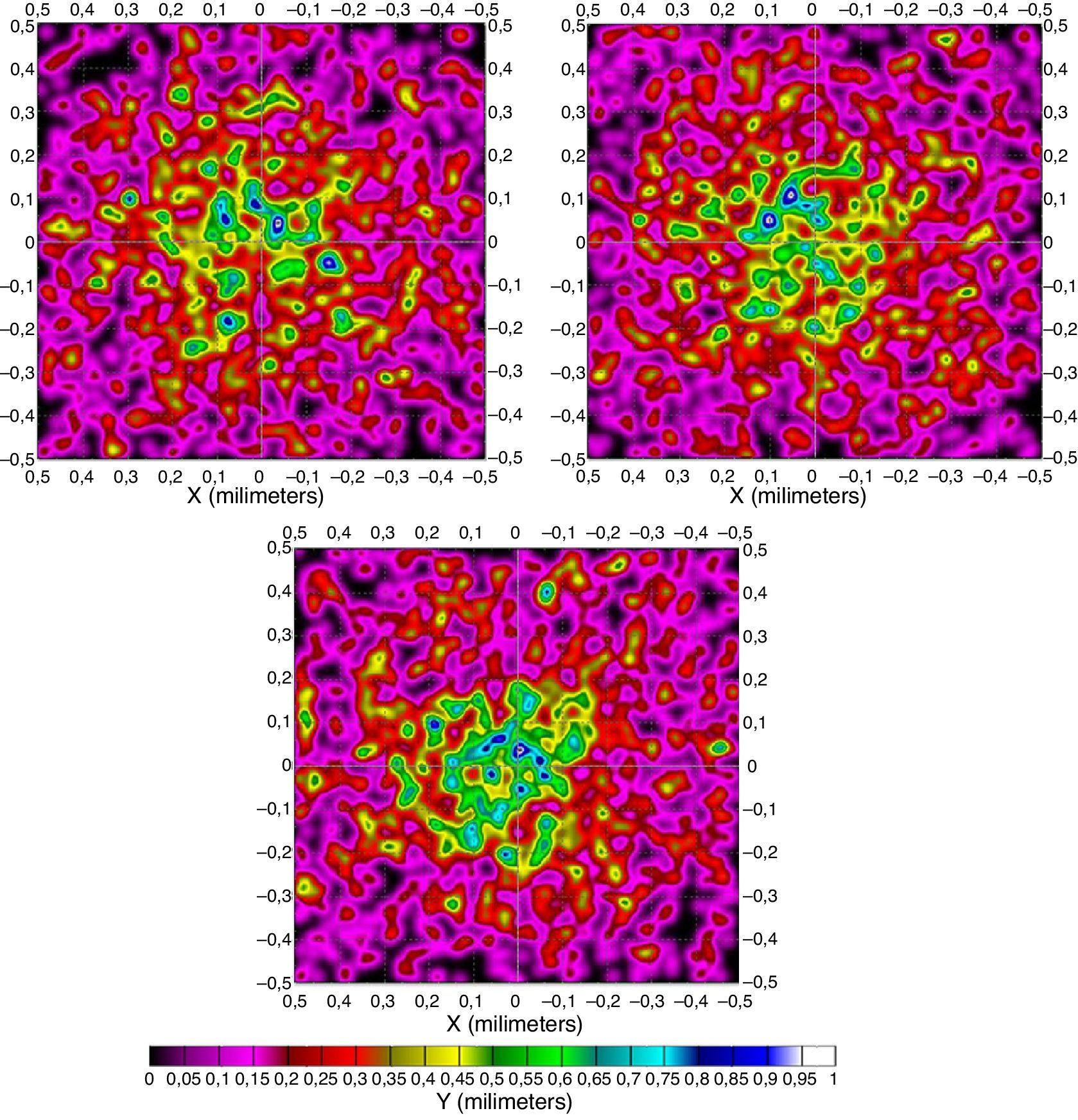
5.5Piel con basaliomaSe pretende simular el cáncer de piel más común en la población humana (basalioma). Para ello se crea en el programa un tipo de piel con un basalioma asociado de propiedades ópticas conocidas y se radia con el mismo láser y las mismas condiciones que las propuestas anteriormente. El patrón de radiación en la superficie de la raíz del folículo se presenta en la figura 11.
Patrón de radiación en unidades de irradiancia, en piel con basalioma en la superficie de la raíz del folículo a distintas longitudes de onda: 550, 600 y 650nm.
Se puede observar un cambio bastante acusado respecto a los tipos de pieles anteriores debido a la absorción de la radiación por parte del basalioma.
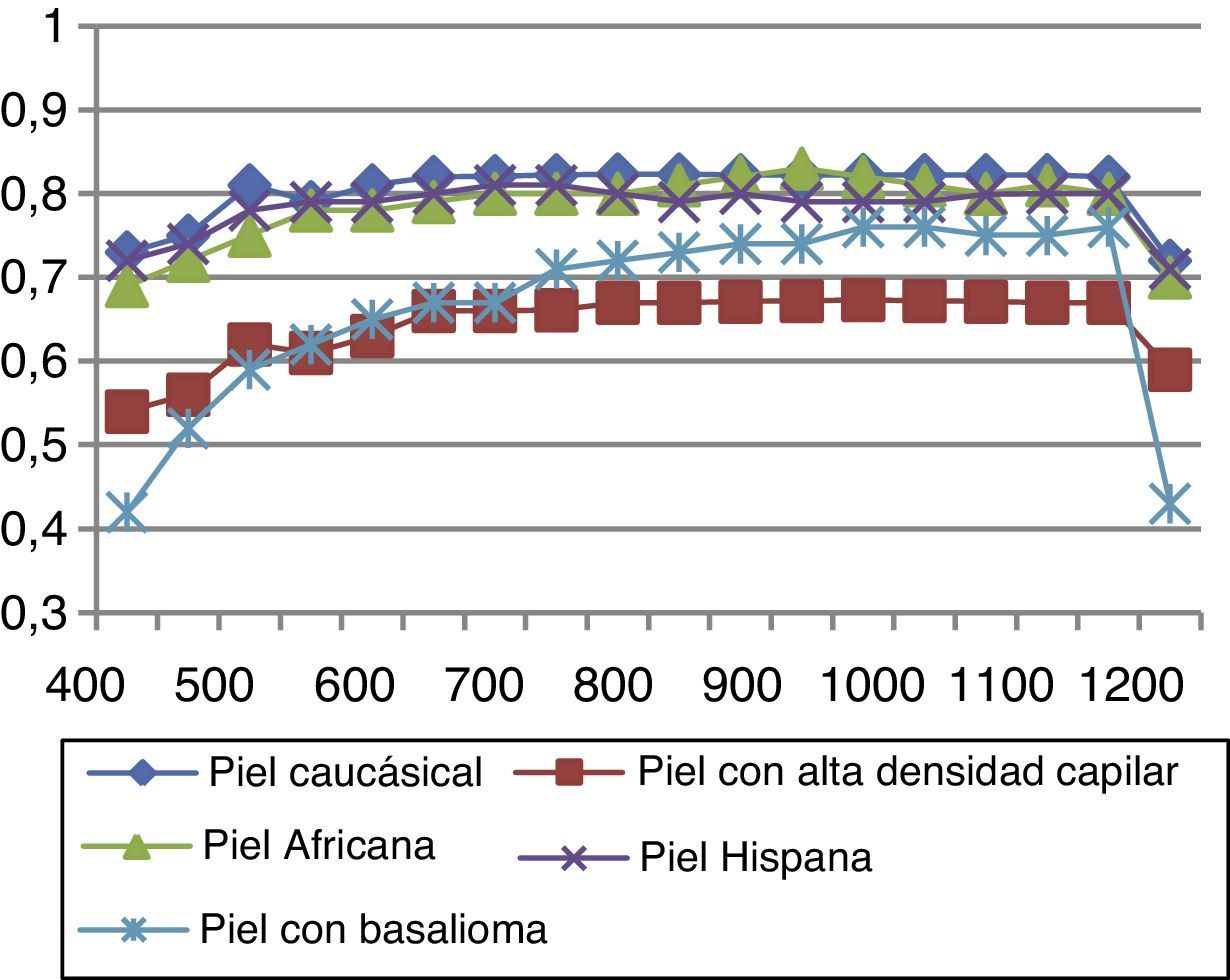
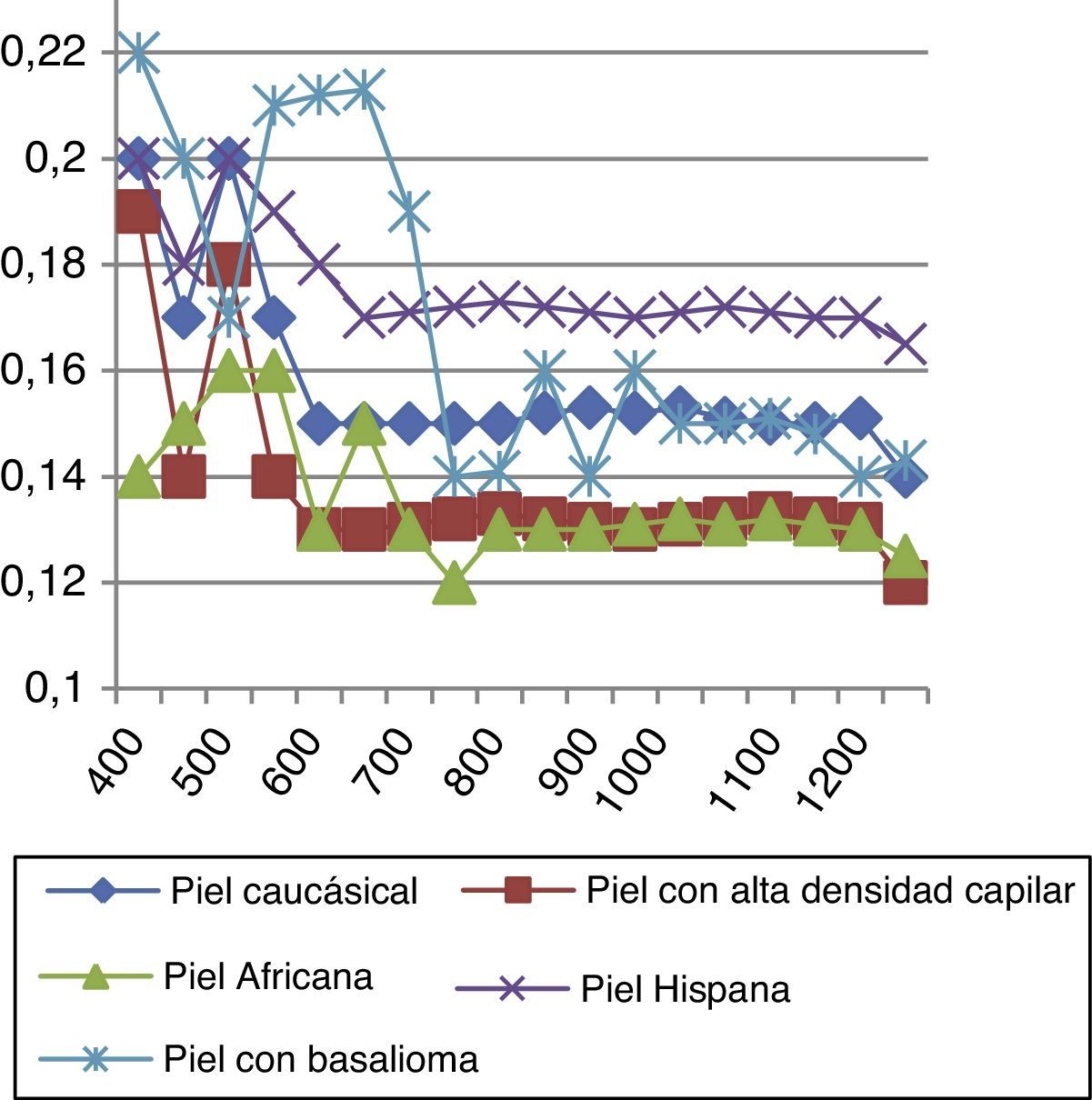
En las figuras 12 y 13 observamos el comportamiento óptico de todos los tipos de pieles estudiados anteriormente en función de la longitud de onda con la que se radia la piel. En una primera aproximación presentamos la irradiancia tanto máxima (fig. 12) como media (fig. 13), con lo que somos capaces de ver de una manera clara cómo caracterizar la piel con elementos cancerígenos.
Comparativa de irradiancia máxima a distintas longitudes de onda (la máxima de las irradiancias obtenidas en las figuras 7-11).
Comparativa de la irradiancia media a distintas longitudes de onda (la media de las irradiancias en las figs. 7-11).
En las figuras se observa que en la irradiancia media tenemos una ventana (500-750nm) en la que sobresale el dato obtenido de la piel con basalioma, consiguiendo un método de detección útil para caracterizar este tipo de cáncer de piel.
Para aplicaciones de fotodepilación, con los datos extraídos de la figura 12, somos capaces de identificar las longitudes de ondas óptimas –y, posteriormente, buscar el tipo de láser que facilitan dichas λ– para la absorción de potencia a la que se produce una mayor irradiancia en la superficie del folículo:
- •
Piel caucásica: el láser que mejor se adapta a estas frecuencias está situado en 1.075nm. Se trata de un láser de neodimio.
- •
Piel africana: el láser que mejor se adecua a este tipo de pieles se encuentra en torno a los 800nm. Se trata de un láser diodo.
- •
Piel con alta densidad capilar: el láser que mejor se adapta a estas frecuencias está situado en 1.123nm. Se trata de un láser de neodimio o 1.152,3nm y de un láser de helio-neón.
- •
Piel hispana: el láser que mejor se adecua a este tipo de pieles se encuentra en torno a 1.000nm de neodimio-YAG.
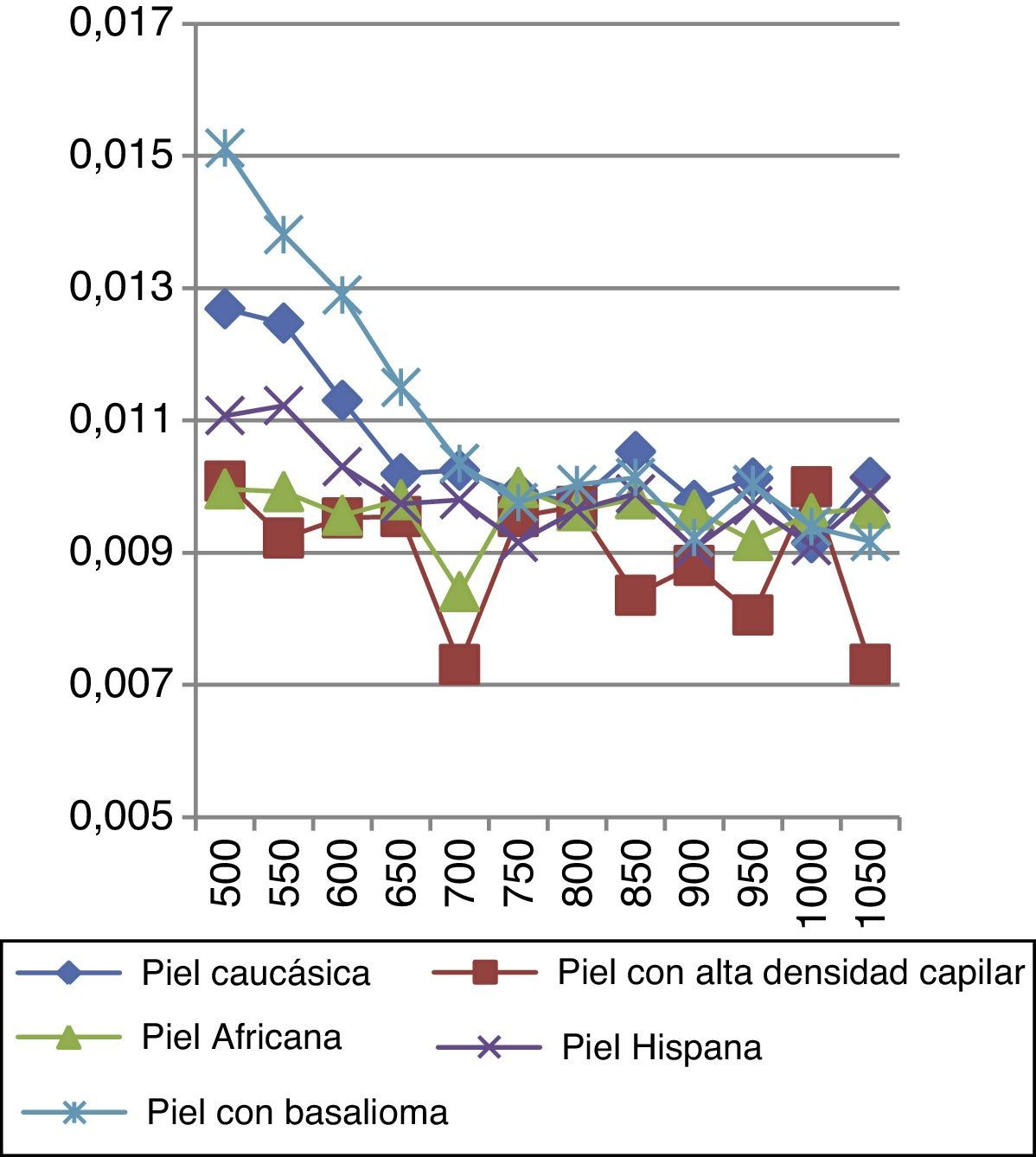
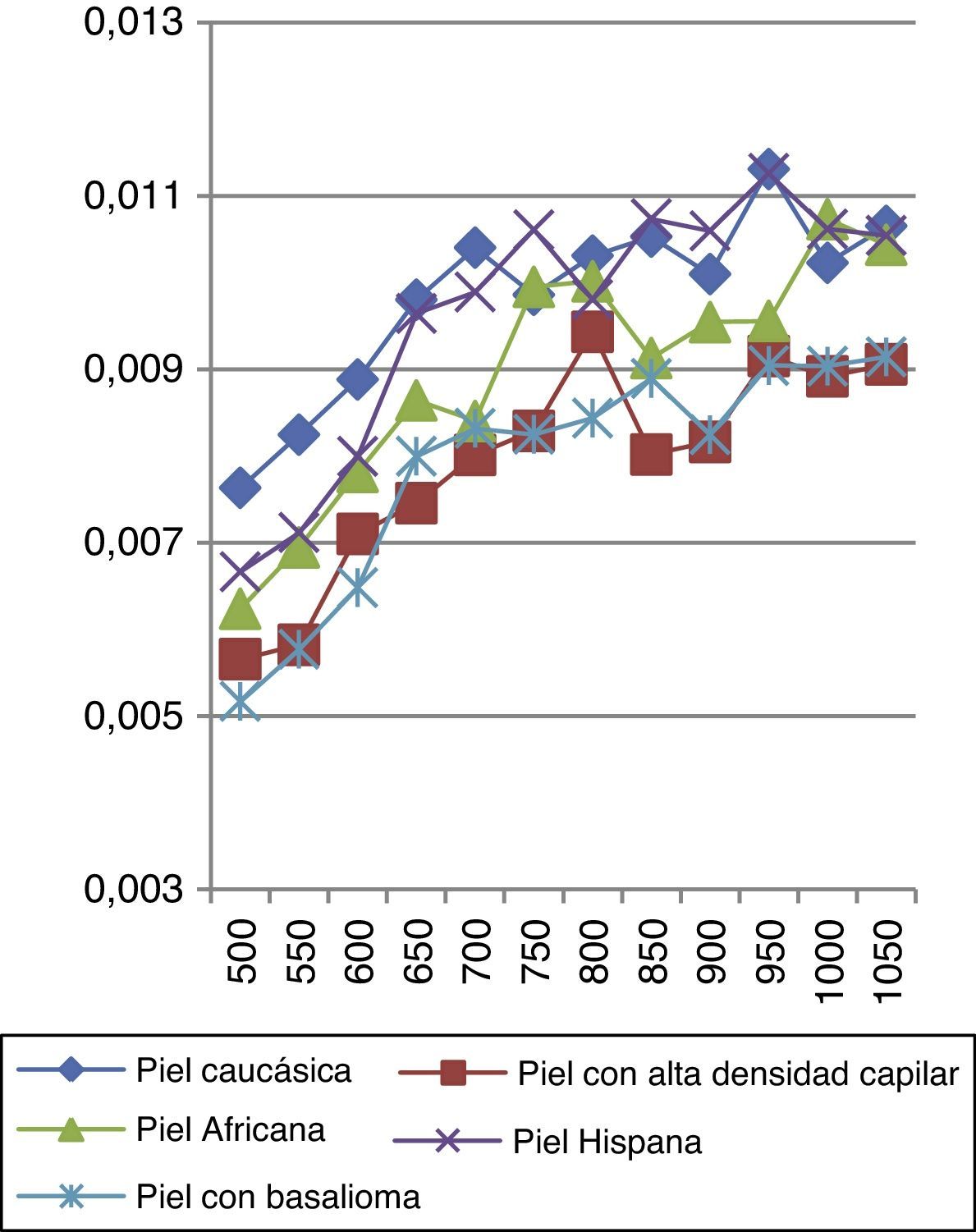
Por otro lado, al realizar un estudio detallado con todas las pieles anteriormente descritas y con la presencia de detectores para obtener datos de potencia transmitida y reflejada, podemos adquirir datos de reflectancia (fig. 14) y transmitancia (fig. 15).
Observamos que todas las pieles presentan las mismas características ópticas de reflectancia, siendo mayor la diferencia entre ellas a longitudes de onda bajas.
En las figuras 14 y 15 se ve cómo el cáncer del basalioma a 500nm presenta un 16% más de reflectancia que una piel caucásica normal, un 9,6% a 550nm, un 12% a 600nm, un 11% a 650nm; esto manifiesta un método eficaz para la detección de basaliomas. De la gráfica también se deduce que es mucho más fácil detectar un basalioma sobre una persona con piel hispana que sobre una muestra caucásica mediante la interacción del láser.
De los datos recopilados, en cuanto a las propiedades de las pieles africanas y de las pieles hispanas a longitudes de onda altas no podemos asegurar su exactitud, sino que habría que corroborar los datos con nuevos medidas experimentales.
Como puede comprobarse para la piel con alta densidad capilar, las medidas de la irradiancia son siempre menores, incluso en la reflectancia y en la transmitancia.
6Conclusión y trabajos futurosEste trabajo presenta un estudio con un simulador de MC para el transporte de fotones en 4 tipos de pieles simuladas. En un trabajo previo [15] los autores compararon con otros programas de simulación con MC, como el de [9], el estudio de diferentes tejidos comprobando la validez de los resultados con el programa empleado aquí.
Las conclusiones extraídas de las simulaciones, resumidas en la tabla 1, concuerdan en cuanto al tipo de láseres que más se emplean en fotodepilación. Se identifica la longitud de onda óptima a la que las distintas pieles absorben potencia en la raíz de los folículos simulados, hecho que tiene importancia para la fotodepilación, al acotar el tipo de láser que debe ser utilizado según el tipo de piel por depilar; sirva esta publicación como contribución para mejorar y difundir el conocimiento sobre el tipo de laser óptimo que se debe utilizar. Un segundo factor fundamental que hay que tener en cuenta, y que no puede ser estudiado con este tipo de simulaciones, es la potencia del láser que se emplee.
Resumen de los resultados obtenidos
| Tipo de piel | Long. de onda a la que se produce la máxima absorción(nm) | Características detectadas | Tipo de láser |
| Caucásica | 1.075 | A longitudes de onda de 450-600nm, se obtiene la mayor diferenciación en el patrón de radiación | Neodimio |
| Africana | 800 | Predominio de la reflexión hasta los 1.000nm | Diodo |
| Alta densidad capilar | 1.123-1.152 | Influencia moderada de los folículos en la respuesta óptica | NeodimioHelio-neón |
| Hispana | 1.000 | Predominio de la reflexión hasta los 800nm | Neodimio-YAG |
| Basalioma | Caracterización por respuesta diferenciadaentre 500-750nmNo domina la transmitancia en torno a 1.000nm |
También se comparan los resultados obtenidos para los 4 tipos de pieles con una piel que presenta basialoma y se observa su comportamiento peculiar. Esta diferencia se encuentra en el rango de longitud de onda de 500-750nm, donde se comprueba que su irradiancia media presenta un pico diferenciador en relación con los otros tipos de pieles.
Otra de las conclusiones de nuestro estudio es que si en un tejido no domina la transmitancia sobre la reflectancia para longitudes de onda de en torno a 1.000nm, no se trata de un tejido «sano» y puede presentar una anormalidad como un cáncer, ya que hemos obtenido el comportamiento óptico de varios tipos de pieles observando que es en la piel del basalioma en la única que predomina la reflectancia a esa longitud de onda.
Este estudio presenta un método de análisis con datos innovadores, hasta donde conocen los autores, en la detección de cánceres de piel específicos (basaliomas), al menos en lo que se refiere a la simulación del patrón de radiación en la superficie de la raíz de un folículo. Esto permite afirmar que se puede extrapolar posteriormente a otro tipo de cánceres o enfermedades de la piel o de otro tipo de tejidos, así como saber en qué tipo de pieles son más fáciles de detectar.
Evidentemente, los datos expuestos necesitan complementarse con un estudio teórico del calentamiento que se produce en el tejido, como siguiente aproximación; un estudio de la posible fluorescencia y presencia de efectos no lineales completaría el análisis del comportamiento óptico del tejido, en concreto de los distintos tipos de pieles, caso que nos ocupa. Pero si nos limitamos al tipo de simulación realizada el siguiente paso sería describir una geometría de fronteras entre capas internas de la piel más compleja que la representada en la figura 4.
Por último, se vuelve a demostrar que las simulaciones permiten disponer de información previa a la experimentación, lo que reduce su coste. Este estudio nos permite restringir el ancho de banda con el que realizar la tarea experimental. Uno de los trabajos futuros que se deriva de la presente publicación es utilizar muestras in vivo o in vitro de distintas pieles y su desarrollo experimental.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Los autores desean expresar su agradecimiento a la biblioteca de la E.T.S.I. Telecomunicación de la U.P.M. por facilitar el acceso a los recursos electrónicos, tramitando el acceso a publicaciones específicas, y a la empresa Lambda Research Corporation© por facilitar el programa de simulación TracePro®. Por último, agradecemos los comentarios del revisor sobre el borrador inicial que han permitido mejorar el artículo.






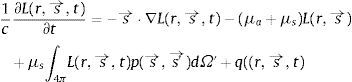
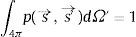

![Trayectoria de varios fotones simulados por Monte Carlo en un tejido multicapa típica de piel de 0,07mm formado por epidermis, dermis, plexos e hipodermis [13]. Trayectoria de varios fotones simulados por Monte Carlo en un tejido multicapa típica de piel de 0,07mm formado por epidermis, dermis, plexos e hipodermis [13].](https://static.elsevier.es/multimedia/02131315/0000003100000003/v1_201506200103/S021313151400042X/v1_201506200103/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)