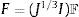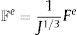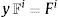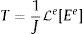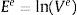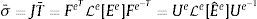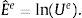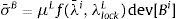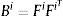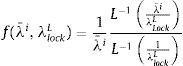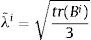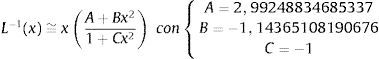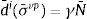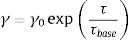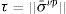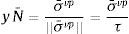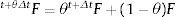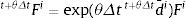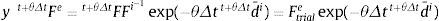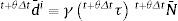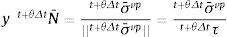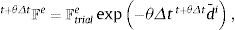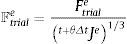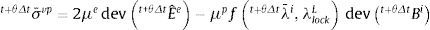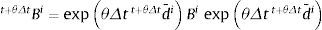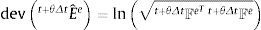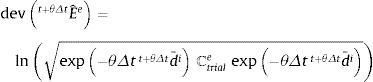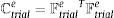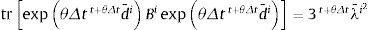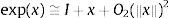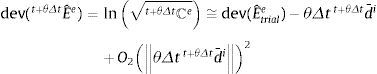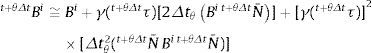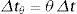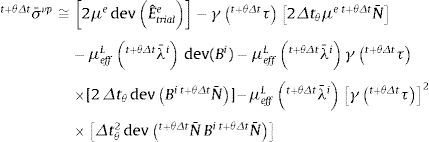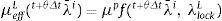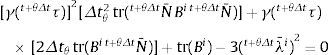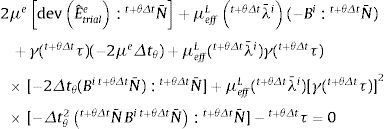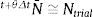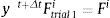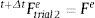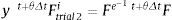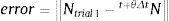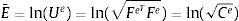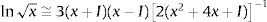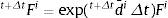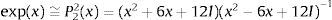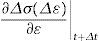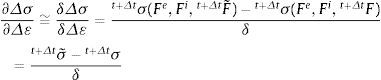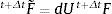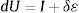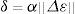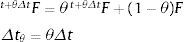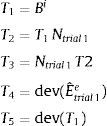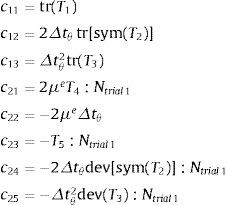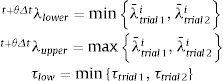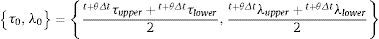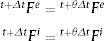Una implementación implícita del modelo viscoplástico de Arruda-Boyce

Resumen

El modelo viscoplástico de Arruda-Boyce (A-B) es la piedra angular para el desarrollo de sofisticados modelos constitutivos de polímeros y tejidos blandos. Se presenta una formulación implícita simple del modelo de A-B junto con los detalles de su implementación como una rutina de material definido por el usuario de ABAQUS-Standard. La formulación hace uso de un esquema de Euler hacia atrás en combinación con procedimientos estándar para la actualización de las tensiones en la configuración relajada. Su implementación prescinde de procedimientos iterativos y del cálculo de descomposiciones polares, autovalores y matrices de rotación. Las raíces cuadradas, exponenciales y logaritmos naturales de los tensores de segundo orden se calculan utilizando aproximaciones de Padé de alto orden, mientras que la matriz de rigidez tangente se calcula utilizando un esquema de diferencias finitas. Resulta así un algoritmo simple para la actualización de las tensiones, sencillo de implementar, pero a la vez preciso y relativamente eficiente en términos de costo computacional. La precisión, la estabilidad y la eficiencia de la formulación propuesta se investigan y se demuestran con una serie de ejemplos. Como resultado, se dan una serie de recomendaciones para ajustar el tamaño del incremento de deformación inelástica y de los residuos de los procedimientos de Newton-Raphson, y para seleccionar los algoritmos más efectivos para evaluar la matriz de rigidez tangente y resolver el sistema de ecuaciones.

Abstract

The Arruda-Boyce viscoplastic model has been the cornerstone for the development of sophisticated constitutive models for polymers and soft tissues. A simple implicit finite element implementation for the Arruda-Boyce viscoplastic model, which is coded as user material routine in ABAQUS-Standard, is presented in this work. The implementation uses the Backard-Euler method and standard stress-update procedures in the relaxed configuration; it has no iterative procedures; it completely avoids the use of eigen-decompositions, polar decompositions and rotation matrices while square roots, exponentials and natural logarithms of second order tensors are computed using high-order Padé approximants. The tangent-stiffness matrix is computed using a finite difference scheme. As a result, the stress-update algorithm turns out to be very simple to code and to implement, but still very accurate and quite efficient in computational terms. The precision, stability and efficiency of the proposed formulation are assessed and demonstrated by means of a number of examples. As a result, a number of recommendations are given to best set the size of the inelastic strain increment and the residuals for the Newton-Raphson procedures; and to select the most effective algorithms for the evaluation of the tangent stiffness matrix and to solve the system of equations.

1

Introducción

El modelo viscoplástico de Arruda-Boyce (A-B) [1,2] es un producto del grupo de modelos inicialmente propuestos por Boyce et al. [3,4] con el objetivo de describir de forma completa el comportamiento inelástico de polímeros. El modelo de A-B fue uno de los primeros de su tipo con la capacidad de reproducir todos los fenómenos característicos del comportamiento de los polímeros estructurales para un rango amplio de deformaciones.

Sus sólidas bases físicas y fenomenológicas han hecho del modelo de A-B un punto de partida para el desarrollo de otros modelos más sofisticados y especializados. El trabajo de Bergström et al. [5] presenta una descripción sucinta de varios de estos modelos a la luz de su aplicación al modelado de polietileno de ultra alto peso molecular (UHMWPE, por sus siglas en inglés); Danielsson [6] presenta una revisión de las reglas de flujo y de las leyes de evolución de las variables internas (incluyendo daño y porosidad), y Anand y Ames [7] proponen una elaborada ley constitutiva basada en el ensamble de «bloques elementales» similares al modelo de A-B.

A diferencia de los modelos elastoplásticos y viscoplásticos clásicos, el modelo de A-B prescinde de una función de fluencia, por lo que es clasificado como un modelo viscoplástico unificado. El modelo de A-B se formula a partir de la descomposición multiplicativa de los gradientes de deformación, donde la deformación plástica se define de forma explícita con una formulación lagrangiana total de Hencky (TLH, por sus siglas en inglés) (véase, por ejemplo, Bathe [8]) y la tensión total se calcula a partir de la deformación elástica. No existen muchos antecedentes sobre la implementación de modelos viscoplásticos unificados con formulaciones TLH. Los trabajos más conocidos son los de Weber y Anand [9], Lush et al. [10] y Sansour [11]; todos ellos utilizan esquemas de integración de Euler hacia atrás. Hay también un trabajo de Bergström et al. [12] que introduce un esquema de integración de orden y tamaño de paso temporal variables para una variación del modelo de A-B.

La calibración y la experimentación son tareas usuales durante las primeras etapas del desarrollo de modelos constitutivos. Por su versatilidad y relativa simplicidad de implementación, se utilizan normalmente con estos propósitos esquemas de integración explícitos que, por otro lado, son computacionalmente ineficientes. La segunda opción son los esquemas implícitos, eficientes desde el punto de vista computacional pero que requieren la elaboración de trabajosos, y muchas veces complejos, procesos de diferenciación (véanse, por ejemplo, Peric y Dettmer [13] y Dettmer y Reese [14]). Es por ello que, normalmente, se prefiere reservar las implementaciones implícitas para las etapas avanzadas de desarrollo de los modelos, cuando la eficiencia computacional se torna relevante.

Se presenta en este trabajo una implementación implícita simple del modelo de A-B. En este contexto, se adapta la formulación matemática del modelo para hacerlo compatible con procedimientos numéricos estándar para la actualización de las tensiones en la configuración relajada, como los propuestos por Weber y Anand [9] y Eterovic y Bathe [15]. La integración en el tiempo se realiza usando un esquema implícito de Euler. Mediante la utilización de aproximaciones y simplificaciones (muchas de ellas inspiradas en el trabajo de Lush et al. [10]), los cálculos en cada paso de tiempo se reducen a resolver un sistema no lineal de 2 ecuaciones con 2 incógnitas. La matriz de rigidez tangente se evalúa de forma numérica mediante perturbaciones del gradiente de deformación total. La formulación propuesta se implementa como una rutina de material definido por el usuario (UMAT, por sus siglas en inglés) del programa ABAQUS-Standard. Su desempeño y precisión se demuestra y discute para una serie de ejemplos.

2

Notación

La notación y las hipótesis de este trabajo son las usuales de la mayoría de las formulaciones en deformaciones finitas. Sin embargo, con el objeto de evitar ambigüedades se da aquí una breve reseña.

La notación para el gradiente de deformación y su descomposición polar es la utilizada en Gurtin [16]:

F	: gradiente de deformación total desde el tiempo 0 hasta el tiempo t.
J = det(F)	: deformación volumétrica desde el tiempo 0 hasta el tiempo t.
F = VR = RU	: descomposiciones polares izquierda y derecha del gradiente de deformación.
V y U	: tensores de elongación izquierdo y derecho.
R	: tensor de rotación.

Se utilizan 2 descomposiciones multiplicativas del gradiente de deformación: la descomposición de Lee, F=F^eFⁱ, donde F^e y Fⁱ son los gradientes de deformación elástico e inelástico, respectivamente (véase Dvorkin y Goldschmit [17]), y la descomposición dada por el producto:

donde J^1/3I da cuenta de las deformaciones volumétricas y el tensor isocórico F contiene la información de las rotaciones de cuerpo rígido y las distorsiones (véase Simo y Hughes [18]). El símbolo I en las expresiones anteriores corresponde al tensor identidad.

El concepto de gradiente de deformación isocórico se utiliza también para los gradientes de deformación elástico e inelástico. Estos son:

Las distintas configuraciones se indican utilizando la notación de Anand y Gurtin [19]. La configuración asociada a un tensor genérico «A» se identifica como A cuando es expresado en la configuración espacial y como A¯ cuando es expresado en la configuración relajada.

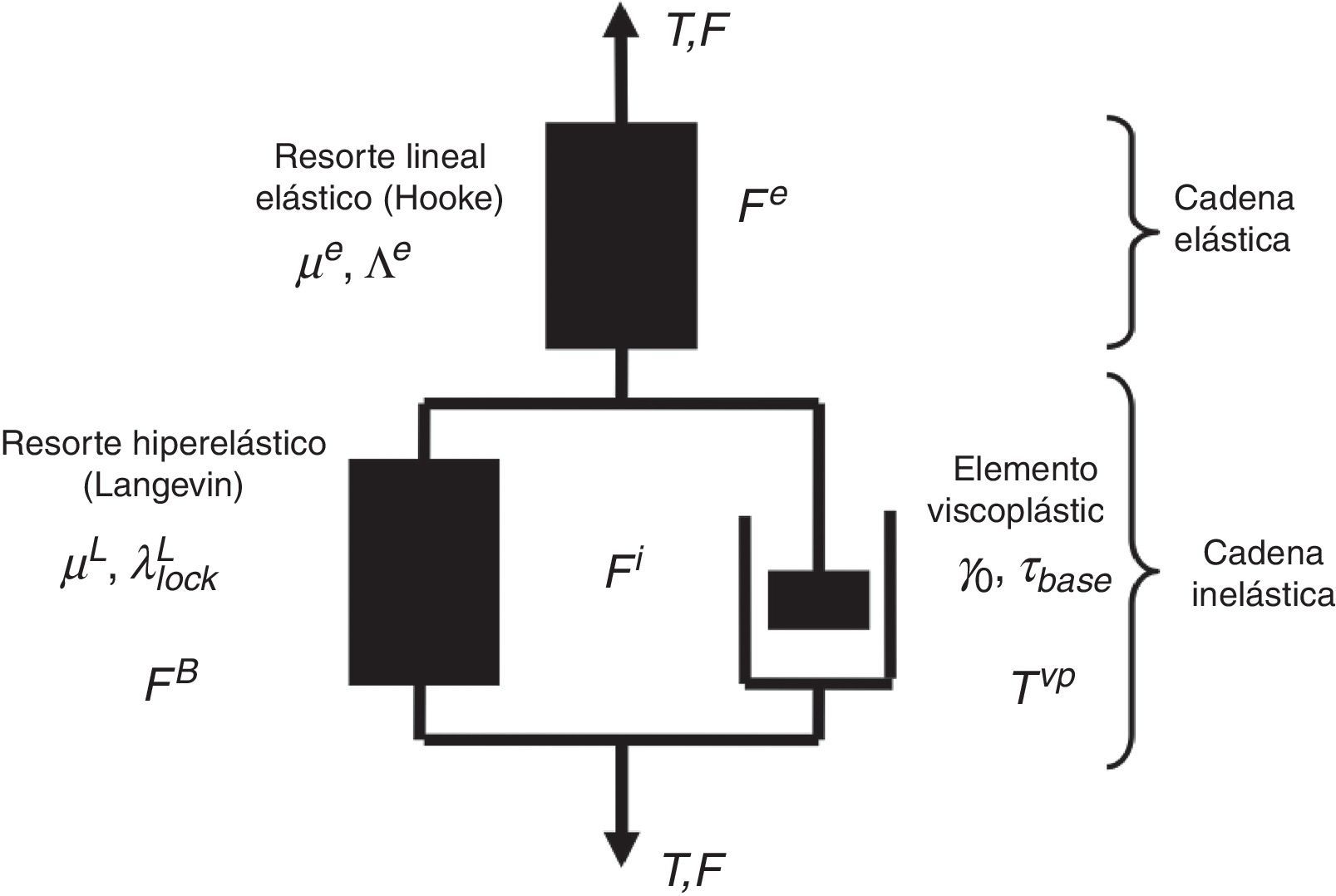
3

El modelo viscoplástico de Arruda-Boyce

El modelo reológico de A-B se ilustra en la figura 1. Este consiste en 2 cadenas dispuestas en serie, una elástica y una inelástica. Estas cadenas se construyen con 3 elementos que se definen en función de 6 parámetros constitutivos [1,2,5]:

• •

  El elemento lineal elástico (resorte de Hooke) forma la cadena elástica y su comportamiento está caracterizado por las constantes de Lamé μ^e y Λ^e.

• •

  El elemento viscoplástico provee la dependencia con la velocidad de deformación. Se ubica en la cadena inelástica y su comportamiento queda caracterizado por la tasa de deformación viscoplástica de referencia, γ₀, y la tensión de corte de referencia, τ_base.

• •

  El elemento hiperelástico (resorte de Langevin) es el responsable del endurecimiento durante la carga y de la recuperación no lineal durante la descarga. Se ubica en la cadena inelástica, en paralelo al elemento viscoplástico. Su comportamiento está caracterizado por el módulo de corte, μ^L, y la elongación de bloqueo, λlockL.

Figura 1.

Modelo reológico de Arruda-Boyce.

La tensión total de Cauchy en la configuración espacial se calcula a partir de la deformación del elemento elástico con la expresión:

donde Le es el tensor constitutivo elástico de cuarto orden y

es la deformación elástica.

La tensión total de Kirchhoff en la configuración relajada es [15]:

donde:

Por su parte, la tensión en el elemento hiperelástico es:

donde:

y λ¯i es la elongación efectiva de la cadena inelástica

La función inversa de Langevin, L⁻¹(·) se aproxima con la fórmula de Cohen [20],

La tensión que impulsa el flujo viscoplástico en la configuración relajada es:

La tasa de deformación inelástica en la configuración relajada es:

donde la magnitud de la tasa de deformación viscoplástica, γ, y la dirección del flujo inelástico, N¯, se calculan a partir de σvp como sigue:

4

El esquema de integración implícita

Se presentan a continuación los detalles de la formulación del esquema de integración. Este tiene asociado un sistema de 2 ecuaciones no lineales cuyas incógnitas son la elongación inelástica, λ¯i, y la tensión de corte efectiva, τ. La integración se realiza utilizando un esquema de Euler hacia atrás. Sobre la base del análisis de las fuentes de error de la formulación, se propone un criterio para limitar el tamaño máximo del incremento de deformación inelástica.

4.1

Formulación

El esquema de integración se formula como una regla implícita general con un parámetro θ que sirve para seleccionar entre un esquema completamente implícito (θ = 1), una regla de punto medio (θ = 1/2) o cualquier esquema estable intermedio (0,5 < θ < 1).

El gradiente de deformación total en t + θΔt es:

El operador de Euler hacia atrás se aplica a los gradientes de deformación inelástico y elástico, con lo que resulta:

donde:

El gradiente de deformación Ftriale=t+θΔtFFi-1 en la expresión (20) puede calcularse con la información disponible al comienzo de cada paso de tiempo.

Finalmente, el gradiente de deformación elástico isocórico se calcula dividiendo la expresión (20) por Jet+θΔt13, de lo que resulta:

donde:

Para deducir la expresión de la tensión que gobierna el flujo viscoplástico se combinan las expresiones (8-11) y (13) para obtener:

La expresión (19) permite reescribir el tensor ^{t + θΔt}Bⁱ de la ecuación (9) como sigue:

Por su parte, la parte desviadora del tensor de Hencky se puede calcular de forma directa a partir del gradiente de deformación elástico isocórico [15]:

Luego del reemplazo de la expresión (23) en la (27) resulta:

donde:

La tensión hiperelástica en t + θΔt, el segundo sumando de la expresión (25), requiere la medida efectiva de las elongaciones, λ¯it+θΔt. Esta se determina mediante el cálculo de la traza del tensor ^{t + θΔt}Bⁱ dado en la expresión (26):

La complejidad de las expresiones (26), (28) y (30) lleva a la introducción de aproximaciones y linealizaciones para hacer el problema matemáticamente tratable.

Se propone reemplazar los mapeos exponenciales en las expresiones (26-30) por la siguiente aproximación de primer orden:

Por su parte, la expresión (28) se reemplaza por la siguiente aproximación de primer orden propuesta por Eterovic y Bathe [15]:

La expresión aproximada de ^{t + θΔt}Bⁱ es el resultado de reemplazar la ecuación (21) en la (26) y de realizar la aproximación (31):

donde:

Por su parte, la expresión aproximada de la tensión que gobierna el flujo viscoplástico es el resultado de reemplazar la ecuación (21) en la (25) y de introducir las aproximaciones (32) y (33):

donde:

El desempeño de estas aproximaciones se discutirá en la sección 4.3.

4.2

Solución del sistema de ecuaciones

La primera de las ecuaciones del sistema resulta de calcular la traza de la expresión (33) (véase la ecuación 30):

donde λ¯it+θΔt y ^{t + θΔt}τ son las incógnitas.

La segunda ecuación, que tiene también a λ¯it+θΔt y ^{t + θΔt}τ como incógnitas, resulta de aplicar el doble producto escalar por N¯t+θΔt a ambos miembros de la ecuación (35):

Es importante notar que los coeficientes de las ecuaciones (37) y (38) son funciones de N¯t+θΔt, que es también desconocido. Para resolver este punto se realiza la aproximación:

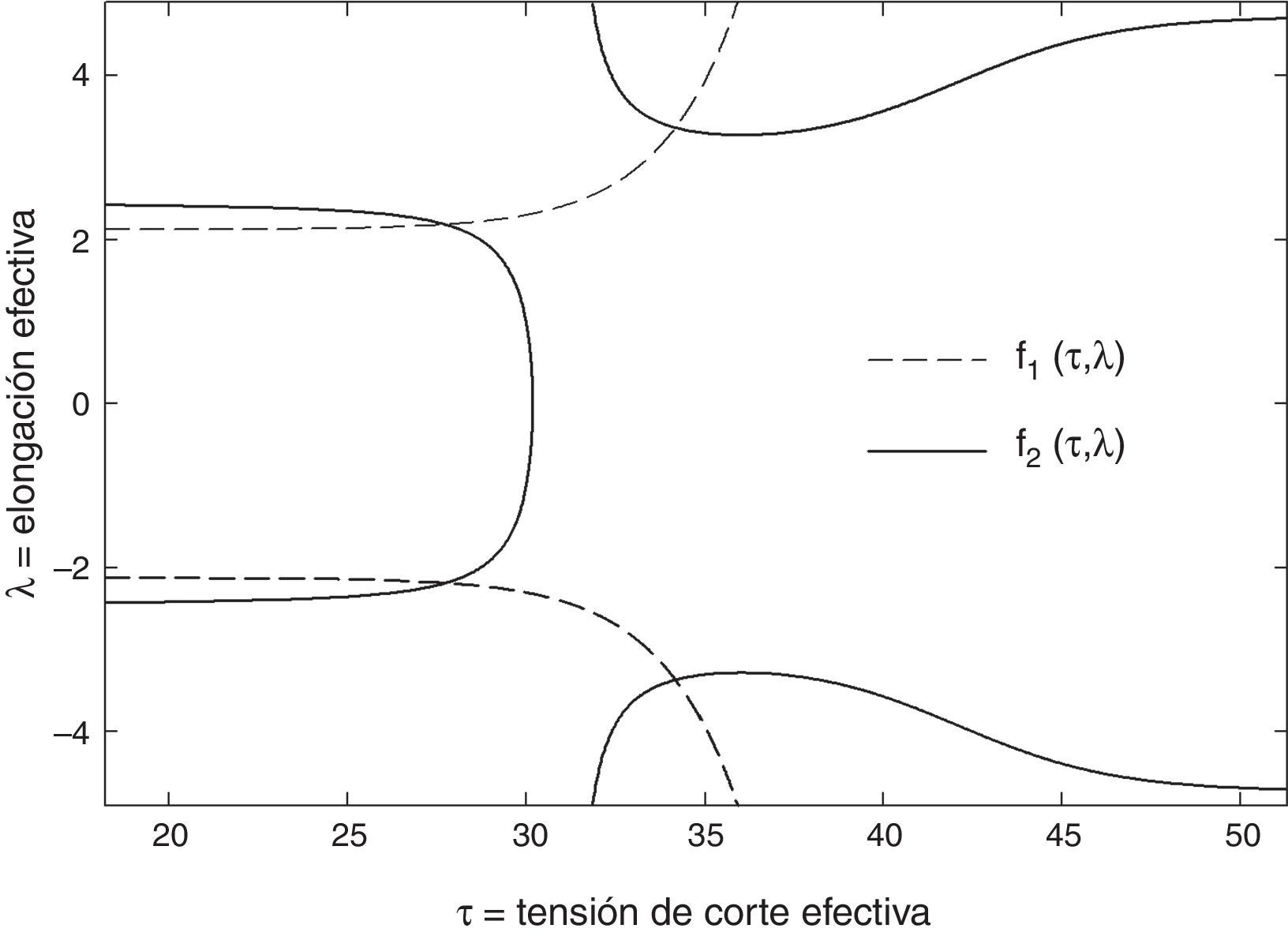
La solución del sistema de ecuaciones no es trivial. La figura 2 ilustra los comportamientos cualitativos de las ecuaciones (37) y (38), que se identifican como f₁(τ, λ) = 0 y f₂(τ, λ) = 0 para un conjunto genérico de propiedades. Se puede observar que las funciones se intersectan en 4 puntos, que son las posibles soluciones del sistema de ecuaciones. Sin embargo, solo una de ellas tiene significado físico.

Figura 2.

Funciones f1τ,λ=0 y f2τ,λ=0 en el plano τλ. Las 4 intersecciones son las posibles soluciones del sistema de ecuaciones no lineales.

Se consideraron 2 estrategias para resolver el sistema de ecuaciones:

• a)

  Un procedimiento de Newton-Raphson de 2 variables. Resultados preliminares mostraron que este procedimiento funciona correctamente para la mayoría de los casos si se le proporcionan estimaciones iniciales razonables de los valores de las incógnitas. Sin embargo, el procedimiento precisa ser refinado para que su desempeño resulte completamente confiable.

• b)

  Un procedimiento de Newton-Raphson en 2 niveles con la capacidad de «encapsular» la solución correcta. Esta estrategia, propuesta por Lush et al. [10], combina la capacidad de un método de bisección para encapsular la solución con la eficiencia del procedimiento de Newton-Raphson para resolver una ecuación escalar con una incógnita.

El procedimiento desarrollado para este trabajo combina las 2 estrategias mencionadas anteriormente. Se implementó así un procedimiento con 2 pasos:

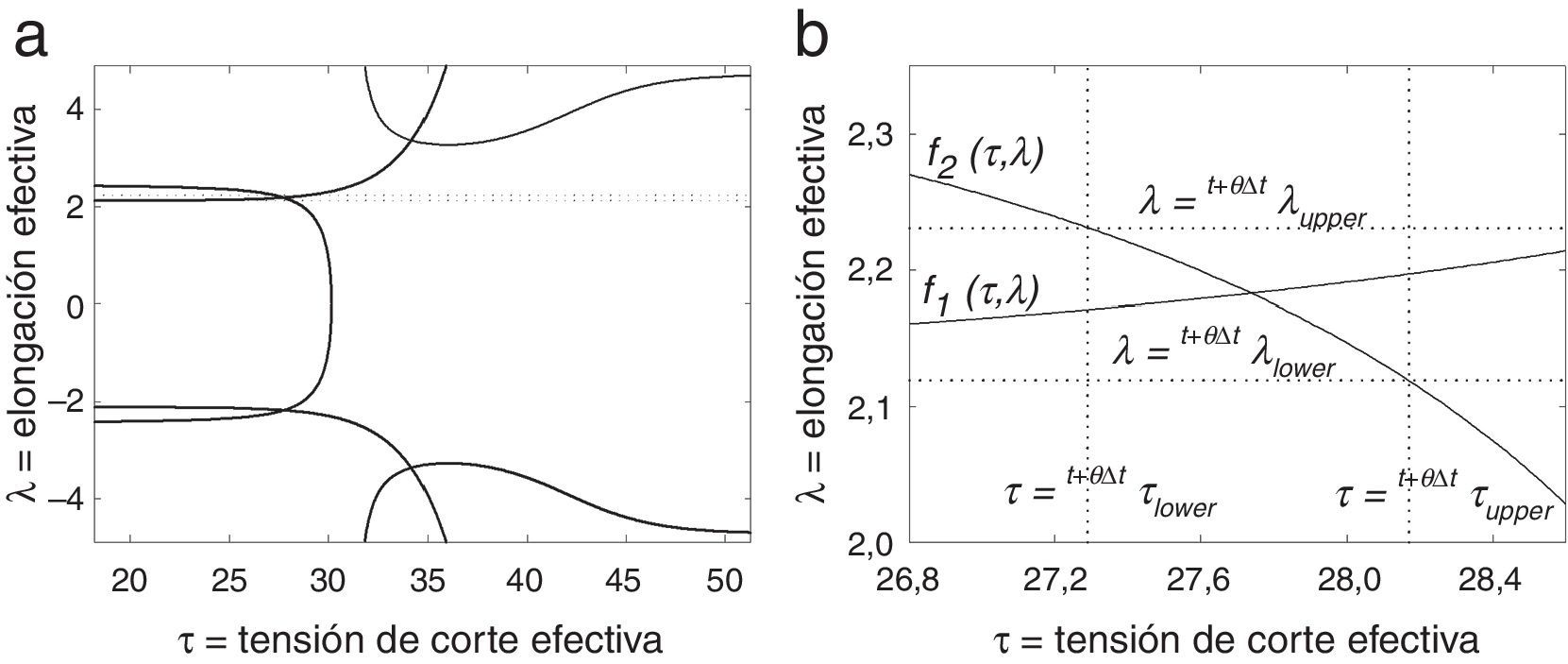
Paso 1: se calculan los límites superiores e inferiores de λ¯it+θΔt y τt+θΔt, que se utilizan para determinar las estimaciones iniciales (λ₀, τ₀). Idealmente, los límites de λ¯it+θΔt y τt+θΔt deberían definir un pequeño subconjunto rectangular en el plano λτ (véase la fig. 2) que contenga la solución con significado físico.

Paso 2: se resuelve el sistema de ecuaciones con un procedimiento de Newton-Raphson de 2 variables con (λ₀, τ₀) como estimaciones iniciales.

Los límites para λ¯it+θΔt se calculan a partir de 2 configuraciones de prueba. En la primera se supone que ocurren solo deformaciones elásticas y que las deformaciones inelásticas se mantienen constantes desde t hasta t + Δt. De esta forma se tiene:

De forma similar, la segunda configuración de prueba asume que solo ocurren deformaciones inelásticas, por lo que:

Los gradientes de deformación inelástica Ftrial 1it+Δt y Ftrial 2it+Δt se utilizan para calcular las elongaciones de prueba λ¯trial 1it+θΔt y λ¯trial 2it+θΔt, respectivamente. El mayor de estos valores se asigna a λuppert+θΔt y el menor a λlowert+θΔt (véase la fig. 3). Por su parte, los límites superior e inferior de ^{t + θΔt}τ se asignan como los valores de las abscisas de las intersecciones de la función f₂(τ, λ) = 0 con las ordenadas λuppert+θΔt y λlowert+θΔt, respectivamente. Los resultados de pruebas preliminares muestran la efectividad de este procedimiento para encapsular la solución con significado físico dentro de límites estrechos.

Figura 3.

a) Funciones f1τ,λ=0 y f2τ,λ=0 con la solución con significado físico encapsulada entre las coordenadas λuppert+θΔt, λlowert+θΔt, τuppert+θΔt y τlowert+θΔt; b) detalle del encapsulamiento solución con significado físico.

4.3

Limitación del tamaño del incremento de deformación

La calidad de las expresiones (37) y (38) para representar la ley de evolución del material depende de la precisión de las aproximaciones en (31), (32) y (39).

El término de error dominante de las aproximaciones (31) y (32) es de la forma O2||θΔt d¯it+θΔt||2=O2||Δγθ||2, lo que sugiere que este puede ser controlado mediante la imposición de un tamaño máximo al incremento de deformación inelástica. Los resultados de pruebas preliminares mostraron que incrementos de deformación inelásticos de hasta Δγ_θ < 0, 5 funcionan correctamente. Sin embargo, se seleccionó un valor umbral conservativo, Δγ_θ < 0, 15, que acota los errores de las expresiones (31) y (32) al 1%, aproximadamente.

Para estimar el error de la aproximación (39), se evaluó la diferencia entre la dirección del flujo plástico de prueba, N_trial, y el que resulta al final del algoritmo de integración, ^{t + θΔt}N:

Los resultados de pruebas preliminares mostraron que el error está en el rango entre 10⁻¹⁷ y 10⁻¹² para incrementos de deformación pequeños y medios, 0 < E < 0,05, y que llega hasta aproximadamente 10⁻¹⁰ para incrementos de deformación grandes: 0,05 < E < 0,13. Estos resultados permitieron concluir que la aproximación (39) no es una fuente de error importante.

5

Implementación del esquema de integración implícito

El esquema de integración implícito es el núcleo de la rutina de material definido por el usuario (UMAT, por sus siglas en inglés). Dada la tensión, T, los gradientes de deformación, {F, F^e, Fⁱ}, las variables internas al inicio del paso de tiempo, ξ=ξ1,ξ1,…,ξn, y el gradiente de deformación total al final del paso de tiempo, ^{t + Δt}F, es la función de la UMAT calcular Tt+Δt,Fet+Δt,Fit+Δt, las variables internas, ξ1t+Δt,ξ2t+Δt,…,ξnt+Δt y la matriz de rigidez tangente.

La implementación de la UMAT hace uso intensivo de las operaciones de evaluación de raíces cuadradas, logaritmos y mapeos exponenciales de tensores de segundo orden. Todas estas evaluaciones tienen un alto costo computacional asociado a la autodescomposición de los tensores. Se propone en este trabajo reducir este costo computacional mediante la utilización de aproximantes de Padé de alto orden (véase Bender y Orszag [21]).

Se presentan a continuación los detalles de la implementación de los aproximantes para la evaluación de raíces cuadradas, logaritmos naturales y mapeos exponenciales de tensores de segundo orden y para el cálculo de la matriz de rigidez tangente. Finalmente se presenta el algoritmo de la rutina de material definido por el usuario.

5.1

Evaluación de raíces cuadradas, logaritmos naturales y mapeos exponenciales de tensores de segundo orden

5.1.1

Raíces cuadradas y logaritmos naturales

El procedimiento de actualización de las tensiones necesita de la evaluación de:

Es importante notar que esta expresión se utilizará para evaluar deformaciones totales, por lo que se necesita una aproximación que proporcione resultados precisos en todo el rango de elongaciones. Para esto se propone utilizar un aproximante de Padé de cuarto orden expandido en el entorno de la matriz identidad [21]:

donde x∈ℝ3×3 e I es la matriz identidad. La precisión de esta aproximación fue evaluada para tensores de deformación asociados a elongaciones en el rango 0,6 < λ < 1,4. En todos los casos el error relativo se mantuvo en el rango entre 10⁻⁵ y 10⁻³, por lo que la precisión de la aproximación se consideró aceptable.

5.1.2

Mapeos exponenciales

El mapeo exponencial se utiliza para actualizar el gradiente de deformación inelástico al final del paso de tiempo t + Δt:

Se propone evaluar este mapeo utilizando el siguiente aproximante de Padé de cuarto orden expandido en el entorno del tensor nulo [21]:

Pruebas preliminares demostraron que la desviación del det(Fⁱ) de la unidad después de utilizar la aproximación (48) para miles de pasos de tiempo nunca superó ±10⁻⁸, por lo que la precisión de la aproximación se juzgó aceptable.

5.2

Cálculo de la matriz de rigidez tangente

La matriz de rigidez tangente en t + Δt es:

Esta se podría evaluar de forma analítica, pero la deducción para el modelo de A-B es un tarea complicada y laboriosa (véase, por ejemplo, Peric y Dettmer [13]). Como se privilegia en este trabajo la implementación rápida de nuevas ideas, se reserva la deducción de las expresiones analíticas para etapas posteriores del trabajo. Se propone aquí un procedimiento numérico para la evaluación de la matriz de rigidez tangente que puede ser fácilmente adaptado para eventuales modificaciones del modelo.

Según el conocimiento de los autores, el único antecedente sobre el cálculo numérico de la matriz de rigidez tangente para una formulación lagrangiana total es el trabajo de Miehe [22], quien utiliza una sofisticada técnica de perturbación. Teniendo como prioridad la simplicidad y la versatilidad, se propone en este trabajo utilizar una técnica más sencilla inspirada en las ideas de Kojic y Bathe [23].

La aproximación numérica de la expresión (49) para una formulación lagrangiana total es

La evaluación de la ecuación (50) requiere la perturbación del gradiente total de deformación, cuya expresión en la configuración espacial es:

donde:

es el tensor de perturbación.

La perturbación (51) se aplica 6 veces para calcular las 6 componentes independientes del tensor dU. Luego, cada conjunto Fe,Fi,t+ΔtF˜ se utiliza como entrada del algoritmo de actualización de las tensiones para obtener σ˜t+Δt, que finalmente se reemplaza en la expresión (50) para calcular cada una de las 6 columnas de la matriz de rigidez tangente.

Con el objetivo de asegurar la precisión del cálculo, el tamaño de la perturbación δ debe mantenerse relativamente pequeño respecto a la norma euclidiana del incremento del tensor de deformaciones:

donde el valor del coeficiente α es dado por el usuario.

A partir de la experiencia adquirida durante este trabajo, se seleccionó el valor α = 10⁻⁵, aun cuando valores de hasta α = 10⁻³ arrojan resultados razonables. Valores α < 10⁻⁵ reducen los residuos en las ecuaciones de equilibrio, pero sin disminuir el número total de iteraciones necesarias para alcanzar el equilibrio. A pesar de su sencillez, y como se demostrará con los ejemplos en la sección 6, la estrategia antes descrita es eficiente y robusta.

5.3

Algoritmo de integración implícito

La implementación del algoritmo de integración implícita para el modelo de A-B es tal y como se describe a continuación:

• 1.

  Los tensores {F, F^e, Fⁱ, ^t+ΔtF} se conocen al comienzo de cada paso de integración. El usuario especifica el valor de θ en el rango 0,5 < θ < 1.

• 2.

  Realizar las siguientes asignaciones:

  

• 3.

  Calcular Ftriale=Ft+θΔt Fi−1 (véase la ecuación (20)) y Eˆtrial1e=lnFtrial1eFtrial1eT con la aproximación de Padé P22(x) de la ecuación (46).

• 4.

  Calcular σ¯trial 1B y λ¯trial 1i con las expresiones (8) y (11), respectivamente. Utilizar Fⁱ como argumento de entrada.

• 5.

  Calcular σ¯trial 1vp= 2μe dev(Eˆtrial 1e)−σ¯trial 1B con la Eˆtrial 1e calculada en el paso 3 y el σ¯trial 1B calculado en el paso 4.

• 6.

  Calcular τ_{trial 1} y N_{trial 1} con las expresiones (16) y (17), respectivamente. Utilizar σ¯trial 1vp como argumento de entrada.

• 7.

  Calcular los siguientes tensores:

  

• 8.

  Calcular los coeficientes del sistema no lineal de ecuaciones dado por (37) y (38) con los tensores calculados en el paso 7:

  

• 9.

  Utilizar las ecuaciones (42) y (43) para calcular Ftrial 2e y Ftrial 2i y luego, con estos, los valores de λ¯trial 2i y τtrial 2 asociados.

• 10.

  Realizar las siguientes asignaciones:

  

• 11.

  Reemplazar λ por λuppert+θΔt en f2(τ,λ)=0 y determinar τ con el método de Newton-Raphson. Utilizar τlow como estimación inicial.

• 12.

  Reemplazar λ por λlowert+θΔt en f2(τ,λ)=0 y determinar el τ con el método de Newton-Raphson. Utilizar la solución de τ obtenida en el paso anterior como estimación inicial.

• 13.

  Asignar el mayor de los 2 valores de τ calculados en los pasos 11 y 12 a τuppert+θΔt y el menor a τlowert+θΔt.

• 14.

  Calcular las estimaciones iniciales para el método de Newton-Raphson como sigue:

  

• 15.

  Calcular la solución del sistema de ecuaciones dado por la (37) y la (38) con el método de Newton-Raphson. Utilizar τ0,λ0 como estimaciones iniciales.

• 16.

  Calcular ^{t + θΔt}γ con la ecuación (15).

• 17.

  IF ^{t + θΔt}γ Δt_θ < 0, 15 THEN

  GOTO paso 18.

  ELSE

  Reiniciar el algoritmo de integración con un incremento de tiempo igual a la mitad del incremento actual.

  ENDIF

• 18.

  Calcular la tasa de deformación inelástica d¯it+θΔt=t+θΔtγ Ntrial 1, donde ^{t + θΔt}γ es la calculada en el paso 16 y N_{trial 1} es la calculada en el paso 6.

• 19.

  Calcular Fit+θΔt=expd¯it+θΔt ΔtθFi con la aproximación de Padé P22(x) dada en la ecuación (48).

• 20.

  Calcular Fet+θΔt=Ft+θΔt Fi−1t+θΔt.

• 21.

  IF θ = 1 THEN

  

  ELSE

  Recalcular d¯it+θΔt a partir de ^{t + θΔt}F^e y ^{t + θΔt}Fⁱ.

  Utilizar la «nueva» tasa del gradiente de deformación d¯it+θΔt para calcular Fit+Δt=expd¯it+θΔtΔtFi y Fet+Δt=Ft+Δt Fi−1t+Δt.

  ENDIF

• 22.

  Calcular Eet+Δt=lnFet+Δt  FeTt+Δt con la aproximación de Padé P22(x) dada en la ecuación (46).

• 23.

  Calcular la tensión total de Cauchy, Tt+Δt=1J2μedev(Eet+Δt)+ketr(Eet+Δt)I, donde k^e = (3Λ^e + 2μ^e)/3.

• 24.

  Almacenar ^{t + Δt}F^e y ^{t + Δt}Fⁱ y reportar la tensión total ^{t + Δt}T.

• 25.

  Calcular la matriz de rigidez tangente de acuerdo con el procedimiento dado en la sección 5.2

Resulta interesante comentar aquí que, en el contexto de los análisis tridimensionales, el procedimiento de actualización de las tensiones se llama 7 veces por iteración. La primera llamada es para el cálculo del tensor de tensiones que reporta el programa de elementos finitos, mientras que las siguientes 6 se utilizan para el cálculo de la matriz de rigidez tangente. Una alternativa para reducir el costo computacional del cálculo de la matriz de rigidez tangente sería utilizar el par λ¯it+θΔt,τt+θΔt, calculado en el paso 15 para la primera actualización de las tensiones, como la estimación inicial de las siguientes 6 llamadas del método de Newton-Raphson. De esta forma se podrían evitar los pasos 9-14 dedicados al refinamiento de las estimaciones iniciales.

El desempeño global del algoritmo de integración se evaluará para 2 variantes en la selección de la matriz tangente y del resolvedor del sistema de ecuaciones global:

• •

  La parte simétrica de la matriz de rigidez tangente en combinación con un resolvedor global simétrico. Esta estrategia tiene 2 beneficios: reduce el número de perturbaciones asociadas al cálculo de la matriz de rigidez tangente y aprovecha el mejor desempeño del resolvedor para matrices simétricas (gradientes conjugados) respecto de su contraparte para matrices no simétricas (GMRES, por sus siglas en inglés).

• •

  Utilizar una matriz de rigidez tangente constante en combinación con un resolvedor para matrices simétricas. Esta opción elimina el costo asociado al cálculo de la matriz tangente (solo precisa ser calculada una única vez) y aprovecha el mejor desempeño del resolvedor para matrices simétricas.

6

Experimentos numéricos

En esta sección se presentan 3 ejemplos. Estos son, en orden de complejidad creciente, un ciclo de carga-descarga de una barra prismática, la indentación de un cilindro rígido en un bloque de polietileno de peso molecular ultra alto (UHMWPE) y la compresión de una corona circular con agujeros. Los 2 primeros ejemplos se utilizan para verificar la implementación y experimentar con el ajuste de los parámetros del algoritmo. Los resultados se comparan con los obtenidos con un esquema de integración explícito hacia delante, que se desarrolló también como parte de este trabajo pero cuyos detalles no se presentan aquí por limitaciones de espacio. El tercer ejemplo muestra la capacidad del esquema de integración propuesto para resolver un problema complejo.

Las constantes de la ley constitutiva del material para los 3 ejemplos son las del UHMWPE del trabajo de Bergström et al. [5]: μe=251,7   MPa,Λe=2898   MPa,μL=6,52   MPa,λlockL=2,92,γ0=1,284⋅10−71/s y τbase=0,962 MPa En todos los casos se utilizó el esquema de integración completamente implícito (θ = 1). Los tiempos de cálculo que se reportan corresponden a los de una notebook Dell Inspiron equipada con un procesador Intel Centrino Duo processor de 1,86 GHz con 4 Gb de RAM.

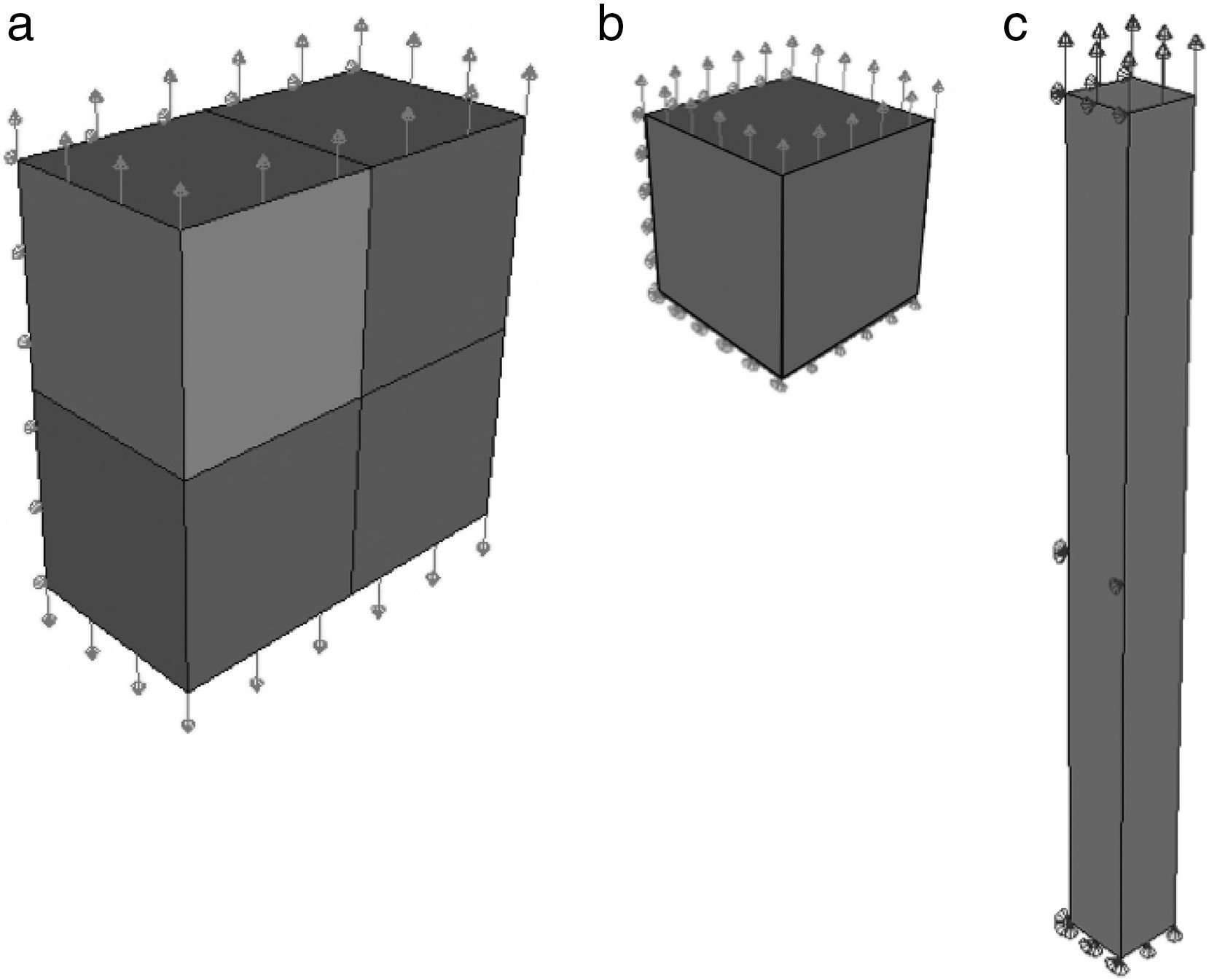
6.1

Tracción y compresión uniaxial de una barra prismática

Se modela en este ejemplo un ciclo de tracción-compresión uniaxial de la barra de dimensiones 2 mm × 2 mm ×1 mm (altura × ancho × espesor) que se ilustra en la figura 4a. El modelo de elementos finitos se limita a un cuarto de la geometría del problema con las correspondientes condiciones de contorno sobre sus planos de simetría (fig. 4b). Para la discretización se utilizó un elemento lineal hexaédrico de 8 nodos de integración reducida, C3D8R [24].

Figura 4.

Tracción uniaxial de una barra: a) geometría completa del problema; b) porción discretizada del modelo; c) geometría deformada.

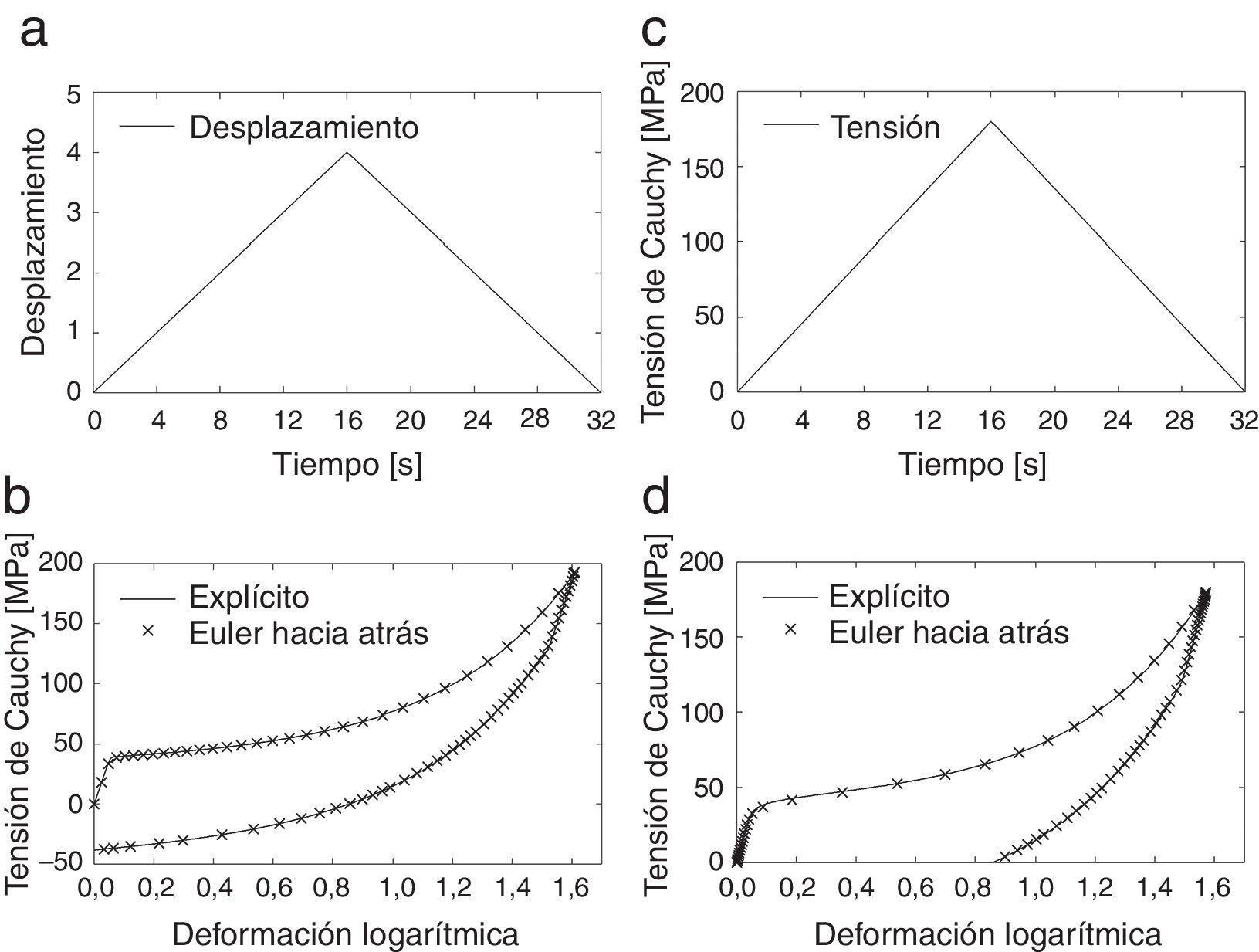
Se estudian 2 casos de carga en los que se aplican los ciclos de carga-descarga controlados por el desplazamiento y por la fuerza, que se grafican en la figura 5a,c. Ambos ciclos de carga se extienden por 32 segundos, divididos en 2 pasos de 16 segundos, el primero para la carga y el segundo para la descarga. En el primer paso se aplica a los modelos una elongación λ_max = 5. En el segundo paso del caso controlado por el desplazamiento se recobra la longitud inicial de la barra, mientras que para el caso controlado por la fuerza se retira la carga aplicada, por lo que la barra queda con deformaciones inelásticas permanentes.

Figura 5.

Tracción uniaxial de una barra prismáticas: a) ciclo de carga controlado por el desplazamiento; b) resultado de tensión vs deformación del ciclo de carga controlado por el desplazamiento; c) ciclo de carga controlado por la fuerza; d) resultado de tensión vs deformación del ciclo de carga controlado por la fuerza.

La figura 5b,d muestra los resultados de tensión versus deformación para los 2 ciclos de carga, mientras que la geometría deformada del modelo se ilustra en la figura 4c. Se muestran también como referencias en estas figuras los resultados calculados utilizando el algoritmo de integración explícito utilizando 10.000 pasos de tiempo. Los acuerdos entre ambas soluciones son excelentes. Los resultados sobre el desempeño del algoritmo en términos de los números de incrementos e iteraciones para alcanzar el equilibrio global se muestran en la tabla 1.

Tabla 1.

Resultados sobre el desempeño del esquema de integración implícito para el ejemplo de la tracción uniaxial de una barra prismática

	Ciclo controlado por desplazamiento	Ciclo controlado por fuerza
Número total de incrementos	83	79
Número total de iteraciones de equilibrio	117	125

A pesar de su similitud, los casos de carga controlados por la fuerza y por el desplazamiento tienen distintos comportamientos desde el punto vista computacional. El caso de carga controlado por la fuerza mostró ser el más demandante, ya que requirió el mayor número de iteraciones para alcanzar el equilibrio. Es interesante mencionar que cuando se utilizaron las matrices de rigidez simétrica y elástica constante (véase el último párrafo de la sección 5.3), el caso de carga controlado por la fuerza no alcanzó la convergencia, mientras que el controlado por el desplazamiento lo hizo en ambos casos.

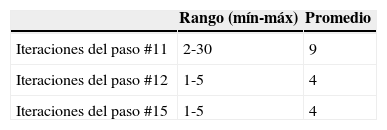
Según se presentó en la sección 5.3, los procedimientos de Newton-Raphson se utilizan 2 veces en el algoritmo de integración: en el refinamiento de la estimación inicial (pasos 11 y 12) y en la solución del sistema no-lineal de ecuaciones (paso 15). La tabla 2 muestra el número de iteraciones para el ejemplo controlado por la fuerza. Se puede observar que los procedimientos para refinar la estimación inicial requieren un número importante de pasos. Sin embargo, estos resultan en una estimación inicial muy precisa de las raíces del segundo procedimiento, el que solo necesita 4 iteraciones. En todos los casos, el residuo absoluto para los procedimientos de Newton-Raphson fue seleccionado igual 10⁻¹⁶.

Tabla 2.

Desempeño de los procedimientos de Newton-Raphson para el problema controlado por la fuerza

	Rango (mín-máx)	Promedio
Iteraciones del paso #11	2-30	9
Iteraciones del paso #12	1-5	4
Iteraciones del paso #15	1-5	4

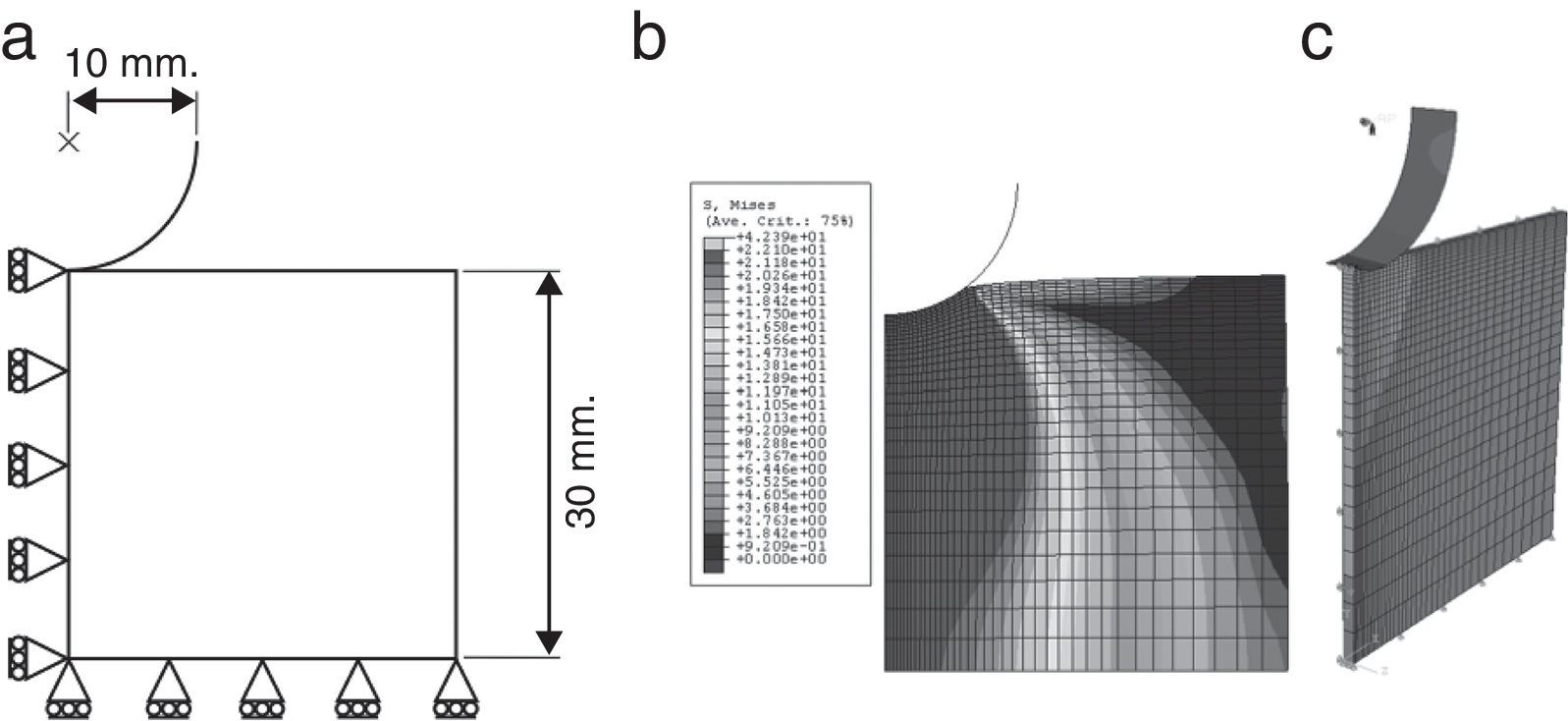
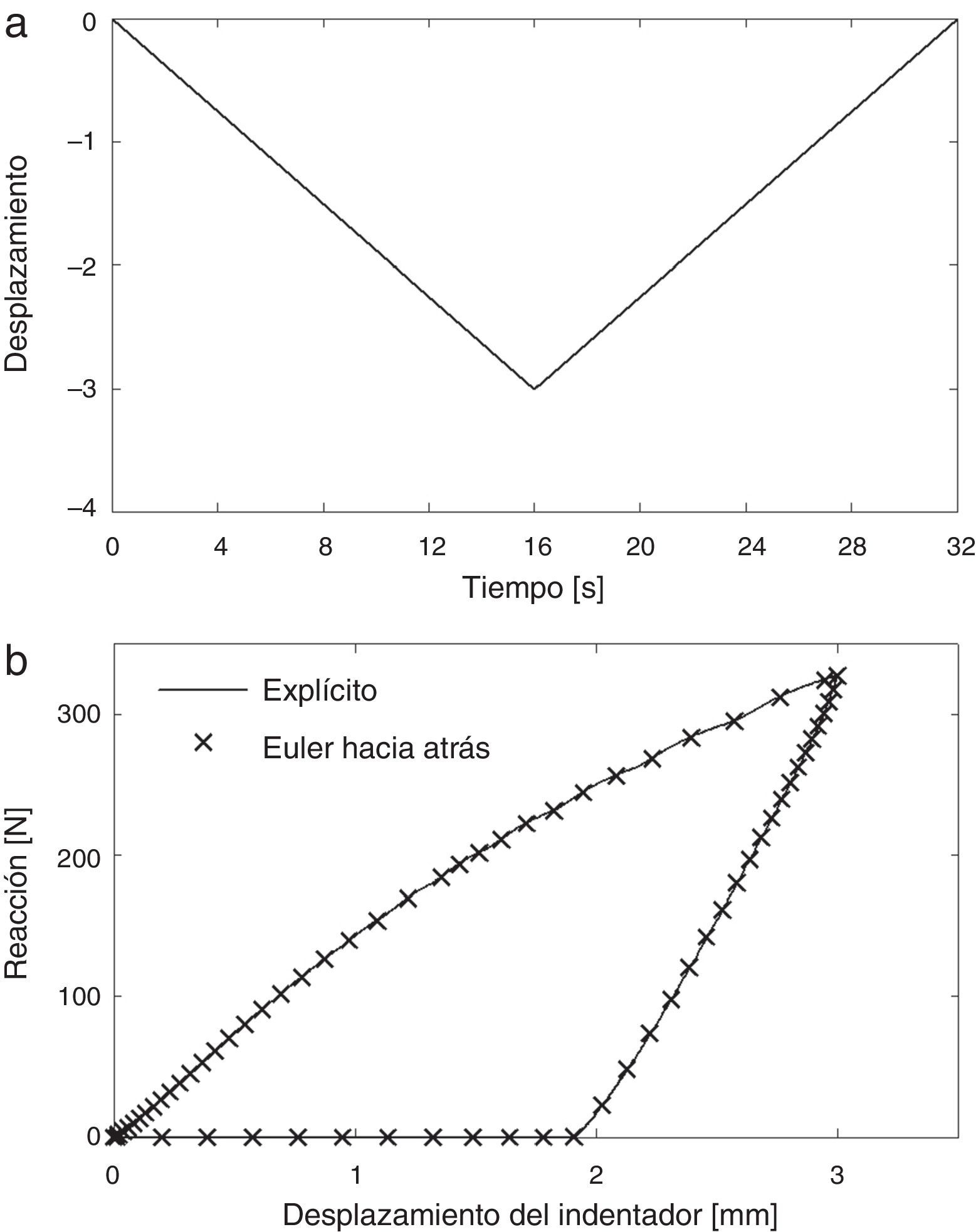
6.2

Indentación de un cilindro rígido en un bloque de UHMWPE

Este ejemplo consiste en la indentación de un cilindro rígido en un bloque de UHMWPE, según se ilustra en la figura 6a. El objetivo de este ejemplo es verificar el desempeño del algoritmo en el contexto de deformaciones no homogéneas y con contacto. El radio del cilindro es de 10 mm y las dimensiones del bloque son 30 mm × 60 mm (altura × ancho). El problema se resuelve simulando un estado de tensión plana con un espesor de 1 mm. El indentador se modela como un cilindro rígido analítico. Dada la simetría del problema, solo se discretiza la mitad de su geometría (fig. 6b,c). El bloque de UHMWPE se discretiza con 1.170 elementos C3D8H, con solo un elemento en la dirección del espesor. La interacción entre el indentador y el bloque se especifica como contacto sin fricción. Según se ilustra en la figura 7a, el ciclo de carga consiste en 2 pasos de 16 segundos de duración cada uno: en el primero se fuerza al indentador a penetrar 3 mm en el bloque (30% del radio del indentador) y en el segundo se regresa el indentador a su posición inicial.

Figura 6.

Indentación de un bloque de UHMWPE: a) geometría y condiciones de contorno del problema; b) modelo deformado; c) vista tridimensional del modelo.

Figura 7.

a) Ciclo de desplazamiento del indentador; b) registros fuerza vs desplazamiento del indentador.

Los resultados se presentan en las figuras 6b y 7b. La figura 6b ilustra la geometría deformada del problema junto con los contornos de la tensión equivalente de von Mises cuando el indentador alcanza la máxima profundidad. El gráfico de la figura 7b muestra el registro fuerza versus la deformación del algoritmo implícito junto con la solución de referencia calculada con el algoritmo explícito. Una vez más, se observa un excelente acuerdo entre ambas soluciones.

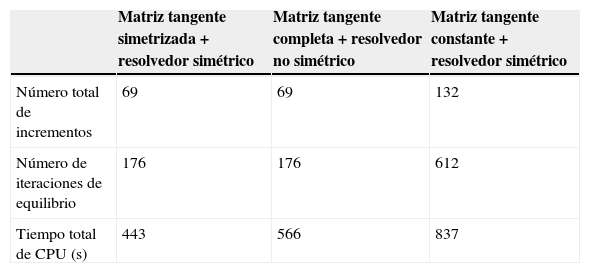
Se investigó el desempeño del esquema de integración para 3 combinaciones de la matriz de rigidez tangente y el resolvedor del sistema global de ecuaciones: la parte simétrica de la matriz tangente en combinación con el resolvedor para matrices simétricas, la matriz tangente completa con el resolvedor no simétrico y la matriz tangente elástica con el resolvedor simétrico. Los resultados se muestran en la tabla 3. Se puede observar que el número de incrementos cuando se utiliza la matriz tangente elástica dobla al de la matriz tangente completa, mientras que el número de iteraciones es 3,5 veces mayor. También se observó que, en contraste con el ejemplo de la barra traccionada, el algoritmo precisa del mismo número de incrementos e iteraciones de equilibrio para la matriz de rigidez tangente simetrizada y para la matriz de rigidez tangente completa. Sin embargo, debe considerarse que este ejemplo involucra, además de la no linealidad del material, la no linealidad de la condición de contacto, por lo que resulta complicado asociar su desempeño únicamente a la naturaleza de la matriz tangente.

Tabla 3.

Desempeño del algoritmo de integración para varias combinaciones de la matriz de rigidez tangente y el resolvedor del sistema de ecuaciones global. Los resultados corresponden al ejemplo de la indentación del bloque de UHMWPE

	Matriz tangente simetrizada + resolvedor simétrico	Matriz tangente completa + resolvedor no simétrico	Matriz tangente constante + resolvedor simétrico
Número total de incrementos	69	69	132
Número de iteraciones de equilibrio	176	176	612
Tiempo total de CPU (s)	443	566	837

6.3

Compresión de una corona circular con agujeros

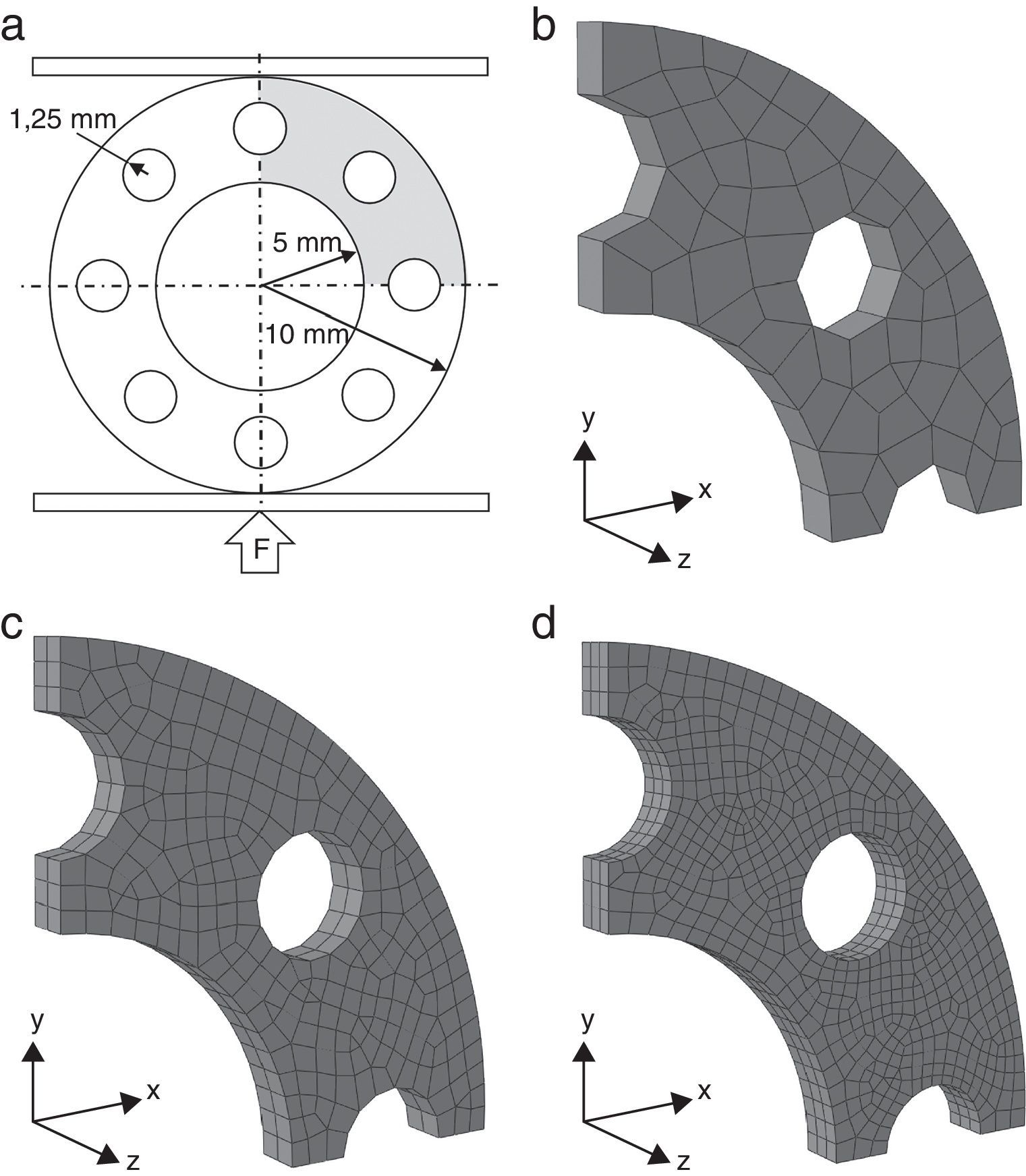
Este ejemplo consiste en la aplicación de un ciclo de carga-descarga en la dirección diametral de una corona circular de UHMWPE. La geometría del ejemplo se ilustra en la figura 8a. Los radios externo e interno de la corona son de 10 y de 5 mm, respectivamente. Los radios de los agujeros en la pared de la corona son de 1,25 mm. El problema se resuelve utilizando un modelo tridimensional de espesor unitario para la corona y una cáscara rígida para modelar el plato de compresión. Solo se discretiza la octava parte del modelo (sector de color gris en la fig. 8a) con las correspondientes condiciones de contorno sobre sus planos de simetría. El contacto entre la corona y el plato de compresión se considera libre de fricción.

Figura 8.

Compresión de una corona circular: a) geometría del ejemplo y discretización; b) malla gruesa; c) malla intermedia; d) malla fina.

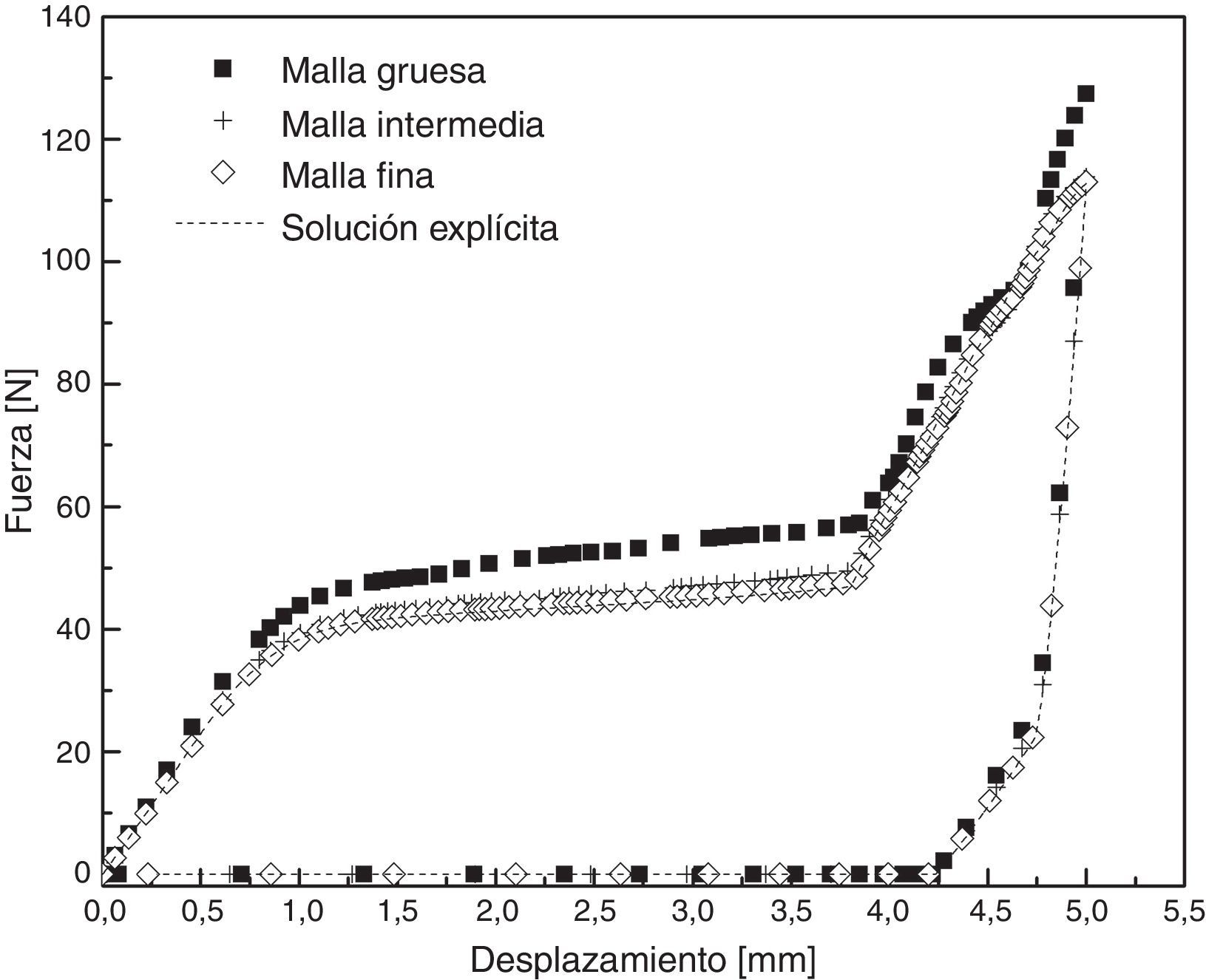
El problema se resolvió para los 3 tamaños de elemento que se ilustran en las figura 8b-d: 1 mm (malla gruesa), 0,5 mm (malla intermedia) y 0,3 mm (malla fina), respectivamente. En los 3 casos se utilizaron los elementos hexaédricos estándar de 8 nodos (C3D8) y cuña de 6 nodos con integración reducida (C3D6). Para calcular la solución de referencia con el algoritmo explícito se utilizó una malla aún más fina, con un tamaño de elemento de 0,25 mm.

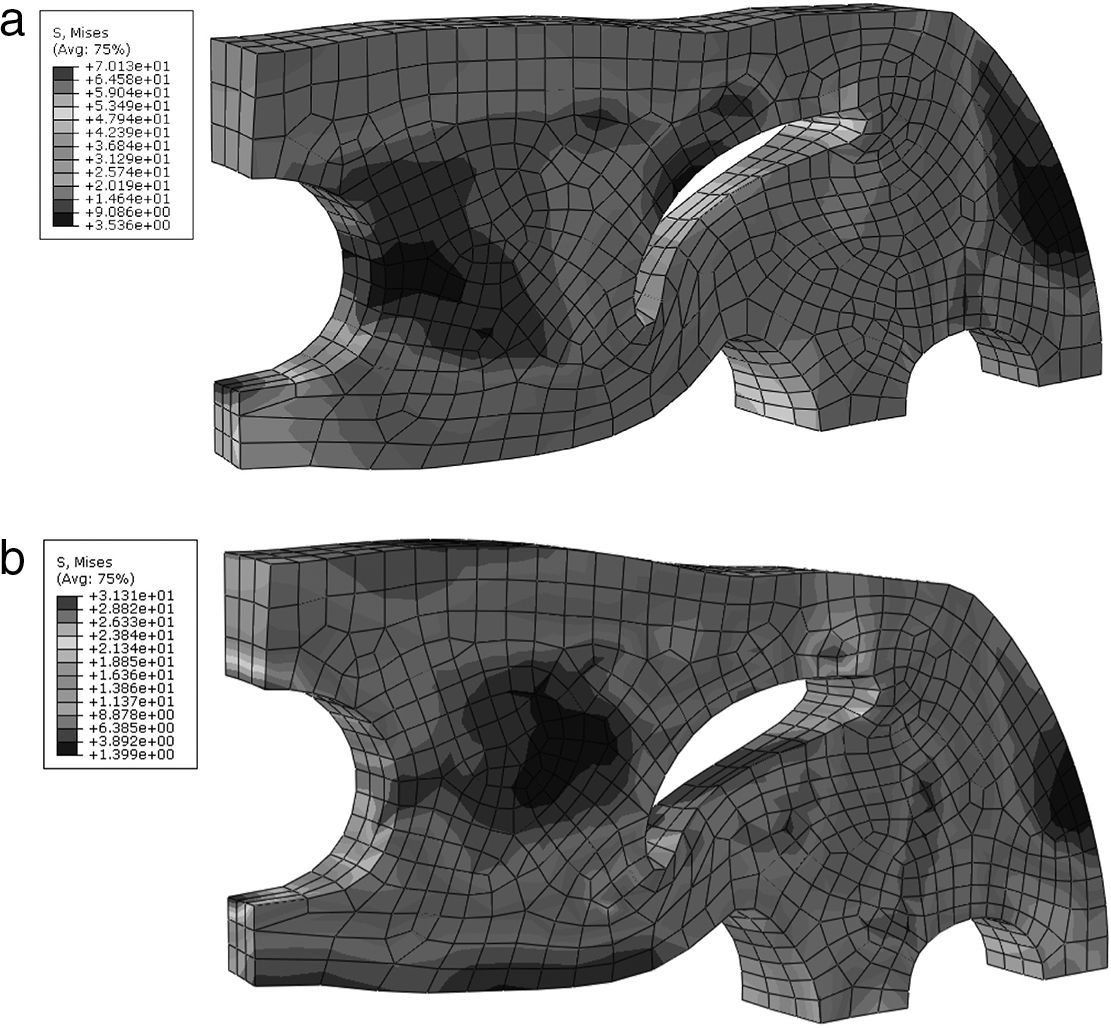
La solución con la malla gruesa precisó 166 incrementos, mientras que las mallas intermedia y fina precisaron 204 y 234 incrementos, respectivamente. Los resultados se presentan en las figuras 9 y 10. En la figura 9 se grafica la fuerza de reacción en el plato como función de su desplazamiento vertical. Se observa que con el refinamiento de la discretización las soluciones implícitas convergen hacia la solución explícita de referencia. Las soluciones de las mallas intermedia y fina son casi coincidentes. Las diferencias entre estas soluciones en puntos característicos de la curva, tales como la carga pico para la máxima fuerza de compresión (113 N) y el desplazamiento al momento de la pérdida de contacto entre la corona y el plato de compresión durante la descarga (4,20 mm), son menores del 0,5%. La figura 10 ilustra la geometría deformada de la corona con el mapa de colores de la tensión equivalente de von Mises para el momento de máxima carga y al final de la simulación.

Figura 9.

Compresión de la corona circular: resultados para el registro fuerza vs desplazamiento.

Figura 10.

Configuraciones deformadas con los contornos de la tensión equivalente de von Misses para: a) el momento de máxima carga, y b) al final del ciclo de carga-descarga (tensiones y deformaciones remanentes).

Los resultados obtenidos muestran la robustez del esquema de integración implícito para resolver un problema demandante, que involucra rotaciones importantes de las direcciones de las tensiones y deformaciones principales durante la historia de carga.

7

Conclusiones

En este trabajo se ha presentado una implementación simple y versátil de un esquema de integración implícito del modelo viscoplástico de A-B.

El esquema propuesto utiliza el método de Euler hacia atrás en combinación con procedimientos estándar para la actualización de las tensiones en la configuración relajada. Mediante la utilización de simplificaciones y aproximaciones, el núcleo del esquema de integración se reduce a la solución para cada paso de tiempo de un sistema de 2 ecuaciones no lineales que tiene como incógnitas la tensión de corte y la elongación inelástica efectivas. El sistema se resuelve de forma eficiente utilizando un procedimiento en 2 etapas. En la primera se encapsula la solución con significado físico y se calcula una estimación inicial de la solución. Esta estimación sirve de semilla para resolver el sistema con un método de Newton-Raphson con 2 variables en la segunda etapa.

Con la única excepción de los procedimientos de Newton-Raphson antes mencionados, el esquema de integración propuesto no requiere procesos iterativos. El procedimiento prescinde del cálculo de autodescomposiciones, descomposiciones polares y matrices de rotación. Las raíces cuadradas, exponenciales y logaritmos naturales de tensores de segundo orden se calculan utilizando aproximantes de Padé de alto orden. La matriz de rigidez tangente se calcula con un esquema de diferencias finitas. Como resultado, el algoritmo para la actualización de las tensiones es muy sencillo, pero al mismo tiempo muy preciso y relativamente eficiente en términos de costo computacional.

El esquema de integración se implementó como una rutina de material definido por el usuario del software de elementos finitos ABAQUS. Su precisión, su estabilidad y su eficiencia se investigaron y demostraron con una serie de ejemplos para los que se compararon las soluciones con las que resultan de utilizar un esquema de integración explícito. Como resultado, se dan una serie de recomendaciones para ajustar el tamaño del incremento de deformación inelástica y los residuos de los procedimientos de Newton-Raphson. Con el objetivo de mejorar el desempeño global de la implementación se exploró la utilización de matrices tangentes simétricas (simetrizada y elástica constante). Los resultados en este sentido mostraron que para algunos casos las matrices de rigidez constantes no permiten alcanzar la convergencia, por lo que es mandatorio utilizar la matriz completa. En otros casos se obtuvo un beneficio marginal, observándose que la reducción del tiempo de cálculo por utilizar las matrices simétricas se compensa por el menor número de iteraciones asociados al uso de la matriz completa.

Es la intención de los autores que el esquema de integración propuesto sea un punto de partida para la rápida implementación y experimentación de nuevos modelos constitutivos para polímeros y biomateriales desarrollados sobre la base del modelo de A-B.

Agradecimientos

Este trabajo ha sido realizado como parte de proyectos de investigación financiados por la Agencia Nacional de Promoción Científica y Tecnológica y el Consejo Nacional de Investigaciones Científicas y Técnicas de la República Argentina y la Universidad Nacional de Mar del Plata.