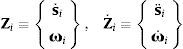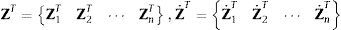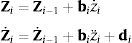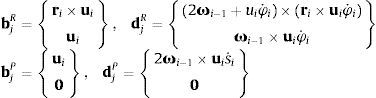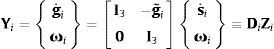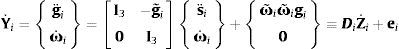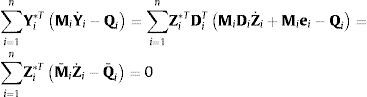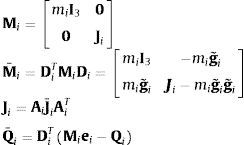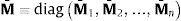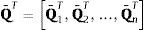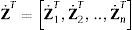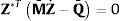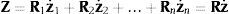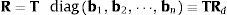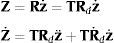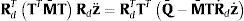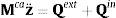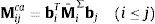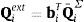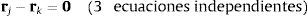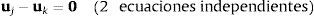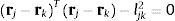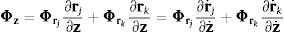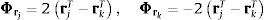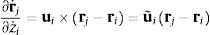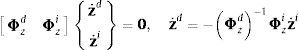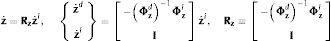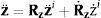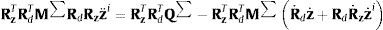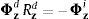Este artículo presenta la implementación eficiente de una formulación dinámica semirrecursiva para la simulación de sistemas multicuerpo de gran tamaño y complejidad, con especiales aplicaciones en el campo de la automoción y en particular en el de los vehículos industriales. Estos sistemas suelen tener un elevado número de restricciones por lo que es habitual trabajar con sistemas de ecuaciones redundantes pero compatibles. El tratamiento matemático de estos sistemas tiene un coste computacional muy elevado, dificultando la obtención de simulaciones en tiempo real.
En este artículo se describen 2 implementaciones para aumentar la eficiencia de estos cálculos. Estos métodos se diferencian en que uno considera a la matriz Jacobiana de las ecuaciones de restricción como una matriz densa, y el otro la considera sparse. El primero resuelve las ecuaciones mediante el uso de matrices densas y el segundo utilizando la librería MA48 de Harwell.
Ambas metodologías han sido implementadas en 2 modelos de sistemas multicuerpo de diferente tamaño. El primer modelo es el de un vehículo tipo chasis-cabina de IVECO, con 17 grados de libertad. El segundo modelo de vehículo es el de un camión con semirremolque, sistema que posee 40 grados de libertad. Tomando como base comparativa para ambos modelos sus implementaciones programadas en C/C++, las mejoras obtenidas en la eficiencia utilizando matrices densas (BLAS) han sido aproximadamente de un 15 y un 50% respectivamente. Mientras que el uso de matrices sparse no ha introducido mejoras apreciables en el primer caso, ha mejorado un 8% los tiempos de las BLAS en el segundo.
This article shows an efficient implementation of a dynamic semi-recursive formulation for large and complex multibody system simulations, with interesting applications in the automotive field and especially with industrial vehicles. These systems tend to have a huge amount of kinematic constraints, becoming usual the presence of redundant but compatible systems of equations. The maths involved in the solution of these problems have a high computational cost, making very challenging to achieve real-time simulations.
In this article, two implementations to increase the efficiency of these computations will be shown. The difference between them is the way they consider the Jacobian matrix of the constraint equations. The first one treats this matrix as a dense one, using the BLAS functions to solve the system of equations. The second one takes into account the sparse pattern of the Jacobian matrix, introducing the sparse function MA48 from Harwell.
Both methodologies have been applied on two multibody system models with different sizes. The first model is a vehicle IVECO DAILY 35C15 with 17 degrees of freedom. The second one is a semi-trailer truck with 40 degrees of freedom. Taking as a reference the standard C/C++ implementation, the efficiency improvements that have been achieved using dense matrices (BLAS) have been of 15% and 50% respectively. The results in the first model have not improved significantly by using sparse matrices, but in the second one, the times with sparse matrices have been reduced 8% with respect to the BLAS ones.
La simulación dinámica precisa y eficiente de sistemas multicuerpo es un tema de gran interés en diversas áreas como maquinaria, robótica, biomecánica, espacio y dinámica vehicular, entre otras. El comportamiento de estos sistemas es profundamente no lineal, con grandes desplazamientos y rotaciones de sólido rígido, lo que dificulta el papel de la imaginación espacio-temporal de los ingenieros e incrementa la importancia de las simulaciones con gráficos 3-D realistas en la percepción de los movimientos resultantes. En la actualidad, las simulaciones con ordenador de sistemas multicuerpo poseen excelentes características de calidad y fiabilidad en los resultados obtenidos, con importantes reducciones de costes y tiempo de desarrollo de productos. La obtención de simulaciones en tiempo real es fundamental en aplicaciones tipo «hardware-in-the-loop» o «man-in-the-loop».
Un sistema multicuerpo es un conjunto de sólidos rígidos y/o flexibles unidos parcialmente entre sí por medio de pares cinemáticos, que permiten unos grados de libertad de movimiento relativo mientras restringen otros. La definición de la posición de todos los sólidos de un sistema multicuerpo requiere de un determinado número de parámetros o coordenadas generalizadas que por lo general no son independientes, sino que están relacionadas mediante las ecuaciones de restricción. Este número de coordenadas suele ser superior al número de grados de libertad del sistema, ya que estos son independientes [6]. El número de ecuaciones de restricción es la diferencia entre el número de coordenadas generalizadas y el número de grados de libertad. Por ejemplo, un cuadrilátero articulado plano tiene un grado de libertad, pero si la posición de cada sólido móvil se define con las 2 coordenadas del centro de gravedad y un ángulo, habrá un total de 9 coordenadas generalizadas. Como consecuencia existirán 8 ecuaciones de restricción que relacionan dichas coordenadas.
Las coordenadas generalizadas más utilizadas pueden agruparse en 3 grupos. En primer lugar se encuentran las coordenadas de punto de referencia, que definen la posición de cada sólido mediante las coordenadas cartesianas de un punto y 3 o más parámetros que describen su orientaron angular. En segundo lugar, las coordenadas relativas, que describen la posición de cada sólido respecto al sólido anterior en la cadena cinemática, utilizando las coordenadas de movimiento relativo permitidas por dicho par. En tercer lugar, las coordenadas naturales, que definen la posición de todos los sólidos mediante las coordenadas cartesianas de puntos y vectores unitarios, compartiendo cuando sea posible dichos puntos y vectores para definir pares sin ecuaciones adicionales. Cada tipo de coordenadas está asociado con un tipo de ecuaciones de restricción, resultando más sencillas las asociadas con las coordenadas naturales. Por otra parte, las coordenadas relativas son las que necesitan un número menor de variables y las coordenadas de puntos de referencia las que permiten plantear las ecuaciones de la dinámica de la manera más sencilla. Para la formulación utilizada en este artículo, inicialmente descrita en la ref. [1], se utilizarán distintos tipos de coordenadas en distintas fases del planteamiento, utilizando en última instancia las coordenadas relativas para llegar a un sistema de ecuaciones diferenciales de reducido tamaño.
La simulación dinámica de los sistemas multicuerpo se puede plantear de diversas formas. Una posibilidad es plantear las ecuaciones diferenciales en coordenadas dependientes y añadirles las ecuaciones de restricción y sus derivadas, llegando a un sistema de ecuaciones algebraico-diferenciales de índice 3. Otra posibilidad es utilizar las ecuaciones de restricción para eliminar las coordenadas dependientes, llegando a un sistema de ecuaciones diferenciales con tantas variables como grados de libertad tiene el sistema. Exceptuando algunos detalles, este es el método utilizado en este trabajo, tratándose con ello de establecer un método que sea al mismo tiempo sencillo y eficiente.
Los métodos de simulación de sistemas multicuerpo se clasifican en 2 grandes grupos: métodos globales y métodos topológicos. Los métodos globales son más sencillos porque proceden siempre de la misma manera, en cualquier tipo de sistema. Por el contrario, los métodos topológicos tratan de aprovechar la topología o conectividad del sistema que se desea analizar. Por ejemplo, si el sistema es de cadena abierta y se utilizan coordenadas relativas, no hay ecuaciones de restricción. Los métodos topológicos son más eficientes que los métodos globales, pero también más difíciles de implementar [1,2]. Es frecuente que los métodos topológicos se formulen de modo recursivo con una complejidad O(N), siendo N el número de elementos, lo cual resulta muy eficiente en sistemas de cadena abierta con gran número de elementos, ya que no necesitan resolver ningún sistema de ecuaciones lineales, cuya complejidad es O(N3). Su aplicación a sistemas de cadena cerrada es realmente muy compleja.
El método descrito en este artículo pertenece a la categoría de los métodos topológicos semirrecursivos. Es topológico porque aprovecha la topología del sistema y es semirrecursivo porque termina resolviendo un sistema de ecuaciones lineales, cuyos coeficientes se han calculado de forma recursiva. La ventaja de esta formulación es que es casi tan sencillo como los métodos globales y tiene la eficiencia propia de los métodos topológicos.
El método que se va a presentar está basado en una doble transformación de velocidades. En un primer momento el sistema se convierte en uno de cadena abierta, lo que puede realizarse de 2 formas. La primera es eliminando algunos pares cinemáticos del sistema y la segunda es eliminando algunos elementos simples como las barras biarticuladas (si están presentes). Ambas metodologías no son excluyentes por lo que se pueden realizar en forma conjunta. A continuación se aplica el teorema de las potencias virtuales en coordenadas de punto de referencia. Seguidamente se introduce una transformación de velocidades de las velocidades cartesianas a las velocidades relativas de los pares, que en un sistema de cadena abierta son independientes. Finalmente se introducen las ecuaciones de restricción de cierre de lazo y se aplica una nueva transformación de velocidades que permite obtener las ecuaciones diferenciales del movimiento del sistema de cadena cerrada en coordenadas relativas independientes. La primera transformación de velocidades tiene un tamaño relativamente grande y se realiza analíticamente. La segunda transformación de velocidades se realiza numéricamente en un sistema de tamaño más reducido, por lo que se puede realizar también de un modo muy eficiente.
Una observación respecto al concepto de «tamaño» en dinámica de sistemas multicuerpo, que es muy diferente de cómo se entiende en otras áreas de la Mecánica Computacional, como por ejemplo el Método de los Elementos Finitos. En dinámica de sistemas multicuerpo un sistema pequeño tiene típicamente entre 1 y 5 grados de libertad y un número de sólidos rígidos entre 2 y 10. Los robots son ejemplos típicos de esta categoría. Un sistema grande puede tener algunas decenas de grados de libertad y un número de sólidos rígidos que se acerque al centenar. Los vehículos pesados pertenecen a esta categoría. Desde el punto de vista de los métodos numéricos, estos tamaños son objetivamente pequeños, pero hay que tener en cuenta por ejemplo que una integración numérica mediante un método de Runge-Kutta de 4.° orden con un paso de 0,001s requiere 4.000 evaluaciones de las ecuaciones diferenciales del movimiento por segundo, y esta es una carga computacional muy importante si se quiere obtener tiempo real. Estos tamaños representan una dificultad a la hora de incrementar la eficiencia numérica. Unidos al carácter secuencial de las operaciones no resulta sencillo aplicar técnicas de paralelización, y se encuentran también en el límite de tamaños para los que la utilización de funciones BLAS (basic linear algebra subprograms) o técnicas de matrices sparse resulta beneficiosa. Un objetivo esencial de este artículo es explicar cómo se pueden aplicar de modo eficiente estas metodologías y qué mejoras en los tiempos de cálculo cabe esperar.
Un último punto a considerar es el propio proceso de integración de las ecuaciones diferenciales del movimiento, que son de orden 2. Estas ecuaciones se reducen a orden 1 evitando problemas de estabilidad por medio del método de la partición de coordenadas [3], y la formulación de Maggi [4,5], uno de los que mejores resultados proporcionan en términos de estabilidad; aunque es considerado «costoso»” en términos computacionales. La formulación presentada en este artículo viene a resolver esta dificultad.
En resumen, el principal objetivo de este artículo es pues el de presentar una formulación dinámica sencilla y muy eficiente para la simulación de sistemas multicuerpo cuya implementación se mejora mediante la introducción de avanzadas librerías matemáticas. Esta formulación está basada en una doble transformación de velocidades mediante la que se obtiene el sistema de ecuaciones diferenciales del movimiento en función de un conjunto de coordenadas relativas independientes.
2Formulación semirrecursiva para sistemas de cadena abiertaEste artículo está basado en la formulación semirrecursiva de Rodríguez et al. [1]. El planteamiento de las ecuaciones de la dinámica para sistemas de cadena abierta es muy sencillo. Utilizando coordenadas cartesianas y aplicando las ecuaciones de Newton-Euler para cada sólido es fácil llegar a un sistema en el que aparecen las fuerzas de restricción entre los sólidos que están unidos mediante un par cinemático. Estas fuerzas internas desaparecen si se aplica el teorema de las potencias virtuales, seguido de una transformación entre las velocidades cartesianas y relativas, según se indica a continuación.
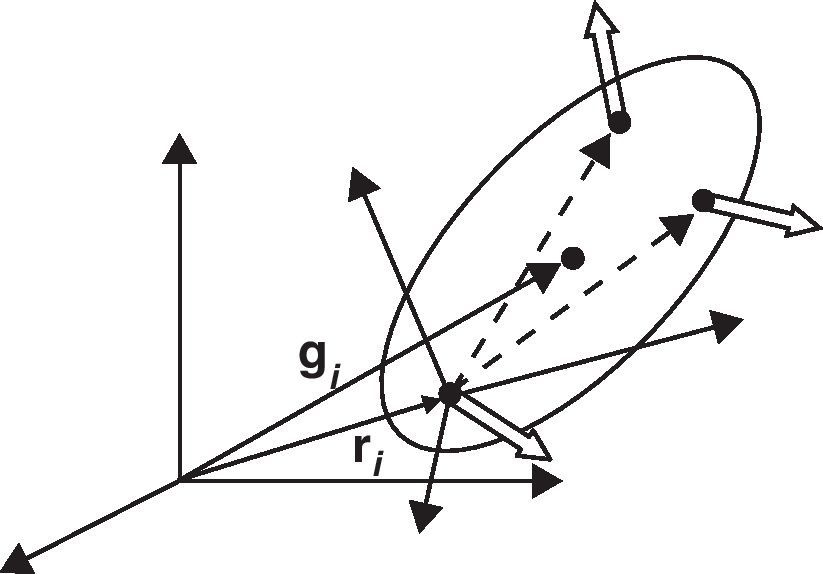
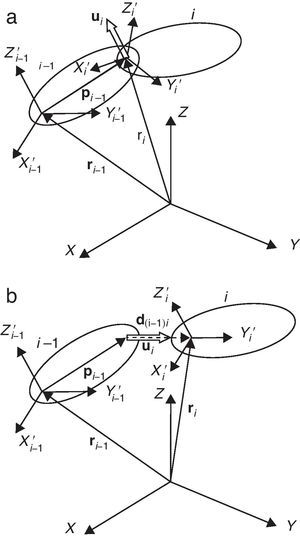
La geometría de cada elemento móvil se define en un sistema de coordenadas que se mueve con él y tiene el origen en su punto de entrada. Para definir los pares del elemento se utilizan coordenadas naturales [6], es decir un conjunto de puntos y vectores unitarios que describen la posición y orientación de sus pares, como puede observarse en la figura 1. La posición de cada elemento se define mediante las coordenadas cartesianas de su punto de entrada y la matriz de rotación que describe su posición angular respecto al sistema de coordenadas global. Es evidente que la posición se define de un modo redundante, pero esto se resuelve con el cambio de coordenadas que se verá a continuación.
Por razones de simplicidad y eficiencia solo se consideran pares de revolución y prismáticos. A partir de ellos puede representarse una amplia variedad de pares. Por ejemplo, una rótula o par esférico es la combinación de 3 pares de revolución, un par cilíndrico es un par de revolución más un par prismático, etc.
Las velocidades y aceleraciones cartesianas se pueden definir mediante los vectores,
donde s˙i y s¨i son respectivamente la velocidad y aceleración del punto del sólido i que instantáneamente coincide con el origen del sistema de referencia inercial.Los vectores Z y Z˙ son los vectores que contienen las velocidades y aceleraciones cartesianas de todos los elementos del sistema,
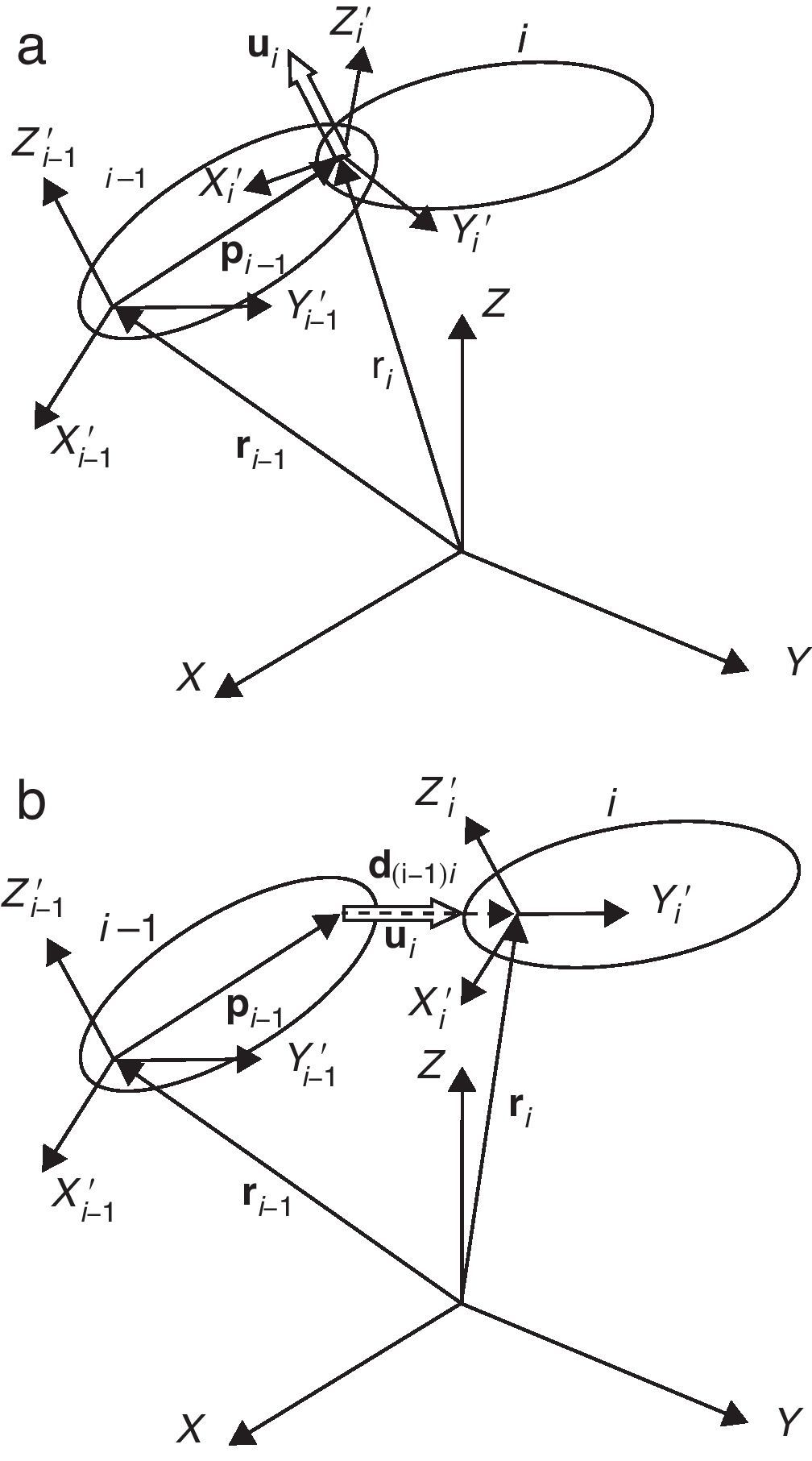
Utilizando puntos y vectores unitarios, los pares cinemáticos entre elementos contiguos se modelan muy fácilmente. Por ejemplo, en un par de revolución entre los elementos i−1 e i (fig. 2), coinciden un punto de salida y un vector unitario del elemento i−1 con un punto de entrada y un vector unitario del elemento i. Para un par prismático ambos elementos comparten un vector unitario, y el punto de entrada del elemento i se encuentra en la línea definida por el punto de salida y el vector unitario del elemento i−1 (fig. 2); en este caso ambos elementos comparten la matriz de rotación.
Como todos los elementos comparten el mismo punto de referencia, las fórmulas recursivas que dan las velocidades y aceleraciones cartesianas del elemento i en función de las del elemento i−1 son muy sencillas, porque no necesitan matrices de transformación:
Los vectores bi y di dependen del tipo de par (prismático o de revolución) que une los elementos i e i−1. Su significado físico puede fácilmente deducirse de la expresión (3) y figura 2. Por ejemplo bi es un vector 6×1 que describe la velocidad cartesiana relativa entre ambos elementos cuando se introduce una velocidad relativa z˙i=1. La parte superior corresponde a la velocidad relativa de traslación y la inferior a la de rotación. Los vectores bi y di responden a las expresiones siguientes:
donde ui es el vector que define el eje del par, ri el vector de posición de dicho par, φ˙i es la velocidad angular relativa entre ambos sólidos, s˙i es la velocidad del punto que instantáneamente coincide con el origen de coordenadas y ωi−1 es la velocidad angular del sólido de entrada.Las ecuaciones del movimiento son más sencillas utilizando velocidades y aceleraciones cartesianas basadas en el centro de gravedad, denotadas como Yi e Y˙i, que se relacionan con Zi y Z˙i de la siguiente forma:
donde g˙i y g¨i son la velocidad y aceleración del centro de masas, ωi y ω˙i la velocidad y aceleración angular del sólido i, y finalmente s˙i y s¨i son la velocidad y aceleración del punto ligado al sólido i que instantáneamente coincide con el origen del sistema inercial de coordenadas.Utilizando las ecuaciones anteriores el teorema de las potencias virtuales se puede expresar de la siguiente forma:
donde el asterisco (*) denota las velocidades virtuales. Las matrices de la ecuación (7) son:donde las matrices Ai y J¯i representan la matriz de rotación y el tensor de inercia en el sistema de coordenadas locales del sólido i respectivamente.Si M¯ es la matriz de inercia, Q¯ el vector de fuerzas y Z˙ el vector de aceleraciones de todo el sistema, se tendrá:
La ecuación de las potencias virtuales (7) toma la forma:
En la ecuación anterior no aparecen las reacciones en los pares, porque son fuerzas internas que se anulan 2 a 2 y no producen potencia virtual. Las velocidades virtuales Z* no se pueden eliminar en la ecuación (12) porque no son independientes. Sin embargo, es posible ahora introducir una transformación entre las velocidades cartesianas y las velocidades relativas de cadena abierta en la forma:
donde la columna j de la matriz R contiene las velocidades cartesianas de todos los elementos situados por encima del par j, consecuencia de introducir una velocidad relativa unidad en el par j, manteniendo nulas todas las demás velocidades relativas.En la implementación realizada se supone que el par de entrada de un sólido (par mediante el que se llega al sólido en el sistema de cadena abierta, recorrido desde el elemento fijo o raíz hacia los sólidos terminales u hojas del árbol), tiene el mismo número que este, y que, como ha sido sugerido por Negrut et al. [2], los sólidos y pares de la cadena abierta han sido numerados desde las hojas o sólidos terminales hacia la raíz o sólido base del árbol. De este modo el elemento padre siempre tiene una numeración mayor que cualquiera de sus elementos hijos. Esta numeración evita el llenado o aparición de elementos no nulos en el proceso de eliminación de Gauss. En este punto es conveniente introducir la matriz de accesibilidad T que define la conectividad o topología del sistema. Sus filas se corresponden con los elementos y sus columnas con los pares. El elemento Tij es 1 si el elemento i está por encima del par j, y en caso contrario es 0. La matriz T es triangular superior; la columna i define los elementos que se encuentran por encima del par i; y la fila j define los pares que se encuentran por debajo del elemento j, es decir entre este y el elemento raíz. Como consecuencia la expresión (13) se puede escribir en la forma:
donde la parte superior de bi, en relación a la ecuación (3), es la velocidad cartesiana del punto de referencia de todos los elementos situados por encima del par i cuando z˙i=1, y z˙j=0,j≠i. Es importante recordar que la velocidad lineal contenida en el vector bi es la velocidad del punto que coincide con el origen del sistema inercial, que es el mismo para todos los sólidos. También la parte inferior de bi es idéntica para todos los sólidos.Cuando se utiliza la ecuación (14) para expresar las velocidades y aceleraciones Cartesianas en función de las relativas, se obtienen las siguientes relaciones entre velocidades y aceleraciones Cartesianas y relativas:
Sustituyendo las ecuaciones (15) en la ecuación (12), multiplicando por RdTTT y teniendo en cuenta que las velocidades virtuales relativas de cadena abierta son independientes, se obtiene el sistema de ecuaciones diferenciales del movimiento en las coordenadas relativas:
o en una forma más compacta:donde el superíndice (ca) hace alusión a la masa del sistema de cadena abierta, (ext) a las fuerzas exteriores e (in) a las fuerzas de inercia dependientes de la velocidad.Es muy interesante considerar el efecto que tiene en las ecuaciones (16) y (17) el producto por la matriz de accesibilidad T. Por ejemplo, el elemento (i,j) de la matriz Mca es:
donde M¯iΣ es la acumulación o suma de todas las matrices de inercia definidas por la ecuación (8), que incluye a los elementos que están por encima del elemento i en el sistema de cadena abierta.Análogamente, el elemento i del vector Qext=RdTTTQ¯ puede expresarse como:
donde Q¯iΣ representa la acumulación o suma de todas las fuerzas en la expresión (8) que actúan en los elementos situados por encima del elemento i. Lo mismo sucede con las fuerzas Qin en la ecuación (17).La matriz y el vector en las expresiones (18) y (19) muestran la ventaja de numerar los sólidos y los pares desde las hojas hacia la raíz: la eliminación de Gauss o la factorización LU mantienen la estructura de ceros en la matriz, evitando algunas operaciones aritméticas.
La ecuación (16) constituye un sistema de ecuaciones diferenciales ordinarias cuya matriz de coeficientes y término independiente pueden ser calculados recursivamente en una forma muy eficiente. Puede añadirse que esta primera transformación de velocidades cartesianas a relativas de cadena abierta se puede realizar analíticamente de un modo muy eficiente.
3Formulación semirrecursiva para sistemas de cadena cerradaSi el sistema es de cadena cerrada las aceleraciones que aparecen en la ecuación (16) no son independientes y es necesario introducir las correspondientes ecuaciones de restricción, que no son otras que las de cierre de cada uno de los pares o elementos que previamente se han eliminado para convertir el sistema en uno de cadena abierta. Las coordenadas relativas de cadena abierta vistas previamente se dividirán en 2 conjuntos, dependientes e independientes.
La primera tarea es expresar las ecuaciones de restricción de cierre de lazo en función de las coordenadas relativas. Después habrá que calcular la jacobiana de dichas ecuaciones y elegir las coordenadas independientes. En un tercer momento habrá que expresar todas las velocidades relativas en función de las independientes con transformaciones similares a las de las ecuaciones (15).
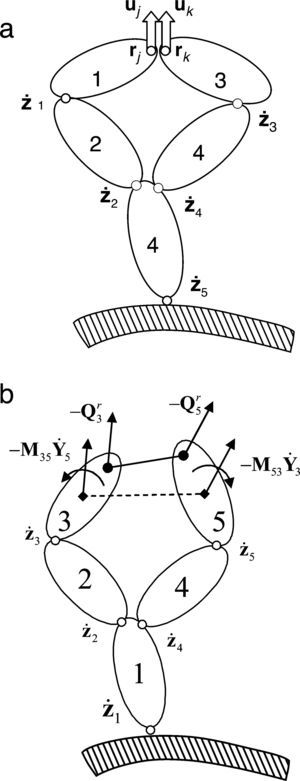
Para hacer el método lo más sencillo posible las ecuaciones de restricción de cierre de lazo se formulan en primer lugar en coordenadas cartesianas y luego se transforman a coordenadas relativas. En este artículo se considerarán 2 formas de abrir los lazos cerrados, que se corresponden con 2 tipos de ecuaciones de restricción de cadena cerrada. El primero consiste en eliminar algunos pares esféricos o de revolución, lo cual es muy habitual en la literatura. El segundo método consiste en eliminar, si las hay, barras biarticuladas (elementos 3-D cuya masa se considera uniformemente distribuida sobre la línea que una las 2 articulaciones esféricas y con un momento de inercia despreciable respecto a dicha línea). Este segundo procedimiento de abrir cadenas raramente aparece en la bibliografía, resultando de gran interés en ciertos sistemas de suspensión de automóviles, donde estas barras son de uso común. Las barras biarticuladas (o rods) son cuerpos rígidos costosos de analizar de modo exacto, por lo que a veces se desprecian sus fuerzas de inercia y se sustituyen por una restricción de distancia constante. Algunos programas comerciales no permiten la introducción de un sólido rígido con 2 pares esféricos, obligando a reemplazar uno de los pares esféricos por una junta universal, eliminando de esta manera la rotación libre alrededor del eje de la barra biarticulada. Abrir un lazo cerrado eliminando barras biarticuladas introduce una sola ecuación de restricción por barra, pero mantener el rod y abrir la cadena cortando por un par esférico introduce 3 ecuaciones de restricción y mantiene las 2 coordenadas relativas de la junta universal. Por otro lado, mientras que un rod puede eliminarse de una forma sencilla, considerar exactamente sus fuerzas de inercia es más complicado.
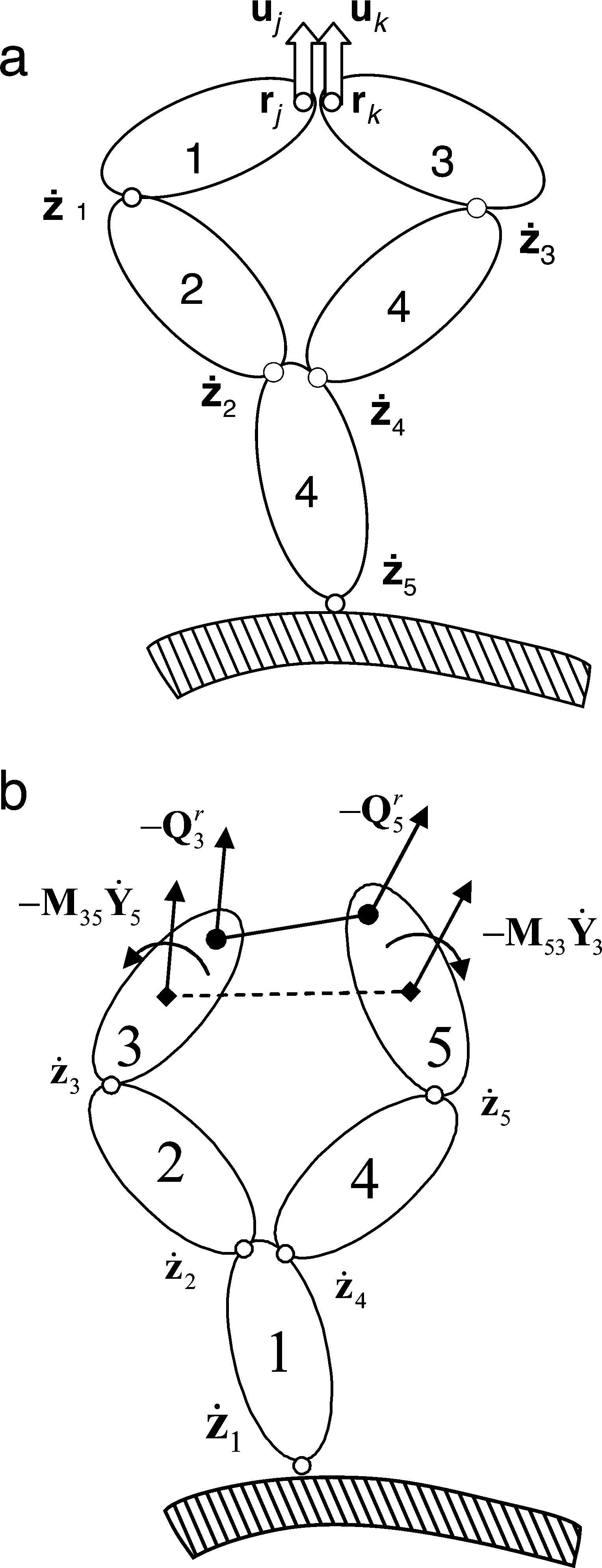
La figura 3 muestra un par de revolución definido mediante coordenadas naturales [6]. Sus ecuaciones de restricción consisten en hacer coincidir 2 puntos y 2 vectores unitarios pertenecientes a cada uno de los sólidos que se unen en dicho par. Las ecuaciones de restricción de cierre de cadena correspondientes a la figura 3 resultan ser muy sencillas:
Para el elemento rod mostrado en la figura 3 es necesaria una única ecuación:
Las ecuaciones de restricción (20)-(22) deben expresarse en términos de las coordenadas relativas z. Esto no es difícil, ya que los puntos rj y rk, y los vectores unitarios uj y uk pueden expresarse en función de las coordenadas relativas del par de la rama correspondiente del sistema de cadena abierta. En realidad no es necesario transformar las ecuaciones de restricción, sino sus correspondientes jacobianas. La matriz jacobiana de las restricciones (20)-(22) con respecto a las coordenadas relativas z puede calcularse utilizando la regla de la cadena de derivación. Por ejemplo, para la restricción de distancia constante (22):
Las derivadas respecto a rj y rk que aparecen en la ecuación (23) son muy fáciles de calcular:
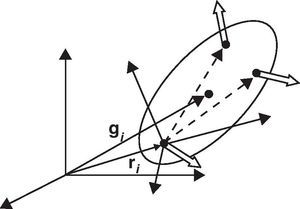
Por otra parte, las derivadas de los vectores rj y rk respecto a las coordenadas relativas z pueden calcularse a partir de la velocidad de estos puntos inducida por una velocidad relativa unidad en cada uno de los pares que están entre el elemento fijo y los elementos j y k, respectivamente. Por ejemplo, si el par i es un par de revolución definido por un punto ri y un vector unitario ui, situado entre el elemento base y el punto rj, la velocidad del punto j originada por una velocidad unitaria en el par i puede expresarse en la forma:
En consecuencia, puede considerarse que el cierre de las ecuaciones de restricción Φz=0 y la correspondiente matriz jacobiana Φz son fáciles de calcular. Utilizando el método de la partición de coordenadas basado en la eliminación de Gauss con pivotamiento total [3,7], se pueden obtener los conjuntos de velocidades dependientes e independientes, dando lugar a la siguiente ecuación de velocidades:
donde se supone que la matriz Φzd es invertible (con esta condición se han seleccionado las coordenadas dependientes). De la ecuación (26) completada con la relación de identidad de z˙i consigo misma, puede obtenerse la matriz Rz de la segunda transformación de velocidades, que relaciona las velocidades relativas de cadena abierta (dependientes) con las independientes de cadena cerrada:Si se deriva respecto al tiempo la ecuación (27) se obtienen las aceleraciones dependientes en función de las independientes, como indica la siguiente expresión:
Introduciendo la segunda transformación de velocidades definida por las ecuaciones (27) y (28) en las ecuaciones dinámicas de cadena abierta (16) se obtiene un sistema de ecuaciones diferenciales ordinarias función de las coordenadas relativas independientes,
En la ecuación (29), se considera implícito en el vector de fuerzas generalizadas externas el término τi, el cual hace referencia a los momentos externos que se introducen en las coordenadas relativas.
En esta formulación todas las características de los rods son tenidas en cuenta de modo exacto, incluyendo el peso, otras fuerzas exteriores y sus fuerzas de inercia. Los detalles acerca de las fuerzas de inercia de los rods que han sido eliminados para abrir las cadenas cerradas no serán incluidos aquí. Es suficiente aclarar que los rods introducen términos de inercia en cada una de las ramas del árbol que conectan. La información topológica para calcular estor términos está contenida en la matriz de accesibilidad T.
4Introducción de funciones BLASEl método de la partición de coordenadas visto previamente es un método muy eficiente para evitar los problemas de estabilidad que surgen durante la integración de las ecuaciones diferenciales del movimiento. Sin embargo, como se mencionó anteriormente, esta operación puede resultar muy costosa, pues debido a la existencia de restricciones redundantes, la obtención de la matriz Rz a partir de la ecuación (27) implica la resolución de un sistema de ecuaciones lineales redundantes aunque compatibles. La utilización de métodos propios de los sistemas incompatibles, como es el caso de las ecuaciones normales propias del método de los mínimos cuadrados, es innecesariamente costosa en este caso y comporta mayores errores numéricos por el incremento en el número de condición de la matriz del sistema.
Existen librerías numéricas muy conocidas como LAPACK [8], que incluyen rutinas muy eficientes para resolver sistemas de ecuaciones lineales, pero en este caso su alcance se limita a matrices cuadradas, no contemplando el caso de sistemas de ecuaciones redundantes y compatibles. LAPACK utiliza las funciones BLAS, programadas en FORTRAN, que en los ordenadores actuales ejecutan operaciones matriciales con una elevada eficiencia. En este artículo se han utilizando las funciones BLAS incluidas en la librería MKL de Intel®[9], para desarrollar funciones similares a las de LAPACK pero solventando sus citadas carencias.
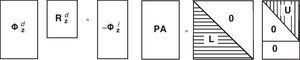
Observando la ecuación (27) se ve que el sistema a resolver Φzd Rzd=−Φzi se basa en una sub-matriz rectangular de la Jacobiana Φzd, como muestra esquemáticamente la figura 4.
Considerando el sistema AX=B para simplificar la nomenclatura, y realizando la factorización LU de la matriz A, el sistema resultante adquiere la forma del esquema en la derecha de la figura 4, donde la matriz P representa la permutación de filas en las matrices A y B. El sistema quedaría como sigue:
La permutación de filas se realiza mediante la función cblas_dswap. La factorización se basa en la función cblas_dger que obtiene ceros en todos los elementos bajo la diagonal mediante actualizaciones de rango uno, lo que constituye un punto fundamental de esta implementación.
El sistema de ecuaciones (30) se resuelve en 2 etapas. Primero, haciendo UX=Y se obtiene el siguiente sistema triangular con las columnas de Y como incógnitas:
siendo la matriz B¯ producto de PB. La segunda etapa es calcular las columnas de X en el sistema triangular UX=Y. Ambas resoluciones con matrices triangulares y múltiples segundos miembros se realizan muy eficientemente mediante actualizaciones de rango uno realizadas por la función cblas_dger de las BLAS.Finalmente hay que señalar que se ha utilizado también la función cblas_dgemm, que realiza el producto general de matrices, con la que se han obtenido la matriz M y el vector b de las ecuaciones (16) y (29).
5Introducción de funciones sparseLa reducción en el número de operaciones aritméticas y de coste computacional que se obtiene al considerar matrices sparse puede ser muy importante, especialmente con matrices de gran tamaño y elevado porcentaje de ceros. En la dinámica de sistemas multicuerpo el tamaño de los sistemas es pequeño en comparación con otras áreas. Es por ello que el uso de técnicas sparse ha tenido éxito principalmente en formulaciones globales, o bien en formulaciones topológicas con elementos flexibles. En ambos casos el tamaño de las matrices difícilmente excede de 1.000×1.000, tamaños considerablemente menores que los acostumbrados en elementos finitos o diferencias finitas. El tamaño de las matrices que aparecen en formulaciones como la de este artículo es bastante inferior al de las que aparecen en las formulaciones globales o con elementos flexibles. A pesar de todo, su utilización puede resultar ventajosa.
Otro factor diferenciador es la densidad de elementos no nulos de las matrices, estando los valores habituales entre un 1 y un 25%. Estos valores son bastante elevados en comparación con otras aplicaciones típicas de matrices sparse.
Si bien ambas características (tamaño reducido y alta densidad de elementos no nulos) parecen estar en desventaja respecto de otras aplicaciones, estas matrices poseen otras propiedades que las hace atractivas para sistemas multicuerpo de un cierto tamaño. Una de estas características es que su cálculo suele ser muy repetitivo y que el patrón de elementos no nulos se mantiene constante durante todo el proceso de simulación. Esto permite realizar un preproceso simbólico al comienzo de las simulaciones, válido para todo el proceso de simulación y permitiendo obtener una importante reducción en los tiempos de cálculo.
La matriz jacobiana del sistema Φz posee una relativamente baja densidad de elementos no nulos y su estructura permanece constante durante todo el proceso de integración de las ecuaciones diferenciales del movimiento. Una de las aportaciones de este trabajo es haber logrado obtener beneficios de las técnicas sparse a pesar del reducido tamaño de estos problemas en comparación con el de otras aplicaciones. A tal fin se ha utilizado la librería de matrices sparse MA48 desarrollada por Harwell [10], usada para la factorización LU de Φz y para obtener la matriz de transformación de coordenadas Rz correspondiente a la ecuación (27).
Existe una amplia variedad de librerías que trabajan con matrices sparse, y a este respecto la referencia [11] contiene un interesante estudio comparativo de varias librerías de funciones sparse aplicadas a la dinámica de sistemas multicuerpo. Según este estudio, las funciones sparse más eficientes resultaron ser las Clark Kent LU (KLU), que están diseñadas especialmente para la simulación de circuitos eléctricos [12,13]. Sin embargo, las funciones KLU, así como muchas otras librerías sparse, no son capaces de trabajar con los sistemas de ecuaciones redundantes pero compatibles propios de la formulación de este artículo. Por ser un área muy especializada, en el caso de las matrices sparse no es factible desarrollar funciones propias, como se ha hecho en el caso de las matrices llenas, como alternativa a las funciones LAPACK.
La librería MA48 es una colección de subrutinas programadas en Fortran 77 para la solución de sistemas de ecuaciones sparse de la forma Ax=b, donde la matriz no simétrica A puede ser cuadrada, rectangular o de rango deficiente, y x y b son vectores. La librería básicamente está compuesta de 4 subrutinas, MA48ID, MA48AD, MA48BD, MA48CD. La primera de ellas fija los parámetros de control y debe llamarse una vez antes de llamar a las restantes subrutinas. La subrutina MA48AD prepara la estructura de datos para la factorización, la MA48BD factoriza la matriz y la MA48CD utiliza los factores L y U para resolver los sistemas Ax=b o ATx=b.
Observando la ecuación (27), el sistema con varios segundos miembros a resolver es el siguiente:
donde Rzd es la parte de Rz relacionada con las velocidades dependientes. La función MA48C/CD no resuelve sistemas con múltiples términos independientes, por lo que hay que llamar repetidamente a la subrutina MA48CD. En la práctica esto no es una dificultad importante.5.1Resultados numéricosCon objeto de mostrar las ventajas relativas, a continuación se presentan los resultados para 2 sistemas multicuerpo de tamaños diferentes. El primero de ellos se corresponde con una furgoneta IVECO DAILY 35C15, que puede considerarse de tamaño mediano, mientras que el segundo ejemplo es una cabeza tractora con semirremolque, que tiene 5 ejes y es un modelo que se puede considerar de gran tamaño y complejidad. Estos modelos representan vehículos reales, donde la geometría de los sistemas de suspensión y las fuerzas actuantes se han considerado de un modo realista. La simulación con la furgoneta IVECO consiste en una maniobra cuya trayectoria sigue una línea recta durante 5s sobre una superficie plana con bandas reductoras de velocidad. La simulación con el modelo de cabina y semirremolque consiste de una maniobra de eslalon de 5s sobre una superficie plana. Para la integración de las ecuaciones diferenciales de ambos ejemplos se ha utilizado el método de Runge-Kutta de orden 4, con un paso de integración de 10-3 s, lo que representa un total de 20,000 evaluaciones de la derivada del vector de estado. En ambos casos las fuerzas de contacto entre las ruedas y el suelo se han modelizado utilizando la fórmula mágica de Pacejka. Los cálculos numéricos se han realizado con un procesador Intel® Xeon® 5160 de 3,0GHz.
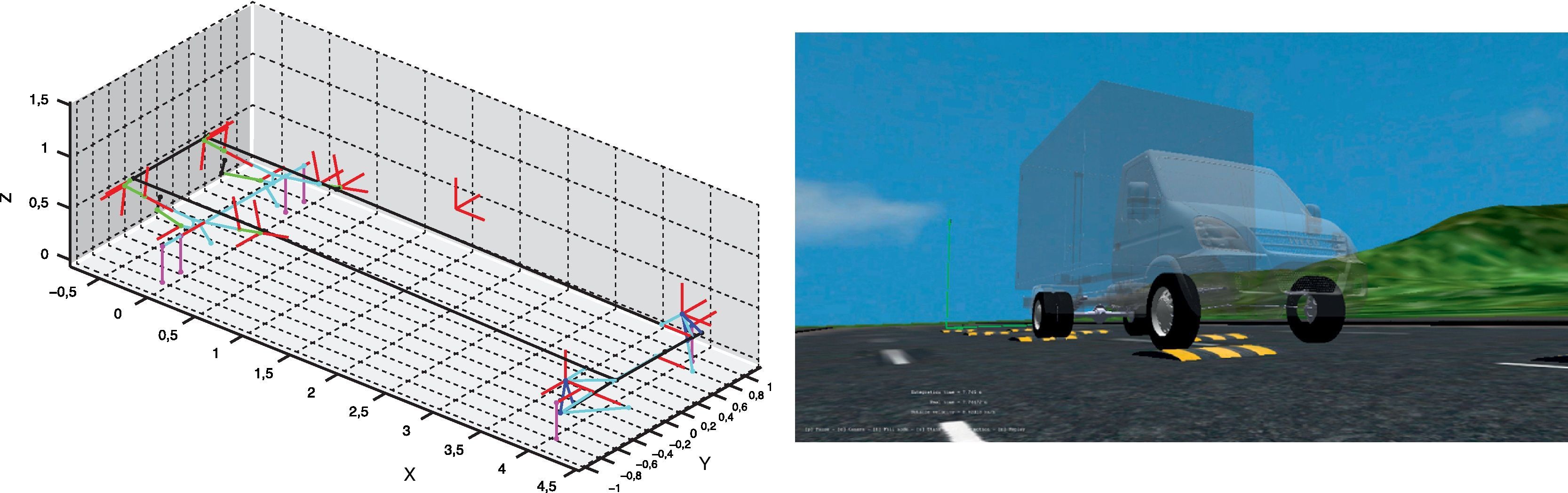
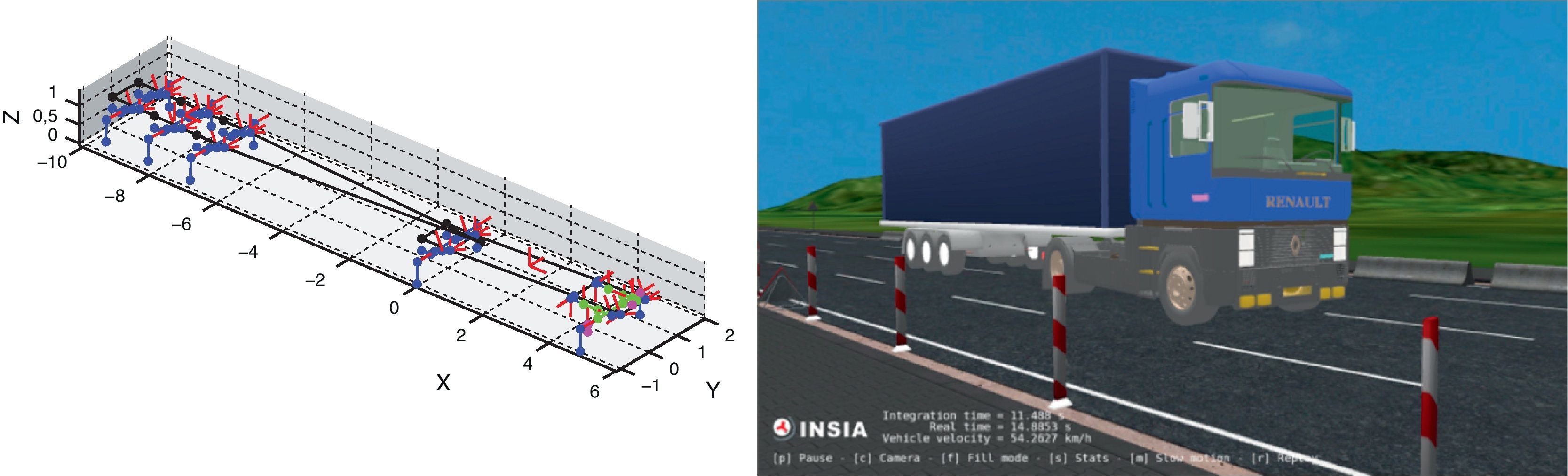
El modelo IVECO posee 17 grados de libertad, 43 cuerpos rígidos (de los cuales 17 son elementos auxiliares sin masa), 4 barras biarticuladas, 47 pares cinemáticos y una coordenada guiada para el sistema de dirección. La matriz Φzd es de tamaño 28×25 y tiene una densidad de elementos no nulos del 22%. La suspensión delantera está formada por un sistema de doble triángulo, con muelles de torsión laterales y por una barra estabilizadora. El sistema de suspensión trasera está compuesto por un eje rígido soportado por ballestas elásticas, amortiguadores telescópicos de doble efecto y una barra estabilizadora. La figura 5 muestra 2 vistas diferentes del vehículo IVECO, una correspondiente al modelo esquemático de los distintos sólidos y pares, y la otra a un modelo CAD.
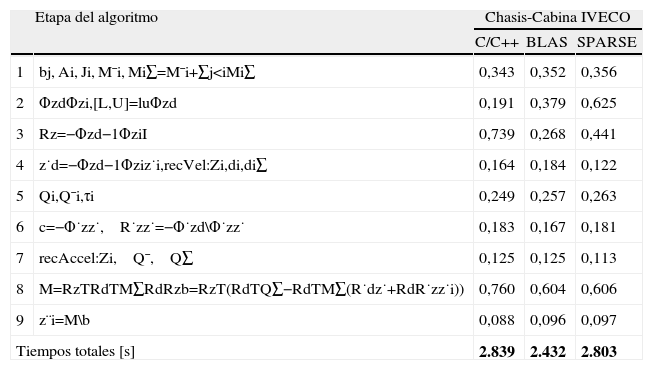
La tabla 1 muestra los tiempos de ordenador obtenidos para las 20.000 evaluaciones del vector de estado en 3 implementaciones diferentes: C/C++ estándar, con funciones BLAS (MKL) y con funciones sparse (MA48). Los pasos 3 y 8 son los más costosos. Puede apreciarse la reducción en los tiempos lograda mediante el uso de las funciones BLAS, y puede verse también que el uso de técnicas sparse en este caso no introduce prácticamente ninguna ganancia.
Tiempos de ejecución para una simulación de 5 s
| Etapa del algoritmo | Chasis-Cabina IVECO | |||
| C/C++ | BLAS | SPARSE | ||
| 1 | bj, Ai, Ji, M¯i, Mi∑=M¯i+∑j| 0,343
| 0,352
| 0,356
| |
| 2 | ΦzdΦzi,[L,U]=luΦzd | 0,191 | 0,379 | 0,625 |
| 3 | Rz=−Φzd−1ΦziI | 0,739 | 0,268 | 0,441 |
| 4 | z˙d=−Φzd−1Φziz˙i,recVel:Zi,di,di∑ | 0,164 | 0,184 | 0,122 |
| 5 | Qi,Q¯i,τi | 0,249 | 0,257 | 0,263 |
| 6 | c=−Φ˙zz˙, R˙zz˙=−Φ˙zd\Φ˙zz˙ | 0,183 | 0,167 | 0,181 |
| 7 | recAccel:Zi, Q¯, Q∑ | 0,125 | 0,125 | 0,113 |
| 8 | M=RzTRdTM∑RdRzb=RzT(RdTQ∑−RdTM∑(R˙dz˙+RdR˙zz˙i)) | 0,760 | 0,604 | 0,606 |
| 9 | z¨i=M\b | 0,088 | 0,096 | 0,097 |
| Tiempos totales [s] | 2.839 | 2.432 | 2.803 | |
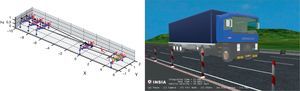
El modelo de camión con semirremolque posee 40 grados de libertad, 5 ejes rígidos, 81 sólidos rígidos (de los cuales 34 son elementos auxiliares sin masa), 89 pares cinemáticos y una coordenada guiada para el sistema de dirección. La matriz Φzd es de tamaño 51×40 y posee una densidad de elementos no nulos del 6,32%. Todos los ejes tienen 2 ruedas. Los sistemas de suspensión del semirremolque y de la parte trasera de la cabeza tractora del camión son de muelles neumáticos y amortiguadores, mientras que la suspensión delantera de la cabeza tractora está compuesta por ballestas elásticas y amortiguadores. La unión entre el semirremolque y la cabeza tractora se ha modelizado con un par esférico. La figura 6 muestra 2 vistas del camión con semirremolque.
La tabla 2 muestra los tiempos de ordenador obtenidos para las 20,000 evaluaciones del vector de estado en 3 implementaciones diferentes: C/C++ estándar, con funciones BLAS (MKL) y con funciones sparse (MA48). Al igual que en el ejemplo anterior, los pasos 3 y 8 son los más costosos, pero ahora las diferencias han aumentado. En este caso tanto las funciones BLAS como las sparse MA48 mejoran significativamente los resultados obtenidos con el C/C++ estándar, resultando en este caso las funciones sparse un poco mejores.
Tiempos de ejecución para una simulación de 5 s
| Etapa del algoritmo | Camión y semirremolque | |||
| C/C++ | BLAS | SPARSE | ||
| 1 | bj, Ai, Ji, M¯i, Mi∑=M¯i+∑j| 0,675
| 0,665
| 0,658
| |
| 2 | ΦzdΦzi, [L,U]=luΦzd | 0,425 | 0,927 | 0,721 |
| 3 | Rz=−Φzd−1ΦziI | 4,032 | 0,655 | 0,616 |
| 4 | z˙d=−Φzd−1Φziz˙i, recVel:Zi,di,di∑ | 0,289 | 0,361 | 0,195 |
| 5 | Qi,Q¯i,τi | 0,273 | 0,275 | 0,275 |
| 6 | c=−Φ˙zz˙, R˙zz˙=−Φ˙zd\Φ˙zz˙ | 0,258 | 0,198 | 0,180 |
| 7 | recAccel:Zi, Q¯, Q∑ | 0,193 | 0,194 | 0,193 |
| 8 | M=RzTRdTM∑RdRzb=RzT(RdTQ∑−RdTM∑(R˙dz˙+RdR˙zz˙i)) | 3,037 | 2,054 | 2,044 |
| 9 | z¨i=M\b | 0,247 | 0,258 | 0,255 |
| Tiempos totales [s] | 9,428 | 5,588 | 5,137 | |
La formulación semirrecursiva para la dinámica de sistemas multicuerpo, con partición de coordenadas y una doble transformación de velocidades, presentada en este artículo, tiene importantes ventajas desde el punto de vista de la estabilidad y de la eficiencia. Su aplicación implica el cálculo de una base del espacio nulo de la matriz jacobiana de las ecuaciones de restricción para cada instante de tiempo. El cómputo de estas operaciones puede redundar en una baja eficiencia numérica especialmente para sistemas de mediano o gran tamaño.
En este artículo se ha presentado una forma muy eficiente de obtener las ecuaciones de la dinámica para sistemas de cadena cerrada mediante una doble transformación de velocidades. En primer lugar, cortando las cadenas cerradas del sistema por algunos pares o eliminando elementos rods se introduce de forma analítica la primera transformación de velocidades cartesianas a relativas. La matriz de accesibilidad permite introducir la topología del sistema de un modo muy sencillo. Luego, la segunda transformación de velocidades es obtenida numéricamente en un sistema de tamaño reducido, expresándose finalmente las ecuaciones diferenciales en función de un conjunto de aceleraciones independientes.
La eficiencia numérica de la formulación ha sido incrementada notablemente mediante el uso de librerías matemáticas como las BLAS o de funciones sparse como la MA48. La reducción en los tiempos de ejecución de las operaciones algebraicas más costosas ha llegado a ser tal, que en el caso del sistema de mayor tamaño, los tiempos totales de simulación se han reducido en casi un 50%. Por último, las funciones utilizadas no solo mejoran la eficiencia, sino que al permitir trabajar con sistemas de ecuaciones redundantes mejoran la versatilidad y robustez de la implementación.
Los autores agradecen el apoyo del Ministerio de Economía y Competitividad de España (antes Ministerio de Ciencia e Innovación) bajo el Proyecto de Investigación TRA2009-14513-C02-01 (OPTIVIRTEST).