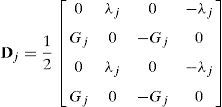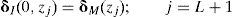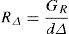Se presenta un método de estrato finito para evaluar los efectos de la acción sísmica en muros de retención, el cual se basa en la teoría de propagación de ondas y superposición modal. El sistema está definido por un muro rígido desplantado sobre un estrato elástico, con capacidad de deslizamiento y volteo de la base. Con este modelo se considera tanto la flexibilidad de la cimentación como la disipación de energía por radiación de ondas. Se demuestra con resultados numéricos que la magnitud de las presiones sobre el muro depende de su capacidad de moverse.
A finite layer method for evaluation of the effects of seismic action on retaining walls is presented, which is based on the wave propagation theory and modal superposition. The system is defined by a rigid wall supported on an elastic stratum, with capacity of sliding and overturning of the base. With this model, the foundation flexibility as well as the energy dissipation by wave radiation is considered. It is demonstrated with numerical results that the magnitude of pressures on the wall depends on its movement capacity.
El problema de muros de retención es uno de los más viejos en ingeniería geotécnica; de hecho, muchos de los principios fundamentales de la mecánica de suelos fueron desarrollados precisamente para permitir un diseño racional de muros de retención. Debido a que varias de estas obras son construidas en zonas sísmicas, es fundamental en el diseño evaluar las presiones dinámicas generadas por el relleno contenido, ya que la posibilidad de fallas por el incremento de las presiones laterales es un problema latente.
Por muchas décadas, el análisis sísmico de muros de retención ha sido basado en la extensión del análisis de equilibrio límite de Coulomb, conocido como el método de Mononobe-Okabe (M-O) [1,2]. Este método, modificado y simplificado por Seed y Whitman [3], ha prevalecido principalmente debido a su simplicidad y a la familiarización que tienen los ingenieros con el método de Coulomb.
Estudios experimentales han demostrado que el método es bastante realista si el desplazamiento activo del muro debido a traslación, rotación o flexión es lo suficientemente grande para generar la formación de la superficie de deslizamiento en el suelo retenido. Sin embargo, en muchos casos reales, como muros de cimentación, muros con refuerzo, estribos de puentes, etc., las restricciones cinemáticas impuestas al sistema de retención no conducen al desarrollo de las condiciones de equilibrio límite y, por tanto, se genera un incremento del empuje dinámico del relleno sobre el muro.
Aunque se han desarrollado soluciones analíticas para este último tipo de problemas basadas en métodos elásticos [4–6], estas predicen exageradas presiones dinámicas sobre el muro en comparación con las obtenidas mediante métodos de equilibrio límite. Este hecho y la escasez de fallas drásticas por grandes empujes de tierra formaron la ampliamente aceptada opinión de que los métodos elásticos eran exageradamente conservadores y, por tanto, inapropiados para usos prácticos. Esta es la principal razón para el casi exclusivo uso del método M-O y sus variantes en la ingeniería práctica.
Los 2 grupos de métodos anteriormente descritos —equilibrio límite y soluciones elásticas— parecen cubrir los 2 casos extremos. Los métodos de equilibrio límite suponen un comportamiento plástico rígido, mientras que los elásticos consideran el suelo como un continuo viscoelástico.
Todas las consideraciones anteriores fueron plenamente aceptadas por mucho tiempo, hasta que Veletsos y Younan [7–9] probaron que las exageradamente altas presiones dinámicas de los métodos elásticos son atribuidas a las hipótesis de rigidez del muro y del terreno de cimentación que son sobreestimaciones de lo que sucede en la realidad. Para subsanar estas limitaciones, estos autores desarrollaron una solución analítica que tiene en cuenta la flexibilidad estructural del muro y/o la posibilidad de rotación respecto a su base. Con estas nuevas hipótesis probaron entonces que las presiones dinámicas dependen fuertemente tanto de la flexibilidad del muro como de la rotación de la base, y que para valores realistas de estos factores, las presiones dinámicas son sustancialmente más bajas que las presiones para el caso de muro rígido y fijo en su base. De hecho, encontraron que las presiones pueden reducirse a niveles de los obtenidos con la solución de M-O si se considera la flexibilidad del muro o su base. Es a la luz de dichos resultados y basados en estas nuevas hipótesis con lo que resurgen los métodos elásticos orientados al diseño sísmico de muros de retención.
En el código sísmico del USACE [10] se definen 3 casos de diseño para muros de retención, basados en las restricciones cinemáticas impuestas. Dependiendo de la magnitud del movimiento del muro, el suelo que forma el relleno puede estar en estado «cedente», «no cedente» o «intermedio», y las presiones generadas sobre el muro se calcularán a partir de dichos estados, utilizando métodos ya sea de equilibrio límite o elásticos.
En este trabajo se presenta un método riguroso y eficiente para determinar la respuesta sísmica de un muro de retención rígido considerando la flexibilidad de la cimentación, esto es, el movimiento de su base en traslación y rotación. Para ello, primero se describe la teoría de propagación de ondas en medios estratificados, y posteriormente se detalla el método propuesto de superposición modal para el análisis de interacción dinámica suelo-muro. Finalmente, se muestra con resultados numéricos la influencia que tiene la flexibilidad de la cimentación en la respuesta sísmica del muro, así como las implicaciones en el diseño de este tipo de estructuras.
Cabe señalar que este método difiere de los conocidos en la literatura en el hecho de que el relleno y el muro están desplantados sobre un suelo de cimentación elástico. Esto permite no solo considerar explícitamente tanto la rotación como la traslación del muro, sino también la disipación de energía por comportamiento histerético (amortiguamiento material) y radiación de ondas (amortiguamiento geométrico). Otra ventaja del método propuesto es que se puede considerar de forma natural la variación de la rigidez del relleno con la profundidad, así como la estratificación del suelo de cimentación. Además, es posible considerar los componentes horizontal y vertical de la excitación.
2Respuestas modales del sueloLa respuesta sísmica de un depósito de suelo es un problema de propagación de ondas cuya solución se puede obtener mediante superposición modal, es decir, por medio de la combinación lineal de modos naturales de propagación y coeficientes de participación modal. En principio, los modos de vibración de un depósito de suelo estratificado horizontalmente podrían obtenerse al resolver un problema de valores característicos continuo. Sin embargo, la ecuación característica del depósito, o ecuación de frecuencias, contiene funciones trascendentes que dificultan enormemente su solución numérica. Para superar esta dificultad, se pueden determinar eigenfunciones discretas en la dirección vertical usando el método de elemento finito, mediante el cual es posible derivar un problema de eigenvalores algebraico cuadrático.
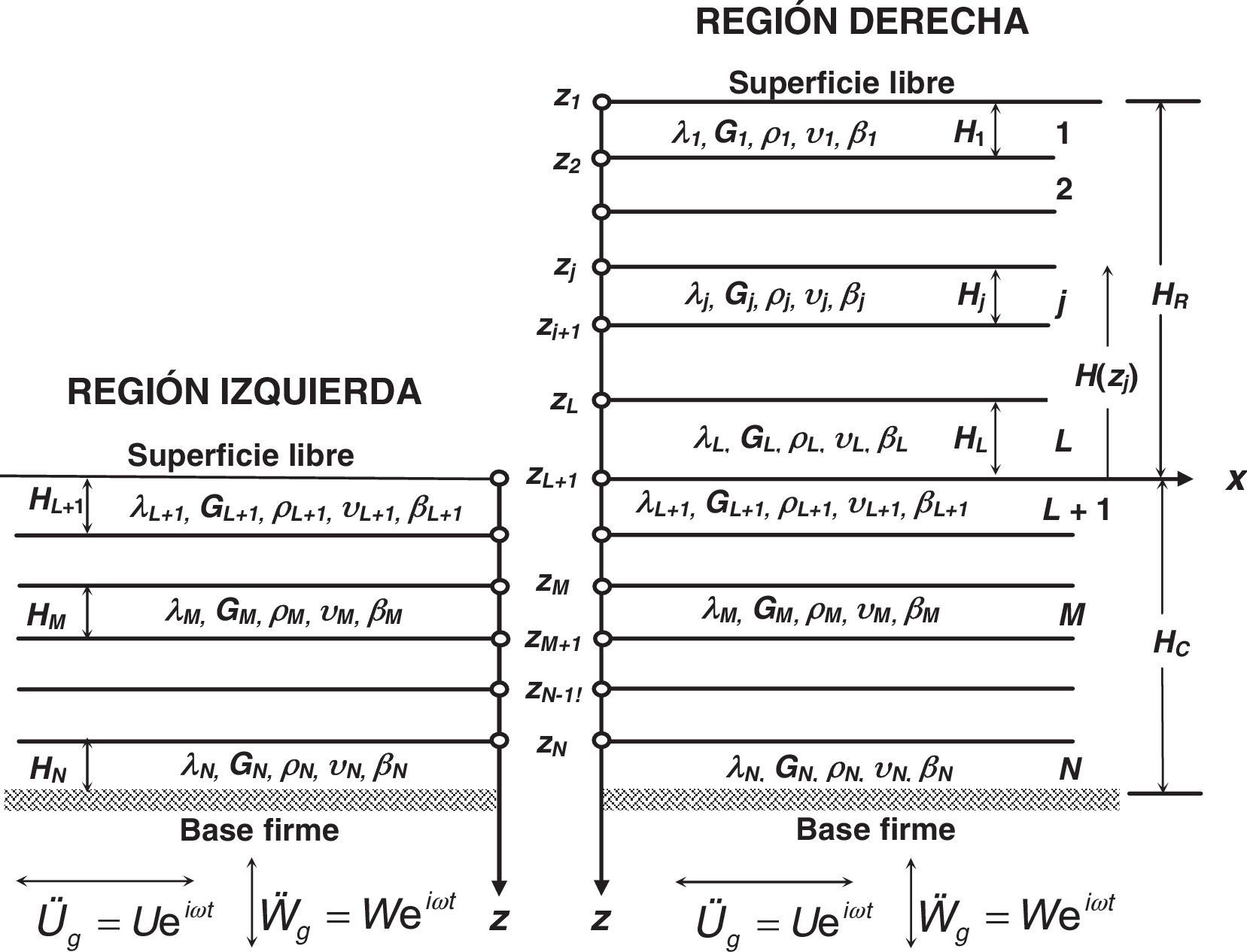
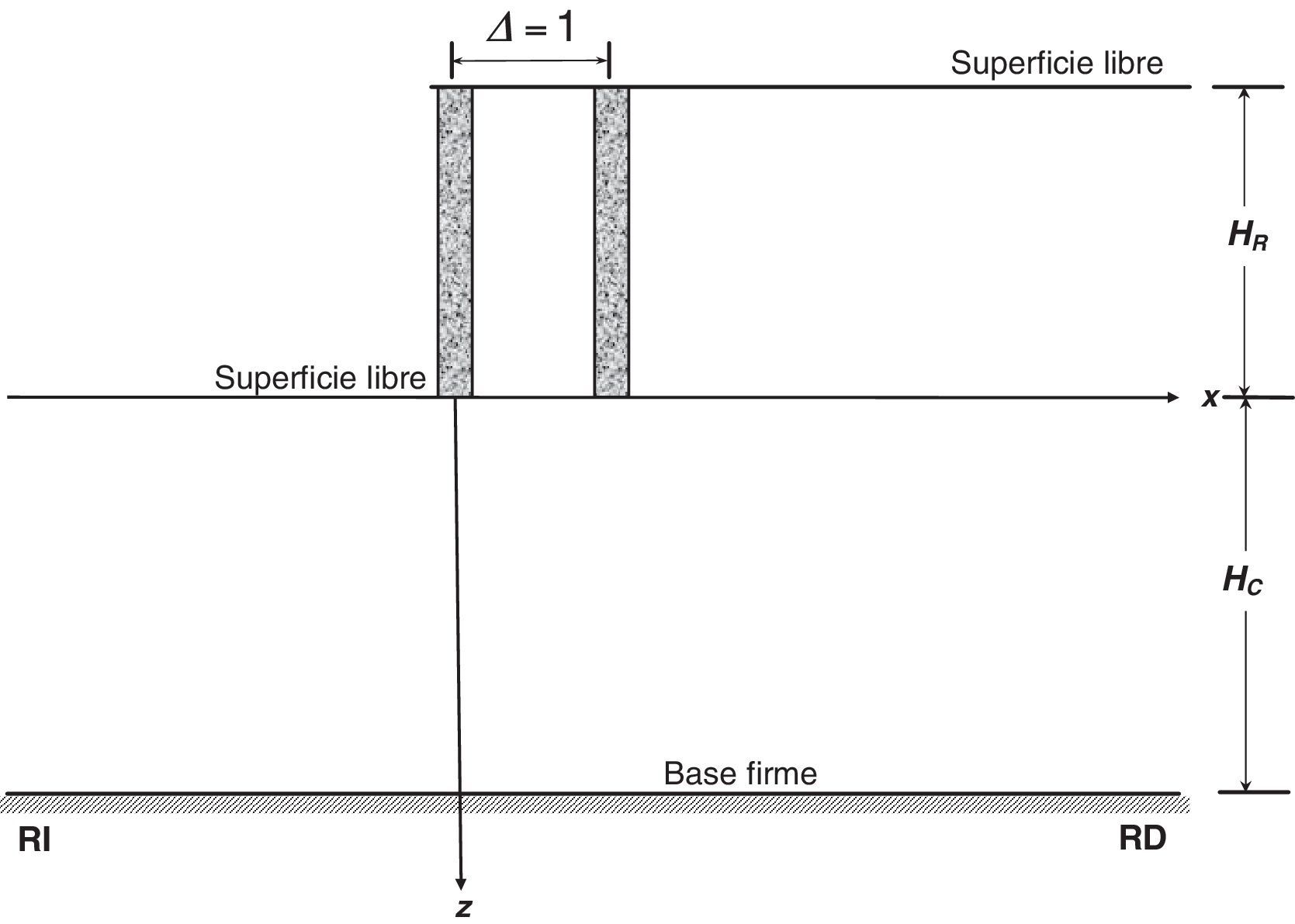
Lysmer y Drake [11] desarrollaron un método eficiente de hiperelementos finitos que consiste en discretizar el depósito de suelo en estratos delgados de longitud infinita, donde se supone que la variación de las eigenfunciones es lineal. Este método permite calcular las frecuencias y los modos naturales del suelo, así como los desplazamientos y fuerzas nodales consistentes que se generan durante la propagación de las ondas. Para fines de análisis, el suelo se divide en 2 regiones: a)la derecha, que contiene el suelo de cimentación y el relleno sobreyaciente (x>0, –HR≤z≤HC), y b)la izquierda, que solamente contiene el suelo de cimentación (x<0, 0≤z≤HC), siendo HR el espesor del relleno y HC el espesor del estrato de cimentación (fig. 1).
En ambas regiones, los estratos que constituyen el depósito de suelo son isótropos, con comportamiento viscoelástico lineal y con continuidad de esfuerzos y deformaciones en las interfases entre ellos. Estos contactos son planos paralelos a la superficie y a la base del depósito. Cada estrato j de espesor Hj se caracteriza por su densidad de masa ρj, relación de Poisson υj y velocidad de ondas de corte Vsj, a partir de los cuales se calculan los módulos de Lamé λj y Gj, que para el caso de un sólido con comportamiento linealmente viscoelástico son valores complejos definidos a partir del amortiguamiento material βj. La base del depósito de suelo se considera rígida, sometida ya sea a la excitación horizontal U¨g o vertical W¨g.
Bajo estas condiciones, el problema algebraico de valores característicos cuadráticos para un depósito de NS capas resulta ser:
donde I y D denotan región izquierda y derecha, respectivamente, ω es la frecuencia de las ondas de tipo armónico, i es la unidad imaginaria, y AS, BS, GS y MS son matrices del sistema de (2NS×2NS), ensambladas a partir de las matrices de estratoEl eigenvalor kl y su correspondiente eigenvector VSl que resultan de la ecuación1 se seleccionan de modo tal que se cumpla la condición de radiación de ondas. De acuerdo con lo anterior, si kl es un eigenvalor con eigenvector que se propaga o irradia en sentido positivo de la forma:se puede demostrar que –kl es otro eigenvalor con eigenvector que se propaga o irradia en sentido negativo de la formadonde Uj y Wj representan los componentes nodales de desplazamiento horizontal y vertical, respectivamente, a la profundidad zj. Es decir, cada nodo tiene asociados 2desplazamientos, uno horizontal y otro vertical, y hay tantos nodos como estratos de suelo. En términos generales, para cada valor de la frecuencia de excitación se obtienen 2NS vectores característicos (modos) linealmente independientes, asociados a 2NS valores característicos (números de onda), con los que se construye la matriz modal VS de (2NS×2NS) cuyas columnas son los vectores VSl.Para las 2 regiones, dichas matrices modales tienen la siguiente forma:
Del valor de k depende la naturaleza del movimiento del modo, de manera que pueden presentarse 4 tipos de modos generalizados descritos en la tabla 1.
Características de los modos
| k | Tipo de modo | Movimiento del modo |
| Real (k=kr) | Real | Se propaga en la dirección x con la velocidad de fase c=ω/kr; cuando kr es positivo, la propagación ocurre en el sentido positivo de x. Este movimiento solo se presenta para suelo no amortiguado |
| Complejo (k=kr+iki) | Complejo | Se propaga en la dirección x con la velocidad de fase c=ω/kr y se irradia (atenuación del movimiento) en el sentido positivo de x cuando ki es negativo. Este movimiento solo ocurre en suelo amortiguado |
| Imaginario (k=iki) | Exponencial | No se propaga, pero se irradia (atenuación del movimiento) en el sentido positivo de x cuando ki es negativo. Este movimiento solo se presenta para suelo no amortiguado; las formas modales son reales |
| Cero (k=0) | Permanente | Corresponde a ondas estacionarias que se propagan en la dirección z. Este movimiento solo ocurre en suelos no amortiguados para las frecuencias naturales de vibración del depósito; las formas modales son reales |
Asimismo, las fuerzas correspondientes a VS pueden obtenerse mediante la integración de los esfuerzos τxz y σx a lo largo del eje z. Para las 2 regiones, las matrices de fuerzas modales se construyen como:
donde KS=Diag [kl] es una matriz diagonal formada con los números de onda y DS es una matriz similar a las matrices AS, BS, GS y MS, ensamblada con las matrices de estrato:De acuerdo con el principio de superposición, la respuesta en cada región puede construirse mediante la suma del campo libre más un campo difractado, el primero generado por la excitación sísmica en la base del depósito y el segundo por la presencia del muro. Así, los campos totales de desplazamientos y fuerzas están dados por:donde δSf y FSf son los vectores de desplazamientos y fuerzas de campo libre, respectivamente, que se calculan como se indica a continuación.Para el caso de propagación vertical, k=0, la ecuación 1 toma la forma:
dondePara resolver la ecuación 15, se imponen en el basamento los movimientos UNS+1o=Ug y WNS+1o=0, siendo Ug la amplitud del movimiento horizontal en la roca basal, y se eliminan los 2 últimos renglones y las 2 últimas columnas de las matrices GS y MS, así como los últimos 2 renglones de los vectores δSf y 0. Para considerar el efecto de la excitación vertical se imponen ahora en el basamento los movimientos UNS+1o=0 y WNS+1o=Wg, siendo Wg la amplitud del movimiento vertical en la roca basal, y se repite el proceso ya descrito para el caso de la excitación horizontal.
El vector de fuerzas de campo libre se obtiene a partir de las ecuaciones 10 y 11, haciendo k=0:
Por otro lado, los desplazamientos y fuerzas nodales de campo difractado, que resultan de la contribución de todos los modos naturales de propagación, se pueden calcular mediante superposición modal de la manera siguiente:
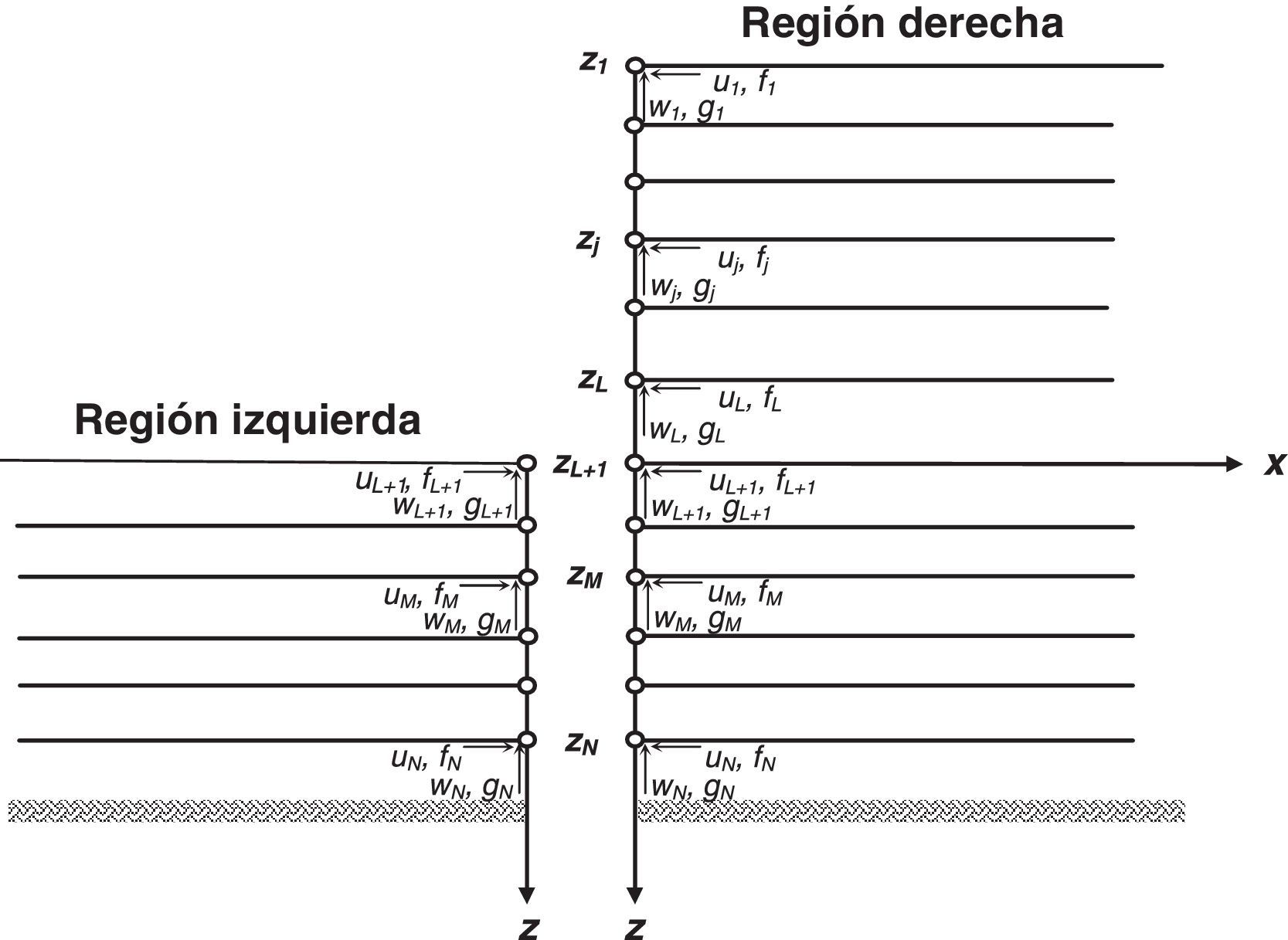
donde VS y PS son matrices de desplazamientos y fuerzas modales, respectivamente, y CS es el vector de coeficientes de participación modal que se obtiene satisfaciendo las condiciones de frontera que se impongan de acuerdo con el problema que se desee analizar.En la figura 2 se muestran esquemáticamente los componentes de los vectores de desplazamientos y las fuerzas totales actuantes en los nodos de ambas regiones.
3Condiciones de fronteraPara satisfacer las condiciones de frontera ante la presencia del muro se utiliza el método de colocación en puntos nodales. En el modelo propuesto los nodos se ubican en la sección x=0, y en ellos es necesario imponer compatibilidad de desplazamientos y equilibrio de fuerzas, como a continuación se muestra:
donde δM es el vector de desplazamientos de cuerpo rígido del muro de retención.Los coeficientes de participación modal pueden determinarse directamente resolviendo el sistema matricial de ecuaciones algebraicas que resultan de sustituir las ecuaciones 13-14 y 18-19 en las ecuaciones 20-23. Sin embargo, para simplificar la solución del problema, se descompuso en 3 pasos que al superponerlos representan correctamente la respuesta total del sistema.
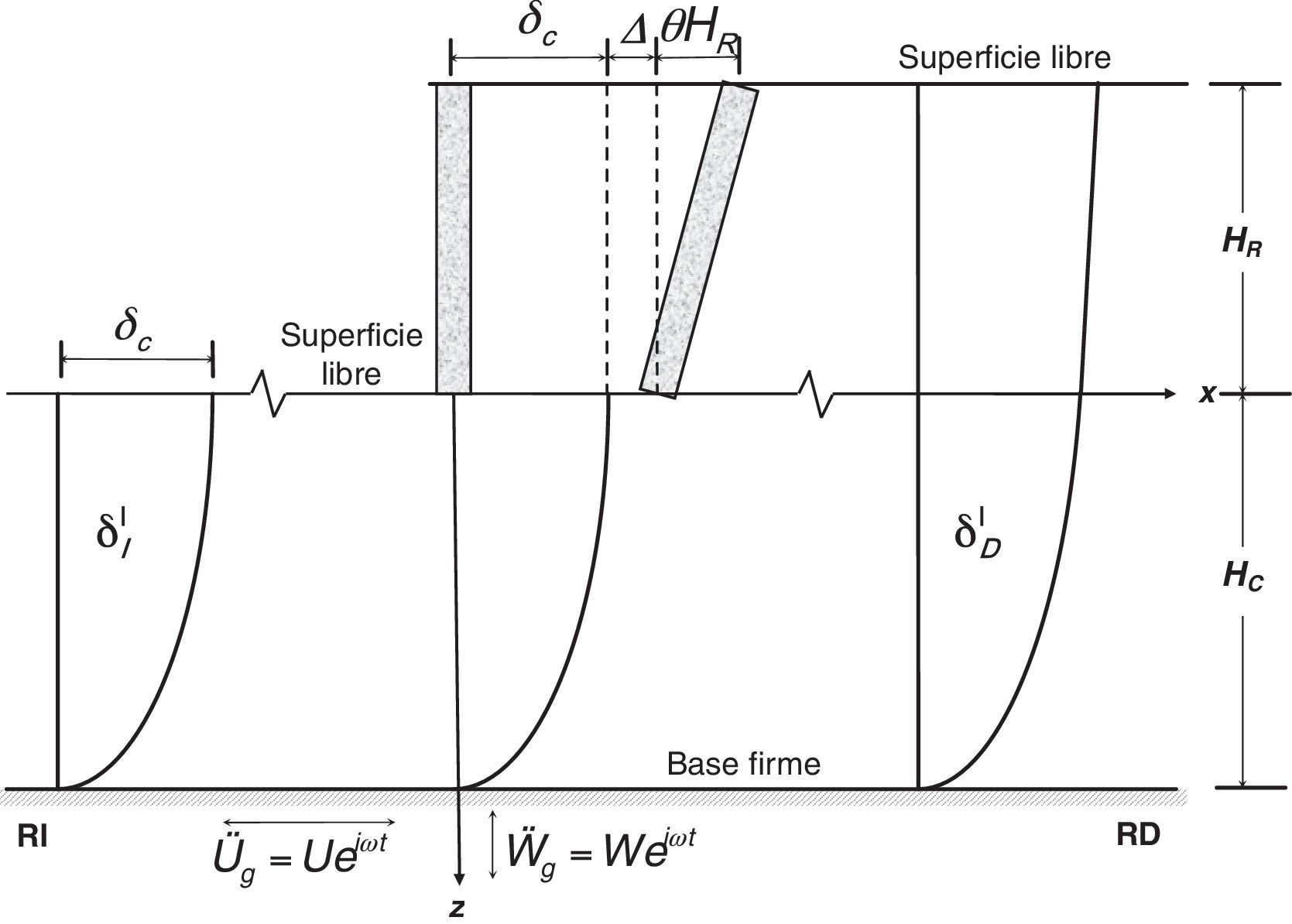
4Método de solución en 3 pasosEn la figura 3 se presenta el modelo acoplado del muro interactuando con el relleno y el suelo de soporte (sistema muro-relleno-cimentación). El movimiento de entrada del sistema muro-relleno-cimentación se especifica al nivel de la roca basal.
El deslizamiento del muro, relativo al movimiento de campo libre δc en la superficie del suelo de soporte, se representa con Δ y el giro con θ. Los campos libres de desplazamientos de la región izquierda y derecha se expresan como δIf y δDf, respectivamente. En seguida se describen los 3 pasos propuestos para la solución del problema.
4.1Paso 1. Excitación en el basamento y muro con base fija (Δ=θ=0)El modelo para este caso se presenta en la figura 4. Aquí no se permite el deslizamiento relativo ni la rotación del muro. En el campo lejano (x=±∞) debe reproducirse la respuesta libre de cada región ante la excitación en la roca basal.
Para obtener los coeficientes de participación modal es necesario especificar la traslación que sufre el muro durante el movimiento de campo libre. Debido a la amplificación de la excitación en el basamento al pasar por el estrato de suelo de cimentación, el vector de desplazamientos del muro para excitación horizontal está dado por:
donde δc=UL+1o es el desplazamiento horizontal de campo libre de la región izquierda en el nodo de la base del muro.Para excitación vertical, el vector está dado por:
donde δc=WL+1o es el desplazamiento vertical de campo libre de la región izquierda en el nodo de la base del muro.Al imponer las condiciones de frontera correspondientes, el sistema resultante de ecuaciones es:
Este es un sistema determinado de 2(NI+ND)×2(NI+ND), ecuaciones lineales complejas. La solución del sistema proporciona los coeficientes de participación modal del paso 1 para las regiones izquierda (CI) y derecha (CD).
Las fuerzas de campo difractado que actúan sobre los nodos del muro de retención se obtienen al sustituir los valores de CD en la ecuación 19. Las fuerzas totales resultan de sumar las fuerzas de campo libre con las de campo difractado de acuerdo con la ecuación 14.
El cortante basal Qb(Δ=θ=0) y el correspondiente momento de volteo Mb(Δ=θ=0) se obtienen de sumar todas las fuerzas horizontales sobre los nodos del muro y los momentos generados por dichas fuerzas, respectivamente.
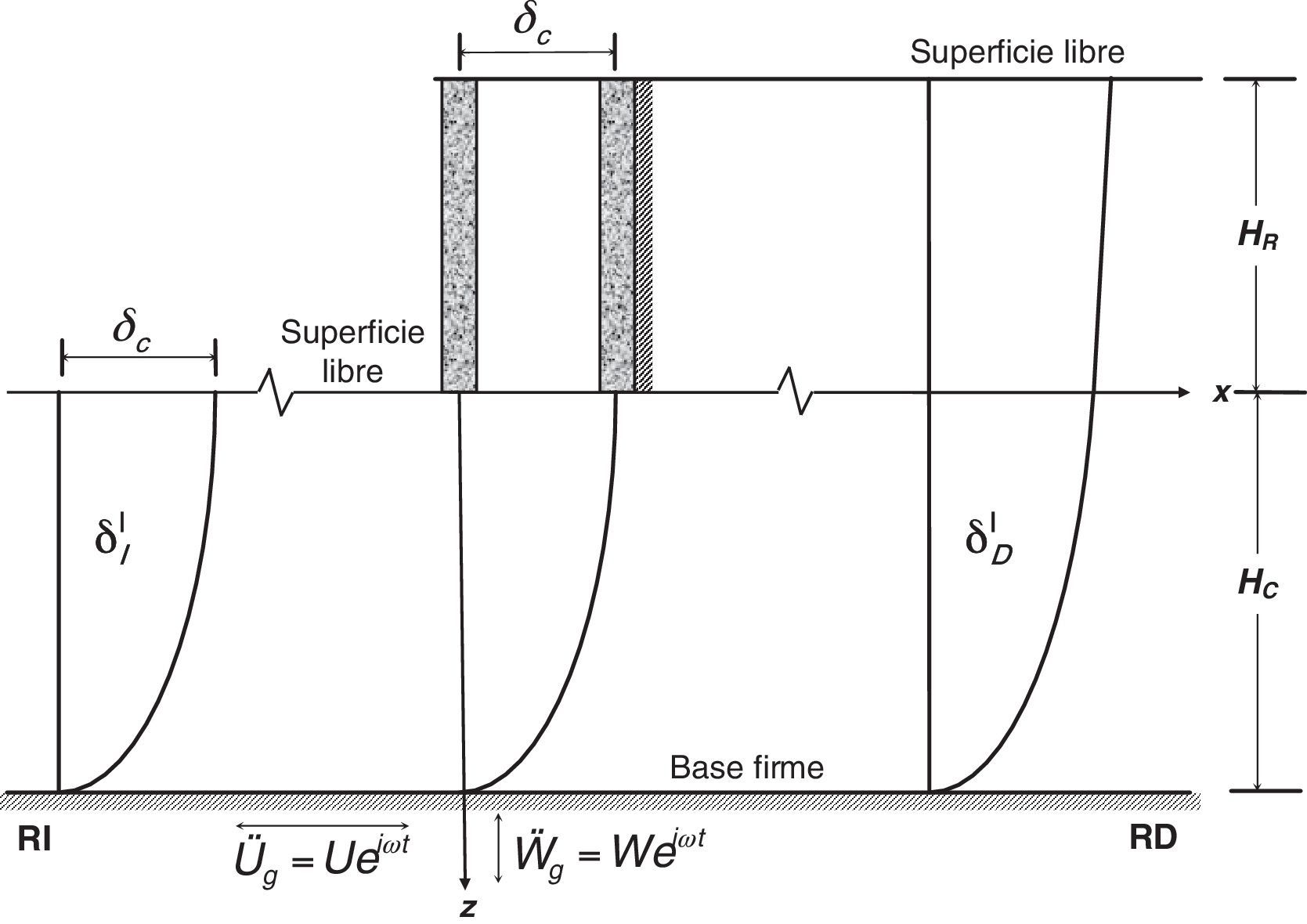
4.2Paso 2. Desplazamiento unitario del muro (Δ=1)El modelo para este caso se presenta en la figura 5. Aquí se considera que el basamento está fijo, por lo que no hay un campo libre, sino solo el campo difractado debido al movimiento del muro.
Si se considera un desplazamiento horizontal unitario (Δ=1) del muro, se tiene que:
Al imponer las condiciones de frontera correspondientes, el sistema resultante de ecuaciones es:
La solución de este sistema de ecuaciones complejas proporciona los vectores de coeficientes de participación modal CI y CD. Con ellos es posible determinar las fuerzas que actúan sobre el muro de retención, así como la fuerza cortante Qb(Δ=1) y el momento de volteo Mb(Δ=1) basales.
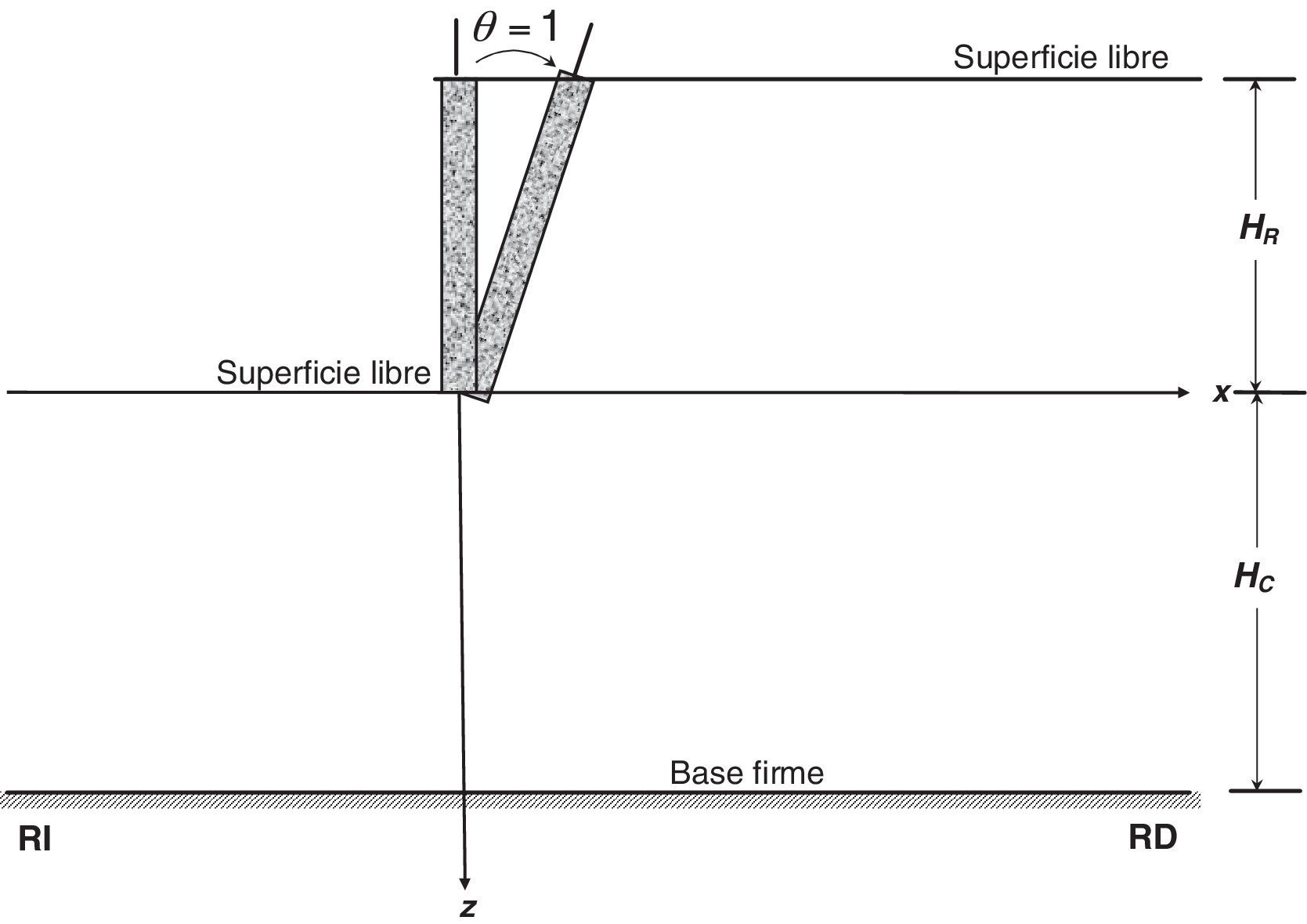
4.3Paso 3. Giro unitario del muro (θ=1)El modelo para este caso se presenta en la figura 6. Al igual que en el caso anterior, aquí solo se genera el campo difractado debido al giro unitario (θ=1) impuesto al muro.
El componente horizontal del desplazamiento en cada nodo del muro se obtiene como el producto de la magnitud del giro por la altura nodal. Así, el vector de desplazamientos se expresa como:
donde hL+1 se toma igual a cero.Al imponer las condiciones de frontera correspondientes, el sistema resultante de ecuaciones es similar al de la ecuación 27.
Al igual que en el caso anterior, la solución proporciona los coeficientes de participación modal y a partir de ellos es posible obtener las fuerzas sobre el muro. Finalmente se determina el cortante Qb(θ=1) y el momento Mb(θ=1) basales.
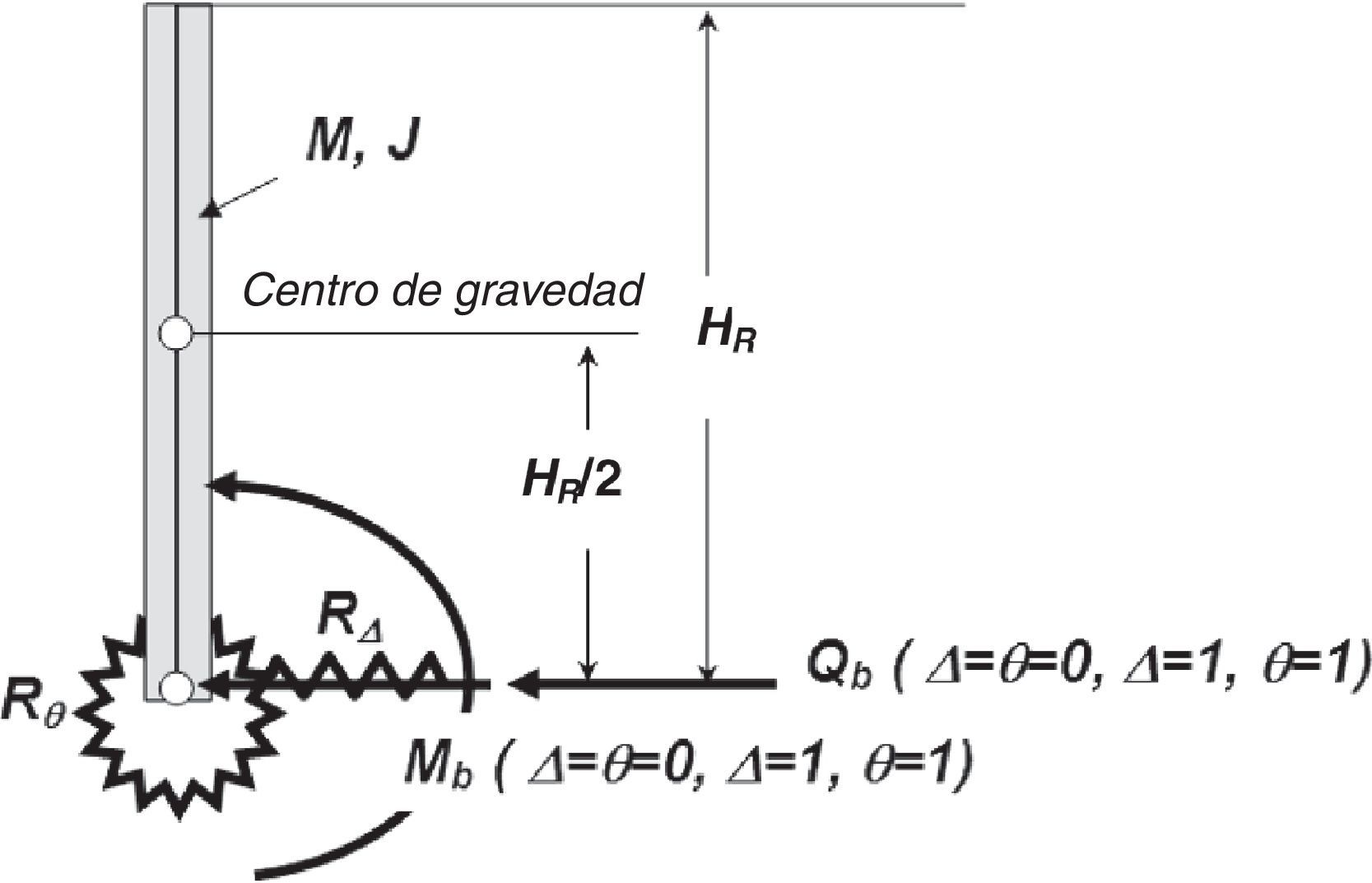
4.4Ecuaciones de equilibrioUna vez obtenidas las fuerzas y momentos totales que resultan de la superposición de las 3 etapas de solución descritas anteriormente, es necesario acoplar la respuesta del sistema muro-relleno-cimentación incorporando las reacciones del suelo de soporte (al deslizamiento RΔ y al giro Rθ) y las características inerciales del muro (masa M y momento de inercia J), que se muestran en la figura 7.
El acoplamiento se hace mediante las ecuaciones de equilibrio que a continuación se muestran.
- •
Equilibrio de fuerzas horizontales:
- •
Equilibrio de momentos en la base del muro:
En las ecuaciones anteriores RΔ y Rθ son los resortes que restringen el deslizamiento y el giro del muro, respectivamente.
Al resolver simultáneamente las ecuaciones 29 y 30, se obtienen los valores del desplazamiento Δ y del giro θ buscados.
Finalmente, las fuerzas y momentos que actúan sobre el muro considerando su interacción con el relleno y el terreno de cimentación se pueden obtener con las ecuaciones siguientes:
5Análisis e interpretación de resultadosPara evaluar la precisión del modelo propuesto en este trabajo, se realizó una comparación contra los resultados obtenidos por Veletsos y Younan [8], quienes son la primera referencia que considera la flexibilidad del suelo de cimentación y que presentan resultados que muestran la influencia del giro del muro. El modelo de estos autores corresponde a un muro desplantado sobre terreno firme al cual se le impuso un resorte en la base que es el que restringe su giro. El material que soporta el muro (relleno) es homogéneo y elástico. La rigidez del resorte Rθ en dicho modelo se determina a partir de:
donde GR y HR son el módulo de rigidez y la altura del relleno, respectivamente, y dθ es un factor de flexibilidad del suelo de cimentación que cuando vale cero indica rigidez infinita del resorte y no permite giro alguno al muro.En el análisis el muro se considera sin masa, mientras que la relación de Poisson, el amortiguamiento y la velocidad de ondas de corte del material homogéneo que forma el relleno son 1/3, 0,05 y 200m/s, respectivamente. Los parámetros del terreno de cimentación (subíndice C) se establecieron respecto a los del material del relleno (subíndice R) con base en las siguientes relaciones υR/υC=1, βR/βC=1 y VsR/VsC=1/4.
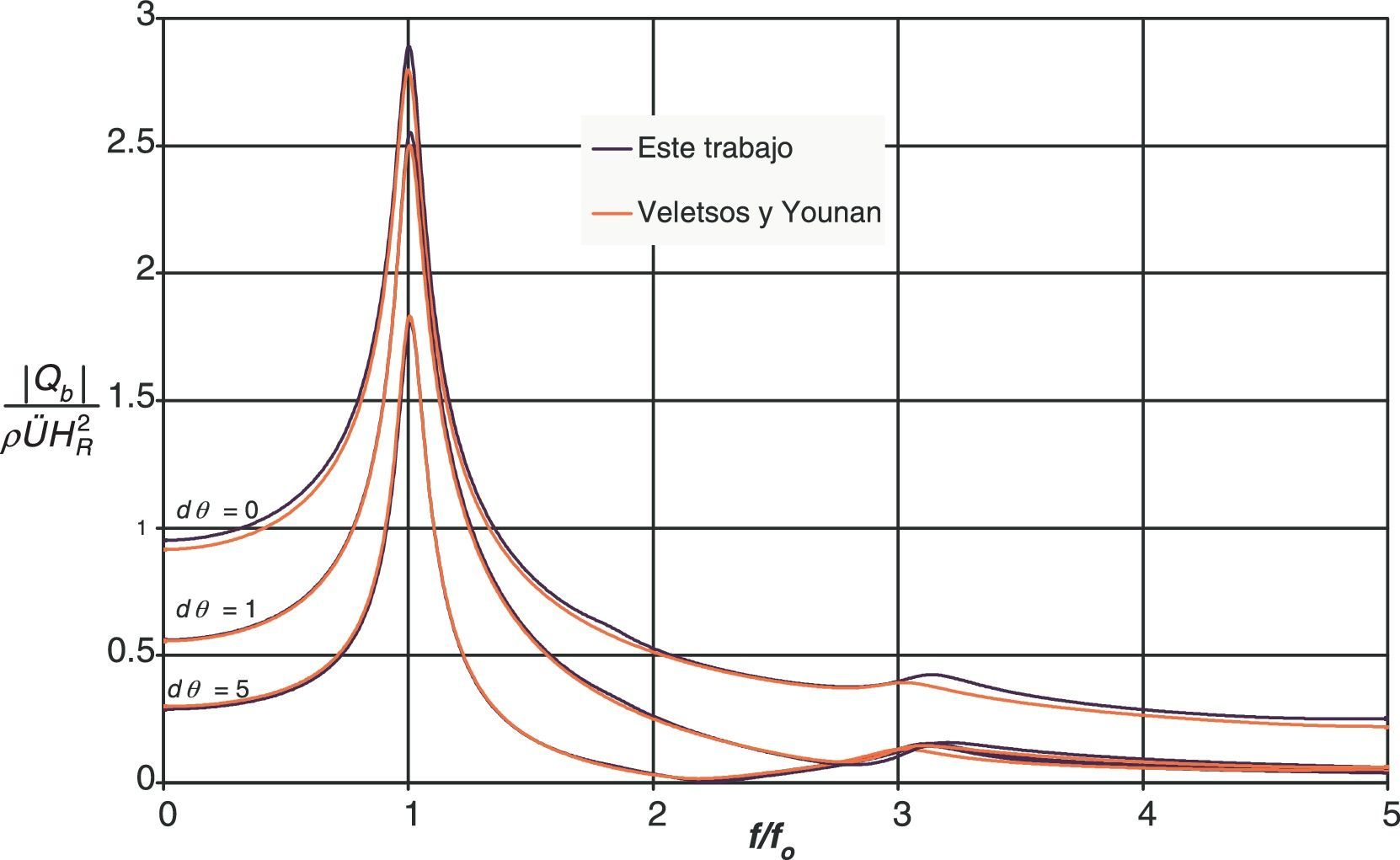
En la figura 8 se presenta una comparación del valor absoluto del cortante basal, |Qb|, de un sistema excitado armónicamente, graficado como una función de la frecuencia natural del relleno que, para un material homogéneo como el del caso analizado, se define como la velocidad de ondas de corte entre 4 veces el espesor del relleno (fo=VsR/4HR). Los resultados se muestran para 3 valores distintos del factor de flexibilidad dθ y están normalizados con respecto a ρU¨gHR2.
Las diferencias que se aprecian con el modelo de Veletsos y Younan se deben a que tales autores no consideran el esfuerzo vertical en la formulación del problema, mientras que el modelo presentado en este trabajo considera de manera rigurosa las componentes horizontal y vertical tanto del esfuerzo como del desplazamiento.
En el dominio del tiempo, el análisis de la respuesta sísmica calculada con el modelo presentado se realizó empleando la síntesis de Fourier. Como señal de excitación se utilizó inicialmente el componente NS del temblor El Centro (California, 1940), que es un sismo representativo de banda ancha. La respuesta considerada fue el valor absoluto del cortante basal máximo, Qb max, normalizado con respecto a ρU¨gHR2, la cual se graficó como una función del período dominante del relleno (To=4HR/VsR). Como una medida del valor de To que puede encontrarse en la práctica, para valores de la velocidad de ondas de corte del relleno en el rango entre 120 y 500m/s y para valores de la altura del relleno (que es igual a la del muro) entre 3 y 15m, los valores de To de interés práctico caen en el rango de 0,024 a 0,5s.
Se presentan 3 casos de estudio: en el primero se analiza la influencia exclusivamente del giro del muro; en el segundo, únicamente del deslizamiento, y en el último caso se muestra la influencia de los movimientos actuando de manera acoplada.
Para los 2 primeros casos se considera un muro desplantado sobre terreno firme, que retiene un relleno de suelo homogéneo con las mismas propiedades que las ya definidas para el ejemplo anterior, sometido a excitación horizontal en su base.
En el primer caso, la rigidez del resorte que restringe el giro se calculó con la ecuación 33 propuesta por Veletsos y Younan. En el segundo caso se decidió seguir la misma idea práctica de los mencionados autores, proponiendo la siguiente expresión para calcular el resorte que restringe el deslizamiento del muro:
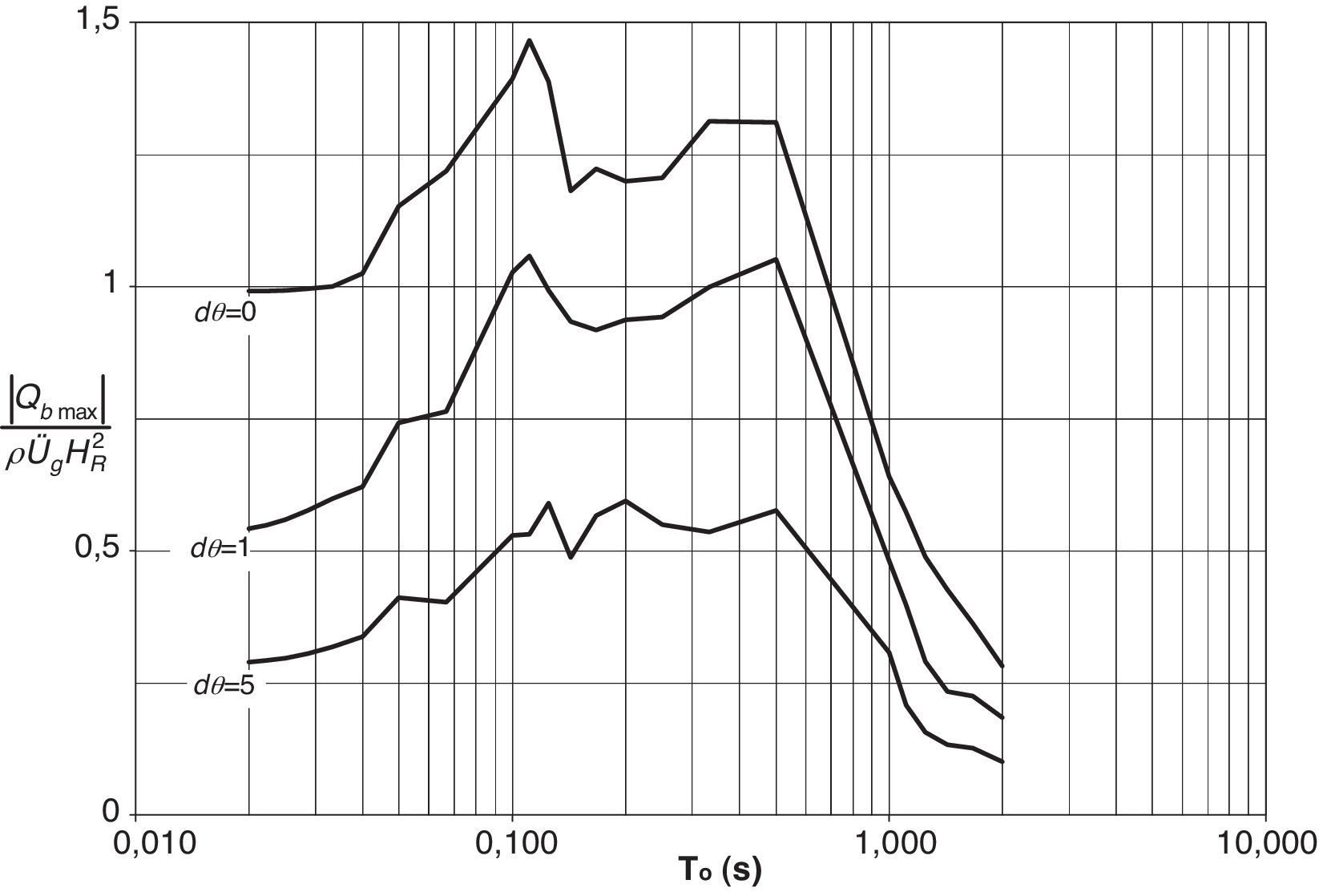
donde RΔ es el resorte que restringe el deslizamiento del muro y dΔ es el factor de flexibilidad correspondiente, cuyos valores se determinaron para los mismos casos que los representados por el factor dθ. Del análisis se obtuvo que, considerando un muro con un ancho de base de 1,6m y una altura HR=3,0m, a un suelo de cimentación con dθ=1 le corresponde un dΔ=0,1, y a uno con dθ=5 le corresponde un dΔ=0,5, aproximadamente.En la figura 9 se presentan los resultados para el primer caso estudiado. El espectro para dθ=5 corresponde a un resorte muy flexible, y para dθ=1, a un valor de flexibilidad intermedio. Estos resultados se comparan con los de un muro sin movimiento alguno, definido por dθ=0.
En dicha figura puede apreciarse que el hecho de permitir el giro al muro redunda en una marcada reducción en el cortante basal. Las reducciones son más notorias para valores de To bajos (muros de poca altura). En el rango de períodos de interés práctico, de 0,2 a 0,5s, la respuesta para el resorte más flexible es de aproximadamente la mitad de la del muro al que no se le permite el giro.
Cabe mencionar que este caso reproduce el presentado por Veletsos y Younan con la misma aproximación que la mostrada en el ejemplo anterior, siendo este el único efecto que puede ser estudiado con el modelo de tales autores, por lo que los resultados que se presentan a continuación son completamente inéditos.
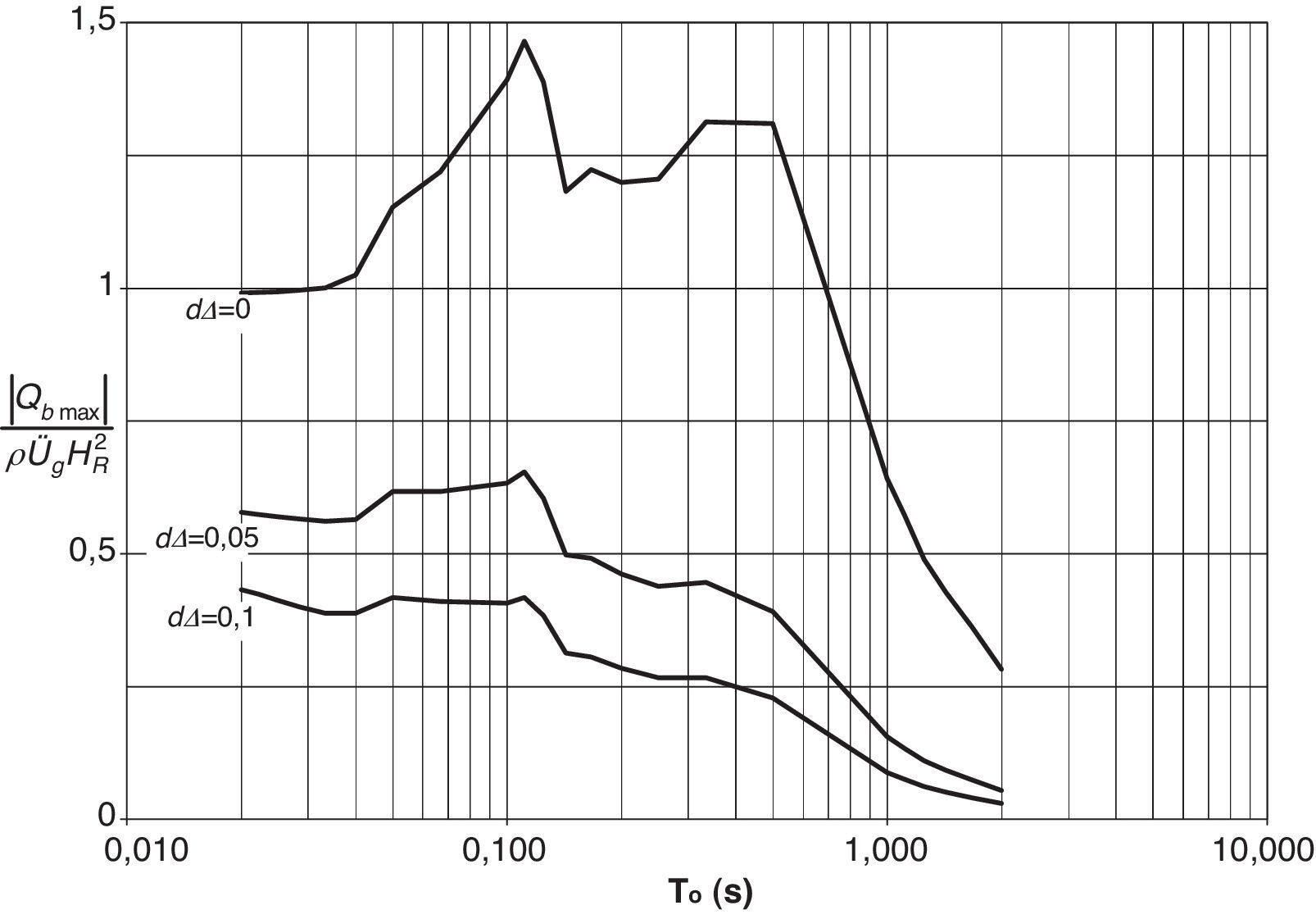
En la figura 10 se presentan los resultados obtenidos para el segundo caso, en el que se estudia exclusivamente el efecto del deslizamiento del muro.
Al analizar los resultados obtenidos con el factor dΔ=0,1, se observó que la magnitud de la respuesta caía drásticamente, por lo que en lugar del resorte originalmente considerado con un factor de flexibilidad dΔ=0,5, que generaría respuestas aún más bajas, se decidió analizar uno con un factor menor, dΔ=0,05, que permitiera verificar la tendencia del comportamiento. Los espectros calculados se compararon con los del muro al que no se le permite movimiento alguno, definido por dΔ=0.
Tal como se aprecia en la figura 10, la flexibilidad del resorte que restringe el deslizamiento del muro reduce drásticamente el cortante basal actuante. Para los períodos de interés práctico en este tipo de estructuras (de 0,2 a 0,5s), las respuestas decayeron aproximadamente el 80% cuando se consideró el resorte de máxima flexibilidad.
También se observa que, para muros con traslación, los espectros tienden a decaer conforme aumenta el periodo del relleno, con lo que se confirma que el efecto de este movimiento en la respuesta sísmica va disminuyendo conforme el muro se va haciendo más alto.
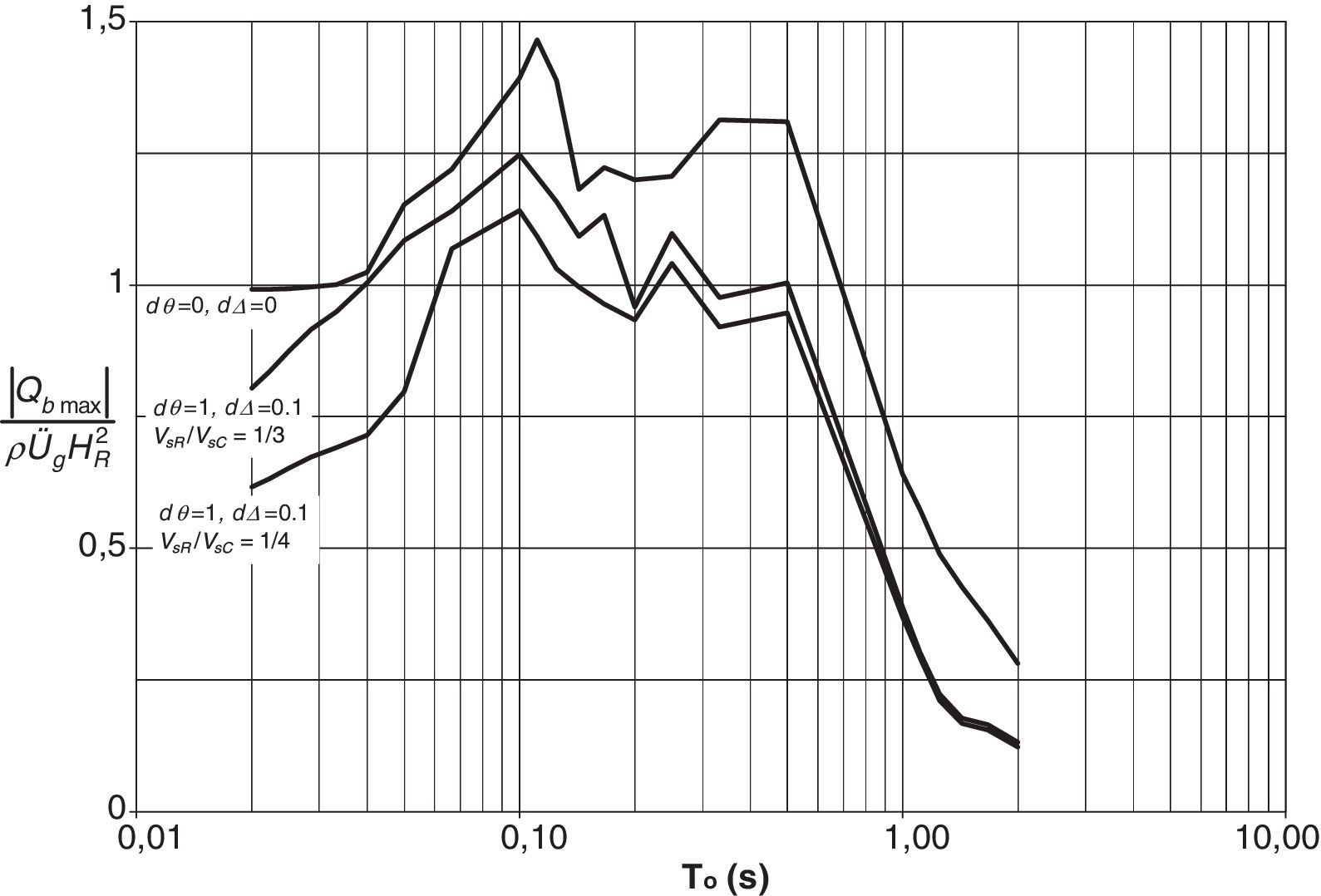
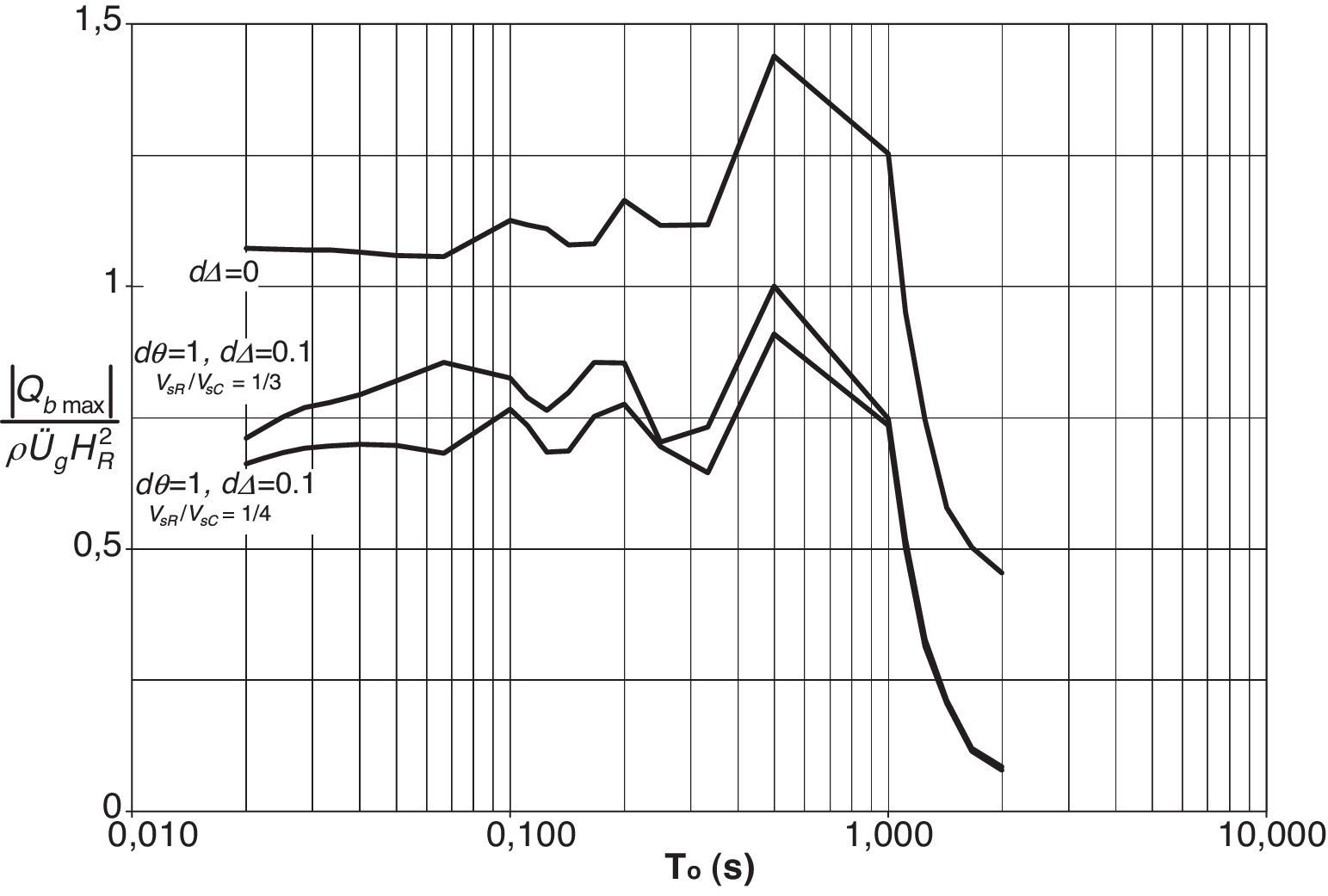
Finalmente, se presenta el caso en el que se consideran los resortes que restringen el giro y el deslizamiento del muro actuando de manera acoplada (dθ≠dΔ≠0). En este análisis se decidió estudiar el escenario con los factores de flexibilidad dθ=1 y dΔ=0,1 con el muro desplantado sobre terreno flexible y homogéneo, con un espesor HC=10m.
Las relaciones entre las propiedades de relleno y las del suelo de cimentación son iguales a las de los ejemplos anteriores, solo que ahora se consideran 2 relaciones de velocidades de ondas de corte, VsR/VsC=1/3 y 1/4, para también analizar el efecto del contraste de rigideces entre ambos materiales.
Los resultados para este caso se presentan en la figura 11, en la que se incluyen también los resultados para el muro desplantado sobre cimentación rígida y sin movimiento alguno (dθ=dΔ=0). En ella puede verse que, en comparación con el espectro de respuesta de base rígida (dθ=dΔ=0), la respuesta disminuye por efecto del movimiento acoplado del muro, pero sin llegar hasta los valores mostrados en las figuras 9 y 10, debido al efecto amplificador del estrato de cimentación flexible. Se aprecia también que dicha amplificación disminuye conforme aumenta la rigidez del estrato de cimentación. La tendencia de los espectros mostrados en la figura 11, al ser más parecida a los de la figura 9, sugiere que el movimiento que más influye en el comportamiento del muro es el de volteo.
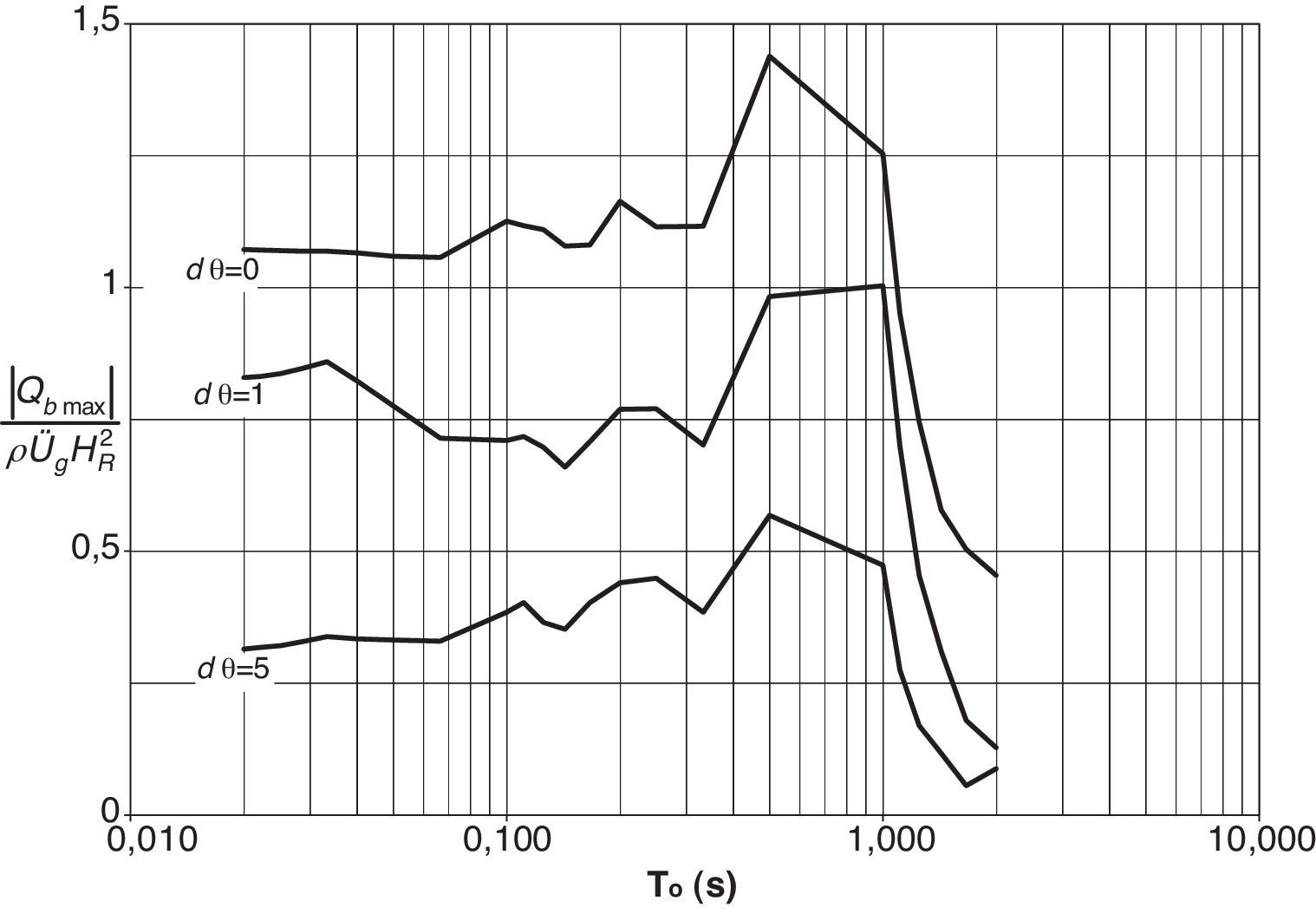
Adicionalmente al análisis realizado con el sismo de El Centro, en California, representativo de un temblor de banda ancha, se realizó otro con el componente EW del sismo SCT, en el Valle de México, en 1985, representativo de un temblor de banda estrecha, bajo las mismas consideraciones y para los mismos casos estudiados. En las figuras 12–14 se presentan los resultados obtenidos de dicho análisis.
A diferencia de los resultados obtenidos con el sismo de El Centro, que muestran espectros planos en la zona de respuestas máximas (meseta espectral), los resultados generados por el sismo SCT muestran espectros con picos resonantes claramente definidos.
Con los resultados anteriores se demuestra el efecto del alto contenido de frecuencias del sismo El Centro, que se visualiza en la meseta definida entre los períodos 0,1 y 0,5s (10 a 2Hz), mientras que el escaso contenido de frecuencias del sismo SCT se visualiza en los picos, definidas en los períodos 0,1, 0,2 y 0,5s (10, 5 y 10Hz).
Las reducciones en la respuesta debido a la flexibilidad de los resortes que actúan ya sea por separado o de manera acoplada son aproximadamente del mismo nivel para los 2 sismos estudiados.
Con los espectros anteriormente mostrados queda de manifiesto el gran efecto reductor de la respuesta que genera la flexibilidad de la cimentación.
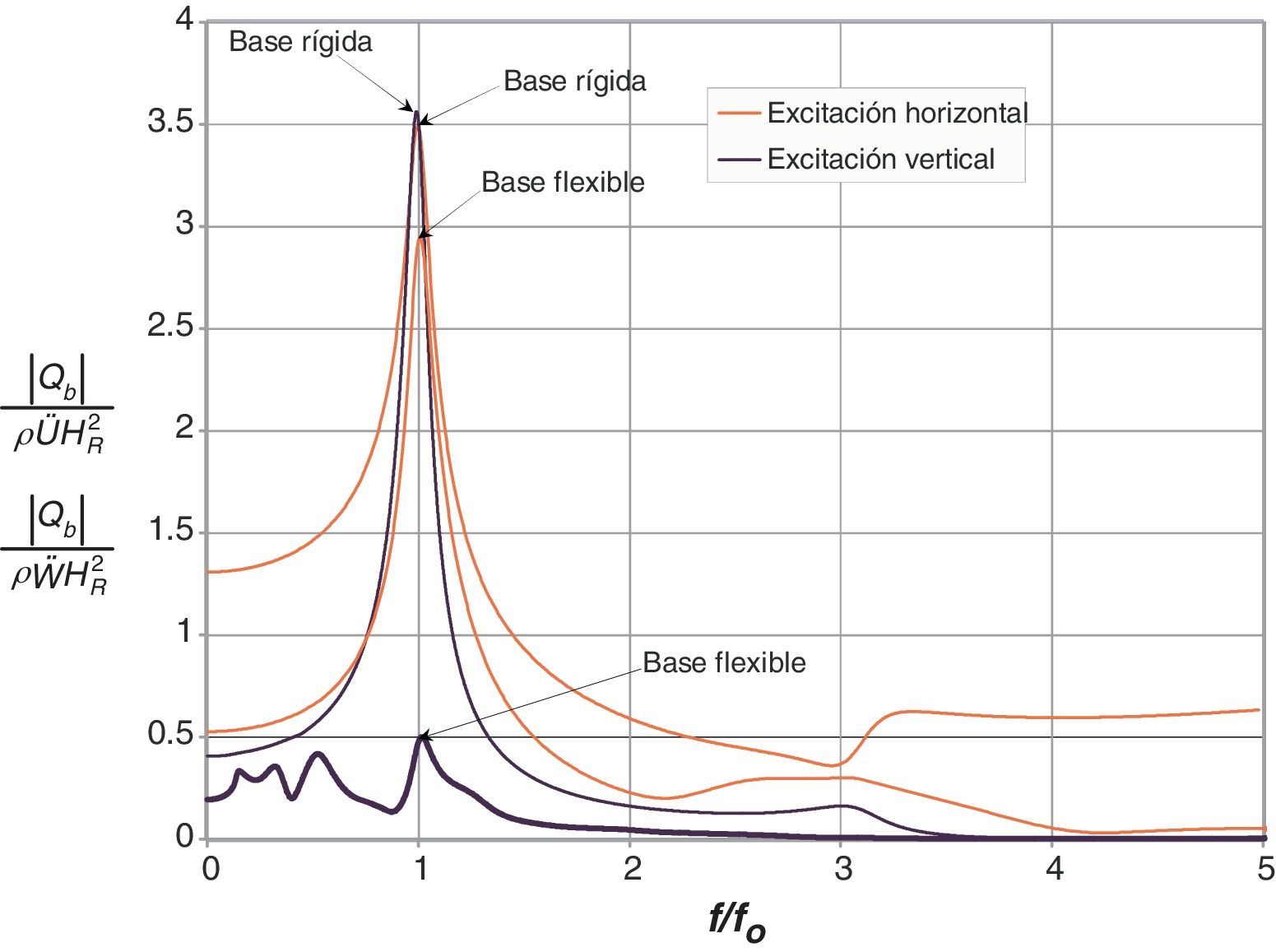
Finalmente se presenta un ejemplo en el que se muestra el efecto de la excitación vertical. Bonola y Avilés [12] han mostrado que el efecto de dicha excitación para un muro desplantado sobre terreno firme puede generar respuestas incluso mayores a las generadas por la excitación horizontal, siempre que el material del relleno esté saturado y la relación de Poisson sea cercana a 0,5, típico de suelos muy deformables.
En la figura 15 se presenta la comparación de la respuesta obtenida con el sistema muro-relleno-cimentación propuesto, considerando excitación armónica tanto horizontal como vertical en su base. Se analiza un muro desplantado sobre un estrato de suelo flexible y sobre terreno firme directamente. El primer caso se caracterizó mediante las siguientes relaciones: HR/HC=1, υR=υC=0,49, βR/βC=1 y VsR/VsC=1. La condición de base rígida en el segundo caso se reprodujo haciendo VsR/VsC=1/4, manteniendo el resto de los parámetros con los mismos valores que para el primer caso. En ambos casos se impidió el movimiento del muro (dΔ=dθ=0) para tratar de obtener la máxima respuesta, ya que al flexibilizar los resortes que restringen el movimiento del muro la respuesta vertical decae considerablemente. La respuesta se normalizó de forma similar a los ejemplos anteriores, considerando U¨g para la excitación horizontal y W¨g para la vertical.
Los resultados obtenidos muestran que, para el caso en que el muro se desplanta sobre base rígida, la tendencia es similar a la observada por Bonola y Avilés [12]. Se aprecia también que el cortante basal generado por la excitación vertical supera al generado por la excitación horizontal alrededor de la frecuencia fundamental, mientras que para las frecuencias restantes la tendencia es a la inversa. Al hacer esta misma comparación para el caso en el que el muro se desplanta sobre base flexible, se observa que la respuesta generada por la excitación vertical es significativamente menor que la generada por la excitación horizontal para todas las frecuencias.
6ConclusionesEn este trabajo se presentó un método riguroso de interacción suelo-estructura para determinar la respuesta sísmica de muros de retención sometidos a excitación horizontal y vertical, considerando la traslación y la rotación de la cimentación como productos de la flexibilidad del suelo de soporte.
En la formulación del problema, además de los resortes que restringen los movimientos de la base del muro, se incluyó un estrato de cimentación flexible que permite considerar la irradiación de las ondas sísmicas. El problema se resolvió mediante el principio de superposición de efectos, descomponiendo la solución en 3 etapas que al combinarlas representan la respuesta total del sistema muro-relleno-cimentación. La primera etapa considera la excitación en el basamento, sin permitir movimiento alguno del muro, y de ella se obtienen las fuerzas sobre el muro y sus momentos correspondientes. En la segunda etapa se impone al muro un desplazamiento unitario, y en la tercera etapa un giro unitario, obteniéndose también las fuerzas y momentos correspondientes. Los resultados de estas 3 etapas se acoplan mediante 2 ecuaciones de equilibrio en las que se incluyen los resortes que restringen el movimiento de la base del muro, así como sus propiedades de inercia. La solución de estas ecuaciones proporciona los movimientos reales de traslación y rotación del muro, con los que se obtienen las fuerzas y momentos definitivos que actúan sobre el muro.
Con la aplicación del método desarrollado se hizo inicialmente una comparación con los resultados obtenidos en el dominio de la frecuencia por Veletsos y Younan [8]. Posteriormente se efectuó un análisis en el dominio del tiempo del que se obtuvieron espectros de respuesta (cortante basal), considerando los movimientos del muro (rotación y traslación) por separado y actuando de manera acoplada, para un sismo representativo de banda ancha y otro de banda estrecha. Los resultados obtenidos muestran que la consideración de estos movimientos reduce de manera considerable las fuerzas que se ejercen sobre el muro. Asimismo, el hecho de considerar un estrato de suelo como cimentación genera una amplificación de la respuesta del relleno que depende del contraste de rigideces entre dicho estrato y el relleno soportado por el muro. Finalmente, se analizó el efecto de la excitación vertical en la respuesta sobre un muro desplantado sobre terreno tanto flexible como rígido, en el dominio de la frecuencia. De acuerdo con los resultados obtenidos, la excitación vertical genera respuestas mayores que la horizontal si la relación de Poisson del material del relleno se acerca a su valor máximo y el muro está desplantado sobre terreno firme. Para un muro desplantado sobre un estrato de suelo, la respuesta generada por la excitación vertical es significativamente menor que la generada por la horizontal en todos los casos.