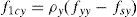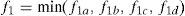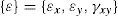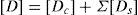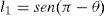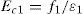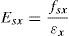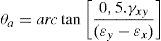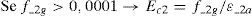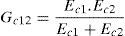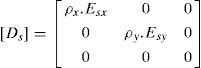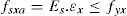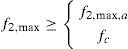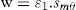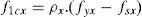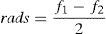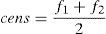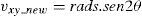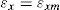Desenvolvimento de uma ferramenta computacional para a análise de elementos de membrana em concreto estrutural

Resumo

Elementos de concreto armado submetidos a esforços de membrana, isto é, forças normais e forças cortantes no próprio plano, são bastante comuns na modelagem de estruturas complexas, tais como hangares, usinas nucleares, estruturas off-shore e vigas caixão de grandes pontes. Apesar de o problema de dimensionamento desses elementos já estar bem resolvido, o mesmo não pode ser dito para o caso da análise de elementos de membrana já armados. Dentro desse panorama, o presente trabalho tem por objetivo apresentar um software implementado na plataforma Matlab e baseado na «Modified Compression Field Theory». De maneira a certificar a performance do programa criado, diversos resultados numéricos foram confrontados com resultados experimentais. Os resultados obtidos revelam que a ferramenta ora desenvolvida possui boa confiabilidade para analisar o desempenho de elementos de membrana em concreto estrutural.

Abstract

Reinforced concrete elements subjected to membrane forces, i.e., elements subjected to in-plane shear and axial stresses are very common for modeling complex structures such as aircraft hangars, nuclear power plants, offshore oil platforms and long-span bridges. While the design of reinforcement for membrane elements is well adressed the same can not be said regarding the analysis of performance of these elements. Into this context, the present paper aims at providing a numerical tool developed in the Matlab platform, taking into account the “Modified Compression Field Theory”. In order to certificate the performance of the proposed tool, extensive numerical results were compared with experimental results available in the literature. The obtained results revealed that the proposed tool is very confident for the analysis of reinforced concrete membrane elements.

1

Introdução

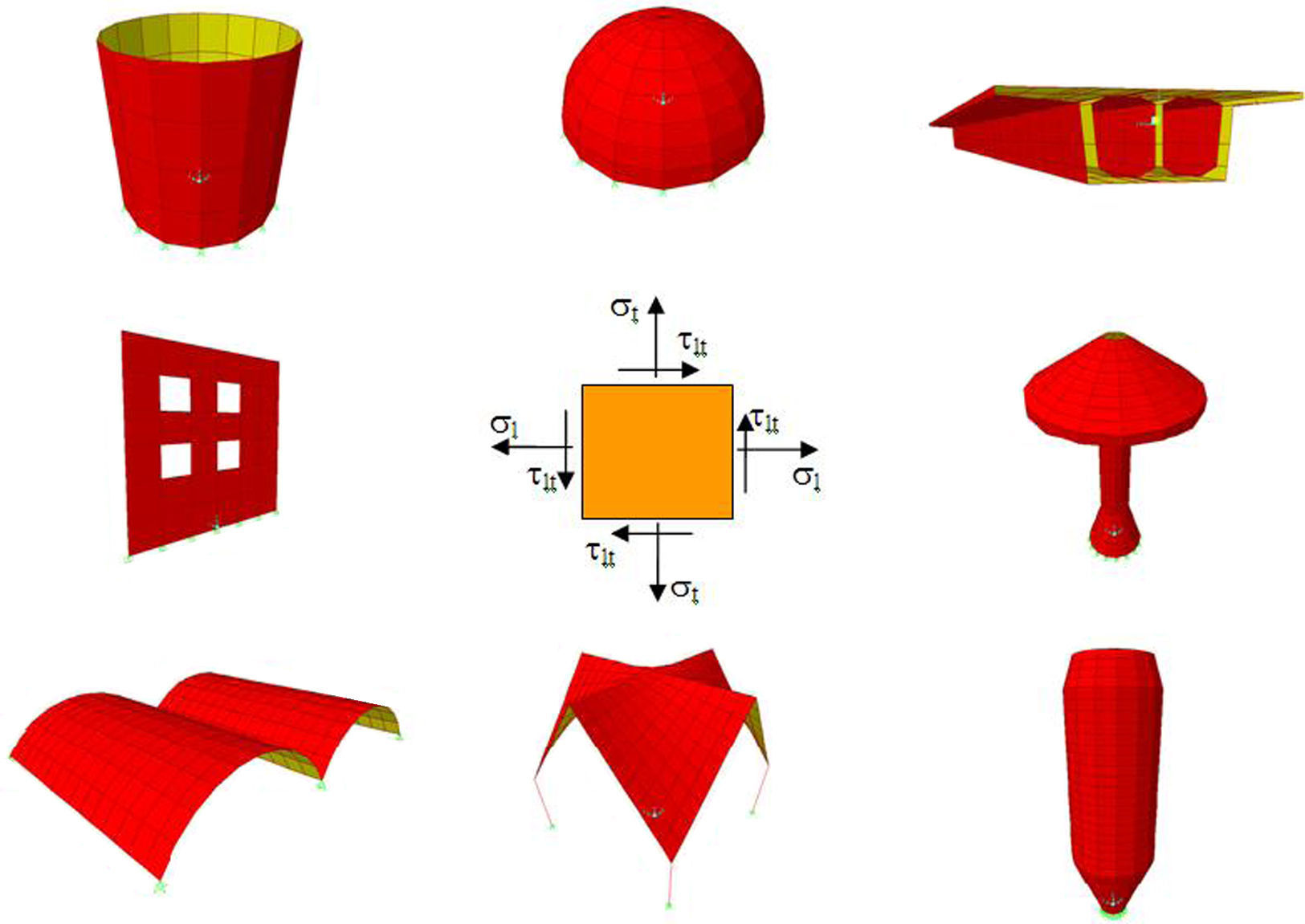
Os elementos de membrana são elementos que estão submetidos apenas a forças normais e de cisalhamento no próprio plano e podem ser utilizados para a modelagem dos mais diversos tipos de estruturas, conforme ilustra a figura 1. A maioria das soluções conhecidas para o dimensionamento destes elementos foi obtida através da verificação das condições de equilíbrio e de resistência, conduzindo a um dimensionamento seguro, baseado no Teorema Inferior da Teoria da Plasticidade. Dentro dessa linha, merecem destaque as publicações de Fialkow [1,2], Gupta [3,4], Hsu [5], Lourenço [6], Lourenço e Figueiras [7], Lourenço e Figueiras [8], Nielsen [9] e Regan [10].

Figura 1.

Estruturas complexas modeladas utilizando elementos de membrana.

Apesar de o problema de dimensionamento estar num estágio aceitável, deve observar-se que as alternativas de solução não são suficientemente difundidas no meio prático. Além disso, o problema de verificação de elementos de membrana, isto é, a análise do comportamento de um elemento plano armado e sujeito a ações no próprio plano, não é um problema trivial como parece ser. Collins et al. [11] relatam que, numa competição internacional, com a participação de 43 líderes mundiais em pesquisa sobre simulações numéricas aplicadas ao concreto armado, não foi possível prever o comportamento carga versus deslocamento de painéis retangulares armados com uma margem de erro inferior a 15%.

Ficou evidente que o insucesso das previsões era fortemente dependente das relações tensão-deformação empregues, as quais basicamente ignoravam a resistência à tração do concreto. Com base nos resultados experimentais da competição realizada, Vecchio e Collins [12] desenvolveram a «Modified Compression Field Theory» (MCFT) e passaram a considerar a resistência à tração do concreto entre fissuras.

De acordo com Vecchio e Collins [12], a análise de um elemento de membrana é dificultada devido ao facto de que novas fissuras podem ser formadas, fissuras preexistentes podem propagar-se e até mesmo fechar-se, e tende a formar-se um sistema estrutural constituído por corpos de concreto conectados pelas barras das armaduras sob a ação de determinados carregamentos. Além disso, os corpos de concreto tendem a unir-se nas superfícies rugosas existentes na interface das fissuras, podendo assim transmitir cisalhamento e compressão nos pontos em contacto.

Um modelo que faz frente ao MCFT proposto por Vecchio e Collins [12] é o «Softened Truss Model», ou Modelo de Treliça Flexibilizado, proposto por Hsu [13]. Trata-se de um método de análise não linear de elementos de membrana que envolve a resolução simultânea de um grande número de equações, tal como se observa no MCFT.

Quando, além dos esforços de membrana (f_x, f_y e f_xy), existem os esforços decorrentes da Teoria das Placas Delgadas, isto é, os esforços associados à flexão do elemento (m_x, m_y, m_xy), pode-se generalizar as soluções citadas anteriormente, tornando a situação de análise ainda mais complexa. Para mais informações sobre o dimensionamento de armaduras em elementos de casca, recomenda-se a leitura dos trabalhos de Gupta [4], Lourenço [6], Lourenço e Figueiras [7], Lourenço e Figueiras [1,8], Regan [10] e Della Bella e Cifú [14].

Tendo em vista a dificuldade do meio prático em obter respostas quanto ao comportamento de elementos de membrana, o presente trabalho tem por objetivo apresentar o desenvolvimento de uma ferramenta computacional criada na plataforma MATLAB para a análise dos referidos elementos. Para tanto, foi criado o programa MEDEA RC_MCFT («Membrane Design and Analysis for Reinforced Concrete Based on the Modified Compression Field Theory»), cuja formulação está fortemente baseada nos trabalhos desenvolvidos por Vecchio e Collins [12], Bentz [15] e Hoogenboom e Voskamp [16].

2

Modified Compression Field Theory

2.1

Breve apresentação

A teoria conhecida como MCFT tem as suas origens na «Diagonal Compression Field Theory (DCFT)» proposta por Mitchell e Collins [17], bem como na «Compression Field Theory (CFT)» proposta por Collins [18]. A proposta original do MCFT foi lançada por Vecchio e Collins [19] a partir do ensaio de 30 painéis de concreto armado submetidos a estados uniformes de deformação.

A versão definitiva do MCFT foi publicada por Vecchio e Collins [12] e, desde então, apenas pequenas modificações foram implementadas no modelo original, conforme atesta o trabalho de Collins and Mitchell [20]. Desde a versão final do modelo, vários outros pesquisadores têm proposto modelos similares, entre eles, os modelos propostos por Hsu e Zhang [21], Zhang e Hsu [22] e Kaufmann and Marti [23].

De acordo com Bentz [15], o MCFT é uma teoria geral para o comportamento carga versus deformação de elementos bidimensionais de concreto armado fissurados submetidos a cisalhamento. O comportamento do concreto sob compressão e tração é baseado em mais de 250 ensaios em equipamentos especialmente desenvolvidos para tal fim. Máquinas similares também foram construídas no Japão e nos Estados Unidos, de maneira que foi possível confirmar a qualidade dos resultados da teoria proposta.

A hipótese mais importante assumida no modelo é que o concreto fissurado pertencente a um elemento de concreto armado pode ser tratado como se fosse um novo material com uma curva própria para o comportamento tensão-deformação. Esse comportamento é diferente do comportamento tradicional obtido do ensaio de corpos de prova cilíndricos submetidos à compressão e leva em conta o efeito de tensões transversais de tração.

As deformações utilizadas no modelo consistem em deformações médias, isto é, reúnem de maneira acoplada efeitos combinados como deformações locais nas fissuras, deformações entre fissuras, aderência-escorregamento e escorregamento entre fissuras. Da mesma maneira, as tensões também são médias, isto é, incluem implicitamente as tensões entre fissuras, tensões nas fissuras, a interface de cisalhamento entre fissuras e o efeito pino propiciado pelas armaduras. Para que que o uso de tensões e deformações médias possa ser considerado adequado, o comportamento médio deve ser medido em distâncias que incluam poucas fissuras.

De acordo com Bentz [15], uma verificação explícita deve ser feita de maneira a penalizar a utilização de relações tensão-deformação médias, garantindo que as tensões médias sejam compatíveis com a condição de fissuração do concreto. Esse processo, denominado «crack check» é uma etapa crucial no MCFT e nas teorias que dele derivam. O processo de verificação consiste basicamente na limitação da tensão principal de tração no concreto a um valor limite, considerando a tensão de tração na armadura que atravessa a fissura e a habilidade de a superfície fissurada transmitir tensões de cisalhamento.

Uma vez que o comportamento geral é baseado em relações médias, melhoradas com o processo de «crack check», o modelo não requer o cálculo explícito de efeitos complementares, tais como: efeito pino, tensões de cisalhamento nas fissuras, tensão nas armaduras nas fissuras, deformações devido ao deslizamento das fissuras e tensões de aderência. Se necessário, os valores comentados anteriormente podem ser calculados por equações de equilíbrio. A simplicidade que se tem no modelo, tendo-se em vista a não consideração explícita dos efeitos complexos mencionados anteriormente, é uma das grandes virtudes da teoria proposta por Vecchio e Collins [12].

A figura 2 procura apresentar de maneira reduzida as relações envolvidas no MCFT para o caso bidimensional, sendo que, para mais informações, se recomenda a leitura na íntegra dos trabalhos de Vecchio e Collins [12,19]. O painel da esquerda apresenta as equações de equilíbrio baseadas nas equações do Círculo de Mohr para tensões. O painel intermediário apresenta as condições de deformação, também resumidas através do Círculo de Mohr. Deve observar-se que, no MCFT, o ângulo da tensão principal no concreto é tomado como sendo igual ao ângulo da deformação principal. O painel da direita ilustra as relações constitutivas para os materiais, nomeadamente aço e concreto. Finalmente, a base de cada painel ilustra as componentes de verificação localizada na fissura, de maneira que as tensões médias possam ser transmitidas.

Figura 2.

Resumo das equações utilizadas no modelo MCFT.

2.2

Descrição do procedimento de «crack check» na «Modified Compression Field Theory»

Apesar de a «Modified Compression Field Theory» ter sua formulação bem conhecida e difundida no meio científico, percebe-se ainda grande dificuldade de implementação numérica do método, tendo-se em vista a pouca divulgação do procedimento conhecido como «crack check», necessário para assegurar que níveis de tensão médios possam ser resistidos localmente numa fissura. Dessa maneira, procura-se apresentar com maior clareza tal procedimento, de maneira que a formulação baseada na MCFT possa ser implementada com toda sua potencialidade.

De acordo com Bentz [15], tornou-se evidente que, no passado, muitos pesquisadores implementaram a MCFT sem a devida inclusão do procedimento «crack check», propiciando dessa maneira respostas inadequadas e potencialmente perigosas. A importância do procedimento «crack check» pode ser demonstrada utilizando o prisma de concreto armado tracionado da figura 3.

Figura 3.

Prisma em concreto armado submetido à tração.

A força total atuante no prisma é dada pela equação (1):

Em que:

N = Força axial total;

N_c = Parcela da força total absorvida pelo concreto = f₁.A_c;

N_s = Parcela da força total absorvida pelas armaduras = f_sx.A_s = ρ.f_sx.A_c;

As relações tensão-deformação para o concreto e para as armaduras podem ser definidas utilizando-se as equações propostas no MCFT e apresentadas em maior detalhe na figura 4.

Figura 4.

Comportamento médio para (a) concreto e (b) armaduras submetidos à tração.

Uma análise equivocada do problema pode produzir o diagrama tensão versus deformação apresentado na figura 5 (a). Este resultado é considerado inadequado, uma vez que as forças carregadas pelo concreto e pelas armaduras foram somadas ao longo de todo o processo de deformação do prisma, o que é particularmente incorreto.

Figura 5.

(a) Comportamento inadequado de deformação do prisma e (b) diagrama de corpo livre na fissura para elemento unidimensional.

Considere agora o diagrama de corpo livre ilustrado na figura 5 (b), sendo que, pelo do lado esquerdo, são consideradas as relações médias utilizadas pelo MCFT e, pelo lado direito, são consideradas tensões locais na fissura, sem que haja a participação do concreto à tração. Analisando o diagrama de corpo livre, fica evidente que, pelo lado direito, a tensão f_sx deve ser limitada pela tensão de escoamento das armaduras e que f₁ = 0. A garantia de que a tensão local na fissura não irá superar a tensão de escoamento do aço é basicamente o procedimento denominado de «crack check» no MCFT. Utilizando a verificação de «crack check», pode-se chegar a um diagrama mais realista do comportamento tensão versus deformação do elemento prismático de concreto armado submetido à tração, conforme ilustrado na figura 6.

Figura 6.

Comportamento tensão versus deformação de prisma de concreto armado considerando o procedimento de «crack check».

Dessa maneira, a explanação anterior dá origem ao procedimento de «crack check» para o caso unidimensional. A dedução de equilíbrio de forças, apresentada na equação (2) possibilita estabelecer o procedimento «crack check» para o prisma ilustrado na figura 3:

Para o caso bidimensional, o procedimento «crack check» torna-se um pouco mais complexo. Primeiramente, deve ser feita uma verificação uniaxial em cada uma das direções das armaduras, acompanhada de uma verificação adicional objetivando responder se há possibilidade de transmissão de cisalhamento na interface da fissura.

Basicamente, assume-se que a fissura não pode transmitir nenhuma tensão axial de tração. Assume-se também que as direções das tensões principais possam rotacionar localmente na fissura e, dessa maneira, o aparecimento de cisalhamento poderá ocorrer na interface da fissura caso as condições de equilíbrio conduzam a essa condição. Implicitamente, assume-se que o concreto está a tentar manter a máxima capacidade de resistência à tração quanto possível, sendo que esse valor máximo obedece a equação constitutiva de «tension stiffening».

Considere agora o diagrama de corpo livre da figura 7, em que um elemento bidimensional de concreto armado é analisado na interface fissurada. Deve observar-se que o corte foi feito na direção do ângulo teta, o mesmo ângulo das fissuras e das direções principais de tensão e deformação no concreto de acordo com o MCFT.

Figura 7.

Diagrama de corpo livre na fissura para elemento bidimensional.

Conforme se pode observar pela figura 7, a tensão principal de compressão no concreto (f₂) é irrelevante para o equilíbrio. As tensões de importância na fissura são basicamente as tensões locais nas armaduras (f_sx-crack e f_sy-crack), bem como o cisalhamento em potencial na interface fissurada (v_ci). Como há 3 resultantes de tensão e apenas 2 equações de equilíbrio disponíveis, o problema pode apresentar mais de uma solução no que se refere ao equilíbrio na fissura.

O procedimento utilizado no MCFT consiste em assumir que o mecanismo de resistência das armaduras é mais rígido do que o mecanismo de cisalhamento na fissura, de maneira que o cisalhamento na fissura é minimizado. A importância dessa hipótese é pequena em comparação com uma hipótese alternativa que considera que o ângulo das deformações principais é mantido localmente na fissura. Por outro lado, importa lembrar que o ângulo das tensões principais, em contraste, irá provavelmente rotacionar localmente na fissura quando comparado com a direção média, devido ao comportamento não linear das armaduras.

De acordo com Bentz [15], a hipótese de minimizar o cisalhamento na interface da fissura tem o efeito de usar toda a capacidade portante do aço na direção mais fraca antes que qualquer tensão de cisalhamento na fissura seja necessária. Uma vez que esse comportamento está a acontecer apenas localmente na fissura, esse efeito não terá influência na resposta global tensão versus deformação.

Somando as forças nas direções x e y da figura 7, pode-se obter as equações que garantem o procedimento «crack check» para o caso bidimensional. Seguindo os passos indicados, pode-se garantir que a tensão na fissura não ultrapassará a tensão de escoamento das armaduras nas direções x e y. Adicionalmente, pode-se garantir que a tensão de cisalhamento na fissura será menor do que um limite máximo calculado em função da abertura de fissura. O fluxograma de cálculo é apresentado a seguir:

• a)

  Inicialmente, calcula-se a tensão principal de tração (f_1a), o máximo cisalhamento possível na interface fissurada (v_cimax = v_ci1) e as tensões médias nas armaduras (f_sx,f_sy);

• b)

  Calcula-se a reserva de capacidade nas direções x e y para as armaduras (f_1cx, f_1cy). Basicamente, f_1cx e f_1cy são as tensões extra necessárias para que ocorra o escoamento das armaduras nas direções x e y:

  
  
  Observe que as equações (3) e (4) constituem o procedimento «crack check», caso se imponha na equação (2) que f_sx-crack = f_yx = f_yy.

• c)

  Calcula-se a condição de escoamento biaxial sem a presença de cisalhamento na fissura (f_1b). Essa verificação garante basicamente que a carga necessária para causar o escoamento biaxial das armaduras na fissura não será ultrapassada:

  

• d)

  Calcula-se a tensão máxima de cisalhamento na fissura para que ocorra o escoamento biaxial (v_ci2) das armaduras:

  

• e)

  Calcula-se a máxima tensão de tração permitida para o equilíbrio nas direções x (f_1c) e y (f_1d):

  
  

• f)

  Seleciona-se o menor valor entre as tensões de tração calculadas:

  

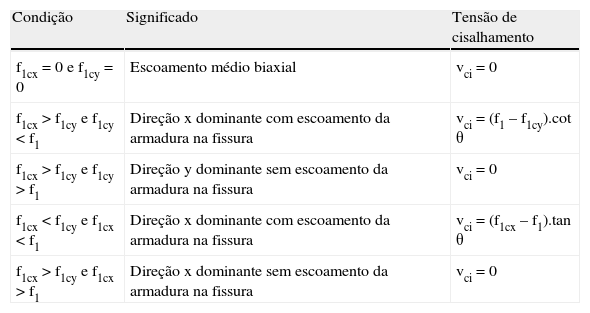
• g)

  Para o cálculo da tensão de cisalhamento na interface da fissura (v_ci), devem utilizar-se os procedimentos descritos na tabela 1. Deve realçar-se que o cálculo não pode ser feito diretamente, uma vez que há mais incógnitas do que equações disponíveis para o problema.

  Tabela 1.

  Tensão de cisalhamento máxima na fissura de acordo com BENTZ [15]

  Condição	Significado	Tensão de cisalhamento
  f1cx = 0 e f1cy = 0	Escoamento médio biaxial	vci = 0
  f1cx > f1cy e f1cy < f1	Direção x dominante com escoamento da armadura na fissura	vci = (f1 – f1cy).cot θ
  f1cx > f1cy e f1cy > f1	Direção y dominante sem escoamento da armadura na fissura	vci = 0
  f1cx < f1cy e f1cx < f1	Direção x dominante com escoamento da armadura na fissura	vci = (f1cx – f1).tan θ
  f1cx > f1cy e f1cx > f1	Direção x dominante sem escoamento da armadura na fissura	vci = 0
• h)

  Finalmente, as tensões nas armaduras na interface fissurada podem ser calculadas, tomando-se por base a tensão de cisalhamento calculada anteriormente:

  
  

2.3

Emprego do «Modified Compression Field Theory» acoplado ao método da rigidez secante

A técnica de solução proposta por Vecchio e Collins [12] é um tanto sofisticada e requer o uso de estratégias apropriadas para a implementação numérica. Dessa maneira, será apresentada na sequência uma estratégia para implementação da MCFT, fazendo proveito de matrizes apropriadas e técnicas numéricas baseadas no Método da Rigidez Secante. A implementação que é aqui apresentada pode ser encontrada em detalhe nos trabalhos de Vecchio [24,25], Bentz [15] e Hoogenboom e Voskamp [16].

De acordo com Bentz [15], uma das maneiras mais eficientes de obter o estado de deformação a partir de um estado de tensão conhecido é através do emprego do Método da Rigidez Secante, em que qualquer curva tensão versus deformação pode ser representada pela equação (12). A figura 8 procura ilustrar a definição de módulo secante e módulo tangente para o concreto e para barras de aço, de acordo com Krpan [26].

Figura 8.

Módulos secante e tangente para (a) concreto e (b) barras de aço.

Basicamente, o vetor das deformações (¿) pode ser relacionado com o vetor das tensões (σ) através da matriz D, definida como sendo a Matriz de Rigidez Secante e apresentada na equação (13). Utilizando-se essa matriz, a solução para qualquer termo desconhecido pode facilmente encontrada com grande estabilidade. Deve observar-se que a Matriz de Rigidez Secante é simétrica e totalmente povoada.

Basicamente, uma estimativa de deformações é efetuada para um dado estado de carregamento. A relação é então verificada utilizando-se o método anterior para calcular as tensões com o emprego da Matriz de Rigidez Secante. Uma nova estimativa para o vetor das deformações é então proposta a partir da Matriz de Rigidez Secante. O procedimento é então repetido até que ocorra a convergência desejada para o nível de carregamento desejado.

De acordo com Selby [27], a Matriz de Rigidez Secante apresentada na equação (13) é calculada em função das direções principais e posteriormente rotacionada para o sistema de eixos cartesiano. A matriz é basicamente constituída por componentes devido ao concreto [D_c] e devido às armaduras [D_s], conforme ilustra a equação (16):

Para a determinação da matriz [D_c], é necessário calcular a mesma nas direções principais e depois rotacionar a mesma para o sistema cartesiano. Esse procedimento pode ser feito empregando a equação (17):

A Matriz de Transformação [T] para o caso bidimensional é composta pelos seguintes termos descritos nas equações a seguir. Deve observar-se que a Matriz de Transformação é descrita em função do ângulo teta, que é o ângulo principal de tensão e deformação para o concreto.

A Matriz [D_c]’ é a matriz de rigidez do concreto na direção principal para o caso bidimensional e é defina pela equação (23):

Uma vez que as armaduras são responsáveis somente pela absorção de força normal, a matriz [D_s] total para as direções x e y será dada pela equação (27):

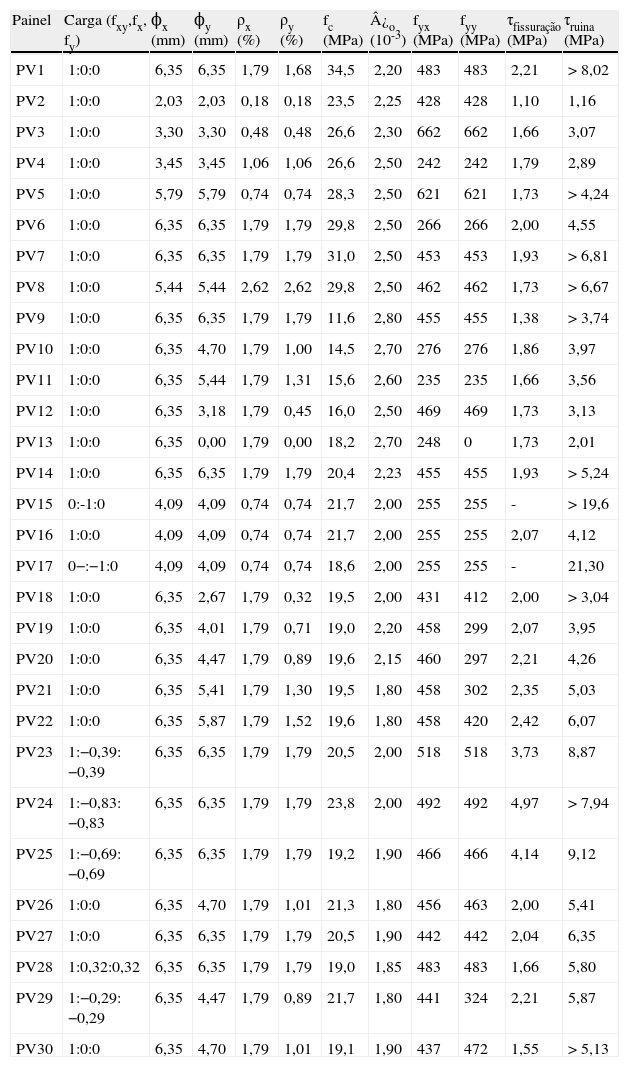
2.4

Principais ensaios experimentais com elementos de membrana

A tabela 2 apresenta uma série de ensaios realizados na Universidade de Toronto por Collins et al. [11], onde se pode visualizar as características dos elementos ensaiados e o tipo de solicitação aplicada. Basicamente, foram ensaiados painéis quadrados de concreto armado com 89 cm de largura e 7 cm de espessura, com resistência à compressão variando entre 11 a 31 MPa. Na maioria dos casos, o carregamento foi aplicado monotonicamente até se atingir o esgotamento (esmagamento do concreto ou rutura da armadura).

Tabela 2.

Resultados experimentais obtidos por Collins et al. [11]

Painel	Carga (fxy,fx, fy)	ϕx (mm)	ϕy (mm)	ρx (%)	ρy (%)	fc (MPa)	¿o (10^-3)	fyx (MPa)	fyy (MPa)	τfissuração (MPa)	τruina (MPa)
PV1	1:0:0	6,35	6,35	1,79	1,68	34,5	2,20	483	483	2,21	> 8,02
PV2	1:0:0	2,03	2,03	0,18	0,18	23,5	2,25	428	428	1,10	1,16
PV3	1:0:0	3,30	3,30	0,48	0,48	26,6	2,30	662	662	1,66	3,07
PV4	1:0:0	3,45	3,45	1,06	1,06	26,6	2,50	242	242	1,79	2,89
PV5	1:0:0	5,79	5,79	0,74	0,74	28,3	2,50	621	621	1,73	> 4,24
PV6	1:0:0	6,35	6,35	1,79	1,79	29,8	2,50	266	266	2,00	4,55
PV7	1:0:0	6,35	6,35	1,79	1,79	31,0	2,50	453	453	1,93	> 6,81
PV8	1:0:0	5,44	5,44	2,62	2,62	29,8	2,50	462	462	1,73	> 6,67
PV9	1:0:0	6,35	6,35	1,79	1,79	11,6	2,80	455	455	1,38	> 3,74
PV10	1:0:0	6,35	4,70	1,79	1,00	14,5	2,70	276	276	1,86	3,97
PV11	1:0:0	6,35	5,44	1,79	1,31	15,6	2,60	235	235	1,66	3,56
PV12	1:0:0	6,35	3,18	1,79	0,45	16,0	2,50	469	469	1,73	3,13
PV13	1:0:0	6,35	0,00	1,79	0,00	18,2	2,70	248	0	1,73	2,01
PV14	1:0:0	6,35	6,35	1,79	1,79	20,4	2,23	455	455	1,93	> 5,24
PV15	0:-1:0	4,09	4,09	0,74	0,74	21,7	2,00	255	255	-	> 19,6
PV16	1:0:0	4,09	4,09	0,74	0,74	21,7	2,00	255	255	2,07	4,12
PV17	0−:−1:0	4,09	4,09	0,74	0,74	18,6	2,00	255	255	-	21,30
PV18	1:0:0	6,35	2,67	1,79	0,32	19,5	2,00	431	412	2,00	> 3,04
PV19	1:0:0	6,35	4,01	1,79	0,71	19,0	2,20	458	299	2,07	3,95
PV20	1:0:0	6,35	4,47	1,79	0,89	19,6	2,15	460	297	2,21	4,26
PV21	1:0:0	6,35	5,41	1,79	1,30	19,5	1,80	458	302	2,35	5,03
PV22	1:0:0	6,35	5,87	1,79	1,52	19,6	1,80	458	420	2,42	6,07
PV23	1:−0,39:−0,39	6,35	6,35	1,79	1,79	20,5	2,00	518	518	3,73	8,87
PV24	1:−0,83:−0,83	6,35	6,35	1,79	1,79	23,8	2,00	492	492	4,97	> 7,94
PV25	1:−0,69:−0,69	6,35	6,35	1,79	1,79	19,2	1,90	466	466	4,14	9,12
PV26	1:0:0	6,35	4,70	1,79	1,01	21,3	1,80	456	463	2,00	5,41
PV27	1:0:0	6,35	6,35	1,79	1,79	20,5	1,90	442	442	2,04	6,35
PV28	1:0,32:0,32	6,35	6,35	1,79	1,79	19,0	1,85	483	483	1,66	5,80
PV29	1:−0,29:−0,29	6,35	4,47	1,79	0,89	21,7	1,80	441	324	2,21	5,87
PV30	1:0:0	6,35	4,70	1,79	1,01	19,1	1,90	437	472	1,55	> 5,13

Observações: Painéis quadrados de 89 cm de largura e 7 cm de espessura, diâmetro máximo do agregado de 6 mm e módulo de elasticidade das armaduras de 200 GPa.

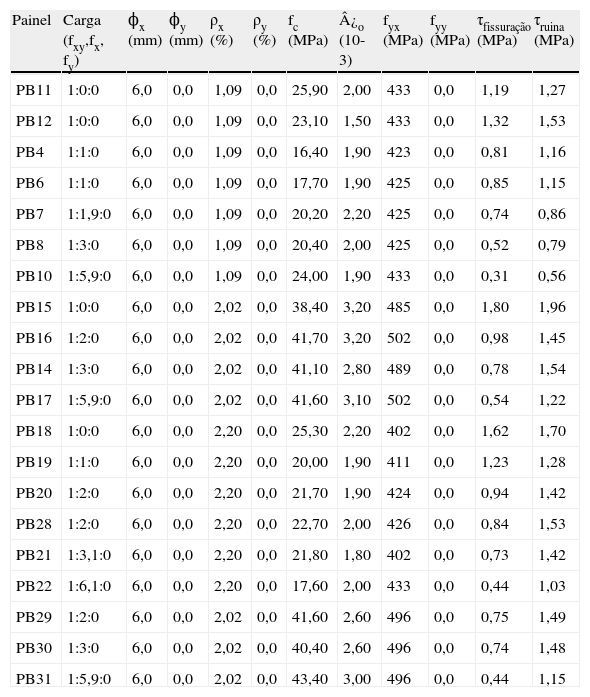
Bhide e Collins [28] também ensaiaram elementos de membrana em concreto armado retangulares com largura de 79 cm e espessura de 7 cm, conforme ilustra a tabela 3. No entanto, as armaduras foram dispostas numa única direção, sendo que, na direção transversal, a tração foi resistida exclusivamente pelo concreto.

Tabela 3.

Resultados experimentais obtidos por Bhide e Collins [28]

Painel	Carga (fxy,fx, fy)	ϕx (mm)	ϕy (mm)	ρx (%)	ρy (%)	fc (MPa)	¿o (10-3)	fyx (MPa)	fyy (MPa)	τfissuração (MPa)	τruina (MPa)
PB11	1:0:0	6,0	0,0	1,09	0,0	25,90	2,00	433	0,0	1,19	1,27
PB12	1:0:0	6,0	0,0	1,09	0,0	23,10	1,50	433	0,0	1,32	1,53
PB4	1:1:0	6,0	0,0	1,09	0,0	16,40	1,90	423	0,0	0,81	1,16
PB6	1:1:0	6,0	0,0	1,09	0,0	17,70	1,90	425	0,0	0,85	1,15
PB7	1:1,9:0	6,0	0,0	1,09	0,0	20,20	2,20	425	0,0	0,74	0,86
PB8	1:3:0	6,0	0,0	1,09	0,0	20,40	2,00	425	0,0	0,52	0,79
PB10	1:5,9:0	6,0	0,0	1,09	0,0	24,00	1,90	433	0,0	0,31	0,56
PB15	1:0:0	6,0	0,0	2,02	0,0	38,40	3,20	485	0,0	1,80	1,96
PB16	1:2:0	6,0	0,0	2,02	0,0	41,70	3,20	502	0,0	0,98	1,45
PB14	1:3:0	6,0	0,0	2,02	0,0	41,10	2,80	489	0,0	0,78	1,54
PB17	1:5,9:0	6,0	0,0	2,02	0,0	41,60	3,10	502	0,0	0,54	1,22
PB18	1:0:0	6,0	0,0	2,20	0,0	25,30	2,20	402	0,0	1,62	1,70
PB19	1:1:0	6,0	0,0	2,20	0,0	20,00	1,90	411	0,0	1,23	1,28
PB20	1:2:0	6,0	0,0	2,20	0,0	21,70	1,90	424	0,0	0,94	1,42
PB28	1:2:0	6,0	0,0	2,20	0,0	22,70	2,00	426	0,0	0,84	1,53
PB21	1:3,1:0	6,0	0,0	2,20	0,0	21,80	1,80	402	0,0	0,73	1,42
PB22	1:6,1:0	6,0	0,0	2,20	0,0	17,60	2,00	433	0,0	0,44	1,03
PB29	1:2:0	6,0	0,0	2,02	0,0	41,60	2,60	496	0,0	0,75	1,49
PB30	1:3:0	6,0	0,0	2,02	0,0	40,40	2,60	496	0,0	0,74	1,48
PB31	1:5,9:0	6,0	0,0	2,02	0,0	43,40	3,00	496	0,0	0,44	1,15

Observações: Painéis quadrados de 89 cm de largura e 7 cm de espessura, diâmetro máximo do agregado de 9,5 mm e módulo de elasticidade das armaduras de 200 GPa.

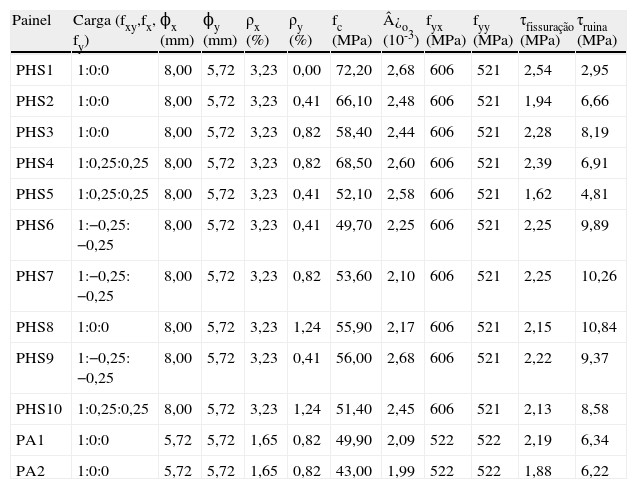
Vecchio et al. [29] ensaiaram elementos de membrana com concreto de alta resistência, com resistência à compressão variando entre 43 a 72 MPa, conforme ilustra a tabela 4. Novamente, foram ensaiadas placas quadradas com 89 cm de largura e 7 cm de espessura. Basicamente, os elementos foram submetidos a solicitações monotónicas de cisalhamento puro (PHS1, PHS2, PHS3, PHS8, PA1, PA2) e combinação cisalhamento-tração (PHS4, PHS5, PHS10) e cisalhamento-compressão (PHS6, PHS7, PHS9).

Tabela 4.

Resultados experimentais obtidos por Vecchio et al. [29]

Painel	Carga (fxy,fx, fy)	ϕx (mm)	ϕy (mm)	ρx (%)	ρy (%)	fc (MPa)	¿o (10^-3)	fyx (MPa)	fyy (MPa)	τfissuração (MPa)	τruina (MPa)
PHS1	1:0:0	8,00	5,72	3,23	0,00	72,20	2,68	606	521	2,54	2,95
PHS2	1:0:0	8,00	5,72	3,23	0,41	66,10	2,48	606	521	1,94	6,66
PHS3	1:0:0	8,00	5,72	3,23	0,82	58,40	2,44	606	521	2,28	8,19
PHS4	1:0,25:0,25	8,00	5,72	3,23	0,82	68,50	2,60	606	521	2,39	6,91
PHS5	1:0,25:0,25	8,00	5,72	3,23	0,41	52,10	2,58	606	521	1,62	4,81
PHS6	1:−0,25:−0,25	8,00	5,72	3,23	0,41	49,70	2,25	606	521	2,25	9,89
PHS7	1:−0,25:−0,25	8,00	5,72	3,23	0,82	53,60	2,10	606	521	2,25	10,26
PHS8	1:0:0	8,00	5,72	3,23	1,24	55,90	2,17	606	521	2,15	10,84
PHS9	1:−0,25:−0,25	8,00	5,72	3,23	0,41	56,00	2,68	606	521	2,22	9,37
PHS10	1:0,25:0,25	8,00	5,72	3,23	1,24	51,40	2,45	606	521	2,13	8,58
PA1	1:0:0	5,72	5,72	1,65	0,82	49,90	2,09	522	522	2,19	6,34
PA2	1:0:0	5,72	5,72	1,65	0,82	43,00	1,99	522	522	1,88	6,22

Observações: Painéis quadrados de 89 cm de largura e 7 cm de espessura, diâmetro máximo do agregado de 10 mm e módulo de elasticidade das armaduras de 200 GPa.

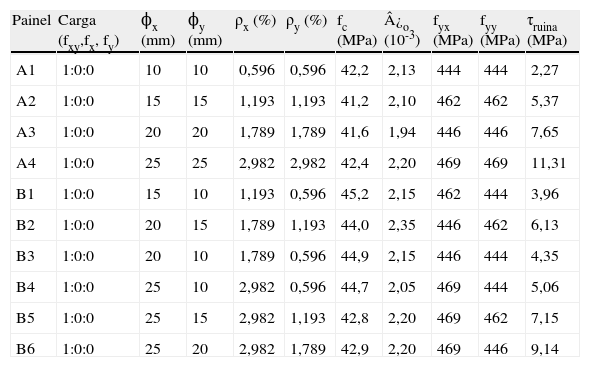
Pang e Hsu [30] submeteram 10 painéis de concreto armado quadrados com 13,97 cm de largura e 17,8 cm de espessura a carregamentos de cisalhamento puro, conforme ilustra a tabela 5. Além dos resultados ora aqui apresentados, que são os mais expressivos na literatura, há ainda os ensaios conduzidos por outros pesquisadores, tais como Yamaguchi et al. [31], Andre [32], Zhang e Hsu [22] e Xie [33].

Tabela 5.

Resultados experimentais obtidos por Pang e Hsu [30]

Painel	Carga (fxy,fx, fy)	ϕx (mm)	ϕy (mm)	ρx (%)	ρy (%)	fc (MPa)	¿o (10^-3)	fyx (MPa)	fyy (MPa)	τruina (MPa)
A1	1:0:0	10	10	0,596	0,596	42,2	2,13	444	444	2,27
A2	1:0:0	15	15	1,193	1,193	41,2	2,10	462	462	5,37
A3	1:0:0	20	20	1,789	1,789	41,6	1,94	446	446	7,65
A4	1:0:0	25	25	2,982	2,982	42,4	2,20	469	469	11,31
B1	1:0:0	15	10	1,193	0,596	45,2	2,15	462	444	3,96
B2	1:0:0	20	15	1,789	1,193	44,0	2,35	446	462	6,13
B3	1:0:0	20	10	1,789	0,596	44,9	2,15	446	444	4,35
B4	1:0:0	25	10	2,982	0,596	44,7	2,05	469	444	5,06
B5	1:0:0	25	15	2,982	1,193	42,8	2,20	469	462	7,15
B6	1:0:0	25	20	2,982	1,789	42,9	2,20	469	446	9,14

Observações: Painéis quadrados de 140 cm de largura e 17,8 cm de espessura, diâmetro máximo do agregado de 19 mm e módulo de elasticidade das armaduras de 210 GPa.

2.5

Desenvolvimento do programa «Membrane Design and Analysis of Reinforced Concrete Using the Modified Compression Field Theory»

2.5.1

Breve descrição do programa

O programa «Membrane Design and Analysis of Reinforced Concrete Using the Modified Compression Field Theory» (MEDEA RC_MCFT) foi criado com o objetivo de se tornar uma ferramenta versátil para a análise de elementos de membrana em concreto estrutural. Para tanto, procurou-se implementar o MCFT na plataforma MATLAB, através dos procedimentos descritos por Vecchio e Collins [12], Vecchio [25], Bentz [15], Bentz [34] e Hoogenboom e Voskamp [16]. O Anexo 1 procura apresentar de maneira resumida o fluxograma do programa.

A figura 9 (a) apresenta a tela de entrada do programa MEDEA RC_MCFT. Após a abertura da tela de entrada do programa, pode então dar-se início à análise de elementos de membrana em concreto armado. Para tanto, basta aceder ao menu «File» e clicar sobre a opção «New». Aquando do acionamento da opção «New», será aberta a tela de entrada de dados ilustrada na figura 9 (b).

Figura 9.

(a) Tela de entrada e (b) introdução de dados no programa MEDEA RC_MCFT.

Conforme se pode observar, o usuário deve fornecer as seguintes informações: diâmetro das barras longitudinais, percentagens de armação, módulo de elasticidade das barras, tensão de escoamento das barras, resistência média do concreto à compressão, diâmetro máximo do agregado, estado de carregamento do elemento de membrana, número de passos de carga e fator de carga para obtenção das curvas de comportamento conforme necessidade do usuário.

Caso o usuário já tenha feito uma análise anterior, os dados podem ser salvos e abertos novamente acedendo ao menu «File» e a opção «Open». Por outro lado, caso o usuário deseje salvar os dados correntes, basta aceder ao menu «File» e, posteriormente, selecionar a opção «Save». A figura 10 (a) ilustra os dados do Painel PV20 ensaiado por Vecchio e Collins [19]. Uma vez que os dados foram descritos, os mesmos devem ser salvos através do menu «File», opção «Save». Em seguida, pode-se selecionar o processamento dos dados através do menu «Process», opção «MCFT», conforme ilustrado na figura 10 (b).

Figura 10.

(a) Descrição dos dados e (b) processamento no programa MEDEA RC_MCFT.

Com o acionamento da opção «MCFT», será aberta uma nova tela para que o usuário escolha o nome do arquivo com os resultados a serem obtidos, conforme ilustra a figura 11 (a). Imediatamente após a escolha do arquivo de saída, o programa iniciará o processamento dos dados de entrada, conforme ilustra a figura 11 (b). Em geral, os processamentos são bastante rápidos para processamentos com até 1 000 passos de carga. Importante relatar que, quanto mais passos de carga forem especificados, melhor será a resposta numérica. Evidentemente, o usuário deve buscar a melhor relação desse parâmetro com o fator de carga, que é utilizado basicamente para definir os incrementos de carga a serem dados ao elemento de membrana em análise.

Figura 11.

(a) Atribuição do nome arquivo de saída com os resultados processados e (b) processamento.

Após o término do processamento, o usuário deve então acionar o menu «Results» e selecionar a opção «Graphs», conforme ilustrado na figura 12 (a). Dessa maneira, o usuário poderá ter acesso a vários gráficos de desempenho para o elemento de membrana descrito. Com a seleção da opção «Graphs», será aberta a tela apresentada na figura 12 (b). Conforme se pode observar, são apresentados os seguintes diagramas de desempenho, desde uma carga pequena até à carga de rutura: tensão de cisalhamento versus deformação de cisalhamento, tensão de cisalhamento versus abertura de fissura, tensão de cisalhamento versus tensão normal nas armaduras nas direções x e y.

Figura 12.

(a) Escolha da visualização de resultados e (b) gráficos de desempenho gerados.

Conforme se pode observar pela figura 12 (b), são apresentadas retas horizontais nos diagramas de tensão de cisalhamento versus deformação de cisalhamento e tensão de cisalhamento versus abertura de fissura. Essas retas referem-se à tensão de cisalhamento informada pelo usuário no início do processamento, na tela de entrada de dados. Dessa maneira, o usuário pode verificar se o estado de tensão descrito é apropriado para o nível de armação informado, tendo em vista a performance completa desde o início do carregamento até à rutura.

Clicando no menu «Results» e, posteriormente, na opção «Output File», o usuário poderá ainda ter acesso aos resultados dos diversos passos de carga. De maneira geral, observa-se que os resultados numéricos obtidos utilizando-se o programa MEDEA RC_MCFT possuem boa precisão quando comparados com os resultados experimentais descritos no item 3 do presente trabalho, conforme visto a seguir.

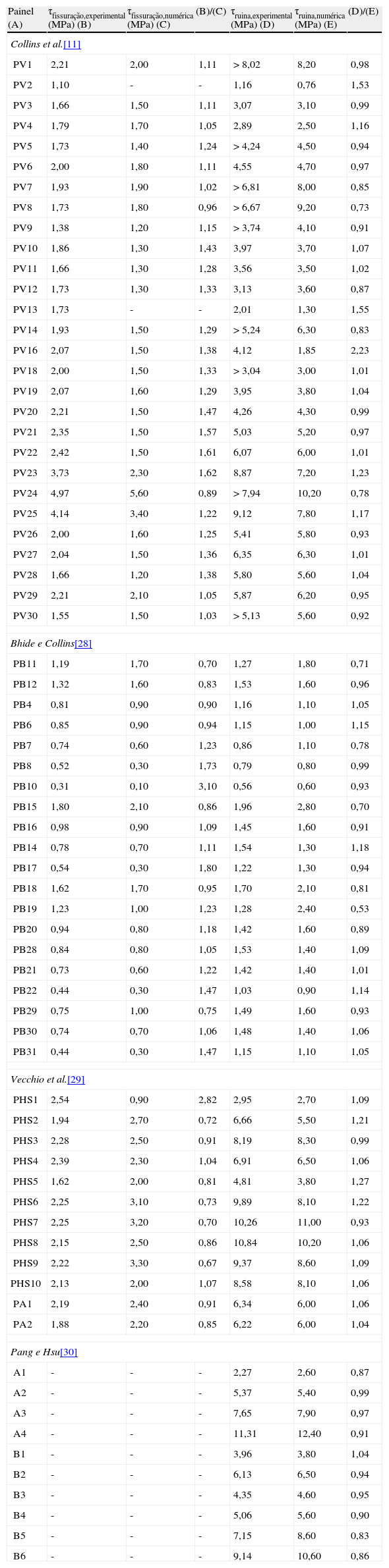
2.6

Validação do programa «Membrane Design and Analysis of Reinforced Concrete Using the Modified Compression Field Theory»

De maneira a comprovar a performance do programa MEDEA RC_MCFT, a tabela 6 procura apresentar uma comparação entre os resultados experimentais descritos no item 3 e os resultados numéricos obtidos utilizando o programa MEDEA RC_MCFT. Conforme se pode observar, foram utilizados os resultados experimentais obtidos por Collins et al. [11], Bhide e Collins [28] e Vecchio et al. [29], com resistência à compressão do concreto variando entre 11,60 e 72,20 MPa. Foram investigados 58 resultados para fissuração e 70 resultados para rutura de placas em concreto armado submetidas a combinações de força normal e força cortante.

Tabela 6.

Resultados numéricos obtidos com o programa MEDEA RC_MCFT e comparados aos resultados experimentais de Collins et al. [11], Bhide e Collins [28], Vecchio et al. [29] e Pang e Hsu [30]

Painel (A)	τfissuração,experimental (MPa) (B)	τfissuração,numérica (MPa) (C)	(B)/(C)	τruina,experimental (MPa) (D)	τruina,numérica (MPa) (E)	(D)/(E)
Collins et al.[11]
PV1	2,21	2,00	1,11	> 8,02	8,20	0,98
PV2	1,10	-	-	1,16	0,76	1,53
PV3	1,66	1,50	1,11	3,07	3,10	0,99
PV4	1,79	1,70	1,05	2,89	2,50	1,16
PV5	1,73	1,40	1,24	> 4,24	4,50	0,94
PV6	2,00	1,80	1,11	4,55	4,70	0,97
PV7	1,93	1,90	1,02	> 6,81	8,00	0,85
PV8	1,73	1,80	0,96	> 6,67	9,20	0,73
PV9	1,38	1,20	1,15	> 3,74	4,10	0,91
PV10	1,86	1,30	1,43	3,97	3,70	1,07
PV11	1,66	1,30	1,28	3,56	3,50	1,02
PV12	1,73	1,30	1,33	3,13	3,60	0,87
PV13	1,73	-	-	2,01	1,30	1,55
PV14	1,93	1,50	1,29	> 5,24	6,30	0,83
PV16	2,07	1,50	1,38	4,12	1,85	2,23
PV18	2,00	1,50	1,33	> 3,04	3,00	1,01
PV19	2,07	1,60	1,29	3,95	3,80	1,04
PV20	2,21	1,50	1,47	4,26	4,30	0,99
PV21	2,35	1,50	1,57	5,03	5,20	0,97
PV22	2,42	1,50	1,61	6,07	6,00	1,01
PV23	3,73	2,30	1,62	8,87	7,20	1,23
PV24	4,97	5,60	0,89	> 7,94	10,20	0,78
PV25	4,14	3,40	1,22	9,12	7,80	1,17
PV26	2,00	1,60	1,25	5,41	5,80	0,93
PV27	2,04	1,50	1,36	6,35	6,30	1,01
PV28	1,66	1,20	1,38	5,80	5,60	1,04
PV29	2,21	2,10	1,05	5,87	6,20	0,95
PV30	1,55	1,50	1,03	> 5,13	5,60	0,92
Bhide e Collins[28]
PB11	1,19	1,70	0,70	1,27	1,80	0,71
PB12	1,32	1,60	0,83	1,53	1,60	0,96
PB4	0,81	0,90	0,90	1,16	1,10	1,05
PB6	0,85	0,90	0,94	1,15	1,00	1,15
PB7	0,74	0,60	1,23	0,86	1,10	0,78
PB8	0,52	0,30	1,73	0,79	0,80	0,99
PB10	0,31	0,10	3,10	0,56	0,60	0,93
PB15	1,80	2,10	0,86	1,96	2,80	0,70
PB16	0,98	0,90	1,09	1,45	1,60	0,91
PB14	0,78	0,70	1,11	1,54	1,30	1,18
PB17	0,54	0,30	1,80	1,22	1,30	0,94
PB18	1,62	1,70	0,95	1,70	2,10	0,81
PB19	1,23	1,00	1,23	1,28	2,40	0,53
PB20	0,94	0,80	1,18	1,42	1,60	0,89
PB28	0,84	0,80	1,05	1,53	1,40	1,09
PB21	0,73	0,60	1,22	1,42	1,40	1,01
PB22	0,44	0,30	1,47	1,03	0,90	1,14
PB29	0,75	1,00	0,75	1,49	1,60	0,93
PB30	0,74	0,70	1,06	1,48	1,40	1,06
PB31	0,44	0,30	1,47	1,15	1,10	1,05
Vecchio et al.[29]
PHS1	2,54	0,90	2,82	2,95	2,70	1,09
PHS2	1,94	2,70	0,72	6,66	5,50	1,21
PHS3	2,28	2,50	0,91	8,19	8,30	0,99
PHS4	2,39	2,30	1,04	6,91	6,50	1,06
PHS5	1,62	2,00	0,81	4,81	3,80	1,27
PHS6	2,25	3,10	0,73	9,89	8,10	1,22
PHS7	2,25	3,20	0,70	10,26	11,00	0,93
PHS8	2,15	2,50	0,86	10,84	10,20	1,06
PHS9	2,22	3,30	0,67	9,37	8,60	1,09
PHS10	2,13	2,00	1,07	8,58	8,10	1,06
PA1	2,19	2,40	0,91	6,34	6,00	1,06
PA2	1,88	2,20	0,85	6,22	6,00	1,04
Pang e Hsu[30]
A1	-	-	-	2,27	2,60	0,87
A2	-	-	-	5,37	5,40	0,99
A3	-	-	-	7,65	7,90	0,97
A4	-	-	-	11,31	12,40	0,91
B1	-	-	-	3,96	3,80	1,04
B2	-	-	-	6,13	6,50	0,94
B3	-	-	-	4,35	4,60	0,95
B4	-	-	-	5,06	5,60	0,90
B5	-	-	-	7,15	8,60	0,83
B6	-	-	-	9,14	10,60	0,86

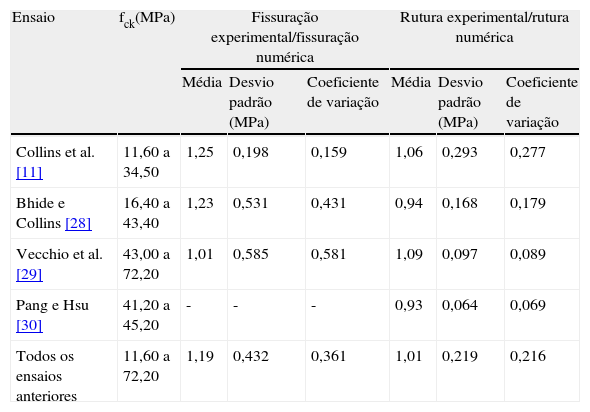
A tabela 7 procura apresentar de maneira resumida os principais resultados numéricos obtidos. Conforme se pode observar, no que se refere a fissuração, o quociente entre os resultados experimentais e os verificados numericamente foi de 1,19, com um desvio padrão de 0,43 e um coeficiente de variação de 36,18%. Já para a rutura, obteve-se um quociente entre a carga de ruína experimental e a carga de rutura numérica igual a 1,01, com um desvio padrão de 0,22 e coeficiente de variação de 21,64%.

Tabela 7.

Resumo dos resultados numéricos obtidos com o programa MEDEA RC_MCFT comparados aos resultados experimentais de Collins et al. [11], Bhide e Collins [28], Vecchio et al. [29] e Pang e Hsu [30]

Ensaio	fck(MPa)	Fissuração experimental/fissuração numérica			Rutura experimental/rutura numérica
		Média	Desvio padrão (MPa)	Coeficiente de variação	Média	Desvio padrão (MPa)	Coeficiente de variação
Collins et al. [11]	11,60 a 34,50	1,25	0,198	0,159	1,06	0,293	0,277
Bhide e Collins [28]	16,40 a 43,40	1,23	0,531	0,431	0,94	0,168	0,179
Vecchio et al. [29]	43,00 a 72,20	1,01	0,585	0,581	1,09	0,097	0,089
Pang e Hsu [30]	41,20 a 45,20	-	-	-	0,93	0,064	0,069
Todos os ensaios anteriores	11,60 a 72,20	1,19	0,432	0,361	1,01	0,219	0,216

Conforme se pode observar pela tabela 7, a fissuração foi melhor capturada para o ensaio de Collins et al. [11], que possui resistência à compressão do concreto variando entre 11,60 a 34,20 MPa. Para este caso, o quociente entre a carga de fissuração experimental e a carga de fissuração teórica foi em média igual a 1,25, com um coeficiente de variação de apenas 15,9%.

Por outro lado, para o ensaio de Vecchio et al. [29] obteve-se um coeficiente de variação bastante alto, indicando que as previsões para este caso são bastante dispersas, apesar do baixo quociente entre a carga de fissuração experimental e a carga prevista numericamente (1,01). Esse facto revela que a previsão de fissuração em concretos com resistência superior a 40 MPa deve ser mais bem formulada no MCFT, tendo-se em vista que o coeficiente de variação procura revelar a representatividade da média.

A carga de rutura foi melhor capturada para os ensaios de Vecchio et al. [29] e Pang e Hsu [30], com coeficientes de variação de apenas 8,9 e 6,9%, respetivamente. Observa-se nesses casos o quociente médio entre a carga de rutura experimental e a carga de rutura numérica com valores médios variando entre 0,93 a 1,09. É interessante notar que os ensaios de Vecchio et al. [29] e Pang e Hsu [30] são aqueles com as maiores resistências à compressão para o concreto, indicando que, no caso de ruína, esse aumento de resistência introduz pouca interferência nas previsões numéricas, ao contrário do que foi observado nas fissurações. Observa-se que o coeficiente de variação obtido na rutura para os ensaios de Collins et al. [11] são os maiores entre todos os outros testados.

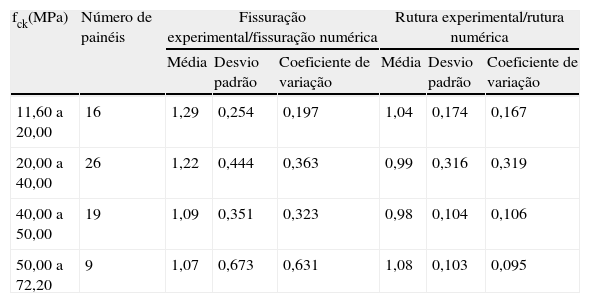
De maneira a investigar o efeito da resistência à compressão do concreto nos resultados numéricos, procurou-se estudar os coeficientes de variação em função das faixas de resistência. A tabela 8 mostra que a fissuração dos painéis é melhor capturada pelo programa MEDEA RC_MCFT na faixa de resistência à compressão do concreto variando entre 11,60 e 20 MPa. Para essa faixa de resistência, obtém-se um coeficiente médio entre a carga de fissuração experimental e a teórica igual a 1,29, com um coeficiente de variação de 25,4%. Por outro lado, observa-se que as respostas numéricas não serão satisfatórias, do ponto de vista de fissuração, para resistências superiores a 20 MPa, uma vez que o coeficiente de variação tenderá a ser superior a 35,1%, podendo chegar a 67,3%.

Tabela 8.

Resumo dos resultados numéricos comparados aos resultados experimentais para diferentes faixas de variação da resistência à compressão do concreto

fck(MPa)	Número de painéis	Fissuração experimental/fissuração numérica			Rutura experimental/rutura numérica
		Média	Desvio padrão	Coeficiente de variação	Média	Desvio padrão	Coeficiente de variação
11,60 a 20,00	16	1,29	0,254	0,197	1,04	0,174	0,167
20,00 a 40,00	26	1,22	0,444	0,363	0,99	0,316	0,319
40,00 a 50,00	19	1,09	0,351	0,323	0,98	0,104	0,106
50,00 a 72,20	9	1,07	0,673	0,631	1,08	0,103	0,095

No que se refere à previsão numérica da ruína dos painéis ensaiados experimentalmente, a tabela 8 revela, surpreendentemente, que as melhores previsões serão para concretos com resistências superiores a 40 MPa, cujos coeficientes de variação serão inferiores a 10,6%. A tabela 8 revela ainda que há uma tendência de cargas de ruínas numéricas mais precisas conforme se aumenta a resistência à compressão do concreto nos painéis. Observa-se que as piores previsões de ruína concentram-se na faixa entre 20 e 40 MPa, em que o coeficiente de variação chega a 31,9%.

Conforme se pode observar, o programa MEDEA RC_MCFT possui uma boa performance e pode ser utilizado como uma ferramenta versátil para a previsão do comportamento de elementos de membrana. Tendo-se em vista a dificuldade em se obter os resultados experimentais de outros ensaios, infelizmente só foi possível validar o programa com os resultados descritos anteriormente. De qualquer forma, as simulações efetuadas com o programa MEDEA RC_MCFT são bastante favoráveis e Conforme se pode observar, estão a favor da segurança, isto é, de maneira geral, o programa fornece cargas de fissuração e colapso que são ligeiramente inferiores às cargas verificadas experimentalmente.

Finalmente, deve observar-se que devem ser feitas melhorias ao MCFT original proposto por Vecchio e Collins [12], de maneira a capturar melhor as cargas de fissuração (para painéis com concretos de resistência à compressão superiores a 40 MPa) e para cargas de ruína (para concretos com resistência entre 20 e 40 MPa). Isso pode ser feito definindo parâmetros multiplicadores de ajuste para as resistências à compressão e tração do concreto.

3

Conclusões

A previsão de comportamento de elementos estruturais utilizando a «Analogia de Treliça» conduz, normalmente, a respostas superestimadas em relação à resistência de elementos estruturais à força cortante e ao momento torçor. Essa dificuldade em prever o comportamento ao cisalhamento tem desafiado pesquisadores desde o começo do século xx e, até hoje, a discussão permanece em aberto, com discussões concentradas nos últimos anos sobre os elementos de membrana.

Conforme mencionado, a análise de elementos de membrana em concreto estrutural não é uma tarefa trivial, uma vez que o comportamento do concreto nos painéis tende a ser diferente do comportamento obtido de ensaios à compressão utilizando corpos de prova cilíndricos. Observa-se que a resistência à compressão numa direção é reduzida pela fissuração devido à tração na direção perpendicular. Além disso, apesar de a resistência à tração ser desprezada no dimensionamento de elementos de membrana, o mesmo não pode ser dito em relação aos procedimentos de análise. Dificilmente é possível obter boas respostas de desempenho se a resistência à tração do concreto for deixada de lado no modelo constitutivo.

Dessa maneira, uma das questões mais importantes para o desenvolvimento de um modelo capaz de simular o comportamento do concreto fundamenta-se na escolha adequada das equações constitutivas. O concreto armado apresenta um comportamento extremamente complexo, devido não só aos efeitos relacionados com o concreto (fissuração, abrandamento, intertravamento entre grãos, resistência entre fissuras, etc.), mas também devido à sua interação com as armaduras (aderência, efeito pino, etc.).

Com o desenvolvimento do MCFT, proposto por Vecchio e Collins [12], pode dar-se um grande avanço na análise de estruturas de concreto submetidas a esforços de membrana. A descoberta e a quantificação do efeito de abrandamento das escoras de concreto comprimido em função de tensões transversais de tração possibilitou um avanço significativo no entendimento da resistência de peças de concreto estrutural sujeitas a tensões de cisalhamento (cortante e torçor).

Porém, deve chamar-se à atenção para o facto de que a análise manual de elementos de membrana em concreto armado utilizando o MCFT é bastante maçante e, por isso, requer o auxílio de métodos computacionais para a otimização do problema. Dessa maneira, o presente trabalho procurou apresentar de maneira resumida o desenvolvimento da ferramenta MEDEA RC_MCFT para a análise de elementos de membrana na plataforma MATLAB. A comparação dos resultados numéricos com resultados experimentais disponíveis na literatura apontam para a boa performance da ferramenta e do MCFT.

A despeito dos bons resultados obtidos pelo programa, observa-se que a formulação original do MCFT necessita de alguns ajustes, de maneira a capturar melhor as cargas de fissuração para com concretos de resistência à compressão superiores a 40 MPa, bem como obter melhores cargas de ruína, para concretos de resistência à compressão entre 20 e 40 MPa.

Finalmente, com a disponibilização da ferramenta numérica ora aqui desenvolvida, bem como da divulgação das nuances embutidas no MCFT (ver Anexo 1), acredita-se que o modelo poderá ser utilizado com menos dúvidas por outros engenheiros. Deve-se realçar que há falta na literatura de descrições mais apuradas acerca dos procedimentos de implementação numérica do modelo e, nesse sentido, o presente artigo vem a superar tais dificuldades. Essas características são fundamentais, uma vez que a Associação Brasileira de Normas Técnicas [35] ainda não apresenta mais informações sobre a análise e dimensionamento de elementos de membrana em concreto estrutural.

Agradecimentos

O autor gostaria de expressar o seu profundo agradecimento ao CNPq (Conselho Nacional de Pesquisa) e à Fundação Araucária pelos investimentos financeiros necessários ao desenvolvimento da presente pesquisa.