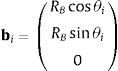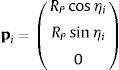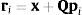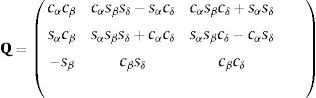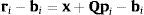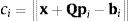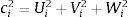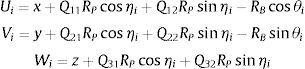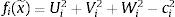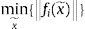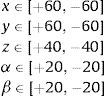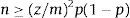El problema de cinemática directa para los robots paralelos se puede enunciar como sigue: dado un conjunto de valores de las variables articulares, se deben encontrar los valores correspondientes en las variables cartesianas, es decir, la posición y orientación del órgano terminal. En muchas ocasiones, el problema de cinemática directa requiere la resolución de un sistema de ecuaciones no-lineales. Los métodos más eficientes para resolver problemas de este tipo suponen convexidad de una función de costo cuyo mínimo es la solución del sistema. La capacidad de tales métodos de optimización para encontrar una solución adecuada depende fuertemente del punto inicial. Un problema bien conocido es la selección de tal punto inicial, el cual requiere información a priori sobre una vecindad convexa donde se encuentra la solución. Este artículo propone un método eficiente para seleccionar y generar el punto inicial basado en aprendizaje probabilístico. El método evita eficientemente los mínimos locales, sin necesidad de intervención humana o información a priori, lo cual lo hace más robusto si se compara con el método Dogleg u otro método de minimización local basado en gradiente. Con el propósito de mostrar el desempeño del método híbrido, se presentan experimentos y su discusión correspondiente. La propuesta se puede extender a otras estructuras con cadenas cinemáticas cerradas, o a la solución en general de sistemas de ecuaciones no-lineales, y por supuesto, para problemas de optimización no-lineales.
The direct kinematics problem for parallel robots can be stated as follows: given values of the joint variables, the corresponding Cartesian variable values, the pose of the end-effector, must be found. Most of the times the direct kinematics problem involves the solution of a system of non-linear equations. The most efficient methods to solve such kind of equations assume convexity in a cost function which minimum is the solution of the non-linear system. In consequence, the capacity of such methods depends on the knowledge about an starting point which neighboring region is convex, hence the method can find the global minimum. This article propose a method based on probabilistic learning about an adequate starting point for the Dogleg method which assumes local convexity of the function. The proposed method efficiently avoids the local minima, without need of human intervention or apriori knowledge, thus it shows a more robust performance than the simple Dogleg method or other gradient based methods. To demonstrate the performance of the proposed hybrid method, numerical experiments and the respective discussion are presented. The proposal can be extended to other structures of closed-kinematics chains, to the general solution of systems of non-linear equations, and to the minimization of non-linear functions.
En años recientes, los robots paralelos se han vuelto una excelente solución para aplicaciones donde se requiere de un posicionamiento preciso. Este tipo de aplicaciones pueden encontrarse en los centros de maquinado, telescopios y simuladores, por citar algunos ejemplos. La cinemática de estas estructuras requiere una solución robusta para aplicaciones exitosas (lo que tiene un papel preponderante cuando se necesita de alta precisión y bajo costo computacional). Para las configuraciones simples, la cinemática de este tipo de estructuras se puede resolver en forma cerrada. Pero en general, las coordenadas generalizadas (posición y orientación) no se pueden expresar en forma analítica como función de las coordenadas articulares [1].
Es conocido que el problema de cinemática directa es más díficil en los robots paralelos, dado que se presenta la multiplicidad de soluciones. Este problema consiste en encontrar los parámetros de posición y orientación del órgano terminal del robot, dando los valores de las variables articulares. Quizá el robot paralelo más conocido es la plataforma Gough-Stewart [2,3]. En particular, el problema de cinemática directa de la plataforma Gough-Stewart general ha sido abordado por muchos investigadores en el pasado. A pesar de ello, debido a la falta de una estrategia efectiva de solución, los esfuerzos en esta dirección continúan. En general han sido utilizadas 4 clases de metodologías: los métodos analíticos, el uso de sensores o transductores adicionales, los métodos numéricos y las redes neuronales. Inicialmente los métodos analíticos se enfocaron en encontrar todas las posibles soluciones del problema de cinemática directa, formulando modelos algebraicos para generar un polinomio. De forma específica los métodos analíticos para resolver la cinemática directa se pueden enunciar de la siguiente forma: (i) se formula un sistema de ecuaciones no lineales y se convierte a un polinomio de orden elevado para después encontrar sus raíces, y así, obtener todas las posibles soluciones [4–7], (ii) se desacoplan los parámetros de posición y orientación, reduciendo la complejidad y acelerando el proceso de solución [8], o (iii) se puede utilizar un enfoque de cuaternion para obtener la solución en forma cerrada para ciertas clases de manipuladores paralelos [9]. Otros métodos analíticos que han sido sugeridos incluyen el método de continuación [10,11], métodos de eliminación [12–15] y análisis de intervalo [5]. Aún no se ha demostrado cómo generalizar estos enfoques analíticos para otras configuraciones de robots paralelos. Adicionalmente y debido al tiempo de cálculo, la mayoría de estas técnicas no son apropiadas para la operación en tiempo real. Por ejemplo, el enfoque de análisis de intervalo requiere al menos 3 o 4 segundos en un sistema de cómputo tipo cluster de 2Ghz, mientras en una computadora simple se requieren de más de 10 segundos. Además, en la actualidad se siguen necesitando esquemas para encontrar una posición y orientación única de entre todas las posibles soluciones al problema de cinemática directa, pues el problema no queda completamente resuelto al encontrar todas las posibles soluciones, sino cuando se da con la solución única que se encuentre dentro del espacio de trabajo de la plataforma.
Por otra parte, también se ha propuesto la instalación de sensores o transductores adicionales sobre el manipulador con el fin de obtener más información sobre el sistema [16]. Sin embargo, el costo adicional de los sensores lo ha hecho poco práctico para resolver el problema de cinemática directa.
Desde otro enfoque, se han propuesto estrategias numéricas para resolver el problema. Pero al utilizarlas de manera aislada no se puede garantizar una solución, y la utilización de altos recursos computacionales restringe su uso práctico. El método iterativo de Newton-Raphson ha sido el método más popular para resolver la cinemática directa de manipuladores paralelos [17–19]. En muchos de los casos, esta estrategia proporciona resultados precisos. Sin embargo, cuando se utiliza el método por sí solo, estos resultados dependen fuertemente de una buena selección de los valores iniciales [20]. Para valores iniciales lejos de la solución final, el método de Newton-Raphson puede tomar un tiempo grande para converger o puede fallar en la convergencia a la solución. En otras propuestas el método de Newton-Raphson se ha modificado y se ha usado en combinacion con un conjunto de ecuaciones no lineales basadas en la expansion en series de Taylor [21]; logrando una convergencia a la solución en menos de 1 ms con una precision de 1e−9 m en movimiento lineal y 1e−9 rad en movimiento angular. Jing-shan et al. [22] propusieron un modelo para la cinemática directa de la plataforma Gough-Stewart empleando coordenadas naturales, lo que provee de un modelo completamente cartesiano solo con términos lineales o constantes, lo que conlleva importantes ventajas para el análisis cinemático y de velocidad aunque los autores no reportan el tiempo de cálculo ni la precisión.
Wang [23] propuso un enfoque numérico que explota una relación lineal entre los pequeños cambios en las variables de las piernas y el pequeño movimiento resultante de la plataforma. Esto ayuda a lograr una solución única de la cinemática directa a través de una serie de pequeños cambios en las variables de las articulaciones. El autor reportó un tiempo de cálculo de 0,4s para 0,01 unidades de error en los parámetros de posición y orientación, lo cual es mayor que los 0,02s obtenidos por Parikh y Lam [24] para los mismos niveles de precisión. En este último trabajo se utilizaron redes neuronales para establecer las condiciones iniciales del método de Newton-Raphson. Otros trabajos que han empleado este enfoque son [25–27] y recientemente Ghasemi et al. [28], para una plataforma Gough-Stewart tipo cable. Sin embargo, las principales desventajas de los métodos basados en redes neuronales son el entrenamiento, prueba y validación. Para cada plataforma específica se demanda una gran cantidad de información sobre el espacio de trabajo.
Refiriéndonos a la robótica en general, los algoritmos evolutivos han comenzado a ser usados para tratar problemas abiertos en esta área. Desde las primeras propuestas [29,30] hasta trabajos recientes, como Zhuang y Huang [31], los algoritmos genéticos han sido usados para generar una trayectoria óptima con experimentos y así tratar el problema de calibración de robots seriales o, como Omran et al. [32], para el control óptimo de manipuladores paralelos. El trabajo presentado por Cabrera et al. [33] aborda el problema de la síntesis de mecanismos usando evolución diferencial para resolver el problema dimensional y multiobjetivo de mecanismos planos. En los últimos 5 años han aparecido reportes donde se utilizan los algoritmos evolutivos tratando el problema de cinemática directa de robots paralelos. Sheng et al. [34] discuten la solución a la cinemática directa de la plataforma Gough-Stewart usando algoritmos genéticos, logrando una precisión promedio de ±0,02 mm y ±0, 02∘. Mientras que Rolland y Chandra [35], reportan un tiempo de cálculo de menos de 1 s para la misma plataforma.
Es claro que no importando cómo se resuelve el problema de cinemática directa, la determinación directa de una solución única continúa siendo un desafío. Se puede identificar una tendencia hacia el uso de algoritmos de optimización y métodos no-lineales. Dado que no hay una relación directa entre las variables a controlar y los grados de libertad, cada variable controlable afecta un grado de libertad y viceversa. Por tanto se involucran funciones no-lineales, entonces no es sorprendente que los métodos de Newton o cuasi-Newton queden atrapados en mínimos locales cuando se intenta resolver el sistema no-lineal.
En este trabajo se presenta un método eficiente para resolver el sistema no-lineal de ecuaciones para el problema de cinemática directa de la plataforma Gough-Stewart general. El método toma ventaja de 2 tipos de optimizadores: un optimizador basado en el método de Dogleg que se usa para encontrar la solución de este sistema de ecuaciones, mientras que un algoritmo de estimación de distribución se ha modelado para seleccionar y generar en forma robusta los puntos iniciales para el sistema usando aprendizaje probabilístico. Se presentan experimentos y su discusión para mostrar el desempeño del método. El método híbrido evita exitosamente quedar atrapado en mínimos locales sin la necesidad de intervención humana, lo cual incrementa la robustez del método cuando se compara con un método simple de Newton.
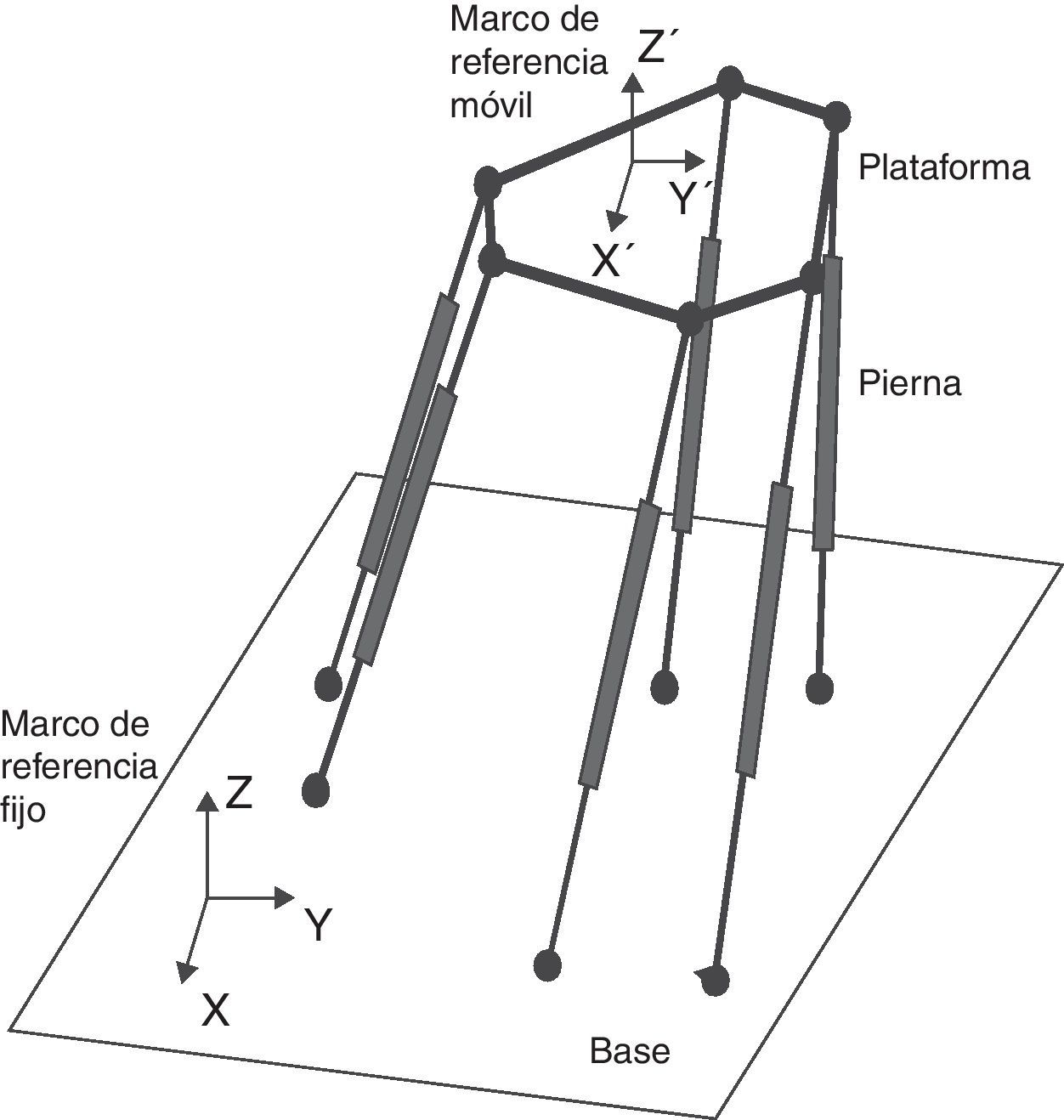
2Formulación del problemaSe seleccionó el manipulador paralelo más conocido como caso de estudio: la plataforma Gough-Stewart, dado que esta estructura puede usarse para aplicaciones donde se requiera alta precisión. En las últimas 2 décadas, muchos aspectos de este manipulador paralelo han sido estudiados y reportados [36–39]. Un modelo cinemático de este manipulador fue formulado por Gosselin [40], y su configuración cinemática consiste de un plato fijo conectado a través de 6 piernas a una plataforma móvil (fig. 1). Cada pierna consta de una articulación prismática (actuador), una articulación esférica fija en su inicio, y una articulación universal en el final móvil. La plataforma fija y la móvil tienen las mismas dimensiones. Con el fin de mejorar la estabilidad del mecanismo, las juntas universales y prismáticas se localizan tan cerca como sea posible.
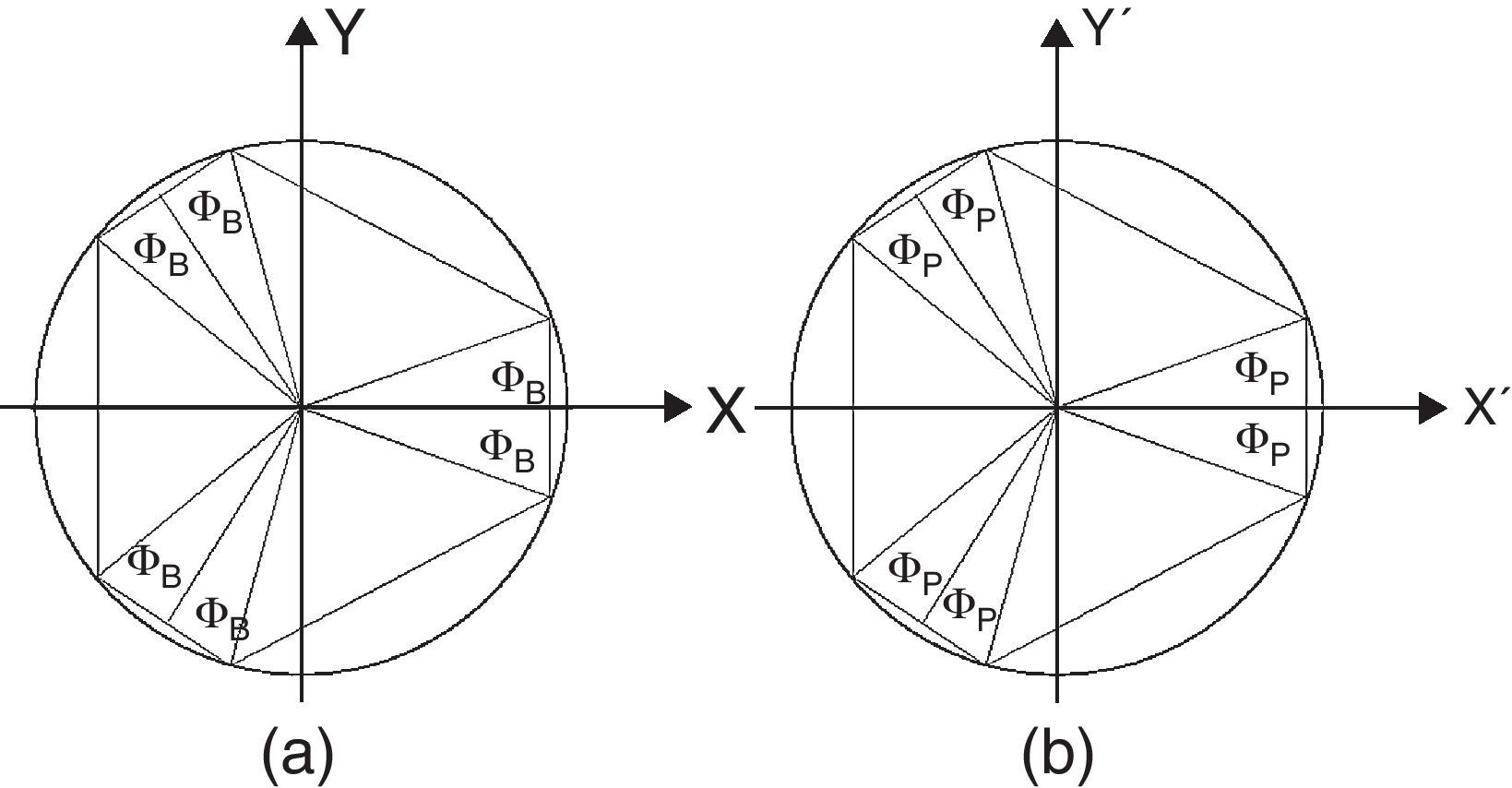
Los puntos centrales de las articulaciones esféricas se localizan en los radios RB, mientras las articulaciones universales se localizan en los radios RP (fig. 2). Bi es el punto central de cada articulación esférica (vértices de un hexágono sobre la plataforma base), y Pi es el punto central de cada articulación universal (vértice de un hexágono sobre la plataforma móvil), figura 2(a) y figura 2(b), respectivamente.
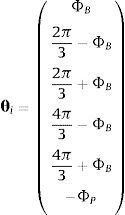
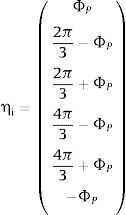
La posición angular entre las articulaciones de conexión es ΦB en la plataforma base, y ΦP en la plataforma móvil. bi puede referirse como el vector de posición de cada punto Bi con respecto al centro de la plataforma base, y pi como el vector de posición de cada punto Pi con respecto a la plataforma móvil. Entonces, se puede escribir:
ydondeyEl vector de posición de la plataforma móvil se define como x (con coordenadas x, y, z), y la orientación se encuentra con la matriz de rotación Q. Así, el vector de posición, con respecto a la plataforma fija de cada articulación universal (en la plataforma móvil), se puede escribir como:
dondeademás α, β, δ representan los ángulos de orientación de la plataforma móvil, y cα=cos(α), cβ=cos(β), cδ=cos(δ), sα=sin(α), sβ=sin(β), sδ=sin(δ).Restando bi en ambos lados de la ecuación (5), se tiene:
La longitud ci de cada pierna se calcula con la norma euclidiana de la ecuación (7) como:
De esta manera, la solución del problema de cinemática inversa se puede escribir como:
dondey Q11, Q12, Q21… son los componentes de la matriz Q.De esta manera, las longitudes individuales de cada pierna se calculan como una función de la posición y orientación de la plataforma móvil. La posición final de la plataforma móvil se puede controlar ajustando ci para un tamaño específico. De la ecuación (10) se puede observar que x, y, z y α, β, δ, las variables posición y orientación, dependen del tamaño de las 6 longitudes, es decir, el problema de cinemática directa consiste en encontrar la posición y orientación dando las 6 longitudes de las piernas. La solución de la cinemática directa es esencial para propósitos de control, simulaciones en línea y análisis de desempeño, tareas primordiales en aplicaciones reales. El problema se reduce a resolver el sistema de ecuaciones no-lineales mostrado en la ecuación (10) para las coordenadas cartesianas; el sistema puede hacerse cuadrado con ecuaciones adicionales usando la matriz de rotación y sus invariantes. Se pueden formular 6 funciones residuales f(x˜)=[f1,…f6] como:
Así, el sistema de 6 ecuaciones con 6 variables de la ecuación (11) puede resolverse dando un vector x˜=[x,y,z,α,β,δ], el cual contiene los valores iniciales para la posición y orientación de la plataforma móvil, y minimizando la función de error siguiente:
donde los elementos de x˜ pueden variar de acuerdo a las siguientes ecuaciones:Es decir, el espacio de trabajo del manipulador se ha definido como un cubo centrado en las coordenadas cartesianas x,y,z=+60,−60,900 donde las unidades son mm. Es necesario especificar que el ángulo de orientación δ ha sido definido con un valor constante de cero grados debido a las restricciones de movimiento de la plataforma.
3Propuesta del optimizador híbridoEl tema principal de esta propuesta es la optimización paramétrica de la cinemática directa de un sistema robótico reduciendo la dependencia a la intervención humana del optimizador. Considerando que si cada una de las partes del sistema está estrechamente relacionada con las demás, los parámetros de minimización del mismo también lo están.
Para resolver el problema se requiere de un optimizador para minimizar la ecuación (12). El optimizador Dogleg [41] es ampliamente conocido por su eficiencia y por ser efectivo. Es un método de minimización/maximización de la familia de los algoritmos de región verdadera, el cual combina la dirección de Cauchy y la de Newton (una dirección basada en el gradiente y otra basada en la información de la segunda derivada, respectivamente). El método Dogleg produce resultados excelentes cuando la función a minimizar es convexa; sin embargo, el método puede quedar atrapado en un mínimo local si no hay convexidad y hay varios mínimos locales. Debido a lo anterior, el método requiere un punto inicial adecuado para converger al mínimo global. De esta manera, si el usuario no tiene información preliminar sobre la posición del mínimo global, no hay certidumbre de encontrarlo. Para tratar con este problema, se propone el uso de un algoritmo de estimación de distribución (EDA, por sus siglas en inglés). Los EDA son algoritmos evolutivos que han mostrado una gran capacidad para la solución de problemas no convexos, que evitan los mínimos locales y no requieren de información de derivadas [42]. La principal función del EDA es aprender y usar las mejores regiones en el espacio de búsqueda para muestrear puntos aleatorios, con el fin de encontrar el óptimo a un bajo costo computacional. Los EDA se derivaron del modelado probabilístico de los algoritmos genéticos (GA, por sus siglas en inglés), y se ha mostrado que son más eficientes que los GA cuando la correlación de las variables es un factor importante para el proceso de optimización. Se espera que el EDA sea capaz de entrenar los parámetros de la distribución para muestrear más intensamente las regiones más prometedoras. Por lo tanto, un EDA que considera las dependencias entre las variables puede ser una estrategia adecuada para tratar este problema.
El optimizador híbrido se construye como sigue: un EDA basado en el modelo gaussiano multivariado, como el EMNAglobal modificado con la distribución empírica de la selección como presentaron Valdez et al. [43], genera los puntos iniciales para el método Dogleg. Para cada punto generado por el EDA se realiza un proceso de minimización local utilizando el Dogleg. De acuerdo con la norma del residuo de la función de costo utilizada por el Dogleg [ecuación (12)] se asigna un valor de aptitud a cada punto generado por el EDA; este valor es utilizado para aprender los parámetros de una distribución gaussiana multivariada, y utilizando esta distribución se generan nuevos puntos y el proceso se repite hasta lograr la precisión deseada en la solución. En cada iteración (generación) la mejor solución encontrada se almacena y al final es devuelta como la aproximación a la solución del sistema. Nuestros experimentos muestran que el optimizador híbrido entrega el óptimo global en el 100 por ciento de los casos. La descripción general del método híbrido se muestra en el algoritmo 3.1. En el paso 4, la evaluación de la función objetivo se refiere a la ejecución del Dogleg, usando cada punto en la población como un punto inicial. Entonces, cuanto menor sea la norma de la ecuación (11), el punto generado por el EDA tiene un mejor valor de función de aptitud. Cuando el Dogleg converge a un punto fuera del espacio de trabajo, la función objetivo toma un valor muy alto (muy malo) de 1, 0e10, para que el EDA aprenda a no generar puntos que convergen fuera del espacio de trabajo. El método de selección en el paso 5 se refiere a la estimación de la distribución empírica de la selección utilizando torneo binario, como ha sido mostrado por Valdez et al. [43]. El paso número 6 involucra la estimación de la media y la matríz de covariancia del modelo gaussiano multivariado usando la distribución empírica de la selección [43]. El modelo de poblacion inicial es una distribución uniforme.
Algorithm 3.1 EDA utilizado para encontrar la solución a la cinemática directa de la plataforma Gough-Stewart
Se llevaron a cabo experimentos para 3.160 puntos en el espacio de búsqueda, generando aleatoriamente (de manera uniforme) una configuración de posición y ángulos x˜={xi,yi,zi,αi,βi,δi}, para después resolver la cinemática inversa y obtener los parámetros de articulaciones, θ˜={θ1,i,θ2,i,θ3,i,θ4,i,θ5,i,θ6,i}. Dado θ˜, se calculó 30 veces la solución a la cinemática directa xˆ por medio del algoritmo 3.1. Si la norma de la diferencia entre la solución conocida y la calculada fue menor de 1e−7, la ejecución se contabilizó como exitosa. Los propósitos de este experimento fueron los siguientes:
- 1.
En primer lugar, mostrar que el algoritmo es capaz de encontrar una solución muy aproximada al óptimo verdadero en todos los experimentos realizados.
- 2.
En segundo lugar, tomando en cuenta que el algoritmo tiene bases aleatorias, es decir, la población inicial es generada de manera aleatoria uniforme y las subsecuentes de manera aleatoria con distribución gaussiana multivariada, mostrar que la solución encontrada por el algoritmo no solo es siempre muy cercana al óptimo real (en una vecindad de radio menor a: 1e−7, cuando la tolerancia física necesaria para cada variable es máximo 1e−6), sino que además la solución encontrada es única en el espacio de trabajo, al menos de acuerdo a rigurosas pruebas estadísticas (miles de ejecuciones para miles de posiciones aleatorias dentro del espacio de trabajo), la solución entregada por el algoritmo es siempre la configuración correcta.
Ambos objetivos se logran mediante la realización de miles de ejecuciones del algoritmo 3.1. Cada ejecución consiste en lo siguiente:
Definición del experimento. En primer lugar se genera una configuración de la estructura, es decir, un conjunto de parámetros x˜; a partir de estos parámetros se encuentran con la cinemática inversa, ecuación (8), los parámetros de las articulaciones, θ˜. Ahora suponemos que no conocemos los parámetros de posición x˜ e intentamos resolver el problema de la cinemática directa a partir de θ˜ con el algoritmo 3.1, dicho algoritmo nos regresa un conjunto de parámetros xˆ={xˆi,yˆi,zˆi,αˆi,βˆi,δˆi}, los cuales, en caso de que la ejecución sea exitosa, deberían ser los mismos o muy aproximados a x˜. Medimos la calidad de la aproximación utilizando la norma: |xˆ−x˜|. El Dogleg tiene una tolerancia de 1e-11 en la norma de la función de coste como criterio de paro. Note que para estos experimentos conocemos la solución exacta ya que partimos de ella; aunque esta solución nunca se usa dentro del proceso de optimización, es utilizada para determinar si el algoritmo funciona adecuadamente como sigue: si la norma es menor que 1e−7, entonces consideramos que la solución se ha encontrado satisfactoriamente.
El proceso del algoritmo 3.1 se repite para el mismo conjunto de parámetros x˜={xi,yi,zi,αi,βi,δi} 30 veces, con el fin de obtener evidencia estadística de que bajo diferentes inicializaciones aleatorias del EDA, la solución encontrada es la misma o muy similar.
Finalmente, se genera otro punto aleatorio, y el proceso se repite 3.160 veces, es decir para i=1…3.160, con el fin de obtener evidencia estadística de que el algoritmo es exitoso al encontrar las configuraciones correctas dentro de todo el espacio de trabajo. Esto quiere decir que aunque el algoritmo se probó con 3.160 puntos distribuidos de manera aleatoria uniforme dentro del espacio de trabajo, el número de ejecuciones totales fue de 3.160×30=94.800, ya que la solución para cada punto se aproximó 30 veces con 30 inicializaciones aleatorias diferentes. Los parámetros de ejecución fueron: 150 generaciones del EDA y un tamaño de población de 100.
Estos parámetros tienen como fin: 1) en el caso del EDA, que sean los de coste computacional mínimo suficientes para que el EDA converja a una solución adecuada; 2) en el caso del número de ejecuciones, que sea un número «suficientemente grande»para proveer evidencia estadística del desempeño del algoritmo. Y fueron determinados 1) empíricamente a través de ejecuciones del algoritmo en el caso del EDA y 2) por medio de la ecuación 14 para el tamaño de muestra, de forma tal que superan el mínimo sugerido para que la evidencia estadística sea significativa [44]. Aplicando la ecuación (14), la muestra adecuada para una prueba de proporciones con 95% de confianza, margen de error de 2, 5% y considerando el peor de los casos (muestra más grande) P=0, 5, el número de puntos sugeridos es de por lo menos 1.537. En este trabajo se usaron 3.160, que es más del doble y por lo tanto provee de mayor confianza y/o menor margen de error. De la misma forma, para calcular el número de ejecuciones para probar la proporción de ejecuciones exitosas de cada punto, y considerando la proporción conocida de ejecuciones existosas de P=0, 9991878, el número de ejecuciones por cada punto debería ser mayor o igual a 5; sin embargo se utilizaron 30, para cumplir con el criterio conservador de usar un número «suficientemente grande», que se considera como mayor a 30 generalmente.
Resultados. Los resultados son satisfactorios. De las 94.800 ejecuciones llevadas a cabo, 94.723 llegaron a la solución correcta. La media de la norma del error, |xˆ−x˜|, para estas ejecuciones fue de 2,576223e−13, la desviación estándar 2,060745e−13, el error máximo 2,603198e−12 y el mínimo 1,24127e−16. Como se puede ver, todos superan con creces el máximo error permitido que es de 1e−7. De 77 casos en que el algoritmo no alcanzó la solución con la precisión deseada nunca fue para el mismo punto, es decir, ya que se resolvió 30 veces la cinemática directa para cada uno de los 3.160 puntos distribuidos uniformemente en el espacio de trabajo, en 77 ocasiones 1 de las 30 ejecuciones del algoritmo no encontró la solución con la precisión deseada, sin embargo para ese mismo punto, las otras 29 ejecuciones sí encontraron la solución con la precisión deseada. En las 77 veces de las 94.800 que no se llegó a la precisión deseada se podía saber que no se había llegado debido a la norma del error en la función, es decir, el algoritmo nunca indica un falso positivo (que indique que se ha encontrado la solución cuando no es cierto y viceversa). El número de evaluaciones del EDA, que es el número de veces que se utilizó un optimizador local, fue en promedio 3.635,627 con desviación estándar de 6.155,476.
Dada la naturaleza estocástica de una parte de la propuesta, se realizó un análisis del coste/tiempo computacional a través de 300 ejecuciones independientes del programa, tanto en serie como en paralelo, con el fin de obtener un intervalo de tiempo suficientemente grande. Las mediciones se repitieron 50 veces para tener un estadístico de la media del tiempo de ejecución y la media y varianza del tiempo de estas ejecuciones. El código fue programado en C y paralelizado con openMP; solo se paralelizó la evaluación de los puntos generados por el EDA, es decir, varias instancias del Dogleg se ejecutan en paralelo. Todos los experimentos se ejecutaron en el SO Linux Open Suse versión 12.1, con el compilador GCC versión 4.6.2, en un procesador intel(R) Core(TM) i7-2600 CPU @3.40 GHz con 4 cores y capaz de levantar 8 hilos (Threads) de forma nativa, con 16.378.164 Bytes (16 GB) de memoria RAM.
Los tiempos de 300 ejecuciones, repetidas 50 veces proporcionaron los resultados que se muestran en la tabla 1. Como se puede observar, los resultados son satisfactorios, y las cuantiosas ejecuciones aportan evidencia estadística de que el algoritmo puede ser utilizado para la solución de la cinemática directa in situ. En particular, se puede resaltar que con una paralización únicamente de la parte de evaluación y con solo 4 cores, se logró una reducción del 67,11% del tiempo con respecto a la ejecución en serie. Actualmente existen equipos especializados para aplicaciones demandantes de computo numérico o tarjetas gráficas (GPU), especializadas también en cómputo de alto desempeño, lo que indica que se pueden lograr reducciones de tiempo mucho mayores.
5ConclusionesEste artículo propone un método híbrido para resolver problemas de optimización global no-convexos. El método se aplica a la resolución de un sistema de ecuaciones no-lineales derivado del problema de la cinemática directa de la plataforma Gough-Stewart general. Se desarrollaron un conjunto de experimentos para validar la propuesta. Obtuvimos evidencia estadística para afirmar que el enfoque toma ventaja de la información obtenida de varias minimizaciones locales para encontrar un punto inicial adecuado para el algoritmo de Dogleg, con el fin de encontrar el óptimo global, es decir, encontrar la solución del sistema de ecuaciones no-lineales.
Los experimentos llevados a cabo muestran que el algoritmo encuentra la solución adecuada en el 100 por ciento de los puntos generados uniformemente en el espacio de trabajo. Adicionalmente, se comprobó a través de experimentos numéricos que la solución que se encuentra es única dentro del espacio de trabajo. Este último punto, aunque no tiene el rigor de una demostración matemática, sí es un argumento fuerte para decir que no se espera encontrar multiplicidad de soluciones del sistema de ecuaciones dentro del espacio de trabajo. Lo anterior, claramente, es importante para el problema físico del cual se deriva el sistema de ecuaciones, ya que evidencia que para un conjunto de parámetros de articulaciones, existe un único conjunto de parámetros de posición y ángulos de la plataforma. Las soluciones encontradas además tienen una precisión excelente para los requirimientos físicos. Los resultados obtenidos muestran que es posible obtener altas precisiones; en consecuencia, el algoritmo propuesto no solo sirve para resolver la cinemática directa/inversa de mecanismos paralelos y no paralelos en general, sino que además podría ser utilizado para realizar aproximaciones alta precisión, buscando obtener errores aún menores. Estas aproximaciones alta precisión pueden tener aplicación directa en la caracterización y análisis los errores de mecanismos de alta precisión.
Finalmente, por medio de un análisis de coste/tiempo computacional se verificó que el algoritmo es altamente paralelizable. Ya que las evaluaciones de los diferentes puntos de la población del EDA son independientes, estas pueden ser llevadas a cabo por diferentes unidades de procesamiento, por lo cual el tiempo de ejecución se puede mejorar aún más haciendo uso de recursos de cómputo como computadoras multicore o GPU, lo que hace factible su implementación en sistemas del mundo real (para tiempo real), ya que el costo computacional del algoritmo paralelizado dependerá principalmente del costo del Dogleg (o algún optimizador local) más que del EDA, puesto que la parte de este último puede ser paralelizada con recursos de cómputo suficientes para alcanzar el tiempo de aproximación deseado.
En conclusión, la propuesta reduce al mínimo la intervención humana debido a que esta no se requiere para resolver el problema de cinemática directa. Adicionalmente, encuentra aproximaciones de alta precisión a la cinemática directa, no requiere información a priori, utiliza un algoritmo poblacional que es capaz de aprender correlaciones entre variables, debido al modelo gaussiano multivariado del EDA. Estas ventajas lo hacen altamente efectivo y eficiente, y pueden ser explotadas en su aplicación en otros mecanismos paralelos.