Las estructuras de forjados reticulares sobre pilares aislados han sido ampliamente utilizadas en el sur de Europa para edificios de viviendas y oficinas entre los años setenta y noventa del siglo pasado. Estas estructuras, proyectadas y construidas con códigos actualmente obsoletos, podrían tener un comportamiento deficiente en caso de terremoto y es necesario evaluar su vulnerabilidad y la necesidad de ser reacondicionadas sísmicamente. Este artículo propone un modelo sencillo de transmisión de esfuerzos en uniones existentes entre forjado reticular y soporte exterior, solicitadas en la dirección normal al plano de fachada. La propuesta tiene en cuenta particularidades de estos forjados tales como la concentración de armaduras orientadas con los nervios y la presencia sistemática de crucetas de punzonamiento. El modelo global consiste en elementos tipo barra para los soportes y tipo placa para el forjado, con uniones entre ambos mediante rótulas a flexión y a torsión. La resistencia de las rótulas a flexión se determina a partir de la estimación de la porción de armadura longitudinal del forjado que transmite directamente momentos al pilar por flexión. La deformación de plastificación de las rótulas se estima con expresiones simples. Como ductilidad de las rótulas a flexión se adopta el valor propuesto por la norma FEMA 356, mientras que para las rótulas a torsión se adopta ductilidad infinita, lo cual es consistente con resultados experimentales previos. Se muestra que la respuesta frente a desplazamientos laterales impuestos monótonamente crecientes obtenida con el modelo propuesto se ajusta adecuadamente a resultados experimentales obtenidos en estudios anteriores, en cuanto a rigidez, resistencia y ductilidad.
Waffle-flat-plate structures have been widely used for residential and office buildings in the South of Europe between the seventies and nineties of the last century. These buildings were designed with old seismic codes and its vulnerability needs to be evaluated to determine whether they need to be seismic retrofitted or not. This article proposes a simple model that represents the moment transfer between plate and column, for existing exterior connections loaded in the direction normal to the building façade. The model takes into account singularities of existing waffle-flat-plate structures such as the concentration of reinforcement in the direction of the joints, and the existence of punching shear reinforcement. The model consists of frame elements for the columns and shell elements for the slabs, both connected with flexural and torsion hinges. The strength of the flexural hinges is obtained by estimating the portion of longitudinal reinforcement of the plate that transfers directly the unbalanced moment to the column by flexure. The yielding deformations of the flexural and torsion hinges are estimated with simple expressions. The ductility of the flexural hinges is taken from FEMA 356, while infinite ductility is adopted for the torsional hinges in accordance with previous experimental studies. It is shown that the proposed model provides a good approximation of the experimental response of the connection under monotonically increasing lateral displacements, in terms of stiffness, strength and ductility.
Las estructuras con forjados bidireccionales planos (de canto constante) sobre pilares aislados han sido recurrentemente utilizadas en la construcción de edificios para viviendas y oficinas, ya que ofrecen un buen aprovechamiento de los espacios, permiten una distribución flexible en planta de los soportes y economizan en materiales y en proceso constructivo. Sin embargo, muchas de estas estructuras han sido proyectadas y construidas con códigos sísmicos obsoletos y se han demostrado significativamente vulnerables frente a terremotos severos [1,2]. Su vulnerabilidad se debe principalmente a la ausencia de detalles de armado que les confiera ductilidad, a la falta de continuidad y bajas cuantías en las armaduras inferiores en la zona de entrega a los pilares, a la formación de rótulas plásticas en pilares, y a su elevada flexibilidad lateral que amplifica los efectos de segundo orden.
La existencia de estructuras ampliamente utilizadas que son vulnerables al sismo justifica el desarrollo de modelos de predicción de su comportamiento. El estudio de los forjados bidireccionales ante las acciones sísmicas se ha centrado fundamentalmente en forjados de losa maciza [1–8], y son escasos los estudios de forjados reticulares sobre soportes aislados [9–11]. Fundamentalmente se ha estudiado: a)la definición de un ancho efectivo de transmisión directa del momento flector al pilar; b)el análisis a punzonamiento debido a la combinación del cortante gravitatorio y la transmisión de momento por cortante excéntrico, y c)la modelización de estructuras completas frente a acciones laterales.
Los modelos de predicción de la capacidad de transmisión de esfuerzos de forjado a pilar que ofrece la ACI-318 [12] son aplicables a los forjados bidireccionales en general. La transmisión de flectores desde el forjado al pilar se basa en 2 mecanismos: uno directo y otro a través de cortantes. La ACI-318 adopta un ancho eficaz geométrico para el momento flector transmitido por flexión directa, C2+3h (siendo C2 la dimensión del pilar en la dirección perpendicular al plano de carga y h el canto de la losa) que resulta razonable en el caso de una distribución de armadura relativamente uniforme y similar en ambas direcciones. Este es el caso habitual de las losas macizas, pero no el de los forjados reticulares tradicionales. En los forjados reticulares la armadura superior (a excepción de la malla electro-soldada de reparto) e inferior no se distribuye uniformemente sino que se coloca en los nervios y alineada con estos en el entorno del pilar. La distancia entre los nervios suele ser del orden de la mitad del ancho eficaz. Ello puede conducir a que, por cuestión de pocos centímetros, el ancho eficaz en el que se supone que el momento flector se transmite del forjado al pilar por flexión directa cuente con uno o con 3 nervios.
La presencia de crucetas de punzonamiento en esta tipología estructural condiciona de forma importante la capacidad y el modo de fallo de una unión forjado reticular-pilar, especialmente en uniones exteriores [1]. Estudios previos han puesto de manifiesto que el punzonamiento bajo acciones sísmicas está altamente correlacionado con el nivel de cortante gravitatorio. Con un cociente de cortante gravitatorio, definido como el cociente entre el cortante gravitatorio y la resistencia a cortante por punzonamiento, por debajo de 0,2 y sin necesidad de armadura de punzonamiento se pueden alcanzar desplazamientos laterales entreplantas superiores al 4% [1,2,4,6]. Los forjados reticulares disponen de menor esbeltez y menor peso propio que las losas macizas, y por tanto un menor cociente de cortante gravitatorio.
La respuesta sísmica de edificios con forjados bidireccionales sobre pilares se ha obtenido habitualmente a partir de modelos de pórticos virtuales planos de barras. Estos modelos adoptan una barra (viga) virtual de un ancho eficaz que se ajusta para reproducir adecuadamente la rigidez de la losa o del forjado reticular. La modelización con elementos barra permite concentrar fácilmente las no-linealidades en rótulas plásticas situadas en los extremos de las mismas. En la literatura hay numerosas expresiones propuestas para determinar anchos efectivos basadas en análisis numéricos 3D, con elementos tipo placa, y en ensayos. Con estos modelos numéricos y con ensayos se ha valorado también la sensibilidad del ancho efectivo ante factores geométricos diversos [13]. No existe un modelo único para estimar el ancho efectivo [7,9,13], fundamentalmente debido a las numerosas variantes constructivas que se emplean para construir los forjados bidireccionales planos y a la influencia que tiene el nivel de fisuración del hormigón en la flexibilidad lateral, la cual depende claramente del nivel de deformación lateral [7,8,14].
Las formas de modelizar uniones entre losas bidireccionales y soportes de hormigón armado se pueden ordenar por orden de complejidad y de requerimientos de tiempo computacional. En un extremo estarían los modelos numéricos con elementos volumétricos (3D) con armaduras embebidas siguiendo los detalles de armado de la unión y relaciones constitutivas avanzadas del acero, del hormigón y de su interacción [15]. En un nivel próximo estarían los modelos basados en teorías avanzadas de la mecánica no-lineal del hormigón armado [16], que emplean elementos tipo fibra para los pilares y elementos bidimensionales (2D) tipo capa para el forjado [17]. En un nivel inmediatamente inferior se situarían los modelos que emplean elementos tipo viga y elementos especiales que representan la penetración/deslizamiento de las armaduras en la unión [18,19].
El análisis riguroso a partir de elementos finitos no lineales, 3D o 2D, de estructuras de hormigón armado sometidas a sismo, aun siendo perfectamente viable, puede resultar complejo y tener un elevado coste computacional cuando se trata de modelizar estructuras completas y realizar cálculos dinámicos en régimen no lineal. Tal como se indica al final del apartado 7, los autores emplearon este tipo de modelización para la unión objeto de estudio utilizando elementos no lineales tipo fibra para los pilares y tipo capa (bidimensionales) para el forjado, y constataron las limitaciones aludidas. Para modelizar estructuras completas y realizar cálculos dinámicos en régimen no lineal utilizables en el proyecto de estructuras de nueva planta y en la evaluación de la vulnerabilidad de estructuras existentes puede resultar beneficioso recurrir a modelos numéricos más sencillos, eficientes y fácilmente aplicables en los programas informáticos frecuentemente empleados en cálculo de estructuras.
Este trabajo propone una modelización numérica relativamente simple para predecir el comportamiento de uniones exteriores forjado reticular-pilar que permite ser aplicada a modelos tridimensionales para estudiar la respuesta en régimen no lineal. El modelo idealiza el forjado como elementos tipo placa, los soportes como elementos tipo barra y representa las no linealidades de los materiales mediante rótulas de flexión y de torsión que conectan el forjado reticular a los soportes. Las rótulas consideran, de forma simplificada, la interacción de los mecanismos de transmisión del momento flector por torsión de la viga de borde y por transmisión directa al soporte. Esta simplificación se justifica por el buen ajuste que se consigue entre datos numéricos y ensayos experimentales. Esta interacción, según constata Farhey [20], se produce cuando la transferencia de flexión directa se extiende más allá del ancho del pilar a los laterales de la losa, y es posible si existe armadura longitudinal en ambas direcciones en esta zona de forma que se puedan formar mecanismos de transferencia tipo biela-tirante [11]. Los modelos numéricos sencillos como el que se propone en esta investigación pueden ser fácilmente implementados en modelos globales y resultan por ello necesarios cuando se trata de estudiar la respuesta no lineal de estructuras de edificios de varias plantas y varios vanos, sometidas a cargas dinámicas de origen sísmico mediante cálculos dinámicos directos o análisis estáticos (método del empuje incremental).
2MetodologíaEn este trabajo se propone un modelo numérico sencillo que permite predecir la respuesta no lineal hasta la rotura de uniones entre forjados reticulares y soportes exteriores sometidos a cargas laterales. El modelo numérico se apoya en resultados experimentales. En los apartados siguientes se describen los pasos y la metodología seguida para desarrollar el modelo. En el apartado 3 se propone un criterio para determinar las barras de armadura longitudinal del forjado que transmiten el momento al pilar por flexión directa, y las barras que emplean un mecanismo de transmisión indirecto basado en la torsión. Determinadas las barras del forjado que emplean cada uno de los 2 mecanismos citados (flexión directa y torsión), se calcula el valor experimental del momento M transmitido por el forjado al pilar a través de cada uno de los 2 mecanismos, a partir de los alargamientos unitarios medidos en las barras en diferentes puntos del ensayo. Para cada valor de M obtenido se calcula la rotación θ correspondiente del forjado de datos experimentales. Representando los puntos (M,θ) en unos ejes cartesianos se obtienen los diagramas momento-rotación en la rótula plástica de flexión y en la de torsión que proporcionan los ensayos. En los apartados 4, 5 y 6 se propone un modelo numérico sencillo y fórmulas para predecir los diagramas momento-rotación anteriores. En el apartado 4 se desarrolla la predicción de la resistencia y del giro de plastificación de la rótula plástica de flexión, y en el apartado 5, de la de torsión. En el apartado 6 se proponen valores de ductilidad para ambos tipos de rótulas acordes con los datos experimentales. Finalmente, en el apartado 7 se implementan los modelos propuestos para las rótulas de flexión y de torsión en un modelo 3D de la unión forjado reticular-pilar, y con él se predice numéricamente la envolvente de los ciclos carga-desplazamiento lateral y se compara con los resultados experimentales. En este mismo apartado se argumenta también cómo puede extenderse el modelo propuesto.
3Diagramas momento-rotación en las rótulas plásticas obtenidos de los datos experimentalesLa figura 1 muestra el modelo a escala 3/5 de una unión exterior forjado reticular-pilar correspondiente a un edificio construido según normativa y prácticas constructivas empleadas entre los años setenta y noventa en España. El modelo se ensayó bajo ciclos impuestos de desplazamiento con amplitud creciente hasta el agotamiento. La definición completa del modelo, sus características geométricas y de armado, las propiedades de sus materiales y su comportamiento histerético se han publicado con anterioridad [11]. La resistencia del hormigón fc y de las armaduras fy eran 19,4MPa y 405MPa, respectivamente. La figura 2 muestra el armado de la unión.
A efectos de determinar la capacidad a flexión de la unión, se puede suponer [11] que el momento flector se transmite del forjado reticular al pilar mediante 2 mecanismos distintos. El primero es un mecanismo de flexión directa en el que se moviliza la armadura longitudinal del forjado que está anclada directamente en el ancho del pilar, más la armadura longitudinal próxima al pilar que es capaz de transmitir esfuerzos a través de un mecanismo de biela-tirante. Los mecanismos biela-tirante han sido empleados en investigaciones experimentales anteriores [19] sobre vigas planas con elevada relación ancho/canto (=24) para determinar el ancho de viga que es capaz de transmitir momentos directamente por flexión al pilar. El segundo es un mecanismo de torsión, por el cual la armadura longitudinal del forjado más alejada del pilar y anclada en la viga de borde del forjado reticular transmite esfuerzos al pilar a través de un mecanismo de torsión en dicha viga de borde. El momento flector máximo que el forjado reticular puede transmitir al pilar mediante el segundo mecanismo está limitado por la resistencia a torsión de la viga de borde.
La figura 3a ilustra el armado longitudinal superior del ábaco y las fuerzas que ejercen las armaduras en ambas direcciones principales. Cuando se trata de uniones de borde, basadas en un mecanismo de bielas y tirantes, las resultantes en ambas direcciones deben equilibrarse con una biela de compresión, que se ha supuesto que pasa por el centro O’ de la armadura de esquina del soporte, en la intersección de los ejes X’-Y’. Si se plantea el equilibrio de momentos respecto este punto, se obtiene la siguiente ecuación:
donde As1,i es el área de una barra genérica i en la dirección 1, y As2,j es el área de una barra genérica j en la dirección 2; xi e yj son las distancias de estas armaduras desde el punto O’ medidas según los ejes X’ e Y’, respectivamente. Se han adoptado como direcciones 1 y 2 las direcciones del plano de carga y normal al plano de carga, tal como hace la norma ACI-318 [12]. El segundo miembro de la ecuación (1) representa el momento en el punto O’ que pueden soportar las m barras dispuestas en la dirección 2 desde el punto O’ hasta la cara exterior de la viga de borde. En esta armadura no se incluye la correspondiente a la cruceta de punzonamiento, cuya capacidad se reserva para el mecanismo de transmisión por torsión. El primer miembro de la ecuación (1) representa el momento de las «n» barras situadas entre la cara del pilar y la prolongación del nervio en la dirección 1 más cercano a dicha cara del pilar. Al área de la armadura situada en la prolongación de dicho nervio se la ha denominado As1,n, y se ha supuesto que solo una parte, determinada por una constante k1, de la capacidad de dicha armadura es capaz de transmitir momentos al pilar mediante un mecanismo directo de flexión. La constante k1 tiene un valor comprendido entre 0 y 1. La armadura paralela a la dirección 1 situada más allá de la prolongación del nervio más cercano a la cara del pilar se supone que no es capaz de transmitir momentos al pilar mediante un mecanismo directo de flexión. Estas barras transmiten momento del forjado al pilar indirectamente a través de torsiones en las vigas de borde del forjado. Las barras cuya área se designa con As1,1, As1,2 hasta As1,n-1 corresponden a la malla electro-soldada de la armadura de reparto que se coloca normalmente en la cara superior del forjado. El sumando del segundo miembro de la ecuación (1) se extiende hasta las m barras paralelas a la dirección 2 que existen entre el punto O’ y el borde del forjado.Para la armadura inferior, situada en la cara lateral del pilar, mediante un razonamiento similar, y a partir de la figura 3b, se obtiene:
En la expresión anterior A′s1 es el área de la armadura inferior en la dirección 1 situada en la prolongación del nervio más próximo a la cara del pilar y k2 es la parte de su capacidad que es capaz de transmitir momentos al pilar mediante un mecanismo directo de flexión. k2 varía también entre 0 y 1. A′s2 es el área de la armadura inferior en la dirección 2 que pasa por el eje del pilar; dj es la distancia entre nervios del forjado reticular y e es la distancia medida según el eje X’ entre el centro del pilar y la prolongación del nervio más cercano del forjado reticular. C1 es la dimensión del pilar en la dirección 1. La biela de compresión tiene una inclinación β con el eje X’ de valor:
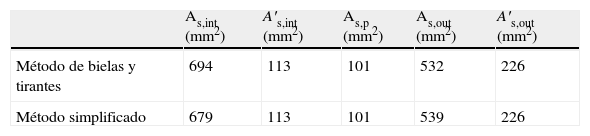
En las ecuaciones (2) y (3) el valor 0,4C1 del numerador del segundo miembro es la distancia desde el centro del soporte a la armadura de esquina medida según el eje Y’, estimada considerando un recubrimiento del 10% de la dimensión del pilar. Aplicando la ecuación (1) al modelo ensayado se obtiene que el área de armadura superior que transmite directamente momentos al pilar vale 694mm2. El valor de la constante k1 que satisface la ecuación en cuestión es de 0,319, lo cual corresponde a una inclinación de la biela comprimida de hormigón del mecanismo biela-tirante muy próxima al valor límite (26,5o) que permite la norma ACI-318 [12].
Para determinar la armadura longitudinal inferior que transmite directamente flexiones al pilar se han considerado las ecuaciones (2) y (3). En el caso de un pilar de sección cuadrada, cuando la armadura longitudinal inferior (en la dirección Y’) que da continuidad a la de los nervios pasa por el eje del pilar (es decir, cuando la prolongación del nervio más próximo al pilar en la dirección Y’ pasa por el centro del mismo y por lo tanto e=0), considerando que β debe ser mayor o igual a 26,5o (ángulo mínimo entre una biela y un tirante que acepta la ACI-318 [12]), se deduce que el cociente dj/C2 debe ser inferior a 1,2, para que la armadura longitudinal inferior situada fuera del ancho del pilar y a ambos lados del mismo pueda transmitir momentos a este directamente por flexión a través del mecanismo de bielas y tirantes. Por el contrario, cuando la armadura longitudinal inferior (en la dirección Y’) que da continuidad a la de los 2 nervios más próximos al pilar es equidistante con el centro del mismo (es decir, cuando e adopta su valor máximo e=dj/2), el cociente dj/C2 se reduce a 0,6. En ambos casos, la armadura longitudinal inferior (según el eje Y’) situada fuera del ancho del pilar y a ambos lados de este que es capaz de transmitir momentos al pilar directamente por flexión a través del mecanismo de bielas y tirantes está afectada por el coeficiente k2, según indica la ecuación (2). Para el modelo ensayado e=0 y el cociente dj/C2 vale 420/240=1,75, y por lo tanto la armadura longitudinal inferior (según el eje Y’) situada fuera del ancho del pilar y a ambos lados del mismo no es capaz de transmitir momentos al pilar directamente por flexión a través del mecanismo de bielas y tirantes. En otras palabras, solo se puede contabilizar como armadura inferior que transmite momentos por flexión directa al pilar la armadura anclada dentro del ancho del mismo.
La primera fila de la tabla 1 («mecanismo de bielas y tirantes») muestra, para el modelo ensayado, el área de armaduras en cara superior, As,int, y en cara inferior, A′s,int, que transmiten momentos por flexión directa al pilar, así como el área de las armaduras que transmiten momentos del forjado al pilar indirectamente a través de torsión en las vigas de borde As,out y A′s,out (para la cara superior e inferior, respectivamente). La segunda fila de la tabla 1 («método simplificado») muestra las áreas estimadas con un método simplificado que se expone en el apartado siguiente. En la tabla también aparece la sección de acero de las barras longitudinales superiores e inferiores de la cruceta de punzonamiento, As,p.
Conocida el área de armadura que transmite momentos flectores del forjado al pilar por flexión directa, y la que transmite momentos indirectamente por un mecanismo de torsión, y conocidas las tensiones en dichas armaduras de datos experimentales se pueden calcular primero los valores de los esfuerzos normales en las barras y después la resultante del momento flector transmitido a través de cada mecanismo. Para el modelo ensayado, las tensiones de las barras se han obtenido a partir de los alargamientos unitarios medidos con los transductores de alargamiento durante el ensayo, adoptando una relación tensión-deformación bilineal sin endurecimiento. Se ha adoptado la hipótesis usual de que la deformación de las secciones es plana, tal como se ilustra en la figura 4. El punto de aplicación de la resultante del bloque de compresiones del hormigón se determina a partir de la consideración de un diagrama de tensiones rectangular (figura 4). La figura 4 muestra una sección transversal con la armadura de acero superior e inferior, As y A′s, respectivamente, así como la armadura longitudinal superior e inferior correspondiente a las crucetas de punzonamiento As,p y A′s.p. Muestra también el diagrama de deformaciones unitarias ¿, correspondientes a la hipótesis de deformación plana, el diagrama de distribución de tensiones y finalmente el diagrama con las fuerzas resultantes de las armaduras a tracción Ns y del bloque de compresiones del hormigón Nc. En flexión positiva los datos experimentales indican que la distancia vertical entre el punto por donde pasa la resultante del diagrama rectangular de compresiones del hormigón y la armadura comprimida es significativamente reducida (oscila entre 4 y 8mm), por lo cual se opta por simplificar el cálculo y despreciar la aportación de la armadura de compresión. En flexión negativa se desprecia también la armadura de compresión por tener un área reducida. Así, el momento resultante experimental M, tanto en flexión positiva como negativa, se obtiene con la siguiente expresión:
donde Ns es la resultante de la armadura longitudinal superior formada por la armadura de los nervios y la armadura de reparto, Ns,p es la fuerza resultante de la armadura longitudinal de las crucetas de punzonamiento, y z y zp son los brazos mecánicos de la armadura longitudinal superior y la armadura longitudinal de punzonamiento, respectivamente.La figura 5 muestra, con pequeños rombos, los puntos del diagrama momento flector-giro de la rótula plástica correspondiente a la armadura superior As,int e inferiorA′s,int que transmiten momentos del forjado al pilar directamente a través de un mecanismo de flexión. Estos puntos se han obtenido a partir de los momentos calculados por el procedimiento anterior y del giro relativo entre forjado y soporte medido con transductores de giro dispuestos durante los experimentos, y cuya posición se indica con las letras I4 e I5 en la figura 1b. La figura 6 muestra con pequeños rombos los puntos del diagrama momento torsor-rotación de la rótula plástica correspondiente a las armadura superior As,out e inferior A′s,out que transmiten momentos flectores del forjado al pilar indirectamente a través de un mecanismo de torsión en las vigas de borde del forjado. Los puntos se han obtenido a partir del momento estimado con la información de los transductores de alargamiento y los giros relativos medidos con los transductores de giro I4 e I1 en la figura 1b. Se aprecia en la figura 6 cómo en torsión negativa (cuando la armadura superior del forjado que acomete a la viga de borde se encuentra en tracción) la capacidad es un 70% inferior al valor en torsión positiva (cuando la armadura inferior del forjado que acomete a la viga de borde se encuentra en tracción), y que además la rótula es más flexible. Esta constatación experimental resulta coherente con los cálculos efectuados mediante el mecanismo de biela-tirante para determinar la armadura superior e inferior, no anclada directamente en el ancho del pilar, que transmitía momentos directamente por flexión. A partir de estos cálculos y en relación a la armadura longitudinal inferior, se determinaba que solo transmitía momentos directamente por flexión aquella anclada dentro del ancho del pilar, ya que no era posible la formación de un mecanismo de bielas y tirantes que permitiera participar a las armaduras longitudinales inferiores situadas fuera del ancho del pilar y a ambos lados del mismo. El que no se pueda formar dicho mecanismo de bielas y tirantes en la cara inferior del forjado imposibilita la interacción entre los mecanismos de biela tirante y el mecanismo de torsión cuando el momento torsor es positivo. Al no darse esta interacción, la capacidad a torsión positiva es mayor que a torsión negativa.
4Predicción de la resistencia y giro de plastificación de la rótula de flexiónEn este apartado se proponen una serie de simplificaciones para calcular de forma sencilla el ancho de la porción de forjado reticular que transmite momentos del forjado al pilar directamente por flexión, en una unión exterior. Para ello se plantean las siguientes simplificaciones: a)la distribución del armado y las cuantías mecánicas en las direcciones 1 y 2 son iguales; b)la totalidad de la armadura inferior está alineada con los nervios (lo cual es aceptable, ya que en la cara inferior del forjado reticular no suele ponerse malla electro-soldada de reparto). De la primera condición se determina que las bielas de compresión en flexión negativa forman un ángulo aproximadamente de 45°. Llamando dc al canto útil del pilar, y a la vista de la figura 7, se puede considerar que, a flexión negativa, el área de armadura superior que transmite momentos directamente por flexión está situada en un ancho de valor C2+2dc. A partir del producto de la cuantía lineal de armadura superior por el ancho C2+2dc, se obtiene el área de armadura superior As,int. En relación a la armadura inferior As’,int que se encuentra alineada con los nervios, su sección se puede estimar como suma de la armadura que atraviesa el soporte y la proporcionada por la ecuación (2) con la condición de β≥26,5°. La segunda fila de la tabla 1 muestra los resultados obtenidos con las simplificaciones anteriores, y se observa que proporciona cuantías próximas a las obtenidas directamente por el método de las bielas y tirantes.
La capacidad última de la porción de forjado que transmite momento directamente por flexión se ha calculado considerando la totalidad de la armadura longitudinal, incluida la de punzonamiento, comprendida en el ancho C2+2dc, y adoptando un diagrama rectangular de tensiones para el hormigón comprimido (fig. 4). En flexión positiva se ha adoptado un ancho de hormigón comprimido de bc=C2+2dc, mientras que en flexión negativa el ancho del bloque de hormigón comprimido adoptado ha sido de bc=1,25C2. Como canto útil se ha tomado dc=0,9C1. Ambos anchos de la zona de hormigón comprimido proporcionan profundidades de la fibra neutra próximas a las obtenidas experimentalmente a partir de los transductores de alargamiento. El momento flector para el cual se produce la fisuración del hormigón se ha calculado de la misma manera a flexión positiva y negativa, adoptando la resistencia a tracción del hormigón que establece la ACI-318 [12] y una sección de ancho igual al de la columna C2. Los valores de la capacidad última a flexión positiva, My+, a flexión negativa My– y del momento de fisuración Mc obtenidos son los siguientes: My+=12,9kNm, My–=42,6kNm y Mc=3,5kNm.
Para estimar la rotación θy para la cual se inicia la plastificación se propone la siguiente expresión que tiene en cuenta la deformación por flexión θb, la deformación por cortante θSH y la deformación del mecanismo de bielas y tirantes θTT.
La deformación por flexión θb se calcula a partir del producto de la curvatura de inicio de plastificación ϕy y la longitud de la rótula plástica de la zona de forjado que transmite momentos directamente por flexión al pilar (ya sea porque está anclada en el ancho del mismo o a través del mecanismo de bielas y tirantes), Lpl. Para determinar Lpl se ha tomado la expresión propuesta por Priestley et al. [21] para vigas y pilares:
donde Ls es la distancia entre la sección crítica (cara interior del soporte) y el punto de contra-flexión o inflexión; db y fy son, respectivamente, el diámetro de la armadura longitudinal traccionada y su tensión de fluencia.Para estimar la deformación del mecanismo de bielas y tirantes se propone el planteamiento que se ilustra en la figura 8 y que se fundamenta en: a)la suposición de que no existe deslizamiento entre el hormigón y el acero, y b)la deformación de las bielas diagonales a compresión es despreciable en relación a la deformación de las barras longitudinales en la dirección transversal (dirección 2). Bajo estas hipótesis, atendiendo a la figura 8, aplicando la ley de senos al triángulo representado (ampliación de la zona sombreada de la figura) y haciendo ¿=¿y, se obtiene:
donde ¿y es la deformación de plastificación del acero. En el mismo triángulo de la figura 8 se puede observar, a partir de la suma de ángulos del triángulo, igual a 180°, la relación:Donde β es el ángulo que forma la biela comprimida de hormigón con la armadura que actúa de tirante. La deformación de plastificación del acero se obtiene a partir de la ley de Hooke:
donde E es el módulo elástico del acero. Determinada la distorsión angular γTT,y correspondiente al inicio de la plastificación de la armadura transversal, el desplazamiento debido a la distorsión angular en la rótula plástica será, según se observa en la figura 8:Aproximando el canto útil de la columna dc a 0,9C1 y considerando una inclinación de la biela de hormigón de 45°, la ecuación anterior resulta:
La deformación δTT implica un giro de valor θTT, según indica la figura 9. Este giro, cuando se produce la plastificación de la armadura que forma el tirante del mecanismo biela-tirante, vale:
Sustituyendo por el valor de δTT,y según (11), se obtiene:
donde xy es la profundidad de la fibra neutra de la sección y df es el canto útil de la misma. Teniendo en cuenta la ecuación (5), la rotación total para la cual se produce la plastificación de la rótula se puede expresar como sigue:El factor a2 es de carácter booleano, con valor 1 si se puede desarrollar el mecanismo de transmisión de bielas y tirantes, y 0 en caso contrario. La deformación por cortante θSH se puede estimar como un 20% de la de deformación por flexión [22], resultando:
La curvatura de inicio de plastificación ϕy se puede determinar a partir de la profundidad de la fibra neutra, xy. Considerando la hipótesis de deformación plana, se obtiene fácilmente la expresión:
donde r es el recubrimiento de la armadura. La profundidad de la fibra neutra a su vez se puede determinar a partir del equilibrio de fuerzas a nivel de sección considerando un diagrama rectangular de tensiones para el hormigón:En la expresión anterior As1 es el área de la armadura de tracción situada dentro del ancho C2+2dc.
5Predicción de la resistencia y giro de plastificación de la rótula de torsiónTal como se ha comentado en la introducción, en las estructuras con forjados reticulares con cocientes de cortante gravitatorio reducidos (del orden de 0,2) las crucetas de punzonamiento no son necesarias, y en caso de estar presentes se pueden tener en cuenta para otras funciones resistentes distintas del punzonamiento. La armadura que forma los brazos de la cruceta de punzonamiento paralelos al borde del forjado colabora junto con la propia armadura de la viga de borde del forjado para transferir, indirectamente, mediante un mecanismo de torsión, parte del momento flector que transmite el forjado reticular al pilar [11].
El cálculo de la capacidad a torsión de la viga de borde del forjado, en la que se incluye la armadura de los brazos de las crucetas de punzonamiento paralelas al borde del forjado, se puede realizar a partir de la formulación propuesta por la norma ACI-318 [12], añadiendo a la misma un factor kri para tener en cuenta la disminución de capacidad última debido a la interacción entre los mecanismos de torsión y de flexión:
donde A0 es el área encerrada en la línea media del cerco y ph es el perímetro de dicha área, At es la sección de la armadura transversal, fyt la tensión de plastificación de la armadura transversal, β’ la inclinación de las bielas de compresión en relación con la armadura longitudinal, s la separación entre cercos y Al el área total de la armadura longitudinal. En correspondencia con la respuesta experimental de la unión ensayada (descrita en el apartado 3) el factor kri toma valor 1 cuando no existe interacción (flexión positiva) y 0,7 cuando esta existe (flexión positiva). Para el especimen ensayado y en base a la ecuación (19), la armadura longitudinal consistente en 4ϕ8mm plastifica antes que los cercos. Estableciendo una inclinación de las bielas de compresión de 60° (límite máximo que se considera aceptable la ACI-318 [12] para la analogía de celosía a torsión) se obtiene la armadura transversal que equilibra la armadura longitudinal. A partir de este valor de armadura transversal, y considerando una inclinación de las bielas de 60°, se obtiene, de la ecuación (18), una capacidad a torsión T de la rótula plástica de 8,83kNm. El momento fisuración Tcr se puede predecir con la fórmula de la norma ACI-318 [12] expresada en unidades del SI (mm y MPa),donde Acp=c1h y Pcp=2(c1+h), en las cuales c1 es la dimensión del soporte en la dirección 1 y h el canto del ábaco del forjado. De la ecuación anterior se determina un momento torsor de fisuración Tcr=3,24kNm.Para estimar el giro para el cual se produce el inicio de la plastificación de la rotula plástica de torsión, a la deformación del mecanismo de bielas y tirantes que transmite directamente momentos por flexión θTT,y hay que añadir la deformación de la celosía tridimensional asociada a la transmisión del esfuerzo torsor θT,y, es decir:
θTT,y se ha calculado ya anteriormente y viene dada por la ecuación (13). El coeficiente a2 de la ecuación (21) es el mismo factor boleano empleado en la expresión (14), y que vale 0 cuando no se desarrolla el mecanismo biela-tirante de transmisión de momentos directamente al pilar (como ocurre a flexión positiva con la unión ensayada). El giro debido a la deformación de la celosía tridimensional asociada a la transmisión del esfuerzo torsor θT,y se puede determinar estudiando la deformación de la celosía espacial virtual que forma la armadura longitudinal y transversal trabajando como elementos a tracción (tirantes), y las bielas inclinadas ficticias de hormigón como elementos a compresión. En el desarrollo siguiente se parte de la consideración de que la armadura longitudinal es la que sufrirá deformaciones plásticas. Como longitud de la rótula plástica a torsión LPl,T de la viga de borde se puede tomar, para simplificar, la distancia entre el nervio exterior mas próximo al pilar y la cara del pilar (figura 3b), y suponer que en toda esta longitud el momento torsor es máximo y constante:En la figura 10a se puede apreciar el giro relativo entre las secciones extremas de la rótula plástica θT. Este giro θT se puede aproximar con θT≈Δ/r0, donde Δ es el desplazamiento relativo entre extremos de rótula de una de las armaduras longitudinales en el plano vertical 1-3, y r0 la distancia entre el centro de torsión y el centroide de la armadura en cuestión. El desplazamiento Δ se puede descomponer en sus componentes horizontal Δh y vertical Δv, según indica el triángulo de deformaciones de la figura 10a.
La figura 10b muestra una proyección del mecanismo de deformación biela-tirante, que es de índole tridimensional, en el plano 1-2. Sin embargo, la componente vertical (dirección 3) de la deformación del mecanismo dejaría el problema indeterminado. Si se establece gráficamente la compatibilidad de deformaciones entre biela y tirante en la dirección normal al plano en la dirección 3, y se acepta, de forma simplificada, que el desplazamiento de cada extremo de barra (biela y tirante) se sitúa en la tangente a los arcos con centros en b y b’, según se trate, respectivamente, de la biela o el tirante, se observa que ambas tangentes resultan paralelas y no van a cortarse. Por tanto, la componente vertical, en la dirección 3, no establece ninguna condición de compatibilidad de deformaciones. Se puede asumir entonces que la condición de compatibilidad de deformaciones queda restringida a la deformación en el plano 1-2.
En el plano 1-2 (figura 10b) se ha supuesto que la biela no varía su longitud. La deformación del tirante cuando se produce la plastificación se determina a partir de la deformación de plastificación del acero, ¿y. A partir de la deformación del tirante, se determina geométricamente la deformación del conjunto, a partir de la intersección de las tangentes a los arcos trazados por los extremos de las 2 barras, con centros de giro en b y b’.
En la figura 10b se puede apreciar que el triángulo sombreado, que determina la condición de compatibilidad de deformaciones entre biela y tirante, es idéntico al correspondiente al mecanismo biela-tirante de la zona de transmisión por flexión mostrado en la figura 8. Por tanto, las expresiones (7) y (8) que derivaban de la figura 8 serán válidas también para determinar γT. Para subrayar que se trata de 2 mecanismos similares pero con variables distintas, las variables de la figura 10 se han diferenciado mediante un apóstrofe, α’, β’.
De estas expresiones (7) y (8), conocida la deformación de plastificación del acero, ¿y, y partiendo de la inclinación de la biela β’, se determina γT. Una vez determinado γT, es posible determinar el desplazamiento horizontal Δh=γTLpl,T, a partir del cual, atendiendo a la figura 10a, es posible determinar el desplazamiento Δ=Δh/sen ϕ. Partiendo de la relación anteriormente mencionada, θT≈Δ/r0, es posible establecer una expresión final para estimar la deformación de plastificación de la rótula plástica a torsión:
El significado de r0 se indica en la figura 10 y vale:
Sustituyendo las expresiones (13) y (23) en la ecuación (21), se obtiene la rotación total de la rótula a torsión correspondiente al inicio de plastificación:
6Definición de los diagramas momento-giro de las rótulas plásticasEn apartados anteriores se han propuesto modelos sencillos para predecir la resistencia y el giro de plastificación de las rótulas de flexión y de torsión, que definen el punto del diagrama momento-giro a partir del cual empieza el comportamiento no lineal. Para definir los diagramas momento-giro de las rótulas en la zona no lineal se adopta el modelo que plantea la norma FEMA 356 [23] para losas bidireccionales con cocientes de cortante gravitatorio inferiores a 0,2 y continuidad del armado inferior, y que está gobernado por los parámetros a, b y c que se ilustran en la figura 11, y cuyos valores son a=0,02rad, b=0,05rad y c=0,2. En las figuras 5 y 6 se han dibujado con línea discontinua los diagramas momento-giro obtenidos para el modelo ensayado, empleando la predicción de resistencia y rotación de plastificación propuesta en los apartados anteriores, y los valores de los parámetros a, b y c de la norma FEMA 356. Tal como se observa en las figuras 5 y 6, se ha despreciado la deformación (giro) para momentos inferiores al de fisuración del hormigón. Si se compara esta línea discontinua con los valores obtenidos experimentalmente (rombos), se observa que existe una buena correlación entre resultados experimentales y predicción, en términos de rigidez elástica inicial, resistencia y ductilidad. El efecto del aumento de resistencia por deformación del acero (strain hardening) se puede incorporar de forma simplificada a los diagramas momento-giro de las rótulas plásticas sustituyendo el tramo horizontal por una recta cuya pendiente aproximada sería del 1% del cociente entre momento y giro de plastificación de la rótula.
Diagrama generalizado fuerza-deformación para elementos de hormigón [23].
Se propone un modelo numérico de unión exterior forjado reticular-pilar en el cual se idealiza el forjado con elementos tipo placa en la zona del ábaco, los nervios y los pilares con elementos tipo barra, y la unión entre los elementos tipo placa y las barras que representan los pilares se realiza mediante un muelle rotacional a flexión (rótula plástica a flexión) y 2 muelles rotacionales a torsión (rótula plástica a torsión). Las no linealidades se concentran en los muelles. El modelo propuesto se ilustra en la figura 12, donde FH indica los muelles a flexión y TH los muelles a torsión. La predicción de las relaciones momento-giro de las rótulas plásticas se obtienen tal y como se ha indicado en los apartados anteriores. En los elementos tipo barra y tipo placa se contempla la deformación por flexión y por cortante, y se reduce a 1/3 la rigidez elástica de los elementos placa y a 3/4 la rigidez elástica del soporte con el fin de tener en cuenta la fisuración del hormigón [7,13]. Esta simplificación se basa en que bajo acciones laterales las solicitaciones máximas se dan en torno a las uniones forjado-pilar, lo que provoca que la degradación de la estructura se concentre en estas zonas. Bajo estas condiciones de acciones sísmicas laterales es razonable suponer que el resto de la estructura se mantiene con una fisuración próxima a la de servicio, que se ha producido durante la etapa de construcción y uso del edificio.
Al emplear rótulas diferentes para la flexión directa y para la torsión de la viga de borde, el modelo propuesto tiene limitaciones a la hora de tener en cuenta directamente la interacción entre ambos mecanismos. En el caso de las uniones objeto de este estudio, el desacoplamiento de los mecanismos de torsión y de flexión directa está justificado por la presencia de crucetas de punzonamiento. Tal como se observa experimentalmente, la unión entre el forjado y el pilar mantiene su capacidad a torsión (fig. 6) cuando la capacidad a flexión se reduce drásticamente (fig. 5). Este comportamiento queda justificado analizando visualmente el modo de rotura. Las figuras 13 y 14 ponen manifiesto que la caída de la capacidad a flexión está provocada por la degradación del recubrimiento de hormigón y la pérdida de adherencia de la armadura longitudinal y transversal, mientras que la cruceta de punzonamiento mantiene su armadura y el hormigón que confina en buen estado, y por tanto mantiene también su capacidad a torsión.
En la figura 15 se compara la envolvente de la relación entre la fuerza lateral aplicada a la cabeza del pilar superior y el desplazamiento horizontal del mismo obtenida experimentalmente, de ensayos con desplazamientos impuestos cíclicos crecientes en amplitud, y la deformación obtenida con el modelo numérico propuesto, con un análisis de empuje incremental. El análisis ha consistido en aplicar, en cada sentido de carga, un desplazamiento horizontal impuesto en el extremo superior del soporte. Se observa que el ajuste es satisfactorio, teniendo en cuenta la simplicidad del modelo numérico propuesto. Experimentalmente se aprecia un endurecimiento progresivo a partir de la plastificación que el modelo numérico propuesto no es capaz de reproducir porque no se ha incluido el fenómeno de endurecimiento por deformación en el comportamiento plástico del acero de las armaduras.
El modelo propuesto puede extenderse y aplicarse a uniones interiores y de esquina, y abordar el comportamiento en 2 direcciones. Para ello la unión entre los elementos tipo placa que idealizan el forjado y los elementos tipo barra que representan los pilares se haría mediante pares de muelles trabajando en serie. Uno de los 2 muelles del par sería una rótula de flexión y el otro una rótula de torsión. En el caso de uniones forjado reticular pilar-interiores serían necesarios 4 pares de muelles (uno para cada una de las 4 caras del pilar). En uniones forjado reticular-pilar en esquina se necesitarían 2 pares de muelles (un par en cada una de las 2 caras ortogonales del pilar en contacto con el forjado). El modelo propuesto está pensado para ser implementado en programas existentes como SAP2000 [24] o similares.
El comportamiento no lineal de las rótulas plásticas del modelo propuesto cuando se someten a cargas arbitrarias de tipo cíclico sigue un modelo histerético poligonal. Este modelo está controlado y se construye a partir de la curva multilineal de las figuras 5 y 6 que constituye el «esqueleto de la curva» y que representa el comportamiento de la rótula bajo cargas monótonas. El esqueleto de la curva esta caracterizado por los parámetros ke+, θy+, Mc+, My+, θd+, kd+, que se ilustran en la figura 16, y sus correspondientes valores en el dominio de momentos negativos ke−, θy−, Mc−, My−, θd−, kd−. El comportamiento cíclico está representado por puntos y segmentos lineales que son función de estos parámetros, y de los valores del momento M y rotación θ en la rótula calculados en pasos anteriores del proceso de cálculo. Al modelo se le introduce un incremento de rotación Δθ, y este responde acomodando dicho incremento en la ley histerética y proporcionando el incremento de momento ΔM correspondiente. El comportamiento histerético a lo largo de los segmentos lineales y los cambios de pendiente de los mismos depende de la historia de deformaciones y sigue una lógica que se expone a continuación. El programa principal proporciona al algoritmo el incremento de rotación deseado Δθ y los parámetros de la historia M-θ seguida por la rótula en pasos anteriores, los cuales están almacenados en la base de datos del programa principal. El algoritmo procesa esta información a través de una primera subrutina que determina si ha habido cambio en la dirección de carga, y en caso afirmativo asigna como pendiente del segmento lineal que debe seguir la relación momento-rotación el valor kun. El valor de kun (pendiente del tramo de descarga) se determina tal como se ilustra en la figura 14 y depende del parámetro α. A partir de los resultados de los ensayos puede tomarse α=2. A continuación, el algoritmo llama a una segunda subrutina que, a partir de la historia momento-rotación, calcula el punto final del segmento de rigidez ki que está siguiendo la curva M-θ en el paso i en curso. Seguidamente comprueba si el nuevo punto, calculado sumando al valor del momento en curso el incremento de momento ΔM=kiΔθ y a la rotación en curso el incremento de rotación Δθ dado, se encuentra dentro del segmento lineal. En caso afirmativo, el nuevo punto se da por válido. En caso contrario, y si todavía no se ha alcanzado la rotación última θu, se modifica la rigidez del segmento adoptando el valor que corresponda según el esqueleto de la curva, y se repite el cálculo. Cuando se sigue un tramo de descarga con pendiente kun, una tercera subrutina controla si el nuevo punto M-θ, obtenido sumando a los valores del paso anterior el incremento de momento ΔM=kunΔθ y el incremento de rotación Δθ, ha cruzado el eje horizontal pasando del dominio de momentos positivos a negativos o viceversa. En caso afirmativo, el algoritmo cambia el segmento que debe seguir la ley histerética asignando una pendiente kr cuyo significado se ilustra en la figura 16. La pendiente kr se calcula con el punto de corte del segmento anterior y el eje horizontal (θp,0), y el punto de máxima deformación θm del esqueleto de la curva alcanzado en ciclos anteriores en el nuevo dominio de momentos. Este punto de máxima deformación se ha identificado con las coordenadas Mm y θm en la figura 16. La primera vez que se cruza el eje horizontal, el algoritmo adopta como punto (Mm,θm) el (My+,θy+) o el (My−,θy−), según el dominio de momentos que corresponda. La subrutina que controla esta ley histerética de las rótulas plásticas recoge la información que resulta paso a paso del modelo y determina si la rigidez asumida es o no realista, procediendo en el segundo caso a su actualización. El usuario puede definir un paso de tiempo inicial, que normalmente se toma inferior por lo menos a la mitad del periodo del modo más alto de vibración del sistema. Cuando la subrutina detecta que hay que actualizar la rigidez, el algoritmo es capaz de reducir el paso de tiempo y ordenar que se repita el paso anterior con un paso de tiempo menor. De esta forma los pasos pueden hacerse más cortos en las zonas en las que se producen cambios de rigidez.
El modelo numérico sencillo propuesto en este trabajo y el algoritmo descrito para al análisis no lineal permiten reducir de forma considerable el tiempo de cálculo. Con objeto de cuantificar esta reducción, la curva envolvente indicada a puntos en la figura 13 se recalculó con un modelo tridimensional de elementos finitos en análisis no-lineal, empleando un programa llamado Engineer's Studio [25]. Engineer's Studio está basado en la teoría de la mecánica no-lineal de hormigón armado desarrollada por Maekawa [16]. En la modelización se emplearon elementos no lineales tipo fibra para los pilares y tipo capa (bidimensionales) para el forjado. El ajuste entre la curva envolvente obtenida con esta modelización y los resultados experimentales fue muy satisfactorio. En Donaire-Ávila y Benavent-Climent [17] se expone una modelización similar realizada para una unión forjado reticular-pilar interior y se explican con detalle los modelos constitutivos del hormigón. El tiempo de cálculo empleado con el modelo numérico sencillo propuesto fue del orden de 25 veces inferior al requerido con el modelo de elementos finitos implementado en el programa Engineer's Studio.
8ConclusionesEn este trabajo se propone un modelo numérico sencillo para predecir el comportamiento de las uniones exteriores forjado reticular-pilar sometidas a cargas laterales. El modelo consiste en una combinación de elementos tipo placa que idealizan la zona del ábaco del forjado, elementos tipo barra que representan los nervios del forjado reticular y los pilares, y muelles rotacionales que conectan los elementos tipo placa con los pilares. En estos muelles se concentran todas las no-linealidades del modelo numérico. Al emplear muelles rotacionales distintos para representar la flexión directa y la torsión, el modelo propuesto no refleja la interacción entre ambos mecanismos. En el tipo de uniones objeto de este estudio, este desacoplamiento está justificado por la presencia de crucetas de punzonamiento que minimizan dicha interacción.
Se proponen hipótesis simplificadoras y fórmulas sencillas para predecir la resistencia y el giro de plastificación de las rótulas, y un criterio comúnmente aceptado para estimar el efecto de la fisuración del hormigón en la rigidez de los elementos tipo placa y tipo barra. La ley momento-giro de las rótulas plásticas estimada con las fórmulas propuestas se compara con la obtenida a partir de mediciones con transductores de alargamiento y de giro obtenidas de ensayos, y se muestra que existe una buena correlación. Finalmente, se compara la envolvente fuerza-desplazamiento lateral obtenida experimentalmente para una unión exterior forjado reticular-pilar con la que predice el modelo numérico propuesto obteniéndose un buen ajuste.
Esta investigación ha sido apoyada por el Gobierno de España (Ministerio de Ciencia e Innovación) a través del proyecto BIA-2011-26816 del Plan Nacional I+D+i, y cofinanciado con fondos de la FEDER de la Unión Europea.






















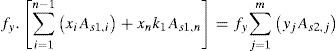

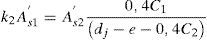
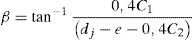
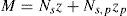




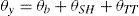
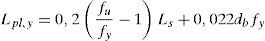

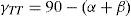

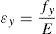
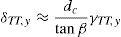
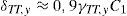


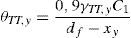
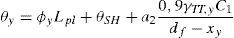
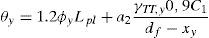
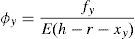
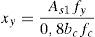
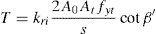
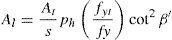
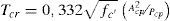
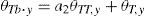
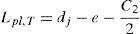

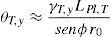
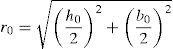
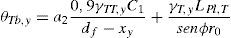
![Diagrama generalizado fuerza-deformación para elementos de hormigón [23]. Diagrama generalizado fuerza-deformación para elementos de hormigón [23].](https://static.elsevier.es/multimedia/02131315/0000002900000004/v1_201311210056/S021313151200048X/v1_201311210056/es/main.assets/thumbnail/gr11.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)




