Influencia de la longitud, diámetro y geometría del implante en la distribución de las tensiones: un análisis con un modelo de elementos finitos

El objetivo de este estudio consistió en evaluar la influencia de la longitud, el diámetro y la geometría de los implantes dentales del Instituto de Biotecnología (Vitoria, España) sobre la distribución de las fuerzas en el hueso. Para este estudio se crearon modelos tridimensionales de elementos finitos con implantes dentales osteointegrados de titanio. Se aplicó una fuerza de 150 N con un ángulo de 30º. Los cuatro sistemas de implantes utilizados fueron: Tiny, Interna Universal, Interna Plus e Interna Wide, y presentaban las siguientes plataformas: 3,5; 4,1; 4,1 (con un cuello de 4,8 mm), y 5,5 mm, respectivamente. Se evaluaron implantes cuyas longitudes fueron 8,5; 10,0; 11,5; 13,0 y 15,0 mm y con los siguientes diámetros: 2,5; 3,3; 3,75; 4,0; 4,5 y 5,0 mm. Los resultados mostraron que el efecto del diámetro del implante sobre la distribución de las fuerzas en el hueso era más significativo que el efecto de la longitud del implante o su geometría. La fuerza máxima se localizó alrededor del cuello del implante y la mayor parte de la fuerza, con independencia del parámetro estudiado, se distribuyó sobre el hueso adyacente a las seis primeras roscas del implante. Sobre la base de estos estudios con modelos de elementos finitos, el uso de implantes de un diámetro superior puede ser más apropiado para disipar las fuerzas actuantes, y de este modo reducir las fuerzas sobre el hueso que rodea el implante. Adicionalmente, el empleo de implantes más cortos y con un diámetro mayor puede ser una alternativa razonable en aquellas zonas limitadas por la altura de la cresta alveolar residual.

La adaptación de la osteointegración implantológica ha revolucionado el campo de la implantología^1,2. Se han descrito diversos factores que podrían estar involucrados en la obtención de una osteointegración satisfactoria, incluidas la geometría y la composición de la superficie del implante^3,4, ausencia de sobrecalentamiento durante la preparación del lecho, óptima calidad y cantidad de hueso, ausencia de sobrecarga, y consecuentemente, distribución de una fuerza intensa al hueso, especialmente durante el período de cicatrización³. De hecho, mientras que una de las razones por las que se produce la pérdida de un implante a corto plazo es el hecho de no haber obtenido una estabilidad primaria, la pérdida de un implante a largo plazo (en estadios avanzados) se relaciona más con una infección o una sobrecarga⁵.

Se ha constatado que la carga transferida al hueso a través del implante y de la prótesis es un factor importante para obtener una distribución adecuada de las fuerzas al tejido óseo⁶. Puesto que la manera como se carga el hueso está relacionada con su respuesta, una sobrecarga continuada podría provocar microfracturas en el hueso, aumentando la tensión y la actividad osteoclástica en la región⁷. De hecho, basándonos en las observaciones clínicas, se ha informado de que durante el primer año de función de un implante intraóseo puede detectarse una pérdida ósea vertical de 1 mm aproximadamente⁸. Subsecuentemente, el índice o tasa de reabsorción ósea puede detenerse o incluso aumentarse en 0,1 mm cada año aproximadamente, incrementándose así el riesgo de pérdida del implante⁹.

Además de la calidad y la cantidad óseas, la longitud, el diámetro y la geometría del implante pueden influir en la distribución de las fuerzas sobre el tejido óseo^10,11. Si se asume este hecho, determinar en qué medida cada uno de estos factores contribuyen a la distribución de las fuerzas en el hueso bajo una carga aplicada será relevante para poder adoptar las decisiones clínicas adecuadas y reducir la fuerza sobre el hueso situado alrededor del cuello del implante, disminuyendo, de este modo, el riesgo de reabsorción ósea.

En este estudio biomecánico los autores investigaron el grado de contribución de estos parámetros (longitud, diámetro y geometría del implante) a la distribución de la fuerza sobre el hueso con la ayuda de un análisis con un modelo de elementos finitos tridimensional (EF 3D) en unos implantes proporcionados por del Instituto de Biotecnología (BTI). El análisis EF 3D es una herramienta matemática exacta y válida utilizada para explorar los efectos de la carga y de los parámetros implantológicos sobre la distribución de las fuerzas en un modelo de hueso¹².

Método y materiales

Implantes

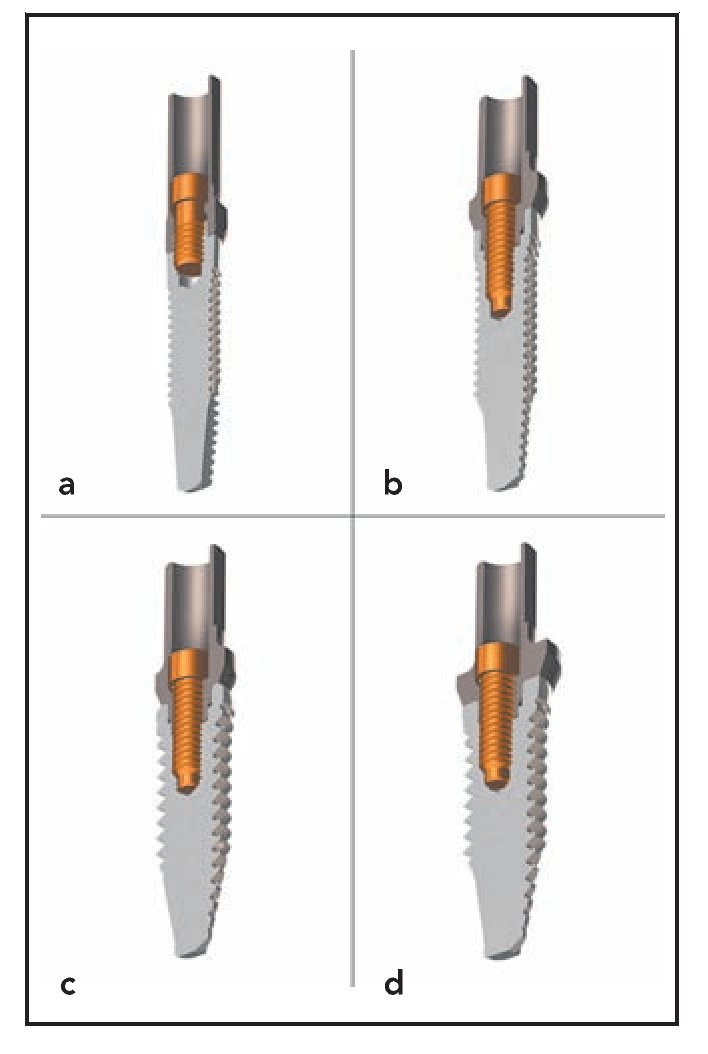
En esta investigación destinada a evaluar los efectos que la geometría, la longitud y el diámetro del implante pueden ejercer sobre la distribución de las fuerzas en el hueso se emplearon 4 implantes BTI con distintas plataformas. La figura 1 muestra de forma esquemática los 4 sistemas de implantes utilizados (Tiny, Interna Universal, Interna Plus e Interna Wide). La principal diferencia geométrica entre los sistemas fue el diámetro de las plataformas (3,5; 4,1; 4,1 [con un cuello de 4,8 mm], y 5,5 mm, para Tiny, Interna Universal, Interna Plus e Interna Wide, respectivamente). Para evaluar la influencia de la longitud y el diámetro se seleccionaron y simularon diferentes modelos de implante para cada plataforma. En resumen, se evaluaron implantes con las siguientes longitudes: 8,5; 10,0; 11,5; 13,0 y 15,0 mm, y cuyos diámetros fueron 2,5; 3,3; 3,75; 4,0; 4,5 y 5,0 mm.

Figura 1 Esquema que muestra los 4 implantes dentales simulados del BTI: (a) Tiny, (b) Interna Universal, (c) Interna plus y (d) Interna Wide.

Modelo de EF

Con objeto de analizar la distribución de las fuerzas provocadas por una carga sobre el hueso localizado alrededor de los implantes dentales se crearon modelos de EF en 3D. En los modelos 3D, por lo general, la fuerza suele representarse por un vector de fuerza de 6 componentes. La fuerza equivalente de von Mises que expresa todos estos componentes como un único valor, se digitalizó para evaluar las variaciones en cuanto a geometría, longitud y diámetro con la ayuda de un programa de software MSC Patran (MSC Software Corporation). Todos los cálculos se llevaron a cabo mediante el programa especializado en cálculo MSC Marc. El software se instaló en un equipo Dell Precision 470 (Dell).

Para este estudio se generaron modelos que contenían un rango de 20.000 a 85.000 elementos, según el tipo de implante. Para los procedimientos analíticos y de engranaje se emplearon elementos isoparamétricos hexaédricos de 8 nódulos (nodos). La estructura ósea se modeló como un cilindro de 20 mm de diámetro, manteniendo en estudio la altura del implante. Los márgenes externos de la sección ósea modelada se redujeron de manera que el desplazamiento de los nódulos en todas direcciones fuera igual a 0. El diámetro del implante era lo suficientemente grande (20 mm) como para hacer que esta condición fuera irrelevante en términos de distribución de las fuerzas sobre el área analizada (el hueso alrededor del implante). El volumen óseo total se consideró un material lineal, isotrópico y elástico dotado de las características del hueso cortical (ε = 1,37 x 10⁴ MPa, Poisson ratio = 0,3)^13,14 y el implante se consideró perfectamente ostoeointegrado. Esto último se consiguió generando una unión nódulo con nódulo entre el hueso y el implante.

Los implantes se simularon como modelos completos hexagonales tridimensionales. El implante de titanio se modeló junto con el pilar de titanio como una sola pieza ( = 1,03 x 10⁴ MPa, Poisson ratio = 0,35). Con el fin de poder utilizar los elementos hexagonales, que proporcionarán unos resultados más exactos comparados con los elementos tetraédricos, las espiras de los implantes se modelaron de forma recta en vez de dotarlas de una configuración en espiral. Se simplificaron los modelos geométricos en 3D del implante y el pilar, la estructura ósea, y los materiales para ahorrar tiempo de digitalización y memoria de trabajo. Puesto que todos los modelos se hallaban sujetos a las mismas simplificaciones, ello no afectó a las conclusiones finales.

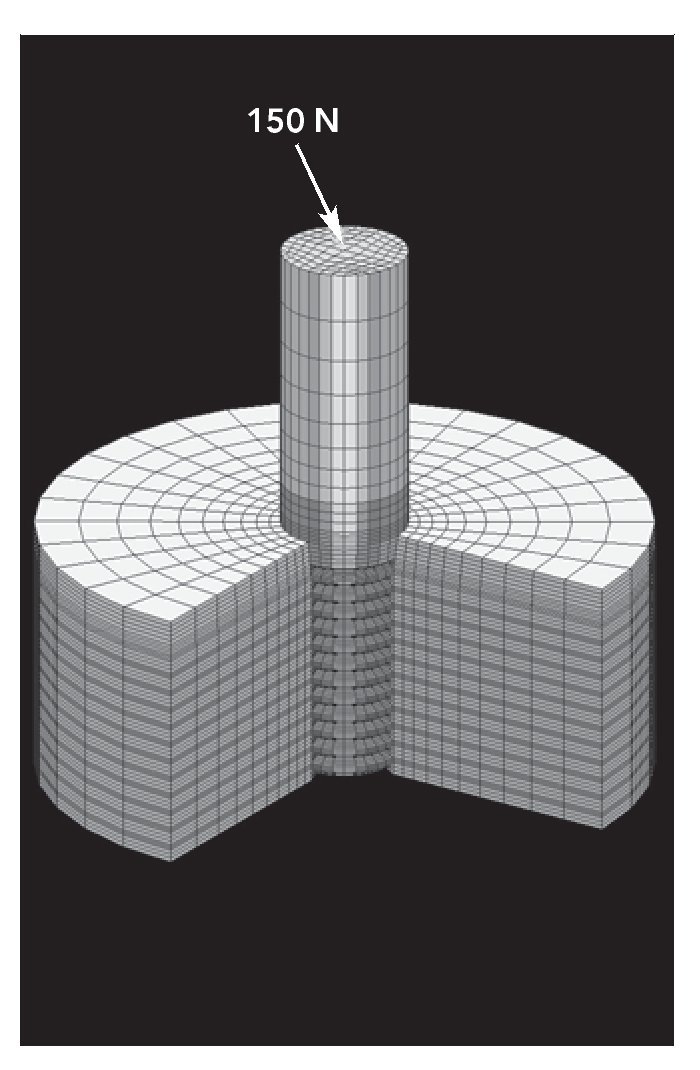
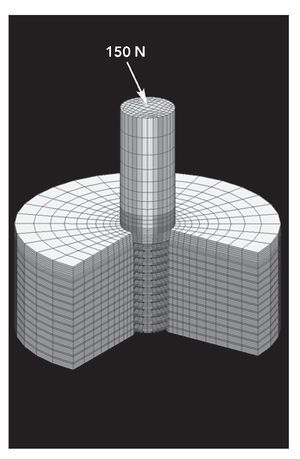
Para analizar la influencia de los parámetros implantológicos citados sobre la distribución de las fuerzas en el hueso, se aplicó una fuerza máxima de 150 N con un ángulo de 30º sobre el plano oclusal atendiendo a la normativa ISO 14801:2003¹⁵. La figura 2 muestra de forma esquemática la configuración implantepilar osteointegrada en la estructura ósea bajo una carga oblicua de 150 N.

Figura 2 Esquema que muestra el modelo implante-pilar osteointegrado en la estructura ósea bajo una carga oblicua de 150 N.

Resultados

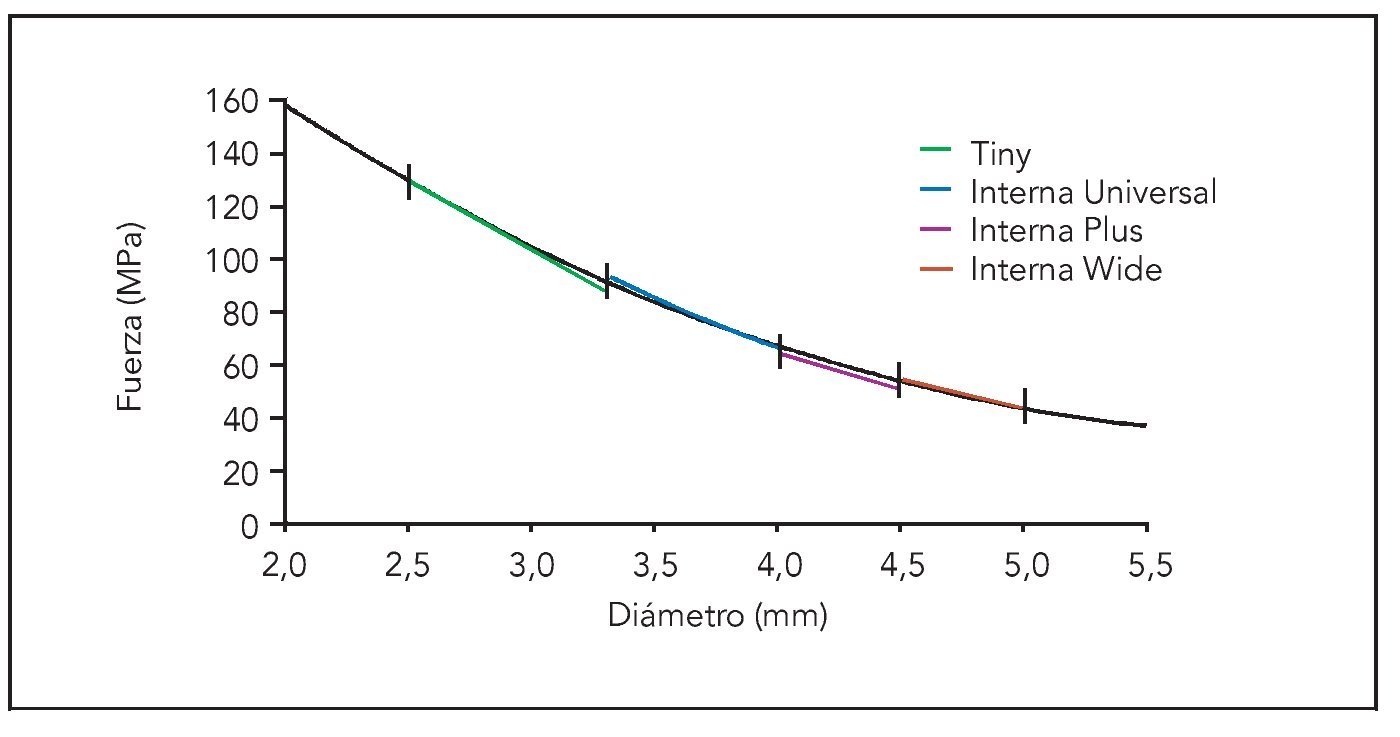
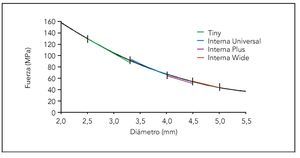
El análisis matemático llevado a cabo con el análisis de EF en 3D demostró que las fuerzas se distribuían de diferente manera sobre el hueso atendiendo al parámetro implantológico estudiado. La aplicación de una fuerza máxima equivalente de von Mises sobre la interfase implante-hueso para las distintas geometrías implantológicas (Tiny, Interna Universal, Interna Plus e Interna Wide), diámetros (que van desde 2,5 a 5,0 mm) y longitudes (que abarcan de 8,5 a 15,0 mm) mostraron una curva de regresión parabólica (R² = 0,99973, figura 3). Esto indica que el efecto del diámetro del implante en la distribución de las fuerzas en el hueso es claramente más significativo que el efecto de la longitud de los implantes o su propia geometría.

Figura 3 Influencia de la longitud, el diámetro y la geometría de los implantes sobre las fuerzas máximas equivalentes de von Mises en el hueso adyacente. Las barras de errores corresponden a la influencia de la longitud del implante con un diámetro constante.

Los valores de tensión más elevados correspondieron a los obtenidos con el implante Tiny, con un diámetro de 2,5 mm y una longitud de 8,5 mm (122,9 MPa), mientras que los valores más bajos se obtuvieron con la simulación de un implante Interna Wide, de 5,0 mm de diámetro y 15,0 mm de longitud (39,6 MPa). Si se aumentaba el diámetro de los implantes Tiny de 2,5 a 3,3 mm, se reducían los valores de tensión en un 30,7 %, mientras que si se aumentaba la longitud (de 8,5 a 15,0 mm), se producía una reducción de tan sólo el 1,71 %. Con los implantes Internal Universal se observaron comportamientos similares. De hecho, la máxima fuerza que actuó sobre el hueso situado alrededor de un implante con un diámetro de 3,3 mm fue 28,2 % superior a la obtenido alrededor de un implante cuyo diámetro era de 4,0 mm, mientras que el hecho de modificar la longitud sólo alteró la fuerza en 2,4 %.

Un hecho interesante observado fue que la diferencia en la reducción de tensiones inducida al aumentar el diámetro del implante fue menos marcada en el caso de los implantes más anchos. El hecho de aumentar el diámetro de los implantes Interna Plus e Interna Wide redujo la tensión en más de un 20 %, mientras que el hecho de aumentar su longitud provocó una disminución de la tensión de un 5 y un 7,6 %, respectivamente. Variar la geometría del implante provocó mínimos cambios en la distribución de las tensiones (figura 3). La modificación de la geometría (manteniendo constantes el diámetro y la longitud) no logró reducir la tensión más que en un 7 % en cualquiera de los implantes estudiados.

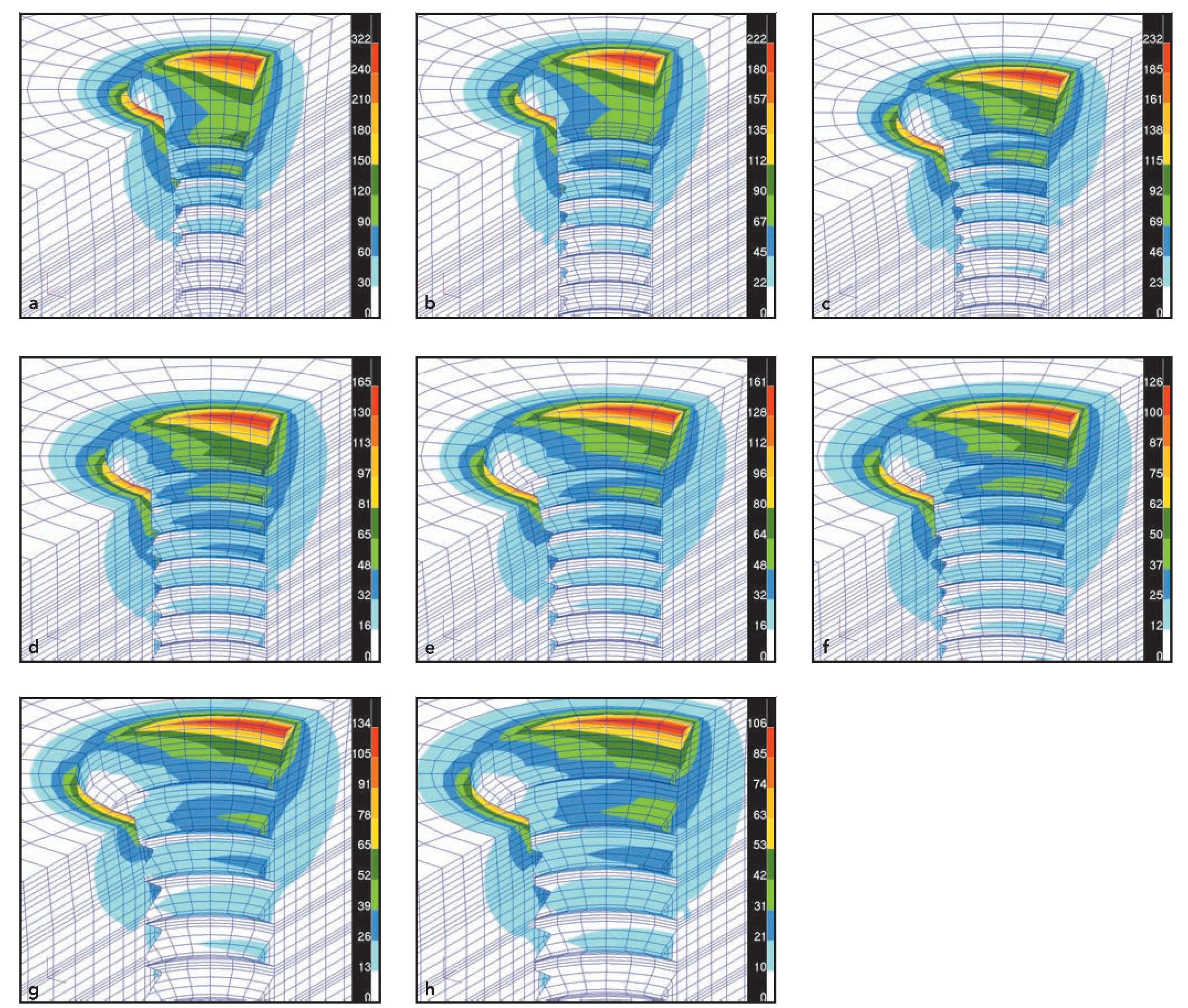
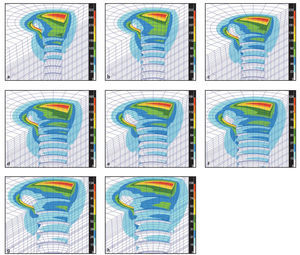
El análisis de EF también reveló una distribución de la tensión desigual o desuniforme en el interior del alvéolo, independiente de la geometría, longitud y diámetro del implante estudiado. La figura 4 ilustra la distribución de la tensión al hueso en implantes con diferentes plataformas (Tiny, Interna Universal, Interna Plus e Interna Wide) y diámetros (2,5; 3,3; 4,0; 4,5 y 5,0 mm), pero con la misma longitud (13 mm). Los resultados mostraron que el área de máxima tensión se situaba alrededor del cuello del implante y disminuía progresivamente en dirección apical al implante. Más aún, el campo sobre el que actuaba la fuerza mostró una considerable disminución al aumentar la distancia desde el lecho del implante.

Figura 4 Distribución de las fuerzas máximas de von Mises en el hueso que rodea el modelo implante-pilar osteointegrado. La longitud del implante se mantuvo constante (13,0 mm) y se evaluó la influencia del diámetro y la geometría del implante. (a) Implante Tiny, 2,5 mm; (b) Implante Tiny, 3,3 mm; (c) Interna Universal, 3,3 mm; (d) Interna Universal, 4 mm; (e) Interna Plus 4 mm; (f) Interna Plus, 4,5 mm; (g) Interna Wide, 4,5 mm, y (h) Interna Wide, 5 mm. Nótense los cambios en la escala de cada figura.

Sin embargo, a pesar de que se había observado una tendencia similar en cuanto a la distribución de las tensiones en todos los implantes estudiados los valores máximos de la fuerza equivalente de von Mises resultaron ser sustancialmente distintos. Por ejemplo, en el implante Tiny de 2,5 mm de diámetro (figura 4a) y en el implante Tiny de 3,3 mm de diámetro (figura 4b) se constató que el área de máxima tensión era la región coronal del tejido periimplantar de ambos implantes, pero los valores registrados para la misma carga disminuyeron al aumentar el diámetro (nótese la escala empleada en cada figura).

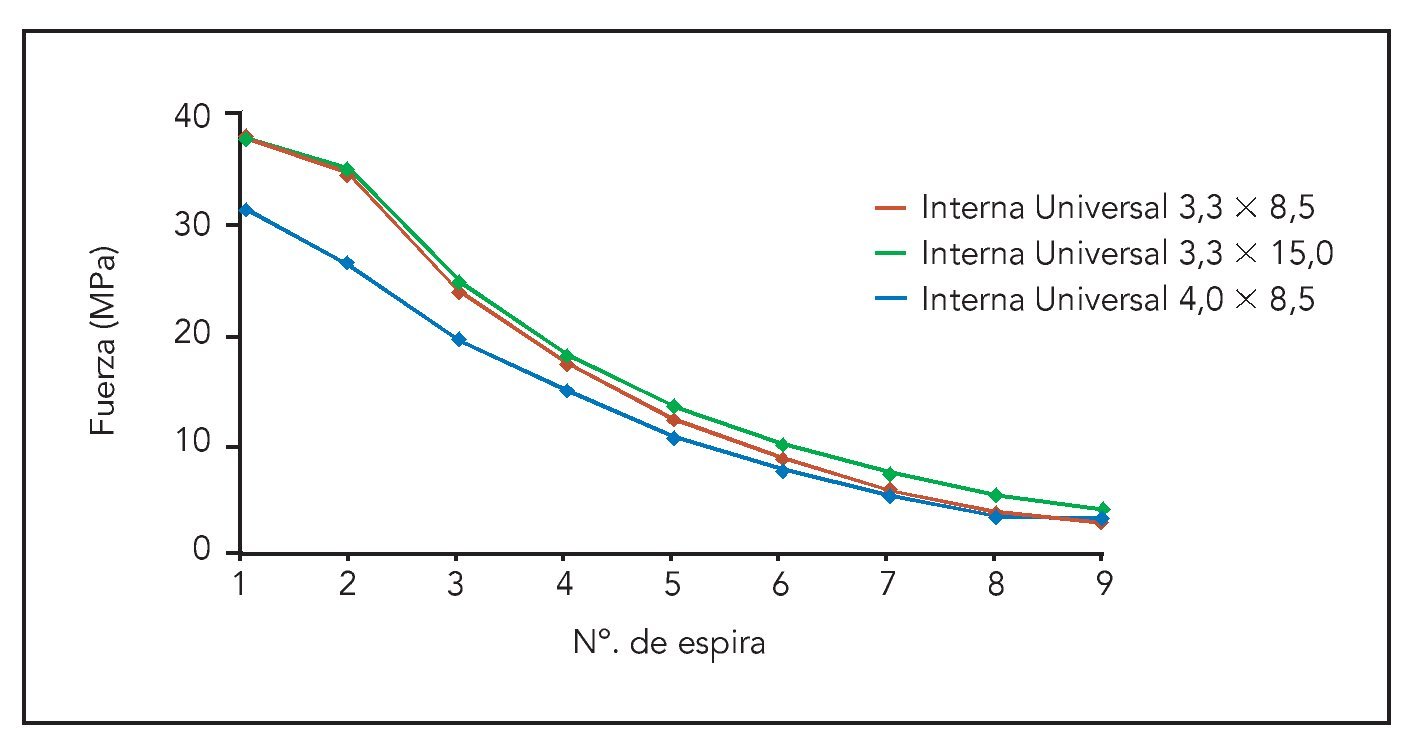
Los autores evaluaron también la influencia de la variación en la longitud, diámetro y geometría de los implantes dentales del BTI sobre la distribución de la fuerza en el hueso adyacente a las roscas de los implantes. En todos los implantes estudiados, los valores de fuerza máximos disminuyeron progresivamente con el número de espiras en la dirección apical del implante (figura 5). Los valores de máxima tensión obtenidos en el hueso adyacente de las seis primeras espiras de los implantes más cortos (8,5 mm) fueron similares, e incluso menores, a los observados en los implantes más largos (15,0 mm) con un diámetro constante. Por el contrario, al aumentar sustancialmente el diámetro de los implantes se redujeron los valores de máxima tensión (figura 5). Estos valores también indicaron que la mayor parte de las fuerzas ejercidas sobre el hueso se localizan en las seis primeras espiras del implante, con independencia de la longitud, el diámetro o la geometría.

Figura 5 Influencia de la variación de la longitud y el diámetro de los implantes dentales del BTI sobre la distribución de las fuerzas en el hueso adyacente de cada espira de los implantes.

Discusión

El análisis de EF en 3D es un método que suele emplearse con frecuencia para analizar la tensión tanto en el campo de la investigación como en el de la industria. De hecho, se ha empleado para analizar prótesis de las articulaciones femorales y rotulianas, además de aplicarse a los implantes dentales¹⁶. Dado que hasta la fecha no se dispone de un método para determinar las deformaciones y la distribución de las fuerzas en el microámbito del hueso adyacente a los implantes osteointegrados in vivo, la simulación matemática que proporciona este método analítico de EF en 3D puede ser una herramienta válida para arrojar luz sobre este tema. El modelo de EF en 3D utilizado en este estudio partió de unas determinadas suposiciones respecto a las estructuras simuladas: la estructura ósea se consideró isotrópica, homogénea y linealmente elástica, mientras que los implantes se consideraron perfectamente osteointegrados en el hueso (100 % interfase implante-hueso). Puesto que estas simplificaciones se hicieron extensibles a todos los modelos, estas condiciones no afectaron a las conclusiones finales.

En el presente artículo, los autores investigaron la influencia de parámetros como la longitud, el diámetro y la geometría de los implantes dentales de BTI expuestos a una fuerza oblicua, sobre la distribución de las tensiones en el tejido óseo. Los resultados extraídos de esta investigación pueden llegar a tener una importancia muy significativa puesto que los 3 parámetros estudiados han resultado afectar la distribución de las tensiones en el hueso^11,13,17. Según la hipótesis de Carter y cols., una fuerza excesiva puede ser perjudicial para el tejido óseo, lo que provocaría una respuesta hipertrófica y una sobrecarga local que podría, a su vez, provocar una pérdida ósea en las zonas donde actuarían las fuerzas¹⁸. Además, se ha constatado que las cargas que generan micromovimientos del orden de las 100 a 200 µm pueden inhibir el crecimiento óseo, inducir la formación de capas fibróticas y aumentar el riesgo de pérdida del implante¹⁹. Si se tiene en cuento esto, la reducción de las tensiones sobre el hueso adyacente a los implantes insertados puede ser de vital importancia para reducir los riesgos de reabsorción ósea y de fracaso implantar.

Los resultados de este estudio demuestran que, en materia de reducción de la distribución de tensiones sobre el hueso, el diámetro del implante es más importante que la longitud o la geometría del mismo. Petrie y Williams¹⁷, en otro estudio de biomecánica en el que se aplicaron cargas oclusales oblicuas, se alcanzaron conclusiones similares. De acuerdo con los resultados del presente estudio, aumentando ligeramente el diámetro de los implantes del BTI, con independencia de la plataforma utilizada, (Tiny, Interna Universal, Interna Plus e Interna Wide) es posible reducir los valores máximos de tensión von Mises en el hueso del 20 al 30 %. El hecho de aumentar la longitud de 8,5 a 15,0 mm tan sólo logró reducir la tensión en un 2-7,6 %, mientras que el hecho de cambiar la geometría de la plataforma no logró una reducción de la tensión que superara el 7 %. Por ello, desde un punto de vista biomecánico, el uso de implantes de diámetro superior puede ofrecer más ventajas a la hora de eliminar o reducir las fuerzas actuantes, de manera que se reducirá la tensión sobre el hueso que rodea al implante.

Otra consideración interesante a tener en cuenta es que las fuerzas máximas equivalentes de von Mises se produjeron en el hueso cortical adyacente al cuello del implante. Este comportamiento coincide con la información descrita en informes previos publicados^20-22. Adicionalmente, la distribución de la tensión sobre el hueso fue desigual y disminuyó al aumentar la distancia desde la localización de la fuerza actuante.

Un hallazgo importante de este informe lo constituye el hecho de que la tensión se distribuye casi por completo al hueso adyacente de las seis primeras roscas del implante, con independencia de su longitud, diámetro o geometría. Puesto que se ha observado que la distribución de la tensión sobre el hueso adyacente de cada espira es similar tanto para los implantes cortos (8,5 mm) como para los largos (15,0 mm) manteniendo un diámetro constante, puede sugerirse que bajo la misma carga oblicua, ambos tipos de implantes presentarán un comportamiento biomecánico comparable. Por ello, desde un punto de vista biomecánico, estos datos apoyan la idea de que en las zonas anatómicas limitadas por la altura de cresta alveolar residual, como las regiones posteriores del maxilar y la mandíbula, puede ser razonable utilizar implantes más cortos y de un diámetro superior.

Nota

Este artículo ha sido financiado por el Instituto de Biotecnología, Vitoria, España. Los autores son investigadores del centro.

---

Correspondencia: Eduardo Anitua,

Instituto Eduardo Anitua, c/José María Cajigal 19, 01005 Vitoria, Spain;

fax: [phone];

e-mail: [e-mail].