A la hora de realizar juicios y tomar decisiones sobre la salud, debemos procesar y comprender información numérica. Por ejemplo, habitualmente recibimos información sobre el riesgo de padecer una enfermedad en probabilidades, porcentajes o fracciones. Sin embargo, muchas personas presentan deficiencias a la hora de comprender esta información. En este trabajo, presentamos una revisión crítica de la evidencia empírica sobre los efectos que tienen las habilidades numéricas en diversos aspectos del proceso que acontece cuando un paciente acude al médico, más concretamente en la percepción de los riesgos médicos y la eficacia de los tratamientos. También describimos los distintos marcos teóricos que pretenden explicar estos efectos y resaltamos algunas de sus limitaciones. Por último, discutimos las ventajas y los inconvenientes de los instrumentos de medida de las habilidades numéricas, y destacamos entre ellos el Berlin Numeracy Test. Concluimos que este test puede evaluar las habilidades numéricas satisfactoriamente en diversos contextos, y planteamos diversas cuestiones que permanecen abiertas, como la relación entre las habilidades numéricas y diversos constructos psicológicos como la inteligencia o la reflexión cognitiva.
When we make judgments and decisions about our health, we are frequently faced with numerical information. For example, we often receive information concerning the risk of suffering an illness in terms of probabilities, percentages or fractions. However, many people have difficulties in understanding this type of information. In this paper, we present a critical review of the existing empirical evidence that documents the influence of numeracy on various aspects of the process that occurs when patients visit their doctor, focusing on perceptions of medical risks and treatment efficacy. We also outline different theoretical frameworks that have attempted to explain the impact of numeracy, highlighting some of their limitations. Finally, we discuss the advantages and disadvantages of existing tools for measuring numeracy, drawing attention to the Berlin Numeracy Test. We concluded that this test can satisfactorily assess numeracy in a wide range of contexts. We also discuss a number of open questions, including the relationship between numeracy and other psychological constructs, such as intelligence or cognitive reflection.
Actualmente debemos comprender y utilizar diferentes tipos de información numérica para solucionar problemas de la vida diaria. Habitualmente estamos expuestos a información sobre diferentes riesgos, entre los que se incluye el de sufrir diferentes enfermedades y sufrir un accidente de coche o un ataque terrorista. Esta información frecuentemente viene dada en probabilidades, porcentajes o fracciones (por ejemplo, “1 de cada 8 mujeres desarrollará cáncer de mama a lo largo de su vida”; Lipkus, Samsa & Rimer, 2001).
La habilidad de las personas para comprender esta información y tomar decisiones a partir de ella está estrechamente ligada a sus habilidades numéricas (es decir, a los conocimientos y las capacidades necesarias para comprender y utilizar la información numérica) (Cokely, Galesic, Schulz, Ghazal & Garcia-Retamero, 2012; Montori & Rothman, 2005; Peters, 2012; Peters et al., 2006; Schwartz, Woloshin, Black & Welch, 1997; véase Reyna, Nelson, Han & Dieckmann, 2009 para una revisión).
Las habilidades numéricas son especialmente relevantes en la interacción médico-paciente, ya que habitualmente implican el intercambio de información cuantitativa (e.g., efectividad de los tratamientos) (Garcia-Retamero, Wicki, Cokely & Hanson, 2014). Sin embargo, la investigación reciente indica que tanto los médicos como sus pacientes muestran dificultades para entender y/o comunicar esta información (Fagerlin et al., 2010; Gigerenzer, Gaissmaier, Kurz-Milcke, Schwartz & Woloshin, 2007; Nelson, Reyna, Fagerlin, Lipkus & Peters, 2008; Schwartz et al., 1997; Woloshin, Schwartz, Byram, Fischhoff & Welch, 2000). Estudios recientes también han puesto de manifiesto que muchas personas presentan escasa habilidad numérica en diversos países (por ejemplo, Estados Unidos y Alemania) (Fagerlin, Ubel, Smith & Zikmund-Fisher, 2007; Galesic & Garcia-Retamero, 2010, 2011; Garcia-Retamero, Galesic & Gigerenzer, 2011; Lipkus et al., 2001; Peters et al., 2006). En España, esta tendencia es especialmente acusada, tal y como muestran los datos recientes sobre el desempeño en escalas que miden las habilidades numéricas (Cokely et al., 2012). Ello podría influir en la calidad y la eficacia de los servicios de salud (Zikmund-Fisher et al., 2010), ya que las decisiones médicas incorrectas pueden implicar gastos económicos elevados (Gigerenzer et al., 2007).
Todo ello pone de manifiesto: la relevancia de determinar hasta qué punto las habilidades numéricas influyen en la percepción de los riesgos médicos, los beneficios derivados de los tratamientos y los juicios y la toma de decisiones sobre la salud, y la importancia de revisar los distintos marcos teóricos que permiten explicar el efecto de las habilidades numéricas en los juicios y la toma de decisiones. Asimismo, dada la relevancia de las habilidades numéricas tanto a nivel teórico como empírico, es fundamental conocer los instrumentos de medida que permiten evaluar estas habilidades, así como las propiedades psicométricas de dichos instrumentos (validez predictiva, convergente y discriminante) y las ventajas e inconvenientes derivados de su uso.
Esta revisión pretende alcanzar estos tres objetivos generales, poniendo especial énfasis en las habilidades numéricas en el contexto de la salud. Entre los instrumentos de medida existentes, destacamos el Berlin Numeracy Test (Cokely et al., 2012; Ghazal et al., 2014; Ghazal, Cokely & Garcia-Retamero, 2014), un instrumento desarrollado recientemente que cuenta con una validez predictiva superior a la de otros instrumentos ampliamente utilizados (Lipkus et al., 2001; Schwartz et al., 1997). Como resaltan Cokely et al. (2012) y Schapira et al. (2012), un buen instrumento de medida permite ajustar la comunicación de información médica a las necesidades de cada persona y fomenta así la toma de decisiones compartida entre el médico y sus pacientes.
Se concluye el artículo discutiendo algunas cuestiones que se podrían abordar en investigaciones futuras relacionadas con los temas revisados, y destacando algunos asuntos que sería importante tener en cuenta en la práctica médica (e.g, cuáles son los formatos de representación de la información que permitirían facilitar la comprensión de riesgos en personas con escasa habilidad numérica).
El efecto de las habilidades numéricas en los juicios y la toma de decisiones sobre la saludEl concepto de habilidades numéricas se ha definido de distintos modos. En las definiciones propuestas se han enfatizado distintos aspectos tales como la capacidad para comprender y utilizar probabilidades y conceptos numéricos básicos, la capacidad para inferir cuáles de los conceptos matemáticos se deben aplicar en distintas situaciones, o la capacidad para procesar dichos conceptos (Montori & Rothman, 2005; Peters et al., 2006; Schwartz et al., 1997). Los niveles más elementales de habilidades numéricas están relacionados con la comprensión del tiempo, la medida, y la estimación; mientras que los niveles superiores se centran en la comprensión de probabilidades, porcentajes o fracciones (Montori & Rothman, 2005; Reyna & Brainerd, 2008; véase Reyna et al., 2009).
En la presente revisión, haremos especial énfasis en las habilidades numéricas relacionadas con la comprensión de conceptos probabilísticos y estadísticos, dada su relevancia para la comprensión de la información de los riesgos para la salud. Cabe destacar que las habilidades numéricas en general se relacionan positivamente con el nivel educativo de las personas (Cokely et al., 2012; Ghazal et al., 2014; Reyna et al., 2009; Rothman, Montori, Cherrington & Pignone, 2008). En los cuestionarios que miden el grado de alfabetización de las personas, se suele considerar las habilidades numéricas uno de los componentes básicos (véase Reyna et al., 2009). No obstante, incluso las personas con alto nivel educativo pueden mostrar serias dificultades a la hora de comprender y utilizar probabilidades y conceptos numéricos básicos (Cokely et al., 2012; Lipkus et al., 2001). Ello indica que un nivel educativo más alto no se traduce necesariamente en habilidades numéricas más avanzadas (Reyna et al., 2009; Rothman et al., 2008).
Las habilidades numéricas influyen en varios aspectos del proceso que acontece cuando un paciente acude al médico, entre ellos la percepción del riesgo de sufrir una enfermedad y los beneficios derivados de los tratamientos médicos, la comprensión de la información que afecta a la toma de decisiones y los comportamientos de salud (Reyna et al., 2009). En primer lugar, el paciente debe entender los riesgos o beneficios asociados a las diversas opciones de tratamiento o pruebas diagnósticas. En este sentido, diversos estudios muestran que las habilidades numéricas son fundamentales para alcanzar una correcta interpretación de la información sobre el riesgo de sufrir efectos secundarios producidos por los medicamentos (Cavanaugh et al., 2008; Estrada, Martin-Hryniewicz, Peek, Collins & Byrd, 2004; Fagerlin et al., 2007a; Gardner, McMillan, Raynor, Woolf & Knapp, 2011).
Asimismo, las personas con bajas habilidades numéricas tienden a mostrar estimaciones sesgadas de la efectividad de las pruebas diagnósticas como la mamografía (Black, Nease & Tosteson, 1995; Davids, Schapira, McAuliffe & Nattinger, 2004; Schwartz et al., 1997), así como del riesgo que tienen de sufrir diversas enfermedades, entre las que se incluye el cáncer de mama (Woloshin, Schwartz, Black & Welch, 1999). La escasez de habilidades numéricas puede llevar también a dificultades a la hora de diferenciar entre niveles de riego de distinta magnitud (como el riesgo de sufrir cáncer de colon o de tener un bebé con síndrome de Down) (Keller & Siegrist, 2009).
Las habilidades numéricas escasas están asociadas también con sesgos que pueden afectar sistemáticamente a la comprensión de los riesgos médicos. Un ejemplo a destacar es el llamado neglect del denominador, que se refiere a la tendencia a centrar la atención en los numeradores de las fracciones e ignorar los denominadores. Esta tendencia puede llevar a estimaciones erróneas de la efectividad de los tratamientos y, por lo tanto, a decisiones médicas inadecuadas (Denes-Raj & Epstein, 1994; Garcia-Retamero & Galesic, 2009; Garcia-Retamero, Galesic & Gigerenzer, 2010; Kirkpatrick & Epstein, 1992; Okan, Garcia-Retamero, Cokely & Maldonado, 2012; Reyna & Brainerd, 2008; Reyna et al., 2009). Ello implica que las habilidades numéricas suponen también un importante componente en el proceso de toma de decisiones informadas (Berger & Hendee, 1989; Gaissmaier et al., 2012; Kalet, Roberts & Fletcher, 1994; Murphy et al., 1994; Schonwetter, Walker, Kramer & Robinson, 1993).
Otro sesgo relevante que puede afectar a la comprensión de los riesgos médicos es el efecto de framing, que se refiere a la influencia que en el proceso de decisión tiene la manera en la que se presenta la información, en términos de ganancias o pérdidas, o de modo más general en términos positivos o negativos (Levin, Schneider & Gaeth, 1998; McNeil, Pauker, Sox & Tversky, 1982; Tversky & Kahneman, 1981). Por ejemplo, diversos estudios en contextos médicos han mostrado que la probabilidad de llevar a cabo comportamientos orientados a la detección de enfermedades es mayor cuando la información se presenta en términos de posibles pérdidas, mientras que la información presentada en términos de posibles ganancias generalmente lleva a comportamientos orientados a la prevención de enfermedades (Banks et al., 1995; Garcia-Retamero & Cokely, 2011; Gerend & Shepherd, 2007; Rivers, Salovey, Pizarro, Pizarro & Schneider, 2005; Rothman, Martino, Bedell, Detweiler & Salovey, 1999).
Diversos estudios han mostrado que las personas con habilidades numéricas o matemáticas escasas se ven afectadas en mayor medida por efectos de framing, posiblemente debido a que muestran más dificultad a la hora de traducir los números de un formato a otro (Garcia-Retamero & Cokely, 2013; Garcia-Retamero & Galesic, 2010a; Peters et al., 2006; Peters & Levin, 2008; Simon, Fagley & Halleran, 2004). Asimismo, las personas con escasas habilidades numéricas se centran en mayor medida en información narrativa y menos en información sobre probabilidades, con lo que pueden llegar a distintas conclusiones sobre la misma información que las personas con altas habilidades numéricas (Dieckmann, Slovic, & Peters, 2009).
La insensibilidad a las probabilidades a priori es otro sesgo de razonamiento que puede afectar a la comprensión de los riesgos médicos. El conocido problema de la mamografía ilustra este fenómeno. En este problema, las personas deben estimar la probabilidad que una mujer tiene de sufrir cáncer de mama, dado que ha recibido un resultado positivo en la mamografía. Para ello ha de tener en cuenta la probabilidad a priori de contraer la enfermedad y la sensibilidad y la tasa de falsos positivos de la prueba (Eddy, 1982; véase también Gigerenzer & Hoffrage, 1995). Las personas frecuentemente ignoran la probabilidad a priori y sobrestiman la probabilidad de que una mujer con un resultado positivo en la prueba sufra cáncer de mama. Investigaciones recientes han mostrado que las personas con habilidades numéricas escasas son más proclives a llevar a cabo estimaciones erróneas y se benefician en menor medida de intervenciones orientadas a reducir este tipo de sesgo (Chapman & Liu, 2009; Garcia-Retamero & Hoffrage, 2013; McNair & Feeney, 2014; Miroslav & Marie, 2011).
No obstante, es necesario tener en cuenta también que las habilidades numéricas altas no siempre están asociadas con menos tendencia a mostrar sesgos de razonamiento. Por ejemplo, Peters et al. (2006) mostraron que las personas con habilidades numéricas altas consideran más atractivas las apuestas de dinero que conllevan la posibilidad de una ganancia (9 dólares) junto con la posibilidad de una pequeña pérdida (5 centavos) que aquellas que conllevan solamente la posibilidad de la misma ganancia pero sin pérdida. Los autores explicaron este hallazgo basándose en la capacidad de las personas con altas habilidades numéricas de extraer un significado afectivo más preciso de la comparación de la ganancia y la pérdida. Es decir, estas personas perciben la posible pérdida como pequeña en comparación con la posible ganancia, lo cual llevaría a evaluar la apuesta de un modo más favorable. Estos resultados muestran que, aunque las habilidades numéricas altas están generalmente asociadas con una mejor comprensión de la información numérica, en ciertas ocasiones pueden llevar también a mostrar sesgos o tomar decisiones inadecuadas.
Es también importante tener en cuenta que toda la evidencia no apunta siempre en la misma dirección. Por ejemplo, un estudio llevado a cabo por Peters, Harty y Fraenkel (2011) mostró que la percepción del riesgo de sufrir efectos secundarios tras tomar una medicación puede variar significativamente dependiendo de si la información presenta el número de personas afectadas frente al número de personas no afectadas. Sin embargo, este efecto de framing se observó independientemente del nivel de habilidades numéricas de los participantes. Los autores concluyen que una posible explicación de este resultado es que son solamente las personas con habilidades numéricas muy elevadas las que no muestran efectos de framing.
Las habilidades numéricas pueden afectar también al papel que prefieren los médicos y sus pacientes en la toma de decisiones sobre su salud (pasivo frente a activo). A lo largo de los años se ha pretendido implicar a los pacientes en la toma de decisiones sobre su salud (Barry, 1999; Gigerenzer & Gray, 2011), de tal manera que estos tengan la posibilidad de decidir qué tratamientos prefieren. Sin embargo, Galesic y Garcia-Retamero (2011a) mostraron que las personas con habilidades numéricas escasas, tanto en Estados Unidos como en Alemania, preferirían tener un papel más pasivo en la interacción con su médico del que realmente tienen, mientras que aquellas con habilidades numéricas altas se sentían satisfechas con su papel (véase Garcia-Retamero et al., 2014, para un estudio similar en médicos). Es posible que ello se deba a que las personas con habilidades numéricas escasas sienten más inseguridad. Ello se debería a las dificultades que experimentan para comprender la información que reciben (Estrada et al., 2004; Fagerlin, Zikmund-Fisher & Ubel, 2005; Galesic & Garcia-Retamero, 2010; Reyna & Brainerd, 2007; Schwartz et al., 1997).
En última instancia, las habilidades numéricas afectan a la comprensión de los resultados médicos y, por consiguiente, a la salud. Por ejemplo, las personas con habilidades numéricas escasas pueden llegar a tener peores resultados médicos cuando su estado de salud depende de su capacidad para seguir instrucciones complicadas sobre los medicamentos (Fagerlin et al., 2007) y presentan mayor riesgo de sufrir diversas enfermedades (como infarto de miocardio, diabetes mellitus o enfermedad pulmonar crónica) (Garcia-Retamero, Andrade, Sharit & Ruiz, en prensa). En esta línea, diversas investigaciones recientes han mostrado que las habilidades numéricas son esenciales en multitud de tareas de la vida cotidiana relacionadas con la salud, tales como la lectura de las etiquetas de los alimentos o de las recetas, la medición de las dosis de los medicamentos y la interpretación de la información sobre la concentración de azúcar en sangre u otros datos clínicos para controlar distintas enfermedades (Apter et al., 2006; Cavanaugh et al., 2008; Estrada et al., 2004; Huizinga et al., 2008; Rothman et al., 2006). Asimismo, las habilidades numéricas escasas se relacionan con peores percepciones de autoeficacia, menos conductas de autocuidado y mayor frecuencia de hospitalizaciones y visitas a urgencias (Apter et al., 2006; Cavanaugh et al., 2008).
Explicaciones del efecto de las habilidades numéricas: marcos teóricos y mecanismos cognitivosLa amplia evidencia empírica revisada sobre el efecto de las habilidades numéricas lleva a plantear varias cuestiones de interés. Por ejemplo, ¿cuáles son los mecanismos cognitivos que permiten explicar la relación entre las habilidades numéricas y los juicios y la toma de decisiones? ¿Las personas con altas y bajas habilidades numéricas procesan la información de modo diferente? Para responder a estas preguntas, Reyna et al. (2009) destacan cuatro marcos teóricos: a) la tradición psicofísica; b) los enfoques computacionales; c) las teorías de procesamiento dual de la información, y d) la teoría de representación borrosa (fuzzy-trace theory).
Desde la tradición psicofísica, se enfatiza la idea de que las representaciones mentales de las magnitudes no son siempre lineales (Dehaene, 1997; Gallistel & Gelman, 2005). Por ejemplo, la diferencia entre los valores 10 y 20 se percibe frecuentemente como mayor que la diferencia entre 110 y 120, a pesar de que en términos absolutos la diferencia sea idéntica. En este sentido, se puede considerar que la percepción de los números está en cierta medida distorsionada. Las personas con habilidades numéricas escasas mostrarían un mayor grado de distorsión al tener representaciones mentales de las magnitudes menos precisas (véase por ejemplo, Peters, Slovic, Västfjäll & Mertz, 2008; Peters, 2012; Reyna et al., 2009). Una de las teorías que ha explicado dicha distorsión en la percepción de las magnitudes es la teoría de la perspectiva (prospect theory) (véase Tversky & Kahneman, 1992). La investigación en esta tradición psicofísica es relevante, por una parte, para explicar los mecanismos causales subyacentes a las habilidades numéricas (Cantlon & Brannon, 2007; Dehaene, 2007; Furlong & Opfer, 2009; Gallistel & Gelman, 2005; Reyna & Brainerd, 1993, 1994; Shanteau, 1992; Siegler & Opfer, 2003) y, por otra, para explicar los mecanismos de los juicios y la toma de decisiones que implican información numérica (Chen, Lakshminarayanan & Santos, 2006; Furlong & Opfer, 2009; Petrova, Pligt & Garcia-Retamero, 2013). Las críticas que ha recibido este enfoque, más concretamente la teoría de la perspectiva, provienen de la carencia de un modelo subyacente que lo explique. Aunque diversas investigaciones han puesto de manifiesto resultados concluyentes (Tversky & Kahneman, 1992), no ocurre lo mismo cuando se modifican o se añaden parámetros (Reyna & Brainerd, 2011).
Desde los enfoques computacionales, se subrayan las limitaciones existentes en la capacidad de procesamiento de la información. La presentación de información numérica en formatos que permiten reducir la carga cognitiva asociada al procesamiento numérico (por ejemplo, subrayando la información relevante y eliminando la irrelevante) puede producir mejoras sustanciales en la comprensión de la información en personas con habilidades numéricas escasas (Peters, Dieckmann, Dixon, Hibbard & Mertz, 2007). Ello parece indicar que las diferencias en las habilidades numéricas podrían estar asociadas, al menos parcialmente, con diferencias en capacidad de almacenamiento y procesamiento de la información (como la memoria de trabajo). Sin embargo, como destacan Cokely et al. (2012), existen muy pocos estudios que hayan investigado directamente cuáles son los procesos cognitivos que siguen las personas con altas y bajas habilidades numéricas para realizar juicios y decisiones basados en información numérica. Una excepción es un estudio llevado a cabo por Cokely y Kelley (2009), que mostró la existencia de diferencias en las estrategias de codificación de la información presentada en los problemas numéricos. Las personas con habilidades numéricas altas llevaron a cabo procesos de búsqueda de información más elaborados y exhaustivos, lo que indica que no se puede atribuir las diferencias en habilidades numéricas únicamente a diferencias en capacidad de procesamiento.
Las teorías de procesamiento dual de la información (Kahneman, 2011; véase también Evans, 2008; Sloman, 1996; Stanovich, 1999) parten de la premisa de que existen dos sistemas distintos de procesamiento: el procesamiento intuitivo o automático (sistema 1) y el procesamiento analítico o controlado (sistema 2). En esta línea, se ha planteado que el procesamiento intuitivo lleva a sesgos y errores en el razonamiento numérico, mientras que el procesamiento analítico está asociado con un razonamiento numérico objetivo y exacto. Por ejemplo, Epstein, Pacini, Denes-Raj y Heier (1996) plantean que la tendencia descrita anteriormente a ignorar los denominadores en las fracciones y centrar la atención en los numeradores (neglect del denominador) está determinada por el predominio del procesamiento intuitivo sobre el analítico. Sin embargo, los datos empíricos no siempre muestran una asociación clara entre procesamiento intuitivo y el efecto del neglect del denominador (véase Gigerenzer & Regier, 1996, y Reyna et al., 2009; para una discusión sobre las limitaciones del marco teórico del doble sistema de procesamiento, véase Cokely & Kelley, 2009).
Algunos autores han planteado que el procesamiento analítico sería más habitual en las personas con altas habilidades numéricas, puesto que este tipo de procesamiento requiere la habilidad de procesar la información numérica de un modo preciso y correcto (Peters et al., 2006). En cambio, en este tipo de tareas las personas con habilidades numéricas escasas se guiarían en mayor medida por un procesamiento de la información afectivo y poco preciso.
Por último, la teoría de representación borrosa (Reyna & Lloyd, 2006; Reyna, 2004; Reyna et al., 2009) explica las diferencias en razonamiento numérico asumiendo la existencia de dos modos de procesamiento de la información: verbatim (codificación de información literal) y quid (codificación poco precisa, que incluye la interpretación de la información que asigna la propia persona). En contraste con las teorías de procesamiento dual destacadas, desde este enfoque se asume que el procesamiento menos preciso puede llevar a un mejor desempeño en tareas numéricas, mientras que el procesamiento de los números exactos puede estar asociado con sesgos y errores en la comprensión. Desde esta perspectiva, los sesgos de razonamiento como la falacia de conjunción (Tversky & Kahneman, 1983) se atribuyen al procesamiento verbatim de la información (Reyna & Mills, 2007; Wolfe & Reyna, 2010), mientras que los efectos de framing mencionados se atribuyen a la preferencia de las personas por el modo de procesamiento quid (Reyna & Brainerd, 1991, 2008).
Asimismo, la teoría de la representación borrosa asume que el efecto del neglect del denominador se debe al solapamiento de las categorías de los numeradores y los denominadores. En las fracciones, la información representada en el numerador (e.g., el número de personas que han fallecido tras una intervención quirúrgica) formaría parte también de la información representada en el denominador (el número total de personas que pasaron por una intervención, que incluye a los que han fallecido y los que no). Este solapamiento llevaría a confusión y, por lo tanto, a centrarse en la información representada en los numeradores (Brainerd & Reyna, 1990; Reyna, 1991, 2004).
La teoría de la representación borrosa asume que las personas con altas habilidades numéricas se guían en mayor medida por el procesamiento quid de los números frente al verbatim. No obstante, esta teoría plantea que estas personas también mostrarán confusión derivada del solapamiento de las categorías de los denominadores y los numeradores (Nelson et al., 2008). Diversas investigaciones (Brainerd & Reyna, 1990; Reyna & Brainerd, 1991) han apoyado esta idea y han etiquetado este tipo de confusiones como “ilusiones de categorías de inclusión”. Esta idea se basa en la amplia evidencia del trabajo original de Piaget en el que los niños más pequeños tienen dificultades para comparar los números relativos del numerador y el denominador, ya que es difícil mantener en su memoria un conjunto numérico cuando una de sus partes ha sido separada (Inhelder & Piaget, 1959; Piaget, 1952). Es más, esta teoría supone que las intervenciones orientadas a centrar la atención en información numérica específica pueden conllevar una ejecución peor en tareas de razonamiento y toma de decisiones (Reyna & Lloyd, 2006). Sin embargo, como destacan Cokely et al. (2012), actualmente no existe un instrumento que permita medir o predecir la tendencia a utilizar representaciones verbatim o quid.
En definitiva, las teorías desarrolladas hasta la fecha son intentos preliminares, aunque fructíferos, para explicar las diferencias en los juicios y la toma de decisiones de personas con altas y bajas habilidades numéricas. No obstante, es necesario llevar a cabo más investigación empírica basada en estas teorías para aclarar la cuestión de los mecanismos específicos que subyacen a dichas diferencias. Para ello resultaría de gran utilidad llevar a cabo un análisis pormenorizado de los procesos mediante los cuales las personas buscan información, determinan cuándo se detiene la búsqueda, y utilizan la información. Todo ello puede dar lugar a distintas estrategias que pueden resultar más o menos efectivas (Garcia-Retamero & Dieckmann, 2006; GarciaRetamero, Ramos & Catena, 2008). Como destacan Cokely et al. (2012), es posible que las habilidades numéricas estén relacionadas con una compleja interacción entre los diferentes mecanismos propuestos, y es necesario determinar cómo se relacionan entre ellos y el peso que tiene cada uno en función de las características específicas de la tarea.
Instrumentos para medir las habilidades numéricasPodemos clasificar los instrumentos de medida de las habilidades numéricas del siguiente modo: a) medidas objetivas, en las que las personas han de realizar cálculos numéricos (véase Black et al., 1995; Galesic & Garcia-Retamero, 2010; Lipkus et al., 2001; Peters et al., 2006; Schwartz et al., 1997; Weller et al., 2013; para una revisión, véase Reyna et al., 2009), y b) medidas subjetivas, en las que las personas expresan el nivel de confianza sobre su propia capacidad para comprender y aplicar las cantidades numéricas (Fagerlin et al., 2007).
Uno de los primeros intentos de evaluar las habilidades numéricas de un modo objetivo incluye varias cuestiones relacionadas con la comprensión de conceptos de riesgo y probabilidad, y fue llevado a cabo por Black et al. (1995). Los autores pidieron a un grupo de personas que especificaran el número de veces que puede salir cara en mil lanzamientos de una moneda no trucada y que respondiesen a otras preguntas relacionadas con el riesgo de sufrir una enfermedad. Posteriormente, Schwartz et al. (1997) desarrollaron una escala con tres ítems que evalúa conocimientos básicos sobre probabilidad, la capacidad de realizar operaciones matemáticas simples en magnitudes de riesgo como porcentajes y proporciones, y la capacidad de realizar conversiones entre dichas magnitudes.
Más recientemente, Lipkus et al. (2001) ampliaron la escala de Schwartz et al. (1997) agregando siete preguntas enmarcadas en un contexto de salud, una de ellas con dos partes: “Si la probabilidad de contraer una enfermedad es del 10%, ¿cuántas personas se espera que contraigan la enfermedad? a) de 100; b) de 1.000”). La escala consta de un total de 11 ítems y una pregunta de práctica (para una traducción del instrumento al español, véase Garcia-Retamero & Galesic, 2013).
La validación de la escala de Lipkus et al. (2001) se llevó a cabo en una población estadounidense de elevado nivel educativo (n = 463). La escala mostró buena consistencia interna (alfa de Cronbach =.54) (Lipkus et al., 2001). Como destacan Cokely et al. (2012), Lipkus et al. (2001) y Reyna et al. (2009), a pesar del alto nivel educativo de la muestra, una proporción considerable de las personas evaluadas mostraron dificultades para contestar preguntas relativamente sencillas que medían las habilidades numéricas. Por ejemplo, el 20% de los encuestados respondió incorrectamente a preguntas básicas relacionadas con la comparación de la magnitud de distintos riesgos (e.g., “¿Cuál de las siguientes cantidades representa mayor riesgo de contraer una enfermedad?: 1%, 5% o 10%?”). Ello indica que las intervenciones dirigidas a fomentar la toma de decisiones compartida en contextos médicos pueden estar abocadas al fracaso si se asume que los pacientes tienen un nivel de habilidades numéricas elevado.
Entre las medidas subjetivas, destaca la escala de Fagerlin et al. (2007). En ella, las personas informan sobre su capacidad de realizar tareas matemáticas y sobre su preferencia respecto al modo de recibir información sobre los riesgos (formato numérico frente a verbal) (véase también Zikmund-Fisher, Smith, Ubel & Fagerlin, 2007). Diversos estudios han mostrado la existencia de correlaciones moderadas o altas entre las medidas objetivas y subjetivas (Fagerlin et al., 2007; Ghazal et al., 2014; Weller et al., 2013; Zikmund-Fisher et al., 2007). Sin embargo, otras investigaciones indican que las personas pueden tener un exceso de confianza a la hora de evaluar subjetivamente su capacidad numérica (Sheridan, Pignone & Lewis, 2003).
Recientemente, Liberali, Reyna, Furlan, Stein, & Pardo (2012) investigaron si las escalas objetivas (Lipkus et al., 2001) y subjetivas (Fagerlin et al., 2007a) medían el mismo constructo, y obtuvieron como resultado que, pese a que estas escalas muestran cierto grado de varianza compartida, sus ítems no saturan en los mismos factores. Ello indica que las escalas no miden necesariamente el mismo constructo y, por lo tanto, no se puede emplear indistintamente. No obstante, cabe destacar que las medidas subjetivas pueden ser de especial utilidad en entornos clínicos, puesto que implican menos carga mental y son menos aversivas que las objetivas (para una revisión, véase Liberali et al., 2012). En cualquier caso, el uso de medidas objetivas es más común.
Diversos estudios recientes han utilizado las escalas de Schwartz et al. (1997) y Lipkus et al. (2001), y han mostrado que estas escalas predicen los niveles de comprensión de los riesgos que presentan las personas así como sus juicios y decisiones (Cokely & Kelley, 2009; Galesic & Garcia-Retamero, 2010; Peters et al., 2006). No obstante, ambas escalas presentan una serie de limitaciones psicométricas, como la dificultad para discriminar satisfactoriamente entre la población con mayor rendimiento (como muestras de estudiantes universitarios, que suelen ser las que han participado en los estudios llevados a cabo sobre el tema). Por ejemplo, Cokely y Kelley (2009) aplicaron la escala de Lipkus et al. (2001) a una muestra de estudiantes universitarios de Estados Unidos, y encontraron que la mayoría de los participantes contestaron más del 80% de los ítems correctamente. Galesic y Garcia-Retamero (2010) también encontraron problemas a la hora de discriminar en un estudio llevado a cabo con muestras representativas de la población de Alemania y Estados Unidos, y hallaron que una media del 68.5% de los ítems fueron contestados correctamente por la muestra alemana y un 64.5% de los ítems por la muestra estadounidense. Ello indica que estas escalas presentan importantes efectos de techo, con puntuaciones distribuidas con asimetría negativa. El Berlin Numeracy Test (Cokely et al., 2012) permite superar esta limitación de las escalas mencionadas y muestra una serie de características ventajosas adicionales.
El Berlin Numeracy TestEl Berlin Numeracy Test (Cokely et al., 2012; véase www. RiskLiteracy.org) es un instrumento breve, flexible y de fácil aplicación, desarrollado con el objetivo de superar las limitaciones psicométricas de los instrumentos previos. Para su elaboración, se comenzó utilizando protocolos verbales en los que se analizaron las respuestas que un grupo de 300 personas de nacionalidad alemana ofrecían a diversos problemas matemáticos. En una segunda fase, se evaluaron 28 ítems que medían habilidades numéricas (12 ítems procedentes de la escala de Lipkus et al., 2001, y 16 ítems nuevos) utilizando el software de categorización DTREG. De este modo, se seleccionaron los cuatro ítems que forman el Berlin Numeracy Test (véase el apéndice).
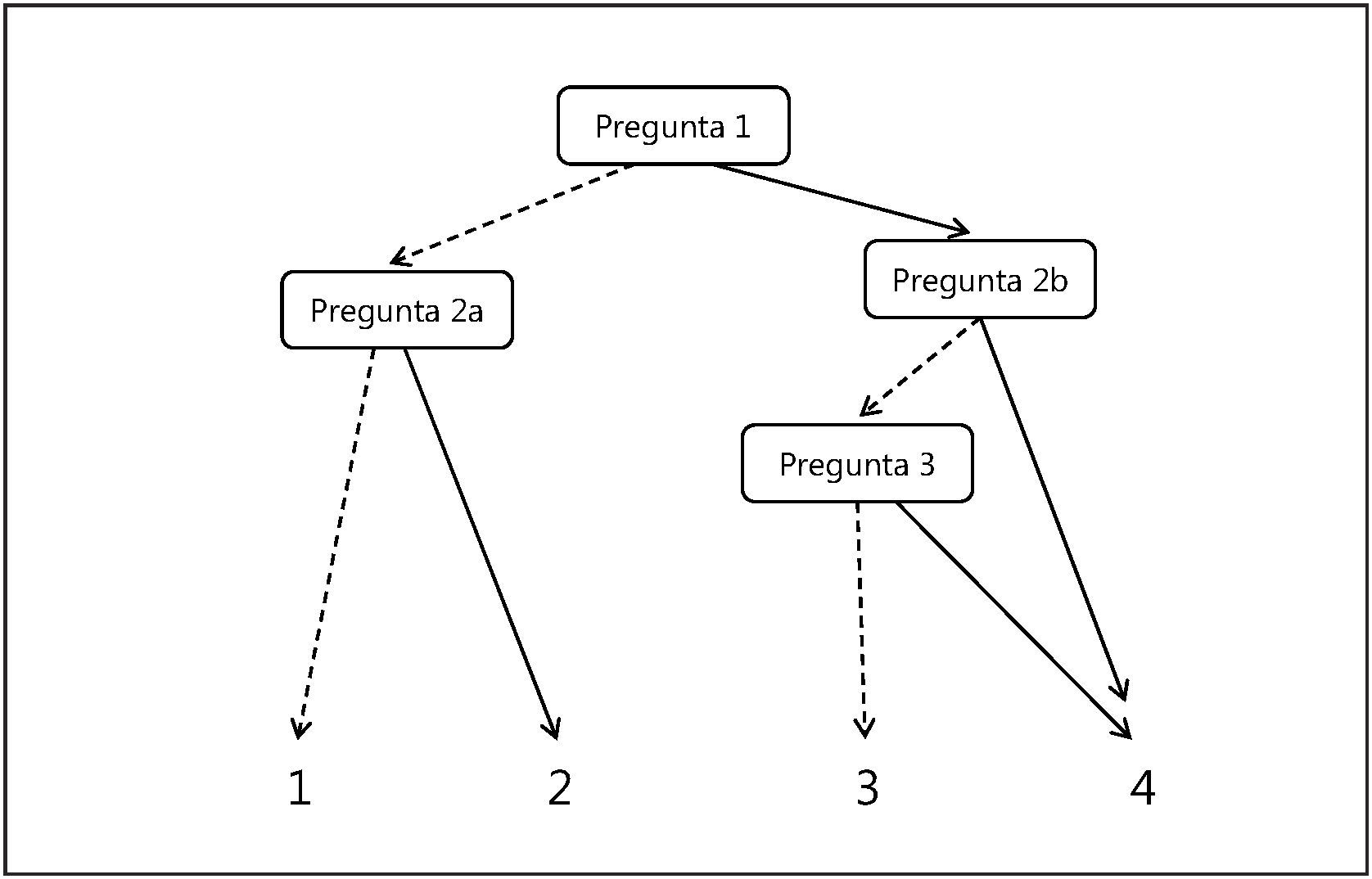
A partir de estos cuatro ítems, se desarrollaron tres formatos distintos de aplicación del test. En primer lugar (y a diferencia de los instrumentos anteriores) una de las versiones del Berlin Numeracy Test (la versión de ordenador) tiene un formato dinámico. Esta versión permite determinar el nivel de habilidades numéricas de los participantes en función de su respuesta a dos o tres preguntas de las cuatro disponibles. Es decir, los participantes no tienen que responder a los cuatro ítems. Por el contrario, su respuesta ante cada uno de ellos determina el ítem que se presentará a continuación. Esta versión del test presenta una estructura en forma de árbol (figura 1), de tal manera que todos los ítems presentan un 50% de probabilidad pretest de respuesta correcta. Dependiendo de si la respuesta a una pregunta es correcta o incorrecta, se presenta después otro ítem más difícil o más fácil. La probabilidad de responder correctamente este ítem es también del 50%.
Asimismo, también hay disponible una versión del test en formato tradicional (papel y lápiz). Esta versión requiere que los participantes respondan a las cuatro preguntas. Por último, para casos en los que haya premura, existe una versión del test que incluye solo el ítem 1. Esta versión permite determinar si las personas se sitúan por encima o por debajo de la mediana de las puntuaciones.
En un estudio, se compararon las propiedades psicométricas de los tres formatos del Berlin Numeracy Test con las de las escalas de Lipkus et al. (2001) y Schwartz et al. (1997). En primer lugar, el alfa de Cronbach del formato en papel y lápiz es superior a los de las escalas de Lipkus et al. (2001) y Schwartz et al. (1997) (α = .59 frente a α = .52 y α = .54). Asimismo, el Berlin Numeracy Test presenta mayor validez convergente y discriminante. Concretamente, las puntuaciones en el test se correlacionan positivamente con medidas de habilidades cognitivas generales, estilos cognitivos y educación y no muestran relación con otras medidas que miden otros constructos diferentes de las habilidades numéricas, como motivación y personalidad (para un estudio con resultados similares, véase Ghazal et al., 2014).
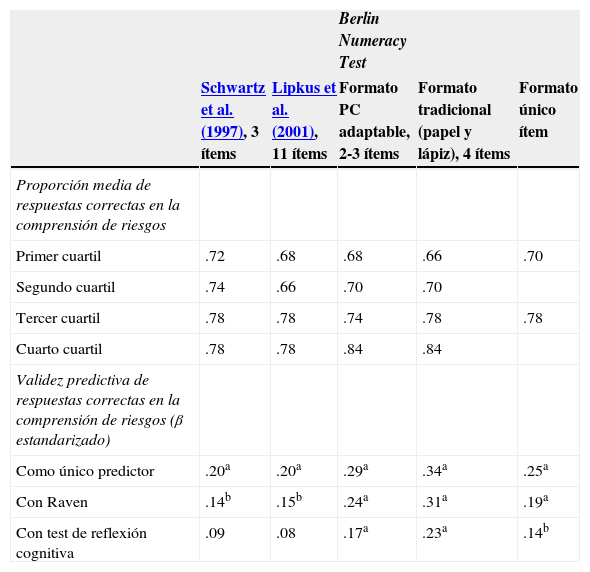
Con la finalidad de evaluar la validez predictiva del Berlin Numeracy Test, se aplicó una batería corta de ítems que miden la comprensión de los riesgos para la salud (Garcia-Retamero & Galesic, 2013). Se comparó la ejecución de dicho test con la de las escalas de Schwartz y Lipkus. Como se puede observar en la tabla 1, el Berlin Numeracy Test presenta mayor validez predictiva. Además, el efecto de las habilidades numéricas medidas con el Berlin Numeracy Test se mantiene aun controlando el efecto de constructos como inteligencia, medida con el test de Raven, o reflexión cognitiva (es decir, la capacidad para suprimir respuestas automáticas e impulsivas y guiarse por procesos controlados conscientemente) (Frederick, 2005).
Propiedades psicométricas de los instrumentos: Validez predictiva
| Berlin Numeracy Test | |||||
|---|---|---|---|---|---|
| Schwartz et al. (1997), 3 ítems | Lipkus et al. (2001), 11 ítems | Formato PC adaptable, 2-3 ítems | Formato tradicional (papel y lápiz), 4 ítems | Formato único ítem | |
| Proporción media de respuestas correctas en la comprensión de riesgos | |||||
| Primer cuartil | .72 | .68 | .68 | .66 | .70 |
| Segundo cuartil | .74 | .66 | .70 | .70 | |
| Tercer cuartil | .78 | .78 | .74 | .78 | .78 |
| Cuarto cuartil | .78 | .78 | .84 | .84 | |
| Validez predictiva de respuestas correctas en la comprensión de riesgos (β estandarizado) | |||||
| Como único predictor | .20a | .20a | .29a | .34a | .25a |
| Con Raven | .14b | .15b | .24a | .31a | .19a |
| Con test de reflexión cognitiva | .09 | .08 | .17a | .23a | .14b |
ap < .01.
bp < .05.
Tabla extraída de Cokely, Galesic, Schulz, Ghazal & Garcia-Retamero (2012). Reproducido con permiso.
Finalmente, el Berlin Numeracy Test ha sido validado en muestras de personas procedentes de 60 países distintos (de los cinco continentes), y ha mostrado una buena discriminación en diferentes muestras, culturas y lenguas (véase Cokely et al., 2012; Garcia-Retamero et al., 2014). En estudios más recientes, se ha mostrado también que las puntuaciones de los pacientes en el Berlin Numeracy Test predicen importantes resultados médicos y conductas, como la probabilidad de sufrir determinadas enfermedades y la cantidad de fármacos que toman los pacientes (Garcia-Retamero et al., en prensa). Todo ello nos lleva a concluir que el Berlin Numeracy Test es un instrumento que permite medir de manera rápida y fiable las habilidades numéricas de las personas, con lo que se superan en gran medida las limitaciones de otras escalas que miden el mismo constructo. No obstante, es necesario tener en cuenta que la distribución de puntuaciones en el Berlin Numeracy Test puede mostrar un sesgo positivo en poblaciones con bajo nivel educativo o de edad avanzada. En ese caso, los autores recomiendan la utilización del test en combinación con los ítems de la escala de Schwartz et al. (1997) (véase Ghazal et al., 2014).
Instrumentos posteriores al Berlin Numeracy TestRecientemente también se han desarrollado otras escalas de medida de las habilidades numéricas. Estas escalas presentan propiedades positivas que hacen aconsejable su uso. No obstante, también presentan algunas limitaciones que no muestra el Berlin Numeracy Test. Así, por ejemplo, el Numeracy Understanding in Medicine Instrument (NUMi) (Schapira et al., 2012) pretende medir diferentes subcomponentes del constructo de las habilidades numéricas. A diferencia de los instrumentos previos, el NUMi se ha desarrollado a partir de la teoría de respuesta al ítem.
Con este instrumento, se miden cuatro habilidades específicas: el sentido del número, la habilidad de interpretar y usar tablas y gráficos, la comprensión de conceptos probabilísticos y la comprensión de estadística. El NUMi pretende ir más allá que el resto de los instrumentos disponibles, midiendo de un modo exhaustivo todo el espectro de aspectos relacionados con las habilidades numéricas, según el marco teórico de los autores. Permite una buena discriminación entre personas con habilidades numéricas bajas. Por ello, podría ser de especial utilidad para identificar a quienes están en mayor riesgo de no comprender la información numérica sobre la salud. No obstante, en comparación con otros instrumentos previos, su aplicación requiere disponer de más tiempo. Además, aún no existen datos que indiquen si las puntuaciones en habilidades numéricas derivadas del uso de este instrumento se correlacionan con los juicios y las decisiones de las personas.
Por otra parte, Weller et al. (2013) han desarrollado recientemente otra escala de habilidades numéricas teniendo en cuenta la teoría de respuesta al ítem. La escala combina ítems de varias escalas de habilidades numéricas existentes (Lipkus et al., 2001; Schwartz et al., 1997) y muestra una distribución de las puntuaciones mejor que la de las escalas previas. De este modo, permite superar algunas limitaciones psicométricas de las escalas de Schwartz et al. (1997) y Lipkus et al. (2001). Sin embargo, los autores resaltan que la distribución de las puntuaciones sigue mostrando un sesgo. Al igual que el NUMi, esta escala tampoco ha sido validada fuera de Estados Unidos ni en distintos tipos de muestras, lo cual contrasta con el Berlin Numeracy Test, que ha sido ampliamente validado.
Discusión y conclusionesEn este artículo se ha revisado la evidencia empírica que muestra la influencia que las habilidades numéricas de las personas tienen en sus juicios y decisiones relacionados con los riesgos para la salud. Se han revisado también los distintos marcos teóricos que podrían permitir explicar el efecto de las habilidades numéricas y hemos destacado los problemas asociados con algunos de ellos. Por último, se ha realizado una revisión crítica de las ventajas y los inconvenientes de los instrumentos de medida de las habilidades numéricas existentes hasta la fecha.
Nuestra revisión no pretende ser exhaustiva, aunque sí hemos intentado presentar una visión general sobre el estado de la literatura en este ámbito. Para concluir, nos gustaría destacar que aún quedan varias cuestiones abiertas, lo cual nos permite incidir en la importancia de seguir investigando sobre este tema. Por ejemplo, una cuestión que aún no se ha investigado es hasta qué punto se relacionan las habilidades numéricas con otros constructos psicológicos como la inteligencia, la memoria de trabajo o la reflexión cognitiva. Se han realizado relativamente pocos estudios sobre esta cuestión. La evidencia existente apunta a cierto grado de varianza compartida, como ponen de manifiesto las correlaciones observadas entre estas variables y las habilidades numéricas (véase Cokely et al., 2012; Cokely & Kelley, 2009; Liberali et al., 2012; Schapira et al., 2012).
No obstante, cabe destacar que el efecto de las habilidades numéricas en la comprensión de riesgos se mantiene aun controlando estadísticamente el efecto de la inteligencia, la reflexión cognitiva o la memoria de trabajo (Cokely et al., 2012; Peters & Levin, 2008; Peters et al., 2006; pero véase también Missier, Mäntylä & Bruine de Bruin, 2012). En la misma línea, otro estudio reciente llevado a cabo por Liberali et al. (2012) mostró, utilizando análisis factorial, que los ítems que miden habilidades numéricas saturan en un factor distinto que los que miden reflexión cognitiva (véase también Weller et al., 2013).
Cabe destacar también que las habilidades numéricas muestran una clara independencia de otros factores como la motivación, la personalidad o la ansiedad frente a los exámenes (Cokely et al., 2012). Asimismo, diversas investigaciones exponen que hay relación entre la ansiedad a las matemáticas y el nivel de habilidades numéricas y encuentran que los participantes con alto nivel de ansiedad muestran mayor número de errores en tareas de suma que aquellos con poca ansiedad (Ashcraft, 2002; Ashcraft & Kirk, 2001). Estos hallazgos apuntan a una relación negativa entre la capacidad de la memoria de trabajo y la ansiedad a las matemáticas. En cualquier caso, sería interesante investigar estas relaciones de un modo más directo y exhaustivo en futuros estudios.
Otra cuestión que aún permanece abierta es la especificidad de dominio de las habilidades numéricas. Aunque generalmente se ha asumido que es posible evaluar las habilidades numéricas independientemente del dominio en que se utilizan (como salud y finanzas), algunas investigaciones recientes han mostrado que las personas tienen mayores dificultades a la hora de realizar tareas numéricas en el ámbito de la salud (Levy, Ubel, Dillard, Weir & Fagerlin, 2014). Ello indica que las habilidades numéricas en el ámbito de la salud pueden no ser totalmente equivalentes a las habilidades numéricas en general. Investigaciones futuras deberían abordar este asunto para aclarar si el dominio en que se lleva a cabo la evaluación de las habilidades numéricas influye a la hora de comprender la información y tomar decisiones basadas en dicha información.
Otra cuestión fundamental es qué formatos de representación de la información podrían mejorar la comprensión de los riesgos médicos. Esta cuestión es de especial relevancia si tenemos en cuenta las importantes deficiencias en habilidades numéricas de la población general. Diversos investigadores han abordado esta cuestión empíricamente (Apter et al., 2008; Fagerlin et al., 2007; Garcia-Retamero & Cokely, 2013; Garcia-Retamero & Galesic, 2013; Lipkus & Hollands, 1999; Peters, Hibbard, Slovic & Dieckmann, 2007; Reyna & Brainerd, 2008; Tubau, 2008).
Entre las recomendaciones derivadas de estas investigaciones, destaca la utilización de formatos transparentes que presentan información sobre riesgos en términos absolutos (e.g., “la ingesta de un fármaco reduce el riesgo de padecer un trastorno de un 8% a un 5%”) en lugar de relativos (“la ingesta de un fármaco reduce el riesgo de padecer un trastorno en un 38%”), las tasas de mortalidad en lugar de las de supervivencia, y las frecuencias naturales en lugar de probabilidades condicionadas (Fagerlin et al., 2007a; Gigerenzer et al., 2007). Estas recomendaciones se basan en estudios que han puesto de manifiesto que el formato de presentación de la información numérica puede afectar sustancialmente a la comprensión (Fagerlin et al., 2007; Gigerenzer et al., 2007; Gigerenzer & Hoffrage, 1995; Hoffrage & Gigerenzer, 1998). Estos estudios también han puesto de manifiesto que los formatos transparentes como las frecuencias naturales pueden ser especialmente útiles para personas con habilidades numéricas escasas (Garcia-Retamero & Hoffrage, 2013).
Asimismo, la información presentada gráficamente mediante apoyos visuales puede mejorar sustancialmente la comunicación y la comprensión de la información (GarciaRetamero & Galesic, 2009, 2010a, 2010b; Garcia-Retamero et al., 2011; Garcia-Retamero & Cokely, 2011, 2013; Lipkus & Hollands, 1999; para una escala de medida de las habilidades gráficas, véase Galesic & Garcia-Retamero, 2011b). De este modo, se puede fomentar la toma de decisiones compartida (Garcia-Retamero et al., 2014). Recientemente, Garcia-Retamero y Muñoz (2013) han puesto de manifiesto que la representación visual de la información numérica mejora considerablemente las inferencias realizadas por las personas mayores con bajas habilidades numéricas. No obstante, es importante tener en cuenta también el nivel de habilidades gráficas de las personas, puesto que, si este es bajo, incluso los apoyos visuales pueden resultar poco eficaces (Gaissmaier et al., 2012; Galesic & Garcia-Retamero, 2011b; Okan, Garcia-Retamero, Cokely et al., 2012; Okan, Garcia-Retamero, Galesic & Cokely, 2012). Investigaciones recientes muestran que la eficacia de los apoyos visuales en personas con habilidades gráficas escasas se puede aumentar usando gráficos dinámicos diseñados para fomentar el procesamiento activo de la información (Okan, Garcia-Retamero, Cokely & Maldonado, en prensa).
También es importante tener en cuenta hasta qué punto los apoyos visuales resultan útiles debido a su naturaleza visual, frente a otras características no relacionadas necesariamente con dicha naturaleza. Por ejemplo, Keller, Siegrist y Visschers (2009) mostraron que los apoyos visuales que muestran información comparativa sobre riesgos pueden ayudar a mejorar la comprensión debido a la presencia de dicha información, y no tanto debido al formato gráfico en sí. Este resultado parece indicar que las personas con habilidades numéricas escasas muestran especiales dificultades para evaluar un único riesgo aislado, puesto que son incapaces de evaluar si el riesgo es alto o bajo. Los resultados de un estudio de registro de movimientos oculares respaldan esta hipótesis y muestran que las personas con habilidades numéricas escasas procesan la información comparativa (como el riesgo asociado con fumar tabaco) de un modo más profundo que las personas con altas habilidades (Keller, 2011). Es necesario llevar a cabo más investigación para establecer con precisión los aspectos específicos de los apoyos visuales que pueden ser especialmente útiles para personas con habilidades numéricas escasas.
En conclusión, las habilidades numéricas tienen un papel fundamental en la comprensión de información de riesgos y en la toma de decisiones, con especial impacto en el ámbito médico. Debido a las diferencias en el nivel de habilidades numéricas de las personas, sería recomendable que los médicos contaran con medios para evaluar dichas habilidades y así poder adaptar la información pertinente a las necesidades de cada paciente. Entre los instrumentos que permitirían llevar a cabo dicha evaluación de una manera rápida, fácil y eficaz, destaca el Berlin Numeracy Test (Cokely et al., 2012), el cual cuenta con las ventajas de ser un instrumento breve y fácil de aplicar que presenta unas características psicométricas superiores a las de otros instrumentos.
AgradecimientosEsta revisión es parte del trabajo de fin de Máster de la primera autora. Nos gustaría dar las gracias a todos los miembros de la comisión evaluadora por sus comentarios. También estamos agradecidas a los dos revisores anónimos por sus valiosos comentarios y sugerencias.
FinanciaciónEste trabajo ha sido posible gracias a los proyectos de investigación PSI2011-22954 y PSI2014-51842-R financiados por el Ministerio de Economía y Competitividad (España).
Q1. De las 1.000 personas que viven en un pequeño pueblo, 500 son miembros de un coro. De esos 500 miembros del coro, 100 son hombres. De los 500 habitantes que no pertenecen a un coro, 300 son hombres. ¿Cuál es la probabilidad de que un hombre seleccionado al azar sea miembro de un coro? Por favor, indique la probabilidad en porcentaje: ______ (Respuesta correcta: 25%)
Q2a. Imagine que tiramos un dado de cinco caras 50 veces. En promedio, de estas 50 tiradas, ¿cuántas veces cree que saldría un número impar (1, 3, o 5) en este dado de cinco caras? ______ de 50 tiradas. (Respuesta correcta: 30)
Q2b. Imagine que tiramos un dado trucado de seis caras. La probabilidad de que salga un 6 al tirar el dado es el doble que la probabilidad de que salga uno de los demás números. En promedio, en 70 tiradas, ¿cuántas veces cree que saldría el número 6? ______ de 70 tiradas. (Respuesta correcta: 20)
Q3. En un bosque, el 20% de las setas son rojas, el 50% son marrones y el 30% son blancas. La probabilidad de que una seta roja sea venenosa es del 20%. La probabilidad de que una seta que no sea roja sea venenosa es del 5%. ¿Cuál es la probabilidad de que en el bosque una seta venenosa sea roja? ______ (Respuesta correcta: 50%)