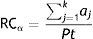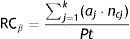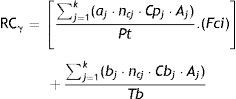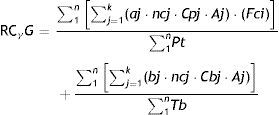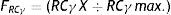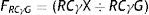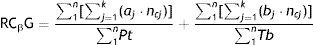The RC algorithm quantitatively evaluates the personal impact factor of the scientific production of isolated researchers. The authors propose an adaptation of RC to evaluate the personal impact factor of research centres, hospitals and other research groups. Thus, these could be classified according to the accredited impact of the results of their scientific work between researchers of the same scientific area. This could be useful for channelling budgets and grants for research.
El algoritmo RC evalúa de forma cualitativa el factor de impacto personal de la producción científica de investigadores aislados. Los autores proponen una adaptación de RC para evaluar el factor de impacto personal de centros de investigación, hospitales y otras agrupaciones de investigadores. Así, estas podrían ser clasificadas en función del impacto acreditado de los resultados de su labour científica entre los investigadores de su mismo ámbito científico, algo que podría ser de utilidad para canalizar presupuestos y ayudas a la investigación.
It is increasingly more essential to implement rationalisation measures to make the best decisions possible when hiring researchers or allocating research funds in competitive events, as well as when raising funds for different research centres (whether they are hospital centres or not), or when calculating their scientific influence amongst similar fields.
In order to do so, we need to have objective and measurable assessment procedures that enable a better assessment of candidates.
One way to evaluate with certain accuracy the research capabilities of a person or a centre, regardless of whether they make many or few publications, is to measure the importance of their research within the scientific context to which they belong. Or, in other words, to evaluate the impact of the results of their researches amongst colleagues. And a way to perform that evaluation lies in writing down the amount of times the articles are cited by colleagues. This could be called the personal impact factor (PIF) of the individual, laboratory, medical department, hospital or research centre.
But the PIF of an individual or centre is not the same as the journals in which the articles are published. Because the impact factor of a journal reflects the amount of times the articles it publishes are cited, and not the impact of the researchers who communicate their results in it. It is known that out of 50% of the citations a journal receives, solely 15% comes from the articles published in it.1 This means that a publication in a journal can have a high impact factor and not be cited many times,1 so influence is very limited, regardless of the high influence that the journal in which the articles are published may have.
The PIF must reflect the amount of times that the articles published by a certain individual or the scientific output of a specific centre are cited, since that is the true impact researches have amongst colleagues of the same field.
The RC algorithm is one of those indicators.2 Its singularity lies in that it performs a qualitative recount of the amount of citations received by each article and book published by a person (and then we will see it performs it by centres as well), taking into account self-citations, the position of the researcher among the authors, the density of the impact in relation to the researcher's total production, the type of article or book assessed (reviews or original research papers), and the length of time since the researcher's last publication. It is more complex and explanatory than the h-index, which only points out the h-amount of articles that have at least an h-number of citations.3
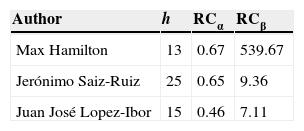
And even though the h-index is a somewhat useful indicator,4 it is not very informative. An example of this is shown in Table 1. In it, Max Hamilton's PIF is shown (he is well-known for his famous depression rating scale), as well as the PIF of other Spanish psychiatrists, using the data provided by the ISI Web Of Knowledge and PubMed-NCBI. Table 1 shows h-indexes, RCα and RCβ (the RCγ index was omitted in this example since its calculation is more complex). Max Hamilton's h-index is inferior than Saiz-Ruiz and López-Ibor's index, and it does not provide much information about the true dimension of said PIF. It does indicate that 13 of his publications are cited over 13 times, but there is no way of knowing if over 13 times means 50, 200 or 1000. Based on the information provided by h, it seems that Hamilton is less influential than Saiz-Ruiz and Lopez-Ibor at an international level; psychiatrists know this is not the case. But RCβ (and RCγ, more sophisticated and explanatory) shows the true dimension of the difference there is by pointing Hamilton's extraordinary PIF (RCβ=539.67) compared to the other two authors.
RC and h-index of some authors.
| Author | h | RCα | RCβ |
|---|---|---|---|
| Max Hamilton | 13 | 0.67 | 539.67 |
| Jerónimo Saiz-Ruiz | 25 | 0.65 | 9.36 |
| Juan José Lopez-Ibor | 15 | 0.46 | 7.11 |
Web Of Knowledge and PubMed-NCBI were consulted on 23/04/2013. Search filters: Hamilton M and depression (Hamilton alone generates 4842 results, most of which do not belong to him); Lopez-Ibor JJ or Lopez Ibor JJ; Saiz-Ruiz J or Saiz Ruiz J (SaizRuiz J does not generate results).
71% of the RCβ value of Max Hamilton comes from the citations he received due to his seminal article “A rating scale for depression”,5 which had a total of 15,477 citations, and 24% of that RCβ value corresponds to his second most cited article (5217), “Development of a rating scale for primary depressive illness”,6 also related to his famous scale.
This is an important reason to calculate the individual PIF of researchers or groups of researchers with the RC algorithm instead of the h-index.
The α version of the RC algorithm (as reflected in (1)) represents the proportion of articles published by an individual that have been cited. It ranges from 0 to 1. And the closer RCα is to 1, it means that the majority of the researcher's production influences others.
where aj are the articles cited and Pt is the total production of articles.If a subject has a RCα=0.85, this means that a large portion of his/her total production is taken into account by his/her colleagues; whereas, if another person has a RCα=0.15, it means that a small proportion of his/her total production is influential.
The raw PIF of a researcher throughout his/her career would be represented by the total amount of citations he/she has received on account of his/her articles, divided by the total amount of published articles:
where, for calculation purposes, aj represents one article (and has a value of “1”) and ncj represents the number of times it is cited.RCα and RCβ are two quite “rough” ways to express the PIF of a subject, since they do not provide qualitative information connected with the type of article published (original or review, for example), the position of the researcher among the authors, self-citations, the time elapsed without scientific activity, etc., although they still are two positively informative indicators.
RCγ is far more explanatory (as reflected in (3)); it gathers the above-mentioned qualitative aspects of each article and book cited.
where aj=is one article (with a value of “1” in the calculation); ncj=number of citations of the article (in the fraction between brackets); Aj=the position of the author in the authorship order of the article (in the fraction between brackets); Cpj=correction for the type of article (original, review, letter to editor, editorial); Fci=correction factor for inactivity; Pt=total number of articles published. And where bj=is a book (with a value of “1” in the calculation); ncj=number of citations of the book (in the fraction outside the brackets); Aj=the position of the author in the authorship order (in the fraction outside the brackets); Cbj=correction for the type of book (original, review, edited book, chapter); Tb=total number of books published.2With RCγ it is possible to provide the PIF value of a subject and, thus, to make comparisons amongst several of them. It may occur that a certain centre is interested in hiring the most influential researcher among his/her peers, or an institution cares about funding a researcher who they can trust and who will obtain results of great interest for his colleagues.
With the purpose of knowing if a same RCγ value corresponds to an individual with a short career, few publications, but of great influence (100 citations each, for instance), compared to another researcher with a more extensive career and less cited articles (30 each), the only datum to take into consideration is the Pt value (total number of articles published) and the Tb value (total number of books published) of each of them.
Development and discussionNevertheless, it is also possible to rate centres from the same research field using RCγ and to compare them. A standard PIF value that allows categorising different hospital departments, research laboratories, hospitals or centres can also be established, based on how far or close they are to that standard PIF value of excellence that can be autonomous, inter-autonomous or public.
To this effect, the RCγ simply needs to be adapted to calculate it in groups: RCγG.
where the fraction numerators contain the sum of the k weighted citations of each of the articles published for each “n” subject from the group under analysis, and the denominator contains the sum of the total number of articles and books published (Pt: articles; Tb: books) of those same “n” subjects.One will simply have to add all the citations (properly weighted according to the position of the author in the authorship order of the article, self-citation, originality, etc., as with RCγ) of each of the published articles received by the individuals that form the scientific staff of the centre, and to divide it by their total production.
It is just a matter of determining if Pt and Tb ought to be all the publications of the group or just those indexed at an international level (those that can actually be tracked, read and cited by their peers). This is a decision that must be adopted and accepted by consensus among the people involved in the assessment process and the authorities that are interested in it.
Another decision that must be made is the time span that will be adopted to evaluate the repercussions of the scientific activity, whether it is of a person or of a centre.
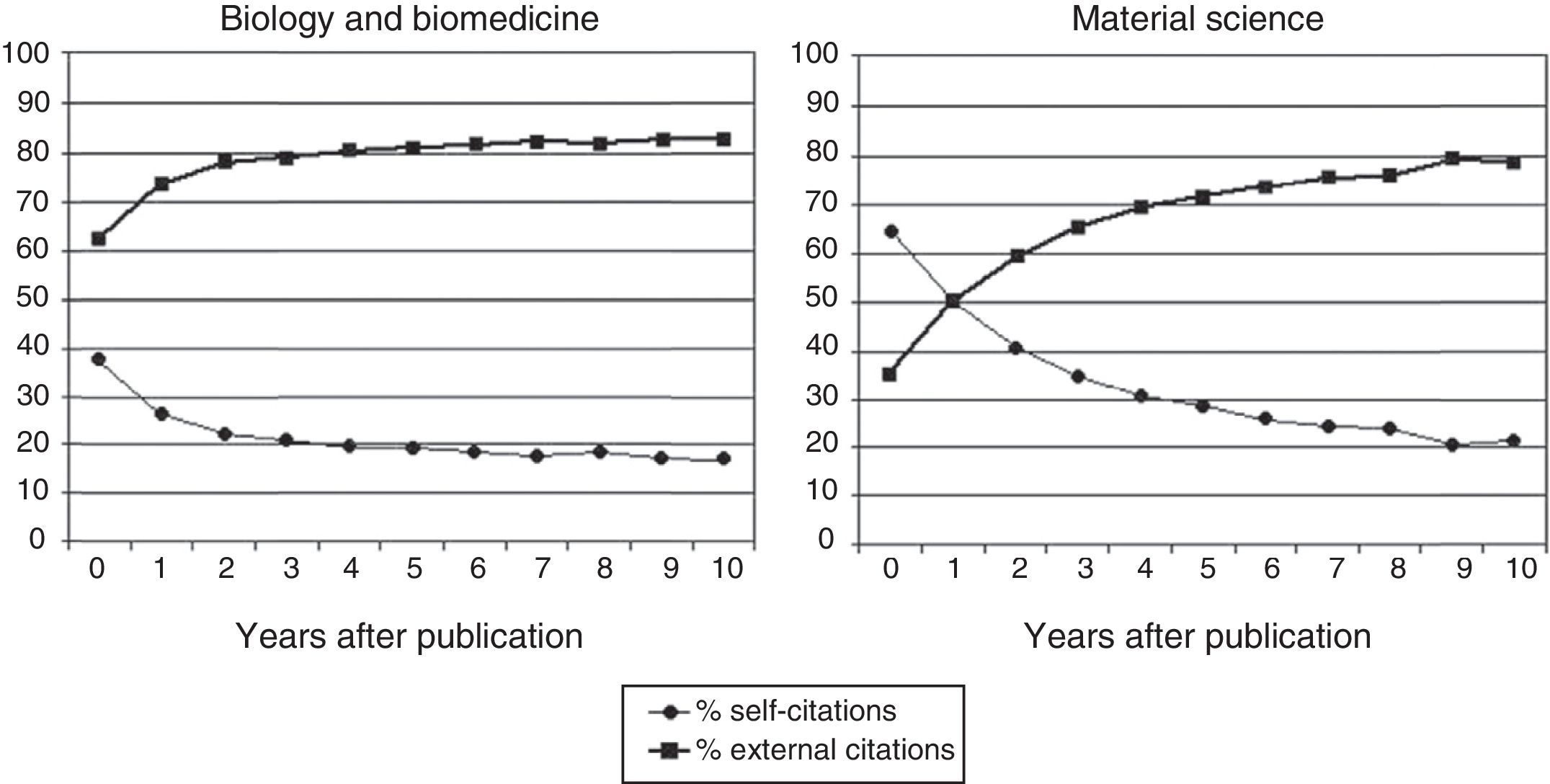
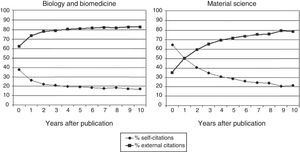
We think that the entire scientific career of people and centres should be taken into consideration. If it were limited to a few years prior to the assessment there would be significant bias because, at least biomedical articles and material science articles begin to be cited by others about three to seven years after they have been published (Fig. 1).7 If the assessment was limited to the citations received within the five previous years, for example, it would be of little use. It is true that the lifespan of a centre is longer than the career of the people who compose it and, therefore, it can receive a considerable amount of citations (higher, in any case, than a potential candidate who belongs to it). But it is also true that it publishes more articles and not all of them will be cited, which reduces the potential inflationary distortion introduced by the factor of time in RCγG by also increasing the denominator in the equation (4).
Evolution, throughout time, of the proportion of self-citations and external citations according to the field of scientific work.
On the other hand, we must take into consideration that, oftentimes, the members of a laboratory or department collaborate by signing the same article. To assess groups with RCγG, this must only be considered once; otherwise, the PIF of that article would be artificially increased when the citations received are multiplied by the number of signatories who belong to the same centre.
Both RCγ and RCγG allow for different types of assessments.
Comparison amongst individualsEither because a well-known researcher wants to be hired for the project, or because financial aid for research is intended for those individuals whose results have a greater impact among their colleagues, the use of RCγ can facilitate making the best decision.
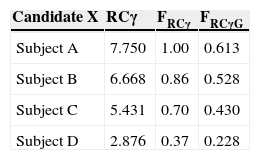
Let's suppose that Centre Z wishes to select three researchers with the best PIF possible. Once the RCγ of each of the proposed individuals is calculated, there are a number of ways to proceed (Table 2). One of them is to simply arrange the RCγ of each candidate in order from the highest to the lowest and to select the first three. Another way to proceed is more graphic and, perhaps, more useful. It would consist of selecting the highest RCγ of the candidates as a reference and obtaining the RCγ fraction (FRCγ) from the rest of the candidates, expressed in how many they are, multiplied by one (5). Centre Z adopts the decision of admitting only those candidates who are in the last quartile of FRCγ (0.75). In the example from Table 2, only Subject B (apart from Subject A, who has been selected as reference) fits in this equation, which means that Centre Z must choose between leaving one position vacant or adjusting its FRCγ criterion.
RCγ use for subject assessment.
| Candidate X | RCγ | FRCγ | FRCγG |
|---|---|---|---|
| Subject A | 7.750 | 1.00 | 0.613 |
| Subject B | 6.668 | 0.86 | 0.528 |
| Subject C | 5.431 | 0.70 | 0.430 |
| Subject D | 2.876 | 0.37 | 0.228 |
| RCγG | |||
|---|---|---|---|
| Centre Z | 12.638 | 1.000 |
Where FRCγ=(RCγ X÷Max RCγ); that is to say, Subject X's RCγ divided by the highest RCγ amongst the proposed candidates (subject A, in the example).
In the PIF comparison of subjects in relation to the centre, FRCγG=(RCγ X÷RCγG). Where RCγG corresponds to the centre's PIF according to (4), which in the example has a value of 12.638.
FRCγ is the RCγ of Subject X divided by the highest RCγ of the proposed candidates.
But Centre Z can choose to act in another way. After all, the two previous ways select the best presented candidates, but not the candidates that Centre Z actually needs. A more selective way to act is to comparatively analyse the fraction between the candidates’ RCγ and Centre Z's RCγ, just as it is calculated in (4), as reference. By using FRCγG(6), Centre Z makes sure it incorporates the most fitting candidate in regards to the PIF profile of its group. In the example from Table 2, Centre Z has a RCγG=12.638. By dividing the RCγ of the candidates between the RCγG of Centre Z, we get the FRCγG values from the right column. If it maintains its requirement to admit subjects that are close to its RCγG in 0.75, it will have to reject all the candidates who have applied, since they lack the type of PIF that Centre Z is interested in maintaining, due to its own reputation and to be successful in potential external assessments.
where RCγX corresponds to Subject X and the RCγG is the one from the centre.However, suppose that Centre Z is not a research facility, but an agency that funds research projects, such as the Carlos III Institute of Health (Instituto de Salud Carlos III), for example, or any other. A criterion to provide this aid may not be what the subject will research of publish, but rather his/her PIF. Since the RCγ reflects the impact of this researcher amongst his/her colleagues, it would be interesting to fund a research project, precisely, of the subject whose study results have the most influence.
Centre Z can select candidates by comparing them through a prefixed standard to calculate FRCγG. That reference model can be a group of researchers (of the same field as the candidate, which are the truly comparable subjects) that has already been funded and of which the RCγG has already been calculated; or it can choose to adopt the RCγG of some department of that speciality that it already knows as a good reference (see below). And, likewise, its selection criterion could be that the candidates reach 0.75 (or any other proportion) of the RCγG of that department.
Comparison amongst centresTo the same extent, hospital departments, hospitals, university lectures, universities and other research centres can be classified by the PIF obtained in their researches, calculated with RCγG, as in (4) (see above).
It is clear that those centres cannot be categorised solely with this criterion. But is seems very useful to maintain a competitive classification of those under this concept; by reputation (that attracts researchers and/or doctors with specialised training) and, also and above all, if that draws funding.
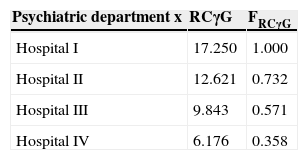
The way to act has already been described. Table 3 shows an example. Imagine you are calculating the RCγG of all the Psychiatry departments (and of any other speciality) of the general hospitals that have them. The one that stands out more by its PIF will be the one taken as reference; and, thus, a classification of such services can be developed according to their FRCγG, as it is calculated in (6).
RCγG use for centre assessment.
| Psychiatric department x | RCγG | FRCγG |
|---|---|---|
| Hospital I | 17.250 | 1.000 |
| Hospital II | 12.621 | 0.732 |
| Hospital III | 9.843 | 0.571 |
| Hospital IV | 6.176 | 0.358 |
Where FRCγG=(RCγG X÷Max RCγG).
RCγG X would correspond to the Psychiatric department from Hospital X, and Max RCγG corresponds to the Psychiatric department with the highest RCγG.
The objective of this classification is to introduce a competition element amongst the Psychiatry departments in order to attain the maximum value of FRCγG (1.000) and to even exceed it. If the Psychiatry department of Hospital III becomes more efficient over time to the point that it exceeds the value of Hospital I (for instance, with a RCγG=23.457 it would exceed it with a FRCγG=1.360) and maintains that for five years, for example, that would become the new RCγG reference value and the classification of the services cited would be modified.
The same thing could be done to classify the professorships of a course in universities. And with research laboratories. And with hospitals as a whole. And with universities.
In order to avoid that just one department (centre, faculty, etc.) is the one that offers the reference RCγG, it could be calculated taking as a basis two or three with the highest PIF of the state. This way, we would get a standard reference model, only adjustable when those two or three departments are consistently exceeded by others, which would become the new models.
Maintaining an adequate FRCγG would be an objective that would improve the quality of the research generated by said centres, aiming not only to publish in the best journals, but also, to become the greatest models amongst peers.
Naturally, the calculations made so far with (4) could be carried out just the same, and with the same purposes, with a RCβ group modification (to which the element connected to the publication of books would have been added), reflected in (7). It is, without doubt, simpler to apply, but the qualitative aspects offered by RCγ would be lost.
Where the fraction numerators contain the sum of k citations of each of the articles published for each “n” subject from of the group under analysis; and the denominator contains the sum of the total production of articles and books published (Pt: articles; Tb: books) by those same “n” subjects.
ConclusionsThe RC Algorithm, both in its individual form (RCγ) and its group form (RCγG), provides an interesting procedure to express the personal impact of individual publications,2 or a group of them, through figures, covering many qualitative values of their scientific production. It also provides a procedure to classify research centres of different types based on the impact (FRCγG) made by their results amongst researchers of the same field.
This allows for the introduction of rational elements for decision making when hiring researchers, when funding researchers and institutions, and when distributing budgets, public or private, amongst the different research centres.
LimitationsNowadays, there are accessible databases (Science Citation Index, Web Of Knowledge, Embase, Scopus, PubMed) that, altogether, make it possible to obtain the number of citations received by the articles of specific researchers, the position of the authors in the authorship order of the article, self-citations, the type of article in question and the publication dates. Google has been testing its own citation searching tool (including books) that could also be useful for these purposes (Google Scholar). Perhaps the most complete database for this purpose is Web Of Knowledge.
One of the limitations of the RC algorithm is, precisely, its dependence on said bibliographic databases, which have a strong pre-eminence of studies published in English. The effectiveness of the RC results depends on the effort that these sources make to include journals in other languages and to ratify the signature of the researchers’ indexed.8,9 Researchers from Spain, for example, tend to have two or three name variations in such databases, which interferes with their identification and the calculations of any indicator based on these data sources.10 For this reason, authors and journals alike should make an effort to attain the ratification of the authors’ signatures.
While it is sought that these databases are as complete as possible, RC algorithm will always be infra-inclusive. It is certainly an unfair limitation with regard to the real total production, but it would affect all the researchers of the same speciality, thus nullifying its restrictive effects.
Another limitation would be that the use of the RC algorithm requires general agreement among the members of the scientific community and the evaluators, in order to standardise the usage criteria. This is why, perhaps, the assessment of departments, hospitals, faculties, universities, etc., should be made by public central bodies, on a basis of a list of researchers affiliated to the different centres, which they could provide.
In spite of everything, and the effort that such an assessment implies, it seems that the use of the RC algorithm could be quite useful, due to its capacity to value the qualitative aspects of scientific individual and group production and its impact on other researchers of the same field.2
Ethical responsibilitiesProtection of persons and animalsThe authors state that no experiments were performed on human beings or animals as part of this investigation.
Data confidentialityThe authors state that this article does not contain patient data.
Right to privacy and informed consentThe authors state that this article does not contain patient data.
Author contributionBoth authors contributed equally to the article content and both approved the final version.
Conflict of interestThe authors declare that there are no conflicts of interest.
Please cite this article as: Cordero-Villafáfila A, Ramos-Brieva JA. La evaluación del factor de impacto individual de investigadores y centros de investigación utilizando el algoritmo RC. Rev Psiquiatr Salud Ment (Barc.). 2015;8:189–194.