Significance of cell number on the bulk elastic properties of auxetic reentrant lattices

Abstract

Auxetics are characterized by a negative Poisson's ratio, expanding/contracting in tension/compression. Given this behavior, they are expected to possess high shear, fracture and indentation resistance, and superior damping. The lack of natural isotropic auxetics promoted an effort to design structures that mimic this behavior, e.g. reentrant model. This last is based on honeycombs with inverted protruding ribs. Commonly, this model is employed in lattices and has been thoroughly studied in terms of mechanical properties and deformation behavior. Given that the amount of cells has an influence in the overall internal structural behavior, there seems to be an absence of data that determines the minimum number of cells for such structure to present internal static bulk properties. Recurring to FEA, this study determines the minimum number of cells to obtain an overall face constrained auxetic lattice with internal bulk elastic behavior, namely in terms of normalized Young's modulus and Poisson's ratio. It is shown that adding reentrant cells increases the Poisson's ratio on an exponential rise to maximum function, reducing the normalized Young's modulus on an exponential decay function. Fundamentally, a minimum number of 13 cells per row to obtain an internal bulk behavior in lattices with constrained faces.

1

Introduction

Auxetics are materials that possess a negative Poisson's ratio (ν), i.e. they expand/contract in tension/compression [1]. Although this behavior may seem counterintuitive, it is supported by the thermodynamic balance enclosed in the classical theory of elasticity, that defines that the limits for this constant are −1 < ν < 0.5 and −1 < ν < 1, respectively, for three [2] and two dimensional approaches [3].

Due to the negative value of this elastic constant, these materials are expected to exhibit enhanced relative shear [4], indentation [5] and fracture resistance [6], and superior vibration damping [7,8] (for reviews on these matters see e.g. [1,9,10]).

Even though, their existence in isotropic forms is theoretically possible, they seem to be absent in nature, given that these materials are found naturally in anisotropic forms. Additionally, there seems to be a preponderance for them to be auxetic only in certain directions, being called semi-auxetics [11]. Some examples of natural materials that may show auxetic behavior are iron pyrite monocrystals [12], cat skin [13], cancellous bone [14], carbon nitride [15], copy paper [16] and human Achilles tendons [17].

Given this lack of natural isotropic auxetics, there is an effort to develop artificial structures that display negative Poisson's ratio since the mid-1980s, by the design of hinging mechanisms [18] and by the transformation of regular foams, by thermo-mechanical processes, into auxetic foams [19].

Since then, there have been developed several structural models that show this deformation behavior, such as chiral [20], nodule-fibril [21], rotating geometries [22], elastic instability [23] and reentrant models [24]. Relatively to the latter, it is the most common employed model, and is fundamentally obtained by the reverse of the vertical ribs of honeycombs into an inverted honeycomb shape.

Even though there are a lot of published works detailing these models and some of its variations (e.g. [25–28]), and given that they are composed by the assembly of basic cellular structures, there seems to be an absence of information on the effect of the number of cells in their internal linear elastic behavior. Furthermore, there seems to be a lack data concerning the minimum number of cells that must be used to obtain lattices with internal elastic bulk behavior.

This study is devoted to the clarification of this matter. Auxetic reentrant lattices with different cell numbers per row/line in a square matrix (m × m) form are subjected to compression simulations by finite element analysis (FEA), where the external faces are restrained, to determine the influence of cell number in the overall internal elastic properties and the minimum number of cells that must be used for them to display internal bulk behavior.

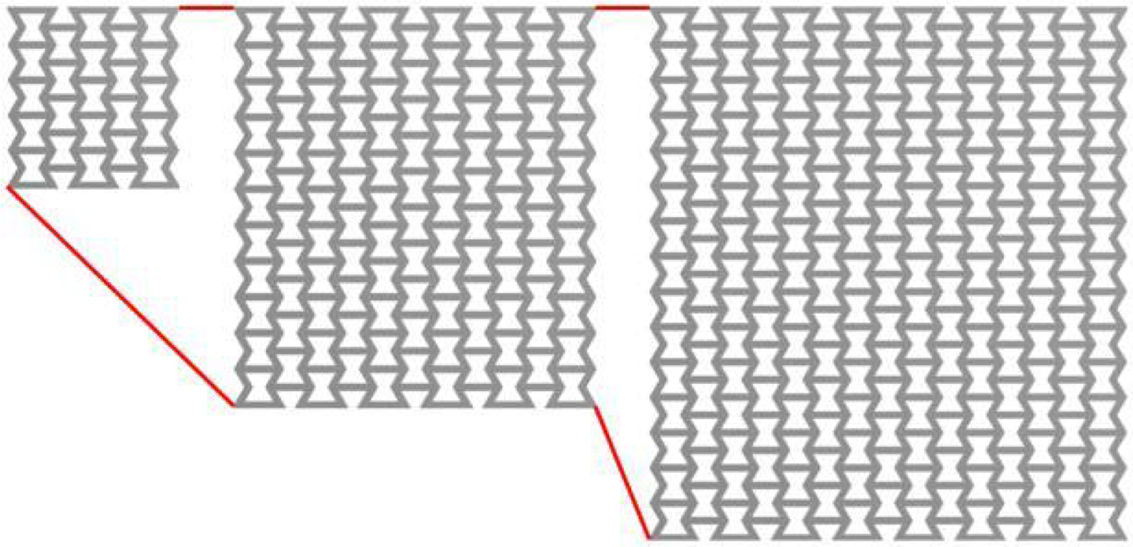
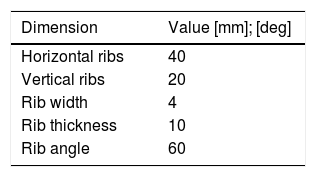
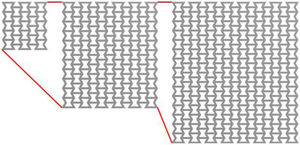
2

Methodology

2.1

CAD models

The cellular matrices that characterize the simulated structures have been modeled by the use of two-dimensional regular auxetic reentrant cells. These have been assembled in square matrices (m × m) with 5, 7, 9, 11, 13 and 15 cells per row (example shown in Fig. 1). The overall dimensions of the auxetic reentrant cells are shown in Table 1.

Fig. 1.

Examples of auxetic reentrant lattice CAD models.

Table 1.

Basic auxetic reentrant cell dimensions.

Dimension	Value [mm]; [deg]
Horizontal ribs	40
Vertical ribs	20
Rib width	4
Rib thickness	10
Rib angle	60

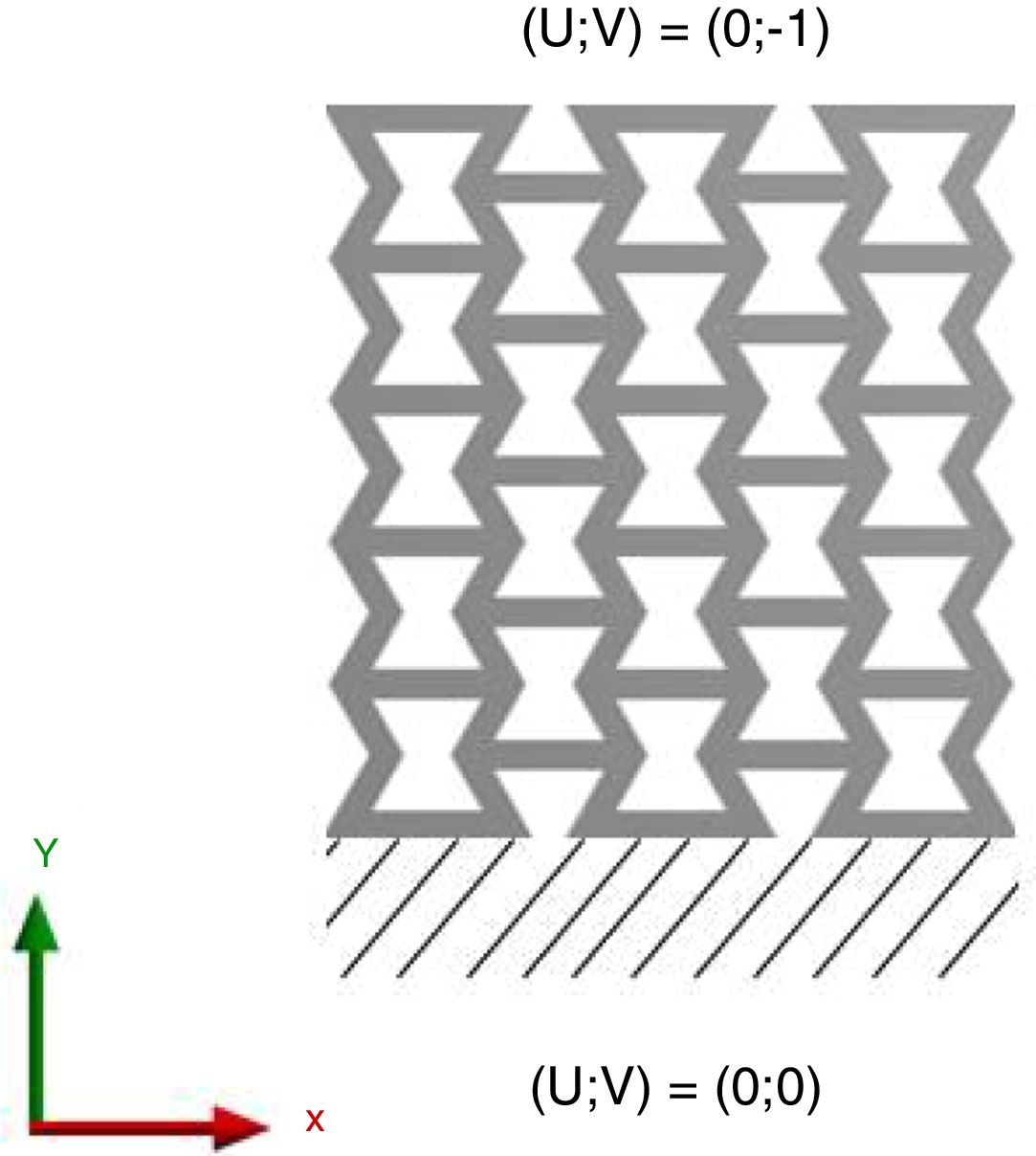
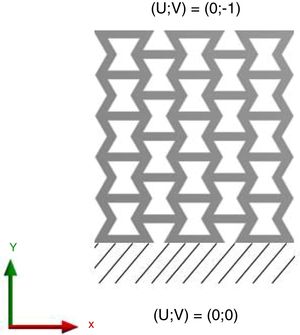
2.2

Finite element analysis

The developed CAD models where subjected to Static Structural FEA using ANSYS 17. In terms of boundary conditions, the lattices had their lower face fixed, while a 1 mm compression displacement is applied in the upper face (Fig. 2). Additionally, the overall input parameters of the simulations are presented in Table 2.

Fig. 2.

Representation of boundary conditions.

Table 2.

Basic auxetic reentrant cell dimensions.

Material	Young's modulus (GPa)	71
	Poisson's ratio (–)	0.33
Formulation	Implicit – isotropic static structural
Mesh	Element type	SHELL181
	Description	Rectangular 4-noded
Solver	Sparse direct equation solver

Additionally, a mesh sensibility analysis was performed on an initial auxetic reentrant lattice (m × m = 3 × 3), by the variation of element size until a stable response is verified in terms of Poisson's ratio and normalized Young's modulus (E*/E).

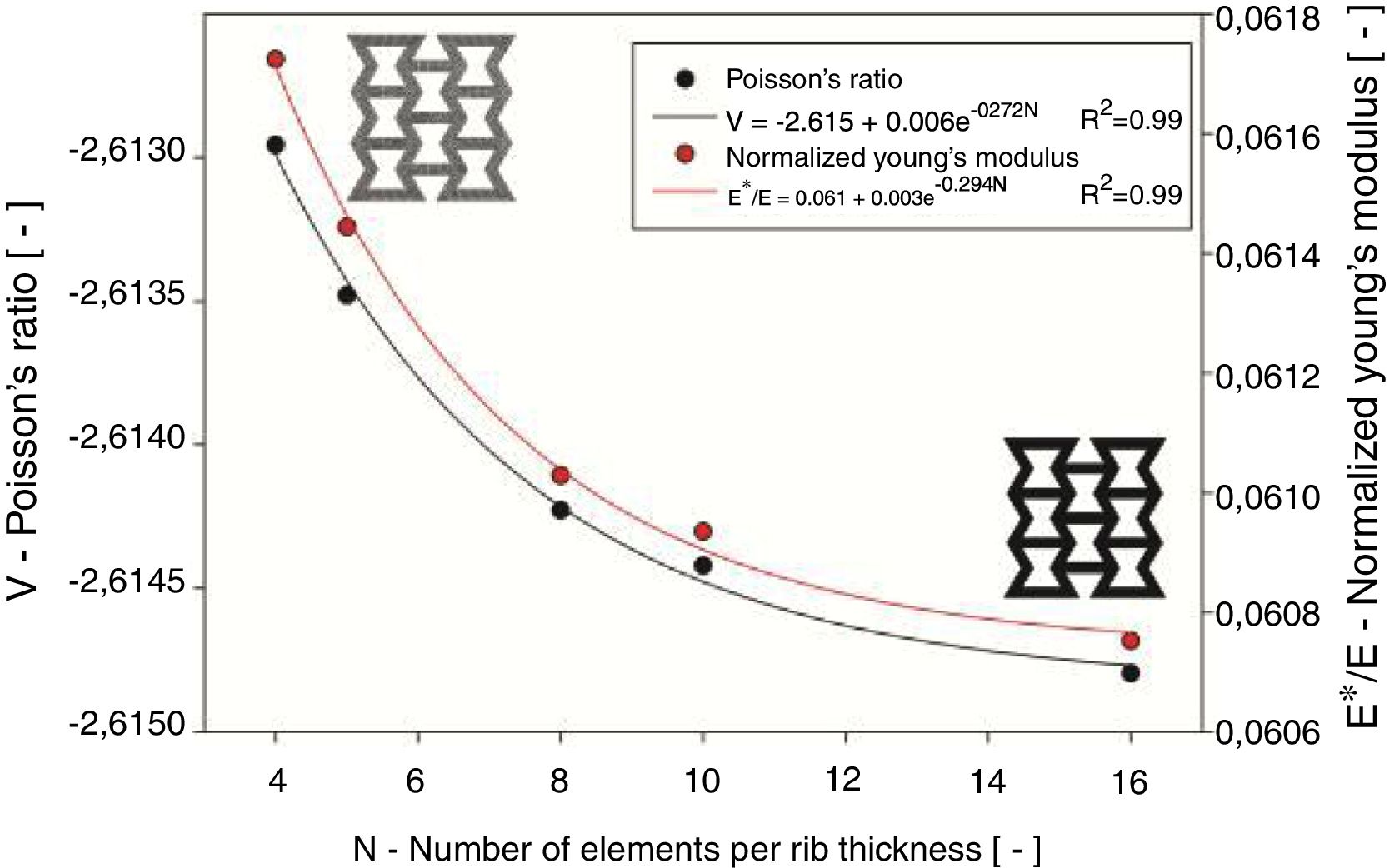
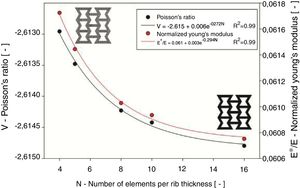
3

Results and discussion

3.1

Mesh sensibility analysis

An initial mesh sensibility analysis was performed to determine the minimum number of elements that must be employed per rib thickness (N) to generate a feasible output of the values of Poisson's ratio and normalized Young's modulus. The results of these initial simulations is shown in Fig. 3.

Fig. 3.

Mesh sensibility analysis results.

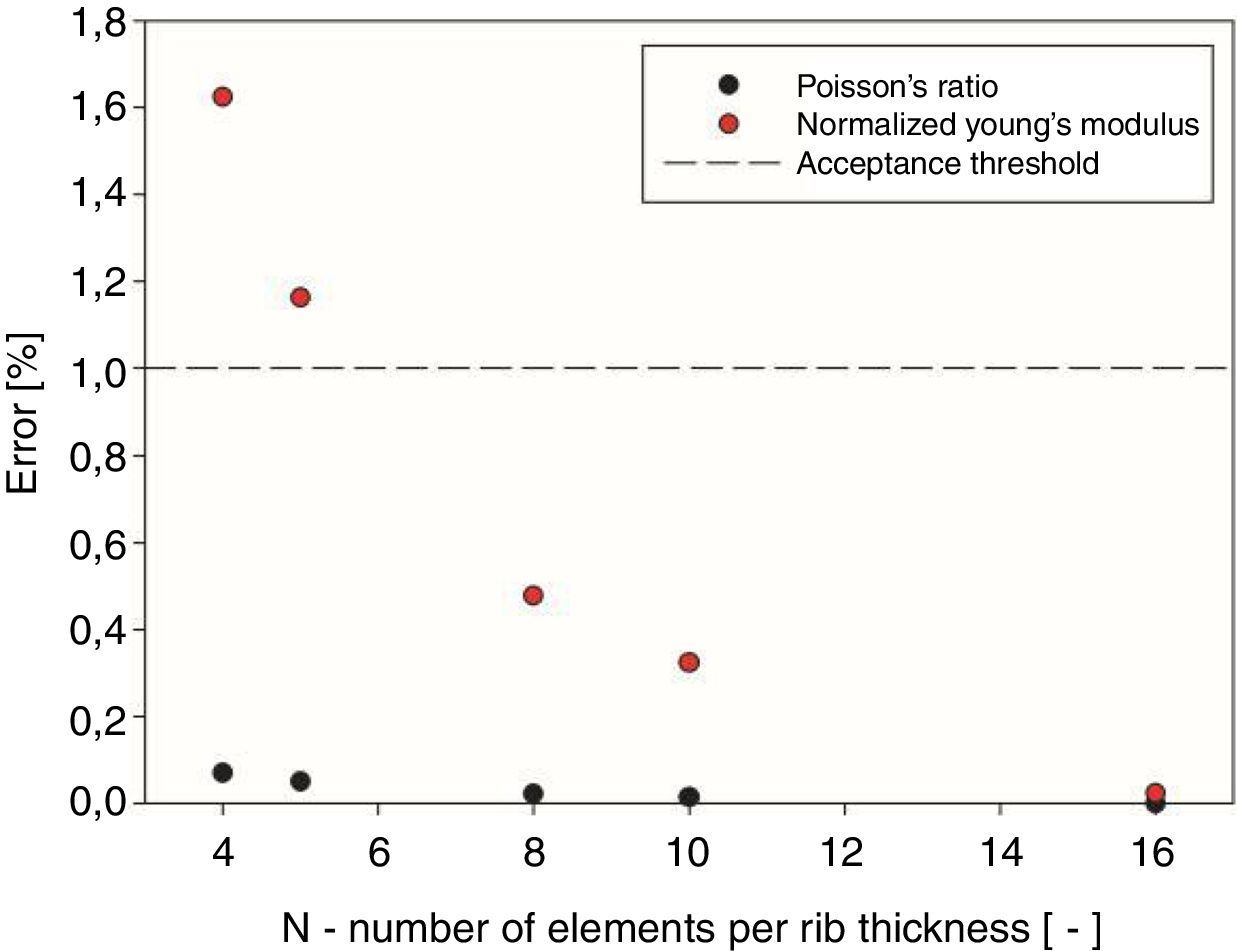
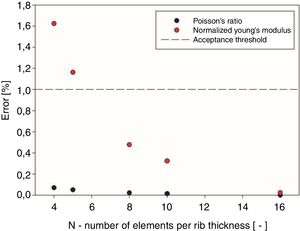
According to this analysis, considering the plotted regressions and the values for which they stabilize, there were calculated the relative errors introduced by the variation of number of elements per rib thickness (Fig. 4). It is shown that for a response variation with less than 1% of error at least 8 elements per rib thickness must be used.

Fig. 4.

Mesh sensibility analysis errors by number of elements per rib thickness.

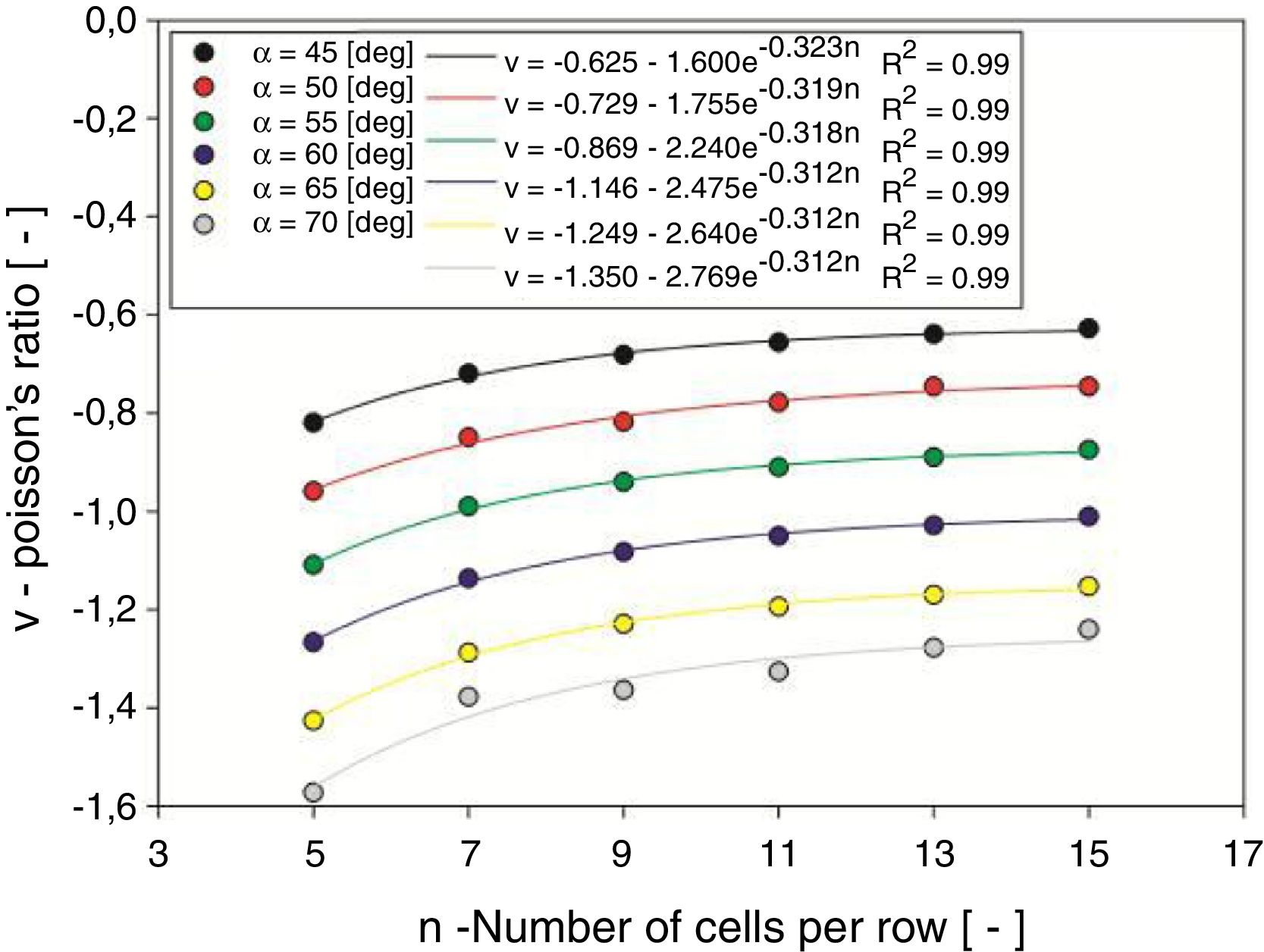
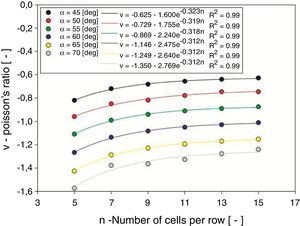
3.2

Poisson's ratio and normalized Young's modulus

Fig. 5 shows the values of Poisson's ratio that were determined by FEA, for the different rib angles (α) and number of cells per row (n). It is shown that these values tend to increase when the number of cells is increased, however, they tend to stabilize following an exponential rise to maximum function, as shown by the performed non-linear regressions. Additionally, for the adopted rib angles, it may also be seen that as these values are increased, there is an increase in auxeticity.

Fig. 5.

Poisson's ratio as a function of rib angle and number of cells per row.

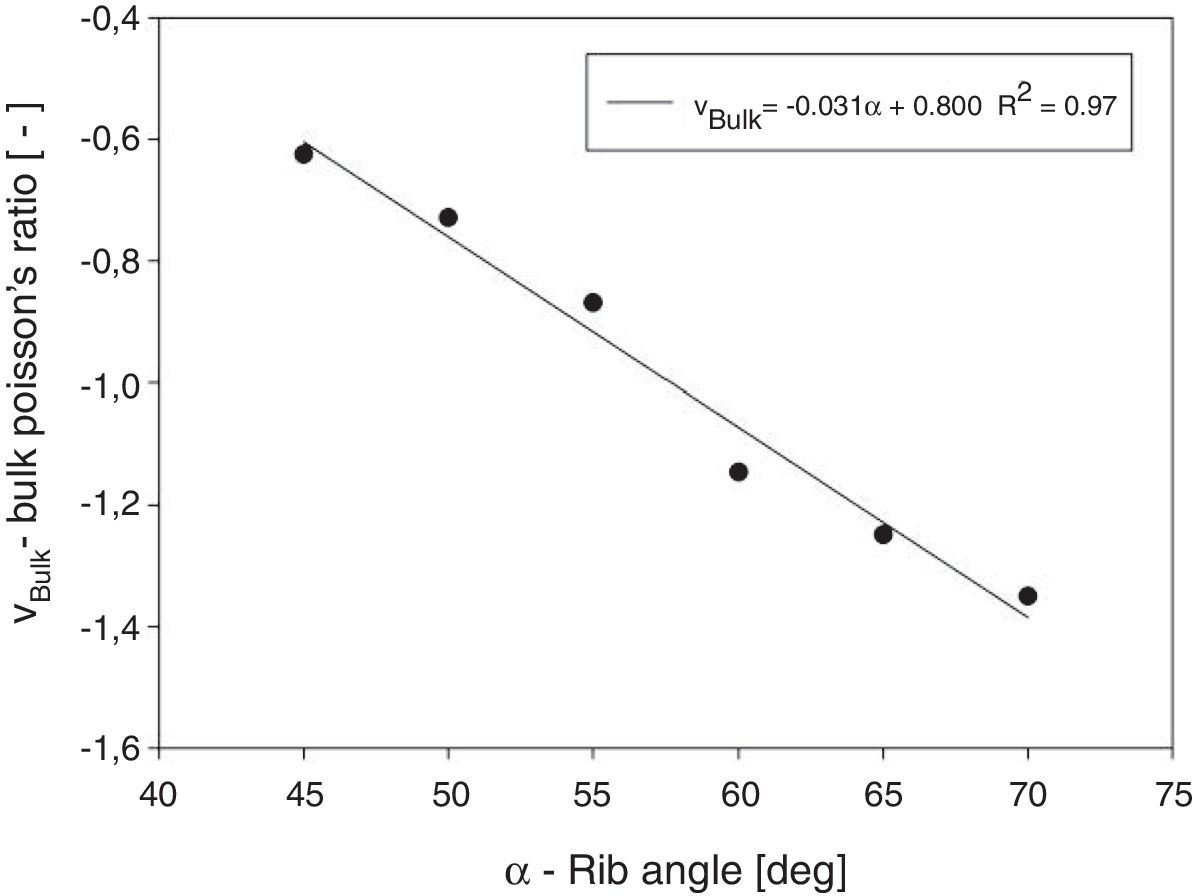
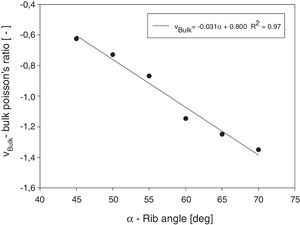
From the referred regressions, it is possible to determine the minimum number of cells for which the Poisson's ratio will stabilize, thus, representing an estimation of the values internal deformation of a lattice with infinite number of cells. These values are plotted in Fig. 6 and represent the rib angle dependent internal bulk Poisson's ratio values and follow a linear function.

Fig. 6.

Internal bulk Poisson's ratio as a function of rib angle.

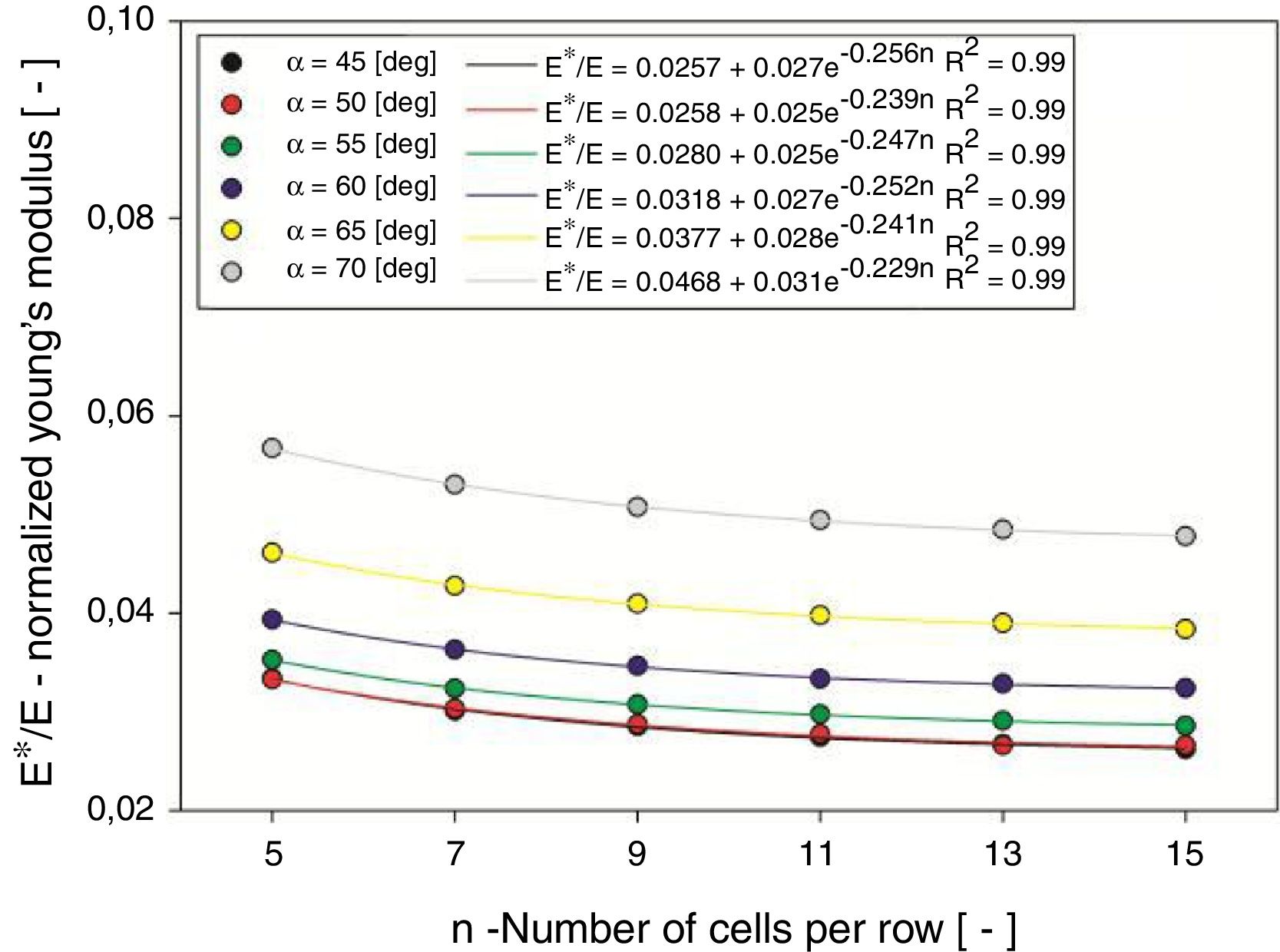
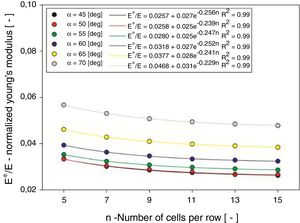
Fig. 7 presents the values of normalized Young's modulus that were determined by FEA, for distinct values of rib angles and number of cells per row. From the numerical results, it is apparent that when the number of cells per row is increased, the normalized Young's modulus decreases on an exponential decay function. However, as the rib angle is increased, so does the normalized Young's modulus.

Fig. 7.

Normalized Young's modulus as a function of rib angle and number of cells per row.

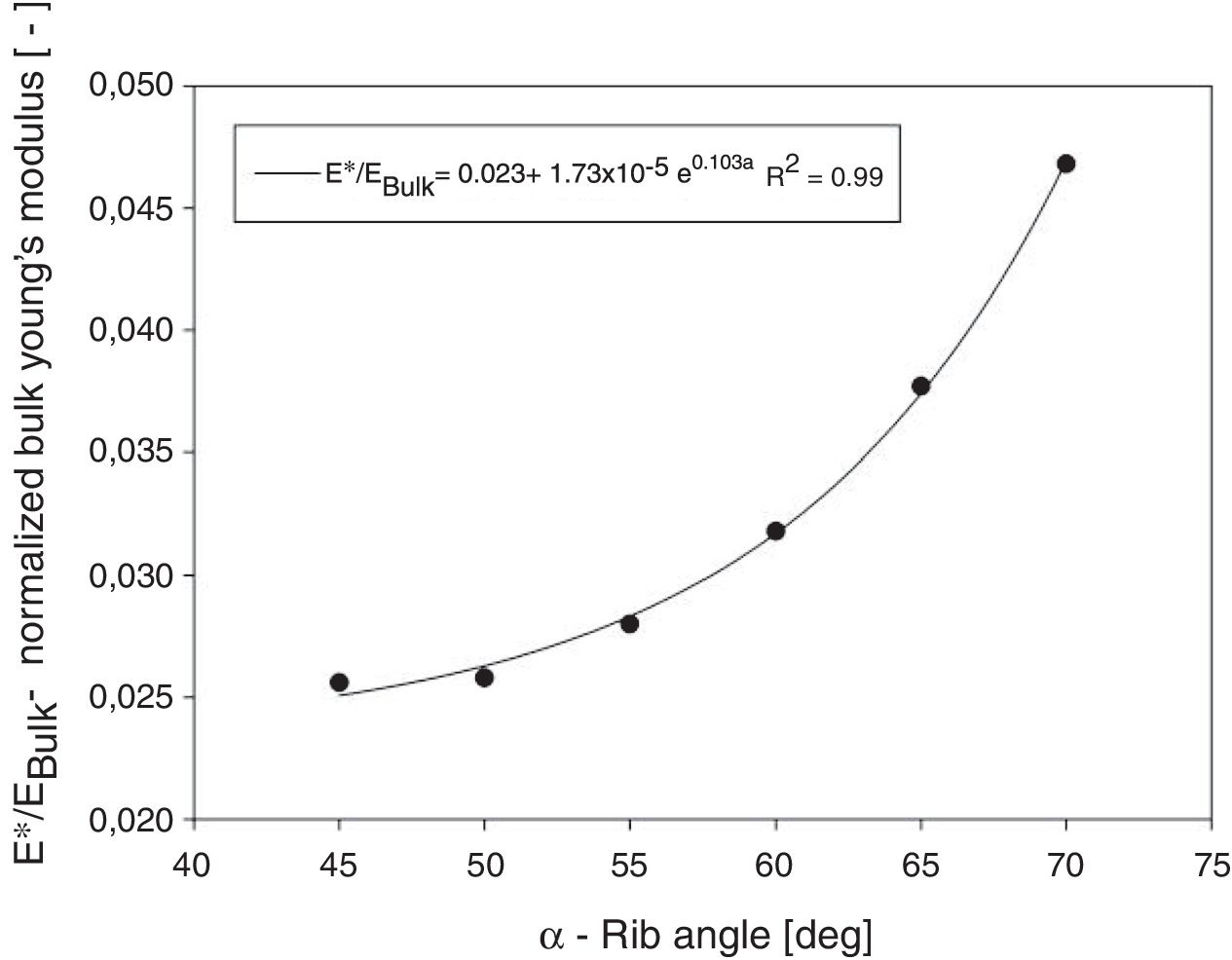
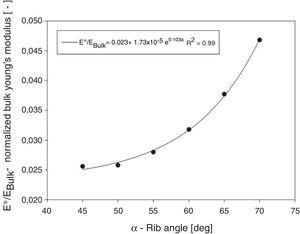
Interpreting the regressions in Fig. 7, and using the method that was described for the Poisson's ratio, the internal bulk values of normalized Young's modulus were determined as a function of rib angle in Fig. 8.

Fig. 8.

Internal bulk normalized Young's modulus as a function of rib angle.

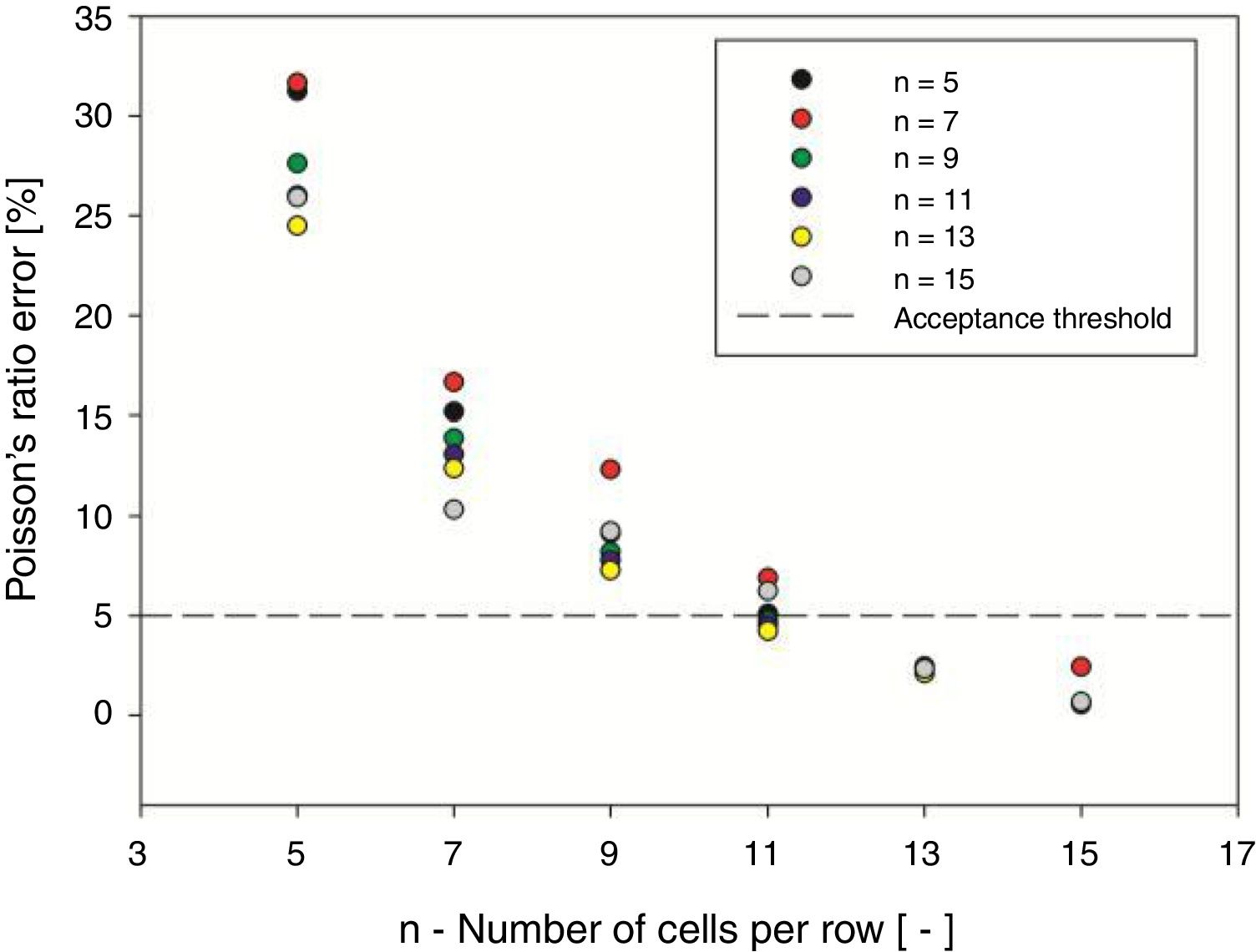
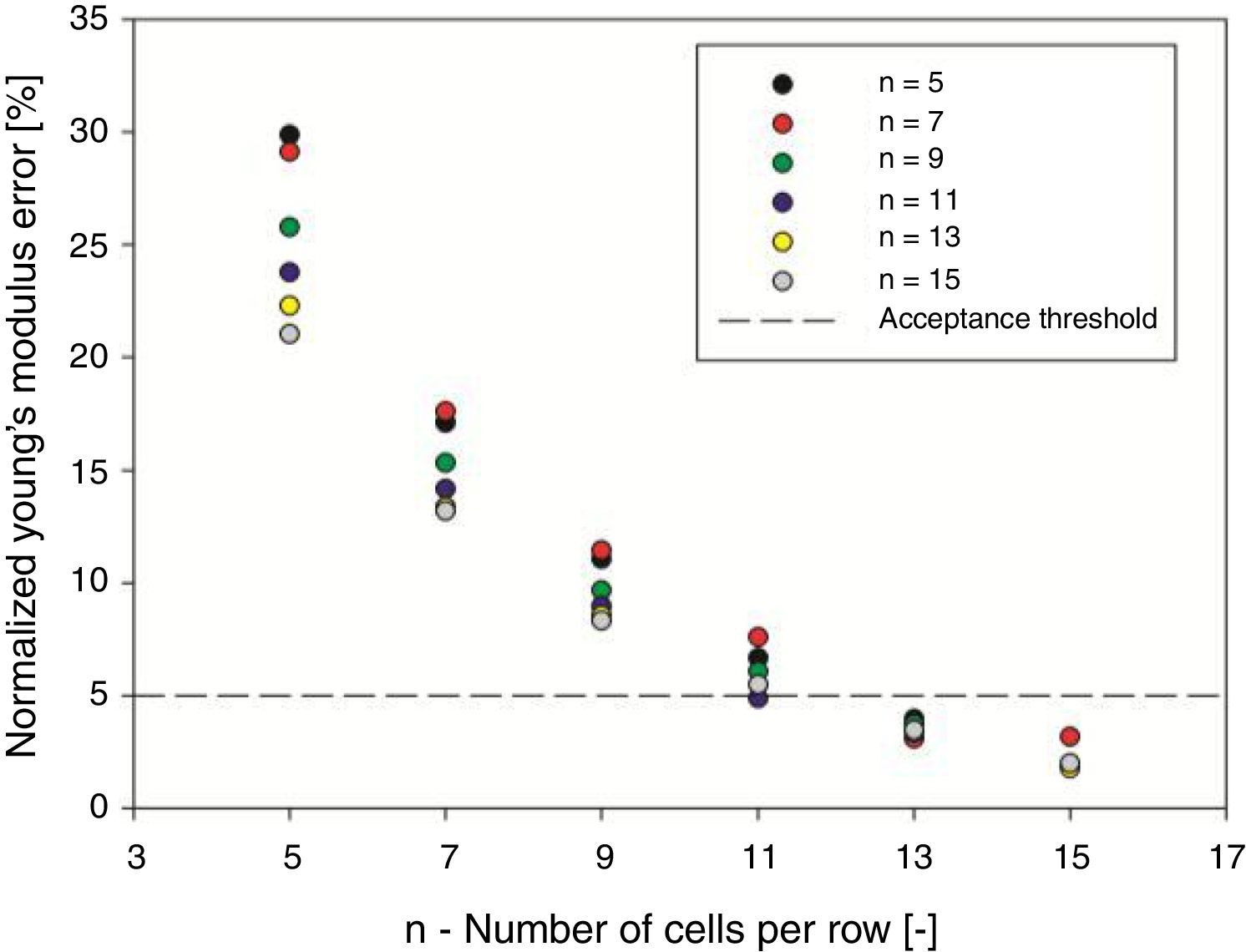
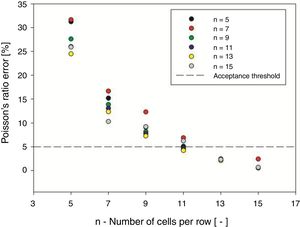
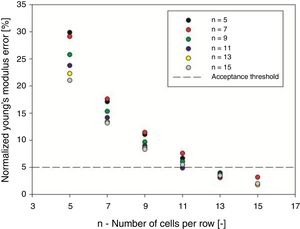
3.3

Minimum number of cells for bulk properties

Based on the deviations from the properties that were determined for the different lattice configurations when compared with the values that were assumed as the internal bulk properties (ν_Bulk and E*/E_Bulk), the values of error when it is considered that such face restrained lattices have internal bulk behavior. These values are represented in Figs. 9 and 10.

Fig. 9.

Poisson's ratio error for different rib angles.

Fig. 10.

Normalized Young's modulus error for different rib angles.

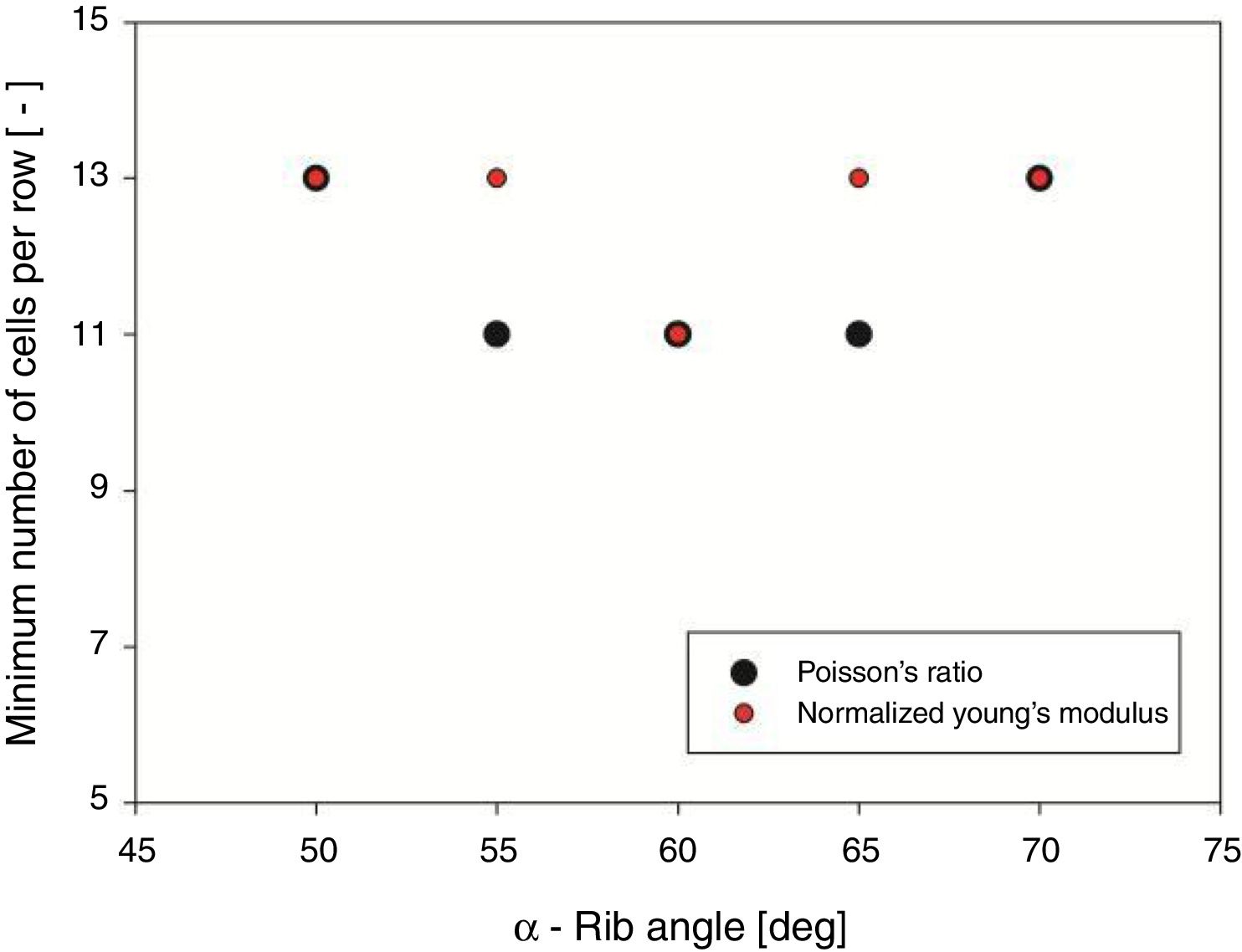
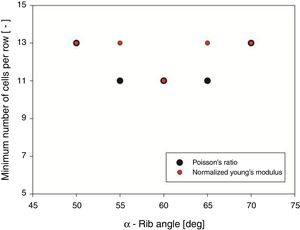
The authors considered an allowable error of 5% as acceptable, and thus, the minimum number of cells to represent internal bulk properties for each of the considered rib angles is shown in Fig. 11.

Fig. 11.

Minimum number of cells to represent internal bulk properties as a function of rib angle.

Considering the information presented in Fig. 11, it may be stated that the minimum number of cells that is able to produce internal bulk properties for the considered rib angles is 13 cells per row.

4

Conclusions

In this study the overall influence of cell number in the internal elastic properties of face restrained auxetic reentrant lattices is explored. Different lattice configurations, based on the assembly of auxetic reentrant cells in the form of a square matrix (m × m) are simulated in compression by the use of FEA. Considering the overall results and discussion of the performed work, the following conclusions were drawn:

• (i)

  Adopting the same base auxetic reentrant cell geometry, as the cell number is increased so do the values of Poisson's ratio. However, the values of normalized Young's modulus tend to decrease.

• (ii)

  The Poisson's ratio tends to increase on an exponential rise to maximum function, while the normalized Young's modulus decreases following an exponential decay function. Both tend to constant values that may be determined as the internal bulk values of these properties.

• (iii)

  In order to obtain an internal bulk behavior from face restrained auxetic reentrant lattices assembled in a square matrix configurations for all rib angles, they must possess at least 13 cells per row and line. However, particularly, for regular auxetic reentrant cells (α = 60°), the minimum number of cells per row is 11.

Acknowledgements

This research was supported by the project iRAIL Innovation in Railway Systems and Technologies Doctoral Programme funds and by national funds through FCT – Portuguese Foundation for Science and Technology and was developed on the aim of the Doctoral grant PD/BD/114096/2015.