The auxetic cellular structures build from inverted tetrapods were fabricated and experimentally tested using uniaxial compression tests in two orthogonal directions. Based on experimental results, the computational models using homogenised material model were developed and validated in LS-DYNA. Furthermore, the computational models based on Smooth Particle Hydrodynamic (SPH) method for simulation of blast loading conditions were developed, verified and validated according to the data available in literature. This computational model was then used to simulate the crush behaviour of composite sandwich panel with auxetic core under blast loading. The results show that the use of the composite sandwich panel with auxetic core reduces the maximum displacement by 33% in comparison to the monolithic plate of the similar mass, while simultaneously a 6% mass reduction can be observed.
Auxetic cellular structures are materials with negative Poisson's ratio, which have some unique and advanced mechanical properties in comparison to other conventional materials [1,2]. The negative Poisson's ratio behaviour is in most cases a consequence of internal structure deformation, while the effect of negative Poisson's ratio can be useful for many different applications to enhance different mechanical properties [2,3]. These properties can be further tailored by using variable cell geometry and density distribution, which can be achieved with functionally graded porosity of auxetic cellular structure. The structures with functionally graded geometry have many advantages in case of the dynamic loading (e.g. impact, blast loading), where the response of the structure can be optimised for specific application needs [4].
Energy absorption properties of auxetic cellular structures are especially important in crash, ballistic and blast protection applications [5]. Blast loading experiments are very expensive, while computational simulations offer an alternative fast estimation of structural response under blast loading conditions [6,7]. In the literature there are only a few reports on the experimental blast loading of monolithic [8] and composite sandwich panels with cellular core [9]. There are however a few recent publications about computational simulations of blast loading of composite panels with auxetic core using empirical ConWep approach [7]. In this work we used a more sophisticated method and detailed approach to simulate the blast loading, i.e. the Smooth Particle Hydrodynamic (SPH) method. The SPH is a meshless method which uses Lagrangian description of leading equations. It was developed for astrophysical high velocity problems [10]. It is applicable in structural mechanics problems, where very large deformation causes convergence problems even if explicit solvers have been applied. The main difference between classical mesh-based approaches and the meshless SPH method is that there is no information flow between mesh and nodes, as for example in the case of the finite elements method (FEM). In the case of SPH method, the particles carry all the information [11].
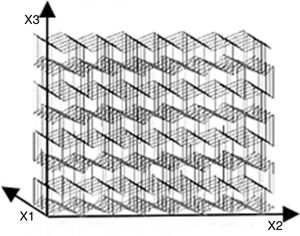
2Experimental testing and numerical modelsThe analysed geometry of the auxetic cellular structure is built from inverted tetrapods [12,4] and fabricated from Ti6Al4V powder using Selective Electron Beam Melting (SEBM) method at the Institute of Materials Science and Technology (WTM), University of Erlangen-Nürnberg, Germany. The specimen's dimensions are 16.2×19.5×21.3mm (6×9×9 unit cells) in the X1, X2 and X3 direction, while the strut thickness is approximately 0.5mm (Fig. 1). The bulk density of the specimens is 636kg/m3.
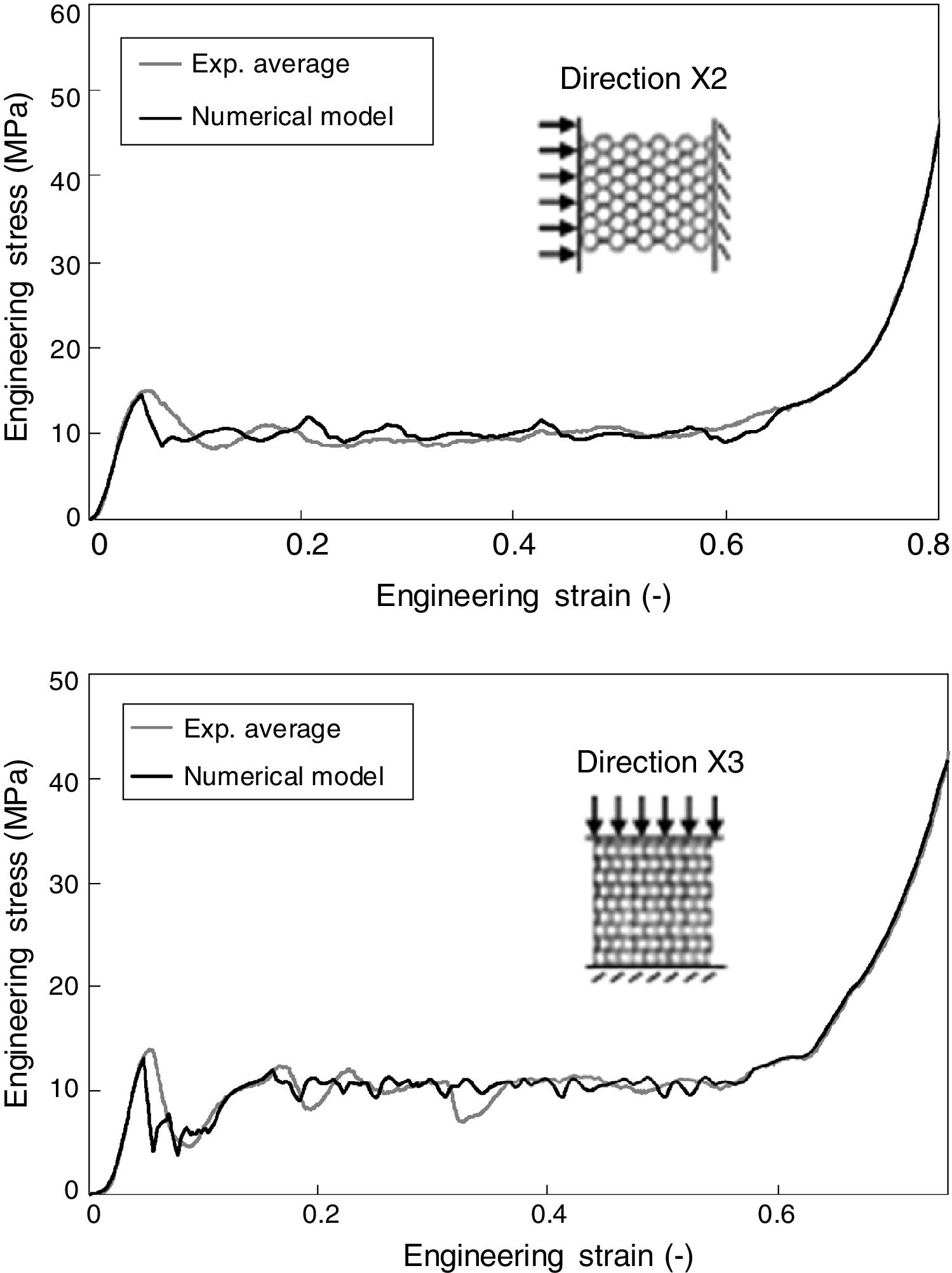
Uniaxial compression tests of auxetic cellular structures build from inverted tetrapods under quasi-static loading conditions were performed on the servo-hydraulic INSTRON 8801 testing machine with position controlled cross-head rate of 0.1mm/s, according to the standard ISO 13314: 2011 [13]. Three specimens were tested only in two directions (X2 and X3) with the maximum applied macroscopic strain of up to 80%. The loading of the auxetic structure in directions X1 and X2 results in similar response of the structure, which has already been observed in [14] and also confirmed by computational simulations. For determination of the compressive response of the tested auxetic structure in three characteristic orthogonal directions (i.e. X1, X2 and X3) it is therefore necessary to test the samples only in two different loading direction, i.e. directions X2 and X3. The recorded load-displacement data were converted to engineering stress-strain data, using the initial specimen's dimensions. The absorbed energy per unit volume (strain energy density) was calculated by integrating the stress–strain relationship.
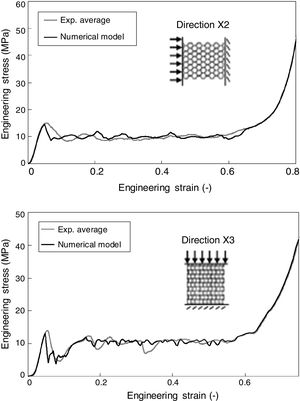
The results from experimental testing were used for validation of the computational models in the LS-DYNA, where a homogenised crushable foam material model (*MAT_63) was applied – specimens were modelled with the solid finite elements in contrast to discrete geometry as used in [4]. The hardening behaviour of material model was defined according to the results of quasi-static uniaxial compression testing. The strain rate sensitivity on the global mechanical response might be for the case of brittle base material as Ti6Al4V neglected, but the mechanical response could be different at higher strain rates due to change of deformation mode to shock mode [15]. The solid finite elements and homogenised material model offer a simple and fast calculation of the global cellular structure's deformation, while it is not possible to observe in detail the deformation process of cellular inner structure. However, the macroscopic computed response under the uniaxial compression loading corresponds very well with the experimental results for both loading directions (Fig. 2).
The comparison of the energy absorption shows even a better fit, with an error (deviation between experimental and numerical results) of only 0.5%. In the case of loading in direction X2, the value of specific energy is 9.66J/kg in the experiment and 9.64J/kg in the simulation. In the case of loading in direction X3, the value of specific energy is 9.19J/kg in the experiment and 9.24J/kg in the simulation. It can be concluded that the homogenised computational model gives very good results for the case of uniaxial compression loading, and can be also used for other loading cases, where compressive deformation is dominant.
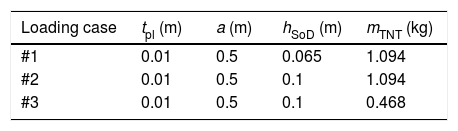
3Blast loadingThe case of blast loading on the composite sandwich panel with auxetic core was studied to additionally observe the crush behaviour of the auxetic cellular structure. The experimental results reported in literature were considered to validate the monolithic steel plate computational model under blast loading [8]. Six different loading cases were analysed in these experiments, where the mass of the explosive and the distance between the plate and the explosive were varied. The study presented in this paper focused on three of these experiments and their data is given in Table 1, where tpl is the plate thickness, a is the width and length of the plate, hSoD is the distance between the TNT and the plate, mTNT is the mass of the TNT explosive.
Experimental data [8].
| Loading case | tpl (m) | a (m) | hSoD (m) | mTNT (kg) |
|---|---|---|---|---|
| #1 | 0.01 | 0.5 | 0.065 | 1.094 |
| #2 | 0.01 | 0.5 | 0.1 | 1.094 |
| #3 | 0.01 | 0.5 | 0.1 | 0.468 |
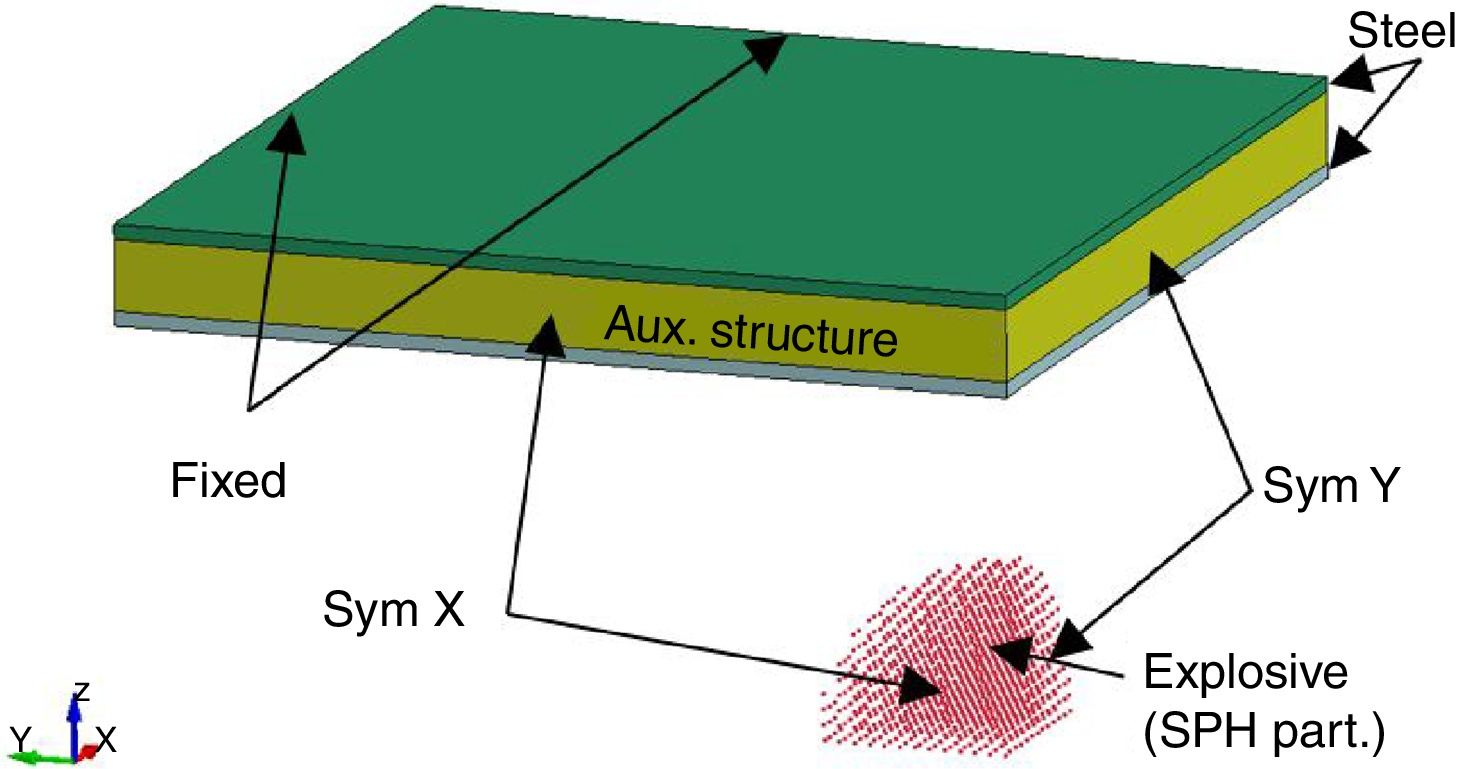
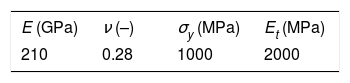
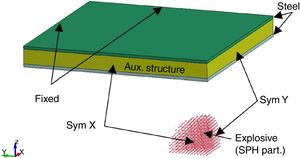
The boundary conditions including the double symmetry and material properties of the plate (Table 2) and explosive were taken from [8,16] and are same for monolithic plate and composite sandwich panel (Fig. 3). The plate was discretised with 3.125 fully integrated solid finite elements.
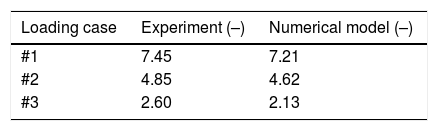
During the verification and validation procedure the appropriate time step, contact formulation and number of the SPH particles were determined based on parametric computational simulations in order to obtain a good correlation with experimental results. The maximum displacement of the plate in the experiment was measured using a simple measuring device in the centre of the plate [8]. The same was done in the computational simulations, where the maximum displacement of a node was measured in the centre of the plate on the opposite side of the explosive. The results of normalised maximum displacement (displacement divided by the thickness of the plate) are presented in Table 3, where a very good correlation between the experimental and computational results is observed for all three loading cases. Only the minor under prediction of displacement in the numerical model is observed, which can be a consequence of the contact between the SPH particles and the plate. Constant material properties without accounting for the strain rate sensitivity used for modelling steel plates in this work will probably not give the accurate results in the case of quasi-static loading or loading at higher strain rates. But for the comparison of the monolithic and sandwich plate's mechanical responses, is the use of such material parameters still appropriate.
After successful validation and verification of the monolithic steel plate model, the computational model (loading case #2) was further developed to study the response of composite sandwich panel with auxetic cellular core. The auxetic cellular structure build from inverted tetrapods in two different directions X2 and X3 was used for the composite structure core. Thickness in the X2 direction is 19.5mm and 21.3mm in the X3 direction, while the bulk density of the auxetic cellular structure is 636kg/m3. The thickness of cover plates for sandwich structure was chosen to be 4mm to enable comparison of results between monolithic and composite plate with the roughly of same mass. The mass of a quarter model of the sandwich composite panel is 4.77kg (direction of the auxetic structure X2) and 4.59kg (direction of the auxetic structure X3), which is in both cases less than the mass of the monolithic plate of 4.9kg.
The boundary conditions were same as in the case of the monolithic plate blast loading (Fig. 3), where only the tied contact between the core and the cover plates in sandwich composite structure was added. The displacement in the case of the sandwich panel was measured on the top cover plate (plate on the opposite side of the explosive).
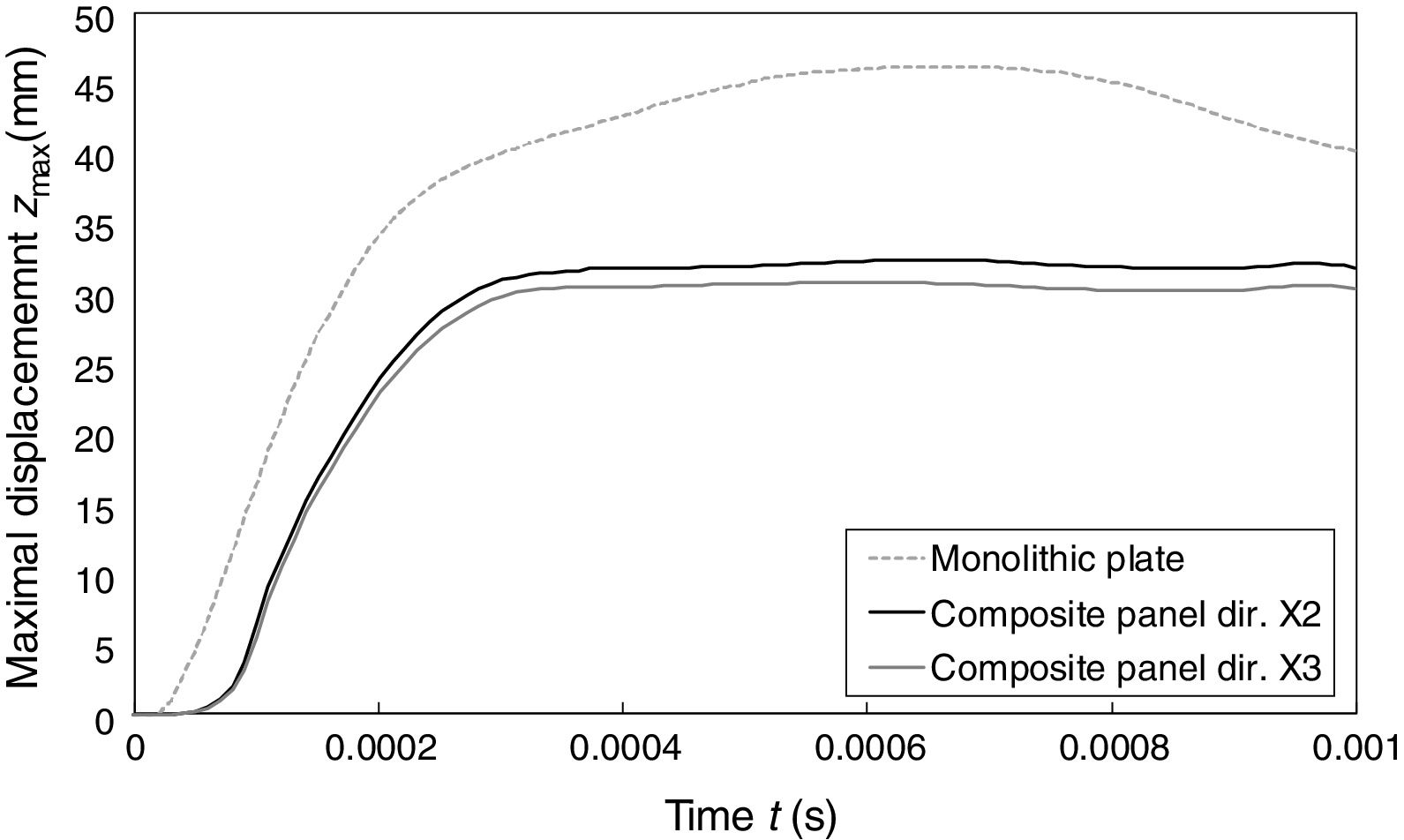
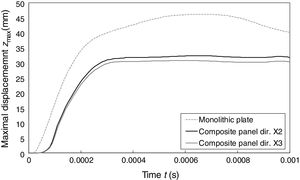
Bottom cover plate of the composite sandwich structure was placed at the same distance from the explosive as in the case of the monolithic plate to obtain the most comparable loading conditions between two analysed cases. The response comparison is shown in Fig. 4, where large influence on the maximum displacement can be observed in the case of sandwich panel. The maximum displacement of the sandwich composite panel has decreased by 33% in comparison to monolithic plate even though the mass of the composite panel is lower by 6%.
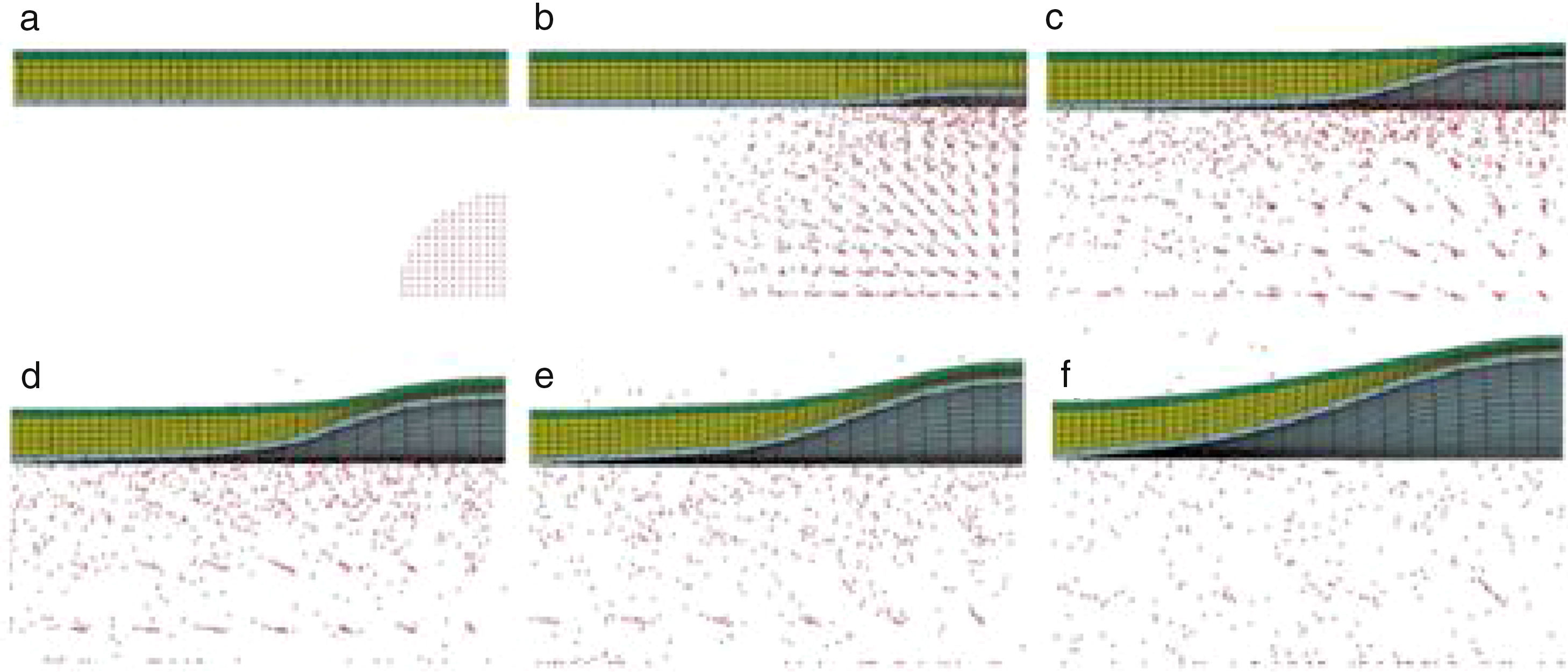
The deformation process of the composite sandwich panel is illustrated in Fig. 5, where the crushing sequence of the auxetic core during blast loading with SPH particles (red particles) is clearly visible. Direct consequence of crushing is a wider area of constant maximum displacement at the top plate that can be observed from Fig. 4.
4ConclusionsThe homogenised computational model of auxetic structure built from inverted tetrapods was developed and validated with the uniaxial compression experimental tests. The simplified computational models with homogenised material model provide fast computational simulations of global auxetic cellular structure behaviour under various loading.
The Smooth Particle Hydrodynamic (SPH) method was used for simulation of crush behaviour of composite sandwich panel with auxetic core under blast loading. The results show that the use of the composite sandwich panel with auxetic core reduces the maximum displacement by 33% in comparison to the monolithic plate of the similar mass. This decrease is due to the energy absorption of the sandwich panel's core, where auxetic cellular structure through crushing dissipates large amount of deformation energy. Such composites can be further enhanced using variable or grade auxetic cellular cores to increase the impact energy absorption through controlled core deformation.
The presented study illustrates great potential of using sandwich structures with auxetic cellular cores. However, the use of discrete computational models would be necessary for more precise observation of the cellular deformation mechanism. This would however result in much longer computational times compared to homogenised computational model. The use of discrete computational models is crucial in order to investigate the influence and potentials of the core with graded porosity to achieve a superior pre-designed response of the composite panels (e.g. smaller accelerations, controllable static displacement after loading, etc.).
The research was performed within the framework of the basic research project J2-8186 entitled “Development of multifunctional auxetic cellular structures”, which is financed by the Slovenian Research Agency “ARRS”. Furthermore, authors acknowledge the financial support from the Slovenian Research Agency (research core funding No. P2-0063).