Desarrollada por Juan Pascual-Leone y sus colaboradores, en el marco de su teoría de los operadores constructivos, la prueba de intersección de figuras (FIT) ha sido ampliamente utilizada en investigaciones básicas y aplicadas que tienen que ver con el desarrollo de la capacidad de memoria de trabajo, como tal y como factor que influye en el logro de aprendizaje. Este trabajo consigna los resultados del análisis psicométrico de la prueba realizado en una muestra de estudiantes colombianos. Los participantes del estudio fueron 146 estudiantes (79 niños y 67 niñas) entre los grados primero y quinto de educación básica primaria (entre 7 y 11 años de edad). Se presenta un análisis de consistencia y un modelo de predicción de la dificultad de cada ítem que se podría considerar indicador de validez de constructo. Se examinan dos escalas propuestas por el autor, así como las diferencias relacionadas con la edad y el sexo.
The figural intersection test (FIT), which was developed by Juan Pascual-Leone and his collaborators within the framework of the theory of constructive operators, has been widely used in basic and applied research concerning working memory capacity both per se and as a factor of learning. This article presents the results of a psychometric analysis of the FIT on a sample of Colombian schoolchildren. The test was applied to 146 primary school children (79 boys and 67 girls) between 1st and 5th grades (7 to 11 years old). An analysis is presented of the internal consistency and a predictive model of the difficulty of each item, which could be considered as an indicator of the construct validity of the test. The two scoring scales proposed by the FIT author, as well as data related to age and gender differences were examined.
Entendida como la cantidad de información que puede activarse (a la que se puede atender) en un momento dado durante la resolución de un problema o la ejecución de una tarea intelectual (Reid, 2009), la capacidad de la memoria de trabajo (MT) es un parámetro del sistema cognitivo que permite identificar niveles o estadios en el desarrollo cognitivo de los individuos (Arsalidou, Pascual-Leone & Johnson, 2011; Pascual-Leone & Johnson, 2005, 2011). Además, esta capacidad es un factor importante en procesos de aprendizaje escolar (e.g., Agostino, Johnson & Pascual-Leone, 2010; Jung & Reid, 2009)
En el contexto de la teoría neopiagetiana del desarrollo cognitivo, propuesta por Juan Pascual-Leone (Pascual-Leone & Johnson, 2005, 2011), y llamada por su autor teoría de los operadores constructivos (TOC), esta capacidad de la MT corresponde al concepto de capacidad mental (o poder M), uno de los constructos centrales de los planteamientos de Pascual-Leone (Pascual-Leone & Johnson, 2005, 2011). Concebida durante los años sesenta y setenta del siglo pasado, esta teoría ha tenido aplicaciones importantes en el ámbito educativo e incluso en el campo de terapia psicológica de corte cognitivo (Greenberg & Pascual-Leone, 2001; Pascual-Leone, Greenberg & Pascual-Leone, 2009).
En términos generales, el poder M es una medida de la capacidad atencional para la activación de unidades internas de información (esquemas) en la realización de una tarea cognitiva. Esta capacidad es limitada con respecto al número máximo de unidades de información que pueden activarse en un momento dado. El límite superior se conoce como capacidad mental estructural (Globerson, 1983; Pascual-Leone & Johnson, 2005). Según la TOC, M aumenta básicamente con la edad, de tal manera que se inicia con un poder M=3 a los 7 años, y se incrementa en una unidad de poder M cada 2 años: 4 a los 9 años, 5 a los 11, 6 a los 13 y 7 a los 15, valor que se mantiene en adelante.
Según la TOC, es posible identificar cuatro características fundamentales que una buena medida de la capacidad M debe tener. Primero, las tareas propuestas para realizar la medición deben minimizar la demanda ejecutiva, lo que puede lograrse con adecuado y suficiente entrenamiento previo en la tarea. Segundo, cada uno de los ítems en el instrumento debe requerir un nivel específico de M para su resolución y todos los ítems deben cubrir la totalidad de un intervalo de M por determinar. Tercero, la medición de la capacidad M debe hacerse en una situación nueva, a fin de minimizar el efecto del aprendizaje previo. Cuarto, las medidas de M deben presentar situaciones adecuadamente engañosas que susciten la activación de esquemas inapropiados a la tarea (Howard, Johnson & Pascual-Leone, 2013; Pascual-Leone, 2013).
A fin de posibilitar la medición de M, Pascual-Leone diseñó la prueba de intersección de figuras (figural intersection test [FIT]), un instrumento que permite evaluar M en un individuo dado. En palabras de su autor: “El FIT lo inventé yo en 1962/1963, en Ginebra, cuando estaba con Piaget, a fin de medir la atención mental. Lo inventé usando el tipo de figuras superpuestas (Abelson figures) que, en neurología clásica, se usaron para estudiar discriminación perceptiva (dibujar y nombrar figuras). Yo cambié las instrucciones para crear una prueba análoga a la inclusión de clases de Piaget, pero en el plano puramente perceptivo: mi análisis metasubjetivo de las pruebas de Piaget y de Witkin me había enseñado ya cómo crear factores engañosos perceptivamente cuando el sujeto tiene que encontrar la intersección de las figuras superpuestas” (J. Pascual-Leone, comunicación personal, 29 de abril, 2014).
Más adelante se describe la prueba en detalle; por ahora, baste decir que la tarea implicada consiste en encontrar y marcar un punto en el área de intersección de grupos de figuras geométricas de diferentes formas y tamaños. Los ítems de la prueba difieren entre sí por el número de figuras cuya intersección debe encontrarse y señalarse. Entre más figuras, mayor será el poder M que se requiere para encontrar su intersección.
En razón de la sólida y sugerente teoría que la respalda y por sus características de aplicación y corrección, la FIT se ha utilizado con frecuencia en la investigación psicológica básica y aplicada. Al respecto, puede mencionarse su uso en estudios sobre el desarrollo de las capacidades intelectuales en el niño (Arsalidou et al., 2010; De Ribaupierre & Pascual-Leone, 1979; Globerson, 1983; Pascual-Leone & Johnson, 2005, 2011); en análisis empíricos sobre la capacidad mental y su relación con la inteligencia general (Howard, Johnson & Pascual-Leone, 2013; Montero, Navarro, Aguilar & Ramiro, 2006; Pascual-Leone, 2013; Pascual-Leone & Ijaz, 1989) y en exploraciones sobre las capacidades intelectuales de poblaciones con condiciones cognitivas especiales (Im-Bolter, Johnson & Pascual Leone, 2006; Navarro et al., 2006).
El FIT se ha aplicado también a poblaciones estudiantiles en varios contextos. Al respecto, se destacan los trabajos sobre los requerimientos cognitivos en el aprendizaje de las ciencias naturales (Ahn, 1995; Cárdenas, 2006; Chu, 2008; Chu & Reid, 2010; Jung & Reid, 2009; Kwon, Lawson, Chunk & Kim, 2000; Niaz & Lawson, 1985; St. Clair-Thompson & Botton, 2009) y en el aprendizaje de las matemáticas (Agostino et al., 2010; Camos, 2008; Orozco & Hederich, 2002). Algunos de estos trabajos fueron realizados sobre muestras de población en Latinoamérica (Cárdenas, 2006; Orozco & Hederich, 2002), sin que en ellos se hayan examinado las características psicométricas del instrumento. Con el presente trabajo se pretende subsanar en parte esta carencia.
Así, atendiendo a su importancia como instrumento que permite operacionalizar uno de los parámetros fundamentales de la capacidad cognitiva de los sujetos y a la necesidad de examinar las características psicométricas del instrumento para el contexto latinoamericano, el presente trabajo proporciona elementos que permiten evaluar la validez de constructo y la confiabilidad del FIT para una muestra de niños colombianos escolarizados de entre 7 y 12 años de edad. Este tipo de validez se establecerá a partir de: (a) la valoración del poder predictivo de la “clase” del ítem sobre su índice dificultad, y (b) el examen de las relaciones entre las puntuaciones de la prueba y la edad, que resultan ser, ambas, predicciones de la teoría.
MétodoDiseñoEl diseño de este estudio puede ser categorizado como investigación instrumental, de acuerdo con la categorización de Montero y León (2007).
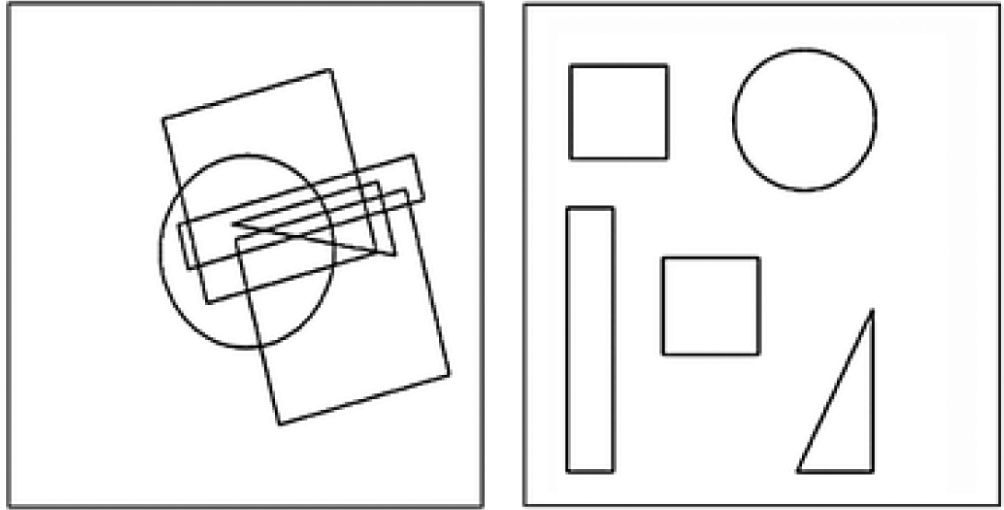
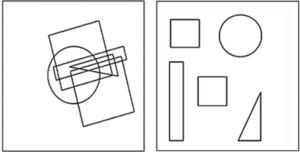
InstrumentoEl FIT se compone de 36 ítems de prueba y seis de entrenamiento, presentados en orden aleatorio de dificultad. Cada uno de los ítems consta de dos grupos de figuras: el “grupo de presentación” en la parte derecha de la hoja y el “grupo de intersección” en la parte izquierda. El grupo de presentación tiene un número de entre dos y ocho figuras geométricas simples separadas entre sí. En el grupo de intersección, estas mismas figuras, y eventualmente otra adicional, pero ahora se encuentran superpuestas unas a otras, de tal manera que hay un área de intersección común a todas las figuras incluidas en el grupo de presentación. Las figuras incluidas en los dos grupos se corresponden en la forma, pero no necesariamente en el tamaño y la orientación. La tarea consiste en encontrar esta área de intersección y marcarla con un punto. En la figura 1 se ilustra un ítem de la prueba.
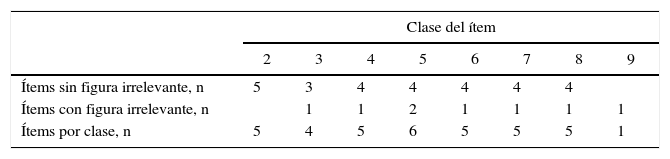
De acuerdo con el autor y como se desprende del tipo de tarea, la dificultad de un ítem depende de dos factores: el número de figuras del conjunto de presentación y la presencia en el grupo de intersección de “figuras irrelevantes”: formas geométricas que, sin estar en el conjunto de presentación, están presentes en la configuración del conjunto de intersección. Así, se calcula la “clase” de cada ítem como el número de figuras del conjunto de presentación en el ítem, más una unidad en el caso en que haya figuras irrelevantes en el conjunto de intersección. La determinación de la clase de cada ítem es fundamental para el cálculo de puntuaciones de la prueba. En la tabla 1 se discriminan los ítems en la prueba por clase, con y sin figura irrelevante.
La prueba es de aplicación individual o grupal. No tiene límites de tiempo. Para la corrección, se han propuesto dos tipos de puntuación (Pascual-Leone & Burtis, 1975). El primero de ellos, llamado FIT2, se utiliza para correlaciones y procedimientos que requieran una medida numérica, y consiste en sumar los valores numéricos de las clases de cada uno de los ítems correctamente resueltos. Esta medida, asimilable a una suma ponderada de ítems, se ubica en un intervalo que va desde 0 (ningún ítem resuelto) hasta 186 (todos los ítems correctamente resueltos).
La segunda puntuación es la FITC (máxima clase lograda), propuesta como una medida absoluta del potencial M del sujeto en cuestión. Para su cálculo se determina primero el porcentaje de ítems correctamente resueltos en cada clase; acto seguido se determina la clase más baja en la cual el sujeto realizó correctamente menos del 70% de los ítems. La clase anterior se considera como la máxima clase lograda (Pascual-Leone & Burtis, 1975).
ParticipantesEl estudio se llevó a cabo con un total de 146 participantes de nivel socioeconómico medio, de ambos sexos, estudiantes de los grados primero a quinto de educación básica primaria de una institución educativa de Bogotá, Colombia, con edades comprendidas entre los 7 y los 12 (media ± desviación típica, 9.48±1.47) años. El 54% de los participantes eran varones y el 46%, mujeres. Los promedios de edad se corresponden con el grado cursado y avanzan según lo esperado, desde el primer grado (7.44±0.26 años) hasta el quinto grado (11.28±0.43 años). Para todos los grados se tomaron los grupos de estudiantes completos.
ProcedimientoLa aplicación de las pruebas se hizo de manera colectiva en grupos escolares completos. Cada participante resolvió el instrumento de manera independiente. Los aplicadores explicaron colectivamente la naturaleza de las tareas y acompañaron a los sujetos a realizar los ejercicios de muestra. No hubo limitaciones de tiempo. Se aseguró a los participantes su anonimato y total confidencialidad. Se contó con consentimiento verbal informado de padres y profesores.
Los resultados fueron codificados y analizados mediante el paquete estadístico SPSS v. 15. Para el examen de la confiabilidad del instrumento, entendida como la medida de su consistencia interna, se calcularon los valores del alfa de Cronbach, corregidos según la fórmula de Kuder-Richarson (KR-20) y el coeficiente de Spearman-Brown para mitades de igual longitud.
Para el análisis de validez de constructo, se examinó el potencial predictivo del número de figuras en el conjunto de presentación y en el conjunto de intersección en el nivel de dificultad de los ítems. Esto se hizo a partir del análisis de un modelo de regresión múltiple.
ResultadosConsistencia internaEl cálculo de la consistencia interna de la prueba se realizó en el presente estudio de dos maneras: (a) la medida por el coeficiente alfa de Cronbach corregida según la fórmula 20 de Kuder-Richardson, y (b) la obtenida por el procedimiento de las dos mitades según la fórmula de Spearman-Brown para mitades de igual longitud.
Los resultados de estos dos procedimientos indicaron α=.9114 y un coeficiente Spearman-Brown para mitades iguales ρ=.8608. Los dos valores son considerados como ampliamente aceptables, de acuerdo con los parámetros comúnmente establecidos, que requieren valores > .7 en los dos casos. El valor de alfa obtenido se puede considerar excelente (Cortina, 1993).
Independientemente del procedimiento empleado, los resultados muestran una muy buena consistencia interna de la prueba. Las diferencias son atribuibles a una distribución inequitativa de la dificultad entre las dos mitades de la prueba. Estos resultados coinciden con los obtenidos por Ahn (1995) y Kwon et al. (2000) en estudiantes de secundaria coreanos, quienes señalaban α=.88, y con los obtenidos por Agostino et al. (2010) en estudiantes canadienses, α=.90.
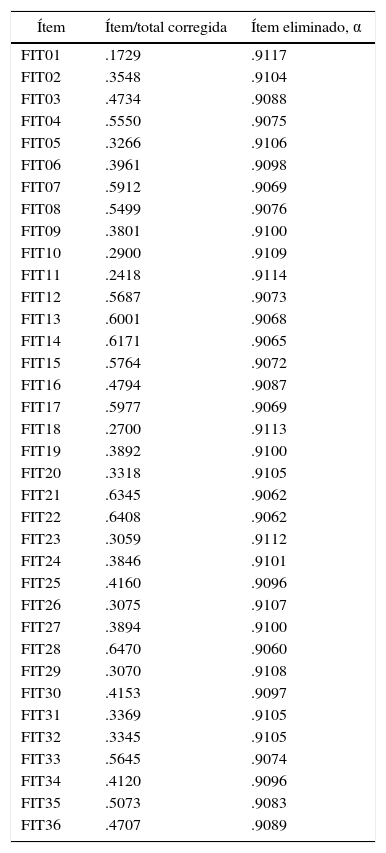
Análisis de ítemsLa tabla 2 presenta los índices de facilidad de cada ítem (porcentaje de respuestas correctas), las correlaciones ítem-total corregidas y el efecto en la consistencia interna de la prueba (alfa de Cronbach) en caso de que el ítem sea eliminado.
Indicadores de consistencia para cada ítem
| Ítem | Ítem/total corregida | Ítem eliminado, α |
|---|---|---|
| FIT01 | .1729 | .9117 |
| FIT02 | .3548 | .9104 |
| FIT03 | .4734 | .9088 |
| FIT04 | .5550 | .9075 |
| FIT05 | .3266 | .9106 |
| FIT06 | .3961 | .9098 |
| FIT07 | .5912 | .9069 |
| FIT08 | .5499 | .9076 |
| FIT09 | .3801 | .9100 |
| FIT10 | .2900 | .9109 |
| FIT11 | .2418 | .9114 |
| FIT12 | .5687 | .9073 |
| FIT13 | .6001 | .9068 |
| FIT14 | .6171 | .9065 |
| FIT15 | .5764 | .9072 |
| FIT16 | .4794 | .9087 |
| FIT17 | .5977 | .9069 |
| FIT18 | .2700 | .9113 |
| FIT19 | .3892 | .9100 |
| FIT20 | .3318 | .9105 |
| FIT21 | .6345 | .9062 |
| FIT22 | .6408 | .9062 |
| FIT23 | .3059 | .9112 |
| FIT24 | .3846 | .9101 |
| FIT25 | .4160 | .9096 |
| FIT26 | .3075 | .9107 |
| FIT27 | .3894 | .9100 |
| FIT28 | .6470 | .9060 |
| FIT29 | .3070 | .9108 |
| FIT30 | .4153 | .9097 |
| FIT31 | .3369 | .9105 |
| FIT32 | .3345 | .9105 |
| FIT33 | .5645 | .9074 |
| FIT34 | .4120 | .9096 |
| FIT35 | .5073 | .9083 |
| FIT36 | .4707 | .9089 |
Las correlaciones ítem-total corregidas son todas positivas y moderadamente altas, salvo el caso del ítem FIT01 (.1719). En coherencia con ello, el alfa resultante de la eliminación de cada ítem es siempre inferior al alfa total, salvo de nuevo en el caso del ítem FIT01, que se incrementa levemente (.912).
Tal y como hemos mencionado, existe un criterio teórico que predice la complejidad cognitiva de un ítem dado como función del número de figuras en el conjunto de presentación más la presencia de figuras irrelevantes en el conjunto de intersección.
Para verificar este supuesto, se estructuró una base de datos cuyos casos son los ítems del instrumento y que contenía sus niveles empíricos de facilidad, el número de figuras en el conjunto de presentación y la presencia de figuras irrelevantes en el conjunto de intersección. A partir de aquí, se calculó un modelo de regresión lineal tomando como variable dependiente el índice de facilidad del ítem y como variables independientes el número de figuras en el conjunto de presentación y la presencia de figuras irrelevantes (0 = no; 1 = sí). Los resultados se presentan en la tabla 3.
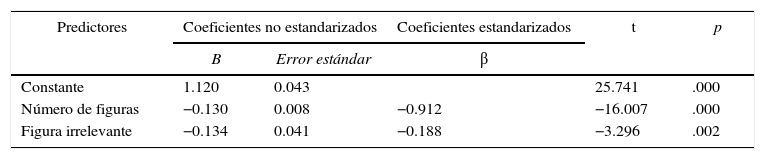
Resultados del modelo de regresión lineal para la predicción de la facilidad de cada ítem
| Predictores | Coeficientes no estandarizados | Coeficientes estandarizados | t | p | |
|---|---|---|---|---|---|
| B | Error estándar | β | |||
| Constante | 1.120 | 0.043 | 25.741 | .000 | |
| Número de figuras | −0.130 | 0.008 | −0.912 | −16.007 | .000 |
| Figura irrelevante | −0.134 | 0.041 | −0.188 | −3.296 | .002 |
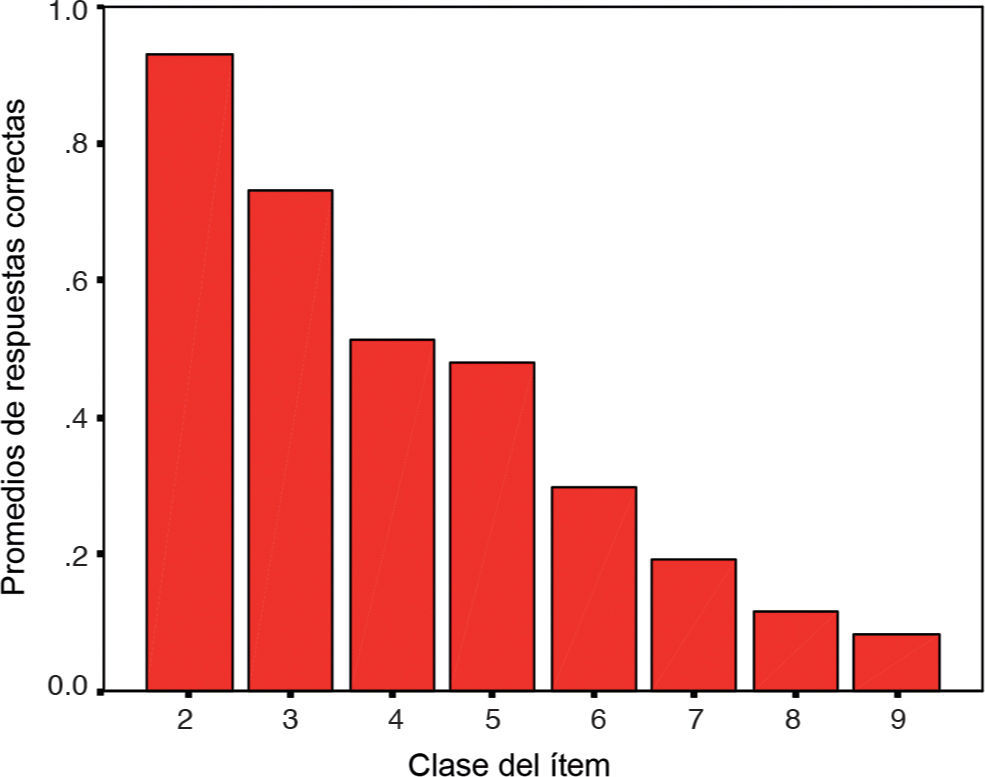
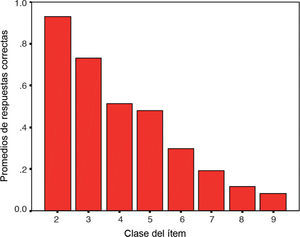
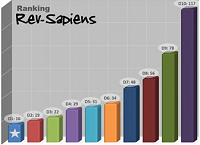
El modelo alcanza a explicar hasta el 88.7% de la varianza de la facilidad del ítem a partir de las variables independientes (R2 ajustado). Vale la pena observar que la presencia de figuras irrelevantes muestra un efecto equivalente al de la presencia de una figura adicional en el conjunto de presentación, lo cual es observable por la similitud de los coeficientes no estandarizados. Así, puede aceptarse que la clase del ítem, tal y como se calculó, es un predictor válido de su nivel de complejidad. La figura 2 presenta el promedio de los índices de facilidad por clase de ítems.
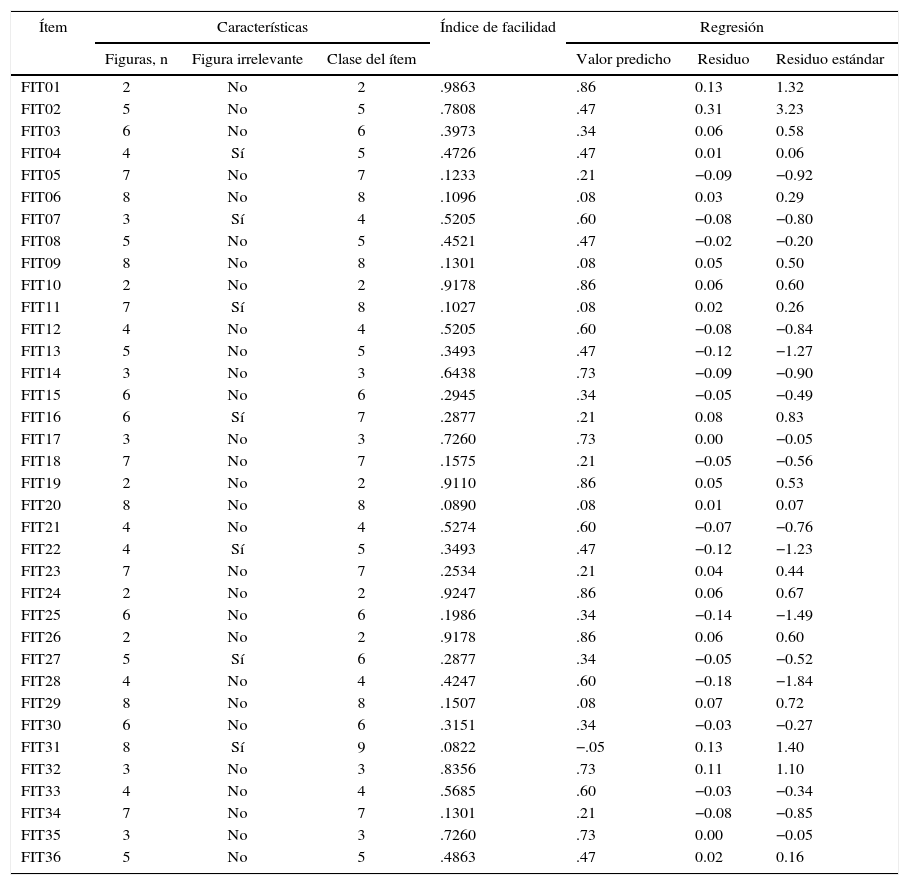
La tabla 4 presenta las características, los índices de facilidad y los ajustes de cada ítem al modelo de regresión. Tal y como se observa, los índices de facilidad varían desde .9863 para el ítem más fácil (FIT01, de clase 2) hasta .0821 para el más difícil (FIT31, de clase 9).
Características de cada ítem y ajustes al modelo de regresión del índice de facilidad
| Ítem | Características | Índice de facilidad | Regresión | ||||
|---|---|---|---|---|---|---|---|
| Figuras, n | Figura irrelevante | Clase del ítem | Valor predicho | Residuo | Residuo estándar | ||
| FIT01 | 2 | No | 2 | .9863 | .86 | 0.13 | 1.32 |
| FIT02 | 5 | No | 5 | .7808 | .47 | 0.31 | 3.23 |
| FIT03 | 6 | No | 6 | .3973 | .34 | 0.06 | 0.58 |
| FIT04 | 4 | Sí | 5 | .4726 | .47 | 0.01 | 0.06 |
| FIT05 | 7 | No | 7 | .1233 | .21 | −0.09 | −0.92 |
| FIT06 | 8 | No | 8 | .1096 | .08 | 0.03 | 0.29 |
| FIT07 | 3 | Sí | 4 | .5205 | .60 | −0.08 | −0.80 |
| FIT08 | 5 | No | 5 | .4521 | .47 | −0.02 | −0.20 |
| FIT09 | 8 | No | 8 | .1301 | .08 | 0.05 | 0.50 |
| FIT10 | 2 | No | 2 | .9178 | .86 | 0.06 | 0.60 |
| FIT11 | 7 | Sí | 8 | .1027 | .08 | 0.02 | 0.26 |
| FIT12 | 4 | No | 4 | .5205 | .60 | −0.08 | −0.84 |
| FIT13 | 5 | No | 5 | .3493 | .47 | −0.12 | −1.27 |
| FIT14 | 3 | No | 3 | .6438 | .73 | −0.09 | −0.90 |
| FIT15 | 6 | No | 6 | .2945 | .34 | −0.05 | −0.49 |
| FIT16 | 6 | Sí | 7 | .2877 | .21 | 0.08 | 0.83 |
| FIT17 | 3 | No | 3 | .7260 | .73 | 0.00 | −0.05 |
| FIT18 | 7 | No | 7 | .1575 | .21 | −0.05 | −0.56 |
| FIT19 | 2 | No | 2 | .9110 | .86 | 0.05 | 0.53 |
| FIT20 | 8 | No | 8 | .0890 | .08 | 0.01 | 0.07 |
| FIT21 | 4 | No | 4 | .5274 | .60 | −0.07 | −0.76 |
| FIT22 | 4 | Sí | 5 | .3493 | .47 | −0.12 | −1.23 |
| FIT23 | 7 | No | 7 | .2534 | .21 | 0.04 | 0.44 |
| FIT24 | 2 | No | 2 | .9247 | .86 | 0.06 | 0.67 |
| FIT25 | 6 | No | 6 | .1986 | .34 | −0.14 | −1.49 |
| FIT26 | 2 | No | 2 | .9178 | .86 | 0.06 | 0.60 |
| FIT27 | 5 | Sí | 6 | .2877 | .34 | −0.05 | −0.52 |
| FIT28 | 4 | No | 4 | .4247 | .60 | −0.18 | −1.84 |
| FIT29 | 8 | No | 8 | .1507 | .08 | 0.07 | 0.72 |
| FIT30 | 6 | No | 6 | .3151 | .34 | −0.03 | −0.27 |
| FIT31 | 8 | Sí | 9 | .0822 | −.05 | 0.13 | 1.40 |
| FIT32 | 3 | No | 3 | .8356 | .73 | 0.11 | 1.10 |
| FIT33 | 4 | No | 4 | .5685 | .60 | −0.03 | −0.34 |
| FIT34 | 7 | No | 7 | .1301 | .21 | −0.08 | −0.85 |
| FIT35 | 3 | No | 3 | .7260 | .73 | 0.00 | −0.05 |
| FIT36 | 5 | No | 5 | .4863 | .47 | 0.02 | 0.16 |
Consecuentemente con el muy buen poder predictivo del modelo de regresión, los residuos estandarizados por ítem muestran valores bajos (< 1.5 desviaciones estándar), salvo un caso: el ítem FIT02 (ítem de clase 5), que muestra un residuo atípicamente alto (3.23). En efecto, este ítem muestra niveles empíricos de facilidad altos (78%), cuando por sus características el valor predicho por la regresión es del 47%, lo cual eleva los promedios de respuestas correctas para la clase 5. Este resultado indica un efecto particular que actúa en los primeros ítems presentados e incrementaría su nivel de facilidad, para desaparecer posteriormente por efecto de la fatiga. Coincidiendo con esta idea, se observa que los niveles empíricos de dificultad de los primeros cuatro ítems (FIT01 a FIT04) son siempre más altos que los predichos por el modelo.
Los resultados indican una fuerte relación negativa entre la clase del ítem (esto es, su dificultad relativa determinada teóricamente) y los porcentajes de logro frente al ítem. En general, puede concluirse que, vistos los resultados en general, las predicciones teóricas sobre la complejidad de los ítems se cumplen para los resultados presentados, lo cual se podría considerar como un indicador de validez de constructo*.
EscalasTal y como se mencionó en los procedimientos de puntuación, para el FIT se calculan dos tipos de puntuaciones: FIT2 (suma ponderada de ítems) y FITC (poder mental, equivalente a la máxima clase lograda corregida por edad).
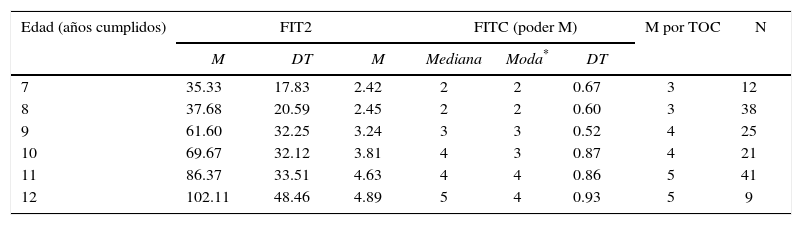
En la medida en que la TOC da a la edad una importancia preponderante como predictor básico de la puntuación en la prueba, no tiene mayor sentido calcular las tendencias centrales de estas dos puntuaciones con independencia de la edad. Por esta razón se presentan en la tabla 5 las estadísticas descriptivas de las dos puntuaciones por franja de edad, además del valor M predicho por la TOC para la edad.
Estadísticas descriptivas de las puntuaciones de la prueba de intersección de figuras
| Edad (años cumplidos) | FIT2 | FITC (poder M) | M por TOC | N | ||||
|---|---|---|---|---|---|---|---|---|
| M | DT | M | Mediana | Moda* | DT | |||
| 7 | 35.33 | 17.83 | 2.42 | 2 | 2 | 0.67 | 3 | 12 |
| 8 | 37.68 | 20.59 | 2.45 | 2 | 2 | 0.60 | 3 | 38 |
| 9 | 61.60 | 32.25 | 3.24 | 3 | 3 | 0.52 | 4 | 25 |
| 10 | 69.67 | 32.12 | 3.81 | 4 | 3 | 0.87 | 4 | 21 |
| 11 | 86.37 | 33.51 | 4.63 | 4 | 4 | 0.86 | 5 | 41 |
| 12 | 102.11 | 48.46 | 4.89 | 5 | 4 | 0.93 | 5 | 9 |
Iniciando por la puntuación FIT2 (suma ponderada de ítems), se observa que las medias son estrictamente crecientes para cada franja de edad y similares entre los 7 y los 8 años, al igual que entre los 9 y los 10, y los 11 y los 12, tal y como espera la teoría, que postula un incremento de una unidad en la capacidad M cada 2 años.
Por otro lado, debe observarse que el promedio de puntajes FIT2 para los 12 años alcanza a distanciarse bastante del obtenido a los 11 años y las desviaciones estándar van incrementándose progresivamente con la edad. Si conservamos el presupuesto teórico de la relación entre edad y puntuación FIT2, esto podría revelar que algunos sujetos pueden mostrar una prematura estabilización de su poder mental M, lo cual explica el aumento de la dispersión en las puntuaciones FIT2 para las franjas de edad más altas (11 y 12 años).
Lo evidenciado por las puntuaciones FITC (poder M) revela las mismas tendencias observadas con respecto a la puntuación FIT2, aunque ahora la interpretación es diferente en tanto tenemos un presupuesto del poder M esperado para cada grupo de edad. Un examen de las medidas del FITC muestra que los sujetos evidencian una tendencia a mostrar un poder M levemente inferior al esperado por la teoría para la edad.
En efecto, los promedios del poder M observado a los 7 y 8 años, que se supondría cercano a 3 unidades, alcanza apenas 2.42 y 2.45, mostrando la estabilidad que predice la teoría en esas dos edades. Confirmando esta apreciación, se observa que el valor de la mediana es de 2 unidades a esas dos edades. Para los 9 y 10 años, momentos en que esperamos M=4, el promedio del poder M observado se sitúa en 3.24 y 3.81, con medianas de 3 y 4, respectivamente; de nuevo levemente por debajo de lo esperado, especialmente para los 9 años. De igual forma, para el periodo entre los 11 y los 12 años, en el que esperamos M=5, los promedios alcanzan apenas 4.63 y 4.81, con medianas de 4 y 5, respectivamente; de nuevo ligeramente por debajo de lo esperado.
Estos resultados son también levemente más bajos que los encontrados por Howard et al. (2013) en niños canadienses de cuarto grado, con edad promedio de 9.81±0.33 años, que logran mostrar un poder M muy cercano a 4. Por otro lado, estos resultados son similares a los reportados por Bentley, Kvasvig y Miller (1990) en niños escolarizados hablantes de lengua zulú en Suráfrica, donde se notó que los valores de M observados se incrementaban hasta llegar a los predichos por la teoría después de efectuar diferentes y repetidos ensayos.
Relaciones con edad y sexoLas correlaciones entre las puntuaciones de la prueba (FIT2 y FITC) con la edad de los participantes son moderadamente altas y ampliamente significativas, tal y como espera la teoría, si bien no son demasiado elevadas por la dispersión de puntuaciones observada antes en los sujetos de más edad (r=.615; p < .001; y r=.785; p < .001).
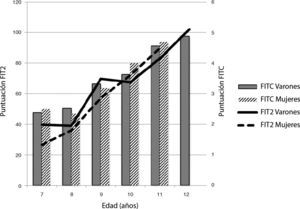
Las relaciones entre las puntuaciones FIT2 y FITC con la edad y el sexo de los sujetos muestran tendencias similares, en tanto son estrictamente crecientes, pero con comportamientos levemente diferentes en la puntuación FIT2, en el sentido de que el promedio de los varones tiende a encontrar una meseta cada 2 años (tal y como predice la teoría), mientras que las mujeres muestran un crecimiento menos escalonado. Estas tendencias no resultan tan acentuadas en la puntuación FITC (figura 3).
Por otro lado, se observan ciertas diferencias leves entre los grupos de sexo con puntuaciones mayores para los varones a los 7 y a los 9 años y para las niñas a los 10 años, especialmente en las puntuaciones FIT2.
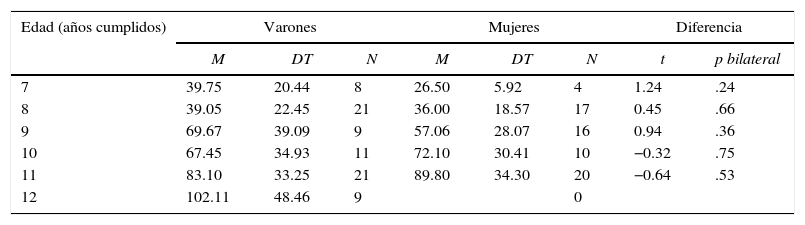
A pesar de que las diferencias entre los grupos de sexo no son significativas para ninguno de los grupos etarios, puede ser interesante observar que, para ambas puntuaciones, el promedio de las puntuaciones de los varones es levemente mayor que el de las mujeres entre los 7 y los 9 años, mientras que entre los 10 y los 11 años el promedio de las mujeres pasa a ser mayor (tablas 6 y 7).
Diferencias entre las medias por grupos de sexo en las puntuaciones FIT2 (suma ponderada de ítems)
| Edad (años cumplidos) | Varones | Mujeres | Diferencia | |||||
|---|---|---|---|---|---|---|---|---|
| M | DT | N | M | DT | N | t | p bilateral | |
| 7 | 39.75 | 20.44 | 8 | 26.50 | 5.92 | 4 | 1.24 | .24 |
| 8 | 39.05 | 22.45 | 21 | 36.00 | 18.57 | 17 | 0.45 | .66 |
| 9 | 69.67 | 39.09 | 9 | 57.06 | 28.07 | 16 | 0.94 | .36 |
| 10 | 67.45 | 34.93 | 11 | 72.10 | 30.41 | 10 | −0.32 | .75 |
| 11 | 83.10 | 33.25 | 21 | 89.80 | 34.30 | 20 | −0.64 | .53 |
| 12 | 102.11 | 48.46 | 9 | 0 | ||||
Diferencias entre las medias por grupos de sexo en las puntuaciones FITC (poder mental)
| Edad (años cumplidos) | Varones | Mujeres | Diferencia | |||||
|---|---|---|---|---|---|---|---|---|
| M | DT | N | M | DT | N | t | p bilateral | |
| 7 | 2.38 | 0.74 | 8 | 2.50 | 0.58 | 4 | −0.29 | .78 |
| 8 | 2.52 | 0.68 | 21 | 2.35 | 0.49 | 17 | 0.87 | .39 |
| 9 | 3.33 | 0.71 | 9 | 3.19 | 0.40 | 16 | 0.66 | .51 |
| 10 | 3.64 | 0.92 | 11 | 4.00 | 0.82 | 10 | −0.95 | .35 |
| 11 | 4.57 | 0.93 | 21 | 4.70 | 0.80 | 20 | −0.47 | .64 |
| 12 | 4.89 | 0.93 | 9 | 0 | ||||
Los resultados indican una prueba con muy buena confiabilidad, entendida esta en términos de su consistencia interna. Esta confiabilidad podría incluso aumentar añadiendo una serie de ítems de prueba con alguna complejidad al inicio del instrumento.
Por otro lado, el análisis de los ítems muestra un alto poder predictivo de la clase del ítem, conformada por el número de figuras del conjunto de presentación más la presencia de una figura irrelevante en el conjunto de prueba, sobre su nivel empírico de dificultad. Esta variable consigue explicar hasta el 88.7% del índice de dificultad del ítem. Esta alta proporción de la varianza explicada señala una alta validez de constructo del instrumento.
El examen de las dos puntuaciones propuestas para el instrumento muestra una tendencia similar. La puntuación FIT2 muestra niveles similares entre los 7 y los 8 años, y entre los 9 y los 10 años, tal y como postula la teoría. Este resultado indica también una buena validez de constructo para el instrumento.
Por otro lado, se observa un aumento progresivo de la desviación típica con la edad, que podría estar señalando una prematura estabilización de la puntuación FIT2 para algunos de los sujetos de la muestra. Esto podría indicar que los casos de baja puntuación FIT2 en la prueba describen a sujetos que avanzaron de acuerdo con lo esperado hasta cierto momento del desarrollo, en el que se estabiliza su puntuación.
El examen de la puntuación FITC, que indica el poder mental de los sujetos, muestra un comportamiento bastante similar al observado en FIT2, especialmente en la estabilidad alcanzada por la puntuación cada 2 años, tal y como predice la teoría.
Examinada la comparación entre la puntuación FITC observada y los valores de poder M predichos por la teoría para los diferentes grupos de edad, se aprecia que lo observado es levemente inferior a lo esperado por la teoría para los diferentes grupos. Ello podría atribuirse a características culturales de la muestra o a su familiaridad con la tarea. Los dos factores deben considerarse para futuras investigaciones; si bien el análisis de los casos publicados en los que se había encontrado esto indica la importancia de realizar repetidos ensayos de la tarea a fin de lograr mayor familiaridad con ella y minimizar la demanda ejecutiva implicada en su realización (Bentley et al., 1990).
Por último, vale la pena mencionar que no se observan diferencias significativas entre sexos en ninguno de los grupos de edad.
Es importante anotar que la evaluación de la capacidad de la memoria de corto plazo o, en términos de Pascual-Leone, el poder M, no es un asunto que se haya resuelto completamente en la investigación psicológica. En un reciente estudio de Demetriou et al. (2013), se examinaron las interacciones entre diferentes parámetros básicos de la cognición humana desde una perspectiva evolutiva: (a) la velocidad y el control del procesamiento; (b) la memoria de trabajo, y (c) la inteligencia fluida (gf). Los resultados constituyen una clara demostración de que estos parámetros son variables latentes diferentes cuyas interacciones cambian dependiendo del nivel de desarrollo del sujeto y su edad.
Para la evaluación de la MT, los investigadores utilizaron multitud de tareas, entre las cuales se mencionan: una tarea que examina memoria visuoespacial (los bloques de Corsi), otra que examina memoria fonológica a corto plazo (recuerdo de palabras), una tarea de recuerdo de disposiciones de figuras geométricas, para la evaluación de la memoria visuoespacial, y dos tareas de memoria numérica de trabajo elaboradas por Case (1985), y una tarea de memoria numérica visual basada en las dos anteriores.
En una réplica a algunos de los resultados de Demetriou, Pascual-Leone (2013) argumenta que estos resultados pueden explicarse en parte por un control inadecuado del balance entre la demanda de M de la tarea con que se evalúa la MT y la capacidad M de los sujetos. Desde el punto de vista de Pascual-Leone, la MT, así como la velocidad de procesamiento y la gf, debe ser entendida desde una perspectiva metasubjetiva, que se opone de manera complementaria y dialéctica a la perspectiva metaempirista adoptada por Demetriou et al. Desde una perspectiva metasubjetiva, la dificultad de un ítem o tarea no es absoluta, sino que está en relación con el nivel de compromiso entre la demanda mental requerida por el ítem y la capacidad mental del participante.
De acuerdo con esta perspectiva, el desempeño correcto en una tarea de velocidad de procesamiento es, efectivamente, una prueba metasubjetiva de eficiencia, pero su significado solo puede apreciarse cuando se calcula la demanda de M de la tarea. La dificultad neta de la tarea depende entonces del principio de equilibrio Md/Mp. De acuerdo con esto, un sujeto puede resolver una tarea que incluye situaciones engañosas (aquellas que activan esquemas irrelevantes para la tarea) si la demanda M de la tarea (en términos de número de esquemas diferentes requeridos para resolverla) es igual o menor que su poder M; si no, el sujeto no logrará resolverla. Esto no se aplica a situaciones facilitantes, en las que las pistas perceptuales de la tarea activen los esquemas relevantes, porque los esquemas automatizados pueden ayudar a resolverla (Baillargeon & Pascual-Leone, 1994). Este principio de compromiso, formulado por primera vez en 1970, hace que la dificultad de una tarea no sea absoluta, como pretende el metaempirismo, sino relativa al poder M de los niños (por lo tanto, a la edad cronológica), así como al nivel de estructuración (demanda ejecutiva, estructuras previamente aprendidas utilizando atención mental, esquemas automatizados que los sujetos tienen en su repertorio) (Pascual-Leone, 1970).
Como se observa, el problema de cómo medir la memoria de trabajo está lejos de tener una respuesta única, adecuada a todas las perspectivas epistemológicas. En este contexto, el instrumento examinado parece ser una muy buena alternativa para la evaluación de la capacidad mental (poder M), durante el desarrollo desde una perspectiva metasubjetiva. La investigación previa indica que las medidas del poder M representan una de las mejores posibilidades de examinar, de manera acultural, variables cognitivas importantes que subyacen a las medidas de la inteligencia humana (Howard et al., 2013). En particular, el instrumento examinado es de aplicación grupal, con mínimos requisitos de alfabetización y de conocimientos y habilidades numéricas, confiable y que presenta alta validez de constructo. Estas características, no muy frecuentes en instrumentos de este tipo, lo muestran como una valiosa herramienta para la investigación.
Una inspección visual de la gráfica presentada indica, sin embargo, que la relación podría no ser lineal, en la medida en que la magnitud de la diferencia entre los promedios de facilidad por clase va disminuyendo progresivamente. En efecto, el examen de una relación logarítmica muestra un leve incremento de la varianza explicada (R2 = 0.913). Hemos preferido no presentar formalmente estos resultados por la ausencia de un modelo teórico que permita realizar una interpretación completa del modelo.
El artículo presenta algunos de los resultados obtenidos en el proyecto “Hacia la construcción de un modelo de procesamiento del sistema de notación decimal”, desarrollado entre 2003 y 2004 en el Centro de Investigaciones de la Universidad Pedagógica Nacional (Bogotá, Colombia) con el apoyo financiero de COLCIENCIAS.