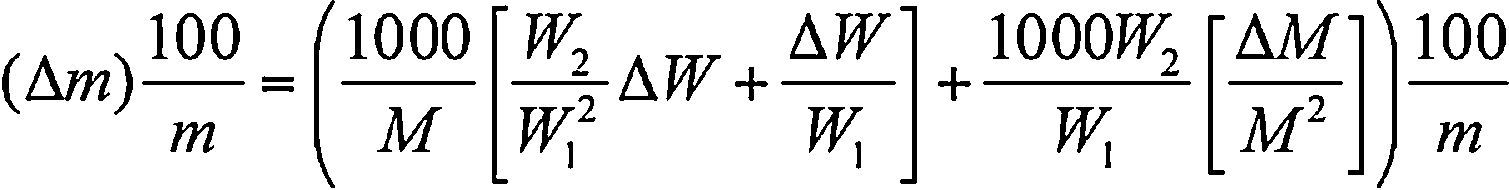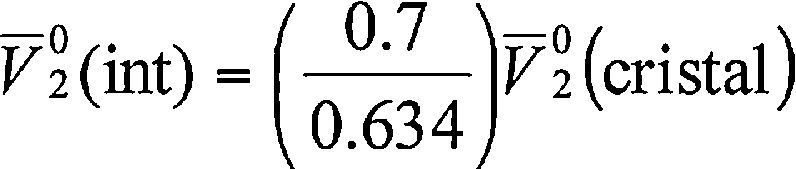COMPORTAMIENTO VOLUMÉTRICO DE LA DL-VALINA EN SOLUCIONES ACUOSAS DE NITRATO DE SODIO A DIFERENTES TEMPERATURAS

RESUMEN

Se determinaron las densidades de la DL-valina (Ácido 2-amino-3-metilbutanoico) en soluciones acuosas de nitrato de sodio en el intervalo de temperaturas desde 283.15 K hasta 318.15 K usando un densímetro de tubo vibratorio Anton Paar DMA 5000. Se calcularon: los volúmenes molares aparentes, los volúmenes molares aparentes a dilución infinita, la segunda derivada de los volúmenes molares parciales a dilución infinita con respecto a la temperatura, así como los volúmenes molares parciales de transferencia y los números de hidratación. Los resultados obtenidos se discutieron en términos de las interacciones predominantes en solución, encontrándose que la DL-valina tiene un efecto disruptor de la estructura del solvente y que a dilución infinita predominan las interacciones soluto-solvente entre el grupo isopropil del aminoácido y los iones sodio y nitrato.

ABSTRACT

Densities of DL-valine (2-amino-3-methylbutanoic acid) in aqueous solutions of sodium nitrate were determined at temperatures ranging from 283.15 to 318.15 K using an Anton Paar DMA 5000 vibrating tube densitometer. The apparent molar volume, infinite dilution apparent molar volume, second derivative of the infinite dilution partial molar volume with respect to temperature, partial molar volume of transfer at infinite dilution and the number of hydration were calculated. The results obtained were discussed in terms of the dominant interactions in solution, it was found that the DL-valine has a disruptor effect in the structure of the solvent and that at infinite dilution solute-solvent interactions are dominant between isopropyl group the amino acid and sodium and nitrate ions.

INTRODUCCIÓN

Es bien conocido que el comportamiento y las propiedades moleculares de las proteínas en las mezclas acuosas es gobernado por muchos factores, como: estructura química, propiedades del disolvente, pH, electrolitos presentes en solución, entre otras¹. La fuerte interacción entre electrolitos y proteínas es la causa de la desviación del comportamiento ideal. Por tanto, este hecho es quizás una de las razones por la que debe estudiarse la influencia de los electrolitos sobre el comportamiento fisicoquímico de las proteínas.

No obstante, ya que este estudio resulta inviable por no decir imposible, debido a la compleja organización estructural de estas macromoléculas biológicas, se recurre al estudio de las interacciones de los bloques de construcción de las proteínas (aminoácidos) en soluciones acuosas de electrolitos, con el fin de entender los finos detalles asociados al comportamiento volumétrico². Por esta razón, es evidente que un estudio directo de las proteínas resulta difícil³ y debido a ello en los últimos años se han usado diversos aminoácidos y péptidos de bajo peso molecular como compuestos modelos en soluciones salinas, con el fin de simular estos complejos ambientes biológicos^4–7. De hecho, existen extensos estudios de propiedades volumétricas y termoquímicas sobre esta área de investigación^8–11.

Además de los argumentos expuestos, otra razón no menos importante está asociada al hecho de que los aminoácidos y péptidos son las unidades estructurales fundamentales de las proteínas, péptidos, ciertos tipos de hormonas, antibióticos y muchos otros compuestos de relevancia biológica. Generalmente, se reconoce que en ausencia de datos termodinámicos experimentales para estas macromoléculas, los aminoácidos y péptidos pueden servir como modelos útiles para la estimación de sus propiedades^12–15.

En virtud a lo anterior y dada la trascendencia del tema, en este trabajo se estudian algunas propiedades volumétricas de soluciones de DL-valina en mezclas acuosas de nitrato de sodio a diferentes concentraciones y a las temperaturas de 283.15, 288.15, 293.15, 298.15, 303.15, 308.15, 313.15 y 318.15 K, con el fin de predecir el efecto que causa la adición de una sal sobre el comportamiento de los aminoácidos. Los resultados obtenidos se discuten en términos de las interacciones predominantes en solución.

MATERIALES Y MÉTODOS

Reactivos

Se empleó DL-valina (Alfa Aesar) y nitrato de sodio (Sigma-Aldrich) ambos con una pureza del 99%. Antes de su uso la DL-valina fue recristalizada dos veces en soluciones acuosas de etanol y secada al vacío a 348 K durante 6 h, después se almacenó en un desecador sobre P₂O₅. El agua utilizada fue desgasificada y doblemente destilada en medio alcalino con KMnO₄ para eliminar la materia orgánica¹⁶, obteniéndose con una conductividad inferior a 2 μS cm^-1.

Preparación de las soluciones

En este trabajo, se prepararon cinco solventes acuosos de nitrato de sodio a concentraciones de (0.0000, 0.0106, 0.0413, 0.1009, 0.4013 y 0.9014) mol kg^-1 que fueron mezclados con cantidades específicas de DL-valina hasta obtener concentraciones en el intervalo de 0.0000 mol kg^-1 hasta 0.4000 mol kg^-1. Las incertidumbres relativas (expresadas en porcentaje) para las concentraciones molales se encontraron en el intervalo de 0.02% a 0.28%, usando la ecuación (1):

Donde M es la masa molar de la DL-valina, W₂ y W₁ es la masa de soluto y solvente respectivamente, ΔM es la incertidumbre asociada a la masa molar de la DL-valina y ΔW es la incertidumbre de la balanza analítica utilizada marca Precisa (±1×10^-5 g).

Determinación de la densidad

Las densidades de las soluciones fueron determinadas en un densímetro de tubo vibratorio Anton Paar DMA 5000, con una incertidumbre de ±1×10^-5 g cm^-3 y un control de temperatura de ±0.001 K desde 283.15 K hasta 318.15 K a intervalos de 5 K. Se verificó el buen funcionamiento del equipo, determinando la densidad del agua bidestilada a diferentes temperaturas, y los datos obtenidos resultaron en buen acuerdo con los reportados en literatura^17–18 como se observa en la Tabla I.

Tabla I.

Densidades del agua bidestilada a diferentes temperaturas: a. Este trabajo, b. Ref. ¹⁷ y c. Ref. ¹⁸

T/K		283.15	288.15	293.15	298.15	303.15	308.15	313.15	318.15
Agua	ρ/g cm^-3
	^a	0.99969	0.99909	0.99819	0.99704	0.99564	0.99402	0.99221	0.99020
	^b	0.99973	0.99913	0.99823	0.99707	0.99568	0.99406	0.99224	0.99024
	^c	0.9997	0.9991	0.9982	0.9970	0.9956	0.9940	0.9922	0.9902

RESULTADOS Y DISCUSIÓN

Las densidades obtenidas para la DL-valina en mezclas acuosas de NaNO₃ aumentan conforme incrementan las concentraciones del aminoácido y del nitrato de sodio, pero disminuyen con el incremento de la temperatura como se observa en las Figuras 1 y 2 respectivamente.

Figura 1.

Densidades de la DL-valina en mezclas acuosas de NaNO₃ (■ 0.0000, × 0.0106, ▴ 0.0413, ♦ 0.1009, + 0.4013, ● 0.9014) mol kg^-1 a temperatura de 298.15 K.

Figura 2.

Densidades de la DL-valina en mezcla acuosa de NaNO₃ 0.0106 mol kg^-1 a diferentes temperaturas. (Todos los sistemas acuosos de NaNO₃ estudiados presentan la misma tendencia en sus datos).

Los valores de los volúmenes molares aparentes V_ϕ para la DL-valina en estas mezclas acuosas de NaNO₃, fueron calculados a partir de los datos de densidad utilizando la ecuación (2)¹⁹.

Donde M es la masa molar de la DL-valina, m es la molalidad del aminoácido en las mezclas acuosas de NaNO₃, ρ y ρ₀ son la densidad de la solución (DL-valina en mezclas acuosas de NaNO₃) y la densidad del solvente (mezclas acuosas de NaNO₃) respectivamente. Las incertidumbres relativas (expresadas en porcentaje) para los volúmenes molares se encontraron en el intervalo de 0.1% a 2.0%, usando la ecuación (3):

Donde Δρ es la incertidumbre del densímetro y Δm es la incertidumbre asociada a la concentración de las soluciones. El término de mayor incertidumbre resulta ser el tercero dentro del paréntesis al lado derecho de la ecuación (3).

Los resultados para las densidades y los volúmenes molares aparentes obtenidos son reportados en la Tabla II. La variación de V_ϕ con respecto a la concentración molal se correlacionó adecuadamente por medio de la ecuación de Masson a las temperaturas de trabajo²⁰, a fin de evaluar los volúmenes molares aparentes a dilución infinita Vϕ0 utilizando la ecuación (4). Para ello se toma la región de mayor concentración donde la tendencia de V_ϕ en función de m^1/2 es lineal; este procedimiento para el cálculo de Vϕ0ha sido previamente utilizado por Frank y Smith²¹, y es comúnmente aceptado debido a que la incertidumbre experimental de V_ϕ aumenta a medida que la concentración disminuye.

Tabla II.

Densidades ρ y volúmenes molares aparentes V_ϕ para la DL-valina en mezclas acuosas de NaNO₃ a las temperaturas de 283.15 hasta 318.15 K

m valina	ρ	Vϕ	ρ	Vϕ	ρ	Vϕ	ρ	Vϕ
mol kg^-1	g cm^-3	cm^3 mol^-1	g cm^-3	cm^3 mol^-1	g cm^-3	cm^3 mol^-1	g cm^-3	cm^3 mol^-1
mNaNO3=0.00000 mol kg^-1
	283.15 K		288.15 K		293.15 K		298.15 K
0.00000	0.99969		0.99909		0.99819		0.99704
0.01050	0.99989	98.77	0.99928	99.11	0.99838	99.37	0.99722	99.66
0.02000	1.00017	93.13	0.99956	93.52	0.99866	93.83	0.99750	94.17
0.03080	1.00049	91.38	0.99987	91.85	0.99896	92.34	0.99779	92.74
0.05090	1.00103	90.87	1.00040	91.29	0.99948	91.83	0.99832	92.09
0.07980	1.00180	90.58	1.00117	90.91	1.00025	91.30	0.99907	91.66
0.09930	1.00233	90.35	1.00170	90.74	1.00077	91.08	0.99959	91.43
0.15230	1.00376	90.10	1.00310	90.49	1.00216	90.84	1.00096	91.19
0.20990	1.00533	89.83	1.00464	90.26	1.00368	90.62	1.00247	90.98
0.24980	1.00641	89.67	1.00571	90.13	1.00474	90.47	1.00351	90.84
0.30210	1.00783	89.50	1.00711	89.93	1.00612	90.32	1.00488	90.68
	303.15 K		308.15 K		313.15 K		318.15 K
0.00000	0.99564		0.99402		0.99221		0.99020
0.01050	0.99582	99.87	0.99421	99.91	0.99239	100.06	0.99039	100.13
0.02000	0.99610	94.37	0.99448	94.63	0.99266	94.92	0.99066	95.17
0.03080	0.99639	92.98	0.99477	93.36	0.99295	93.64	0.99094	93.92
0.05090	0.99691	92.44	0.99528	92.74	0.99346	93.03	0.99145	93.27
0.07980	0.99765	92.00	0.99603	92.26	0.99419	92.65	0.99218	92.89
0.09930	0.99816	91.77	0.99653	92.09	0.99469	92.40	0.99267	92.71
0.15230	0.99953	91.54	0.99788	91.85	0.99604	92.16	0.99401	92.45
0.20990	1.00102	91.30	0.99936	91.61	0.99750	91.95	0.99547	92.20
0.24980	1.00205	91.18	1.00039	91.49	0.99853	91.79	0.99649	92.05
0.30210	1.00340	91.04	1.00173	91.32	0.99986	91.62	0.99783	91.86
mNaNO3=0.01064 mol kg^-1
	283.15 K		288.15 K		293.15 K		298.15 K
0.00000	1.00056		0.99995		0.99905		0.99788
0.05097	1.00192	90.44	1.00128	90.90	1.00035	91.39	0.99917	91.76
0.08072	1.00272	90.27	1.00207	90.72	1.00113	91.19	0.99994	91.59
0.09956	1.00322	90.20	1.00257	90.64	1.00162	91.11	1.00042	91.51
0.20069	1.00592	89.95	1.00523	90.37	1.00424	90.86	1.00301	91.25
0.25061	1.00724	89.87	1.00653	90.29	1.00553	90.76	1.00428	91.15
0.30022	1.00856	89.76	1.00783	90.18	1.00680	90.67	1.00554	91.06
0.35005	1.00987	89.70	1.00913	90.11	1.00807	90.60	1.00680	90.98
0.39684	1.01110	89.62	1.01034	90.05	1.00927	90.53	1.00798	90.92
	303.15 K		308.15 K		313.15 K		318.15 K
0.00000	0.99648		0.99486		0.99304		0.99103
0.05097	0.99776	92.12	0.99612	92.51	0.99429	92.86	0.99227	93.28
0.08072	0.99851	91.94	0.99687	92.35	0.99503	92.70	0.99300	93.10
0.09956	0.99899	91.87	0.99734	92.26	0.99550	92.63	0.99347	93.03
0.20069	1.00155	91.62	0.99988	91.98	0.99801	92.36	0.99596	92.74
0.25061	1.00281	91.54	1.00114	91.86	0.99925	92.25	0.99718	92.64
0.30022	1.00406	91.44	1.00237	91.78	1.00047	92.16	0.99839	92.56
0.35005	1.00530	91.36	1.00361	91.69	1.00170	92.07	0.99960	92.47
0.39684	1.00647	91.28	1.00476	91.64	1.00284	92.02	1.00073	92.40
mNaNO3=0.04132 mol kg^-1
	283.15 K		288.15 K		293.15 K		298.15 K
0.00000	1.00231		1.00166		1.00073		0.99954
0.05038	1.00365	90.44	1.00298	90.81	1.00202	91.26	1.00082	91.64
0.07998	1.00443	90.30	1.00376	90.70	1.00279	91.14	1.00157	91.52
0.09896	1.00494	90.24	1.00425	90.63	1.00328	91.07	1.00206	91.46
0.20069	1.00763	90.02	1.00691	90.43	1.00590	90.88	1.00464	91.27
0.25093	1.00895	89.95	1.00821	90.37	1.00718	90.81	1.00591	91.20
0.29985	1.01023	89.89	1.00947	90.31	1.00843	90.73	1.00714	91.13
0.34962	1.01152	89.83	1.01075	90.24	1.00968	90.68	1.00838	91.08
0.40049	1.01284	89.76	1.01205	90.17	1.01096	90.62	1.00964	91.03
	303.15 K		308.15 K		313.15 K		318.15 K
0.00000	0.99811		0.99647		0.99463		0.99261
0.05038	0.99937	92.07	0.99773	92.36	0.99588	92.76	0.99384	93.09
0.07998	1.00012	91.93	0.99847	92.24	0.99661	92.65	0.99457	92.94
0.09896	1.00060	91.85	0.99894	92.17	0.99708	92.58	0.99504	92.86
0.20069	1.00317	91.63	1.00148	91.96	0.99958	92.39	0.99753	92.69
0.25093	1.00442	91.54	1.00273	91.89	1.00081	92.33	0.99875	92.63
0.29985	1.00564	91.47	1.00393	91.82	1.00200	92.27	0.99993	92.57
0.34962	1.00687	91.42	1.00515	91.76	1.00320	92.22	1.00113	92.51
0.40049	1.00813	91.35	1.00639	91.72	1.00443	92.16	1.00235	92.45
mNaNO3=0.10086 mol kg^-1
	283.15 K		288.15 K		293.15 K		298.15 K
0.00000	1.00580		1.00509		1.00409		1.00285
0.05034	1.00714	90.02	1.00641	90.39	1.00540	90.79	1.00414	91.21
0.08080	1.00795	89.91	1.00721	90.30	1.00619	90.69	1.00492	91.10
0.10084	1.00849	89.87	1.00774	90.27	1.00671	90.64	1.00544	91.06
0.20070	1.01113	89.72	1.01034	90.14	1.00929	90.50	1.00799	90.90
0.25102	1.01245	89.67	1.01165	90.10	1.01058	90.45	1.00926	90.85
0.29998	1.01374	89.62	1.01290	90.05	1.01183	90.40	1.01049	90.79
0.34969	1.01502	89.58	1.01418	90.01	1.01309	90.35	1.01173	90.76
0.39866	1.01629	89.52	1.01542	89.96	1.01432	90.31	1.01295	90.70
	303.15 K		308.15 K		313.15 K		318.15 K
0.00000	1.00138		0.99970		0.99782		0.99560
0.05034	1.00266	91.56	1.00096	91.98	0.99907	92.30	0.99684	92.64
0.08080	1.00343	91.47	1.00173	91.87	0.99984	92.18	0.99760	92.52
0.10084	1.00394	91.42	1.00223	91.83	1.00034	92.13	0.99810	92.47
0.20070	1.00646	91.29	1.00473	91.67	1.00281	91.98	1.00056	92.27
0.25102	1.00772	91.23	1.00597	91.62	1.00405	91.92	1.00179	92.21
0.29998	1.00894	91.18	1.00718	91.57	1.00524	91.88	1.00298	92.16
0.34969	1.01016	91.14	1.00839	91.52	1.00645	91.82	1.00419	92.10
0.39866	1.01136	91.11	1.00958	91.48	1.00764	91.78	1.00536	92.05
m NaNO3=0.40131 mol kg^-1
	283.15 K		288.15 K		293.15 K		298.15 K
0.00000	1.02287		1.02185		1.02059		1.01912
0.05034	1.02419	89.33	1.02315	89.72	1.02189	90.00	1.02040	90.32
0.08028	1.02498	89.26	1.02393	89.66	1.02265	89.94	1.02116	90.26
0.10084	1.02551	89.24	1.02446	89.62	1.02318	89.91	1.02168	90.23
0.20044	1.02809	89.16	1.02701	89.54	1.02571	89.84	1.02419	90.14
0.25074	1.02939	89.12	1.02828	89.51	1.02697	89.81	1.02544	90.10
0.29995	1.03064	89.09	1.02952	89.48	1.02820	89.78	1.02666	90.07
0.35005	1.03191	89.06	1.03077	89.46	1.02944	89.75	1.02789	90.04
0.39786	1.03311	89.04	1.03196	89.43	1.03061	89.73	1.02906	90.01
	303.15 K		308.15 K		313.15 K		318.15 K
0.00000	1.01744		1.01558		1.01354		1.01130
0.05034	1.01871	90.71	1.01684	91.03	1.01479	91.35	1.01254	91.64
0.08028	1.01946	90.64	1.01758	90.97	1.01553	91.27	1.01328	91.54
0.10084	1.01998	90.60	1.01810	90.93	1.01604	91.23	1.01379	91.50
0.20044	1.02246	90.50	1.02056	90.81	1.01850	91.08	1.01623	91.33
0.25074	1.02370	90.45	1.02179	90.78	1.01972	91.04	1.01745	91.29
0.29995	1.02491	90.42	1.02299	90.74	1.02091	91.01	1.01864	91.26
0.35005	1.02613	90.39	1.02420	90.71	1.02212	90.97	1.01984	91.22
0.39786	1.02728	90.37	1.02534	90.69	1.02325	90.95	1.02098	91.19
mNaNO3=0.90145 mol kg^-1
	283.15 K		288.15 K		293.15 K		298.15 K
0.00000	1.05001		1.04857		1.04694		1.04513
0.05002	1.05132	87.87	1.04986	88.24	1.04821	88.64	1.04639	88.97
0.08010	1.05209	87.84	1.05063	88.20	1.04897	88.60	1.04714	88.93
0.09997	1.05261	87.82	1.05114	88.18	1.04947	88.58	1.04764	88.91
0.20072	1.05518	87.78	1.05369	88.12	1.05199	88.54	1.05013	88.86
0.25066	1.05645	87.76	1.05494	88.10	1.05322	88.52	1.05135	88.84
0.30012	1.05769	87.74	1.05616	88.08	1.05443	88.50	1.05255	88.82
0.35005	1.05893	87.73	1.05739	88.07	1.05564	88.49	1.05375	88.80
0.40188	1.06021	87.71	1.05866	88.05	1.05689	88.47	1.05499	88.79
	303.15 K		308.15 K		313.15 K		318.15 K
0.00000	1.04315		1.04102		1.03862		1.03587
0.05002	1.04440	89.32	1.04225	89.62	1.03985	89.95	1.03709	90.25
0.08010	1.04514	89.29	1.04299	89.59	1.04059	89.91	1.03782	90.23
0.09997	1.04563	89.27	1.04348	89.58	1.04107	89.90	1.03831	90.21
0.20072	1.04810	89.22	1.04593	89.53	1.04350	89.83	1.04072	90.16
0.25066	1.04931	89.20	1.04713	89.51	1.04469	89.81	1.04190	90.15
0.30012	1.05049	89.19	1.04831	89.49	1.04587	89.79	1.04307	90.13
0.35005	1.05168	89.17	1.04949	89.47	1.04704	89.78	1.04423	90.11
0.40188	1.05291	89.15	1.05070	89.46	1.04825	89.76	1.04543	90.10

Donde S_V es la pendiente límite experimental²².

En la región de dilución infinita, el volumen molar aparente es igual al volumen molar parcial de la DL-valina Vϕ0=V¯20²³, y los resultados obtenidos para Vϕ0 se presentan en la Tabla III, observándose que ellos disminuyen con el incremento de la concentración del cosolvente NaNO₃, lo cual puede ser interpretado como una contracción del volumen a dilución infinita debido al incremento de las interacciones soluto-cosolvente. Así mismo, los valores de Vϕ0 aumentan con el aumento de la temperatura, lo que podría ser atribuido a un debilitamiento de las interacciones que resultan del incremento de la energía cinética de las partículas.

Tabla III.

Volúmenes molares aparentes a dilución infinita Vϕ0 para la DL-valina en mezclas acuosas de NaNO₃ a las temperaturas de 283.15, 288.15, 293.15, 298.15, 303.15, 308.15, 313.15 y 318.15 K

m NaNO3/mol kg^-1	Vϕ0/cm^3 mol^-1	SV /cm^3 mol^-2 kg	R^2
283.15 K
0.00000	91.53	-3.69	0.9992
0.01064	90.77	-1.83	0.9949
0.04132	90.65	-1.39	0.9970
0.10086	90.20	-1.06	0.9960
0.40131	89.45	-0.65	0.9963
0.90135	87.94	-0.36	0.9983
288.15 K
0.00000	91.82	-3.42	0.9989
0.01064	91.19	-1.82	0.9965
0.04132	91.06	-1.39	0.9949
0.10086	90.60	-1.01	0.9963
0.40131	89.81	-0.61	0.9968
0.90135	88.29	-0.38	0.9984
293.15 K
0.00000	92.10	-3.24	0.9996
0.01064	91.66	-1.80	0.9994
0.04132	91.49	-1.37	0.9979
0.10086	90.97	-1.04	0.9985
0.40131	90.12	-0.62	0.9962
0.90135	88.69	-0.35	0.9985
298.15 K
0.00000	92.44	-3.20	0.9999
0.01064	92.07	-1.84	0.9981
0.04132	91.86	-1.32	0.9987
0.10086	91.38	-1.07	0.9932
0.40131	90.45	-0.69	0.9990
0.90135	89.04	-0.40	0.9982
303.15 K
0.00000	92.77	-3.17	0.9987
0.01064	92.46	-1.87	0.9969
0.04132	92.28	-1.46	0.9981
0.10086	91.74	-1.01	0.9981
0.40131	90.81	-0.71	0.9928
0.90135	89.39	-0.37	0.9966
308.15 K
0.00000	93.11	-3.26	0.9998
0.01064	92.81	-1.88	0.9994
0.04132	92.55	-1.32	0.9952
0.10086	92.16	-1.08	0.9996
0.40131	91.12	-0.69	0.9998
0.90135	89.69	-0.37	0.9977
313.15 K
0.00000	93.45	-3.32	0.9992
0.01064	93.20	-1.90	0.9957
0.04132	92.95	-1.25	0.9980
0.10086	92.48	-1.10	0.9982
0.40131	91.41	-0.72	0.9970
0.90135	90.01	-0.39	0.9988
318.15 K
0.00000	93.85	-3.74	0.9996
0.01064	93.58	-1.87	0.9990
0.04132	93.29	-1.32	0.9974
0.10086	92.80	-1.18	0.9992
0.40131	91.66	-0.75	0.9984
0.90135	90.32	-0.34	0.9993

También se analizó el efecto de la temperatura sobre el comportamiento del volumen molar aparente a dilución infinita Vϕ0 y éste se discute en términos de las interacciones hidrofóbicas e hidrofílicas y efecto del soluto sobre la estructura del solvente¹⁴. Para lo cual, los valores experimentales de Vϕ0 fueron correlacionados con la temperatura usando la ecuación (5).

Donde A, B y C son parámetros ajustables y T es la temperatura absoluta. En particular para estos sistemas los valores de ∂²Vϕ0/∂T² resultaron positivos para la mezcla binaria DL-valina + agua y negativos para la DL-valina + mezclas acuosas de NaNO₃, como se observa en la Tabla IV. Lo cual indica, según Hepler que en el primer sistema la DL-valina tiene un efecto formador de la estructura del agua; mientras que en los demás sistemas, la DL-valina tiene un efecto disruptor de la estructura del solvente mixto (mezclas acuosas de NaNO₃)²⁴

Tabla IV.

Valor de ∂²Vϕ0/∂T² de la DL-valina en mezclas acuosas de NaNO₃ a diferentes temperaturas

m NaNO3/mol kg^-1 en solución acuosa	∂^2Vϕ0/∂T^2
0.00000	0.00058±0.00004
0.01064	-0.00059±0.00007
0.04132	-0.00061±0.00009
0.10086	-0.00045±0.00007
0.40131	-0.00049±0.00007
0.90135	-0.00058±0.00004

Para examinar las interacciones moleculares predominantes en solución se determinaron los volúmenes molares parciales de transferencia a dilución infinita △Vϕ0 que fueron obtenidos con la ecuación (6) y los resultados se presentan en la Tabla V.

Tabla V.

Volúmenes molares parciales de transferencia a dilución infinita ΔVϕ0 para la DL-valina en agua hasta las mezclas acuosas de NaNO₃

m NaNO3/mol kg^-1	0.01064	0.04132	0.10086	0.40131	0.90135
T/K	ΔVϕ0 /cm^3 mol^-1
283.15	-0.75	-0.88	-1.33	-2.08	-3.59
288.15	-0.63	-0.76	-1.22	-2.01	-3.53
293.15	-0.44	-0.61	-1.13	-1.98	-3.41
298.15	-0.37	-0.58	-1.06	-2.00	-3.40
303.15	-0.31	-0.49	-1.03	-1.96	-3.38
308.15	-0.31	-0.56	-0.95	-2.00	-3.42
313.15	-0.25	-0.50	-0.98	-2.05	-3.44
318.15	-0.27	-0.57	-1.05	-2.19	-3.54

Los valores negativos obtenidos para ΔVϕ0 de la DL-valina en las mezclas acuosas de NaNO₃ podrían explicarse con ayuda del modelo de superposición de coesferas hidratadas²⁵ y del concepto de que en el estado de dilución infinita las interacciones soluto-soluto están ausentes^26-27. Además, de acuerdo con Mishra y Ahluwalia, los valores negativos de los volúmenes de transferencia obtenidos en este trabajo son el resultado del predominio en solución de la interacción soluto-cosolvente: ion-hidrofóbica, que ocurre entre el grupo isopropil –CH(CH₃)₂ del aminoácido DL-valina y los iones Na⁺ y NO₃⁻ del cosolvente⁸. Mientras que los valores negativos para ΔVϕ0son el resultado del efecto que pudiera tener el nitrato de sodio sobre las moléculas de agua en las coesferas de hidratación y sobre la molécula de soluto²⁸.

Consecuentemente, el predomino de dichas interacciones produce un aumento en el número de moléculas de agua liberada desde la esfera de solvatación hacia la fase voluminosa, produciéndose así una disrupción local en la estructura del solvente^29-30, este resultado es consistente con el criterio de la segunda derivada del volumen molar a dilución infinita con respecto a la temperatura, como lo sugiere el análisis de ∂²V20/∂T².

Por otra parte, los valores negativos obtenidos para ΔVϕ0pueden ser también explicados con ayuda de la ecuación (7) propuesta por Shahidi y colaboradores³¹.

En esta construcción, los volúmenes molares parciales a dilución infinita son consecuencia de las siguientes contribuciones: ΔV_VW que es el volumen de van der Waals, ΔV_V es el volumen asociado a los espacios vacíos en solución y ΔV_S es el volumen de contracción debido al efecto de electrostricción. Asumiendo que ΔV_VW y ΔV_V tienen la misma magnitud en agua que en soluciones acuosas, es decir son nulos, se deduce que cualquier variación de los volúmenes de transferencia es sólo consecuencia del efecto de electrostricción V_S²⁹. El signo negativo para ΔVϕ0 indica una disminución en el volumen a causa del efecto de electrostricción.

Esta situación nos advierte, que la presencia del nitrato de sodio en el sistema (DL-valina + mezclas acuosas de NaNO₃) aumenta el efecto de electrostricción alrededor de la DL-valina, como lo reflejan los números de hidratación, que se obtienen a continuación:

Los números de hidratación N_H para la DL-valina a cada temperatura y concentración de NaNO₃ se calcularon con ayuda del modelo propuesto por Millero³², a partir del volumen molar parcial del aminoácido, mediante la ecuación (8).

Donde V¯20 es el volumen molar parcial a dilución infinita de la DL-valina obtenido experimentalmente, V¯20(int) es el volumen molar parcial intrínseco de la DL-valina, que se puede expresar como la adición del volumen de van der Waals y el volumen debido al efecto de empaquetamiento³³, V¯20(elect) es el volumen molar parcial de electrostricción debido a la hidratación del aminoácido. Los valores de V¯20(int) pueden ser obtenidos del volumen molar de un cristal de la DL-valina utilizando la ecuación (9).

Donde V¯20(cristal) es el volumen molar de los cristales del aminoácido, y se obtiene dividiendo la masa molecular de la DL-valina entre su densidad en estado puro³⁴. Esta ecuación fue originalmente usada por Millero, para evaluar el comportamiento de aminoácidos en agua; sin embargo, también ha sido usada por otros investigadores en solventes acuosos mixtos^35-40. Una vez conocido el volumen de electrostricción es posible determinar la cantidad relativa de moléculas de agua alrededor del aminoácido hidratado utilizando la siguiente ecuación:

En este modelo se asume que por cada molécula de agua que pase desde la fase voluminosa hasta la región cercana al aminoácido el volumen decrece en (V¯E0–V¯B0). En este trabajo, para evaluar el término (V¯E0–V¯B0) fueron usados los valores de: −2.9, −3.3, −4.0 cm³ mol^-1 a 288.15, 298.15 y 308.15 K reportados por Yan y colaboradores⁴, en adición a los extrapolados por Páez y colaboradores³⁶ de: −2.7, −3.1, −3.6, −4.6 y −5.5 cm³ mol⁻¹ para las temperaturas de 283.15, 293.15, 303.15, 313.15 y 318.15 K. Finalmente los números de hidratación pueden ser obtenidos como una aproximación utilizando la ecuación (10) y los resultados se muestran en la Tabla VI.

Tabla VI.

Números de hidratación N_H para la DL-valina en mezclas acuosas de NaNO₃ a diferentes temperaturas

m NaNO3/mol kg^-1	0.01064	0.04132	0.10086	0.40131	0.90135	0.01064
T/K	NH
283.15	2.50	2.78	2.83	3.00	3.27	3.83
288.15	2.23	2.45	2.49	2.65	2.92	3.45
293.15	2.00	2.14	2.19	2.36	2.63	3.10
298.15	1.77	1.88	1.95	2.09	2.38	2.80
303.15	1.53	1.62	1.67	1.82	2.08	2.47
308.15	1.29	1.37	1.43	1.53	1.79	2.15
313.15	1.05	1.10	1.16	1.26	1.50	1.80
318.15	0.81	0.86	0.92	1.01	1.22	1.46

Es evidente que los números de hidratación N_H de la DL-valina en las mezclas acuosas de NaNO₃ aumentan conforme aumenta la concentración del cosolvente y disminuyen con el aumento de la temperatura. Este hecho sugiere que el aumento de las interacciones entre la DL-valina y los iones Na⁺ y NO₃⁻ del cosolvente generan un aumento en el efecto de electrostricción sobre las moléculas de agua, mientras que el aumento de la temperatura provoca una deshidratación de las especies solvatadas⁴¹.

CONCLUSIONES

En este trabajo se obtuvieron valores de densidad no reportados para el sistema de DL-valina en mezclas acuosas de NaNO₃ a las temperaturas desde 283.15 K hasta 318.15 K a intervalos de 5 K. A partir de los datos experimentales de densidad obtenidos se calcularon propiedades volumétricas encontrándose que los volúmenes molares aparentes a dilución infinita Vϕ0resultaron positivos y disminuyen con el aumento de la concentración del NaNO₃ e incrementan con el aumento de la temperatura. La segunda derivada de Vϕ0con respecto a la temperatura muestra que la DL-valina se comporta como un soluto disruptor de la estructura del solvente mixto (mezclas acuosas de NaNO₃). Los volúmenes molares parciales de transferencia a dilución infinita ΔVϕ0indican que las interacciones dominantes se establecen entre los iones Na⁺ y NO₃⁻ del cosolvente y la parte hidrofóbica del aminoácido, generando un aumento en la contracción del volumen a causa del efecto de electrostricción. Finalmente, los resultados de los números de hidratación N_H utilizando el método de Millero, muestran un efecto de deshidratación a medida que se incrementan los valores de temperatura; sin embargo, este parámetro no mostró sensibilidad a los cambios en los valores de la concentración del NaNO₃ en las mezclas.

Agradecimientos

Los autores agradecen a la Universidad de Córdoba por el apoyo brindado para la realización de este trabajo.