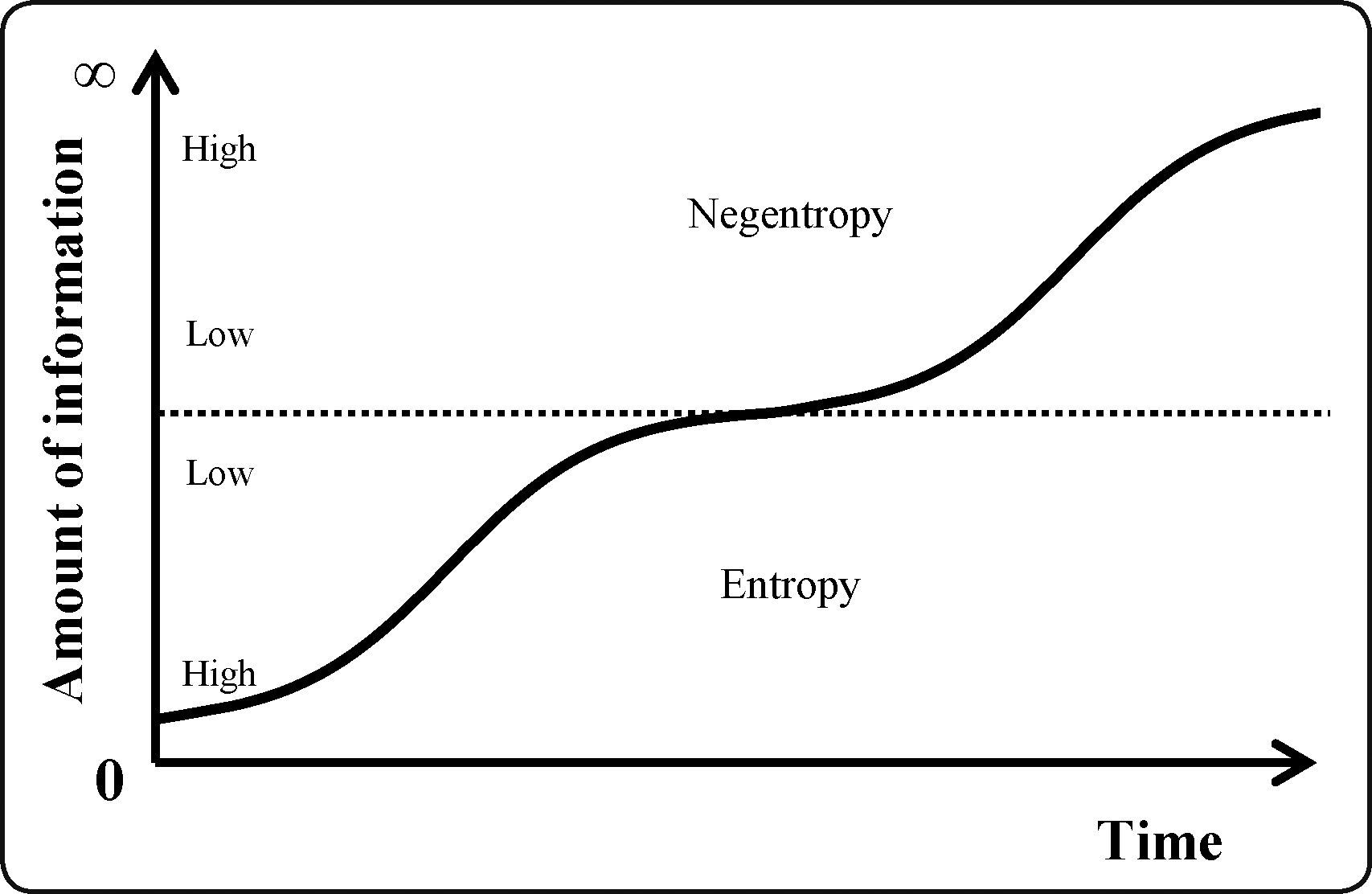
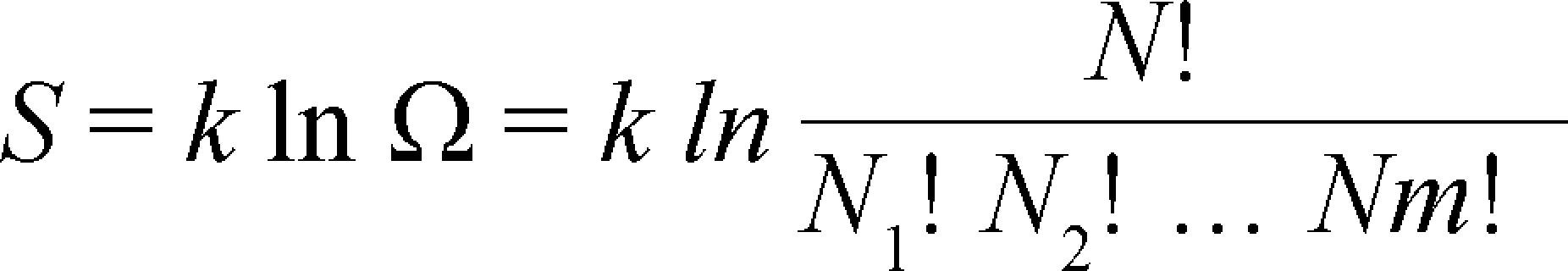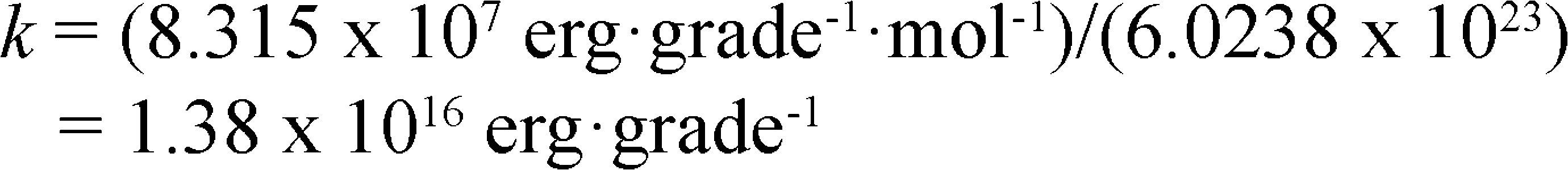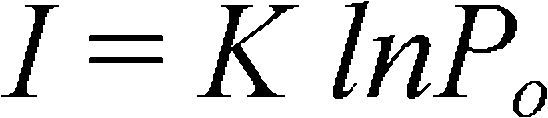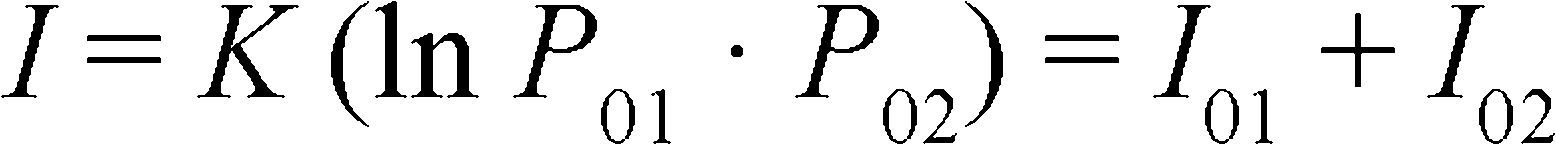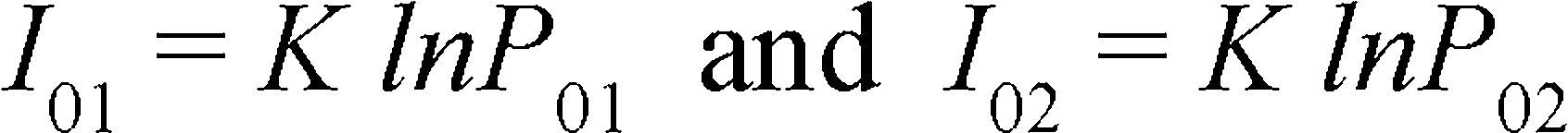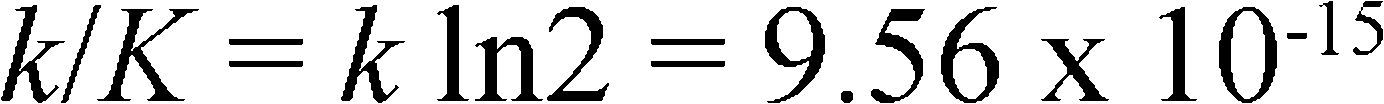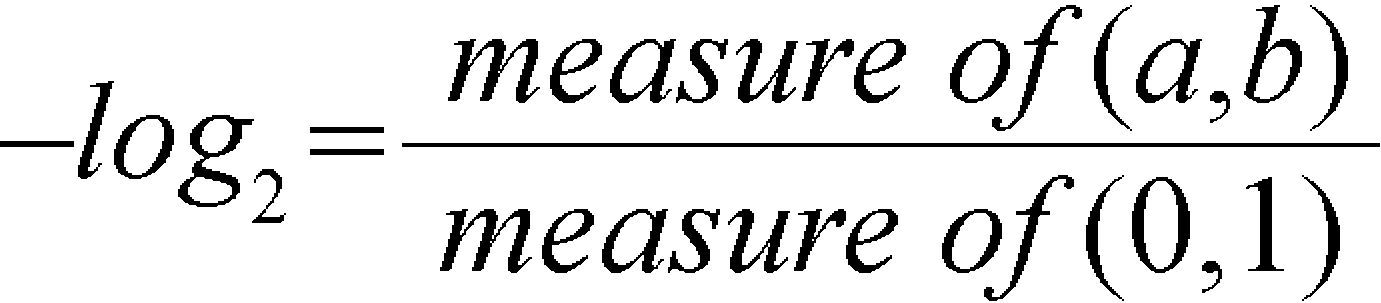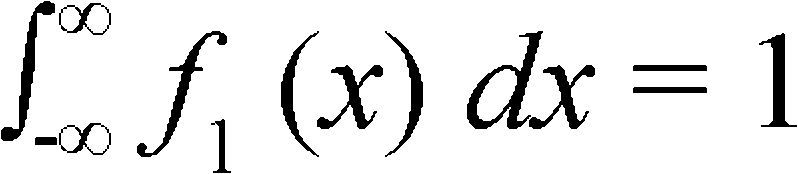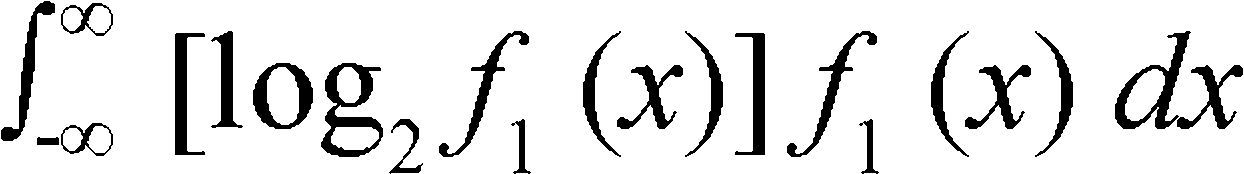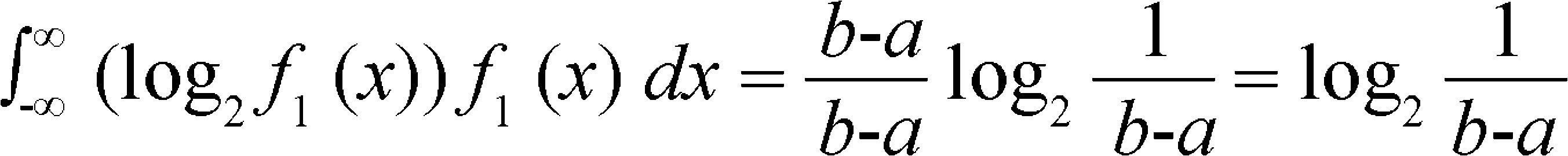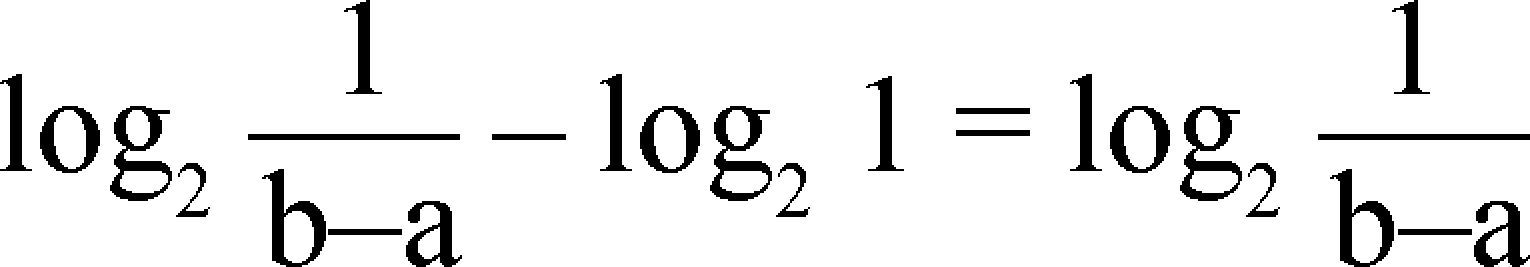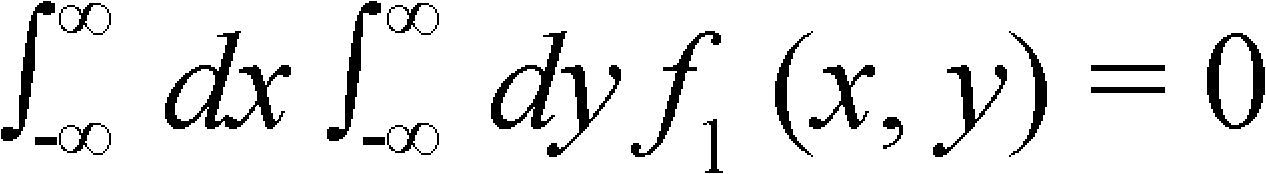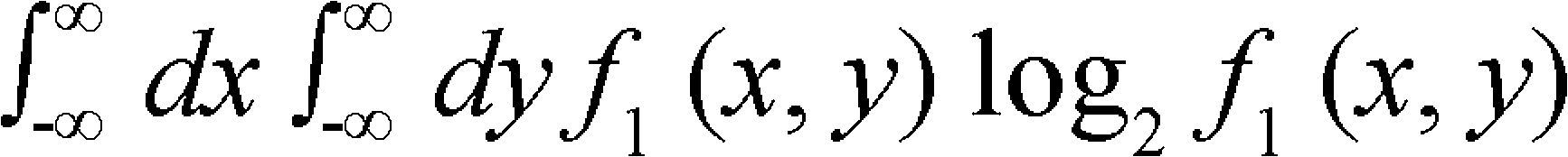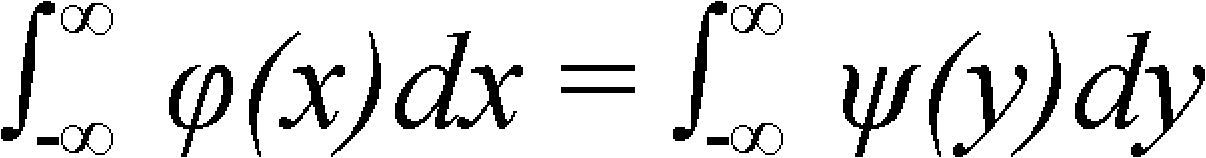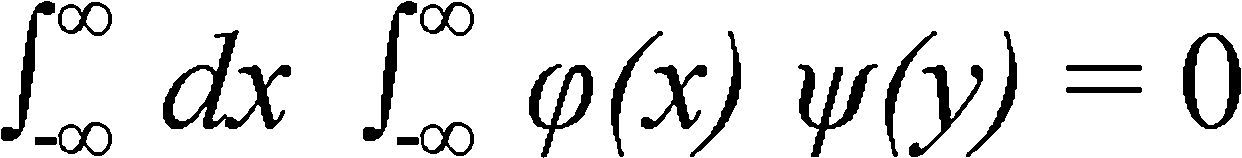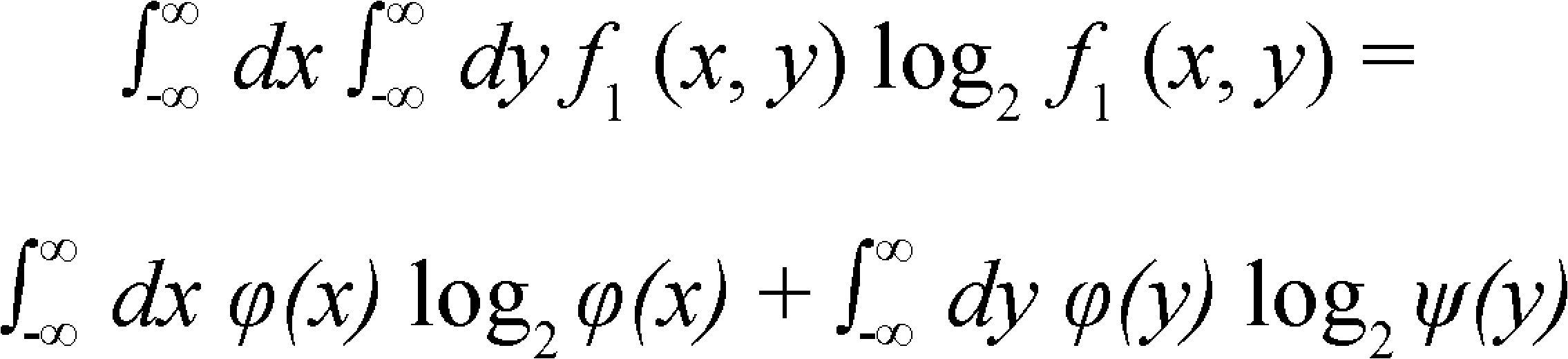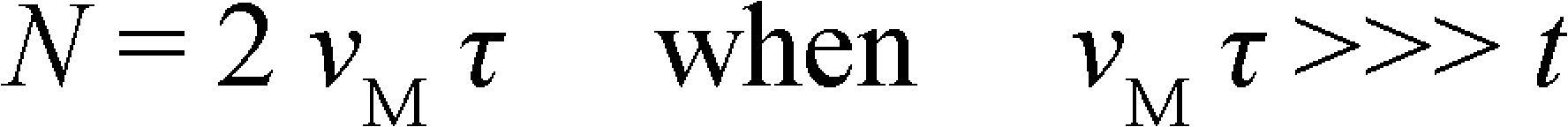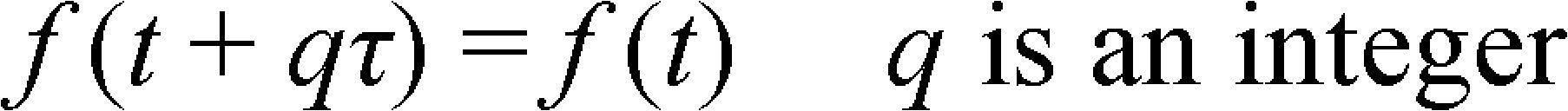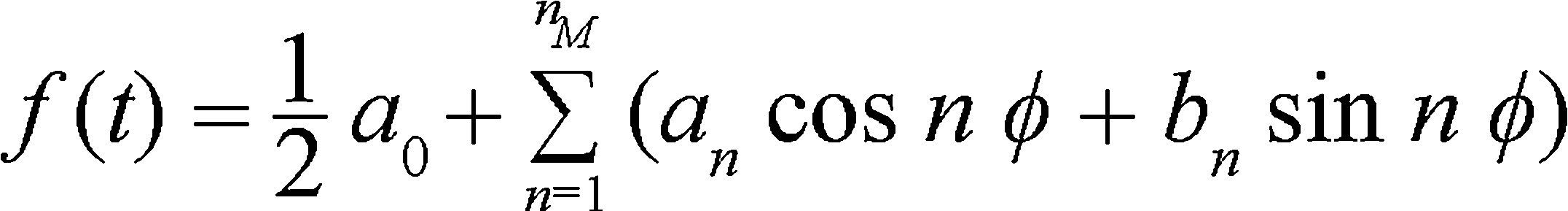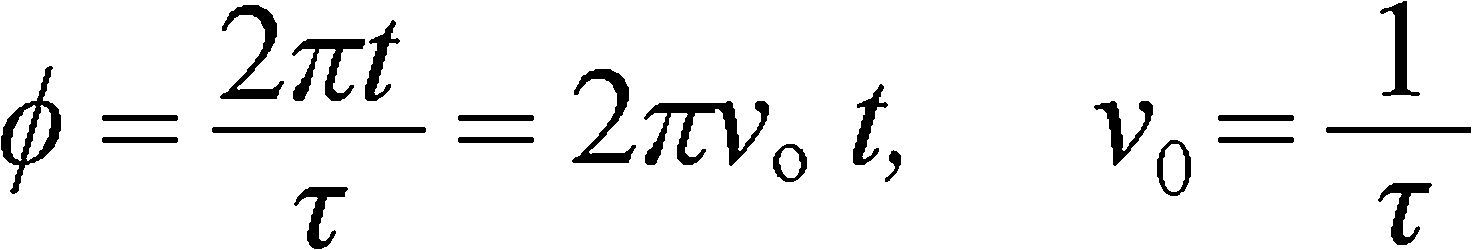For years, links between entropy and information of a system have been proposed, but their changes in time and in their probabilistic structural states have not been proved in a robust model as a unique process. This document demonstrates that increasement in entropy and information of a system are the two paths for changes in its configuration status. Biological evolution also has a trend toward information accumulation and complexity. In this approach, the aim of this article is to answer the question: What is the driven force of biological evolution? For this, an analogy between the evolution of a living system and the transmission of a message in time was made, both in the middle of environmental noise and stochasticity. A mathematical model, initially developed by Norbert Wiener, was employed to show the dynamics of the amount of information in a message, using a time series and the Brownian motion as statistical frame. Léon Brillouin's mathematical definition of information and Claude Shannon's entropy equation were employed, both are similar, in order to know changes in the two physical properties. The proposed model includes time and configurational probabilities of the system and it is suggested that entropy can be considered as missing information, according to Arieh Ben–Naim. In addition, a graphic shows that information accumulation can be the driven force of both processes: evolution (gain in information and complexity), and increase in entropy (missing information and restrictions loss). Finally, a living system can be defined as a dynamic set of information coded in a reservoir of genetic, epigenetic and ontogenic programs, in the middle of environmental noise and stochasticity, which points toward an increase in fitness and functionality.
Durante años se han propuesto vínculos entre entropía e información de un sistema, pero sus cambios en tiempo y en sus estados estructurales probabilísticos no han sido probados en un modelo robusto como un proceso único. Este documento demuestra que incrementos en entropía e información de un sistema son las dos sendas para cambios en su estado configuracional. También, la evolución biológica tiene una tendencia hacia una acumulación de información y complejidad. Con este enfoque, aquí se planteó como objetivo contestar la pregunta: ¿Cuál es la fuerza motriz de la evolución biológica? Para esto, se hizo una analogía entre la evolución de un sistema vivo y la transmisión de un mensaje en el tiempo, ambos en medio de ruido y estocasticidad ambiental. Se empleó un modelo matemático, desarrollado inicialmente por Norbert Wiener, para mostrar la dinámica de la cantidad de información de un mensaje, usando una serie de tiempo y el movimiento Browniano como estructura estadística. Se utilizó la definición matemática de información de Léon Brillouin y la ecuación de la entropía de Claude Shannon, ambas son similares, para conocer los cambios en las dos propiedades físicas. El modelo propuesto incluye tiempo y probabilidades configuracionales del sistema y se sugiere que la entropía puede ser considerada como pérdida de información, de acuerdo con Arieh Ben-Naim. Se muestra una gráfica donde la acumulación de información puede ser la fuerza motriz de ambos procesos: evolución (incremento en información y complejidad) y aumento en entropía (pérdida de información y de restricciones). Finalmente, se puede definir a un sistema vivo como la dinámica de un conjunto de información codificada en un reservorio de programas genéticos, epigenéticos y ontogénicos, en medio de ruido y estocasticidad ambiental, que tiende a incrementar su adecuación y funcionalidad.
What is life? Technically, it could be defined as cells with evolutionary potential, make up by organic matter and getting on in an autopoyetic metabolism[1]. Organisms use energy flow gradients at different organization levels in accord with physical laws. The living systems have three principal functions as self-organizing units: a) compartmentalization, b) metabolism, and c) regulation of input and output information flux[2]. The layer between internal and external environment of organisms controls matter, energy and information flows; metabolism regulates epigenetic and autopoyetic processes; biological information is a program (and a set of programs) that operates both physiology and functionality, codified in the DNA[3].
Darwinian theory of evolution by means of variation, natural selection and reproductive success of heritable variation in populations and organisms, can be defined as an ecological process that change the covariance of phenotypic traits (as expression of genetic, epigenetic, ontogenic and environmental factors) in living organisms or biological systems grouped at different organization levels[4]. Natural selection operates on biological systems that have three features: a) variability, b) reproductivity, and c) heritability; one result of natural selection is a tendency toward to an increase in fitness and functionality of biological systems in an environmental stochasticity (both biotic and abiotic). Fitness is a measure of reproductive success of changes in allele frequency of organisms on a determinate ecological noise, conditioned on the phenotype or genotype[5].
In this paper, an analogy between a biological system and a message was made; it was also considered the environmental stochasticity as the noise when a message is transmitted. Thus, the biological system is analogous to the amount of information of a message (for example: genetic information) that is transported to the next generation inside an ecological noise. This favors the use of the Norbert Wiener model of message's transmission in a telephonic line with noise[6]. In our model, it has been considered that information could be as simple as a binary unit (bit, 0 and 1), but it can grow by the additive property[7,8].
The amount of information defined by Wiener[7] (p. 62) is the negative of the quantity usually defined as statistical entropy. This principle of the second law of thermodynamics can be understood for a closed system as the negative of its degree of restrictions[9] (p. 23), i.e., its structuration level. Also, G.N. Lewis in 1930 (cited by Ben-Naim[10] p. 20) quotes: “Gain in entropy always means loss of information”.
In relation to information theory, Léon Brillouin in his book “La información y la incertidumbre en la ciencia”[11] (p. 22-25) wrote that entropy is connected with probabilities as is expressed in equations by Ludwig Eduard Boltzmann and Max Planck, and suggested that information is a negative entropy[12,13] or negentropy[12]. But instead of using the term of entropy, Arieh Ben-Naim[10] (p. 21) proposes to replace it by “missing information”.
Nevertheless, the second law of thermodynamics neither implies one-way time, nor has a statistical probabilities model. For this reason, in this paper it was employed a time series tool and the Brownian motion as a model to simulate the dynamics of the amount of information of a message, as an analogous of a biological system. This approach shows that biological information could be carried by “some physical process, say some form of radiation” as Wiener[7] wrote (p. 58). What wavelength? Brillouin[11] (p. 132), in his scale mass-wavelength equals a mass of 10−17 g to a wavelength of 10−20 cm; for this scales, it could be important to consider k, the Boltzmann constant, because its value is 1.38 x 10−16 erg/°K, in unities of the system cm, g, second. Likewise, a quantum h can be expressed as h = 10−33 cm; this smaller length “plays a fundamental role in two interrelated aspects of fundamental research in particle physics and cosmology”[14] and “is approximately the length scale at wich all fundamental interactions become indistinguishable”[14]. Moreover, it is necessary to mention that Brownian motion is a thermic noise that implies energy of the level kT (where T is temperature) by degree of freedom[11] (p. 135). It was hypothesized that this radiation could be the wavelength of photons incoming on Earth's surface, irradiated by the photosphere of the Sun at a temperature of 5760 °K; after the dissipation of high energy photons to low energy ones, through irreversible processes that maintain the biosphere, the temperature of the outgoing photons that Earth radiates to space is 255 °K[15]. This incoming radiation support plant photosynthesis, evapotranspiration flow, plant water potential, plant growth, energy for carbon-carbon bonds (or C-H, C-O, O=O, etc.), and food of the trophic chains in ecosystems, among other energy supported processes.
The question to answer in this paper is: What is the driven force of biological evolution? The possible answer is that driven force is the dynamics of the amount of information in a biological system (genetic and epigenetic messages). Antoine Danchin[16], in a similar approach, proposes that mechanical selection of novel information drives evolution. In the next section, it will be described the mathematical model of the dynamics of message transmission, as a proposal to explain the nature of biological evolution.
THE MODELShannon entropy formula is[17] (p. 291):
Where Ω is the number of microstates or possible arrangements of a system, for N particles that can occupy m states with occupations numbers (n1, n2, ….., nm) and k is the Boltzmann constant, that is R (the ideal gas constant) divided by the Avogadro′s number:
and Brillouin information (I) formula[18] (p. 1) is:
Where K is a constant and Po is the number of possible states of a system, keeping in reserve that the states have a priori the same probability. The logarithm means that information has the additive property.
For example, if the configuration states of two independent systems are coupled in this way: P0 = P01 · P02
with
The constant K can be equal to 1/(ln2) if information is measured in binary units (bits) (op. cit., p. 2); nevertheless, if information of Brillouin's formula is compared with Shannon entropy formula, and K is replaced by k, the Boltzmann constant, then information and entropy have the same unities: energy divided by temperature[18] (p. 3). The relationship, between entropy and information, if temperature -in centigrade scale- is measured in energy units is:
The problem to associate entropy and information as concepts and in unities is that information is not a change between an initial and a final state, and it lacks of statistical treatment of possible configurations as in thermodynamical statistics. Thus, Norbert Wiener[7] developed the next model, where information has a time series and their distribution follows the configuration of the Brownian motion (chapter III).
For this, Wiener[7] (p. 61) established that the amount of information of a system, where initially a variable x lies between 0 and 1, and in a final state it lies on the interval (a, b) inside (0, 1), is:
The a priori knowledge is that the probability that a certain quantity lies between x and x + dx is a function of x in two times: initial and final or a priori and a posteriori. In this perspective, the a priori probability is f1(x) dx and the a posteriori probability is f2(x) dx.
Thus, it is valid to ask: “How much new information does our a posteriori probability give us?”[7] (p. 62). Mathematically this means to bind a width to the regions under the curves y=f1(x) and y=f2(x), that is initial and final conditions of the system; also, it is assumed that the variable x have a fundamental equipartition in its distribution. Since f1(x) is a probability density, it could be established[7] (p. 62):
and that the average logarithm of the breadth of the region under f1(x) may be considered as an average of the height of the logarithm of the reciprocal of f1(x), as Norbert Wiener[7] wrote using a personal communication of J. von Neumann. Thus, an estimate measure of the amount of information associated with the curve f1(x) is:
This quantity is the amount of information of the described system and it is the negative of the quantity usually defined as entropy in similar situations[7] (p. 62). It could also be showed that the amount of information from independent sources is additive[7] (p. 63). Besides: “It is interesting to show that, on the average, it has the properties we associate with an entropy”[7] (p. 64). For example, there are no operations on a message in communication engineering that can gain information, because on the average, there is a loss of information, in an analogous manner to the loss of energy by a heat machine, as predicted by the second law of thermodynamics.
In order to build up a time series as general as possible from the simple Brownian motion series, it is necessary to use functions that could be expanded by Fourier series developments, as it is showed by Norbert Wiener in his equation 3.46, and others, in his book on cybernetics[7] (pp: 60-94).
It is possible to apply equation (5) to a particular case if the amount of information of the message is a constant over (a, b) and is zero elsewhere, then:
Using this equation to compare the amount of information of a point in the region (0, 1), with the information that is the region (a, b), it can be obtained for the measure of the difference:
It is important to say that this definition of the amount of information can be also applicable when the variable x is replaced by a variable ranging over two or more dimensions. In the two dimensional case, f(x, y) is a function such that:
and the amount of information is:
if f1(x, y) is the form φ(x) ψ(y) and
then
and
this shows that the amount of information from independent sources is additive[7] (pp: 62-63).
For this model, it would be interesting to know the degrees of freedom of a message. It would be convenient to take the proposal of Léon Brillouin[18] (pp: 90-91), who made the next development:
A certain function f(t) has a spectrum that does not include frequencies higher than a certain maximum limit: νM and the function can be expanded over a time interval τ. The outstanding question is: How much parameters (or degrees of freedom) are necessary for to define the function?
If it is established that there is N degrees of freedom and
To choose the independent parameters for the function, it was considered the interval 0 < t < τ and that it is suitable to know the function values before 0 and after τ, without any addition of information to the message f(t). Thus, it is chosen a periodic function that reproduces in an indefinite way the solution curve of the function f(t) between 0 and τ as:
and use a periodic function with a period τ; thus, applying a development of a Fourier series, it is obtained:
with
as was stated by Brillouin[18] (pp: 90-91).
This means that the degrees of freedom bound to a message could be a periodic function that is dependent on the amount of information and the time interval.
DISCUSSIONIt has been demonstrated a mathematical model that correlates the accumulation of information with biological evolution, by means of additive information (it could be genetic and epigenetic). Biological systems can be assimilated as messages transmitted to the next generation in the middle of an environmental noise, biotic and abiotic. What kind of information? It could be as simple as binary units (bits, 0 and 1), which can be a set in a wavelength of a photon and that can be assembled into integrative structures. For example, in computer technology the hardware is the physical support of an ensemble of structured information (algorithms hierarchically organized); this informatics programs run on a binary system where an alpha-numeric character is formed with a set of binary units, i. e., a byte (byte is equals to 8 bit series), and then, they can form data (words), concepts, sentences, routines, algorithms, programs and sets of programs as in computers software. The DNA is a genetic information code and it must have epigenetic, ontogenic and autopoyetic programs that regulate (by expression or restriction) its development. The genetic pleiotropy in organisms is when a gene affects more than one phenotypic trait, and it exhibits the gene modulation by an epigenetic process.
The mathematical model also shows that changes in information and entropy could be the same process: an increase in entropy normally means a loss of structure or restrictions of a system. On the contrary, the evolution of a biological system usually means an enlargement in its amount of information and complexity that drives to an increase in its fitness and functionality. Biological systems are information building systems[19–21], i.e., genetic and epigenetic capacity to generate developmental functional complexity (phenotype), as is quoted by Elsheikh[22] in his abstract, but organisms also face to environmental networks, where there are stochasticity, random processes (positive or negative) and, sometimes, chaos[23,24].
Two emergent attributes of biological organisms are phenotype and behavior. Phenotype is a synthesis of equilibrium between internal and external environments, and behavior is a driven force in individual evolution[25–27]. A path frequently transited by evolutionary changes is the mutualistic symbiosis[1]. In this sense, the transmission of biological messages (organisms) to the next generation increases its possibilities to improve the amount of information, if the message is redundant and symbiosis is a way to form additive messages. For example, if the organism A has three traits and become a functional unity with the organism B, which has other three different traits and both can share all traits; then, they have 9 binomial sets of traits.
Finally, it is necessary to point out that information create programs and a set of programs that drive toward power-law behavior of organisms. Behavior also has two sources: a) phylogenetic memory (i.e., genetically codified routines and conducts), and b) algorithms induced by epigenetic modulation and environmental noise or stochasticity. It is already known that ecological behavior of organisms is the driven force to its evolution (accumulation of information) or its degradation (loss of structures and information).
CONCLUDING REMARKSFigure 1 makes a synthesis of the role of information on the evolution of biological systems and on changes in entropy. Mathematically, the origin of matter in the universe could have begun above zero entropy[15], and matter evolution drives to form organization levels with increasing complexity and information. The transition between both is called abiotic matter, and living systems must be carried by the degrees of freedom due to the product of the Boltzmann constant by temperature (kT). The big source of heat on the Earth is the Sun that is at 5760 Kelvin degrees at the photosphere and the Earth average temperature in the biosphere actually is ca. 288 °K. Then, organisms absorb high energy solar photons and they use that energy for photosynthesis or as food in the trophic chain by means of dissipative processes. Living organism “eat” high energy photons and they distribute them among photons with low energy. The entropy of photons is proportional to the number of photons[15] in a system and on the Earth's energy balance, Lineweaver and Egan[15] (p. 231) say: “when the Earth absorbs one solar photon, the Earth emits 20 photons with wavelengths 20 times longer”.
Likewise, Karo Michaelian[28] (p. 43) wrote: “Direct absorption of a UV photon of 260nm on RNA/DNA would leave 4.8eV of energy locally which, given the heat capacity of water, would be sufficient energy to raise the temperature by an additional 3 Kelvin degrees of a local volume of water that could contain up to 50 base pairs”. In this discerment, solar photons increase the degrees of freedom, in structure and functionality, of living organisms. One degree of freedom is an independent parameter of a system and it could be considered as novel information of it.
Finally, it is important to say that information can be the driven force of biological evolution. Life, as a state, can be defined as a dissipative system that has a structural biomass or hardware, genetic and epigenetic programs or software and metabolic-ontogenic interface that regulates flows of matter, energy and information, in order to have an autopoyetic homeostasis, behavior and increases in its fitness and functionality. Furthermore, a living system is an unique set of programs reservoir that evolves in face to ecological noise, stochasticity and, sometimes, chaos.
The authors are grateful to Edmundo Patiño and César González for their observations to the original manuscript and to three anonymous reviewers. This study was financed by the Dirección General de Asuntos del Personal Académico of the Universidad Nacional Autónoma de México, UNAM (Grant PAPIIT IN-205889).