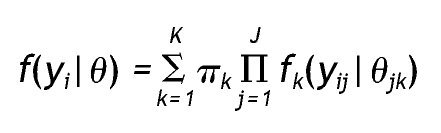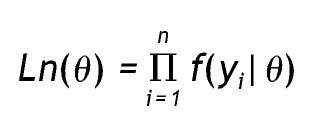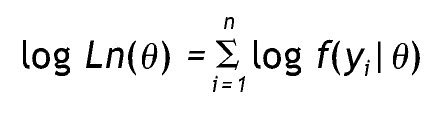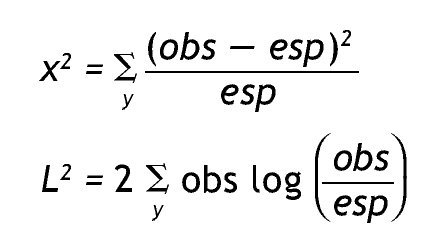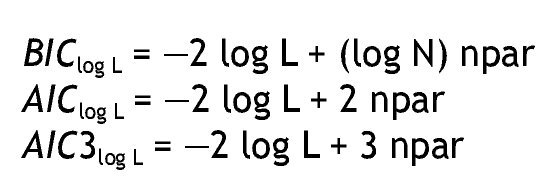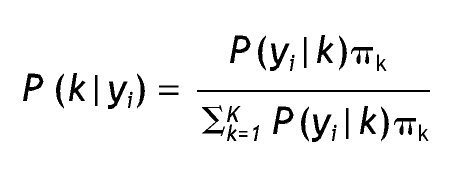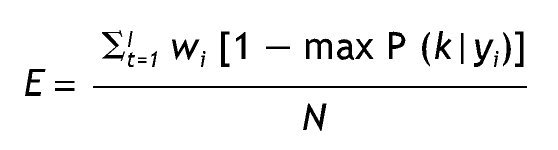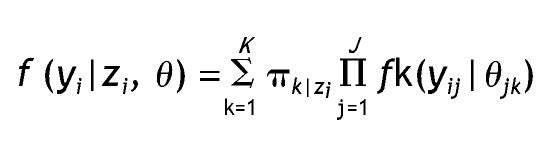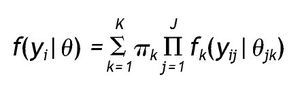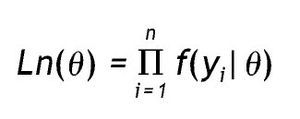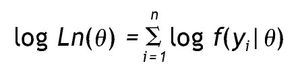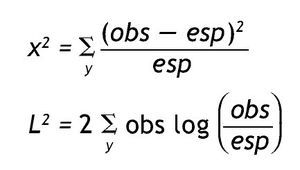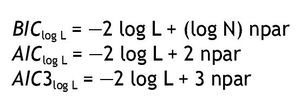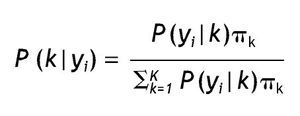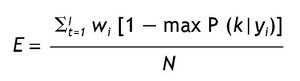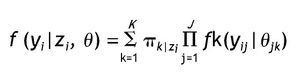Introducción
En numerosas ocasiones se manifiesta la necesidad de clasificar a individuos u otros objetos según algún constructo que no se puede medir directamente, por lo cual se recurre a indicadores del mismo. En ese sentido, el análisis de clases latentes (LCA), basado en un modelo probabilístico, es una herramienta útil cuando se tienen variables manifiestas nominales, ordinales, continuas o conteos; se utiliza cada vez con mayor frecuencia en la clasificación de trastornos conductuales y psiquiátricos 1,2 y cobra particular relevancia en el campo del abuso de sustancias, donde gran parte de las variables son categóricas 3.
El hecho de desarrollar tipologías de uso de sustancias, en lugar de focalizarse de manera exclusiva en patrones problemáticos, permite detectar problemas menores de consumo de sustancias que no logran ser identificados con los criterios de dependencia y medidas unidimensionales 4,5, los cuales han mostrado notables deficiencias. DiFranza y Ursprung 6 revisaron 37 estudios con el objetivo de revisar los criterios de clasificación de dependencia al tabaco, y observaron una carencia de evidencia de validez predictiva de los criterios diagnósticos, como también ausencia de medidas de validez y fiabilidad de los instrumentos oficiales, los cuales excluyen los fumadores no cotidianos al valorar la dependencia. Por ello, es necesario recurrir a otras metodologías para identificar patrones de uso de sustancias. Por ejemplo, el análisis de cluster ha permitido identificar tipologías de fumadores adolescentes canadienses situacionales y ubicuos, superando esa tipología a las reglas típicas de frecuencia y cantidad para definir el estatus de fumador 7.
A diferencia de otros modelos estadísticos empleados para obtener tipologías de usuarios, el LCA se distingue por incorporar variables discretas no observadas para explicar la relación entre variables observadas (manifiestas o indicadoras), sin basarse en los supuestos tradicionales del modelado (distribución normal, relaciones lineales y homogeneidad de varianzas). Es un método estadístico que permite encontrar subtipos de casos relacionados a partir de las variables observadas, las cuales se utilizan para estimar los parámetros del modelo. Como señala Goodman 8 las clases se forman en función de una variable latente categórica que genera una división en clases latentes exhaustivas y mutuamente excluyentes, y en cada clase latente las variables observadas son estadísticamente independientes.
En el contexto de la dependencia al tabaco, el LCA ha permitido identificar diferentes gradientes de intensidad en una muestra de jóvenes adultos estadounidenses 9. A partir de la clásica puntuación del test de Fagëstrom, el 66 % de los participantes de la muestra presentaba un nivel muy bajo de dependencia, el 17 % bajo, el 9 % moderado y el 9 % nivel alto. Por otra parte, a través del LCA se identificó una clase no dependiente (50 %), otra clase con una cantidad moderada de características de dependencia (31 %) y, finalmente, una clase intensamente afectada (19 %). Si bien la clasificación por ambos métodos fue bastante congruente, el LCA identificó un porcentaje mayor de fumadores con problemas graves de dependencia en relación con lo que sugieren los criterios convencionales.
El hecho de disponer de mejores herramientas para identificar los patrones de uso y abuso de sustancias tiene implicaciones también en el campo preventivo y de intervención terapéutica. De hecho, ha permitido identificar subtipos de fumadores alemanes categorizados en la fase de precontemplación según el modelo transteórico de Prochaska y Velicer 10, tomando como variables indicadoras los pros y contras de no fumar y la autoeficacia para dejar de fumar 11.
A partir de considerar la relevancia del LCA para abordar la clasificación de los trastornos adictivos, este trabajo se propuso, por una parte, revisar aspectos teóricos del LCA, y por otra valorar su aplicación a través del estudio de la conducta de fumadores de cigarrillos mayores de 18 años de España, en función de 5 variables indicadoras: cantidad de cigarrillos, intención de dejar de fumar, auto-percepción como fumador y frecuencia de fumar del padre y de la madre cuando era niño.
Características del análisis de clases latentes
El LCA se basa en el concepto de probabilidad y recurre a los datos observados para estimar los parámetros del modelo: la probabilidad de cada clase latente, cuya suma debe ser igual a 1 (tamaño); y las probabilidades de respuesta condicional, lo cual representa la probabilidad de una respuesta particular en una variable observada condicionada por la pertenencia a una clase latente determinada.
Como señalan Vermunt y Magidson 12 el modelo de cluster de clases latentes para variables observadas mixtas se puede expresar como:
Donde yi representa las respuestas de un sujeto u objeto en un conjunto de variables observadas, K es el número de clases, πk indica la probabilidad de pertenecer a una clase latente k (tamaño de la clase k), J indica el número total de indicadores y j un indicador particular, y fk(yij|θjk) implica la función de distribución univariante de cada uno de los elementos yij de yi, condicionada por el conjunto de variables indicadoras j de la clase k. Es decir, que la función de densidad de un conjunto de respuestas de un sujeto en un conjunto de variables observadas es igual a la suma de la probabilidad de pertenecer a cada una de las clases por el producto de la función de densidad de cada indicador condicionado por la clase.
Estimación de parámetros en análisis de clases latentes
Los parámetros del modelo de clases latentes se estiman por el método de máxima verosimilitud (ML), es decir, que la solución consiste en valores de parámetros que maximizan la función de probabilidad y su logaritmo natural 13. La verosimilitud de un modelo se define como la probabilidad de que cada conjunto de datos haya sido generado por el modelo; es la formulación del modelo a través de la distribución conjunta de los datos y se expresa de la siguiente forma:
Donde yi representa un conjunto de datos particular, n es el número de casos θ y comprende los parámetros del modelo. Dado que Ln(θ) (o simplemente L) siempre es un valor muy pequeño, se utiliza el logaritmo (log L o LL), ya que es una función monótona creciente y no afecta el orden de las mediciones. Así, el producto pasa a ser una suma:
Debido a que esa función es siempre negativa y pequeña, generalmente se utiliza menos dos veces el logaritmo de verosimilitud (—2LL), que varía entre [0, ∞); los valores que tienden al infinito indican que el modelo no genera el conjunto de datos, y valores más cercanos a cero señalan que el modelo genera los datos, es decir, que el error es mínimo 14.
Para aproximarse a los estimadores máximos verosímiles de los parámetros del modelo se recurre al algoritmo de maximización de la esperanza (EM), o al algoritmo de Newton-Raphson. Ambos algoritmos son iterativos; el algoritmo más utilizado en este caso es EM, que comienza con valores iniciales arbitrarios de parámetros y continúa con una serie de pasos de estimación y reestimación de parámetros hasta que se logra un criterio determinado, esto es, cuando la diferencia entre las estimaciones es más pequeña que cierto criterio, por lo cual se converge a un máximo de una función de verosimilitud 15. Su mayor uso se debe a que presenta notable robustez con respecto a los valores iniciales y es relativamente fácil para programar 16.
Lo ideal es que el algoritmo de estimación converja en un máximo global, pero en ocasiones converge en un máximo local, que es la mejor solución, pero en un espacio de parámetros determinado, no un máximo global. Los máximos locales se relacionan con la complejidad del modelo, siendo más comunes a medida que se incrementa el número de clases latentes 13. Para evitar soluciones de máximos locales se debe correr el algoritmo de estimación varias veces con distintos valores iniciales, y si se obtienen soluciones diferentes se debe examinar la distribución de cada una de las soluciones y considerar como mejor la que es más frecuente o la que presenta mejor ajuste (mayor probabilidad). Otra manera de evitar máximos locales es simplificar el modelo, lo cual reduce el número de parámetros que se estiman 15.
Otro aspecto relacionado con la estimación de los parámetros es la identificación del modelo, es decir, si existe suficiente información en la tabla de contingencia de datos observados para estimar los parámetros del modelo propuesto 16. Un modelo identificado es aquel que presenta sólo una solución mejor; en cambio, si el modelo es no identificado existe más de una. Una de las causas de no identificabilidad es especificar un modelo con numerosas clases latentes, debido a que para cada nueva clase latente se deben estimar más parámetros, y el número máximo de parámetros estimables está limitado por los grados de libertad disponibles. Otras causas posibles son muestras pequeñas y tablas de contingencia muy dispersas 17. Una forma para evaluar la identificabilidad es correr el algoritmo de estimación varias veces con valores iniciales distintos, y si las soluciones son semejantes es indicio de que el modelo es identificado 16. Además, se puede evaluar la matriz hessiana (matriz de derivadas de segundo orden de todos los parámetros), que en los casos donde el modelo es no identificado resulta ser de rango incompleto 18.
Selección del modelo y criterios de bondad de ajuste
Como señalan Linzer y Lewis 19 una de las ventajas del LCA es la variedad de herramientas disponibles para evaluar el ajuste del modelo y determinar el número apropiado de clases latentes. Los modelos con más parámetros proveen un mejor ajuste a los datos, mientras que los modelos con menos clases tienden a tener un peor ajuste, por lo que el objetivo es encontrar el modelo más parsimonioso que tenga un ajuste aceptable a los datos observados 16. Lo habitual es comparar las frecuencias predichas por el modelo y las observadas a partir de los datos, si resultan similares el modelo se considera aceptable, lo contrario ocurre si se observan diferencias.
Las dos medidas más comunes para evaluar el ajuste en el análisis de tablas de contingencia son el estadístico χ 2 de Pearson y la razón de verosimilitud (L 2):
y representa un patrón de respuestas. Ambos estadísticos tienen distribución chi-cuadrado asintótica, lo cual significa que esa distribución es una buena aproximación cuando el número de observaciones en cada celda es suficientemente grande, y si el valor obtenido es menor que un valor crítico determinado (usualmente 0,05) se considera que el modelo no ofrece un buen ajuste a los datos. L 2 tiene la ventaja de permitir comparar modelos anidados; si la diferencia de los modelos en L 2 resulta significativa implica que es necesario un modelo más complejo para lograr un ajuste adecuado, lo opuesto sucede si la diferencia es no significativa 15,16.
Sin embargo, generalmente los modelos de clases latentes comprenden tablas de contingencia de gran tamaño, con celdas dispersas, por lo que los estadísticos anteriores no se pueden aproximar con la distribución chi-cuadrado, por lo cual resulta útil analizar medidas comparativas de bondad de ajuste. En este sentido, las medidas más utilizadas son los criterios de información bayesiana (BIC) y de Akaike (AIC), que evitan algunas de las limitaciones de los estadísticos anteriores, penalizando por el número de parámetros del modelo a estimar (AIC, BIC) y el tamaño de la muestra (BIC), siendo preferidos en situaciones en que tales valores son elevados 16. Los criterios de información se basan en log L y se expresan como:
Valores menores en los criterios de información son indicativos de un mejor ajuste. Si bien en algunos estudios el AIC3 ha mostrado un mejor desempeño 20,21, no existe "un" criterio mejor para todos los modelos; debe recordarse que el objetivo es obtener el modelo que presente un ajuste adecuado y que sea el más parsimonioso.
Además, para comparar modelos con distinto número de clases latentes se ha propuesto 22 una medida de bootstrapping condicional en función de la diferencia en el valor log L. A partir de considerar como verdadero un modelo B con k + 1 clases latentes (menos restringido), se evalúa la diferencia en el ajuste entre dicho modelo B y un modelo A con k clases (más restringido), y si la diferencia resulta significativa se rechaza el modelo A; en cambio, si la diferencia no es significativa se rechaza el modelo B a favor del modelo A, ya que es más parsimonioso.
Otra manera de comparar modelos es considerar el error de clasificación; para comprenderlo revisaremos primero cómo se realiza la asignación de los casos a las clases latentes. Esta clasificación se basa en la probabilidad posterior de pertenencia a una clase latente k dado un patrón de respuestas determinado yi, que recurriendo al teorema de Bayes se expresa como:
Después de tal cálculo, se procede a clasificar a los casos que presentan un patrón de respuestas determinado en la clase latente con mayor probabilidad posterior 23, lo cual se conoce con el nombre de asignación modal. También se puede considerar un valor crítico para la clasificación, por ejemplo, clasificar sólo los casos que presentan una probabilidad de pertenencia a una clase determinada mayor a 0,75. Esto último se relaciona con el error de clasificación, es decir, cómo de apropiadamente son asignados los casos con cierto valor de respuesta a una clase latente determinada. Como señalan Vermunt y Magidson 18 el error de clasificación se basa en la asignación modal para cada vector de respuestas y en las frecuencias de dichos vectores, considerando el tamaño de la muestra; su expresión es:
Donde wi agrupa patrones de respuesta idénticos se utiliza como un recuento de frecuencias. Valores de error de clasificación más cercanos a cero son indicadores de una mejor clasificación.
Extensiones del análisis de clases latentes
El modelo de clases latentes expuesto anteriormente es susceptible de numerosas modificaciones. Las más habituales, como señala McCutcheon 16, son: a) restricción de los parámetros a valores determinados, por ejemplo, indicar que la probabilidad sea igual a un valor específico para una clase latente determinada; y b) restricción de igualdad de variables indicadoras, lo que implica que dos o más variables indicadoras tengan índices de error idénticos con respecto a cada clase latente, reduciendo de esta manera el número de parámetros a estimar.
Por otra parte, la inclusión de covariables es un añadido para la predicción de la pertenencia a una clase latente determinada, por lo que el modelo general presentado inicialmente resulta en:
Donde zi denota los valores de las covariables. Es importante tener en cuenta que se está realizando un conjunto adicional de supuestos de independencia, lo que implica que las variables indicadoras se asumen independientes de las covariables dada la clase latente. Otra manera de incluir covariables es considerar que tienen efectos directos sobre las variables indicadoras, lo que permite relajar el supuesto acerca de la influencia de las covariables sobre las indicadoras sólo a través de variables latentes 12,24.
Otra modificación del modelo de clases latentes presentado en un comienzo implica la flexibilización del supuesto de independencia de las variables indicadoras al interior de cada clase latente, es decir, permitir dependencia local. Incluir en un modelo dependencia local, tal como mencionan Vermunt y Magidson 12, previene de terminar con soluciones de muchas clases latentes (aunque existe el riesgo de que se oculten clases relevantes) y puede generar una mejor clasificación, dado que plantear que dos variables son localmente dependientes es equivalente a señalar que contienen cierta información superpuesta, por lo que no se debería utilizar para determinar la probabilidad de pertenencia a una clase determinada.
Análisis de clases latentes y otros métodos estadísticos
El LCA es semejante en cuanto a objetivos al análisis de cluster, en el que se pretende encontrar grupos o tipos de casos en función de los datos observados, de manera tal que el grado de similitud sea máximo dentro de los grupos, y mínimo entre los grupos. Una diferencia notable es que el LCA se basa en un modelo probabilístico y se asume que los datos se generan a partir de una mezcla de distribuciones de probabilidad subyacente. En el análisis de cluster la asignación de los sujetos u objetos a las clases se realiza basándose en medidas de distancia; además, la influencia de un sujeto sobre una clase es de 0 o 1, por lo que el resultado es incorrecto si la clasificación es errónea. En cambio, como se señaló antes, en el LCA los sujetos son asignados a las clases en función de la probabilidad de pertenencia posterior 25. El análisis de cluster se limita a variables de tipo cuantitativas intervalores, por lo que el LCA ofrece considerables beneficios, ya que extensiones del modelo tradicional incorporan variables indicadoras de distintos niveles de medición.
Otra ventaja del LCA es que la elección del número de clases es menos arbitraria, ya que cuenta con varias medidas que permiten evaluar el ajuste de los modelos. Además, en el LCA no se necesita estandarizar las variables, a diferencia del análisis de cluster, donde se estandarizan las variables con el fin de homogeneizar varianzas y evitar obtener cluster dominados por las variables con varianza muy grande, aunque la estandarización no resuelve el problema asociado con las diferencias de escala, ya que las clases son desconocidas y no es posible desarrollar una estandarización al interior de los cluster25.
Por último, cabe señalar que las covariables son tratadas de manera diferente en ambos análisis. Es habitual que después de realizar un análisis de cluster se lleven a cabo estudios posteriores para evaluar las diferencias entre las clases resultantes con respecto a una o más covariables. Por el contrario, como se mencionó antes, el modelo de clases latentes se puede extender para incorporar covariables, lo que permite desarrollar de manera simultánea la clasificación y descripción de la clase, aunque esto no siempre ocurre, ya sea debido a limitaciones impuestas por el tamaño de la muestra ya sea porque se prefiere obtener el modelo más simple y efectuar a posteriori las comparaciones de interés.
Por otra parte, se han señalado similitudes metodológicas entre el LCA y el análisis factorial 17. Ambos son útiles para la reducción de datos y se refieren a constructos no observados que se infieren a partir de los datos. Además, determinar el número de clases latentes es semejante a determinar el número de factores; en ambos casos a medida que el número de clases o factores aumenta, el ajuste del modelo es mejor, pero el objetivo es hallar un equilibrio entre el ajuste a los datos y el número de clases o factores requerido.
Uebersax 17 también señala relaciones entre LCA y el análisis de rasgo latente, ambos considerados como variaciones del análisis de estructuras latentes, aunque en el primero la variable latente que determina la estructura de los datos es nominal, mientras que en el segundo la variable es continua. En ambos las variables indicadoras, en principio, se asumen independientes, condicionales a los valores de la variable latente.
Aplicación del análisis de clases latentes: tipología de fumadores
Método
Muestra
Los datos se obtuvieron de un estudio sobre hábitos relacionados con el tabaco realizado a nivel nacional por el Centro de Investigaciones Sociológicas, dependiente del Ministerio de la Presidencia en convenio con el Ministerio de Sanidad y Consumo de España durante el mes de febrero de 2008 26. En dicho estudio participaron 2.002 personas mayores de 18 años. En primer lugar se seleccionaron de manera aleatoria teléfonos-hogares entre los registrados en la guía telefónica correspondientes a estratos definidos a partir del cruce de 17 comunidades autónomas y la cantidad de habitantes dividido en 7 categorías. Luego se seleccionó a una persona residente en el hogar mediante cuotas de sexo y edad.
Instrumento
Los datos sobre hábitos relacionados con el tabaco se obtuvieron a través de cuestionarios que se aplicaron vía entrevista telefónica personal. En particular, aquí se recupera información sobre variables señaladas como relevantes en la literatura sobre consumo de cigarrillos 27-29, las cuales son:
1. Cantidad de cigarrillos. "Aproximadamente, y por término medio, ¿cuántos cigarrillos fuma usted al día?" La cantidad de cigarrillos se categorizó de la siguiente manera: 1 = 1 a 7; 2 = 8 a 12; 3 = 13 a 20; 4 = 21 o más.
2. Intención de dejar de fumar. "¿Ha intentado usted dejar de fumar alguna vez?" 1 = sí, más de una vez; 2 = sí, una vez; 3 = no, nunca.
3. Auto-percepción como fumador. "Le gusta a usted ser fumador/fumadora (3), lo lamenta (1), o le da igual (2)?".
4. Frecuencia de fumar del padre cuando era niño. "Cuando usted era niño/niña, ¿su padre fumaba?" 1 = no; 2 = sí, alguna vez, ocasionalmente; 3 = sí, habitualmente.
5. Frecuencia de fumar de la madre cuando era niño. "Cuando usted era niño niña, ¿su madre fumaba?" 1 = no; 2 = sí, alguna vez, ocasionalmente; 3 = sí, habitualmente.
(1)En el ambiente del software R una de las librerías más completas para el LCA es poLCA, desarrollada por Linzer y Lewis 31, la cual permite estimar modelos de clases latentes para variables indicadoras con cualquier número de resultados posibles. Sin embargo, a la fecha, las variables ordinales son tratadas como nominales, por lo que se prefirió utilizar Latent Gold. Haughton, Legrand y Woolford 32 ofrecen una excelente revisión de tres programas para LCA: Latent Gold, poLCA y MCLUST.
Procedimiento
Para el análisis del modelo de clases latentes se utilizó el software Latent Gold 4.0 30(1). Se desarrollaron modelos de 1 a 6 clases latentes. Se evaluó el valor de L2 y se compararon los modelos en las medidas que tienen en cuenta tanto la bondad del ajuste como la parsimonia: BIC, AIC y AIC3 (basándose en LL).
Resultados
La muestra inicial estaba compuesta por 2.002 personas, de las cuales 513 (25,62 %) informaron fumar actualmente. Dos personas no especificaron la cantidad de cigarrillos consumidos, por lo que no se incluyeron en el análisis. Además, las preguntas sobre auto-percepción y frecuencia de fumar de los padres comprendían opciones de respuestas "No sabe (o no recuerda)" y "No contesta". Los individuos que señalaron tales opciones fueron excluidos del análisis. Finalmente, los fumadores actuales resultaron ser 498; 55,2 % varones y 44,8 % mujeres, con una edad promedio de 41,71 años (DT = 13,75).
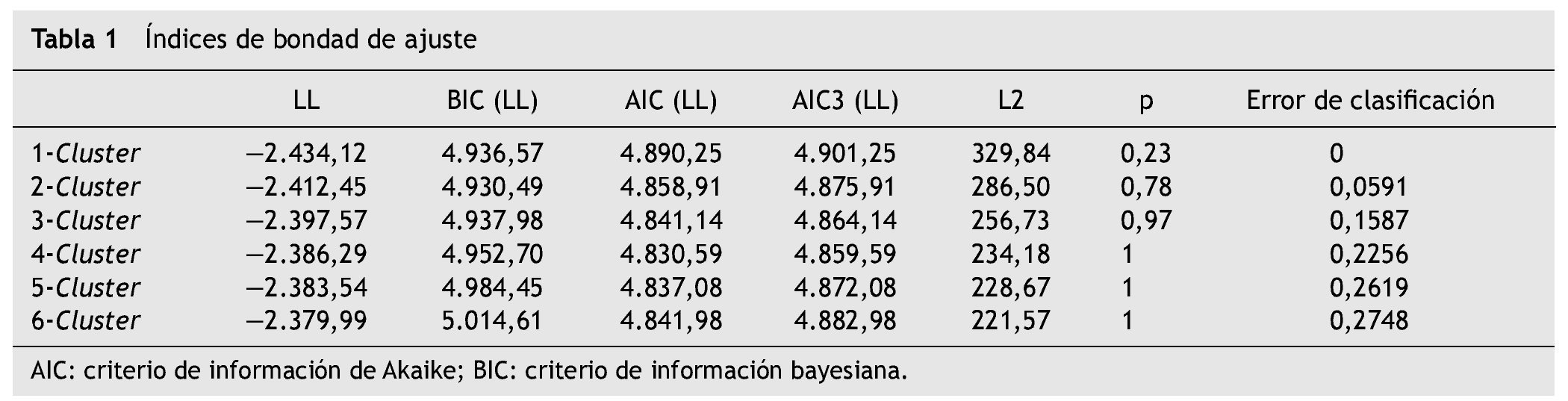
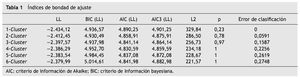
A partir del AIC y AIC3 se observó que el modelo de 4 clases latentes fue el que mejor se ajustaba a los datos (AIC = 4.830,59; AIC3 = 4.859,59) y según el BIC el mejor modelo fue el de 2 clases (BIC = 4.930,49). Además, se consideró el error de clasificación, en el modelo de 4 clases fue del 22,56 %, mientras que en el de 2 clases sólo 5,91 % (tabla 1). Para evaluar cuánto mejoraba el ajuste del modelo de 4 clases en relación con el modelo de 2 clases se recurrió al bootstrapping condicional, que el programa calcula en función de la diferencia en LL, exactamente es —2 la diferencia de LL, que resultó en un valor de 52,32. El valor p asociado con el incremento en clases fue menor a 0,05, lo cual significa que el modelo de 4 clases ofrece una mejora significativa sobre el modelo de 2 clases. Teniendo en cuenta estos resultados se eligió el modelo de 4 clases latentes. El software Latent Gold permite inspeccionar fácilmente el supuesto de independencia local a través de los residuos bivariados; valores mayores a 1 indican que el modelo no logra explicar la asociación entre dos indicadores 24. En este sentido, el modelo de 4 clases no presentó dependencia local.
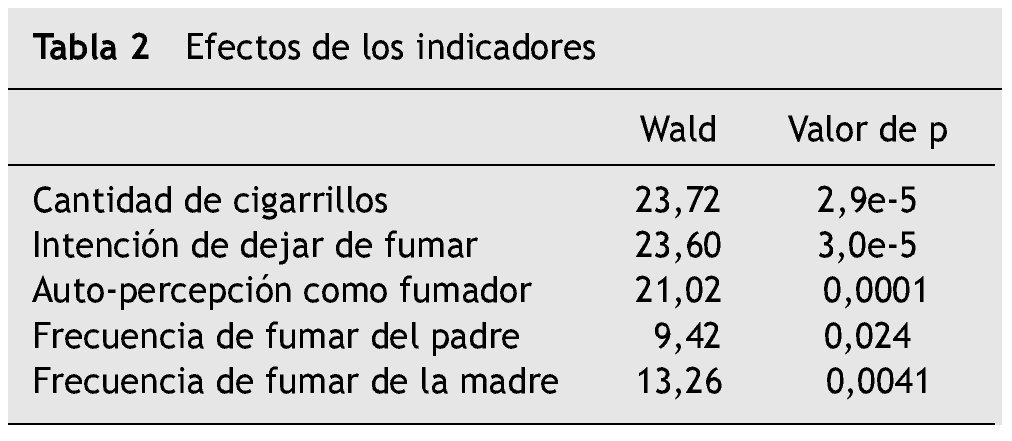
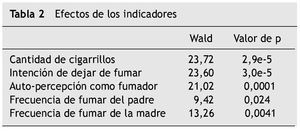
Además, el software utilizado permite valorar los efectos asociados a cada una de las variables indicadoras a través del estadístico Wald, el cual se evalúa bajo la hipótesis nula de que los efectos asociados con cada indicador son nulos. Se considera un valor p = 0,05, por lo que un valor p < 0,05 significa que conocer la respuesta a ese indicador contribuye a discriminar entre las clases. Todos los indicadores resultaron ser significativos para diferenciar las clases (tabla 2).
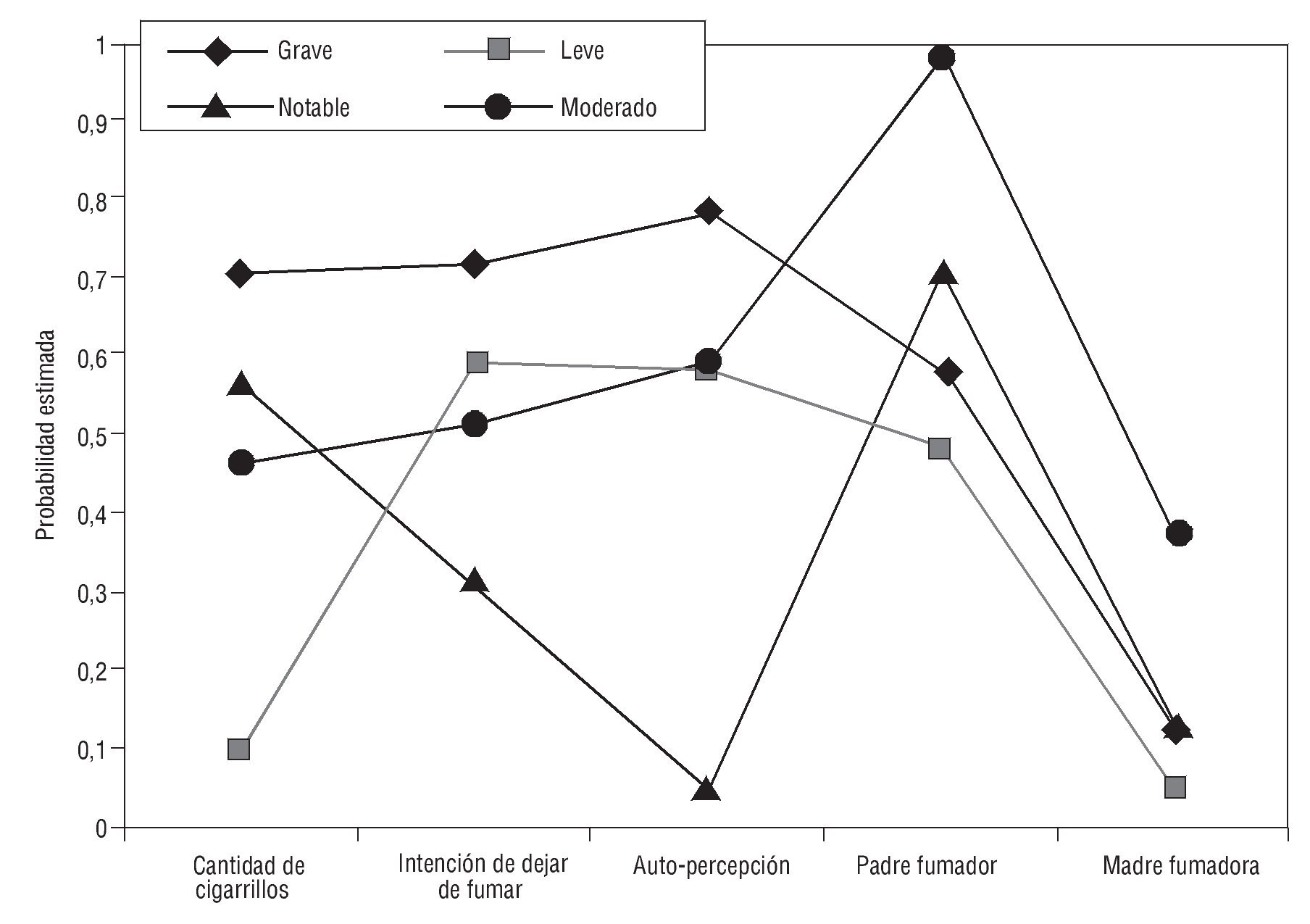
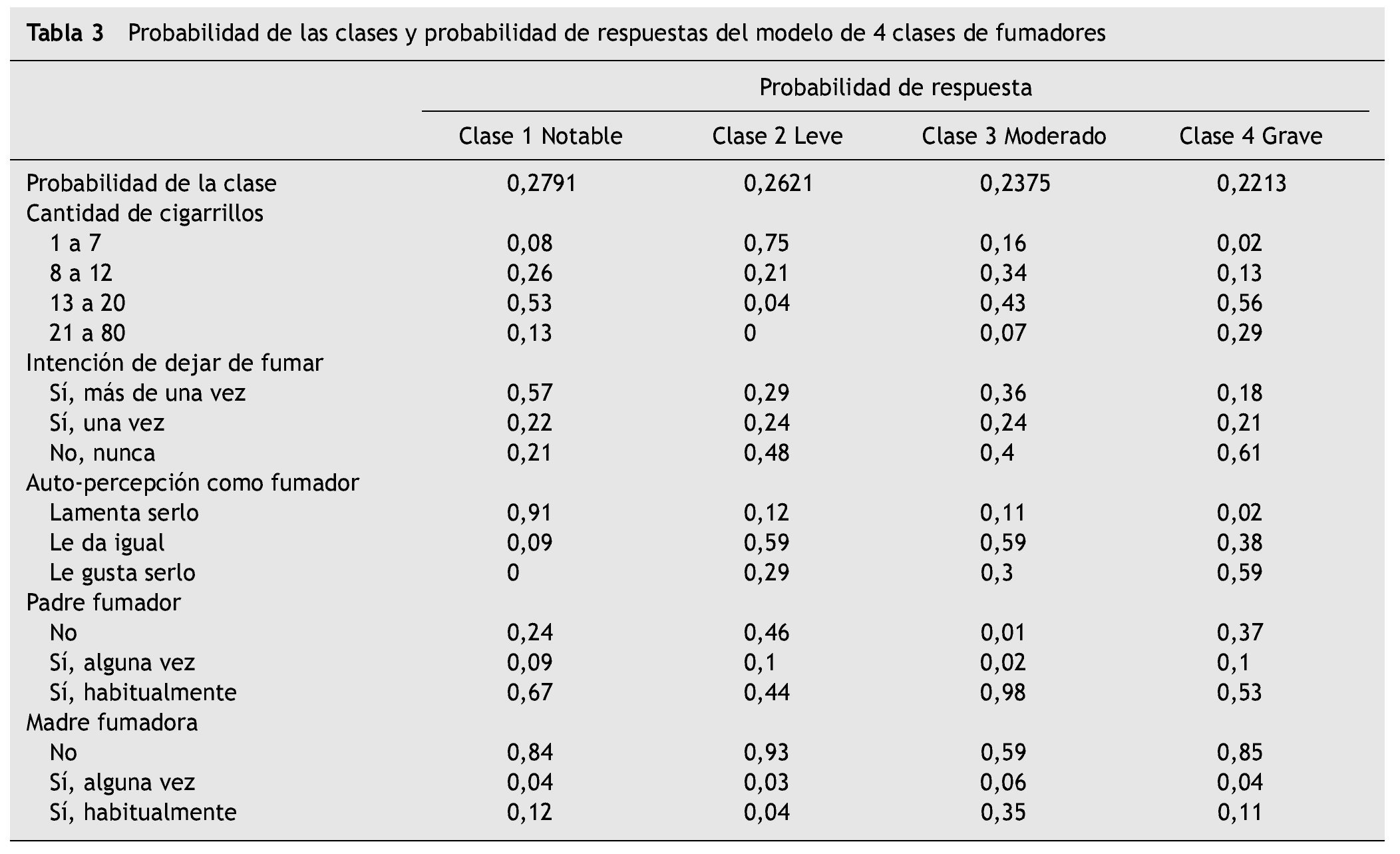
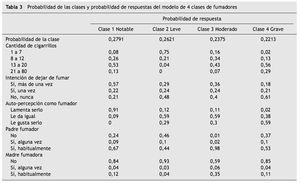
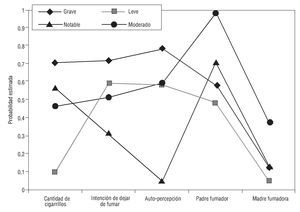
El tamaño de las clases fue: clase 1 = 27,91 % de la muestra; clase 2 = 26,21 %; clase 3 = 23,75 %; y clase 4 = 22,13 %. Posteriormente, se analizaron las probabilidades de respuesta en las variables indicadoras en cada clase latente. La clase 1 comprendió personas caracterizadas por consumir entre 13 y 20 cigarrillos por día (probabilidad [P] = 0,53), haber intentado dejar de fumar en más de una ocasión con una probabilidad considerable (P = 0,60) y tener una auto-percepción como fumadores altamente negativa (P = 0,91); señalan que, cuando eran niños, sus padres fumaban habitualmente (P = 0,67), a diferencia de sus madres, quienes eran en su mayoría no fumadoras (P = 0,84); esta clase se denominó "fumadores notables". La clase 2 mostró consumir principalmente entre 1 y 7 cigarrillos por día (P = 0,75), con mayor probabilidad de no haber intentado dejar de fumar (P = 0,48), señalando con mayor probabilidad que le da igual ser fumador (P = 0,59), con padres fumadores y no fumadores en semejante proporción (P = 0,53 y 0,46; respectivamente) y madres fundamentalmente no fumadoras (P = 0,93); a esta clase se le asignó el nombre de "fumadores leves". En la clase 3 las personas informaron consumir de 8 a 12 o de 13 a 20 cigarrillos por día (P = 0,34 y 0,43; respectivamente), con intención media de dejar de fumar (sí, P = 0,52; no, P = 0,48), manifestando que le da igual ser fumador (P = 0,59), con alta probabilidad de que el padre haya sido fumador habitual (P = 0,98) y en menor proporción la madre (P = 0,35); esta clase se denominó "fumadores moderados". Por último, la clase 4 presentó mayor probabilidad de consumir de 13 a 20 cigarrillos por día o más (P = 0,56 y 0,29, respectivamente), sin intención de dejar de fumar (P = 0,61) y percibiéndose de manera positiva como fumador (P = 0,59), con mayor probabilidad de que sus padres fuesen fumadores habituales (P = 0,53), pero madres principalmente no fumadoras (P = 0,85); esta clase se denominó "fumadores graves". En la tabla 3 se muestra el tamaño de las clases y la probabilidad de cada nivel de las variables indicadoras. Latent Gold presenta en un gráfico la probabilidad de cada variable indicadora según la clase, y en el caso de variables ordinales muestra la media re-escalada en el rango 0-1, calculada en función del valor mínimo, máximo y el rango de toda la población (para cada indicador) (fig. 1).
Figura 1. Probabilidad estimada de las variables indicadoras en el modelo de 4 clases latentes.
Discusión
El LCA es una herramienta útil para categorizar sujetos u objetos cuando se tienen variables manifiestas nominales, ordinales, continuas o conteos. Está basado en un modelo probabilístico y brinda mejores posibilidades de análisis que otras herramientas estadísticas.
El método de estimación que se utiliza es el de máxima verosimilitud, siendo el algoritmo de maximización de la esperanza el más utilizado. Para evaluar el ajuste de un modelo se consideran los estadísticos basados en chi-cuadrado, χ 2 de Pearson y la razón de verosimilitud L2, y se recurre primordialmente a los criterios de información BIC, AIC y AIC3, basados en LL. Otro aspecto que permite evaluar un modelo es el error de clasificación, el cual informa en qué medida son asignados los casos con determinado valor de respuestas a una clase latente determinada. Además, se puede obtener el tamaño de cada clase latente.
Los programas de análisis estadístico habituales (SPSS, Statistica, Stata, entre otros) no tienen incorporados paquetes para desarrollar el LCA. Se han desarrollado varios programas específicos, entre los que se cuentan programas comerciales (Latent Gold y Mplus) que brindan al usuario una interfaz de fácil manejo, y programas de acceso libre, ya sea en forma de librería (poLCA, MClust, e1017 y gllm en R; PROC LCA y PROC LTA en SAS) o individuales (LEM y MMLSA, entre otros) (para una exposición más amplia véase Uebersax 17).
El LCA ha sido utilizado en distintas ciencias: educación 33, psicología 34, medicina 35, economía 36, demografía 37 y ciencias políticas 38. En el campo del uso de sustancias ha mostrado ser una herramienta muy útil para identificar patrones de consumo. En particular, en el ejemplo analizado, el LCA permitió obtener un modelo de 4 clases de fumadores de cigarrillos a partir de variables observadas tales como la cantidad de cigarrillos que se fuma por día, la intención de dejar de fumar, la auto-percepción como fumador y los antecedentes parentales de fumadores. De esta manera, se ha logrado obtener una imagen más precisa del consumo de tabaco, superando así los criterios clásicos focalizados en patrones problemáticos. Sin embargo, si bien se utilizaron variables indicadoras relevantes para caracterizar la conducta de consumo de tabaco disponibles en la base de datos empleada, es probable que la comprensión de nuevas variables permita obtener modelos con mejor ajuste y más parsimoniosos.
Numerosas extensiones se han presentado a partir del modelo clásico del LCA, entre las que se encuentran la incorporación de variables exógenas que actúan como covariables, las restricciones sobre los parámetros, y el permitir asociación entre variables indicadoras al interior de una clase latente, alterando así el supuesto clásico de independencia local. En relación con este último punto, recientemente Henry y Muthén 39 propusieron el LCA multinivel, aplicándolo a un estudio de fumadoras norteamericanas. Como señalan los autores si las muestras son seleccionadas de manera aleatoria de la población, el LCA con efectos fijos es adecuado; sin embargo, si se emplea otro método de muestreo, comprendiendo por ejemplo distintas comunidades dentro de un país, un modelo multinivel posiblemente ofrezca una tipología más precisa. Retomando el ejemplo analizado en este trabajo, y considerando que se presentó uno de los modelos más simples de LCA, queda pendiente revisar modelos que consideren alguna/s de las extensiones del modelo de clases latentes, como por ejemplo, la incorporación de covariables y la valoración de modelos multinivel.
Más allá de las limitaciones señaladas, el poder disponer de mejores herramientas estadísticas para identificar patrones de uso y abuso de sustancias repercute no sólo directamente a nivel descriptivo, sino también en las medidas preventivas y terapéuticas que generalmente se desarrollan en función de categorías de consumidores.
Si bien los desarrollos iniciales del LCA datan de la década de los sesenta, en los últimos 20 años se han producido los mayores avances, progreso facilitado por el adelanto de la tecnología. Actualmente se cuenta con muy buenas herramientas comerciales, como Latent Gold y Mplus; sin embargo, los paquetes para el ambiente de R, el cual se basa en un lenguaje de programación, son muy prometedores, sobre todo considerando que R cuenta con una comunidad de desarrolladores abierta y numerosas fuentes de información.
Conflicto de intereses
Las autoras declaran que no existe conflicto de intereses.
*Este estudio ha sido financiado por el Consejo Nacional de Investigaciones Científicas y Técnicas.
*Autor para la correspondencia.
Correo electrónico:cereyna@psyche.unc.edu.ar (C. Reyna).
Recibido el 4 de noviembre de 2010.
Aceptado el 5 de enero de 2011