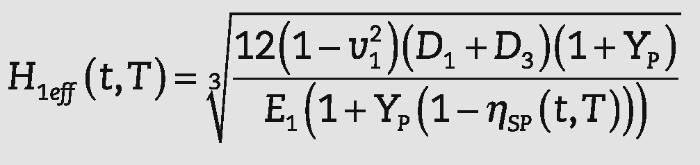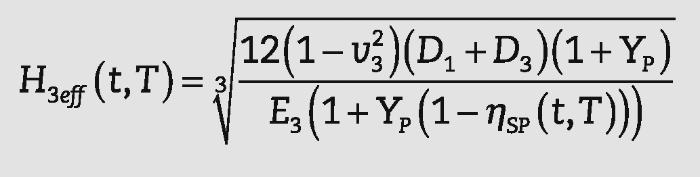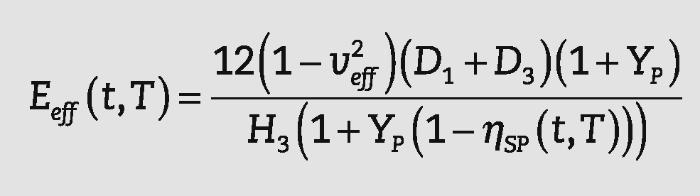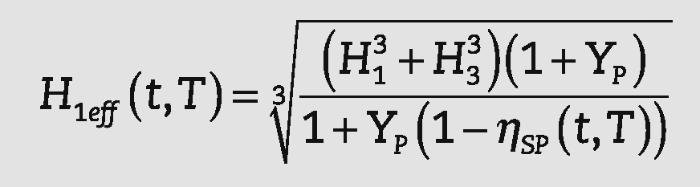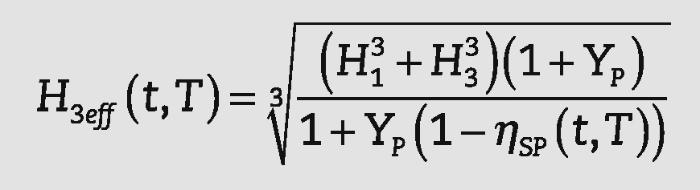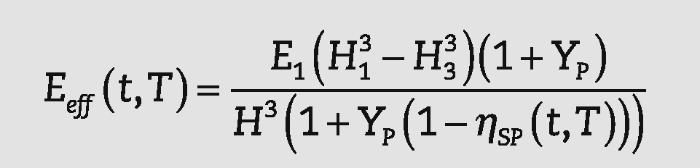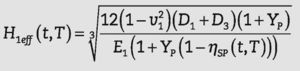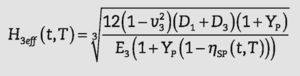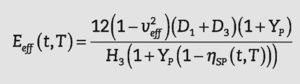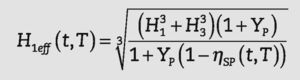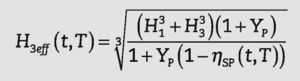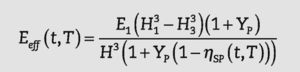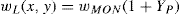En los últimos años, el uso de vidrio laminado como elemento estructural se ha incrementado considerablemente en construcciones arquitectónicas, sobre todo en fachadas, cubiertas, escaleras o ventanas de seguridad. El cálculo de estos elementos tipo sándwich no es sencillo debido a la combinación de las propiedades mecánicas del vidrio (elástico-lineales) con las del polímero interior (viscoelástico-lineales). Recientemente, algunos autores han propuesto el concepto de espesor efectivo para el cálculo simplificado de elementos de vidrio laminado bajo carga estática, utilizando un modelo monolítico con una rigidez equivalente igual a la del elemento laminado. Debido a la variación de propiedades del laminado con la temperatura, introducidas por el polímero viscoelástico, para cada cambio de temperatura se tiene un espesor efectivo diferente, lo que conlleva un mayor número de evaluaciones para cada una de las situaciones de trabajo del elemento laminado. En este trabajo se propone el concepto de módulo de elasticidad efectivo como una alternativa más eficiente para el cálculo con modelos de elementos finitos. La metodología propuesta se valida mediante ensayos experimentales realizados en placas de vidrio laminado sometidas a una carga uniformemente distribuida.
In recent years, the use of laminated glass as a structural element has increased considerably, mainly in facades, roofs, stairs or security windows. Laminated glass elements are sandwich structures which presents a complex behaviour due to the combination of the mechanical properties of glass layers (linear-elastic) with the properties of the polymeric interlayer (linear-viscoelastic). Recently several authors have proposed the concept of effective thickness in order to simplify the laminated-glass static calculations, using a monolithic model with an equivalent flexural stiffness equal to that of the laminated element. Due to the variations of the laminated glass properties with temperature, introduced by the viscoelastic polymeric interlayer, for each different temperature, a different effective thickness must be determined. This particularity implies a large number of assessments for each of the possible working situations. In this work, the Young's modulus concept is proposed as an efficient alternative to be used in finite elements models. The proposed methodology is validated by experimental tests on laminated glass plates under uniformly distributed load.
El vidrio laminado es un material compuesto formado por la unión de dos o más capas de vidrio y una o más capas intermedias de un material polimérico1, 2, 3, 4, 5. El vidrio laminado combina las propiedades del vidrio con las ventajas de un material polimérico, es decir, el comportamiento del laminado es el de una estructura compuesta6, 7. Generalmente, las capas poliméricas utilizadas presentan un comportamiento viscoelástico8, 9, 10, 11, esto es, las propiedades mecánicas son dependientes de la temperatura y del tiempo. El butiral de polivinilo (PVB) es el material más común para las capas intermedias y se comercializa en espesores de 0,38 mm o valores múltiplos del mismo (0,76 mm, 1,12 mm, 1,52, etc.)12.
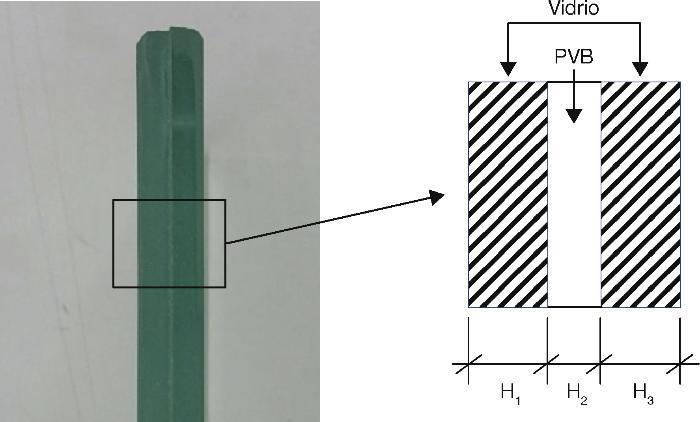
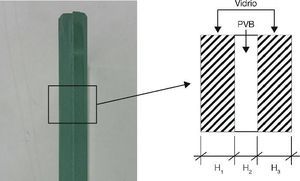
La configuración más simple que se presenta en el vidrio laminado consiste en tres capas: dos de vidrio y una intermedia polimérica (Figura 1).
Figura 1. Elemento básico de vidrio laminado.
Los primeros trabajos sobre elementos de vidrio laminado fueron realizados por Hooper13, que desarrolló un modelo para vigas a flexión en cuatro puntos y realizó ensayos en vigas simplemente apoyadas. Behr et al.14 realizaron ensayos en vigas de vidrio monolítico y vidrio laminado y Edel15 llevó a cabo los primeros estudios sobre el efecto de la temperatura en vigas de vidrio laminado. Los primeros modelos para vidrios laminados multicapa (varias capas de vidrio y varias capas intermedias de polímero) fueron propuestos por Noville et al.16.
El auge experimentado en los últimos años en la utilización del vidrio laminado, ha favorecido el estudio del comportamiento mecánico de este tipo de elementos. Así se han propuesto varios modelos para el cálculo de desplazamientos y tensiones en elementos de vidrio laminado ante cargas estáticas17, 18, 19, 20, 21. En el caso de placas, Foraboschi22, 23 realizó estudios donde se presentan modelos matemáticos para calcular placas de vidrio laminado y Galuppi et al.4, 5 propusieron expresiones para el cálculo de desplazamientos en elementos de vidrio laminado con diferentes condiciones de contorno, utilizando el concepto de espesor efectivo. Este concepto ha sido recientemente extendido al comportamiento dinámico por López-Aenlle et al.24, 25.
En los modelos analíticos y numéricos, el comportamiento del vidrio se suele modelizar como elástico lineal, mientras la capa polimérica se modeliza con un comportamiento viscoelástico-lineal. Los elementos de vidrio laminado son sencillos de modelizar con programas de elementos finitos mediante modelos 3D pero, debido al pequeño espesor de la capa polimérica respecto al resto de dimensiones del laminado se requiere utilizar una discretización muy fina que implica una malla con un número muy elevado de elementos. Recientemente, algunas publicaciones han propuesto el concepto de espesor efectivo para el cálculo de elementos de vidrio laminado, utilizando un modelo monolítico con un espesor equivalente tal que presente los mismos desplazamientos, tensiones, etc., que el modelo de vidrio laminado1, 2, 3, 4, 5. El espesor efectivo puede ser usado tanto con ecuaciones analíticas como en modelos de elementos finitos.
Como alternativa al espesor efectivo, en este trabajo se propone el concepto de módulo de elasticidad efectivo para el cálculo simplificado de elementos de vidrio laminado utilizando modelos monolíticos. En este trabajo, se deduce el concepto de módulo de elasticidad efectivo en placas laminadas a partir del modelo propuesto por Galuppi y Royer Carfagni4. La metodología propuesta se valida en una placa sometida a carga constante y los resultados experimentales se comparan con las predicciones analíticas.
Modelos analíticos para el cálculo simplificado de elementos de vidrio laminadoAunque los elementos laminados suelen tener materiales iguales en las capas de vidrio, es decir, E1 = E3 (Figura 1), existen vidrios laminados denominados como híbridos, donde ambas capas de vidrio presentan distintas propiedades E1 ≠ E3. La formulación que se presenta en los siguientes epígrafes se desarrolla de manera general para una placa híbrida, manteniendo así la generalidad de la misma. En el caso de tratarse de una placa de materiales iguales, las ecuaciones son de aplicación directa introduciendo la relación: E1 = E3. Además, se incluyen las variables tiempo ‘t’ y temperatura ‘T’ para tener en cuenta las variaciones en las propiedades mecánicas que experimenta el vidrio laminado debidas a la capa polimérica.
Aunque el concepto de espesor efectivo fue introducido por Benninson et al.1, los recientes trabajos de Galuppi y Royer Carfagni3, 4, 5 amplían y presentan la utilización de este con- cepto a un mayor número de cargas, geometrías y condiciones de contorno. Por esta razón, la metodología propuesta en este artículo para el cálculo con el módulo de elasticidad efectivo en placas se basa en los estudios y modelos de cálculo pro- puestos por Galuppi y Royer Carfagni4, 5.
En el caso de placas de vidrio laminado la deformación viene dada por:
donde g(x,y) es la forma que adopta la deformada de una placa monolítica de sección constante y sometida a las mismas con- diciones de carga y apoyo que la placa laminada en estudio. La función g(x,y) se aproxima en este caso por el primer tér- mino del desarrollo en serie de la deformada correspondiente a una placa monolítica4, 5. La rigidez a flexión D(t,T)s vienedefinida por:
donde:
y
En la expresión (5), G2(t,T) es el módulo de relajación a cor- tante de la capa polimérica y el subíndice «SP» indica placa sometida a carga estática. El coeficiente depende de la geometría de la placa y de sus condiciones de apoyo. Los valores más habituales de dicho coeficiente se encuentran tabula- dos en5.
La ecuación (2) se puede expresar también como:
donde:
Si E1 = E3 y v1 = v3, se concluye que en la expresión del coe- ficiente Yp coincide con el coeficiente YB obtenido para vigas21.
Espesor efectivoEl espesor efectivo para calcular desplazamientos se puede definir como el espesor de un elemento de vidrio monolítico con la misma longitud y anchura que el laminado y que pro- duce el mismo desplazamiento que el del elemento laminado bajo la misma carga y condiciones de contorno1, 2. Como el comportamiento de los elementos de vidrio laminado es dependiente de la temperatura y del tiempo, el espesor efec- tivo también depende del tiempo y de la temperatura.
La rigidez D(t,T)s en placas de vidrio laminado, dada por la ecuación (6), se puede considerar como una rigidez a flexión efectiva, es decir, la deformada de una placa monolítica con rigidez D(t,T)s será igual que la de una placa de vidrio lami- nado. A partir de esta rigidez efectiva se puede definir:
• Un espesor efectivo, Heff(t,T)s, considerando un módulo de elasticidad constante.
• Un módulo de elasticidad efectivo, Eeff(t,T), considerando una placa de espesor constante.
En el caso de placas, se necesitan tres parámetros para definir la rigidez de la placa (espesor, módulo de elasticidad y coefi- ciente de Poisson). El espesor efectivo Hieff, con módulo de elas- ticidad Ei y coeficiente de Poisson vi, se obtiene a partir de:
donde la rigidez D(t,T)s viene dada por la expresión (6).
En el caso de utilizar un modelo con espesor constante, todavía se desconocen los valores correspondientes al módulo de elasticidad y al coeficiente de Poisson. Con el objetivo deobtener valores razonables para el módulo de elasticidad efec- tivo Eeffs, se pueden tomar valores para el coeficiente de Poisson iguales a los del vidrio. Es decir:
donde: o bien:Las expresiones del espesor efectivo propuestas por Galuppi y Carfagni4, así como las obtenidas en este trabajo para el módulo de elasticidad efectivo se presentan en la Tabla 1.
Tabla 1. Espesor efectivo y módulo de elasticidad efectivo
| Modelo | Ecuacion | |
| Espesor efectivo (4) | E1 ≠ E3 ν1 ≠ ν3 | |
| Modulo de elasticidad efectivo | E1 ≠ E3 ν1 ≠ ν3 | |
| Espesor efectivo | E1 = E3 ν1 = ν3 | |
| Modulo de elasticidad efectivo | E1 = E3 ν1 = ν3 |
Tanto las ecuaciones del módulo de elasticidad efectivo como las del espesor efectivo indicadas en la Tabla 1, se han deducido a partir de la rigidez D(t,T)s dada por la ecuación (2). Por lo tanto, cuando se calcula del desplazamiento de una placa mediante ecuaciones analíticas, ambos métodos proporcionarán el mismo resultado. Sin embargo, cuando se utiliza un modelo numérico monolítico para el cálculo, el concepto de módulo de elasticidad efectivo es mucho más sencillo de implementar, ya que se utiliza un modelo mono- lítico de espesor constante mientras que las propiedades del material se definen dependientes del tiempo y de la temperatura. La utilización del concepto de espesor efectivo sería mucho más difícil de implementar, se definirían pro- piedades constantes del material, pero sería necesario modificar el espesor de la placa para cada instante de tiempo.
Aplicación prácticaEn este apartado se indica cómo calcular deformadas en pla- cas de vidrio laminado utilizando un modelo monolítico y los conceptos de módulo de elasticidad y espesor efectivo indi- cados en el apartado «Espesor efectivo». Se va a considerar que los espesores de las capas de vidrio tienen el mismo módulo de elasticidad: E1 = E3. En este caso, la deformada de la placa laminada wL(x,y,t,T) se puede expresar como:
donde D(t,T)s viene dado por la ecuación6 y wMON(x,y) es la deformada de un modelo monolítico con rigidez:
Sustituyendo las ecuaciones (3) y (6) en la ecuación (13) se obtiene:
O alternativamente:donde βSP(t, T) = (1 − ηSP(t, T)). Para los casos particulares en los que ηSP(t, T) = 1, es decir, el comportamiento es asimilable al de una placa monolítica, la ecuación se simplifica a wL(x,y) = wMON y para el ηSP(t, T) = 0, donde el comportamiento es asimilable a dos placas superpuestas,
.De la expresión (14) se deduce que para calcular la defor- mada de una placa laminada sólo se necesita la deformada de una placa monolítica con la misma carga y condiciones de contorno y el coeficiente ηSP(t, T).
Validación experimentalCon el objeto de validar experimentalmente las ecuaciones del espesor3, 4 y del módulo de elasticidad efectivos, se realizaron ensayos experimentales en una placa de vidrio laminada apoyada en cuatro puntos y sometida a carga dis- tribuida.
Caracterización de los materialesPara las capas de vidrio se consideró un módulo de elasticidad E1 = E3 = 70 GPa y un coeficiente de Poisson v1 = v3 = 0.2121. Por otro lado, para el PVB se utilizaron los datos del mate- rial obtenidos en estudios previos21. Las propiedades tanto del vidrio como del PVB utilizados se recogen en la Tabla 2. Asimismo, en la Tabla 3 se presentan los coeficientes de la serie de Prony del módulo de relajación del PVB que permitenreconstruir la curva maestra del material21.
Tabla 2. Propiedades mecánicas del vidrio y del PVB
| Glass | PVB | |||||||
| E (Young's Modulus) | ν (Poisson's ratio) | ρ (Density) | E0 (Instantaneous tensile modulus) | K (Bulk Modulus) | ν (Poisson's ratio) | ρ (Density) | C1 C1 (WLF: Tref=20¿) | |
| [GPa] | [kg/m3] | [GPa] | [GPa] | [kg/m3] | ||||
| 70 | 0,21 | 2.500 | 1,19 | 2 | 0,3908 | 1.030 | 12,60 | 74,46 |
Tabla 3. Coeficientes de la serie de Prony para el PVB
| τi [s] | ei |
| 2.36600000000000E-07 | 2.342151953E-01 |
| 2.26430000000000E-06 | 2.137793134E-01 |
| 2.16668000000000E-05 | 1.745500419E-01 |
| 2.07327300000000E-04 | 1.195345045E-01 |
| 1.98389580000000E-03 | 1.362133454E-01 |
| 1.89837195000000E-02 | 6.840656310E-02 |
| 1.81653498300000E-01 | 4.143944180E-02 |
| 1.73822593210000E+00 | 7.251952800E-03 |
| 1.66329270788000E+01 | 2.825459600E-03 |
| 1.59158978189400E+02 | 2.712854000E-04 |
| 1.52297789909670E+03 | 4.293523000E-04 |
| 1.45732380763177E+04 | 9.804730000E-05 |
| 1.39449999999999E+05 | 5.274937000E-04 |
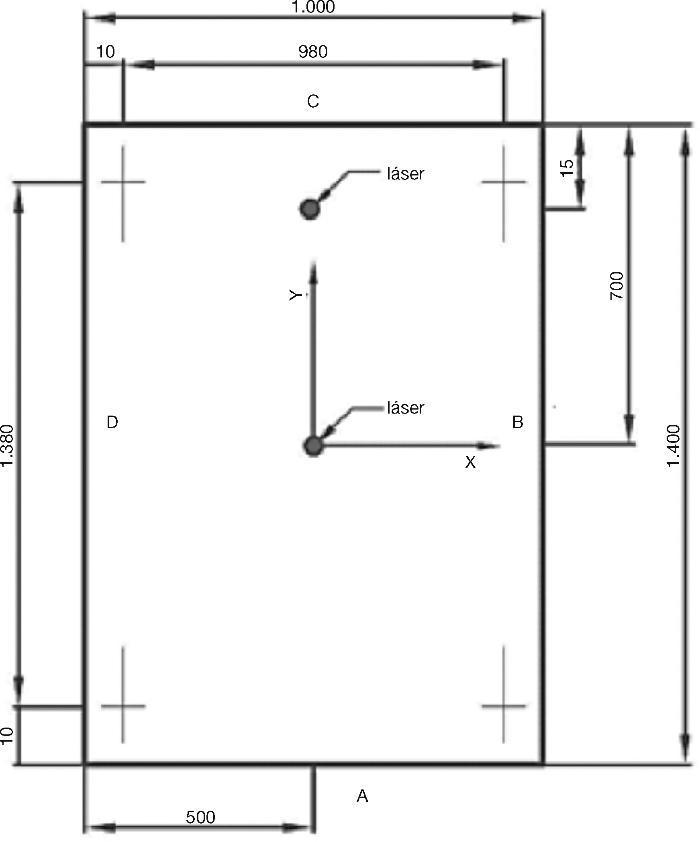
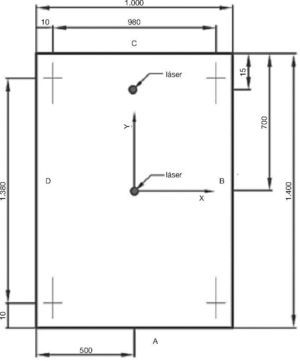
Para validar la ecuación (15), que permite predecir desplaza- mientos en placas, se realizaron ensayos en una placa de dimensiones a = 1.4 m, b2 = 1 m y espesores de H1 = 8 mm, H2 = 0.76 mm y H3 = 8 mm (Figura 2). La placa se apoyó en las cuatro esquinas sobre 4 bolas de madera de 5 cm de diámetro y se sometió a una carga uniformemente repartida en su superficie (Figura 3).
Figura 2. Esquema del ensayo. Cotas en milímetros.
Figura 3. Esquema del ensayo.
Esta carga se aplicó colocando 52 ladrillos perforados de dimensiones 11 × 10.2 × 24 cm colocados de canto y con la soga del ladrillo paralela a la dirección menor de la placa, de tal forma que aportan una carga de q = 914.2 N/m2. Para lograr una mejor uniformidad de la carga, entre los ladrillos y la capa de vidrio se colocó una placa de poliestireno expandido de 2 cm de espesor y masa despreciable. Los ensayos se realiza- ron a una temperatura T = 21.5 °C.
Los desplazamientos se midieron en el centro de la placa y en el punto medio de uno de los bordes de menor longitud (Figura 2). Los desplazamientos se registraron con dos sensores láser de la marca Acuity modelo AccuRange AR700-12, conec- tados a un sistema de adquisición de datos NI CompactDAQ con módulo de entrada analógica NI9239.
Teniendo en cuenta las dimensiones de los apoyos, la dis- tancia libre entre apoyos se reduce a a = 1.38 m en las caras más largas y b = 0.98 m en las otras dos. En la Figura 2 se puede ver un esquema con la posición de ensayo y los puntos medi- dos.
Modelo numéricoLos desplazamientos en los puntos indicados en la Figura 2 se predijeron con la ecuación (15). Para ello se necesita conocer la deformada de un modelo monolítico, que se puede obtener de la literatura para los casos más comunes, o también mediante un modelo numérico.
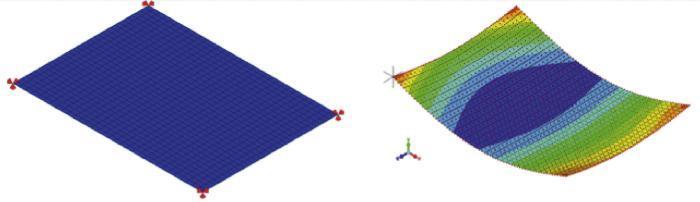
En este caso se realizó un modelo de elementos finitos con el programa LISA, utilizando elementos cuadráticos con inte- gración reducida de tipo «shell-quad8». La malla se indica en la Figura 4. Las dimensiones de la placa equivalente monolí- tica se toman L = 1.38 m, b = 0.98 m y H = 16.38 mm. A este modelo monolítico se le aplicó una carga q = 914.2N/m2 uni- formemente repartida obteniéndose unos desplazamientos en el punto central de w = 1.9 mm y un desplazamiento en el borde w = 0.74 mm. La deformada de la placa completa se puede ver en la Figura 4.
Figura 4. Malla de la placa monolítica con elementos tipo shell Quad 8 (izquierda) y deformada de la placa (derecha).
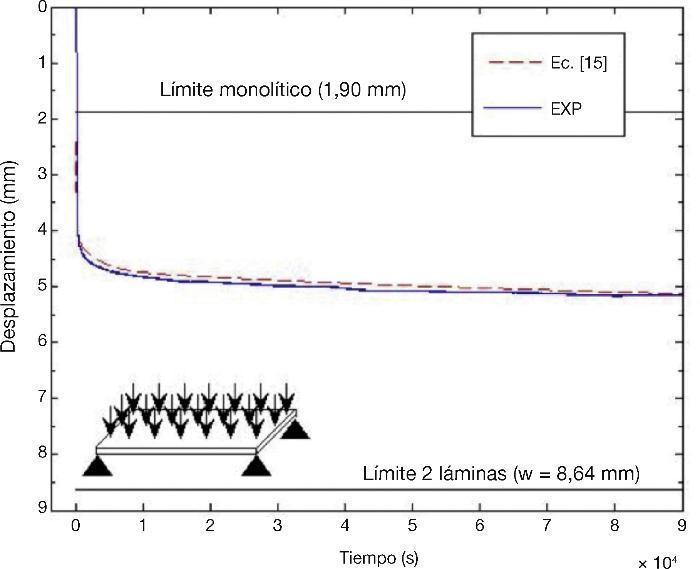
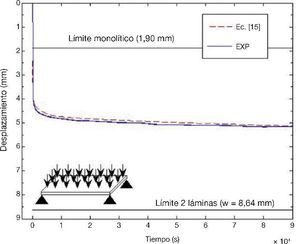
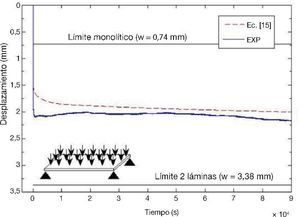
ResultadosLos desplazamientos en los puntos mencionados anterior- mente de la placa laminada se determinaron con la ecuación (15) y las predicciones numéricas junto con los resultados experimentales se muestran en las figuras 5 y 6.
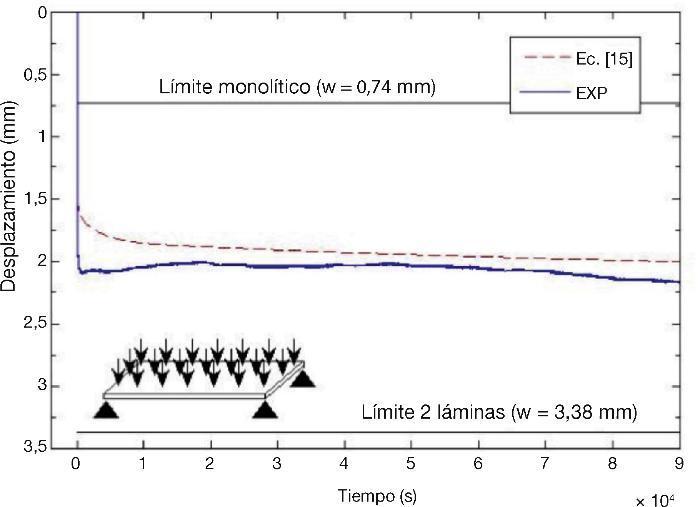
En la Figura 5 se muestra el desplazamiento en el centro de la placa, en la que se puede observar que la ecuación (15) predice el desplazamiento con un error menor al 1%.
Figura 5. Desplazamiento del punto central.
En cuanto al desplazamiento en el borde (Figura 6) el error medio es aproxidamente del 10%. Al inicio del ensayo se pro- duce en este punto un desplazamiento mayor del esperado (se observa que en el tramo 0 < t < 2 104 s el desplazamiento experimental se reduce con carga constante) y que puede ser debido a efectos dinámicos en el proceso de carga.
Figura 6. Desplazamiento punto lateral.
La duración del proceso de carga fue aproximadamente de 100 segundos. Los ladrillos utilizados para aplicar la carga empezaron a colocarse por el borde A (Figura 2) y los últimos en colocarse fueron los del borde C (Figura 2), es decir, el borde en el que estaba colocado uno de los sensores láser de desplaza- miento.
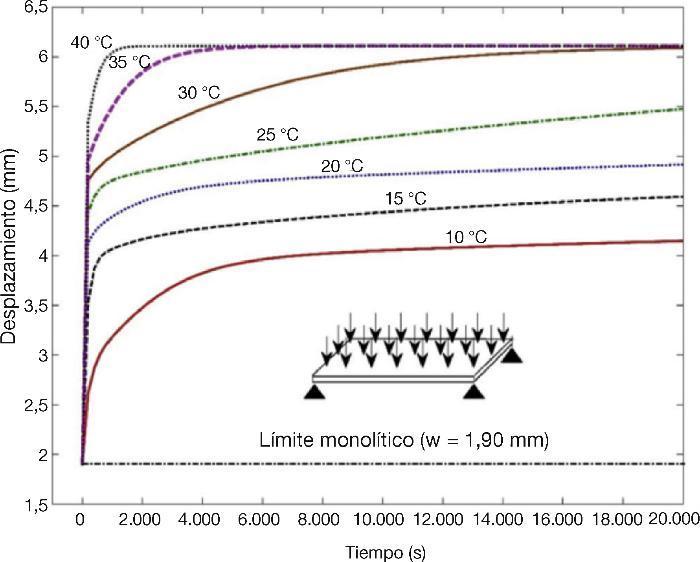
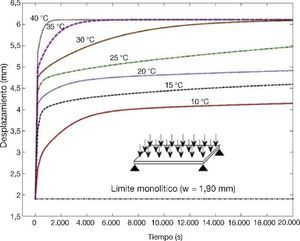
En lo que respecta al efecto de la temperatura en los des- plazamientos de la placa, esta influye en la velocidad de deformación, es decir, en el tiempo necesario para alcanzar un determinado valor de desplazamiento. A medida que aumenta la temperatura, aumenta la velocidad de deforma- ción. En la Figura 7 se han representado los desplazamientos predichos en el centro de la placa para el ensayo de la Figura 3, para temperaturas desde 10 °C hasta 40 °C, en la que se puede observar que la temperatura no afecta al desplazamiento máximo alcanzado, es decir, el valor máximo es indepen- diente de la temperatura. Sin embargo, a medida que dismi- nuye la temperatura se necesita más tiempo para alcanzar ese valor máximo.
Figura 7. Desplazamiento estimado en el punto central a diferentes temperaturas.
ConclusionesEn los últimos años, se han propuesto diversos modelos para el cálculo de desplazamientos en elementos de vidrio lami- nado bajo carga estática. Sin embargo, en el predimensiona- miento y en el cálculo práctico de estos elementos, resulta útil utilizar modelos simplificados. Benisson et al.1, 2 y Galuppi y Royer Carfagni3, 4, 5 han propuesto el cálculo simplificado de estos elementos utilizando el concepto de espesor efectivo, que consiste en utilizar un modelo monolítico con un espesor efectivo que proporciona la misma rigidez (rigidez equivalente o efectiva) que la del elemento de vidrio laminado, de tal forma que los desplazamientos de ambas elementos sean iguales.
En componentes de vidrio laminado, el espesor de las capas de vidrio frente al espesor de la capa polimérica es mucho más pequeño que las otras dimensiones del elemento. Por esta razón, las mallas de elementos finitos utilizadas para el cál- culo de estos elementos suelen ser muy densas (muchos ele- mentos 3D). Por otro lado, las propiedades mecánicas de los materiales viscoelásticos y, por tanto, también los desplaza- mientos y las tensiones dependen del tiempo. Estos dos fac- tores hacen que el cálculo estático de estos elementos sea de un gran coste computacional.
Como variable adicional, el carácter viscoelástico de la capa polimérica influye en el comportamiento del laminado siendo, por tanto, la rigidez efectiva dependiente del tiempo y de la temperatura. Si en el modelo monolítico equivalente se consi- dera constante el módulo de elasticidad, se obtiene un espesor efectivo Heff que depende del tiempo y de la temperatura. Aunque tanto el método de módulo de elasticidad efectivo como el de espesor efectivo proporcionan los mismos resultados, si se pretende realizar los cálculos con un modelo de elementos finitos, resulta más sencillo utilizar un modelo monolítico de espesor constante donde se implemente el módulo de elastici- dad efectivo Eeff dependiente de dichas variables.
En este trabajo se han deducido las ecuaciones para el módulo efectivo, Heff en placas de vidrio laminado a partir del modelo de Galuppi y Royer Carfagni. Dichas ecuaciones se pueden utilizar como una alternativa al concepto de espesor efectivo, tanto en elementos laminados con de capas de vidrio de igual espesor como híbridas (distinto espesor).
Con el objeto de validar los conceptos de espesor y módulo de elasticidad efectivos, se realizaron ensayos estáticos en una placa de vidrio laminado sometida a carga uniforme- mente distribuida. Durante los ensayos se registraron los desplazamientos de varios puntos con sensores láser. Los resultados obtenidos indican que la metodología práctica pro- puesta predice los desplazamientos en placas de vidrio lami- nado con un error menor del 10%, lo cual se pueden considerar razonable en cálculos prácticos de Ingeniería.
Agradecimientos
Los autores agradecen la financiación económica recibida del Ministerio de Economía y Competitividad a través del pro- yecto de investigación BIA2011-28380-C02-01 y del Instituto Universitario de Tecnología Industrial de Asturias (IUTA) a través del proyecto SV-14-GIJÓN-1.12.
Recibido 9 Enero 2015
Aceptado 27 Febrero 2015
Autor para correspondencia. aenlle@uniovi.es