The procedures of the proposed BM decision-making method with IvIFSs and matching willingness are given as follows. First, the matching willingness is computed through Algorithm 1 and Algorithm 2. Then, the IvIFS BM model considering the matching willingness is constructed through the multiobjective programming method. Third, the BM model is transformed into a biobjective BM model using NIvSF and SF. Finally, the optimal BM scheme is obtained through Algorithm 3. (Fig. 1)

Fig. 1.

Solution idea for BM decision-making with IvIFSs.

(0.14MB).

Computation of matching willingness

In Section 3, the matching willingness wjχ and wkγ are unknown. This subsection will introduce two approaches to determine them. The procedures of Algorithm 1 for determining wjχ are displayed below.

Algorithm 1:

Input: IvIFS F¯jχ={,,...,}.

Step 1: Compute the positive-ideal IvIFS of side χ, i.e., F¯j*χ={,,...,}, where IvIFN =<[pF¯j*χk,L,pF¯j*χk,R],[qF¯j*χk,L,qF¯j*χk,R]> is calculated by:

Step 2: Compute the negative-ideal IvIFS of side χ, i.e., F¯j∘χ={,,...,}, where IvIFN =<[pF¯j∘χk,L,pF¯j∘χk,R],[qF¯j∘χk,L,qF¯j∘χk,R]> is calculated by:

Step 3: Calculate the positive distance between F¯jχ={,,...,} and F¯j*χ={,,...,} by Eq. (7), namely, Dj*χ. Calculate the negative distance between F¯jχ={,,...,} and F¯j∘χ={,,...,} by Eq. (7), namely, D∘jχ.

Step 4: Calculate the closeness degree cjχ of χj, where cjχ is computed by:

Step 5: Calculate the matching willingness wjχ of χj, where wjχ is computed by:

Output: Matching willingness of χj, i.e., wjχ.

Similarly, the procedures of Algorithm 2 for determining wkγ are displayed below.

Algorithm 2:

Input: IvIFS F¯kγ={,,...,}.

Step 1: Compute the positive-ideal IvIFS of side γ, i.e., F¯k*γ={,,...,}, where IvIFN =<[pF¯k*γj,L,pF¯k*γj,R],[qF¯k*γj,L,qF¯k*γj,R]> is calculated by:

Step 2: Compute the negative-ideal IvIFS of side χ, i.e., F¯k∘γ={,,...,}, where IvIFN =<[pF¯k∘γj,L,pF¯k∘γj,R],[qF¯k∘γj,L,qF¯k∘γj,R]> is calculated by:

Step 3: Calculate the positive distance between F¯kγ={,,...,} and F¯k*γ={,,...,} by Eq. (7), namely, Dk*γ. Calculate the negative distance between F¯kγ={,,...,} and F¯k∘γ={,,...,} by Eq. (7), namely, Dk∘γ.

Step 4: Calculate the closeness degree ckγ of γk, where ckγ is computed by:

Step 5: Calculate the matching willingness wkγ of γk, where wkγ is computed by:

Output: Matching willingness of γk, i.e., wkγ.

From the above descriptions, Algorithm 1 is divided into five steps, which do not require many computations. The computational complexity is as follows: Step 1 requires only n Max operations; Step 2 requires only n Min operations; Step 3 requires no more than 21n2 operations; Step 4 requires only 2n operations; Step 5 requires no more than 2n operations. The complexity of the computation of Algorithm 2 is the same as that of Algorithm 1. Furthermore, the matching willingness of the bilateral agents can be determined through Algorithm 1 and Algorithm 2.

Construction of the BM model

First, the BM variable vjk is introduced, i.e.,

Consequently, a BM matrix V=[vjk]m×n can be established. In accordance with IvIFSs F¯jχ={,,...,} and F¯kγ={,,...,}, the matching willingness wjχ and wkγ, and the BM matrix V=[vjk]m×n, a BM Model (16) can be built, i.e.,

where =wjχ=<[pF¯jχk,L,pF¯jχk,R],[qF¯jχk,L,qF¯jχk,R]>wjχ, =wkγ=<[pF¯kγj,L,pF¯kγj,R],[qF¯kγj,L,qF¯kγj,R]>wkγ. The objectives of Model (16) are to maximize the IvIFN satisfactions in consideration of the matching willingness. The constraints of Model (16) are the one-to-one matching between the bilateral agents.

Transformation of the BM model with NIvSFs

To solve Model (16), IvIFNs and should be transformed into NIvSFs. Through the use of Eqs. (5) and (6), IvIFNs =<[p~F¯jχk,L,p~F¯jχk,R],[q~F¯jχk,L,q~F¯jχk,R]> and =<[p~F¯kγj,L,p~F¯kγj,R],[q~F¯kγj,L,q~F¯kγj,R]> are transformed into NIvSFs [sF¯jχk,L,sF¯jχk,R] and [sF¯kγj,L,sF¯kγj,R], where

Remark 2

From Yue et al. (2016), it is realized that αF¯jχk can be treated as the support ratio of Λ(χj)=γk from side χ, and αF¯kγj can be treated as the support ratio of Λ(χj)=γk from side γ.

Then, NIvSFs [sF¯jχk,L,sF¯jχk,R] and [sF¯kγj,L,sF¯kγj,R] are transformed into SFs sF¯jχk and sF¯kγj, where:

In Eqs. (19) and (20), θF¯jχk stands for the optimism attitude of χj towards γk, and θF¯kγj stands for the optimism attitude of γk towards χj. Through Eqs. (17)-(20), we know that a higher IvIFN satisfaction corresponds to a larger score, and vice versa. Moreover, the BM Model (16) can be changed into the following BM Model (21) with SFs, where the model constraint is still the one-to-one quantitative matching.

Ordinarily, the priorities of the agents of each side are treated as the same. From this point, the BM Model (21) can be translated into a biobjective BM Model (22):

To solve the above biobjective BM Model (22), a new optimization algorithm is introduced. The ideas of the new algorithm are as follows: First, solve the maximum and minimum values of a single objective function in Model (22) under the same constraints. Then, we transform Model (22) into a single objective model according to the idea of obtaining as much satisfaction as possible. The procedures of the new optimization algorithm are exhibited below.

Algorithm 3:

Input: SFs sF¯jχk and sF¯kγj.

Step 1: Find the maximum value Bχmax through the solution of BM Model (23):

Step 2: Find the minimum value Bχmin through the solution of BM Model (24):

Step 3: Find the maximum value Bγmax through the solution of BM Model (25):

Step 4: Find the minimum value Bγmin through the solution of BM Model (26):

Step 5: Transform the BM Model (22) into the following BM Model (27) in accordance with the idea of the new optimization algorithm:

Output: Maximum values Bχmax and Bγmax, minimum values Bχmin and Bγmin.

From the above description, it is also known that Algorithm 3 consists of five steps, and its calculation is more complex than Algorithm 1 or Algorithm 2, as shown below. The implementation process of Step 1 of Model (23) shall not exceed 2mn iterations, which is the same as the other steps.

Remark 4

If the priority of the agent of sides χ and γ is not the same, AHP technology can be used to acquire the priority of the agent of each side.

In this section, a novel method for solving the BM problem on the basis of IvIFSs and matching willingness is exhibited.

Step 1: Find matching willingness wjχ through the use of Algorithm 1.

Step 2: Find matching willingness wkγ through the use of Algorithm 2.

Step 3: Construct the BM Model (16) in accordance with IvIFSs F¯jχ and F¯kγ, matching willingness wjχ and wkγ, and the BM matrix V=[vjk]m×n.

Step 4: Transform IvIFN =<[p~F¯jχk,L,p~F¯jχk,R],[q~F¯jχk,L,q~F¯jχk,R]> into NIvSF [sF¯jχk,L,sF¯jχk,R] through the use of Eq. (17).

Step 5: Transform IvIFN =<[p~F¯kγj,L,p~F¯kγj,R],[q~F¯kγj,L,q~F¯kγj,R]> into NIvSF [sF¯kγj,L,sF¯kγj,R] through the use of Eq. (18).

Step 6: Transform NIvSFs [sF¯jχk,L,sF¯jχk,R] and [sF¯kγj,L,sF¯kγj,R] into SFs sF¯jχk and sF¯kγj through the use of Eqs. (19) and (20), respectively.

Step 7: Convert BM Model (16) into BM Model (21).

Step 8: Convert BM Model (21) into the biobjective BM Model (22).

Step 9: Transform BM Model (22) into BM Model (27) through the use of new optimization.

Step 10: Gain the optimal BM scheme through the solution of Model (27).

A BM case study in the field of knowledge innovation management shows the feasibility of the presented decision-making method.

A technology service company for a knowledge management system in Shenzhen provides cross-industry knowledge management system purchase, customization and matching services for suppliers and demand enterprises through its service platform. At present, the company's service platform has received the purchase intention of five enterprises χ1,χ2,...,χ5 to purchase a knowledge management system in advance to improve the efficiency of their internal knowledge management and meet their long-term needs. During this period, six suppliers γ1,γ2,...,γ6 on the platform expressed their trading intention. Five enterprises χ1,χ2,...,χ5 evaluate six suppliers γ1,γ2,...,γ6 mainly from the aspects of system performance, purchase price and after-sales service and then give the preference of IvIFS, F¯jχ={,,...,}, j∈M, as shown in Table 2. Considering the evaluation of the payment method, enterprise quotation, enterprise reputation and enterprise scale, six suppliers γ1,γ2,...,γ6 gave their preferences for IvIFS towards five enterprises χ1,χ2,...,χ5, F¯kγ={,,...,}, k∈N, as shown in Table 3. Finally, the technology service company is required to act as an intermediary to provide a reasonable BM scheme for demand enterprises and suppliers according to their IvIFS preference information.

To provide enterprises and suppliers with a more effective BM scheme, a calculation process is described according to the IvIFS preferences F¯jχ (j=1,2,...,5) and F¯kγ (k=1,2,...,6), which are the original input values.

Step 1: Find matching willingness wjχ(j∈M={1,...,5}) through the use of Algorithm 1. The uncomplicated calculation procedures are revealed below.

Algorithm 4:

Input: IvIFS F¯jχ (j=1,2,...,5).

Step 4.1: Gain the positive-ideal IvIFS F¯j*χ={,,...,} through the use of Eq. (8).

Step 4.2: Gain the negative-ideal IvIFS F¯j∘χ={,,...,} through the use of Eq. (9).

Step 4.3: Obtain the positive distance Dj*χ between F¯jχ(j∈M) and F¯j*χ and the negative distance D∘jχ between F¯jχ(j∈M) and F¯j∘χ through the use of Eq. (7), where r,α,β,γ=1,0.4,0.4,0.2.

Step 4.4: Gain closeness degree cjχ(j∈M) through the use of Eq. (10).

Step 4.5: Gain matching willingness wjχ(j∈M), i.e., w1χ=0.1815, w2χ=0.1765, w3χ=0.2758, w4χ=0.1599, w5χ=0.2063.

Output: Matching willingness wjχ (j=1,2,...,5).

Step 2: Determine the matching willingness wkγ(k∈N={1,...,6}) through the use of Algorithm 2. The uncomplicated calculation procedures are revealed below.

Algorithm 5:

Input: IvIFS F¯kγ (k=1,2,...,6).

Step 5.1: Gain the positive-ideal IvIFS F¯k*γ={,,...,} through the use of Eq. (12).

Step 5.2: Gain the negative-ideal IvIFS F¯k∘γ={,,...,} through the use of Eq. (13).

Step 5.3: Obtain the positive distance Dk*γ(k∈N) between F¯kγ(k∈N) and F¯k*γ and the negative distance Dk∘γ(k∈N) between F¯kγ(k∈N) and F¯k∘γ through the use of Eq. (7), where r,α,β,γ=1,0.4,0.4,0.2.

Step 5.4: Gain closeness degree ckγ(k∈N) through the use of Eq. (14).

Step 5.5: Gain matching willingness wkγ(k∈N), i.e., w1γ=0.145, w2γ=0.1662, w3γ=0.173, w4γ=0.1411, w5γ=0.1778, w6γ=0.1969.

Output: Matching willingness wkγ (k=1,2,...,6).

Step 3: Construct the following BM Model (16) in accordance with IvIFSs F¯jχ(j∈M) and F¯kγ(k∈N), matching willingness wjχ(j∈M) and wkγ(k∈N), and the BM matrix V=[vjk]5×6:

=wjχ and =wkγ are calculated by Definition 3.

Step 4: Transform IvIFN =<[p~F¯jχk,L,p~F¯jχk,R],[q~F¯jχk,L,q~F¯jχk,R]> into NIvSF [sF¯jχk,L,sF¯jχk,R] through the use of Eq. (17), as displayed in Table 4, with η=1. The support ratio αF¯jχk is displayed in Table 5.

Table 4.

NIvSF [sF¯jχk,L,sF¯jχk,R].

	γ1	γ2	γ3	γ4	γ5	γ6
χ1	[0.1105,0.1263]	[0.1086,0.1239]	[0.1357,0.1521]	[0.106,0.117]	[0.109,0.1207]	[0.103,0.1198]
χ2	[0.0993,0.112]	[0.1119,0.1271]	[0.1133,0.1192]	[0.0977,0.1051]	[0.1181,0.1286]	[0.1178,0.1377]
χ3	[0.1859,0.2049]	[0.1706,0.1783]	[0.1749,0.1967]	[0.1538,0.1716]	[0.1987,0.2192]	[0.1903,0.1994]
χ4	[0.0999,0.1078]	[0.1036,0.1128]	[0.1074,0.1226]	[0.0969,0.1067]	[0.1007,0.1219]	[0.072,0.0768]
χ5	[0.1231,0.1413]	[0.1165,0.1224]	[0.1441,0.1604]	[0.1231,0.1323]	[0.1228,0.1349]	[0.1238,0.1306]

Table 5.

Support ratio αF¯jχk.

	γ1	γ2	γ3	γ4	γ5	γ6
χ1	0.1692	0.1526	0.2103	0.1606	0.1606	0.1467
χ2	0.1503	0.1732	0.1668	0.1443	0.1759	0.1895
χ3	0.1753	0.1538	0.1671	0.1389	0.1896	0.1753
χ4	0.1669	0.1759	0.2002	0.1586	0.1759	0.1225
χ5	0.1659	0.1517	0.2072	0.1659	0.1576	0.1517

Step 5: Transform IvIFN =<[p~F¯kγj,L,p~F¯kγj,R],[q~F¯kγj,L,q~F¯kγj,R]> into NIvSF [sF¯kγj,L,sF¯kγj,R] through the use of Eq. (18), as displayed in Table 6 with η=1. The support ratio αF¯kγj is displayed in Table 7.

Table 6.

NIvSF [sF¯kγj,L,sF¯kγj,R].

	γ1	γ2	γ3	γ4	γ5	γ6
χ1	[0.0936,0.1009]	[0.0907,0.1091]	[0.1015,0.1125]	[0.0852,0.0885]	[0.1227,0.1405]	[0.1188,0.1289]
χ2	[0.0716,0.0824]	[0.0951,0.1]	[0.1118,0.118]	[0.1024,0.1076]	[0.0974,0.1138]	[0.1206,0.1453]
χ3	[0.0668,0.0711]	[0.0967,0.1133]	[0.0951,0.1115]	[0.0732,0.0824]	[0.0992,0.1118]	[0.1304,0.1526]
χ4	[0.1079,0.1135]	[0.1043,0.1206]	[0.098,0.1098]	[0.0803,0.0838]	[0.113,0.1253]	[0.1229,0.1393]
χ5	[0.0962,0.1079]	[0.1114,0.1255]	[0.1098,0.1207]	[0.0909,0.1002]	[0.1111,0.1239]	[0.1244,0.1482]

Table 7.

Support ratio αF¯kγj.

	γ1	γ2	γ3	γ4	γ5	γ6
χ1	0.15	0.1462	0.1682	0.1386	0.2068	0.1901
χ2	0.1192	0.1521	0.1824	0.1723	0.1602	0.2139
χ3	0.1122	0.182	0.1633	0.1284	0.1695	0.2445
χ4	0.1713	0.1701	0.1447	0.1259	0.1884	0.1996
χ5	0.1517	0.1802	0.1708	0.1356	0.1688	0.1929

Step 6: Transform NIvSFs [sF¯jχk,L,sF¯jχk,R] and [sF¯kγj,L,sF¯kγj,R] into SFs sF¯jχk and sF¯kγj through the use of Eqs. (19) and (20), respectively, as demonstrated in Table 8 and Table 9 with θF¯jχk=θF¯kγj=0.6.

Table 8.

SF sF¯jχk.

	γ1	γ2	γ3	γ4	γ5	γ6
χ1	0.12	0.1178	0.1455	0.1126	0.116	0.1131
χ2	0.1069	0.121	0.1168	0.1021	0.1244	0.1297
χ3	0.1973	0.1752	0.188	0.1645	0.211	0.1958
χ4	0.1046	0.1091	0.1165	0.1028	0.1134	0.0749
χ5	0.134	0.12	0.1539	0.1286	0.1301	0.1279

Table 9.

SF sF¯kγj.

	γ1	γ2	γ3	γ4	γ5	γ6
χ1	0.098	0.1017	0.1081	0.0872	0.1334	0.1249
χ2	0.0781	0.098	0.1155	0.1055	0.1072	0.1354
χ3	0.0694	0.1067	0.1049	0.0787	0.1068	0.1437
χ4	0.1113	0.1141	0.1051	0.0824	0.1204	0.1327
χ5	0.1032	0.1199	0.1163	0.0965	0.1188	0.1387

Step 7: Convert BM Model (16) into BM Model (21) in accordance with SFs sF¯jχk and sF¯kγj, i.e.,

Step 8: Convert BM Model (21) into the biobjective BM Model (22) under normal circumstances, i.e.,

Step 9: Transform BM Model (22) into BM Model (27) through the use of Algorithm 3. The calculation procedures are revealed below.

Algorithm 6:

Input: SFs sF¯jχk and sF¯kγj (j=1,2,...,5; k=1,2,...,6).

Step 6.1: Solve the BM Model (23); then maximum value Bχmax is gained, i.e., Bχmax=0.7293.

Step 6.2: Solve the BM Model (24); then minimum value Bχmin is gained, i.e., Bχmin=0.5823.

Step 6.3: Solve the BM Model (25); then maximum value Bγmax is gained, i.e., Bγmax=0.6238.

Step 6.4: Solve the BM Model (26): then minimum value Bγmin is gained, i.e., Bγmin=0.4767.

Step 6.5: Transform the BM Model (22) into the following BM Model (27) in accordance with the calculation results of Steps 6.1–6.4, i.e.,

Output: Maximum values Bχmax and Bγmax, minimum values Bχmin and Bγmin.

Step 10: By solving Model (27), we can acquire the optimal objective function value θχ*+θγ*=1+0.6179=1.6179 and the optimal BM matrix V=[vjk*]5×6, as demonstrated in Table 10.

Table 10.

Optimal BM matrix V=[vjk*]5×6.

	γ1	γ2	γ3	γ4	γ5	γ6
χ1	0	0	1	0	0	0
χ2	0	0	0	0	0	1
χ3	0	0	0	0	1	0
χ4	0	1	0	0	0	0
χ5	1	0	0	0	0	0

As a result, the optimal BM scheme Λ* is gained, Λ*=ΛM*∪ΛS*, where ΛM*={(χ1,γ3),(χ2,γ6),(χ3,γ5),(χ4,γ2),(χ5,γ1)}, ΛS*={(γ4,γ4)}.

Remark 5

It should be emphasized that the decision-making method proposed in this paper is based on IvIFSs. However, the methods proposed in Yue et al. (2016) and Yue and Zhang (2020) were actually based on IvIFNs rather than IvIFSs, which cannot be used to directly solve the IvIFS BM problem displayed in this paper. The proposed decision-making method uses the distance measure for IvIFSs directly for calculating the matching willingness of the bilateral agents, which can reduce information loss. The proposed decision-making method solves the BM problem under the fuzzy background of IvIFS by building the BM model considering the matching willingness of the bilateral agents. It not only expands the solution approach of the BM problem in knowledge innovation management under the IvIFS environment but also provides a reference for solving the BM problem and other decision-making problems considering the matching willingness under other intuitionistic fuzzy environments.

If the priorities of agents of sides χ and γ are not the same, then let ωχ and ωγ be the weights of agents of side χ and γ, respectively. Moreover, the objective function of Model (27) is turned into f=ωχθχ+ωγθγ. As a result, Model (27) is translated into the following BM model:

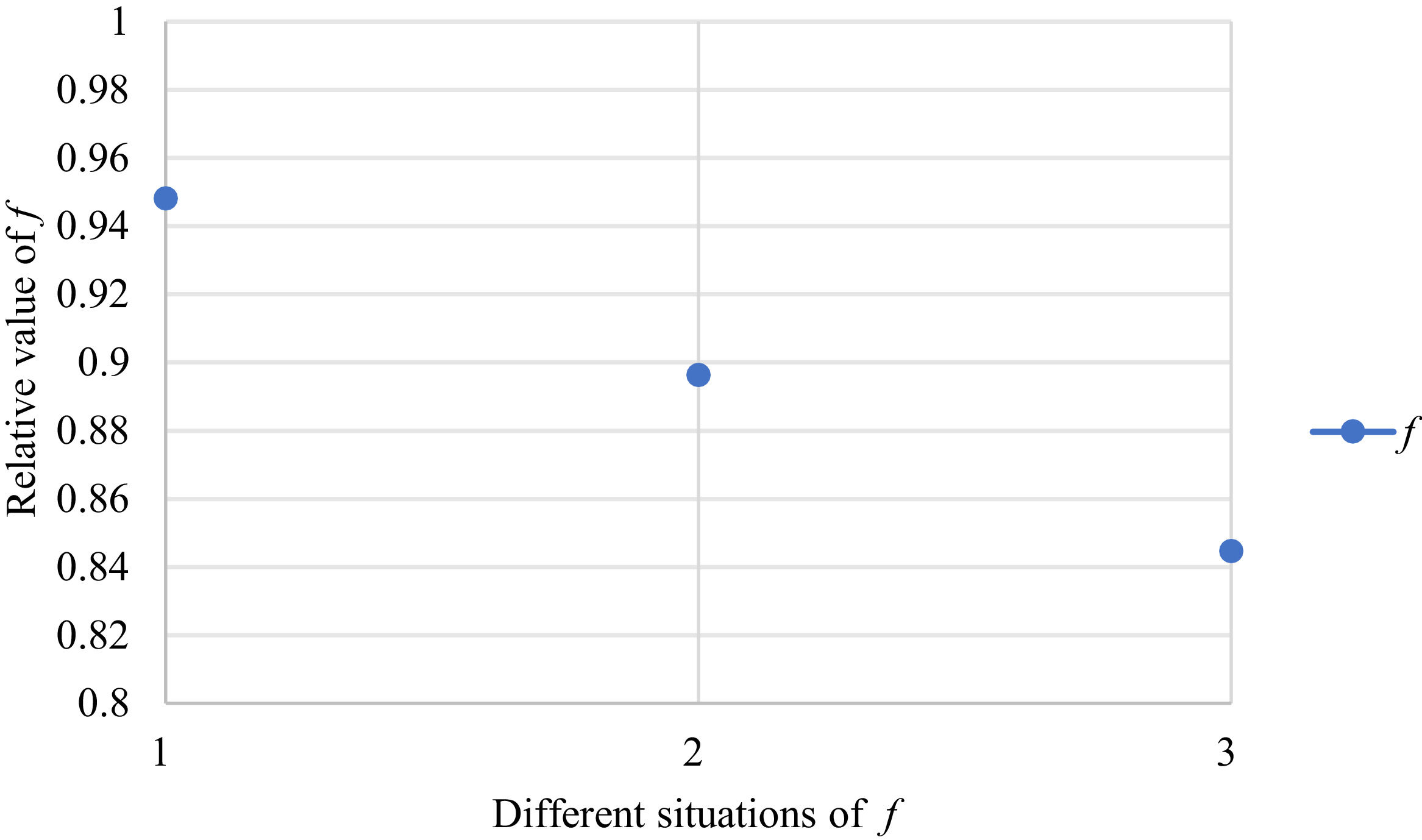
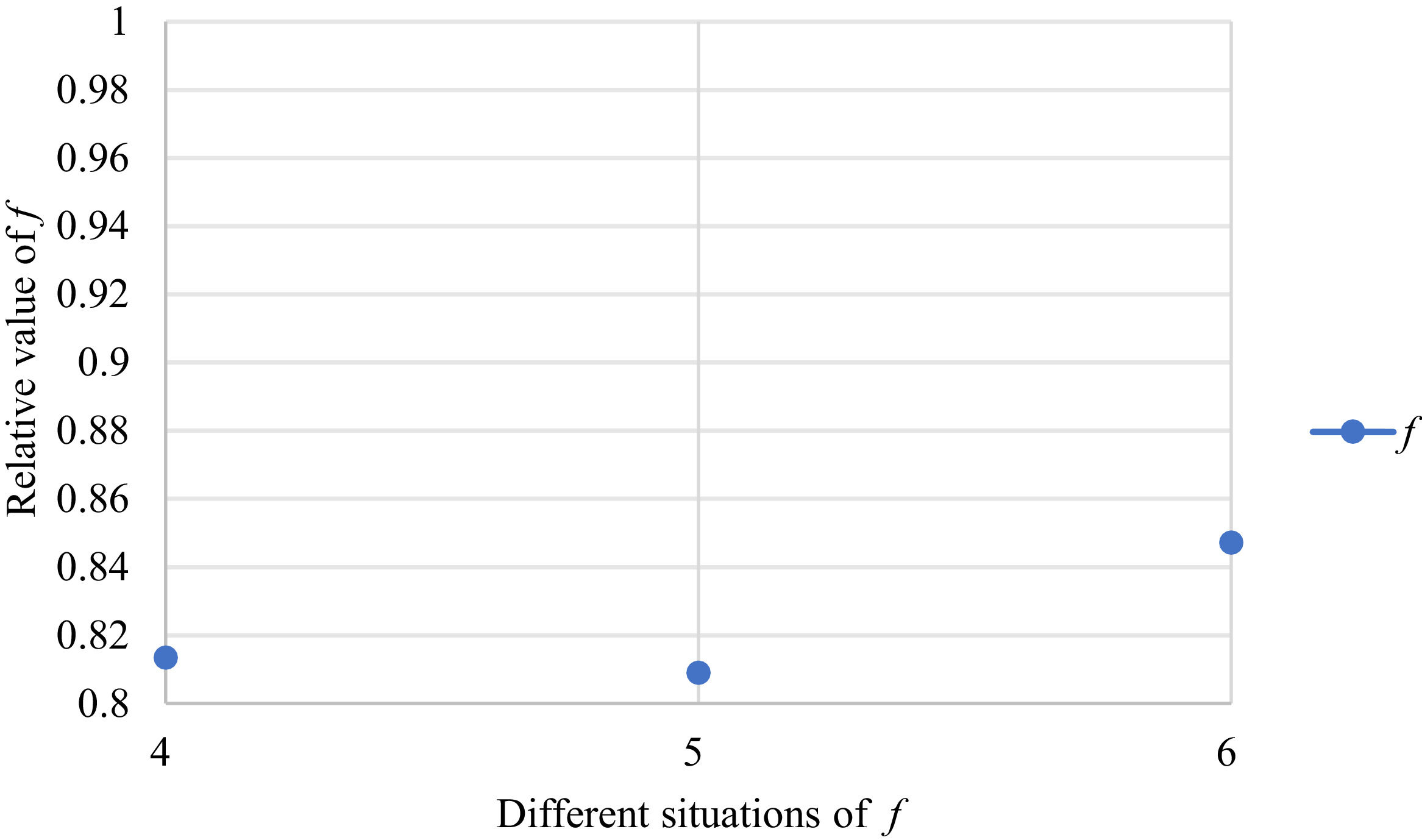
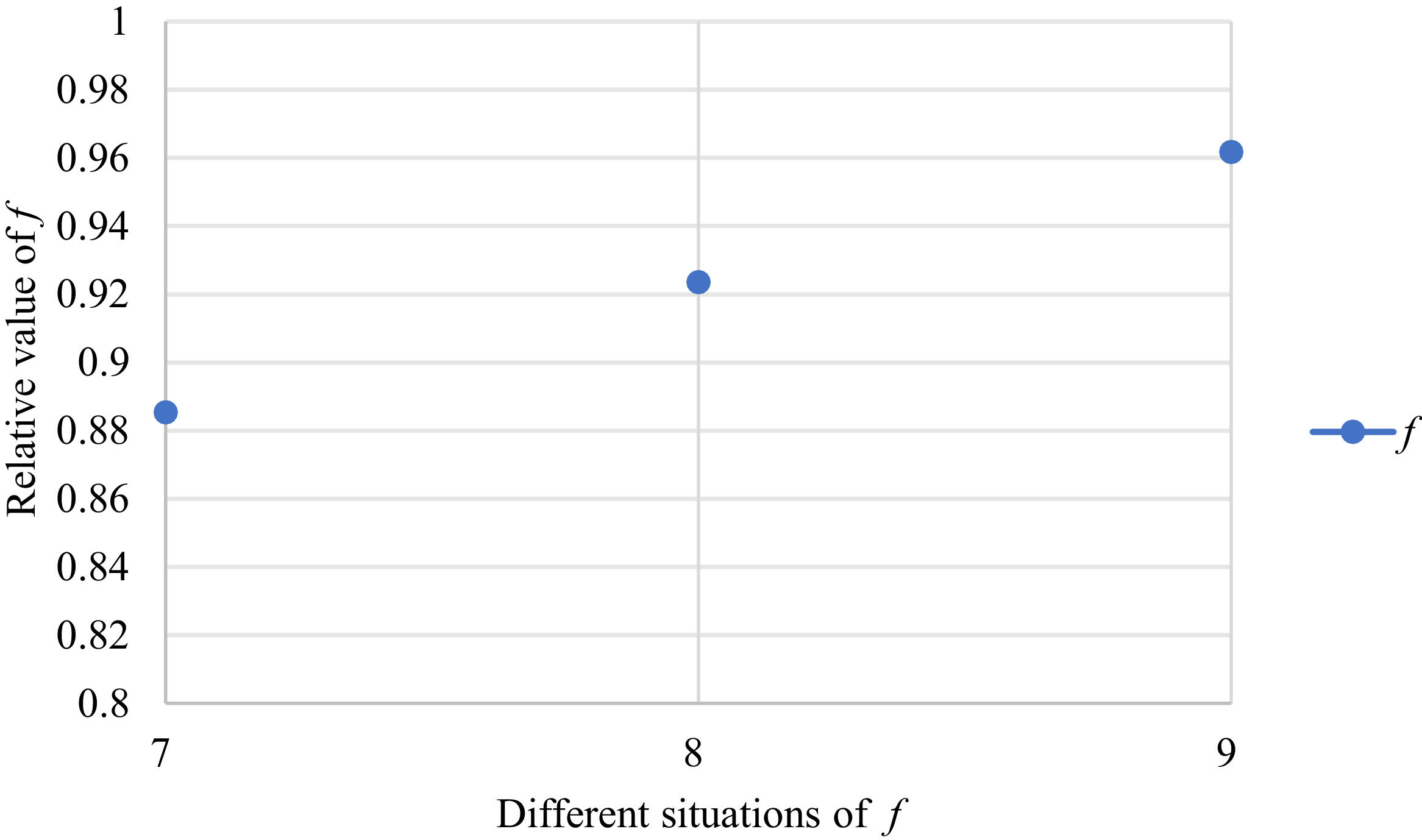
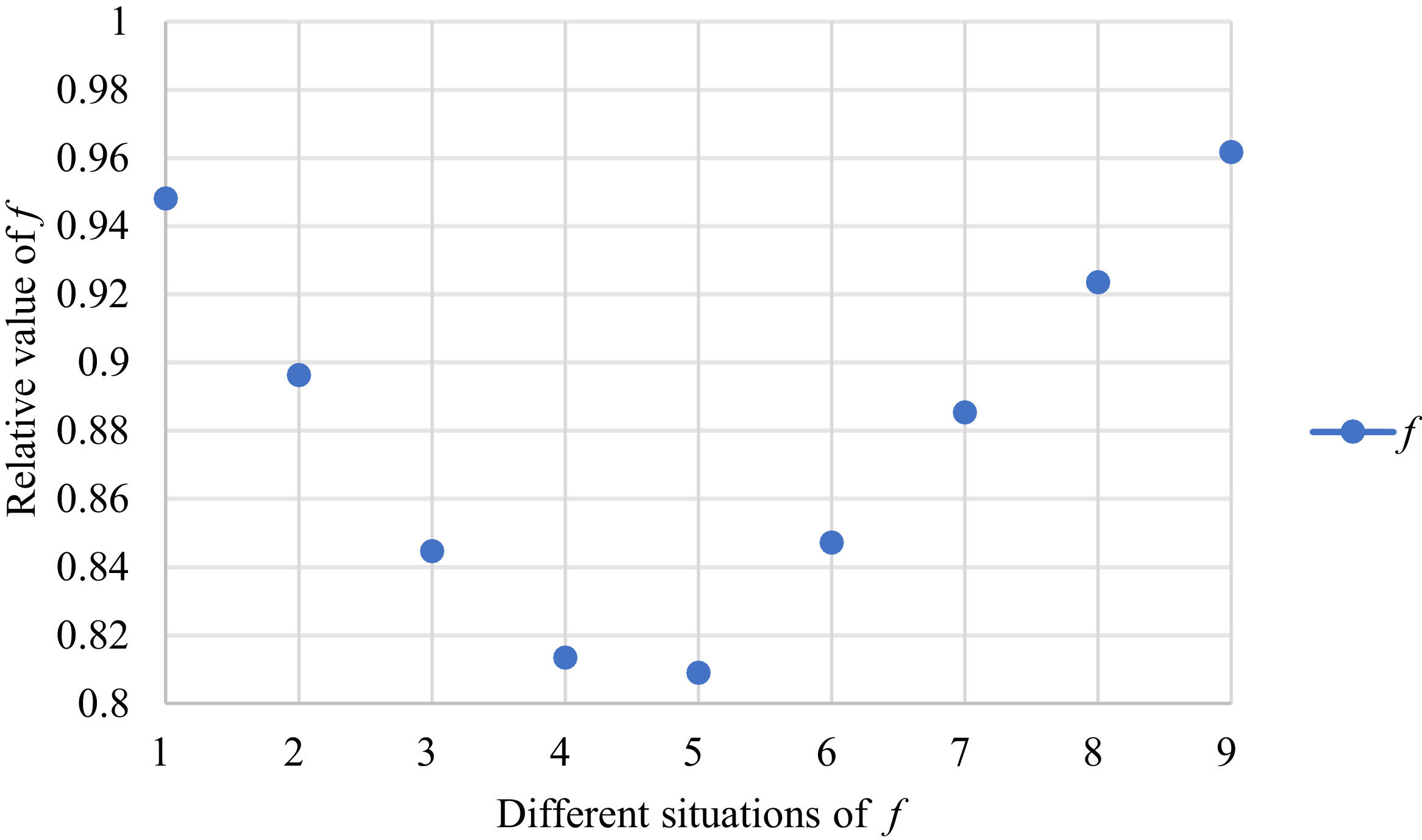
Fig. 2 reveals the tendencies of the objective function f from Situation I to III. Fig. 3 reveals the tendencies of objective function f from Situation IV to VI. Fig. 4 reveals the tendencies of objective function f from Situation VII to IX. In light of Figs. 2-4, the overall tendencies of f from Situation I to IX can be acquired, as displayed in Fig. 5. From the figure, we can see that objective function f decreases first and then increases, reaching the minimum in Situation V.

Fig. 2.

Tendencies of f from Situation I to III.

(0.11MB).

Fig. 3.

Tendencies of f from Situation IV to VI.

(0.11MB).

Fig. 4.

Tendencies of f from Situation VII to IX.

(0.11MB).

Fig. 5.

Tendencies of f from Situation I to IX.

(0.13MB).

As shown in Figs. 2-5, we mainly discuss the impact of the different priorities of the bilateral agents on the objective function f=ωχθχ+ωγθγ. Fig. 5 shows a comprehensive comparison. The results show that when the priorities of the bilateral agents differ greatly, the value of the objective function is also greater; however, when the priorities of the bilateral agents gradually tend to be equal, the value of the objective function gradually decreases and tends to be the minimum.

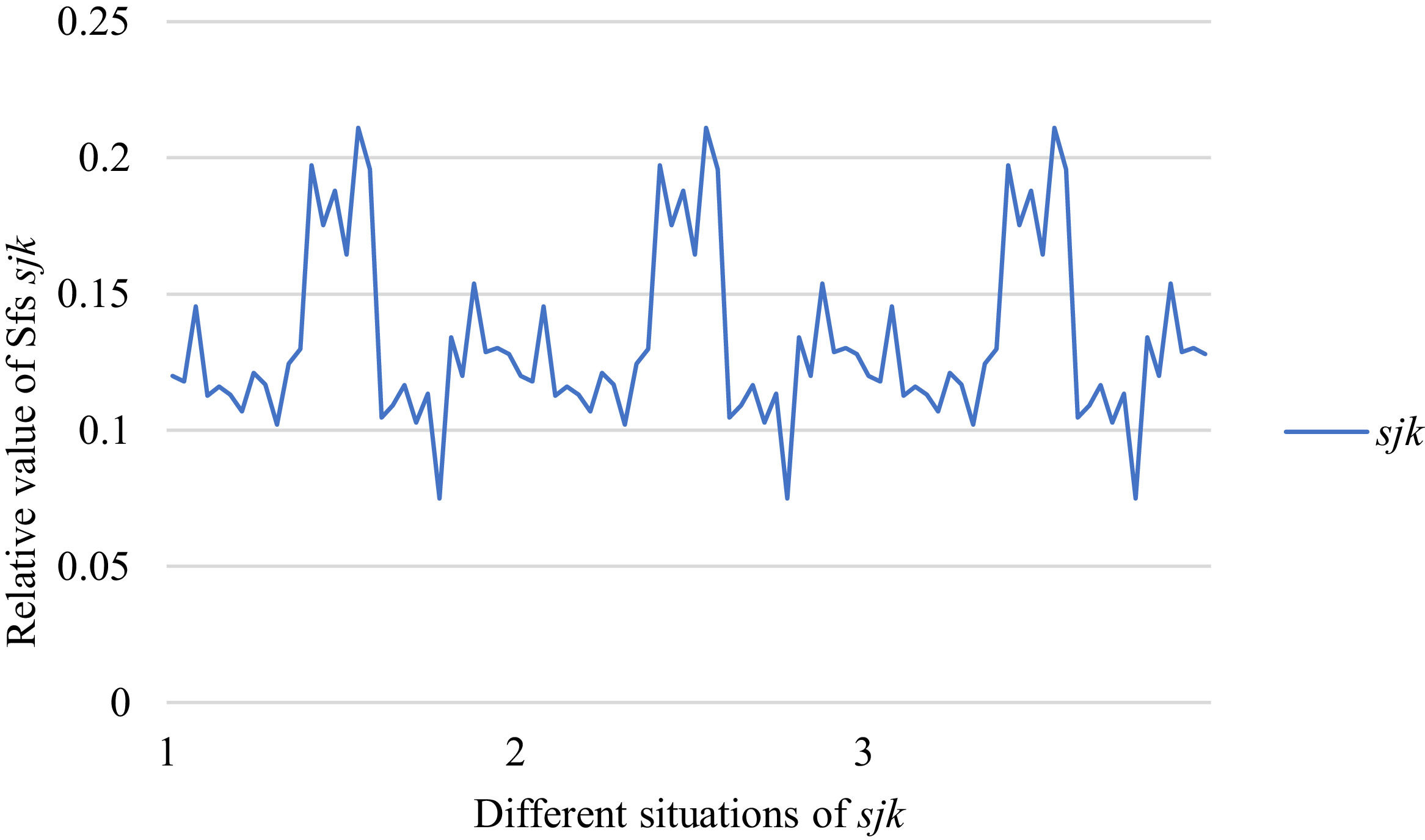
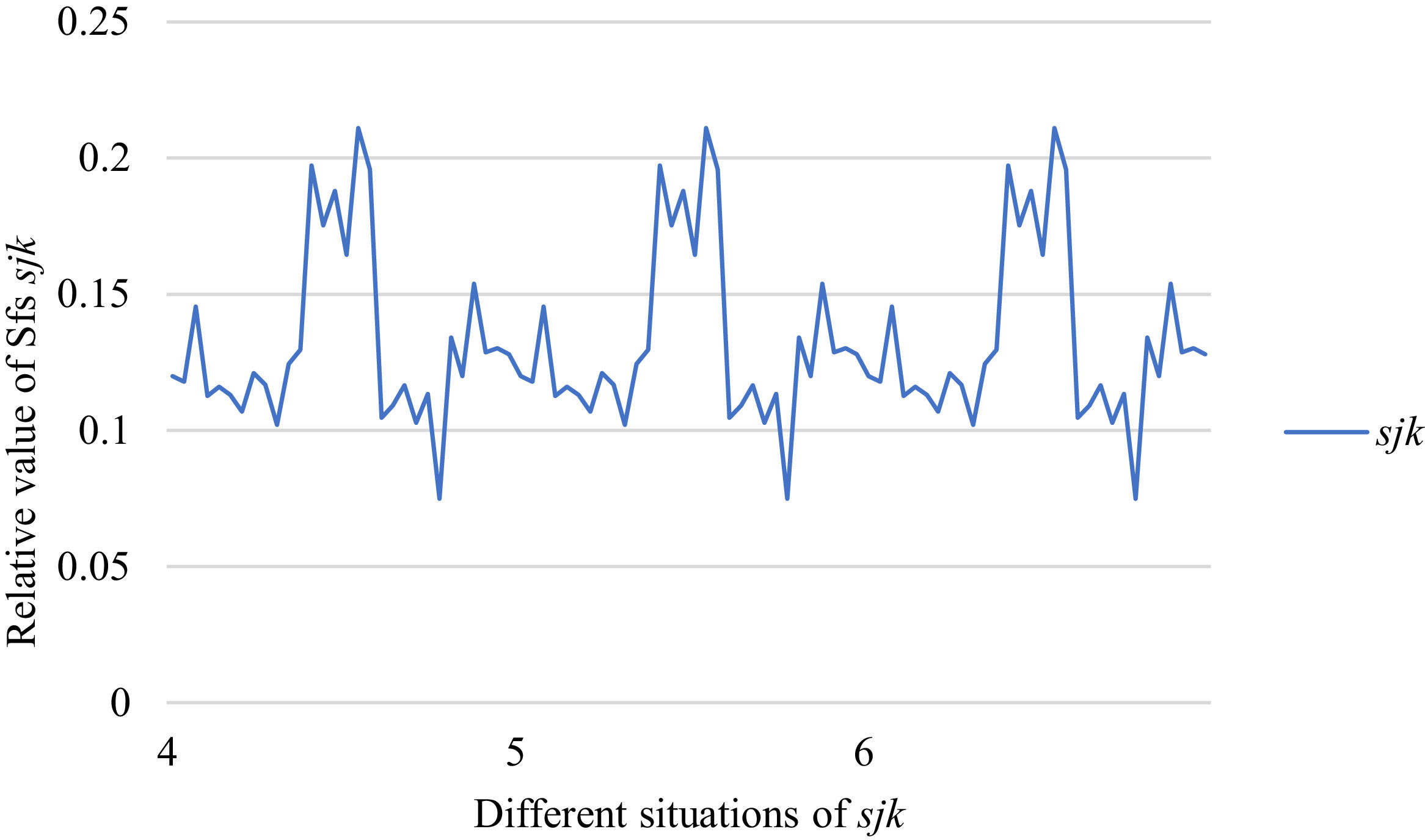
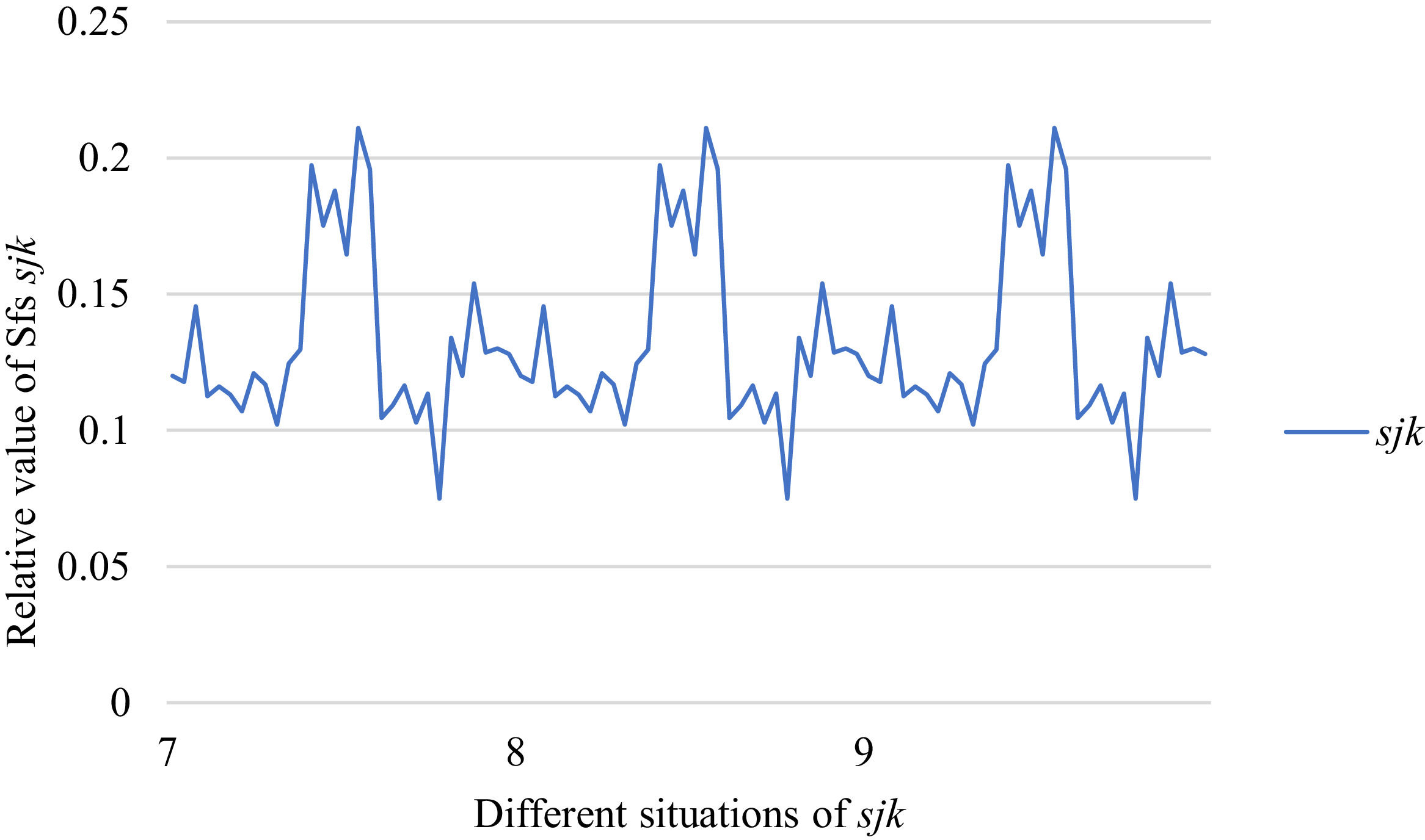
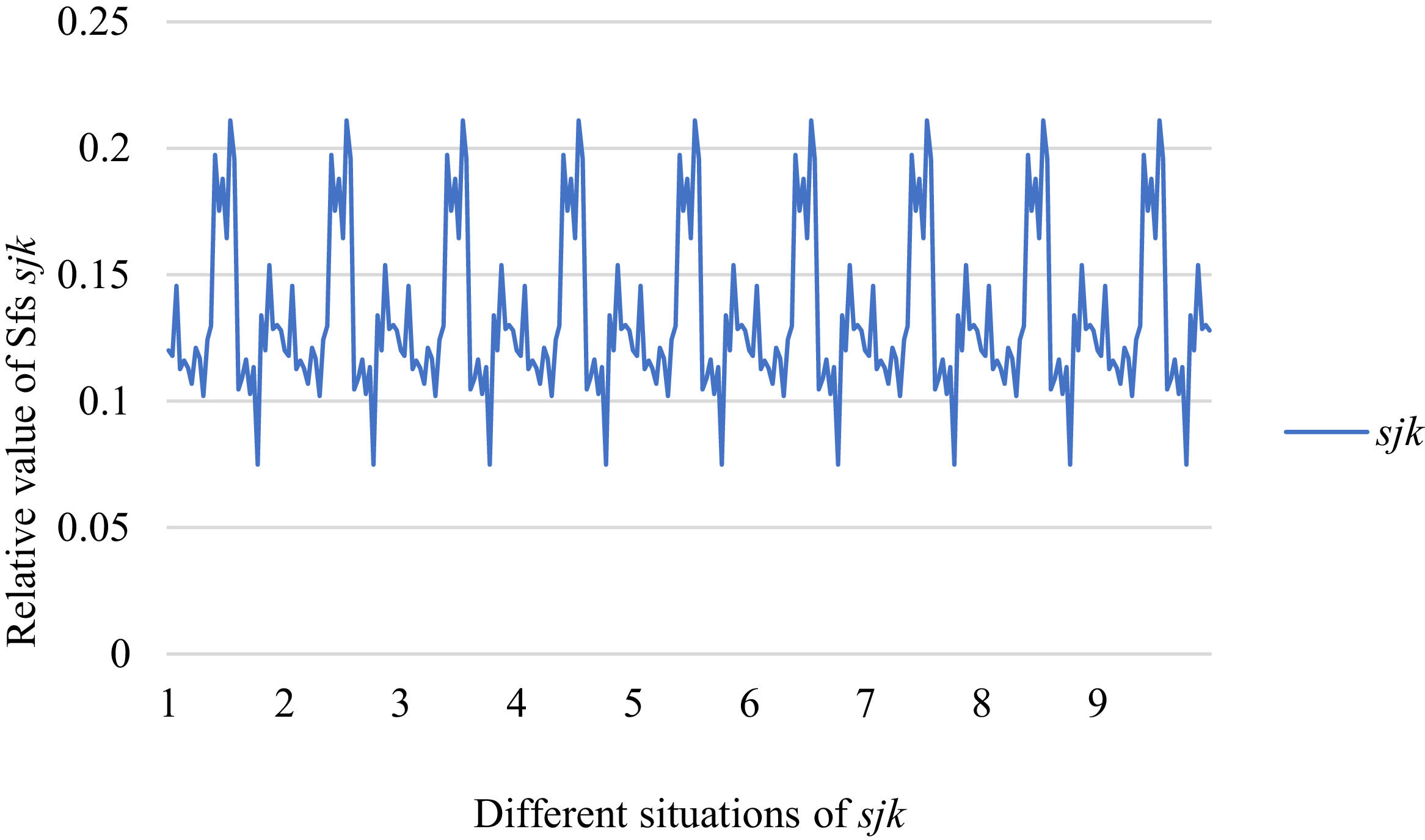
Fig. 6 reveals the tendencies of SFs sF¯jχk from Situation I to III. Fig. 7 reveals the tendencies of SFs sF¯jχk from Situation IV to VI. Fig. 8 reveals the tendencies of SFs sF¯jχk from Situation VII to IX. In light of Figs. 6-8, the overall tendencies of SFssF¯jχk from Situation I to IX can be acquired, as displayed in Fig. 9. From Fig. 9, we can see that SFs sF¯jχk fluctuates periodically from Situation I to IX.

Fig. 6.

Tendencies of SFs sF¯jχk from Situation I to III.

(0.15MB).

Fig. 7.

Tendencies of SFs sF¯jχk from Situation IV to VI.

(0.14MB).

Fig. 8.

Tendencies of SFs sF¯jχk from Situation VII to IX.

(0.15MB).

Fig. 9.

Tendencies of SFs sF¯jχk from Situation I to IX.

(0.19MB).

As shown in Figs. 6-9, we mainly discuss the impact of the different priorities of the bilateral agents on SFs sF¯jχk. Fig. 9 shows a more comprehensive comparison. The results show that when the priorities of the bilateral agents are different, there is no significant change in the value of SFs sF¯jχk.

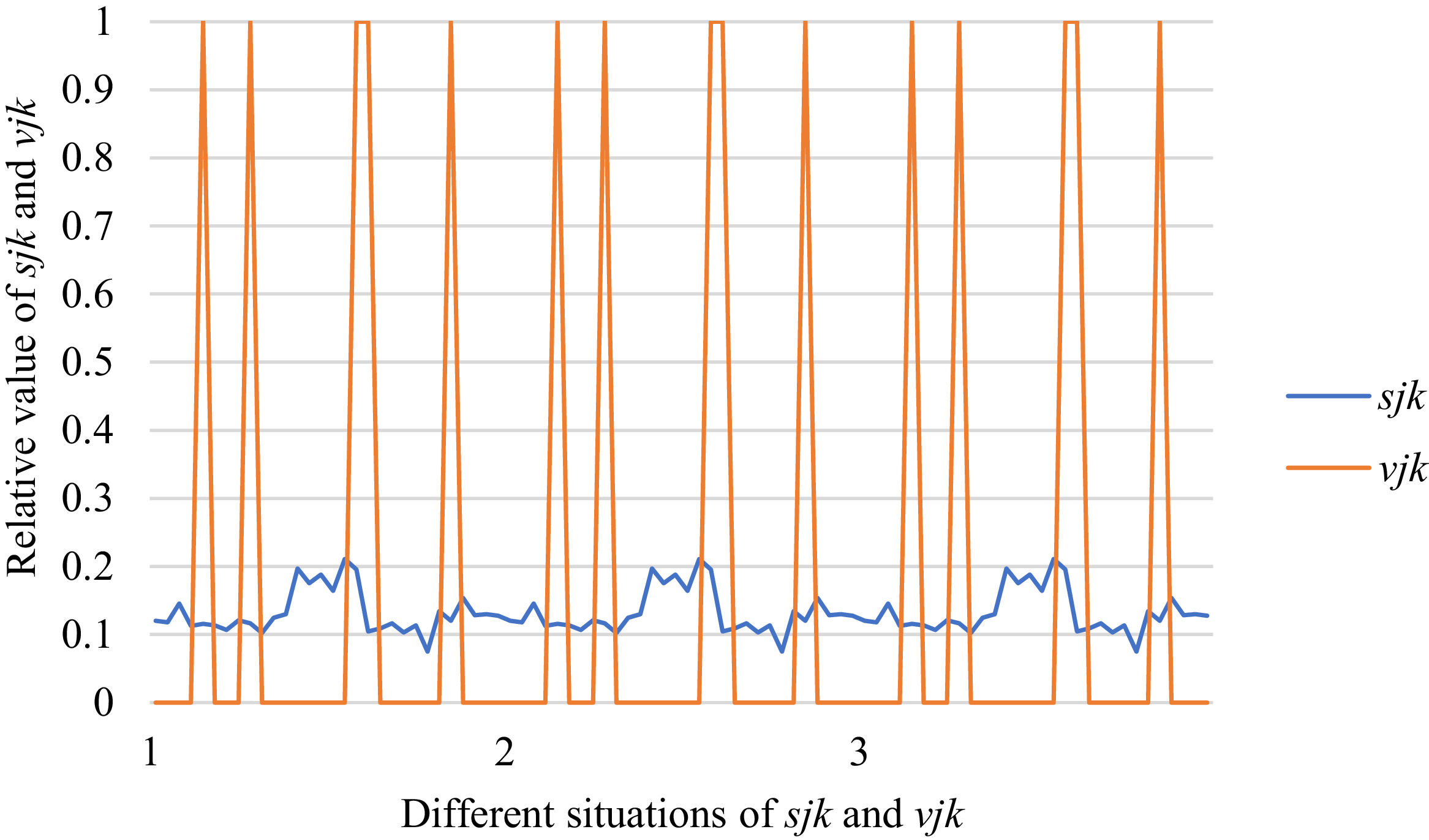
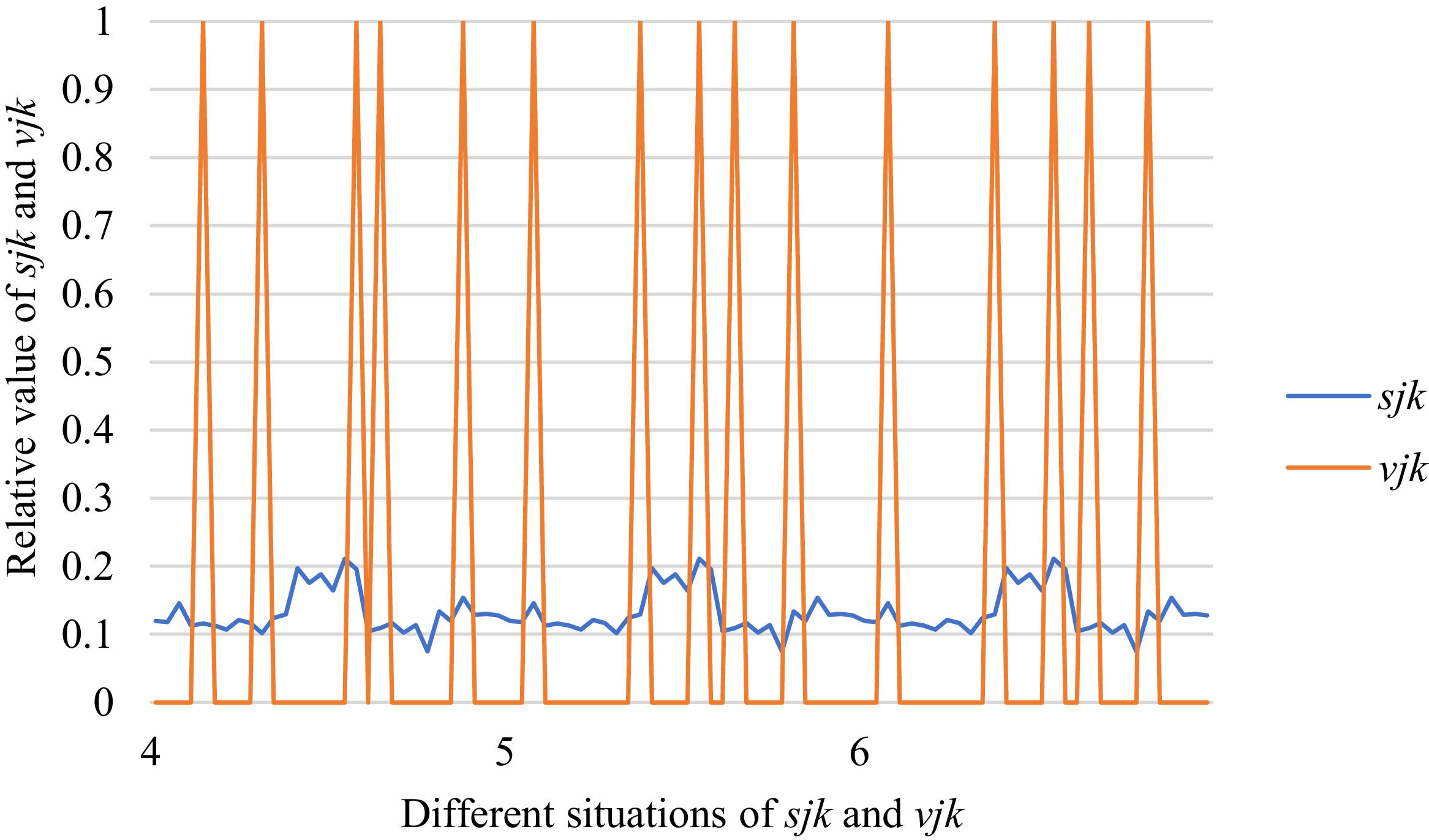
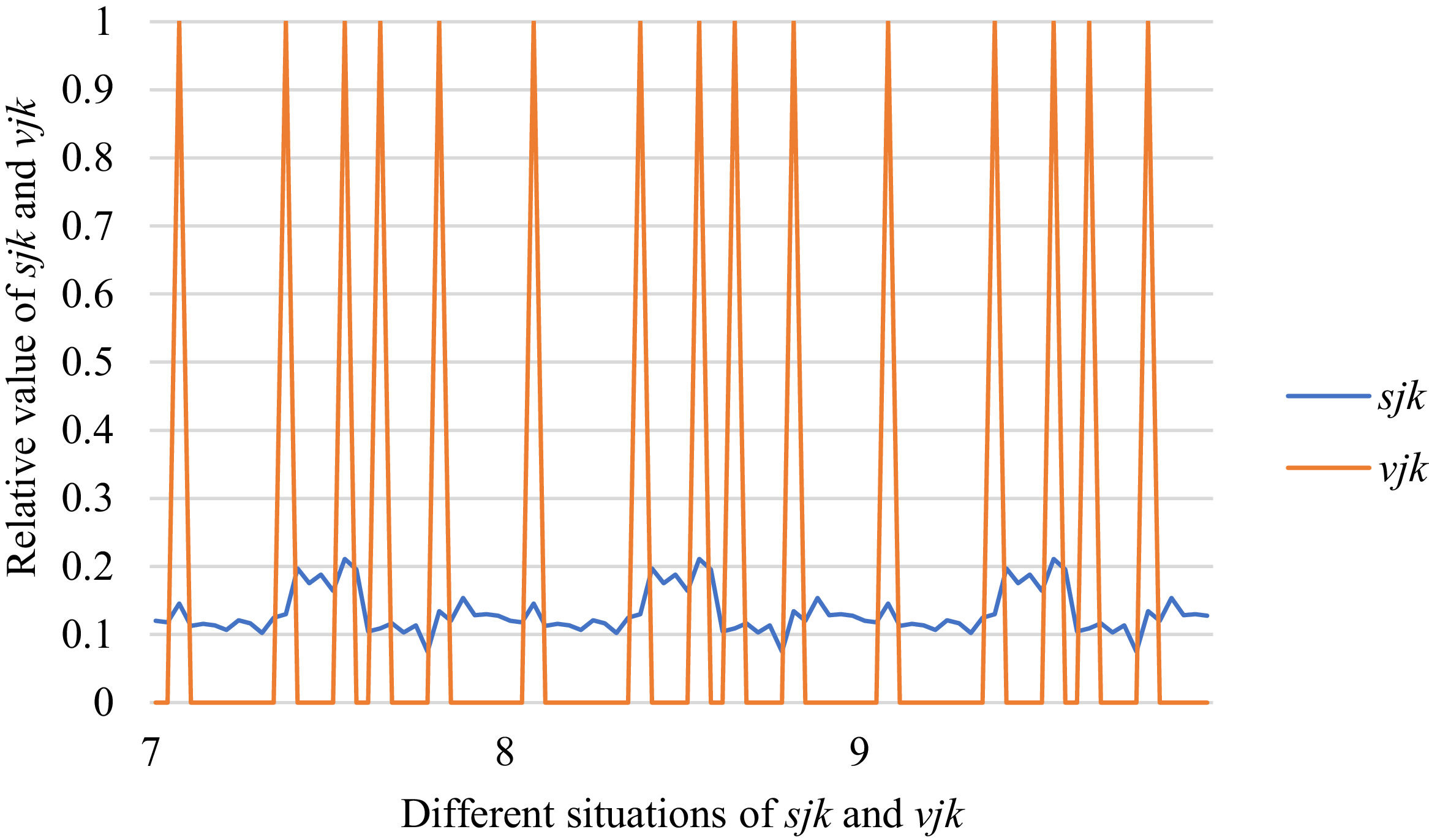
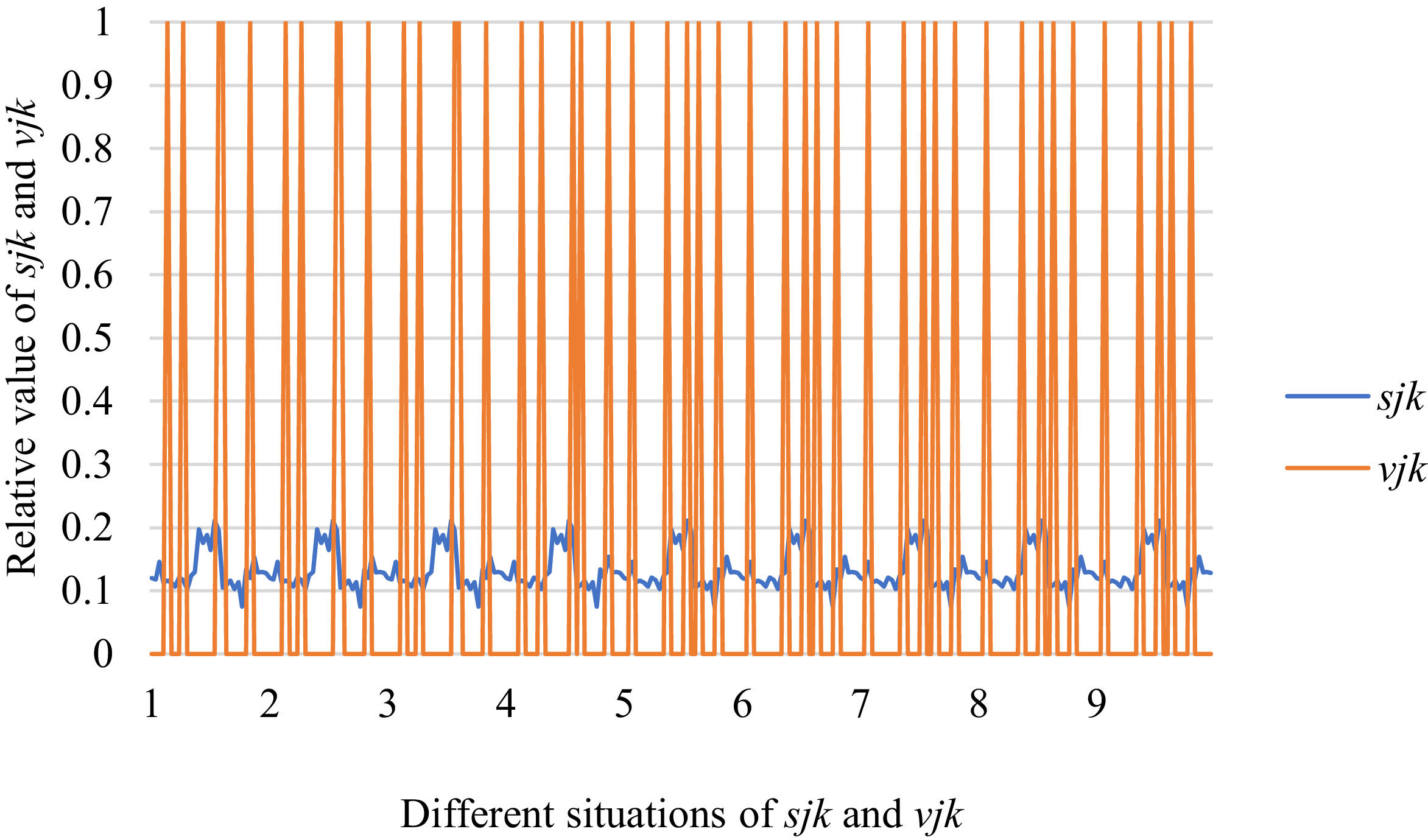
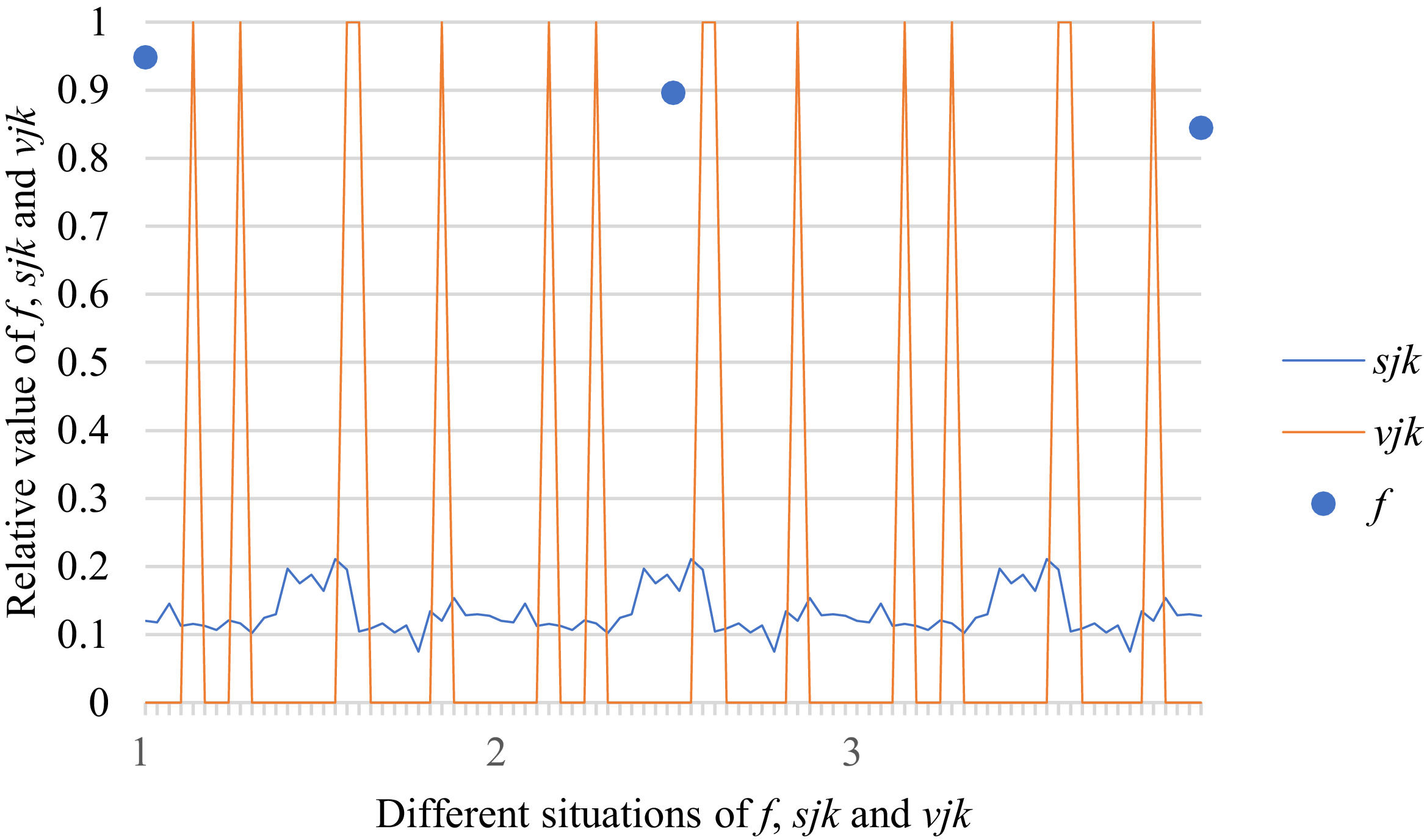
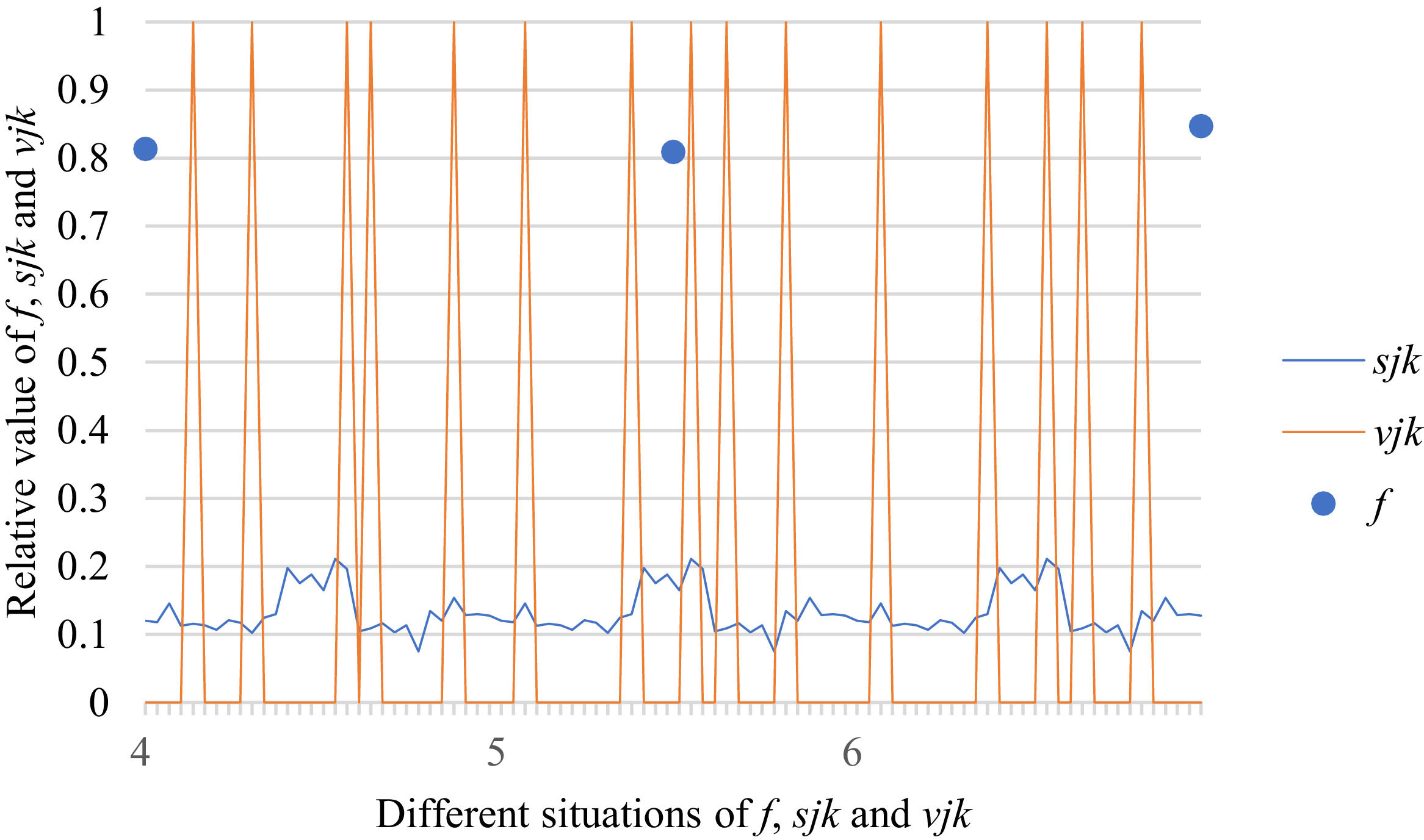
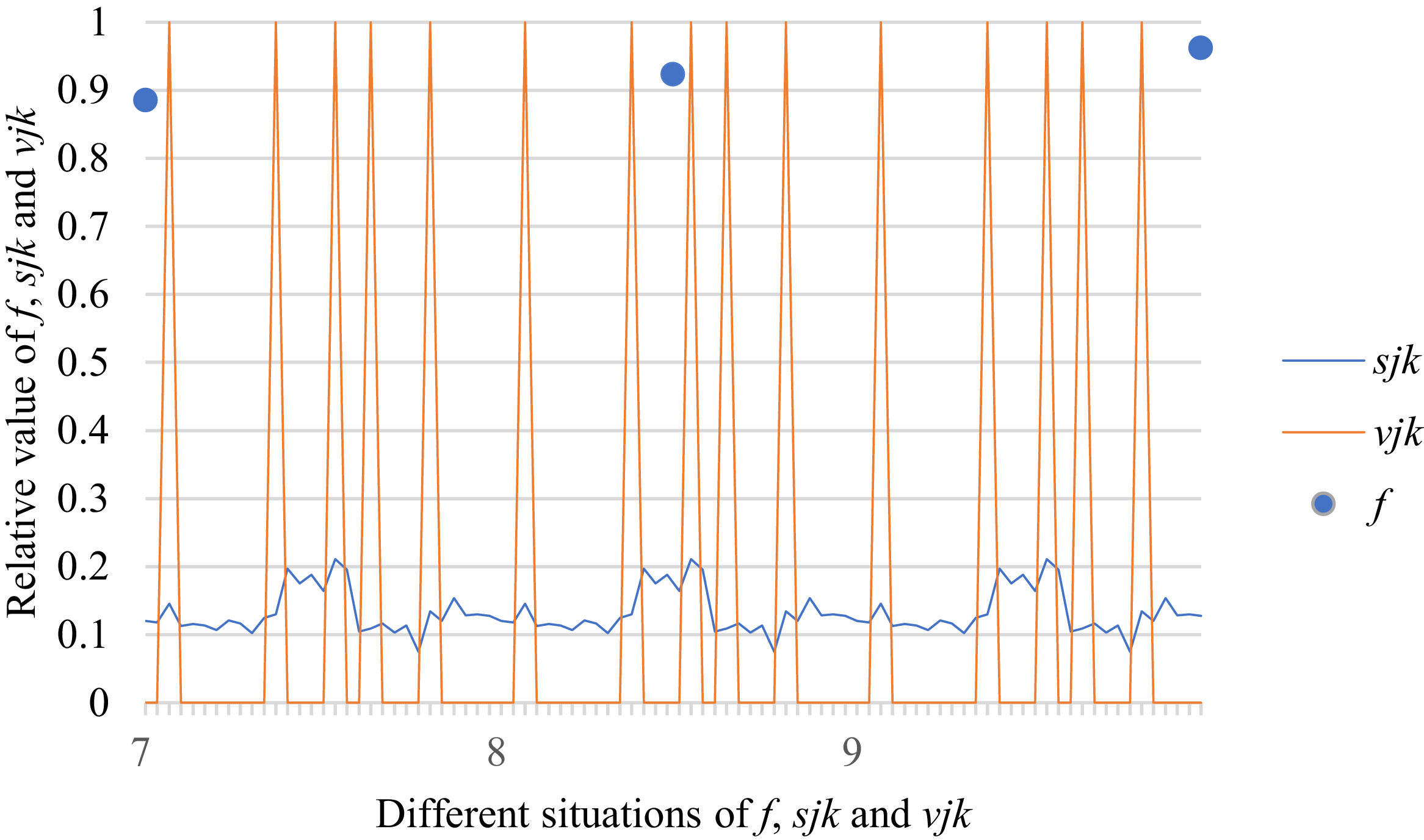
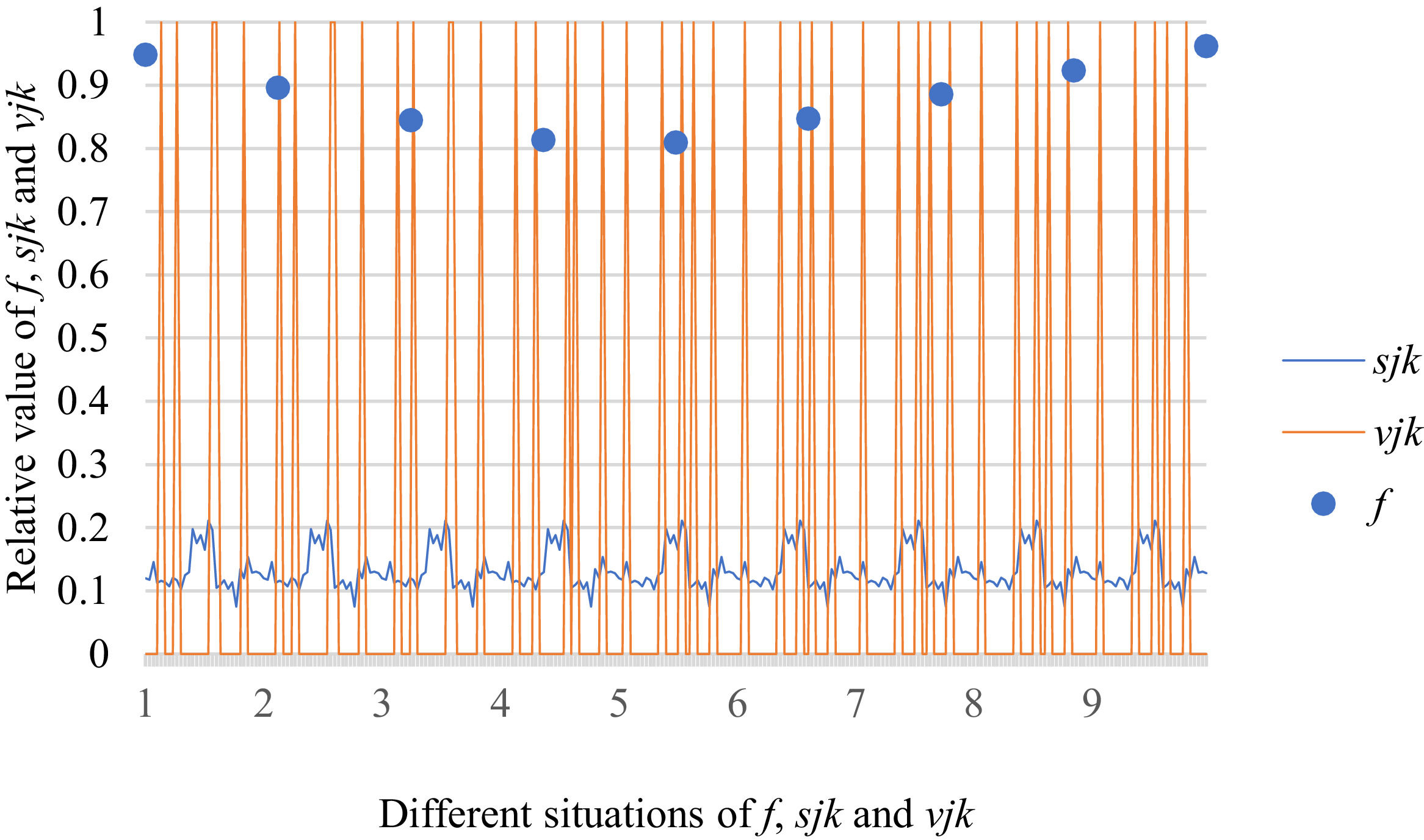
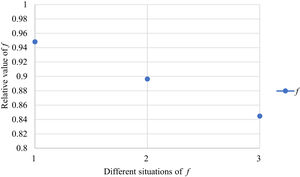
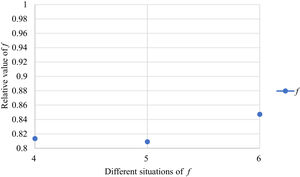
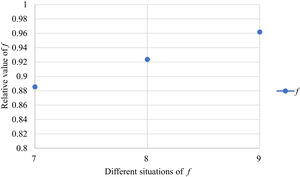
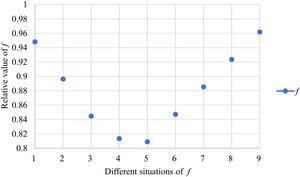
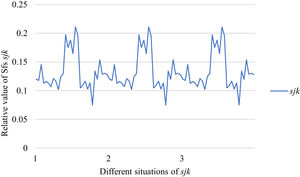
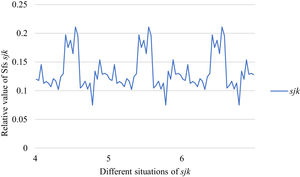
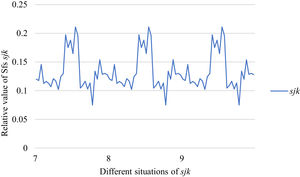
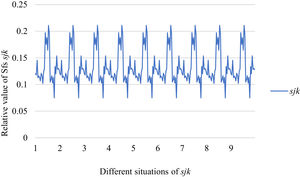
Fig. 10 reveals the tendencies of the relationships among SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 from Situation I to III. Fig. 11 reveals the tendencies of the relationships among SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 from Situation IV to VI. Fig. 12 reveals the tendencies of the relationships among SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 from Situation VII to IX. In light of Figs. 10-12, the overall tendencies of the relationships among SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 from Situation I to IX can be acquired, as displayed in Fig. 13. From the figure, we can see that SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 are different in some situations.

Fig. 10.

Relationships among SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 from Situation I to III.

(0.26MB).

Fig. 11.

Relationships among SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 from Situation IV to VI.

(0.29MB).

Fig. 12.

Relationships among SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 from Situation VII to IX.

(0.28MB).

Fig. 13.

Relationships among SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 from Situation I to IX.

(0.4MB).

As shown in Figs. 10-13, we further discuss the influence of the difference priorities on SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6. Fig. 13 shows a more comprehensive comparison and results. The results show that the priority difference of the bilateral agents has no significant impact on SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6.

Fig. 14 reveals the tendencies of the relationships among the objective function f, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 from Situation I to III. Fig. 15 reveals the tendencies of the relationships among the objective function f, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 from Situation IV to VI. Fig. 16 reveals the tendencies of the relationships among the objective function f, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 from Situation VII to IX. In light of Figs. 14-16, the overall relationships among the objective function f, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 from Situation I to IX can be acquired, as displayed in Fig. 17. From the figure, we can see that the objective function f is different in all situations; meanwhile, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 are different in some situations.

Fig. 14.

Relationships among the objective function f, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 from Situation I to III.

(0.25MB).

Fig. 15.

Relationships among the objective function f, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 from Situation IV to VI.

(0.27MB).

Fig. 16.

Relationships among the objective function f, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 from Situation VII to IX.

(0.27MB).

Fig. 17.

Relationships among the objective function f, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6 from Situation I to IX.

(0.41MB).

As shown in Figs. 14-17, we further discuss the influence of the different priorities of the bilateral agents on the objective functionf, SFs sF¯jχk and optimal BM matrix V=[vjk*]5×6. Fig. 17 shows a more comprehensive comparison and results. The results show that the different priorities of the bilateral agents will have a significant impact on the objective function value f in this experimental analysis but it has no significant impact on SFs sF¯jχk and the optimal BM matrix V=[vjk*]5×6 in this experimental analysis. Considering this experimental analysis, shows that the priority of the agent is only one of the factors affecting the determination of the optimal BM scheme but is not the decisive factor. However, if the same analysis is performed for the other examples, the results may not be exactly the same.

Examining the BM problem of knowledge innovation management under an interval intuitionistic fuzzy set environment, a matching decision-making method is proposed. In the method, the matching willingness of the bilateral agents is obtained by developing a novel algorithm, and a BM model considering IvIFSs and the matching willingness is constructed. The optimal BM scheme is obtained through the model solution. An enterprise knowledge management case study verifies the effectiveness of the presented BM method. The method proposed in this paper is applicable to a variety of intuitionistic fuzzy preference environments considering the matching willingness of the bilateral agents and can also be applied to other decision-making problems in enterprise knowledge innovation management.

Compared with the existing methods, the presented approach exhibits the following salient features: (1) The displayed approach uses the TOPSIS technology to compute the matching willingness directly on the basis of the IvIFS preferences, which can avoid information loss as much as possible. The computational algorithms of matching willingness can be regarded as a generalization of the existing approaches. (2) The displayed approach establishes the BM model using IvIFSs and matching willingness, which can mirror agents’ behaviours that are overlooked in some existing approaches. (3) The displayed approach uses a new optimization algorithm to solve the developed BM model, which is a new approach and supplement to the existing algorithms. (4) The gained BM scheme can reflect agents’ matching willingness, which has been overlooked in many existing approaches.

Future research will mainly focus on the following areas: (1) the BM problem with IvIFSs needs an in-depth study, where the matching willingness of a single agent towards the agents of the other side is not at the same level. (2) Considering that stable matching has an impact on the satisfaction of the bilateral agents and that an unstable BM scheme may reduce the satisfaction of the bilateral agents, we will additionally study the relevant theories and methods for stable matching in the IvIFS environment. (3) This paper mainly focuses on the IvIFS environment; therefore, the calculation algorithm of matching willingness under other intuitionistic fuzzy preferences needs to be further studied.