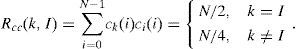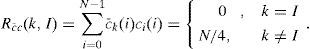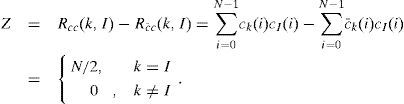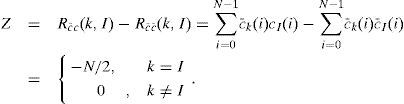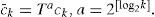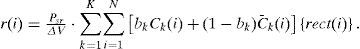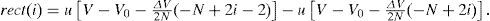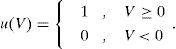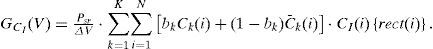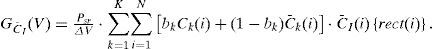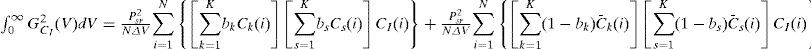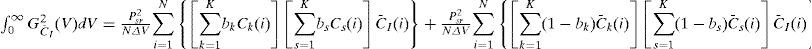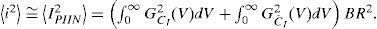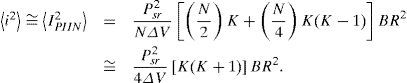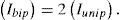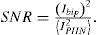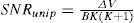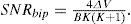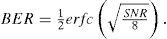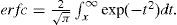This study analyzes and calculates dual unipolar and bipolar coded configurations of spectral-amplitude-coding optical code division multiple access (SAC-OCDMA) systems by using simulation methods. The important feature of the SAC-OCDMA systems is that multiple access interference (MAI) can be eliminated by code sequences of a fixed in-phase cross-correlation value. This property can be effectively canceled multiple access interference by using balance detection schemes. This study uses Walsh-Hadamard codes as signature codes for the unipolar and bipolar schemes. The coder and decoder structures are based on optical filters of fiber Bragg gratings (FBGs). The simulation results of unipolar/bipolar coding structures are first presented by commercial simulation obtained using OptiSystem software. The simulation results show that the bit error rate (BER) through use of the bipolar coding method is superior to the unipolar scheme, especially when the received effect power is large. When the system needs good performance to transmit multimedia data, we can use bipolar scheme in the network. If the users only transmit voice data, the unipolar method can be employed. The eye diagram also shows that the bipolar encoding structure exhibits a wider opening than the unipolar encoding structure. The flexible implementation of codewords assigns and integratable hardware designs for the scheme with FBGs to realize dual coding OCDMA system is proposed.
Optical code-division multiple access (OCDMA) systems are yielding increasingly more attention for applications in optical communications [1]. The advantage of OCDMA includes the ability for multiple users to access the network simultaneously and asynchronously with a high level of transmission security. Based on encoding schemes, the OCDMA system can be classified into (1) time domain and frequency domain encoding, and (2) spectral amplitude coding (SAC)-OCDMA systems, the latter of which are based on the frequency domain and have been receiving more attention over the past decade [2,3].
The important feature of the SAC-OCDMA systems is that multiple access interference (MAI) can be eliminated by code sequences of a fixed in-phase cross-correlation value. This property can be effectively canceled multiple access interference by using balance detection schemes [2-3, 5].
In recent years, fiber Bragg grating (FBG) has been widely used to implement in many systems such as sensor system [4] and coding system. The FBGs can realize the encoder and decoder for the SAC-OCDMA systems [5-7], and two different encoding structures of the SAC-OCDMA systems have been proposed. Using different encoding structures and signature codes influences the SAC-OCDMA system’s performance [8]. The main signature codes for the SAC-OCDMA systems are the M-sequence, MQC, and Walsh-Hadamard codes. This paper focuses on the SAC-OCDMA system for two encoding structures: bipolar and unipolar. This study also provides a comparison of the performance of the two encoding structures by using Walsh-Hadamard codes. A code with the length of N, the weight of w, and in-phase cross-correlation of λ is expressed as S(N, w, λ) [3,5].
The rest of this paper is organized as follows: Section 2 presents the Walsh-Hadamard codes’ construction and properties; Section 3 provides a description of the system; Section 4 details the system’s performance analysis and numerical results; Section 5 shows the simulation results; and lastly, Section 6 offers a conclusion.
2Code Construction and PropertiesThe SAC-OCDMA system assigns each user one spectral amplitude codeword Ck, and CK=(CK(0), CK(1),…, CK(N−1)), which is a sequence binary code of length N.
Let HN be an N×N Hadamard matrix in {0,1} unipolar form. The Walsh-Hadamard codes have the property that any two different row sequence code’s cross-correlation from HN is exactly N/4, where N is the number of optical sources divided into the optical spectrum. Every user codeword is obtained by selecting the rows of a Walsh-Hadamard matrix. All rows contain N / 2 “0” and N / 2 “1”. For example, the codeword for user k, where k ∈{0,1,...,N−1} and N=4, is as follows:
The first row, comprising bit “1”, cannot be used in spectral codes. Hence, only N-1 sequence codes are in our coding systems. If some code families have the property of Rcc(k,I)=Rc¯c(k,I) for k ≠l, then the influence of MAI from other users is cancelled by computing Rcc(k,I)-Rc¯c(k,I).
The cross-correlation between Ck and Cl is expressed by the following:
and
A balanced detector of the decoder for user #k implements the correlation subtractions, expressed as follows:
The MAI coming from other users is shown to be completely cancelled. In addition, the Walsh-Hadamard codes also have a property for a complementary coding scheme, which is expressed as follows:
In the system adopting the complementary Walsh-Hadamard codes method, user #k sends Ck for bit “1” and c¯k for bit “0” when the encoder uses the bipolar encoding structure. The codeword Ck and its complement c¯k can be found to have the following relationship:
where T is the operator shifting vectors cyclically to the right by one place (e.g., TCK=(CK(N−1), CK(0), CK(1),…, CK (N−2))).
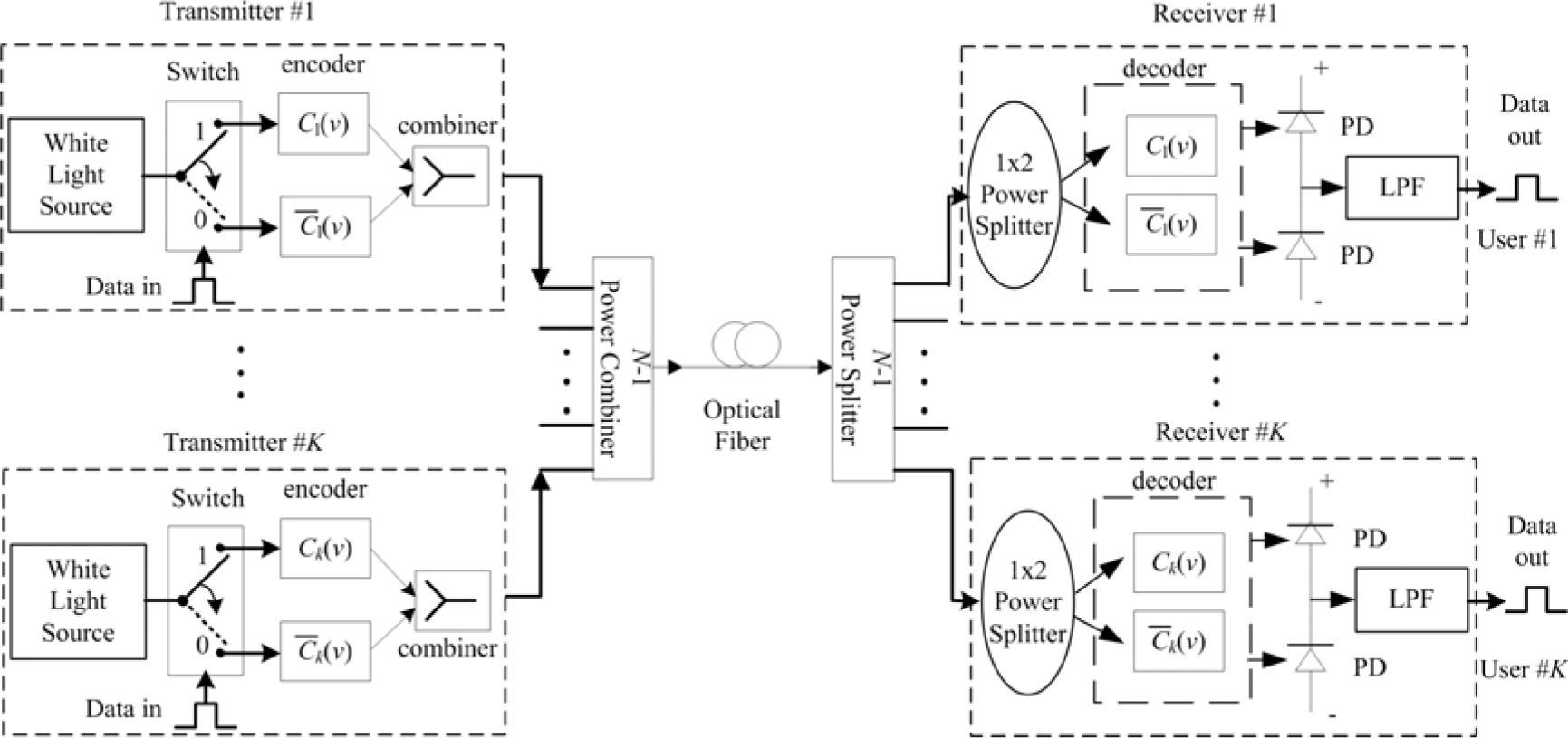
3System DescriptionA block diagram has been proposed for the use of the Walsh-Hadamard codes in a bipolar encoding structure for the SAC-OCDMA system, as shown in Fig. 1[5].
We use a series of FBGs in the system architecture because each FBG has its central wavelength, the component of the central wavelength is reflected and the rest of the wavelength is transmitted.
At the transmitter, the spectrum of white light sent to user #k’s spectral component can be expressed as Ck when the data bit is “1”; in contrast, it sends c¯k (the complementary spectral component of user #k) when the data bit is “0”. All of the transmitter’s signals are collected by the power combiner. Then the signal is broadcast to the power splitter via the optical fiber.
With the unipolar encoding structure for the SACOCDMA system, the user #k spectral is sent to the spectral component when the data bit is “1”. However, when the data bit is “0”, it does not send any spectral component.
At the receiver, the power splitter divides the received signal into k-th (N-1) parts. In each user’s receiver, the code spectrum is split into two by a 1×2 power splitter, and then enters two ports of spectral decoders: the direct decoder (at the additive branch) and the complementary decoder (at the subtractive branch). The direct decoder has the same spectral characteristics as user #k (Ck(i)), and the complementary decoder has the complementary wavelength component of user #k(c¯k(i)). The outputs from these decoders are detected by two photodetectors; the MAI is effectively cancelled by balanced photodetection. The low-pass filter (LPF) is then used to recover the original data.
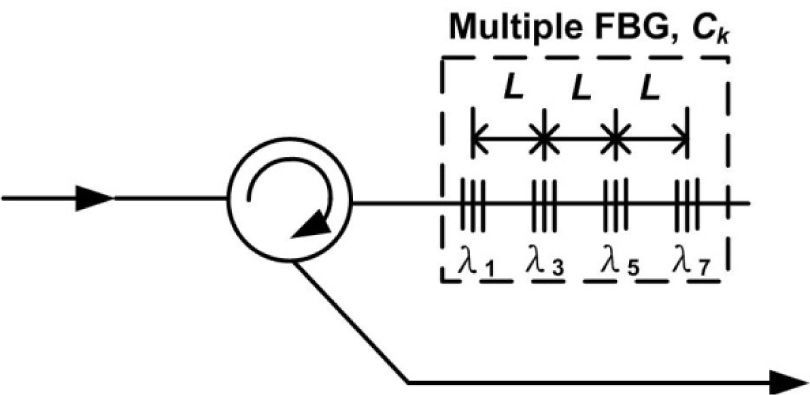
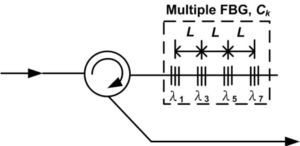
The encoder and decoder structures are proposed based on a series of FBGs with Walsh-Hadamard codes, as shown in Figs. 2 and 3, respectively [6]. When a broadband source passes through a series of FBGs, the spectral components are reflected back according to the user #k codeword sequence CK(i), and all of the complementary spectral of user #k (i.e., c¯k(i) code) pass the FBGs to the output, as shown in Fig. 2.
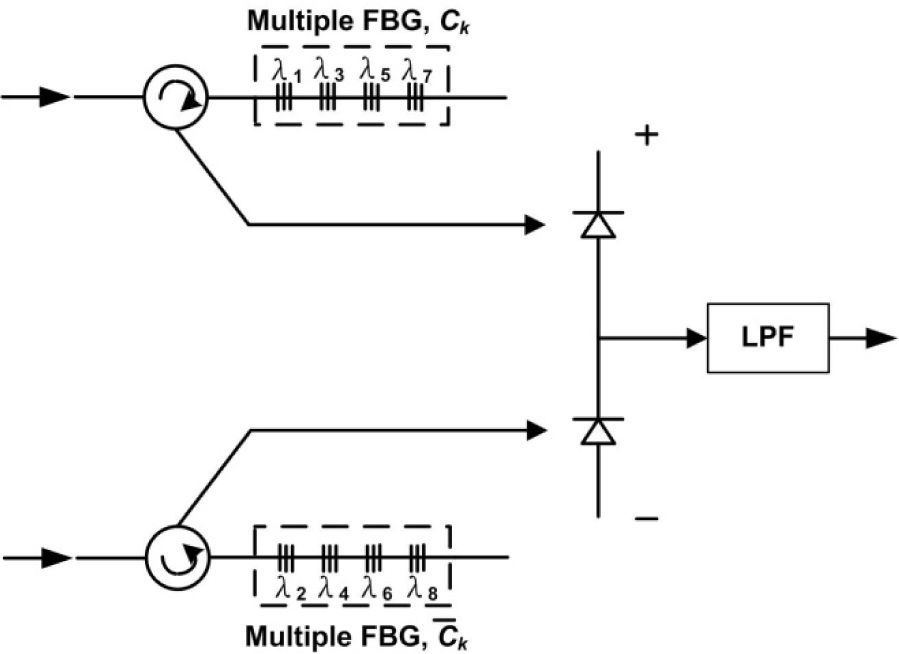
In the decoder shown in Fig. 3, we use a series of FBGs to reflect the spectral of user #k, so that the upper photodetector signal is r(i)Ck(i), where r(i) is the receiver signal and Ck(i) is the user #k codeword sequence. In contrast, the bottom photodetector signal is r(i)C¯k(i), where C¯k(i) is user #k’s complementary codeword sequence.
4System Performance AnalysisThe proposed system contains three types of noise: contained shot noise, thermal noise, and phase-induced intensity noise (PIIN). This study only considers the dominant noise of PIIN; thus, the variance of the photocurrent effect by the PIIN can be expressed by the following:
where I is the average photocurrent; B is the receiver’s noise-equivalent electrical bandwidth; τc is the coherence time of source.
The power spectral density (PSD) of the received optical signals can be expressed by the following:
where Psr is the effective power from the source power at the receiver, K is the number of the user, and bk is the data bit of user #k. The rect(i) function in Eq. (8) is expressed by the following:
where u(v) is a step function expressed by the following:
Therefore, the PSD at the PDCl and PDc¯I of the l-th receiver with one bit can be expressed by the following:
And
The balance calculations of the output current Ibip can be expressed by the following:
where R is the photodiode responsivity.
Using (10) and (11) yields the following:
And
The noise at PDCl and PDc¯I is independent; thus, the power of noise in the photocurrent can be expressed by the following:
When the user data is bit “1”, substituting Eqs. (13) and (14) into Eq. (15) yields the following:
An assumption of the user data bit’s probable occurrence of “0” and “1” leads to the following:
The system performance of signal-to-PIIN noise ratio (SNR) can be expressed as follows:
By using (12), (16), (17) and (18), we can calculate the SNR for the unipolar and bipolar encoding structures with the following:
and
Based on the approximation of the Gaussian distribution, the bit-error rate (BER) expression of the SAC-OCDMA system can be expressed as follows:
where erfc is the complementary error function, which can be expressed by the following:
5Simulation ResultsIn the simulation setup, we compare the performance of the unipolar and bipolar schemes for the SAC-OCDMA systems by OptiSystem software version 7.0 with the following parameters: the code length of the Walsh-Hadamard codes is 8, and the data bit rate is 200 Mbs. The data bit source we adopted was a PRBS generator component to generate random binary codes, and the sequence code is 210 – 1. The transmission link is a signal mode fiber with no attenuation, and the dispersion influence. The central wavelength of the optical fiber is set to 1550 nm, and the transmission distance is 20km. The bandwidth of each wavelength is equal to 0.4 nm.
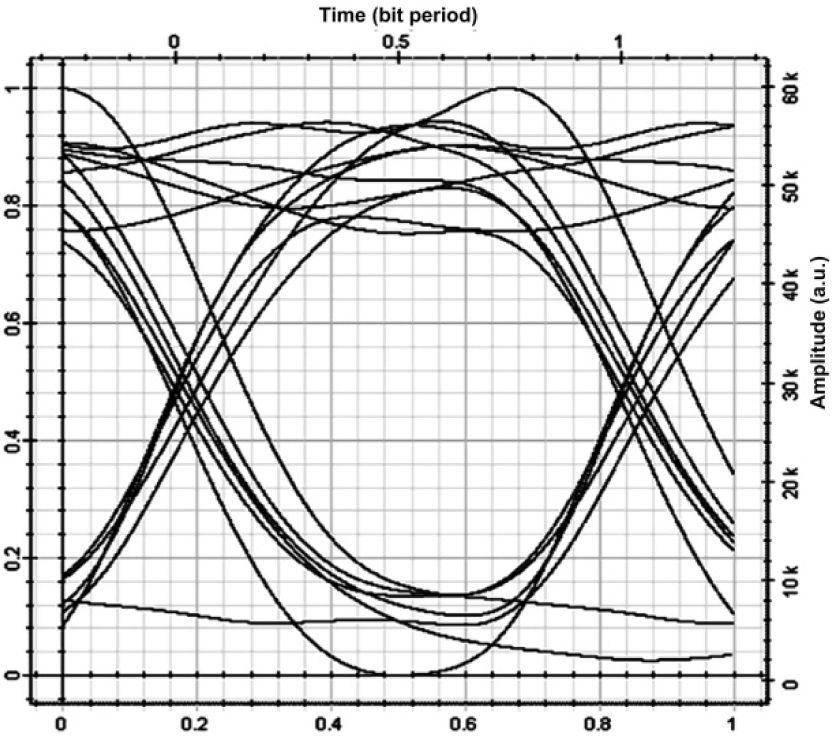
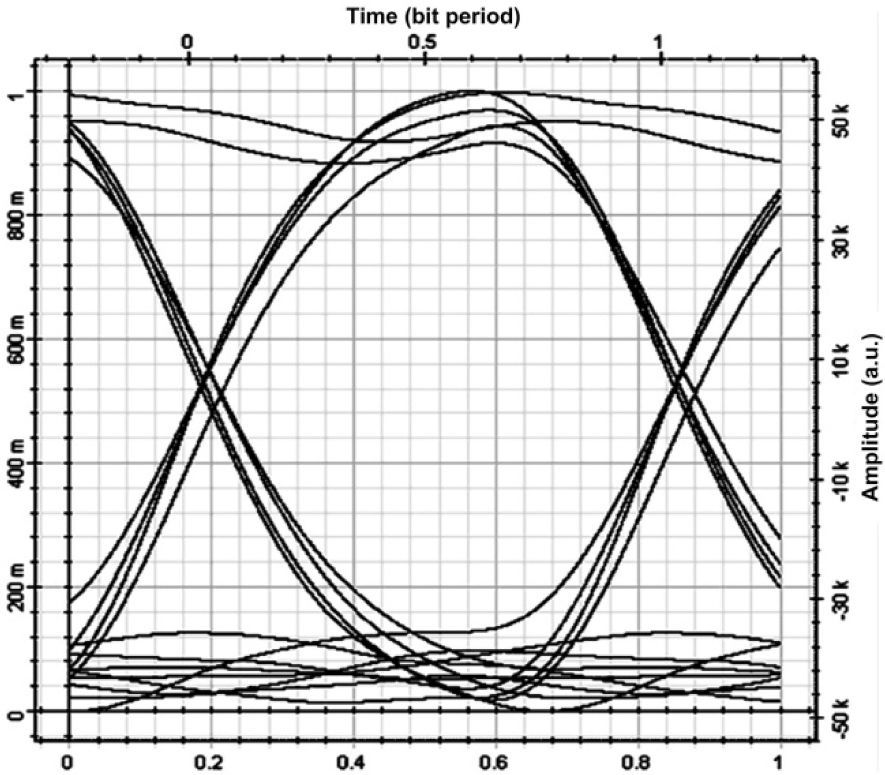
There are three simultaneous active users to analyze the performance of unipolar/bipolar encoding structures in SAC-OCDMA network. Figs. 4 and 5 present the eye diagrams of the unipolar and bipolar encoding structures in our proposed SAC-OCDMA systems, respectively. A comparison between these two figures shows that the eye opening for the SAC-OCDMA system with the bipolar encoding structure is significantly greater than that of the common ones with the unipolar encoding structure.
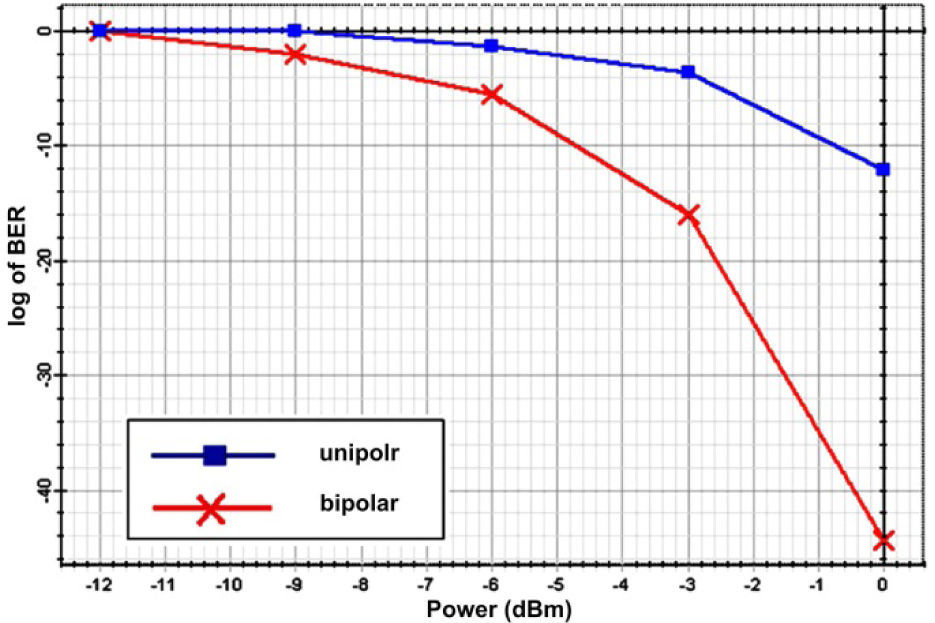
Furthermore, the simulation result indicates that the bit-error-rate (BER) of the bipolar encoding structure is smaller than the unipolar encoding structure shown in Fig. 6.
Fig. 6 shows the user BER relative to the white light source power of the unipolar and bipolar encoding structures. The figure shows that the BER curves indicate that when the white light source power is increased, the BER performance in both the unipolar and bipolar systems is decreased. However, the BER of the bipolar encoding structure can be enhanced strongly when the transmitted source is larger than -3 dBm. For this reason, we can infer that the bipolar encoding structure is more suitable for high transmission rate system such as video data, and unipolar coding structure can be used in low data rate scenarios such as audio data in our duo spectral Walsh-Hadamard codes based on SAC-OCDMA systems.
6ConclusionsThis study presents dual coding OCDMA system performance induced by PIIN effects, and demonstrates the simulation result of unipolar and bipolar SAC-OCDMA systems. The results indicate that, for the bipolar encoding structure of the SACOCDMA system, BER performance is superior to that of the unipolar method. The advantage in the system can choice bipolar or unipolar coding method depends on which data formats are transmitted. If we need good performance the bipolar scheme is employed, or we can use unipolar technique for low data rate such as voice data. The bipolar coding scheme’s eye diagrams show wider openings than the unipolar encoding structures. The simulation and the mathematical derivation results show the same trends as these two systems. In conclusion, when SAC-OCDMA systems use bipolar coding schemes, they have superior performance and spectral efficiency to the unipolar encoding structures in the same code family. Besides, the proposed structure can use dual unipolar/bipolar coding method at the same time without changing the decoding structures on the receiver end.
AcknowledgementsThis work was supported in part by the National Science Council under Grant No. NSC 101-2221-E-150-066-.