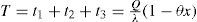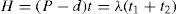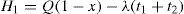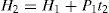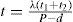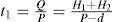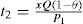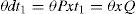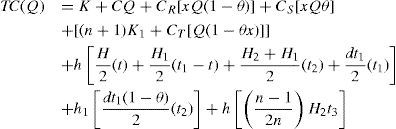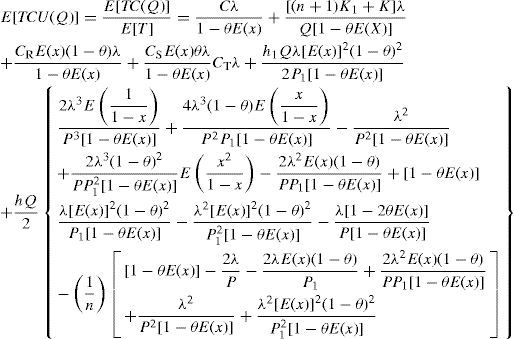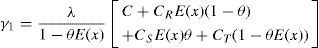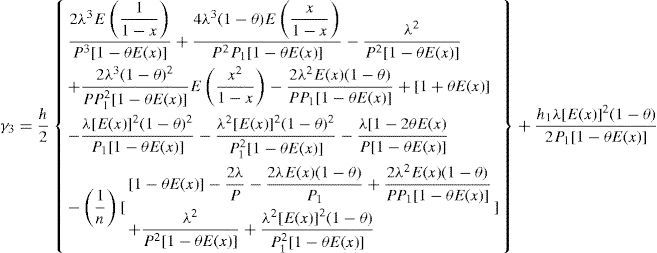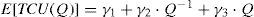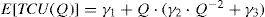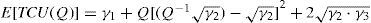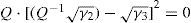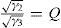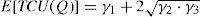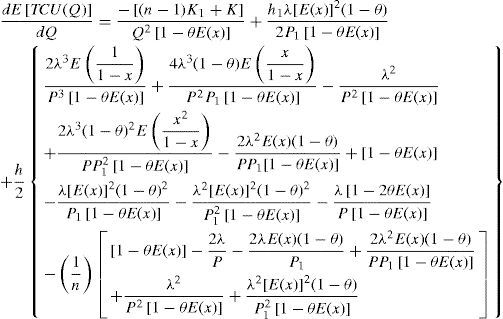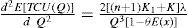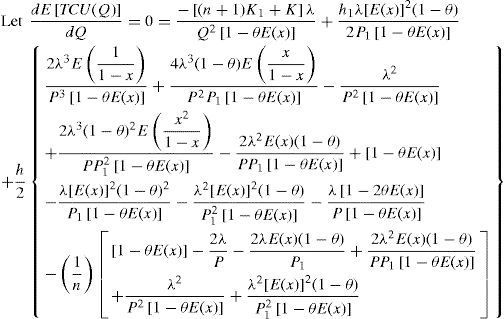A conventional approach for solving an economic production quantity (EPQ) model with multi-delivery policy and quality assurance is to use mathematical modeling for deriving the system cost function and to employ differential calculus for proving convexity of the cost function before determining the optimal operating policy. This paper presents a simplified solution procedure to reexamine a specific EPQ model [1] and demonstrates that both, the optimal manufacturing lot size and the long-run cost function can be derived without derivatives. The proposed approach may enable practitioners—with little knowledge of calculus—to understand such a real life vendor-buyer integrated system with ease.
This paper proposes a simplified solution procedure for deriving the optimal replenishment lot size as well as the optimal total system cost for an imperfect economic production quantity (EPQ) model with discontinuous issuing policy. The EPQ model was first introduced by Taft, 1918[2] to assist manufacturing firms to determine the most economic production lot size that minimizes the long-run average production-inventory cost. Thereafter, it has been often adopted by production and inventory control practitioners to help them in their routine decision-makings [3], such as when to initiate a production run and how large a replenishment lot size should be. During the past decades, based on the concept of EPQ, many production systems with imperfect quality items, unreliable machine, and more complicated or practical features have been extensively studied (see Shih [4], Rosenblatt and Lee [5], and others [6-19]).
Recently, because supply chains management has received broad attentions by practitioners as well as by academic scholars, studies that incorporate multiple or periodic deliveries of finished items into EPQ models (i.e., situations in real-life vendor-buyer integrated system in supply chains environment) have been extensively carried out. Schwarz [20] studied a one-warehouse N-retailer deterministic inventory system with the objective of determining the stocking policy which minimizes the long-run average system cost per unit time. Goyal [21] investigated the integrated inventory model for a single supplier-single customer problem. He proposed a method that is typically applicable to those inventory problems where a product is procured by a single customer from a single supplier. He gave an example to illustrate his proposed method. Many different vendor-buyer models with various practical features have been broadly examined ever since (see Banerjee [22], Hahm and Yano [23], and others [24-29]).
Chiu et al. [1] studied an EPQ model with a (n+1) multi-delivery policy and partial reworking of defective items produced. They derived the optimal replenishment lot size by the conventional approach. That is, by using differential calculus on the long-run average cost function with the need to prove optimality first. Grubbström and Erdem [30] proposed the algebraic approaches to solve the economic order quantity (EOQ) model with backlogging without reference to the use of derivatives. This study adopted such a similar solution procedure to reexamine the problem in Chiu et al. [1] and demonstrated that the optimal batch size and a straightforward formula for total system costs for such a particular EPQ model can be derived without derivatives.
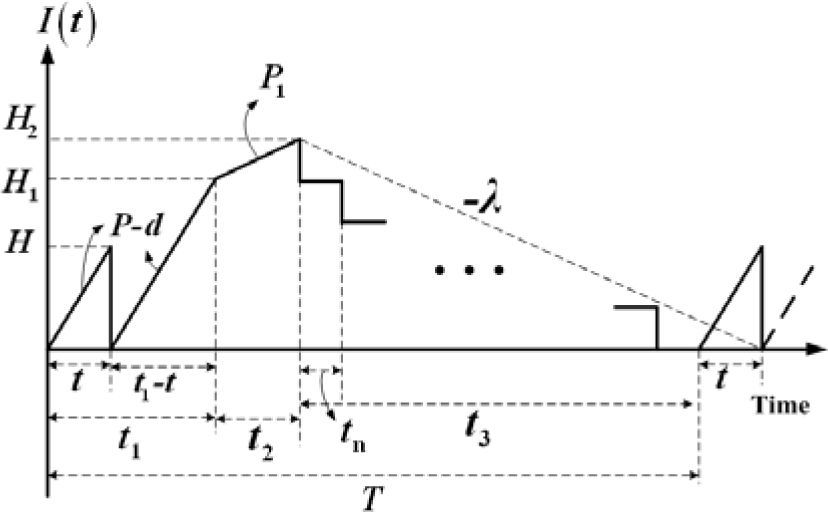
2Problem description and formulationReconsider the EPQ model [1] with a (n+1) multi-delivery policy and partial rework. It is assumed that a manufacturing system may randomly produce x portion of defective items at a production rate d. No shortages are allowed in the system; hence, it is assumed that the constant annual production rate P has to be larger than the sum of annual demand rate λ and production rate of defective items d. That is, (P-d-λ)>0, where d can be expressed as d=Px. Among nonconforming items a θ portion is scrap and the other (1-θ) portion can be repaired at a rework rate P1, which is done within the same cycle when regular production process ends. A (n+1) delivery policy is adopted (see Figure 1). Under such policy, an initial delivery of finished items is distributed to the buyer to satisfy the product demand during the producer regular production time and rework time. At the end of the rework time, a fixed quantity of n installments of the finished products, are delivered to the customer at a fixed interval of time. In comparison with the first delivery starts after rework process, this (n+1) delivery policy can lower holding costs for both vendor and buyer (see Figure 2 in Chiu et al. [1]). To ease readability, in this paper we adopted the same notation from the modeling sections in Chiu et al. [1]:
On-hand inventory of perfect quality items in EPQ model with (n+1) delivery policy and partial rework [1].
C=unit production cost,
h=holding cost per item per unit time in producer’s side,
K=setup cost per production run,
CR=unit rework cost,
CS=unit disposal cost,
h1=holding cost or each reworked item,
K1=fixed delivery cost per shipment,
CT=variable delivery cost per item,
Q=production lot size to be determined for each cycle,
H=the level of on-hand inventory in units to satisfy product demand during manufacturer’s regular production time t1 and rework time t2,
H1=maximum level of on-hand inventory in units when regular production ends,
H2=the maximum level of on-hand inventory in units when rework process finishes,
T=cycle length,
t=the production time needed for producing enough perfect items to satisfy product demand during t1 and t2,
t1=the production uptime for the proposed EPQ model,
t2=time required for reworking of defective items,
t3=time required for delivering the remaining quality assured finished products,
n=number of fixed quantity installments of the finished batch to be delivered to customer during t3,
tn=a fixed interval of time between each installment of products delivered during t3,
I(t)=on-hand inventory of perfect quality items at time t,
TC(Q)=total production-inventory-delivery costs per cycle for the proposed model,
E[TCU(Q)]=the long-run average costs per unit time for the proposed model.
The following basic formulas can be obtained according to the model description and to Figure 1.
TC(Q) (Equation 10) consists of setup cost, variable production and rework cost, disposal cost, fixed and variable delivery cost, holding costs for finished products during t1 and t2, holding costs for defective items during t1, for reworked items during t2, and for finished products during t3.
The expected E[TCU(Q)] can be derived by taking into account the randomness of defective rate x, and substituting all related parameters from Equations 1 to 9 in TC(Q) as follows [1].
3The proposed simplified solution procedureUnlike conventional method applying differential calculus to the long-run average cost function E[TCU(Q)] with the need of proving its optimality, this paper uses a simplified algebraic approach for solving such a specific EPQ model.
Let γ1, γ2, and γ3 denote
Equation 11 becomes
or
With further rearrangement of Equation 16 we have
Therefore, we obtain
Notice that if the second term of Equation 18 equals zero then E[TCU(Q)] is minimized.
That is
or
Substituting Equations 13 and 14 in Equation 20 and with further derivations, we derive the optimal replenishment lot size as
Notice that Equation 21 is identical to Q* in Chiu et al. [1], which was derived using the conventional differential calculus approach (see Appendix). Furthermore, let us suppose in Equation 18, that the optimal replenishment lot size Q* is used, E[TCU(Q*)] becomes
3.1Numerical example with further verificationTo enable users to easily compare research results obtained in this paper to those that were given in Chiu et al. [1], in this section we adopted the same numerical example as used in their paper. Consider that a product can be made at an annual rate of 60,000 units, and this item has a stable annual demand rate of 3,400 units. During production process, a random defective rate x is assumed to follow uniform distribution over the interval [0, 0.3]. Among nonconforming items a portion θ=0.1 is considered to be scrap and other portion can be repaired, at a rework rate P1=2,100 units per year. Additional parameters include C=$100, K=$20,000, K1=$4,350, h=$20, h1=$40, CS=$20, CR=$60, and CT=$0.1.
Case 1. Suppose n=4 and the proposed (n+1) delivery policy has a total of five shipments. From computations of Equations 21 and 22, we obtain the optimal replenishment lot size Q*=3495 and E[TCU(Q*)]=$436799.
Case 2. Let n=3 and the proposed (n+1) delivery policy has a total of four shipments as it was analyzed in Chiu et al.’s second scenario. Applying Equations 21 and 22, once again, we have Q*=4219 and E[TCU(Q*)]=$435712.
We noticed that both of the aforementioned results are identical to those given in Chiu et al. [1]. Furthermore, for the computation of the long-run average costs per unit time E[TCU(Q*)], the proposed Equation 22 is simpler than Equation 11.
4ConclusionsThis research note presents a simplified solution procedure to reexamine the problem in Chiu et al. [1]. We demonstrated that both, an optimal replenishment lot size and a straightforward formula for the long-run average cost function for such a particular EPQ model can, be derived without derivatives. This alternative approach may enable practitioners—with little knowledge of calculus—to understand and manage such a real-life vendor-buyer integrated problem with ease.
The authors greatly appreciate the support of the National Science Council (NSC) of Taiwan under grant number: NSC-100-2410-H-324-007-MY2.
To show that Equation 21 is identical to Q* as was derived by the use of differential calculus approach [1], we can differentiate E[TCU(Q)] (Equation 11) with respect to Q, the first and the second derivatives of E[TCU(Q)] are shown in Equations A-1 and A-2.
Equation A-2 results positive [1], so E[TCU(Q)] is a convex function for all Q different from zero. The optimal lot size Q* can be obtained by setting first derivative of E[TCU(Q)] equal to zero (see Equation A-1)
With further rearrangement, we can obtain Q* identically as shown in Equation 21.




![On-hand inventory of perfect quality items in EPQ model with (n+1) delivery policy and partial rework [1]. On-hand inventory of perfect quality items in EPQ model with (n+1) delivery policy and partial rework [1].](https://static.elsevier.es/multimedia/16656423/0000001100000003/v2_201505081636/S1665642313715414/v2_201505081636/en/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)