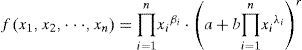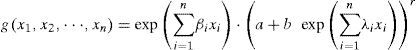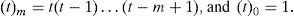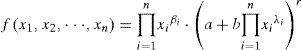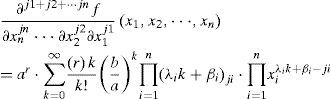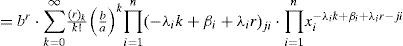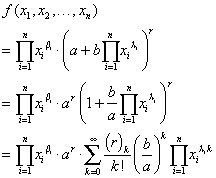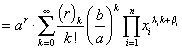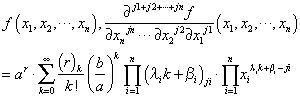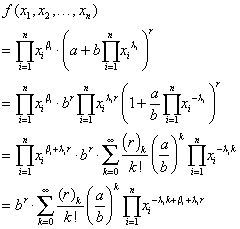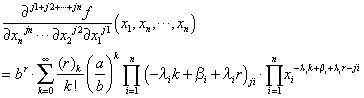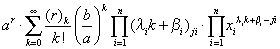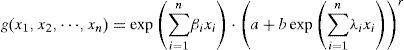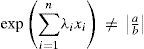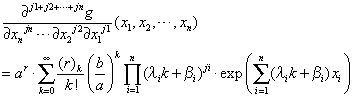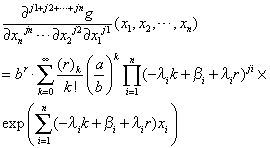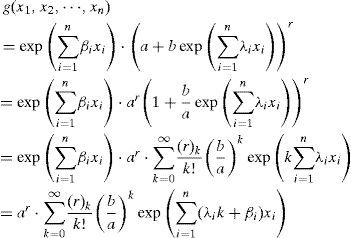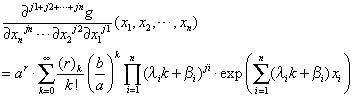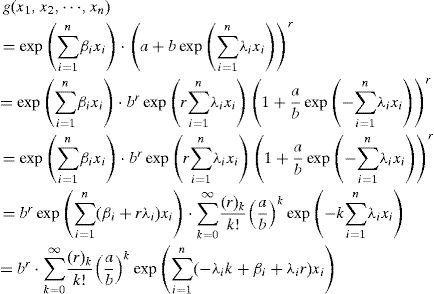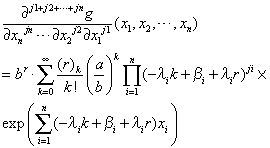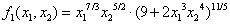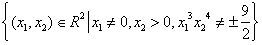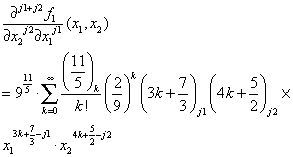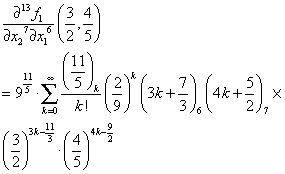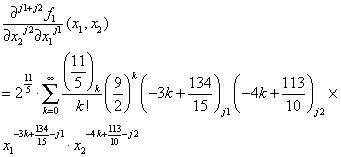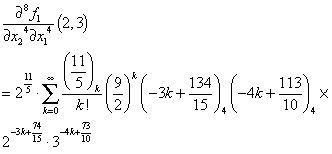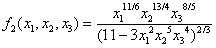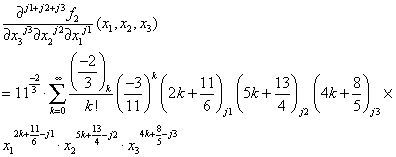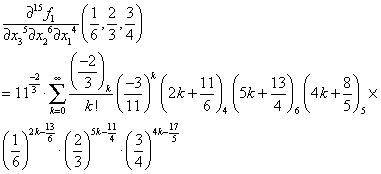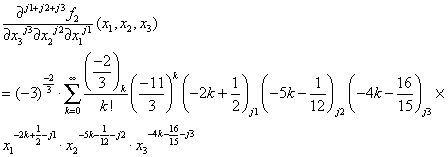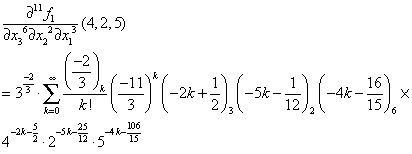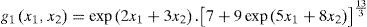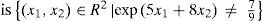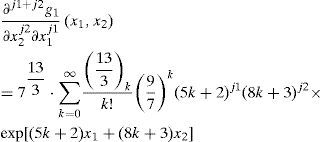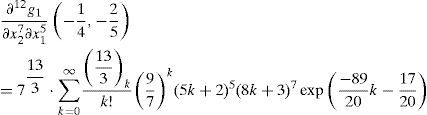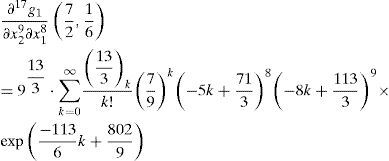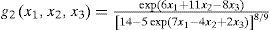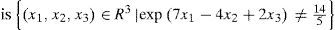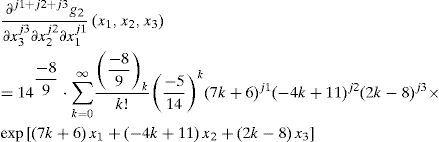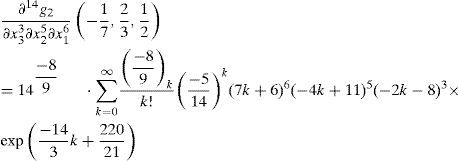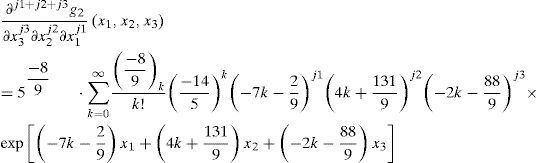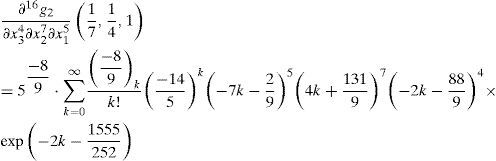This paper considers the partial differential problem of two types of multivariable functions and uses mathematical software Maple for verification. The infinite series forms of any order partial derivatives of these two types of multivariable functions can be obtained using binomial series and differentiation term by term theorem, which greatly reduce the difficulty of calculating their higher order partial derivative values. On the other hand, four examples are used to demonstrate the calculations.
In calculus and engineering mathematics, the evaluation and numerical calculation of the partial derivatives of multivariable functions are important. The Laplace equation, the wave equation, and other important physical equations involve the partial derivatives. The evaluation of the m -th order partial derivative value of a multivariable function at some point, generally, requires two procedures: the determination of the m -th order partial derivative of the function, and the substitution of the point into the m -th order partial derivative. These two procedures become increasingly complex calculations for increasing order of partial derivative, thus manual calculations become difficult. The present study considers the partial differential problem of the following two types of n -variables functions
where n is a positive integer, a, b,r, βi, λi are real numbers for all i = 1,..,n, a,b ≠ 0, and ar, br exist. We can obtain the infinite series forms of any order partial derivatives of these two types of multivariable functions using binomial series and differentiation term by term theorem; these are the major results of this study (i.e., Theorems 1 and 2), which greatly reduce the difficulty of calculate their higher order partial derivative values. The study of partial differential problems can refer to [1-24]. The methods adopted in [1-5] are different from the methods used in this paper, and [6-24] studied the evaluation of the partial derivatives of different types of multivariable functions using differentiation term by term theorem and complex power series method. [25] considered two differential equations whose independent variables involve the partial derivatives. [26] discussed the distance functions whose expressions contain the partial derivatives, and [27] found the solutions of some type of partial differential equation. In this article, some examples are used to demonstrate the proposed calculations, and the manual calculations are verified using Maple.
2Main ResultsSome notations used in this paper are introduced below.
2.1Notations2.1.1∏i=1nci=c1×c2×…×cn where n is a positive integer, ci are real numbers for all i = 1,.., n.
2.1.2Suppose that t is any real number, and m is any positive integer. Define
2.1.3Suppose that n is a positive integer, ji are non-negative integers for all i = 1,.., n. For the n- variables function f(x1, x2, …, xn), its ji times partial derivative with respect to xi for all i = 1,.., n, forms a j1 + j2 + … + jn -th order partial derivative, denoted as ∂j1+j2+⋅⋅⋅jnf∂xnjn⋅⋅⋅∂x2j2∂x1j1x1,x2,⋅⋅⋅,xn
The followings are two important theorems used in this study.
2.2Binomial series(1+u)r=∑k=0∞(r)kk!uk, where u,r are real numbers, and |u|<1.
2.3Differentiation term by term theorem ([28, p230]).For all non-negative integers k, if the functions gk:(a,b)→R satisfy the following three conditions: (i) there exists a point x0 ∈ (a, b) such that ∑k=0∞gk(x0) is convergent, (ii) all functions gk(x) are differentiable on the open interval (a, b), and (iii) ∑k=0∞ddxgk(x) is uniformly convergent on (a,b), then ∑k=0∞gk(x) is uniformly convergent and differentiable on (a,b). Moreover, its derivative ddx∑k=0∞gk(x)=∑k=0∞ddxgk(x).
The following is the first major result in this study, we determine the infinite series forms of any order partial derivatives of the n -variables function (1).
2.4Theorem 1Suppose that n is a positive integer, a, b,r,λi,βi are real numbers for all i = 1,.., n, a, b≠0, and ar,br exist. If the n -variables function
satisfies that xiβi,xiλi,xiλir exist, xi ≠ 0 for all i = 1,.., n, and ∏i=1nxiλi≠±ab.
Case A. If ∏i=1nxiλi
Case B. If ∏i=1nxiλi>ab∂j1+j2+⋅⋅⋅jnf∂xnjn⋅⋅⋅∂x2j2∂x1j1x1,x2,⋅⋅⋅,xn
Proof Case A. ∏i=1nxiλi>ab
Because
(Because ∏i=1nxiλi
By differentiation term by term theorem, differentiating ji-times with respect to xi (i = 1,..,n) on both sides of Equation (5), we have: the j1 + j2+ … + jn-th order partial derivative of
Case B. If ∏i=1nxiλi>ab
Because
Using differentiation term by term theorem, differentiating ji -times with respect to xi (i = 1,..,n) on both sides of Equation (6), we obtain:
2.5Remark 1If ∏i=1nxiλi
is uniformly convergent. Thus, we can use differentiation term by term theorem to prove Equation (3) holds. The same reason that we can employ differentiation term by term theorem to confirm Equation (4) holds.
The following is the second major result in this study, we obtain the infinite series forms of any order partial derivatives of the n -variables function (2).
2.6Theorem 2If the assumptions are the same as Theorem 1. Suppose that the n-variables function
satisfies that a+bexp∑i=1nλixir exists, and
Case A. If exp∑i=1nλixi
Case B. If exp∑i=1nλixi>ab, then
Proof Case A. exp∑i=1nλixi Because
By differentiation term by term theorem, differentiating ji-times with respect to xi (i = 1,..,n) on both sides of Equation (9), we obtain: the j1 + j2 + … + jn -th order partial derivative of g(x1,x2,…,xn),
Case B. exp∑i=1nλixi>ab
Because
Using differentiation term by term theorem, differentiating ji-times with respect to xi (i = 1,..,n) on both sides of Equation (10), we obtain:
2.7Remark 2The same reason as that in Remark 1, we can use differentiation term by term theorem to prove Equations (7) and (8) hold.
3ExamplesFor the partial differential problem of the multivariable functions in this study, four examples are proposed. Theorems 1 and 2 are used to obtain the infinite series forms of any order partial derivatives of these functions, and to evaluate some of their higher order partial derivative values. Additionally, Maple is used to calculate the approximations of these higher order partial derivative values to verify the manual calculations.
3.1Example 1Suppose that the domain of the two-variables function
is3.1.1If x13x24>92. Using Case A of Theorem 1 yields: any j1 +j2-th order partial derivative of f1(x1, x2),
Therefore, the 13-th order partial derivative value of f1(x1,x2) at 32,45
Next, we use Maple to verify the correctness of Equation (13).
>f1:=(x1,x2)->x1^(7/3)*x2^(5/2)*(9+2*x1^3*x2^4) ^(11/5);
>evalf(D[1$6,2$7](f1)(3/2,4/5),22);
7.123326797821678044703.1011
>evalf(9^(11/5)*sum(product(11/5-j,j=0..(k-1))/k!* (2/9)^k*product(3*k+7/3-p,p=0..5)*product(4*k+5/2-q,q=0..6)*(3/2)^(3*k-11/3)*(4/5)^(4*k-9/2),k=0.. infinity),22);
7.123326797821678044705. 1011
3.1.2If x13x24>92. By Case B of Theorem 1, the j1 +j2 -th order partial derivative of f1(x1,x2),
Thus, the 8-th order partial derivative value of f1(x1,x2) at (2,3),
>evalf(D[1$4,2$4](f1)(2,3),18);
1.11843022977422795.1013
>evalf(2^(11/5)*sum(product(11/5-j,j=0..(k-1))/k!*(9/2)^k*product(-3*k+134/15-p,p=0..3)*product(-4* k+113/10-q,q=0..3)*2^(-3*k+74/15)*3^(-4*k+73/10), k=0..infinity),18);
1.11843022977422796.1013
3.2Example 2Assume that the domain of the three-variables function
is (x1,x2,x3)∈R3x1>0,x2>0,x3≠0,x12x25x34≠±113
3.2.1If x12x25x34<113. Using Case A of Theorem 1, we obtain: any j1 + j2 + j3-th order partial derivative of f2(x1,x2,x3),
Thus, the 15-th order partial derivative value of f2(x1, x2, x3) at 16,23,34
>f2:=(x1,x2,x3)->x1^(11/6)*x2^(13/4)*x3^(8/5)/((11-3*x1^2*x2^5*x3^4)^2)^(1/3);
>evalf(D[1$4,2$6,3$5](f2)(1/6,2/3,3/4),14);
5.3261668131349.107
>evalf(11^(-2/3)*sum(product(-2/3-j,j=0..(k-1))/k!*(-3/11)^k*product(2*k+11/6-p,p=0..3)*product(5*k+ 13/4-q,q=0..5)*product(4*k+8/5-s,s=0..4)*(1/6)^(2* k-13/6)*(2/3)^(5*k-11/4)*(3/4)^(4*k-17/5),k=0.. infinity),14);
5.3261668131350.107
3.2.2If x12x25x34>113. Using Case B of Theorem 1 yields: any j1+j2+j3-th order partial derivative of f2(x1,x2,x3),
Hence, the 11-th order partial derivative value of f2(x1,x2,x3) at (4,2,5),
>evalf(D[1$3,2$2,3$6](f2)(4,2,5),14);
-0.000019108587954897
>evalf(3^(-2/3)*sum(product(-2/3-j,j=0..(k-1))/k!*(-11/3)^k*product(-2*k+1/2-p,p=0..2)*product(-5*k-1/12-q,q=0..1)*product(-4*k-16/15-s,s=0..5)*4^(-2*k-5/2)*2^(-5*k-25/12)*5^(-4*k-106/15),k=0.. infinity),14);
-0.000019108587954897
3.3Example 3If the domain of the two-variables function
3.3.1If exp(5x1+8x2)<79. By Case A of Theorem 2, we obtain: any j1+j2-th order partial derivative of g1(x1,x2),
Therefore, the 12-th order partial derivative value of g1(x1,x2) at −14,−25
>g1:=(x1,x2)->exp(2*x1+3*x2)*(7+9*exp(5*x1+8* x2))^(13/3);
>evalf(D[1$5,2$7](g1)(-1/4,-2/5),22);
5.855345231176575279854.1014
>evalf(7^(13/3)*sum(product(13/3-j,j=0..(k-1))/k!* (9/7)^k*(5*k+2)^5*(8*k+3)^7*exp(-89/20*k-17/10), k=0..infinity),22);
5.855345231176575279879.1014
3.3.2If exp (5x1+8x2)>79.. Using Case B of Theorem 2 yields: any j1 + j2-th order partial derivative of g1(x1,x2),
Therefore, we can determine the 17-th order partial derivative value of g1(x1, x2)at 72,16,
Maple was used to verify the correctness of Equation (25):
>evalf(D[1$8,2$9](g1)(7/2,1/6),22);
1.028551772875461091101.1068
>evalf(9^(13/3)*sum(product(13/3-j,j=0..(k-1))/k!*(7 /9)^k*(-5*k+71/3)^8*(-8*k+113/3)^9*exp(-113/6*k+ 802/9),k=0..infinity),22);
1.028551772875461091120.1068
3.4Example 4Suppose that the domain of the three-variables function
3.4.1If exp(7x1−4x2+2x3)<145. By Case A of Theorem 2, we obtain: any j1 + j2 + j3-th order partial derivative of g2(x1, x2, x3),
Thus, the 14-th order partial derivative value of g2(x1,x2,x3) at −17,23,−12,
>g2:=(x1,x2,x3)->exp(6*x1+11*x2-8*x3)/((14-5*exp (7*x1-4*x2+2*x3))^8)^(1/9);
>evalf(D[1$6,2$5,3$3](g2)(-1/7,2/3,-1/2),22);
-1.324276036594542259720.1016
>evalf(14^(-8/9)*sum(product(-8/9-j,j=0..(k-1))/k!*(-5/14)^k*(7*k+6)^6*(-4*k+11)^5*(2*k-8)^3*exp(-14/3 *k+220/21),k=0..infinity),22);
-1.324276036594542259721.1016
3.4.2If exp(7x1−4x2+2x3)>145. Using Case B of Theorem 2 yields: any j1 +j2 + j3 -th order partial derivative of g2(x1,x2,x3),
Hence, the 16-th order partial derivative value of g2(x1,x2,x3)at 17,14,1,
>evalf(D[1$5,2$7,3$4](g2)(1/7,1/4,1),40);
-7.22751822579461952474808.1020
>evalf(5^(-8/9)*sum(product(-8/9-j,j=0..(k-1))/k!*(-14/5)^k*(-7*k-2/9)^5*(4*k+131/9)^7*(-2k-88/9)^4* exp(-2*k-1555/252), k=0..infinity),22);
-7.227518225794619524748.1020
4ConclusionThis article proposed two methods (i.e., the binomial series and the differentiation term by term theorem) to solve the partial differential problem of some multivariable functions. The two methods can be applied to evaluate any order partial derivatives of general multivariable functions. Further studies on related applications will be conducted in the future. Moreover, other calculus and engineering mathematics problems will be considered and solved using Maple.