Digitisation has raised concerns about how it can transform the growth of productivity in firms and its divergence around the world. Given that literature has focused mainly on confirming firm productivity gaps, research on the explanatory role of digital-based complementarities in productivity gaps has been scarce. This work aims to provide evidence on the digital divide and its causes in small and medium-sized enterprises (SME) and in large firms. Using a sample of 5,840 Spanish SMEs and large firms during the 1991–2016 period, results reflect a growing divergence in total factor productivity, both for SMEs and for large firms. Moreover, they also show that the productivity gap becomes more evident when firms develop digital-based complementarities, particularly those derived from ICT investment, R&D activities and product innovation. Firm strategies and policy implications of the results obtained are also discussed.
The film Blade Runner, directed by Ridley Scott, was released in 1982. In Los Angeles, 2019, bioengineering has been developed in such a way that it is possible to manufacture artificial human beings, called replicants. The film, which portrays a dystopian future, has become a cult classic. Economically, it suggests a future dominated by large corporations, where the Tyrell Corporation has achieved a dominant position as a result of its capacity for innovation in the biomedical field.
Could an economic future, controlled by some large corporations that have all the market power, become a reality? Can digitisation lead to a situation where the global frontier of innovation is dominated by a few large corporations? Or, on the contrary, is this just science fiction and economic dynamism will always feed a large group of new adventurous firms, mainly small and medium-sized enterprises (SME), preventing the concentration of market power? The study of productivity, and especially total factor productivity, will help us answer these kinds of questions.
In this context, the technological revolution has emerged as one of the main factors responsible for productivity growth (Lafuente, Acs, Sanders & Szerb, 2019). This is why economic activities are increasingly influenced by new waves of innovation and investment in digitisation technologies, such as the Internet, e-commerce, robotisation, the Internet of Things (IoT), artificial intelligence (AI), and collaborative platforms, amongst others, which have constituted a new way of structuring firms with the consequent impact on the production gap (Trajtenberg, 2018).
The importance of productivity lies in the fact that it is the main indicator of an economy's long-term growth potential (Comin, 2017). The literature shows the existence of a direct relationship between productivity growth and capital deepening (capital per worker or per hour worked), as well as with the efficiency of the combined total factors of production (hereinafter, ‘TFP’) (Díaz-Chao, Miralbell-Izard & Torrent-Sellens, 2016). The right combination of these two factors, therefore, enables sustained long-term growth of the economy (Timmer, Inklaar, O'Mahoney & Van Ark, 2010).
Contrary to what was thought, there has been a clear downward trend in aggregate productivity in developed countries, which has reopened the debate on technological effects on productivity (Berlingieri, Blanchenay & Criscuolo, 2017; Bryne, Fernald & Reinsdorf, 2016; Cette, Fernald & Mojon, 2016). In this context, the literature has captured the growing importance of productivity convergence as associated with new technologies and the way in which firms interact on an international market, thus varying the productive capacity of firms along the global frontier of innovation and digitalisation change (Berlingieri et al., 2017). Thus, convergence, indicating the proximity in terms of productivity of a given firm to the leading firms, and divergence, indicating dispersion in productivity, have become key concepts in academic discussions on productivity and internationalisation.
Two consequences have, therefore, been identified. Firstly, that despite digitalisation, there is a discussion about the real effects of technology on productivity (Berlingieri et al., 2017; Bryne et al., 2016; Cette et al., 2016). Secondly, that entrepreneurially there has been a very notable increase in the productivity gap, which means that the problem is not that productivity does not grow in frontier firms (sector leaders, also called ‘gazelle companies’), where it is understood as those firms that are on the global productivity frontier, defined as the most productive firms in each economic sector. While non-frontier firms (follower) are those that are not close to the productivity frontier, due to innovation diffusion problems (Añón-Higón, Mañez, Rochina-Barrachina, Sanchis-Llopis & Sanchis-Llopis, 2017; Berlingieri et al., 2017; Cette et al., 2016).
Under this prism, this article intends to go beyond the confirmation of the existence of productive divergence and aims to explain its reasons for a sample of SMEs and large industrial firms. In fact, two new contributions to the literature are tested: to assess whether divergence exists only between large firms and SMEs, or also amongst the SMEs themselves. Therefore, we intend to answer the following questions: What is the role of dimension in the divergence of business productivity? Specifically, is the growing gap in productivity between large firms, or between small and medium-sized enterprises? And, secondly, in trying to explain this divergence: What are the foundations of the divergence in productivity? In particular, what role do digital-based complementarities play in explaining the growing divergence in TFP?
Results show divergence in both SMEs and large firms. Results also suggest that larger, more capital-intensive industries, with a higher skilled labour force, are closer to the frontier, with frontier firms defined as those with a higher average output, and non-frontier firms as all the rest–following Andrews, Criscuolo and Gal (2015), frontier firms are the 10% most productive firms in each year of the sample. In addition, according to the results, the role of digital-based complementarities has a notable importance in the growth of TFP, highlighting expenditure and investment in R&D, investment in information and communications technology (hereinafter, ‘ICT’), and product innovation.
The rest of this paper is structured as follows. The second section reviews the literature that analyses the reality of productivity insofar as there is divergence/convergence, as well as the relationship between TFP and digital transformation as a generator of such divergence/convergence. Section 2 also postulates the working hypotheses. The third section presents the methodology used to make the corresponding TFP estimates, as well as the Blinder-Oaxaca decomposition. The fourth section presents the database used in this study, Encuesta sobre Estrategias Empresariales (Business Strategy Survey, ESEE), and analyses its validity, as well as the different variables used throughout the article, which enable verification of the hypotheses posed. In the fifth section, the main research findings are analysed. A closing section provides the conclusions and discussion of the main results.
Theoretical background and hypothesesRelated workIn recent decades, there has been an increase in the literature on the analysis and estimation of productivity (Aiello, Pupo & Ricotta, 2014). Several papers have shown that economic performance is associated with differences in the dispersion of within-industry productivity across firms (Añón-Higón et al., 2017). However, recent research at the firm level has focused on technology levels, demand, and market structure as a driver of productive divergence (Bartlesman, Haltiwanger & Scarpetta, 2013; Draca, Sadun & Van Reenen, 2006; Syverson, 2011). According to these works, production divergence at the firm level can occur due to “[…] the effect of competition (Schmitz, 2005; Syverson, 2004), the size of sunk costs (Collard-Wexler, 2013), and the interaction of product market rivalry and technology spillovers (Bloom et al., 2007)” (Syverson, 2011, p. 329).
These new perspectives have highlighted the importance of heterogeneity between firms and industries in terms of productivity (Andrews et al., 2015; Crespi, 2013). Some of the main determinants of firm productivity heterogeneity are directly associated with digitalisation (Gal, Nicoletti, Renault, Sorbe & Timiliotis, 2019), as well as with those factors associated with the need to increase investment in R&D (Añón-Higón, Mañez & Sanchis-Llopis, 2018; Aw, Roberts & Xu, 2008; Ballestar, Grau-Carles & Sainz, 2019) and the importance of innovation (Foster et al., 2017, 2018). Innovation can be divided into product innovation and process innovation. While product innovation has a positive effect on productivity (Bernard, Redding & Schott, 2010), process innovation is associated with internal value processes, which offer a more precise reasoning to support the technical efficiency of firms (Ballestar et al., 2019; Gunday, Ulusoy, Kilic & Alpkan, 2011).
Under this perspective, the efficient and combined use of the different resources (tangible and intangible) by firms generates a new organisational capability, which becomes a differentiating component in relation to competitors (Amit & Schoemaker, 1993). The capability of firms to use these resources also leads to an improvement in productivity (Mikalef et al., 2020).
Furthermore, intangible resources include those associated with robotisation, innovation, and digitisation, amongst others, which have increased the level of TFP (Brynjolfsson & Hitt, 2000; Edquist & Henrekson, 2017; Jorgenson, Ho & Stiroh, 2008; Pellegrino & Zingales, 2017). However, the impact of the second wave of ICT (i.e. machine learning, Internet of Things, cloud computing, big data, 3D printing) on industry is still being analysed, because this increase in productivity is associated with business divergence/convergence.
In this context, there has been an in-depth discussion on whether this reality is maintained continuously over time, generating a greater divergence between firms, or whether, on the contrary, it leads to productive convergence between firms (Añón-Higón et al., 2017; Bartlesman et al., 2013; Berlingieri et al., 2017). The literature shows evidence that the productivity gap between frontier and non-frontier firms has widened in the last decade and, therefore, the process of productivity convergence within the industry has come to a halt (Andrews, Criscuolo & Gal, 2016; Añón-Higón et al., 2017). That is why the mechanisms that generate a greater gap between frontier and non-frontier firms are determined by the firms that are, on the one hand, more capital and labour intensive, and, on the other hand, are closer to the frontier. Furthermore, the literature questions how new technologies and spillovers fail to diffuse across all firms, ultimately leading to a widening of the productivity gap. However, the use of public policies aimed at improving and investing in digitalisation would reduce this gap.
Hence, as indicated by Berlingieri et al. (2017), p. 5): “It is therefore important to understand not only the link between the observed divergences in wages and productivity, but also how structural changes, such as globalisation and digitisation, affect this link”.
Hypotheses developmentThese circumstances have led to the analysis of the potential for productivity heterogeneity amongst firms. In this sense, in the last decade a vast body of literature has addressed the question of whether national firms tend towards global productive convergence or, on the contrary, a productivity deviation and a clear divergence amongst firms exists (Bartlesman et al., 2013). In this regard, the literature provides a description of frontier firms (those defined as the most productive on average) versus non-frontier firms (the remaining firms) (Andrews et al., 2015; Syverson, 2004). This discussion has arisen as a result of the international crisis that began in the third quarter of 2007, which had a significant impact on the productivity of economies, industries and firms (Añón-Higón et al., 2017).
An abundant amount of literature has analysed the distance between frontier and non-frontier firms at the international level (Andrews et al., 2016; Añón-Higón et al., 2017). In this sense, this bibliography shows how productivity growth of lagging firms is mostly related to the evolution of national frontier productivity, not to the international frontier (Iacovone & Crespi, 2010).
It should be mentioned that those firms considered frontier (also called "gazelle" companies) are fundamental for job creation (Bartlesman, Dobbelaere & Peters, 2014; Decker, Haltiwanger, Jarmin & Miranda, 2016b; Henrekson & Johansson, 2010). In this sense, it is possible to postulate that:
Hypothesis 1 The divergence in TFP between leader and follower industrial firms has increased.
It should be noted that there is an increase in production divergence both in inter- and intra-size, which raises the question on whether divergence is the result of intra-dimensionality (between SMEs and large firms) or inter-dimensionality (between both groups). This research proposes a set of hypotheses associated with the distribution between firms (SMEs and large firms) (Garicano, Lelarge & Van Reenen, 2016; Moral-Benito, 2016). To that end, the impact of the TFP in terms of intra-industry divergence is analysed. We therefore raise hypotheses on the existence of divergence between firms of the same size in the industry (Criscuolo, Timmis & Johnstone, 2016). Thus, it is proposed that:
Hypothesis 1a The divergence in TFP increases between leader and follower SMEs.
Hypothesis 1b The divergence in TFP increases between leader and follower large firms.
Under this line of research, we contribute to the analysis of the relationship between digitalisation and productivity at the firm level. But how is the situation of productivity at firm level with respect to the use of digitalisation? The analytical study conducted by Corrado, Haskel and Jona-Lasinio (2017) shows the need for better use of digital technologies to improve the overall effect of efficiency in Spain. Along these lines, it should be noted that, in order to achieve growth in productivity, investments must be made in physical and human capital, taking into account the need for human capital to have a better capacity to use digitalisation in order to generate more added value (Van Laar, Van Deursen, Van Dijk & De Haan, 2017).
In recent decades, discussions about investment in digitalisation and its impact on the productive dynamics of firms have been prolific (Autor, 2015; Cusolito, Lederman & Peña, 2020; Van Ark, 2014). This is a clear sign of how the phenomenon of technological innovation has an increasingly prominent weight in the production cycle associated with economic growth, both in the short and long term (Edquist & Henrekson, 2017; Graetz & Michaels, 2018). Nonetheless, the discussion on this dynamic does not entail a single path of analysis, as there is a wide range of empirical studies that show a negative relationship between both variables (Van Ark, 2016). In recent years, however, the literature has increasingly shown a positive and significant relationship between the use of digitalisation and productivity improvement (Corrado et al., 2017; Edquist & Henrekson, 2017; Mohnen & Hall, 2013).
For this reason, a second group of hypotheses is put forward, based on the relationship between the variables that affect SMEs and large firms in terms of their divergence or convergence between productivities. The divergence in productivity between SMEs and large firms increases due to the fact that large firms have access to a greater amount of resources in the context of digitalisation (human capital, access to technology, amongst others) that make them more competitive. However, SMEs and large firms tend to have very different competitive advantages (Díaz-Chao, Sainz & Torrent-Sellens, 2015). SMEs have greater flexibility to adapt to changes, while large firms have a higher market power, circumstances that hinder the comparison between both groups of firms. For this reason, once the inter-industry divergence has been contrasted, this study carries out an intra-industry analysis, involving a contrast of SMEs and large firms.
The specialised literature shows a clear relationship between digitalisation and the improvement of TFP (Hall, Lotti & Mairesse, 2013). In this context, under the assumption of a positive relationship between digitisation and productivity, the second working hypothesis is configured (Andrews et al., 2015; Bartlesman et al., 2013).
Hypothesis 2 Digitalisation explains the productive divergence in the industry.
This hypothesis implies that the expansion of digital-based complementarities has not been balanced amongst firms, generating a productive gap amongst SMEs and concentrating its benefits on increasing productivity in firms with a higher average productive value (Sorbe, Gal, Nicoletti & Timiliotis, 2019). This same situation occurs for large firms. Associated to this second hypothesis, the following can be verified:
Hypothesis 2.a Digital-based complementarities explain the productivity divergence between SMEs.
Hypothesis 2.b Digital-based complementarities explain the productivity gap between large firms.
In order to test the research hypotheses, this study models and estimates TFP associated with a sample of Spanish industrial firms extracted from the Encuesta sobre Estrategias Empresariales (Business Strategy Survey, ESEE) of the SEPI Foundation for the period 1991–2016. Then, we apply the Blinder-Oaxaca decomposition technique, which enables the acceptance or rejection of the hypotheses associated with the predictive relationship between the two groups of firms analysed (frontier and non-frontier). Moreover, the productive divergence in relation to the set of variables under study will be taken into consideration.
In this context, the objective of this paper is determined by the analysis of divergence/convergence in the TFP of frontier and non-frontier firms for a total of 5840 firms in the Spanish industrial fabric in the period between 1991 and 2016. It comprises a total of 157,680 observations (the study uses an analysis of a panel of data) that enable a better understanding of the productive situation of the Spanish industrial fabric (Añón-Higón et al., 2017; Ballestar et al., 2019).
Model of total factor productivity (TFP)The model used in this research is based on the estimation of a Cobb-Douglas type production function with three production factors. The application of this production function is due to the fact that it is one of the simplest, as well as the most widely used in the literature (Bloom et al., 2019; Edquist & Henrekson, 2017; Harris & Moffat, 2017). The functional form of the production function is as follows:
Where, Y is the value added (AV) of the firm and = 1, …, N for the period t = 1991, …, 2016, which depends on the variable A defined as the TFP, L is the labour factor, K is the quasi-fixed capital factor, M are the intermediate inputs. The parameters βl, βk, βm are the elasticities of the labour, capital and intermediate cost, respectively.In order to work in a linear way, it applies the Napierian logarithms, enabling the transformation of an exponential function into a linear one:
β0 is a measure of the TFP level common to all the firms that make up the sample, and uit represents the error term, which includes all those factors of the business reality. While uit is either not observable or it corresponds to variables determined by external circumstances, i.e., it is an identically distributed error term that captures unexpected shocks to production or measurement error. This term is also a random component that firms do not consider when making their decisions (Iootty, Pena & De Donato, 2019).
The function [2] is directly related to the technology index or TFP; therefore, if we rewrite the function [2] we obtain [3]:
Blinder-Oaxaca decompositionThe Blinder-Oaxaca decomposition is an econometric technique that enables the comparison of two population groups and thus the observation of differences based, firstly, on the existence of a common component, and secondly, on the category that differentiates the analysed groups (Barcenilla, Gimenez & López-Pueyo, 2019; Castany, López-Bazo & Moreno, 2005; Karunaratne, 2007).
This decomposition divides the differential of the variable into two distinct groups. The first explains the differential characteristics of each group that have some impact on productivity (for example, investment in R&D or use of robots, amongst others). A second residual group allows us to hypothesise about different virtual contexts and enables, not only to analyse differences in the average, but also in the overall distribution. It is also based on multiple regression coefficients by means of regressors (Jann, 2008). In the Blinder-Oaxaca decomposition, the bias is eliminated by self-selection and, in a specific case, the estimate is made by specifying the OLS (Castany et al., 2005; Lamorgese & Petrella, 2016).
Therefore, the Blinder-Oaxaca decomposition is considered to be the mean value of the conditional expectation function (Schneider, 2018).
As we can see, it is a linear function; therefore, the basis of the Blinder-Oaxaca decomposition is obtained by the equation [5], which is estimated in two linear regressions, for each of the comparison groups.
Where (ΔE[X]β′) shows the difference in assignments, while the (E[X]Δβ) is the contribution of a change of structure.More flexible estimates are used to calculate the decomposition of Blinder-Oaxaca. The literature shows the existence of the problem of determining how the base structure would prevail in the absence of discrimination. To overcome this circumstance and extend the discrimination component, three alternative methods of decomposition are proposed: Cotton (1988); Neumark (1988), and Oaxaca and Ransom (1994). Cotton (1988) suggests weighting the differences of the x's by the average of the coefficient vectors, while Neumark (1988) and Oaxaca-Ransom (1994) propose the use of the coefficients obtained from the regression of the grouped data.
Estimation functions and methodsTotal factor productivityWe estimate the relationship of divergence/convergence between firms, as well as the relationship between digitalisation, using two types of models. The next model estimates individual TFP from the Cobb-Douglas production function. As explained above, we expect divergence effects to be time dependant. Therefore, we estimate the long-term effects on logarithmic levels and assume that differences in productivity will be reflected in the long run. The parametric productivity equations (derived from equation [2]) will explain the individual effects that will take the form of [6]:
The methodology proposed by Wooldridge (2009) is used to estimate the parametric function. As indicated by Olley and Pakes (1996), these estimates find that production factors and inputs tend to be correlated due to a problem of simultaneity. If the firm responds to a positive production shock by expanding output, then there is a correlation between the error term and the independent variables. Therefore, the authors assume that variables L and M are fluctuating input variables, while on the contrary, K is a static or quasi-fixed variable, affected by the distribution of productivity shocks, uit, which is also conditioned by the information given with respect to the productivity variable, coming from the period t-1 and present values ui.
Olley and Pakes (1996) also indicate that capital may not be correlated with productivity. In this case, if capital levels are correlated with variable inputs, as is the case with the labour variable, this could imply that a negative bias in one of the variables also influences the other variable negatively, since both are estimated simultaneously. In order to solve this problem, Olley and Pakes use investment as a proxy for unobserved productivity shocks.
Depending on the database used, a situation may arise in which the database does not provide the necessary information to carry out the estimate using the Olley and Pakes model, and therefore an alternative variable to the investment must be sought. Levinsohn and Petrin (2000); 2003 use intermediate goods as a proxy to value unobserved productivity shocks to intermediate inputs. They conclude that the use of investment as a proxy entails two problems. The first is that investment is a very unequal variable (lumpy), because it incorporates substantial adjustment costs and therefore does not respond "smoothly" to productivity shocks. Secondly, this proxy is linked to the fact that many firms do not make investments during some periods of time and, therefore, investment is only valid for those that report investment different from zero. The OLS and Random Effect are used as alternatives for robustness checks.
Blinder-Oaxaca decompositionThus, once the TFP estimation is made, the model is specified. The TFP index is a function of the productive level and the innovative action of each firm. According to the theoretical arguments presented so far, the specification of the analysis is done by means of a linearisation with respect to the TFP. Likewise, the firms and the temporary effects are set as control variables. The number of variables selected is determined on the basis of the firm's complementarity effects of digitisation, and the function is taken on the basis of the model set out in Castany et al. (2005).
On the basis of the above arguments on the Blinder-Oaxaca decomposition, the specified model is determined by linear regression based on the TFP index. In this method, the capital deepening (DEEPCAP) is controlled, as well as the digital-based complementarities by ICTI, research and development (R&D), R&D workers (R&DEMP), and finally, the dichotomous variables corresponding to product innovation (PRODIN), process innovation (PROCIN), and robotics (RBN). Therefore, the empirical model can be expressed as follows:
In this research, estimation is applied through the decomposition of Blinder-Oaxaca. This has been widely used to study wage differentials between diverse types of workers (Boeri & Ours, 2013; Fortin, Lemieux & Firpo, 2011), although in the present study it is applied to analyse productivity differentials at the firm level. This methodology enables an analysis of how much of the TFP differential between frontier and non-frontier firms can be explained by differences in their characteristics or by differences in the performance of those characteristics (Battisti, Del Gatto & Parmeter, 2018). The Blinder-Oaxaca decomposition “permits identifying the relative importance of firm characteristics and returns very easily” (Castany et al., 2005, p. 8).
Following the exposition of Oaxaca (1973) with the modification made by Castany et al. (2005), the method of decomposition of the productive gap of the two analysed groups (frontier and non-frontier) is applied in the following way. Firstly, identical TFP regions are estimated for each group:
Where TFPF and TFPNF represent the logarithm of the TFP of the frontier (F) and non-frontier (NF) group, respectively. βF and βNF, are the vectors of the coefficients to be estimated in each group, XFit and XNFit, represent the vectors of the observed characteristics for group, and, finally, uFit and uNFit, correspond to the error term of each equation.Secondly, we decompose the average TFP differential between the two groups, expressed as:
The Blinder-Oaxaca decomposition evaluates the productivity differential in the mean distribution of characteristics, that is, comparing the mean characteristics of frontier and non-frontier firms.
As far as the use of alternative models is concerned, the result of the difference can be written as:
Where the first term, D in Eq. (11), is the part of the productivity difference that is explained by group differences in regressors (TFP difference), the second term is the productivity increase by investment in digitisation in group 1, and the third is the underpayment to group 2 due to digitisation. Eq. (12) is put into practice under the assumption of a non-discriminatory production structure by assigning weight proportions of frontier firms (PF) and non-frontier firms (PNF) to the digitisation structure and β* is defined as;Information sourceThis research is based on the SEPI Foundation's Encuesta sobre Estrategias Empresariales (Business Strategy Survey, ESEE), sponsored by the Ministry of Industry. ESEE is a data panel survey consisting of approximately 2200 Spanish manufacturing firms per year, as every year the aim is to maintain the representativeness of the sample.
ESEE provides data from 1990 to 2016 (last year available). This means that there is a total of approximately 55,000 observations. Consequently, this panel data permits a very detailed study of the microeconomics of productivity and employment as well as the analysis of changes in Spanish manufacturing firms during various stages of the business cycle (Camiña, Díaz-Chao & Torrent-Sellens, 2020). The ESEE data panel enables us to conduct the TFP estimation at a microeconomic level in a wide range of pre- and post-international crisis years.
In the first year of the sample, 5% of all manufacturing firms were randomly selected for industrial strata with a volume of workers comprising between 10 and 200 individuals. However, at the same time as the survey was launched, firms with more than 200 workers were asked to actively participate, and 70% of them agreed (Castiglionesi & Ornaghi, 2013).
The ESEE database contains a set of segmented information for manufacturing firms with more than 200 employees (large firms) and firms with 10 to 200 employees (SMEs). Due to this division, SMEs are classified differently in ESEE than by the European Commission (Camiña et al., 2020; European Commission, 2012). In the case of the ESEE, the limit used to define SMEs is 200 workers, while the European Commission uses a maximum size of 250 workers. This difference is due to the sampling procedure used by the ESEE: “In this survey, all large manufacturing firms (more than 200 workers) are included in the sample. However, for SMEs (from 10 to 200 workers), stratified, proportional and systematic sampling is used by industries (national economic activity two-digit classification code, NACE) and size of the firm” (Camiña et al., 2020, p. 6). With regard to data entry, ESEE provides detailed information for 20 economic sectors (Appendix A), which are representative of the Spanish industrial fabric.
Variables and indicatorsTable 1 presents a summary of the main dependant and explanatory variables included in the models used at the productivity level. The selection of these variables is consistent with the literature dealing with the TFP estimation. However, additional variables that will permit testing the second group of hypotheses are also included.
Variables.
| variable | measures | mean | s.d. | skewness | kurtosis | references |
|---|---|---|---|---|---|---|
| dependent | ||||||
| Added Value (AV)1 | Euros | 14.59 | 1.90 | 0.27 | 2.63 | Faggio, Salvanes and Van Reenen (2010) / Añón-Higón et al. (2017)) |
| Independents | ||||||
| Labour (NL) | Labour | 14.28 | 1.78 | 0.27 | 2.44 | Fu and Moral-Benito (2018) |
| Capital Stock (CS) | Euros | 14.75 | 2.36 | 0.02 | 2.60 | Fu and Moral-Benito (2018) |
| Intermediate Inputs (INTIN) | Euros | 14.92 | 2.3 | −0.07 | 3.19 | Levinsohn and Petrin (2003)) |
| Others | ||||||
| Capital deepening (DEEPCAP) | Capital per worker | 11.22 | 1.04 | −0.38 | 5.52 | Criscuolo, Andrews and Gal (2019) |
| R&D expenditure (R&D) | Euros | 12.34 | 2.07 | −0.15 | 3.77 | Raymond, Mairesse, Mohnen and Palm (2015) |
| R&D workers (R&DEMP) | Staff in R&D activities | 1.85 | 1.31 | 0.78 | 3.86 | Graetz and Michaels (2018) |
| ICT Investment (ICTI) | Euros | 1.52 | 1.37 | −0.47 | 2.72 | Autor and Salomons (2018) |
| Frequency | ||||||
| Variable | Measures | No | Yes | Skewness | Kurtosis | Bibliography |
| Use of industrial robots (ROB) | (yes/no) | 11,487 | 4243 | 2.93 | 9.58 | Camiña et al. (2020)/Ballestar, Díaz-Chao, Sainz and Torrent-Sellens (2020a) |
| Product innovation (PRODIN) | (yes/no) | 38,272 | 10,947 | 0.99 | 2.09 | OECD (2018) |
| Process innovation (PROCIN) | (yes/no) | 33,034 | 16,186 | 1.08 | 2.36 | OECD (2018) |
Notes: The continuous variables have been considered on a logarithmic basis. Data in real terms.
All the vacinal terms have been deflated using a Paasche referenced to the prices’ variation of intermediate consumption (raw materials, energy, and external services). High values of kurtosis and symmetry were detected, suggesting potential problems in the estimation of the market share, workers in R&D, and in the use of robots. For this reason, VIF tests will be conducted.
ResultsIn this section, the results obtained from the TFP estimate will be analysed using fixed effects. This will permit detecting the existence of divergence or convergence of the firms under study for the period analysed. Likewise, by using the Blinder-Oaxaca decomposition, we will be able to contrast the reality of the Spanish industrial fabric with respect to the TFP divergence/convergence at the firm level, taking into account capital deepening, market share, the use of new technologies (investment in R&D, workers assigned to R&D, ICTI, innovation in process and product, and the use of robots), as well as economic activity.
Divergence / convergence total factor productivityThis section analyses the divergence/convergence trend between the division of the 10% of firms with a higher average value (frontier firms) with respect to the remaining 90% (non-frontier firms) for the period between 1991 and 2016. The literature selects as the frontier firms a fixed number of firms per industry over time, usually the top 5% or 10% (Andrews et al., 2015; Añón-Higón et al., 2017). For this research we have selected the top 10% due to the variability in terms of incorporation and closure of firms included in the ESEE sample. This fact makes it possible to capture the change of frontier firms over time (Añón-Higón et al., 2017).
Table 2 reflects the TFP estimation. All coefficients are positive and significant. In the analysis of the (individual and complementary) explanatory factors of productivity and employment for Spanish industries, we have estimated the TFP by means of Levinsohn and Petrin (2003)), following the methodology of recent international research (Aiello et al., 2014; Van Beveren, 2012). In this sense, we answer the set of hypotheses associated with hypothesis 1 on divergence/convergence in Spanish industry (large firms and SMEs).
Total factor productivity (TFP) estimation. 1991–2016.
| SMEs | Large firms | Total Industry | |||||||
|---|---|---|---|---|---|---|---|---|---|
| OLS | FE | LP | OLS | FE | LP | OLS | FE | LP | |
| Coefficients | |||||||||
| Labour | 0.64⁎⁎⁎ | 0.61⁎⁎⁎ | 0.62⁎⁎⁎ | 0.53⁎⁎⁎ | 0.53⁎⁎⁎ | 0.55⁎⁎⁎ | 0.62⁎⁎⁎ | 0.59⁎⁎⁎ | 0.60⁎⁎⁎ |
| (0.003) | (0.007) | (0.005) | (0.009) | (0.002) | (0.03) | (0.003) | (0.003) | (0.01) | |
| Intermediate Cost | 0.25⁎⁎⁎ | 0.30⁎⁎⁎ | 0.26⁎⁎⁎ | 0.25⁎⁎⁎ | 0.36⁎⁎⁎ | 0.32⁎⁎⁎ | 0.25⁎⁎⁎ | 0.31⁎⁎⁎ | 0.27⁎⁎⁎ |
| (0.003) | (0.005) | (0.005) | (0.007) | (0.007) | (0.01) | (0.004) | (0.004) | (0.007) | |
| Capital | 0.16⁎⁎⁎ | 0.12⁎⁎⁎ | 0.12⁎⁎⁎ | 0.20⁎⁎⁎ | 0.12⁎⁎⁎ | 0.13⁎⁎⁎ | 0.16⁎⁎⁎ | 0.12⁎⁎⁎ | 0.10⁎⁎⁎ |
| (0.003) | (0.003) | (0.003) | (0.006) | (0.001) | (0.02) | (0.002) | (0.003) | (0.001) | |
| Statistics | |||||||||
| N° Obs. | 31,329 | 9974 | 41,303 | ||||||
| Adj. R2 | 0.854 | 0.894 | – | 0.763 | 0.789 | – | 0.916 | 0.913 | |
Notes: Data in real monetary log-levels. Estimation methods: OLS (Ordinary Least Square), FE (Fixed Effect) and LP (Levinsohn and Petrin). Estimated coefficients: Standardized coefficients. Standard errors of the standardized coefficients in brackets.
Table 2 shows the summary statistical results of the coefficients of the variables used in the estimation of TFP using the Ordinary Least Square (OLS) method, the fixed effects (FE) and, finally, the Levinsohn and Petrin (LP) method. The estimation shows results similar to those of the literature on the conclusions given by the OLS and FE methods. Likewise, labour and intermediate inputs represent 85%−90% of the variation in the value added of the analysed firms, while the use of capital represents 12%−20%. This confirms that most of the firms analysed are more labour-intensive, although they produce with a high level of capital for manufacturing.
It should be noted that Levinsohn and Petrin's (2003) more robust method uses labour as a free variable, intermediate inputs as a proxy variable, and capital as a state variable. Using intermediate inputs as a proxy to detect unobserved productivity shock lower values of labour, while capital increases slightly, where it plausibly implies a correction of simultaneity and endogeneity bias.
The tests conducted to determine if data meets the assumption of collinearity indicate that multicollinearity is not a concern (for all variables and explanatory indicators, Tolerance > 0.10 and VIF < 10; the correlation matrix is presented in Appendix A).
Table 3 shows the descriptive statistics with respect to TFP at the firm level, which indicates that the average of the 10% most productive firms (frontier firms) has a higher value in proportion to the 90% of less productive firms (non-frontier firms) for SMEs and large firms. As might be expected, this table reflects that the average TFP is higher in large firms, which is confirmed by the equality of means test that rejects that the average TFP is the same in the two subsamples. The percentiles at 25%, 50%, 75% and 90% show that TFP is always higher in frontier firms. Thus, it is confirmed that the differences in TFP between these groups of firms are not homogeneous throughout the range of TFP levels.
Descriptive statistics of TFP for frontier and non-frontier firms. 1991–2016.
Notes: Data in real monetary log-levels. Standard Deviation (S.D.) in brackets.
Table 4 shows the digital transformation activity variables for SMEs, large firms, and total industry. The table shows the main statistical data on the main variables of the digital transformation analysed with regards to frontier and non-frontier firms. In this sense, for the three cohorts analysed as a whole, it is stated that, for frontier firms, there is greater investment in R&D, as well as greater capital deepening. This presupposes that the 90% least productive firms operate mainly in ICTI, in product innovation, and in process innovation. They average values of 20–35% for PRODIN, and 32–50% for PROCIN, which is expected to have a positive effect on productivity. It can also be seen that in terms of robotisation, it has a greater weight in 90% of non-frontier firms. Data is also expected to have a greater impact on the growth of TFP in this group of firms, expecting a trend towards convergence with frontier firms.
Descriptive analysis of the independent variables for frontier and non-frontier firms, by firm size. 1991–2016.
Note: Data in real monetary log-levels and in dichotomous form (1, yes; 0, no). Standard Deviation (S.D.) in brackets. Frequency in percentage.
The Table B.1 (Appendix B) reflects years 1991, 2000, 2010 and 2016, which have been selected in order to make a comparison with respect to the productive variables (TFP, labour productivity, and capital deepening) allowing a comparative analysis between frontier and non-frontier firms.
When analysing the evolution segmented by SMEs, it is evidenced that, in frontier firms, the TFP shows a positive accumulated value from 1991 to 2016 (1%), while negative growth values are shown in terms of labour productivity (0.8%). Capital deepening shows a positive value (1%). On the other hand, in large firms TFP (0.6%), labour productivity (1%) and capital deepening (1.4%) show positive and growing values throughout the period analysed. This situation is a clear indication of the lack of a structural production base in Spanish SMEs. Moreover, for the period between 2000 and 2016, the trend is positive for TFP (2%) and capital deepening (0.6%), and negative for labour productivity (0.3%).
In the case of non-frontier firms, during the aggregate period 1991–2016, TFP (0.5%) and capital deepening (2%) increased, while labour productivity shows positive values (0.7%). The situation is similar for the periods ranging from 2000 to 2016 and from 2010 to 2016. In the case of large firms, results evidence a cumulative increase of 1% for the frontier firms’ TFP in the period 1991–2016. This circumstance is also evidenced in terms of capital deepening with a cumulative positive value of 1%. On the other hand, for 90% of non-frontier firms, the accumulated TFP for the years 1991–2016 shows a positive value of 0.5%, as well as for the capital deepening of 2%, while for labour productivity the variation in value is 0.8% (Appendix B).
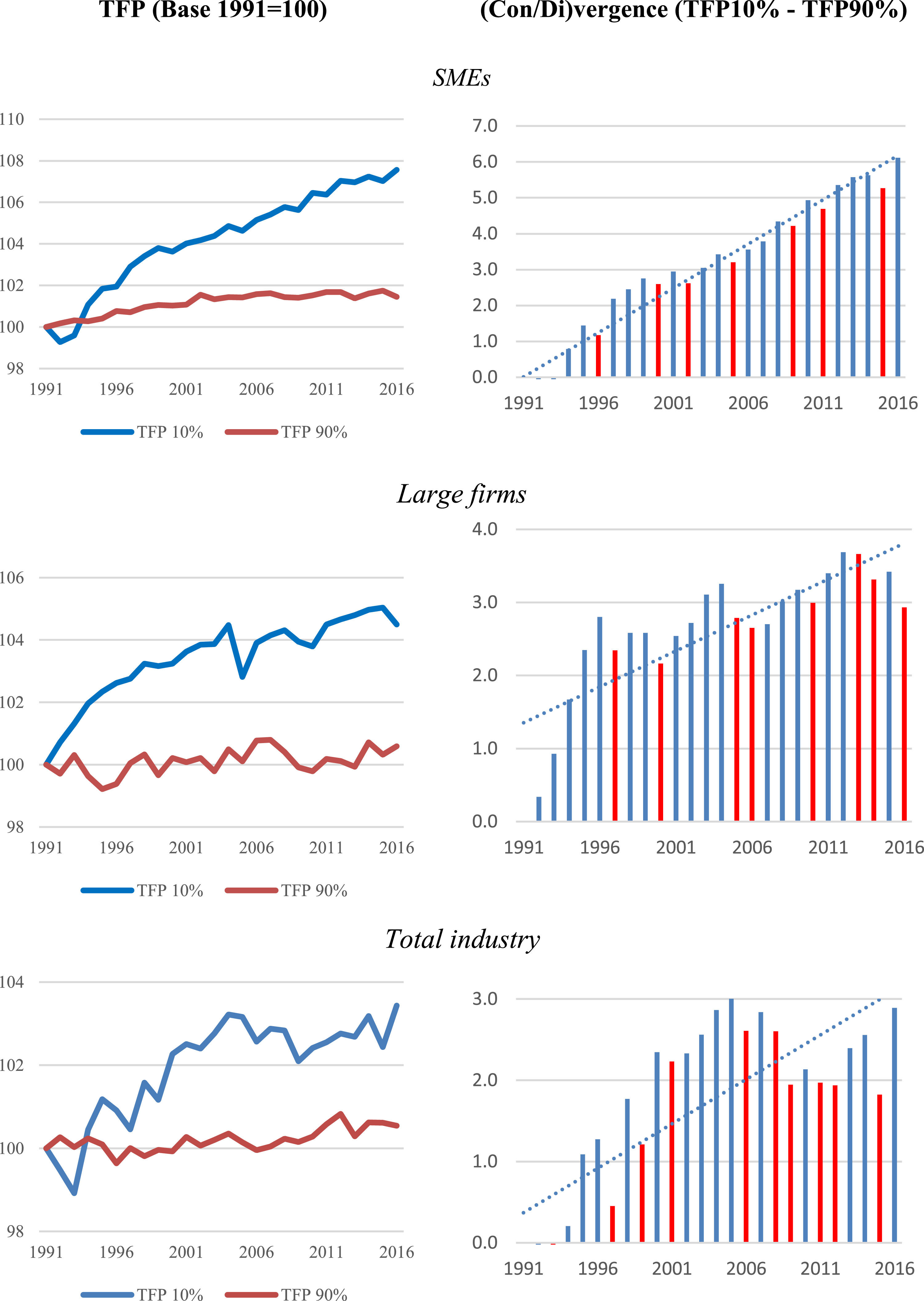
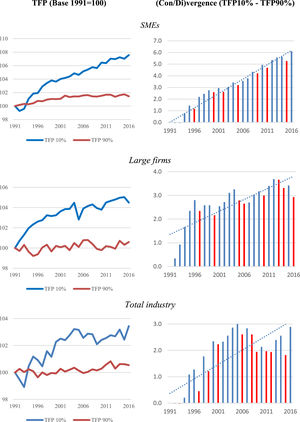
Fig. 1 shows how divergence has increased as a result of the more moderate progress of the TFP of follower firms with respect to frontier firms. This is true of both SMEs and large firms. The results corresponding to SMEs show a clear increase in the average annual TFP of frontier firms, with a clear accumulated divergence of 6% in the period analysed.
Average distribution of TFP in large firms and SMEs (frontier versus non-frontier firms) (1991–2016) (Base 1991 = 100)
Note: Notice that the graphs on the right, the blue colour shows year-on-year divergence, while the red colour is year-on-year convergence, likewise the dotted line is the trend of the divergence value.
Based on the results obtained in Fig. 1, it can be stated that, in general terms, there is a clear divergence in the group of firms analysed from 1994 onwards. The divergent trend reveals that, for both SMEs and large firms, divergence grows and accelerates from the year 2000. From 2000, the percentage evolution of the divergence is increasing, with values of 3% for the SMEs and 8% for large firms.
In this sense, it should be noted that, for large firms, the acceleration of the divergence occurs mainly at the beginning of the 2000s, while for SMEs there is a constant evolution of divergence throughout the years analysed.
The next step to be taken would be to study the average distribution of TFP by each group of analysis (frontier and non-frontier firms) in relation to the distribution of new cohorts (two cohorts represented in decades and one for five years). This distribution will allow us to observe the evolution of the TFP variable for each of the divisions carried out (Autor & Salomons, 2018; Pellegrino & Zingales, 2017). In this case, due to the extended period analysed in this article, the three periods (1991–2000, 2001–2010; 2011–2016) can be observed.
In order to carry out this analysis, a statistical contrast is used to check the differences between the distribution functions. These are based on the concept of first-order stochastic dominance and, in turn, allow a classification to be established for the compared distributions. In this case, the Kruskal-Wallis test is used, which allows us to test and verify TFP relationships between periods (Gonçalves, 2013).
The Kruskal-Wallis test is a non-parametric range-based test that can be used to determine whether there are statistically significant differences between two or more groups of an independent variable in a continuous dependant variable. It is considered the non-parametric alternative to unidirectional ANOVA, which is considered an extension of the Mann-Whitney test to allow the comparison of more than two independent groups, as is our case, where we have three comparative groups (Mahmood, Qasim, Khan & Husnain, 2014).
The results obtained by the Kruskal-Wallis test in Table 5 show a significance level of 0.0001 (i.e., p = 0.0001) for non-frontier SMEs, which is below the significance level of 0.05. It therefore reveals a statistically significant difference in the average TFP between the three distinct groups of the independent variable, agreed for each of the periods (i.e. "1991 to 2000″, "2001–2010″ and "2011–2016″). In relation to large firms, the significance level for the 10% of frontier firms is 0.771 (i.e., p = 0.771), which is below the significance level of 0.1. This indicates that there is a statistically significant difference in the average TFP between the three distinct groups of the independent variable; this result is similar for 90% of non-frontier firms. In other words, for large firms and for the two groups analysed, we find a significant average difference in TFP.
Kruskal-Wallis test for year cohorts. 1991–2016.
Under hypothesis 2 of this research paper aims at assessing whether digitisation explains the productive divergence in the industry (SMEs and large firms). Table 6 shows that, for industry as a whole and for large firms, the top 10% of the most productive firms have a higher reward in terms of the overall digital transformation than the remaining 90%. For SMEs as a whole we find the opposite case, i.e., we see how digital transformation has a greater impact on less productive firms. This is why the breakdown of Blinder-Oaxaca shows that, in the sample analysed, the difference in TFP between groups is statistically significant. This implies an unequal situation between 10% of the frontier firms and 90% of the follower, or non-frontier, firms.
Estimation of TFPs for 10% of frontier firms and 90% of non-frontier firms. 1991–2016.
| SMEs | Large firms | Total industry | ||||
|---|---|---|---|---|---|---|
| 10% | 90% | 10% | 90% | 10% | 90% | |
| ITCI | −0.002 | −0.001 | 0.120⁎⁎⁎ | 0.010 | 0.030 | −0.030⁎⁎ |
| (0.007) | (0.020) | (0.040) | (0.010) | (0.020) | (0.010) | |
| R&D | 0.010* | 0.22⁎⁎⁎ | 0.040 | 0.120⁎⁎⁎ | 0.140⁎⁎⁎ | 0.280⁎⁎⁎ |
| (0.010) | (0.02) | (0.030) | (0.010) | (0.020) | (0.021) | |
| PRODIN | 0.050* | 0.180⁎⁎⁎ | −0.080 | 0.070* | −0.092 | 0.173⁎⁎⁎ |
| (0.030) | (0.060) | (0.130) | (0.040) | (0.049) | (0.041) | |
| PROCIN | −0.020 | −0.080 | −0.190 | 0.010 | −0.032 | −0.151⁎⁎⁎ |
| (0.020) | (0.060) | (0.130) | (0.040) | (0.002) | (0.041) | |
| R&DEMP | 0.0001 | 0.004 | 0.006⁎⁎⁎ | 0.001* | 0.001⁎⁎⁎ | 0.001 |
| (0.001) | (0.003) | (0.002) | (0.006) | (0.002) | (0.001) | |
| ROB | −0.009 | −0.070* | −0.100 | −0.080⁎⁎⁎ | −0.080* | −0.091⁎⁎⁎ |
| (0.020) | (0.040) | (0.080) | (0.030) | (0.039) | (0.032) | |
| N° | 276 | 618 | 151 | 1110 | 613 | 1542 |
| Adjusted R2 | 0.376 | 0.255 | 0.193 | 0.149 | 0.277 | 0.303 |
Notes: Data in real monetary log-levels. Estimation methods: OLS (Ordinary Least Square) Robust. Estimated coefficients: Standardized coefficients. Standard errors of the standardized coefficients in brackets.
The linear regression model uses TFP as the dependant variable, while selecting variables associated with the digital transformation as separate regressors (Ballestar et al., 2020a). The results obtained clearly support the existing evidence of positive and significant coefficients for investment in R&D and product innovation in the three groups of firms analysed, as well as for both groups (frontier and non-frontier firms).
From Table 6 it can be also clearly seen that the performance of the different variables analysed varies between the groups of firms. The levels of workers assigned to R&D were favourable for large firms and for the industry as a whole, both for the 10% of frontier ‘gazelle’ firms as a whole and for 90% of follower firms. The results also indicate that robotisation has negative but significant values for all the group of firms. It seems that robotisation shows a negative result in the growth of TFP in the whole of Spanish industry, generating greater discrimination in productive growth.
The summary of the analysis of the Blinder-Oaxaca decomposition is reported in Table 7 below. As shown in the table, the probability of having a higher TFP is 11.19 for the group of 10% of frontier firms, and 9.14 for 90% of non-frontier firms, which implies an increase of 2.05 units of productive change between both groups. This implies that nearly 33% of the increase in productivity is due to the change in the effect of digital transformations on the coverage of the two groups. The remaining 67% of the increase is attributed to the change in the composition of the explanatory variables.
Blinder-Oaxaca decomposition estimates. 1991–2016.
| Mean | 0 | 1 | Cotton | Reimers | Neumark | |
|---|---|---|---|---|---|---|
| Group 1: | 11.19⁎⁎⁎ | |||||
| Group 2: | 9.14⁎⁎⁎ | |||||
| Difference: | 2.05⁎⁎⁎ | |||||
| Explained: | 0.37⁎⁎⁎ | 1.38 | 1.68 | 1.53 | 1.46 | 1.12 |
| Unexplained: | 1.68⁎⁎⁎ | 0.67 | 0.37 | 0.52 | 0.59 | 0.93 |
| % Unexplained: | 67.0 | 82.0 | 74.5 | 71.3 | 54.6 | |
| % Explained: | 33.8 | 18.8 | 25.5 | 28.7 | 45.4 | |
| Mean pred. High (H): | 11.193 | |||||
| Mean pred. Low (L): | 9.140 | |||||
| Raw Difference (R): | 2.052 | |||||
| - Due to Endowments (E): | 0.677 | |||||
| - Due to Coefficients (C): | 1.682 | |||||
| - Due to interaction (CE): | −0.306 |
Table 7 also shows the endowment factor, which implies that if non-frontier firms had the same productivity characteristics (in Mincer's sense), their TFP would be higher–the wage log would be, on average, 0.68 higher. The most cautious estimates, though, are those that describe the explained and unexplained part of the gap in relation to TFP–the unexplained coefficient is in absolute values more than twice the coefficient of the explained part of the equation.
On the whole, this analysis shows how the gap between 10% and 90% was decomposed into components. The results of the decomposition analyses indicate that certain digital factors together explain a large part of the TFP inequalities. In relation to the selected predictor variables (ITCI, R&D, PRODIN, PROCIN, R&DEMP and ROB) they explain 33% of the TFP of non-frontier firms and 18% of frontier firms.
In addition, the table shows how the explained and unexplained portions of the outcome gap vary according to the decomposition used. In this case, the decompositions of Cotton, Reimers, and Neumark have been used. The results obtained show that, regardless of the decomposition used, there is a clear difference in the average values of the R&D, ITC, workers in R&D, innovation product, innovation process and robotisation, which significantly explain the difference in TFP between the 10% of most productive firms and 90% of follower firms.
Likewise, the following Table 8 shows which digital-based complementarities variables generate a productivity gap between frontier and non-frontier firms. In this table we take the different decompositions (Blinder-Oaxaca, Cotton, Reimers, and Neumark). Based on the results obtained by focusing on the Neumark decomposition, it can be seen that there is a variable which positively influences the growth of TFP non-frontier firms: product innovation. However, in the case of frontier firms, it is the set of digital-based complementarities variables which imply an improvement in TFP for frontier firms: investment in R&D, innovation in process, and employees dedicated to R&D. ICTI and robotisation do not show any implication of improving TFP for the gazelle group or for the follower group, as they take a value of 0.
Blinder-Oaxaca decomposition estimates. 1991–2016.
Where, C are coefficient; CE is interaction; D = 0 and 1 are the analysis groups.
This study has reviewed the literature on two key issues in the Spanish economy, namely the discussion on divergence or convergence between frontier firms (10% of firms with the highest production values) and non-frontier firms (the remaining 90% of firms) during the period between 1991 and 2016. The relationship between TFP growth and the use of ICTI, investment in R&D, and robotisation, amongst other variables, has also been analysed.
Productive divergence/convergenceThe relevant analysis carried out on the TFP variable has shown a concrete reality. In this sense, it has been possible to observe a clear divergence between gazelle and follower firms, understanding divergence as a dispersion in productivity and convergence as the closeness in productivity to leading firms (Berlingieri et al., 2017). The tangibility shown by long-term trends in TFP is confirmed by the literature (Andrews et al., 2015; Cuadrado, Moral-Benito & Solera, 2020).
The literature has indicated a divergence between frontier and non-frontier firms in recent years. For example, Añón-Higón et al. (2017)) observe a clear divergence between leading and follower firms in European industry for the period between 2003 and 2014. Similarly, Andrews et al. (2016) evidence such divergence for a sample of 24 OECD countries. Thus, divergence has been determined by the analysis of the entire industrial fabric of nations, without making a distinction between SMEs and large firms.
In trying to assess hypothesis 1 on the increase in TFP divergence between leading and follower industrial firms, our results are similar to the conclusions reached in the literature (Criscuolo, Gal & Menon, 2014), but we obtain new results, which can potentially enlarge the extant research. As regards to economic and institutional factors at the firm level, we find that firm size plays a significant role as a determinant of the distance of firms from the Spanish frontier in terms of TFP. In particular, we show how leading firms increase their distance from follower firms over the years under analysis.
It is worth noting how a debate is opening on the divergence of non-frontier firms from frontier firms in the case of Spanish industry. The literature shows that there has been a divergence between leading and follower firms in recent years (Andrews et al., 2016; Añón-Higón et al., 2017; Criscuolo et al., 2014).
Results also confirm hypothesis 1a, which states that TFP divergence increases between leading and following SMEs, and hypothesis 1b, which posits the same with respect to large companies. A productive divergence for the Spanish industry as a whole is evidenced throughout the years of the observed sample.
Likewise, this reality shows a clear polarisation between groups of firms, which increasingly leads to a production gap between the most productive 10% and the remaining 90% (Berlingieri et al., 2017). In this sense, it can be concluded that SMEs are less ICT-intensive, so the introduction of ICTI generates significant efficiency gains, maintaining the productive dispersion between groups. Likewise, large firms with more intensive uses of digitisation depend more on what surrounds the use of technology (for example, organisational change or human capital), which may hinder the reduction of productivity differences between firms. In other words, the level of intensity of the uses of technology and its path in terms of efficiency improvements strongly influence the potential for divergence/convergence in productivity (Cette et al., 2016; Díaz-Chao et al., 2015).
Naturally, the dynamics generated in the national economy can lead to an increase in production divergence in the long term (Bahar, 2018; Decker, Haltiwanger, Jarmin & Miranda, 2016a). In this sense, there has been much debate in the literature about the causes of the international crisis in productivity growth (Andrews et al., 2015; Añón-Higón et al., 2017; Bahar, 2016; Syverson, 2016). When we analyse the reality of the Spanish industrial fabric under the temporal period analysed in this investigation, we look at the reality of TFP trends by sub-periods, where three periods "1991–2000″, "2001–2010″ and "2011–2016″ have been distributed. It has been clearly observed, through the Kruskal-Wallis test, that for both frontier and non-frontier firms there is a divergence in the average TFP with respect to the three periods. This result shows a clear average divergence of TFP. Therefore, there is a clear productive variability between groups in the long term (Bahar, 2018; Decker et al., 2016a).
Digital-based complementarities and TFPThe second group of hypotheses examined the differences between frontier and non-frontier firms, focusing on the question of how digital-based complementarities affect the improvement of TFP, as well as the generation of business production divergence.
Through the decomposition of Blinder-Oaxaca and other alternatives, where the estimate has been replicated through more flexible alternatives such as Cotton (1988); Neumark (1988); Oaxaca-Ransom (1994), as proposed by Jann (2008), it has been possible to verify how in frontier and non-frontier firms the incentive mechanisms in relation to investment in R&D, and the use of ICT are influential with respect to the productive difference. Therefore, it can be deduced that the returns on investment in the innovation variables (product) generate a competitive advantage related to TFP (Camiña et al., 2020; Gal et al., 2019).
Regarding robotisation, although the literature shows a positive and significant relationship with the productivity of the firms (Müller, Fay & Vom Brocke, 2018), the results obtained in this research show a negative relationship for both frontier and non-frontier firms. However, this relationship is significant for non-frontier firms, both for SMEs and for large firms. In view of these results, hypothesis 2 is partially confirmed for SMEs (hypothesis 2a) and large firms (hypothesis 2b).
Limitations and further researchThis study has certain limitations. In addition to some of the variables used in the assessment of new technologies, perhaps the most significant limitation is the estimation of TFP. However, the data from the study allows us analysing and obtaining a correct estimate. Nevertheless, researchers should consider new approaches to the availability of data for other territories or groups of firms.
This research has analysed digitalisation, as well as investment in R&D, amongst other variables that are considered to be the main variables in the evolution of industry 4.0. Unfortunately, we do not have all the values needed to construct this digital transformation, so the lack of data with regard to Internet of Things, cloud computing, additive manufacturing or 3D printing limits our conclusions. In this sense, the capacity for transformation (Camiña et al., 2020; Frank, Dalenogare & Ayala, 2019) constitutes a future research avenue.
Finally, it is proposed for future research to include a deeper understanding of the relationship between different levels of TFP growth and the competitive strategy of large and small Spanish firms. As well as an update of the sample in terms of the period analysed.
Firm strategy and policy implicationsIn this context, business management and public policy should intensify programmes to support ICT investment processes, to enable envisioning and encouraging the digital transformation and entering a phase of greater competitiveness. Special mention should be made of those programmes that emphasise knowledge management that may involve the assessment of both strategic and transformational capabilities. In this context, reference could be made to human capital, as well as the management of innovation, technology, digitisation, and robotisation, amongst others (Camiña et al., 2020).
Therefore, it has been observed that for firms in the Spanish industrial fabric there are barriers to innovation that limit the capacities and potential for improving productivity, so that comprehensive strategies and policies should be aimed at seeking the complementarity of new knowledge in order to improve productivity (Andrews et al., 2016). In this regard, capital deepening and robotisation are the variables that have a direct influence on the TFP growth of both SMEs and large firms. However, in relation to the frontier firms of large firms it shows a negative relationship.
Similarly, a clear commitment to and promotion of second wave digital transformation processes must be made (Ballestar, Camiña, Díaz-Chao & Torrent-Sellens, 2020b). Therefore, it is important to take into consideration strategies and public policies that promote the dissemination of knowledge, so that SMEs can take advantage of this wave (including innovation, training and capitalisation mechanisms) in the most efficient way possible to provide incentives to improve productivity and internationalisation of firms in a competitive market (Bartlesman et al., 2014).
This economic dynamic and firm commitment implies that the SMEs with the highest degree of innovation and leadership in the competitive context mentioned above could take advantage of all the competitive and productive potential in the long term, thus reducing the productivity gap on the global frontier (Andrews et al., 2016; Añón-Higón et al., 2017; Ballestar et al., 2019).
The results obtained in this research suggest that three types of public policy are required for small firms in the Spanish industrial fabric to improve their productivity. First, public policies must actively and jointly promote investment in R&D, as well as the use of ICT, organisational change, and the training of employers and workers (Díaz-Chao et al., 2015). Secondly, incomplete public policies designed to promote the use of ICTI and the correct consideration of all the co-innovative factors will not allow sustained growth in productivity in the medium and long term. Lastly, public policies must encourage internationalisation, as the introduction of international competition enables the phenomenon of learning-by-exporting to be more closely linked to productivity.
ConclusionThis research has concluded that the growth of TFP, as well as the generation of greater production divergence is due to greater investment in ICT, R&D activities, as well as product innovation. These results suggest that, in its current form, digitisation and its complementarities are driving differences in productivity amongst the fabric of industrial firms in Spain. So that the following firms are not left behind, some strategic actions and comprehensive public policies are proposed. These actions should consider the multidimensionality of causes related to the productivity gap. Based on the results obtained, it is of special importance to attend to the complementarities that are established between the uses of digitalisation, R&D activity and product innovation. This would imply continuing to expand and adapt human capital stocks, reorganize firms to better adapt them to digital transformation, and continue to promote their internationalisation processes, so that, through learning-by-exporting, they continue to improve their productivity levels.
See Table A1, Table A2, Table A3
Descriptive and frequency statistics (dimension: value 0, 200 employees or fewer; value 1, more than 200 employees) of the sample of Spanish manufacturing firms. 1991–2016.
Correlation matrix.
| SMEs | ||||
| Added Value | Intermediate Cost | Labour | Capital | |
| Added Value | 1 | |||
| Intermediate Cost | 0.806⁎⁎⁎ | 1 | ||
| Labour | 0.931⁎⁎⁎ | 0.797⁎⁎⁎ | 1 | |
| Capital | 0.809⁎⁎⁎ | 0.745⁎⁎⁎ | 0.832⁎⁎⁎ | 1 |
| Large firms | ||||
| Added Value | Intermediate Cost | Labour | Capital | |
| Added Value | 1 | |||
| Intermediate Cost | 0.747⁎⁎⁎ | 1 | ||
| Labour | 0.883⁎⁎⁎ | 0.769⁎⁎⁎ | 1 | |
| Capital | 0.741⁎⁎⁎ | 0.701⁎⁎⁎ | 0.766⁎⁎⁎ | 1 |
| Total industry | ||||
| Added Value | Intermediate Cost | Labour | Capital | |
| Added Value | 1 | |||
| Intermediate Cost | 0.885⁎⁎⁎ | 1 | ||
| Labour | 0.963⁎⁎⁎ | 0.882⁎⁎⁎ | 1 | |
| Capital | 0.886⁎⁎⁎ | 0.844⁎⁎⁎ | 0.898⁎⁎⁎ | 1 |
*p < 0.1.
⁎⁎p < 0.05.
See Table B.1
Descriptive analysis of the independent variables for frontier and non-frontier firms for Spanish manufacturing firms by different years. 1991, 2000, 2010 and 2016.
Notes: TFP refers to the logarithm of total factor productivity; labour productivity refers to the logarithm of output-labour; capital deepening refers to the log-capital-labour ratio. Data in real monetary levels. Standard Deviation (S.D.) in brackets.