Research on cognitive development suggests that the human being has a number sense called "Approximate Number System" (ANS). There are also different characteristics for the representation system of symbolic numbers, called "Accuracy Number System". In this context, the aims of the study were: (a) to identify and longitudinally evaluate the development of symbolic and non-symbolic magnitude representation skills; and (b) analyse the relationships between these skills and mathematical achievement. The present longitudinal study was carried out with a sample of 31 Early Childhood Education participants, for two years, with four evaluations timing. Results suggested that at the age of 4 years, symbolic magnitude processing abilities increased quickly until they surpass non-symbolic ones. On the other hand, the comparison of symbolic magnitudes had a higher predictive value on mathematical performance at the ages evaluated. It is discussed whether these skills may be of interest as detection and assessment tools in the field of mathematics, as well as for interventions in students with mathematics learning difficulties.
La investigación sobre el desarrollo cognitivo indica que el ser humano posee un sentido numérico al que se viene denominando “Sistema de Aproximación Numérica” (SAN). Existen también características diferentes para el sistema de representación de números simbólicos, denominado “Sistema Numérico Preciso” (SNP). En este contexto, los objetivos del estudio han sido: (a) identificar y evaluar longitudinalmente el desarrollo de las habilidades de representación de las magnitudes simbólicas y no-simbólicas; y (b) analizar las relaciones entre dichas habilidades y la competencia matemática. El presente estudio longitudinal, se ha llevado a cabo con una muestra de 31 participantes de Educación Infantil, durante dos años, con cuatro momentos de evaluación. Los resultados sugieren que en 3° de Educación Infantil (5 años), las habilidades de procesamiento de magnitud simbólica se incrementan rápidamente hasta superar a las no-simbólicas. Por otro lado, la comparación de magnitudes simbólicas ha tenido un mayor valor de predicción sobre el rendimiento matemático en las edades evaluadas. Se discute si estas habilidades pueden ser de interés como instrumentos de detección y evaluación en el ámbito de las matemáticas, así como para intervenciones en alumnado con dificultades de aprendizaje de las matemáticas.
Children’s arithmetic development has often been related to their ‘number sense’ (Dehaene, 2011; Devlin et al., 2022), which means having, among others, the ability to handle and represent non-symbolic magnitudes (e.g. points or other concrete objects). Research into cognitive development indicates that we possess a number sense known as the Approximate Number System (ANS) (Odic & Starr, 2018) that is considered innate. Numerous studies suggest that animals and humans share this congenital and universal ability to represent non-symbolic magnitudes (Bryer et al., 2022), the accuracy of which increases with age (Dehaene, 2011). Non-symbolic skills emerge early and develop over time (Braeuning et al., 2021). Libertus et al. (2011) assessed non-symbolic skills, finding that four-year-old children are able to complete a non-symbolic comparison task. Toll et al. (2015) also examined non-symbolic skills with a greater range of 1 to 100, finding similar results for four-year-old schoolchildren. Other studies (Barroso et al., 2021) explored non-symbolic comparison in children aged five years and older, concluding that it maintains a developmental continuum throughout childhood and even into adulthood (Hyde et al., 2014). During childhood development, non-symbolic skills are constantly reorganised until by adulthood they can successfully discriminate between sets with a ratio of 10:11 (Wang et al., 2021).
However, the symbolic number representation system, also known as the Precise Number System (PNS), has different characteristics: (1) it is an acquired system affected by the language faculties (Xenidou-Dervou et al., 2015); (2) it represents quantities precisely (Mussolin et al., 2014); and (3) with age, it can manipulate increasingly larger range with higher accuracy (Praet & Desoete, 2014). The ability to approximate numbers non-verbally is a relevant factor in quantitative reasoning throughout human development (Wang et al., 2021).
Research has also shown that symbolic skills usually appear at the age of five, generally before the start of formal education (Kolkman et al., 2013). Gilmore et al. (2007) argue that children can perform this task with the help of the ANS. It is plausible that they convert Arabic numerals into non-symbolic numerosities, showing a matching ability enabling the transformation process from a non-symbolic to a symbolic representation (Barth et al., 2009). This is one of the skills they must develop in order to achieve an understanding of the interconnections between symbols and the quantities they represent.
The relationship between symbolic and non-symbolic skills is subject to debate among researchers (Goffin & Ansari, 2019) and raises a number of unresolved research questions (Wong et al., 2022). Symbolic and non-symbolic skills are known to be different (Kolkman et al., 2013) and are based on two distinct systems that do not share the same underlying capacity (Xenidou-Dervou et al., 2015). Matejko and Ansari (2016) found that symbolic and non-symbolic magnitude processing skills have different developmental trajectories and that the development of the two formats is only related to each other in the first year of formal schooling (Grade 1 of primary school) when symbolic magnitude processing skills subsequently affect non-symbolic ones.
Other researchers consider that both non-symbolic and symbolic comparison skills are to some extent based on the ANS (Chen & Li, 2014; Van Marle et al., 2014). In addition, many studies have focused on analysing the relationship between non-symbolic and symbolic representation skills (Gobel et al., 2014; Kolkman et al., 2013; Toll et al., 2015). This correlation has at times not been as evident (Fazio et al., 2014). The results obtained are not fully consistent, meaning that the development of both trajectories is not clearly explained. One factor hindering this clarification is the use of overly difficult assessment tasks (Xenidou-Dervou et al., 2015) such as approximate sums. Due to this discrepancy, we believe it is relevant to determine the influence of symbolic processing on non-symbolic processing in the developmental age range of four to seven years, for which there are fewer conclusive results.
There is still ample scope for research into the association between non-symbolic representation and mathematical ability, which has not been completely resolved. Several studies have found positive correlations between non-symbolic representation skills and mathematical ability in children and adults (Chen & Li, 2014; Schneider et al., 2017). However, others have found no correlation between ANS accuracy and mathematics (Nosworthy et al., 2013; Lyons et al., 2014; Sasanguie et al., 2014).
Nonetheless, the literature has reached a certain consensus that symbolic skills have a significant impact on mathematical ability. Along these lines, Bugden and Ansari (2011) found this correlation to be significant among students in the first two years of primary school. Similarly, Toll et al. (2015) concluded that symbolic comparison skills are the most important predictor of mathematical ability. Van Marle et al. (2014) also researched the role of symbolic skills as a potential mediator of the relationship between non-symbolic magnitude processing in three to four-year-olds and mathematics at the end of the first year of early childhood education (ECE). They refer to a multiple mediation model that predicts the relationship between the ANS and mathematical performance mediated by the PNS. Similar results have also been found in six-year-old schoolchildren (Gobel et al., 2014). Finally, Scalise and Ramani (2021) conducted a longitudinal study with three to five-year-olds, finding that symbolic comparison skills are related to the development of subsequent understanding of cardinality, addition and problem-solving skills. It should also be taken into account that the developmental context has a significant impact on the chances of success, given that cognitive stimulation and emotional support are also critical variables in the adjustment of academic performance (Heckman, 2011).
In this context, the current study has two objectives: (1) to identify the developmental trajectories of non-symbolic and symbolic magnitude representation skills, which are assessed with magnitude comparison tasks. The available evidence shows discrepancies regarding the connections between these two comparison skills. (2) to analyse the relationship and mediation between symbolic and non-symbolic magnitude representation skills and mathematical ability in ECE from four to five years of age and the beginning of the second year of primary school (six to seven years of age). As suggested, several studies have focused on different age ranges and different amounts within and outside the subitisation range, generating diverse and non-matching results (Hutchison et al., 2020). This study focuses on the age range of four to seven years, with the hypothesis that the relationships between these three types of skills (symbolic comparison, non-symbolic comparison and mathematical performance) will differ as a function of the age and variation in the participants’ schooling over time.
MethodParticipantsForty-seven students in the 3rd year of ECE with typical development were selected incidentally to participate in a longitudinal study on the development of mathematical skills with four assessment stages. For various reasons, this initial sample eventually ended up with a total of 31 participants. The 16 participants lost were due to change of school, refusal of informed consent or other reasons unknown to the researchers. The sample consisted of 20 girls and 11 boys with an average age of 5.2 years [SD = 3.32 years; range 4(9) to 5(9)] in the first evaluation session. The participants were pupils of a middle-class public charter school in a city with 130,000 inhabitants.
InstrumentsTest of symbolic and non-symbolic numerical magnitude processing (Nosworthy et al., 2013). This tests symbolic magnitude processing skills using 56 pairs of Arabic digits (between 1 and 9) and non-symbolic comparison using 56 pairs of dot arrays in a printed booklet. The ratio (small/large) between pairs of numbers and dot arrays ranged from 0.11 to 0.89 (e.g. the ratio between 3 and 5 would be 0.60). Stimuli with relatively smaller proportions are presented sooner than those with larger proportions. The participants are given two minutes for each comparison type and have to mark with a pencil the element of the pair that is larger or in which there are more. McDonald’s Omega coefficient value for the symbolic comparison subtest was 0.735, and 0.722 for the non-symbolic comparison.
Test of Early Mathematics Ability (TEMA-3; Ginsburg & Baroody, 2003). This test assesses formal and informal concepts and skills in different domains: counting, number comparison, numeral literacy, mastery of number facts, calculation skills and understanding of mathematical concepts. It consists of 72 items and it has a McDonald’s Omega coefficient of 0.853.
ProcedureParticipants were individually assessed in a school setting appropriate for this type of test, in a quiet room in the school during school hours and respecting break times. The assessments were carried out by the authors, who have experience with this type of test. Each individual assessment was carried out in two sessions with a maximum duration of approximately 45min, following the instructions in the corresponding test administration manual. The timeline of the assessments under the longitudinal study and the tests administered at each stage are specified in Table 1.
Timeline of the longitudinal study assessment with the tests administered at each stage (T)
| Tasks administered | Early Childhood Education(5 years)(1st term) | Early Childhood Education(5 years)(3rd term) | Primary Education (Year 1)(6 years)(1st term) | Primary Education (Year 2)(7 years)(1st term) |
|---|---|---|---|---|
| T1Start of year | T2End of year | T3Start of year | T4Start of year | |
| Comparison of symbolic and non-symbolic magnitudes | X | X | X | X |
| Test of Early Mathematics Ability (TEMA-3) | X | X | X |
Prior to starting the study, written informed consent was obtained from both the parents of the participants and the school. All applicable legal and ethical protocols were followed during the course of the study, both in relation to authorisations and data protection. This study followed the International Code of Conduct for Humanities and Social Sciences of the Centre for Research Ethics and Bioethics.
Data analysisFirstly, descriptive analyses were carried out to examine the trends in the data and their distribution in order to explain the results of the sample used in the study. Similarly, inferential analysis was performed using repeated measures ANOVA, taking into account the administration of the same tests at different stages of development and post-hoc Bonferroni tests to assess the differences between the specific means. The data meet the condition of sphericity (Mauchly’s W), with the associated probability being greater than p > .05 (W = 917, p = .33). Correlations were also calculated to study the association between two numerical variables and their increasing or decreasing trend. Linear regression analyses were performed to study the predictive weight of symbolic and non-symbolic comparison on mathematical competence at the different stages, revealing the percentage of variability in early mathematical competence when taking magnitude comparison skills as predictor variables. Finally, a simple mediation analysis was carried out with PROCESS (3.4.1) using the causal steps approach (Baron & Kenny, 1986) and based on regression analysis, with the aim of establishing a possible causal explanatory model of the relationship between the ANS and mathematical competence and its mediating variables.
ResultsDevelopment of symbolic and non-symbolic magnitude processing skillsThe students were highly accurate with both symbolic and non-symbolic comparisons, which may suggest a good understanding of the instructions. Additional statistical analyses were carried out of the total number of correct items. Table 2 shows the statistical values calculated for the study variables at the four assessment stages.
Mean, standard deviation and range calculated for the longitudinal study variables. Assessment stages T1, T2, T3 and T4
| Symbolic comparison | Non-symbolic comparison | TEMA-3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | T1 | T2 | T3 | T4 | T1 | T2 | T4 | |
| M | 31.29 | 39.51 | 44.45 | 51.74 | 35.35 | 39.38 | 43.80 | 47.64 | 18.45 | 25.87 | 48.03 |
| SD | 10.40 | 7.99 | 9.18 | 5.34 | 6.56 | 6.37 | 6.14 | 6.21 | 4.22 | 5.85 | 8.23 |
| Range | 9−55 | 15−51 | 18−56 | 40−56 | 25−47 | 25−47 | 27−54 | 36−56 | 9−28 | 13−42 | 32−67 |
To assess how symbolic and non-symbolic magnitude processing skills change over the period between the third year of ECE (four to five years old) and the beginning of the second year of primary school (six to seven years old), a repeated measures ANOVA was conducted with the task type (symbolic vs non-symbolic) and assessment stage (T1, T2, T3 and T4) as comparison factors. This analysis revealed that there was no principal effect for the task type: F(1, 30)=0.053, p=.819, η2 = 0.002. However, there was a principal effect for the assessment stage: F(3, 90)=56.19, p< .0001, η2 = 0.65, with accuracy increasing over time. There was also a task x time interaction effect: F(3, 28)=11.48, p< .0001, η2 = 0.27. The participants performed better on the non-symbolic task (M=35.35, SD=6.56) than the symbolic task (M=31.29, SD=10.4) at T1, while performance on the symbolic comparison improved over the course of the longitudinal study more than the non-symbolic task (MT1=31.29, MT2=39.51, MT3=44.45; MT4=51.74). Post-hoc Bonferroni corrections were conducted to examine the quantitative characteristics of the task x time interaction. The participants showed better results in the non-symbolic task at T1 (p < .0001). At T2 and T3 the differences were not significant (p=.33). The data suggest that non-symbolic performance is superior to symbolic performance at the first assessment stage (T1) (four-year-old ECE students). Subsequently (T4), once again there were statistically significant differences at the beginning of the second year of primary school (seven years old), when the results in the symbolic task were clearly superior to the non-symbolic task (p < .0001). Meanwhile, the results of the correlations (Table 3) indicate that symbolic and non-symbolic performance correlates significantly at T1 (r(31)=0.57, p< .001), T2 (r(31)=0.68, p< .001]), T3 (r(31)=0.60, p < .0001) and T4 (r(31)=0.65, p < .0001).
Pearson correlations calculated between the different tests administered in the longitudinal study
| Variable | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. CS1 | 1 | 0.577** | 0.500** | 0.314 | 0.352 | 0.324 | 0.296 | 0.130 | 0.331 | 0.303 | 0.406* |
| 2 CNS1 | 1 | 0.183 | 0.183 | −0.093 | 0.079 | 0.014 | 0.061 | 0.265 | 0.239 | 0.315 | |
| 3. CS2 | 1 | 0.685** | 0.608** | 0.420* | 0.680** | 0.366* | 0.422* | 0.392* | 0.482** | ||
| 4. CNS2 | 1 | 0.378* | 0.521** | 0.497** | 0.515** | 0.328 | 0.295 | 0.426* | |||
| 5. CS3 | 1 | 0.604** | 0.590** | 0.352 | 0.108 | 0.240 | 0.257 | ||||
| 6. CNS3 | 1 | 0.264 | 0.229 | 0.290 | 0.327 | 0.459** | |||||
| 7. CS4 | 1 | 0.654** | 0.340 | 0.387* | 0.505** | ||||||
| 8. CNS4 | 1 | 0.330 | 0.356* | 0.326 | |||||||
| 9. TEMA-3 T1 | 1 | 0.819** | 0.717** | ||||||||
| 10. TEMA-3 T2 | 1 | 0.708** | |||||||||
| 11. TEMA-3 T4 | 1 |
To investigate the nature of the relationship between symbolic and non-symbolic performance at the assessment stages, several regressions were carried out to determine whether symbolic and non-symbolic performance at T1, T2 and T3 predicted scores at T2, T3 and T4 respectively (see Table 4). The first linear regression (1.a) using the symbolic score of T2 as the dependent variable (and the symbolic and non-symbolic comparison of T1 as the predictor variable) is statistically significant: F(2, 30)=5.09, p< .013. In this model, only the T1 symbolic scores predict a unique variance in T2 symbolic scores (the non-symbolic comparison had no predictive value).
Results of the linear regression analysis (1.a and 1.b) to predict symbolic comparison skill based on scores in symbolic and non-symbolic comparison tests as predictor variables at T1, T2, T3 and T4
The second linear regression (1.b.) using the symbolic score of T3 as the dependent variable and the symbolic and non-symbolic scores of T2 as predictor variables was significant: F(2, 30)=8.308, p<.001. In this case, only the T2 symbolic scores (but not the T2 non-symbolic scores) predicted a unique variance in T3 symbolic scores.
Finally, the linear regression using the symbolic score of T4 as the dependent variable and the symbolic and non-symbolic scores of T3 as predictor variables was significant: F(2, 30)=7.919, p< .002. Only the symbolic scores of T3 predicted a unique variance in T4 symbolic scores. Once again, the non-symbolic score had no predictive value for the symbolic score. Another series of linear regression analyses (2.a) was conducted with the non-symbolic scores of T2, T3 and T4 as the dependent variable and the symbolic and non-symbolic scores of T1, T2 and T3 as predictors (see Table 5).
Results of the linear regression analysis (2.a, 2.b and 2.c) to predict non-symbolic comparison skills based on scores in symbolic and non-symbolic comparison tests as predictor variables at T1, T2, T3 and T4
| T2 | T3 | T4 | ||||
|---|---|---|---|---|---|---|
| β | t | β | t | β | t | |
| Symbolic comparison | 0.311 | 1.418 | 0.119 | 0.539 | 0.337 | 1.51 |
| Non-symbolic comparison | −0.004 | 0.017 | 0.439** | 0.199 | 0.026 | 0.117 |
The prediction with the symbolic and non-symbolic score at T1 on the non-symbolic score at T2 was not significant: F(2, 30)=1.527, p = .235 and the symbolic and non-symbolic scores at T1 did not predict a unique variance. The second linear regression (2.b.) using the non-symbolic score of T3 as the dependent variable and the symbolic and non-symbolic scores of T2 as predictor variables was significant: F(2, 30)=5.403, p<.01. Only the non-symbolic scores of T2 predicted a unique variance in T3 non-symbolic scores. In the last linear regression calculated (2.c.) the non-symbolic score of T4 was used as the dependent variable and the symbolic and non-symbolic scores of T3 as predictor variables. These were not significant: F(2, 30)=1.99, p=.056. Neither the symbolic scores nor the non-symbolic scores of T3 predicted a unique variance in the non-symbolic scores of T4.
Symbolic and non-symbolic magnitude processing and mathematical competenceTable 2 shows the mean scores of the participants in TEMA-3 at three stages of the study: (T1), (T2) and (T4). In the last assessment (six to seven years old) the participants had already completed the first year of primary school and were starting the second year. The means show an important advance in the development of mathematical skills (MT1 = 18.45, MT2 = 25.87, and MT4 = 48.03), along with a greater standard deviation and an increase in the differences in terms of mathematical competence as the participants advance with their schooling. The differences were significant between T1 and T2: t(31) = -12.13, p < .0001 and also between T2 and T4: t(31) = -21.22, p < .0001. These differences suggest an improvement in mathematical skills between the last year of ECE and the beginning of the second year of primary school. Subsequently, regression analysis was conducted for T1, T2 and T4 to calculate the unique contribution of the two types of magnitude processing to the mathematical results of TEMA-3.
Table 6 shows the standardised beta coefficients and significance levels of the regression models at each stage of the mathematics performance assessment. At T1 (the start of the third year of ECE) the two magnitude processing components explain a variation of 15%. However, neither symbolic nor non-symbolic comparison had a significant effect on performance in TEMA-3. The same occurs at T2 where the variation is 16%, with no significant effect of magnitude processing. At T4, magnitude processing explains 25% of the variance in TEMA-3, but only symbolic comparison has a significant effect: F(2, 30)=4.79, p < .016. The predictive effect of the non-symbolic comparison was not significant in any of the regression analyses performed.
Results of the regression analysis of symbolic and non-symbolic comparison in the results of TEMA-3 at the different assessment stages
| T1 | T2 | T4 | ||||
|---|---|---|---|---|---|---|
| β | t | β | t | β | t | |
| Symbolic comparison | 0.268 | 1.23 | 0.358 | 1.49 | 0.510* | 2.366 |
| Non-symbolic comparison | 0.110 | 0.507 | 0.049 | 0.207 | −0.008 | −0.036 |
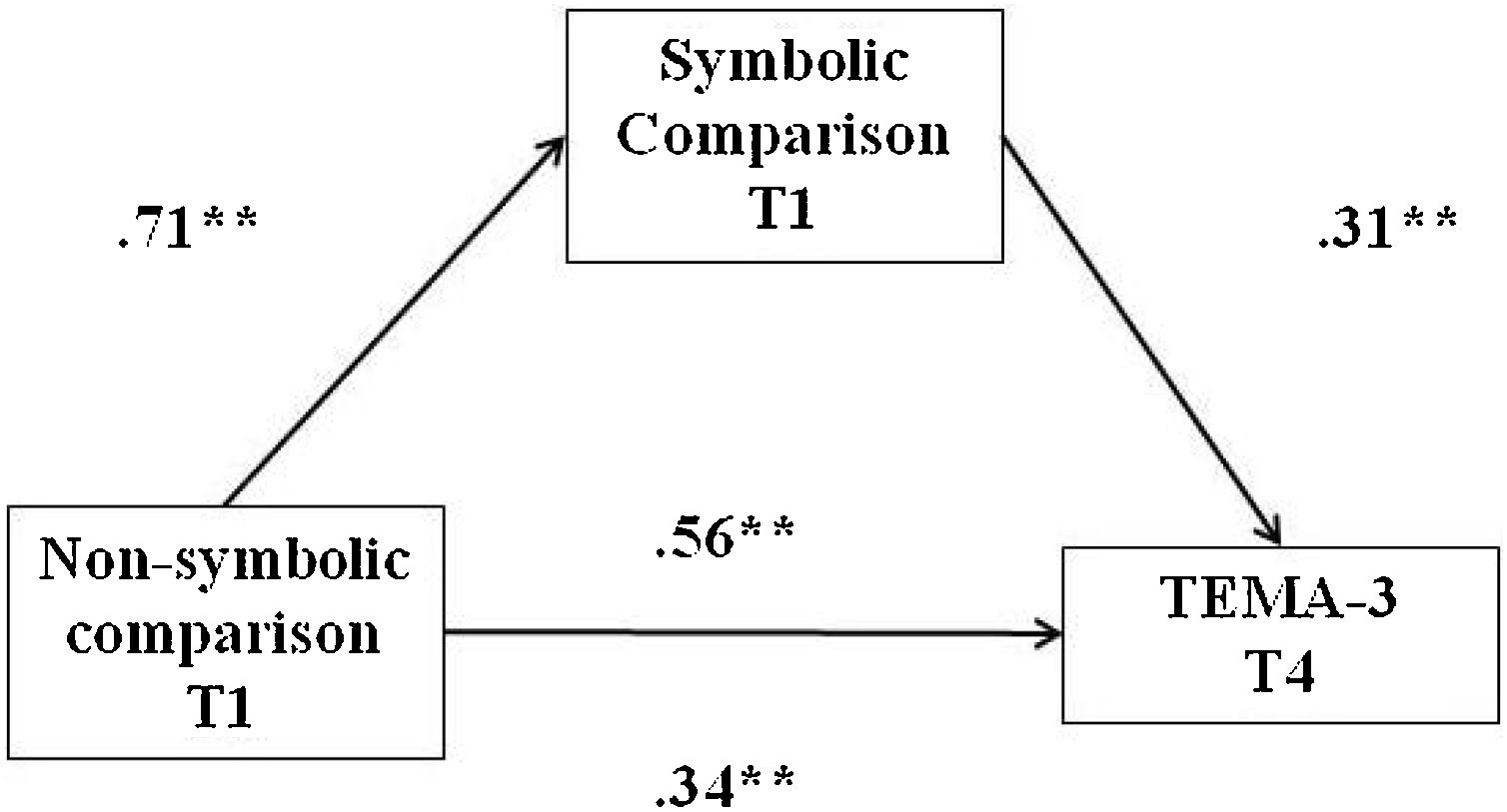
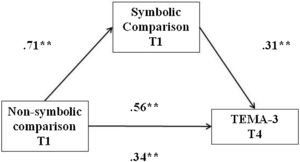
The mediation analysis conducted to determine the effect of the symbolic component on mathematics performance yielded a mediation model where non-symbolic comparison at T1 predicts mathematics performance at T4, mediated by symbolic comparison (see Figure 1).
Finally, with regard to the analysis of the indirect effects of non-symbolic comparison (VI) on mathematical competence (DV) considering the mediating role of symbolic comparison, the following results were obtained: β=0.18, SD=0.08, 95% CI=0.04−0.38. Considering the confidence interval, it can be seen that the effect of the mediating variable is statistically significant. To sum up, non-symbolic comparison skills at T1 had an effect on early mathematical competence at T4, which is mediated by symbolic comparison skills at T1. Similarly, the results deriving from the calculation of the inverse model with non-symbolic comparison as the mediating variable have also been included. The results were as follows: β=0.15, SD=0.07, 95% CI=0.001−0.292. In light of the results, the effect of non-symbolic comparison at T1 as a mediating variable in the prediction of symbolic comparison at T4 is significant, but with values very close to zero in the confidence interval, it is no longer significant at T2 (β=0.14, SD=0.08; 95% CI = −0.009−0.325). This pattern was also repeated at T4 (β=0.11, SD=0.07, 95% CI = −0.03−0.27).
DiscussionThe first aim of this study was to identify the developmental trajectories of non-symbolic and symbolic magnitude representation skills through assessment with magnitude comparison tasks. Very few longitudinal studies of these trajectories have been conducted. The study by Matejko and Ansari (2016) was limited to analysis of a single academic year at the beginning of formal education: five-year-old participants perform better on the non-symbolic task than on the symbolic task. However, as they learn mathematics more formally, the advantage of non-symbolic skills disappears. Our results support this conclusion. At each stage of the assessment, the predictor variable (symbolic comparison) had more weight than non-symbolic comparison. As they learn more about the symbolic representation system, students’ advantages in terms of non-symbolic ability seem to have less influence. The first year of formal schooling is an important period for the development of symbolic processing skills (Nosworthy et al., 2013). They grow rapidly until they match and eventually surpass non-symbolic processing skills. The present data replicate these findings, as well as showing that symbolic processing skills have a different developmental trajectory to non-symbolic skills in the transition from ECE to primary school, where symbolic skills improve at a faster rate (Malone et al., 2021).
In the school context of the present study, at the beginning of the second year of primary school (seven years old) after one year of formal schooling, the results suggest that the developmental trajectories for symbolic and non-symbolic skills are divergent and may continue to be so in the future, remaining different from each other until adulthood (Lyons et al., 2012). The question of how children learn the meaning of symbolic numbers remains unanswered. Our results show that symbolic and non-symbolic skills are not as closely linked as might be expected during a period when students are rapidly developing fluency with symbolic numbers. If symbolic and non-symbolic formats had the same underlying representation throughout the first year and beginning of the second year, the changes in one system would lead to changes in the other. However, no such relationship was found over the entire period studied (2 years). Changes in non-symbolic performance are not always related to changes in symbolic performance at the different assessment stages, eventually reaching a point where they are independent to each other. Before reaching that stage, our mediation analysis suggests that symbolic processing contributes to the explanatory power of non-symbolic processing in relation to mathematical performance.
However, not all the available evidence points to these different developmental trajectories for symbolic and non-symbolic magnitude processing. In the study of magnitude processing skills from ECE through to the first year of primary school, Toll et al. (2015) found a moderate relationship between the development of symbolic and non-symbolic skills, suggesting that the two formats influence each other. The results also show that symbolic comparison is the most significant predictor of number line estimation and basic mathematical achievement. However, our reverse mediation analysis does not show that symbolic processing is mediated by non-symbolic processing. In line with Matejko and Ansari (2016), one explanation for the contrasting results could be the differences between tasks. The magnitude comparison task in our study used digits from 1 to 9, while Toll et al. (2015) used digits ranging from 0 to 100. In the present study, there was no statistically significant relationship between the development of the trajectories of the symbolic and non-symbolic formats, except at T4. This probably indicates that the speed of the change in symbolic and non-symbolic processing skills differs over time, especially after formal education has already begun.
The second aim of this study was to determine the associations between symbolic and non-symbolic magnitude representation skills and their influence on mathematical performance. We found a significant effect of symbolic skills on mathematical performance, but not for non-symbolic skills. The literature also yields different results, especially in relation to non-symbolic comparison. Fazio et al. (2014) proposed three hypotheses for the relationship between non-symbolic and symbolic skills and mathematical ability, concluding that non-symbolic skills can have direct, indirect or independent effects on mathematical performance. Our results suggest that there may be an influence of non-symbolic skills on mathematical skills through symbolic skills (see the mediation analysis). However, there is limited direct input from non-symbolic processing so the third hypothesis of Fazio et al. (2014) seems more plausible. These results coincide with those of Van Marle et al. (2014), who found that the relationship between non-symbolic skills and mathematical performance is mediated by symbolic skills, in line with the mediation model in our study. Overall, the results obtained show that symbolic processing has an important impact on mathematical performance in the age range studied. This is in line with the results of Li et al. (2018) at five to seven years of age. However, this is not the case for eight-year-olds, for whom the impact of symbolic processing ceases to be significant for mathematical performance assessed with TEMA-3. On the other hand, Schneider et al. (2017) found that magnitude processing is associated with lifelong mathematical competence across a wide range of mathematical tasks and that the association is stronger for symbolic than for non-symbolic numerical magnitude processing, as our results also show. Moreover, symbolic number processing is a consistent and significant predictor of arithmetic achievement scores, while non-symbolic number processing is not (Bartelet et al., 2014).
Finally, the results of Xenidou-Dervou et al. (2017) show that symbolic and non-symbolic comparisons have different developmental trajectories, with symbolic comparison improving more than non-symbolic comparison. Both these skills are better longitudinal predictors of students’ future mathematical performance than variables such as IQ and working memory. Non-symbolic comparison appears to be moderately predictive only at ECE level, while symbolic comparison predicts mathematical performance well over the three years of the longitudinal study.
Limitations and future lines of researchOne limitation of this study is the limited size of the sample, meaning that the results should be viewed with caution to avoid false extrapolations. Furthermore, tasks assessing symbolic and non-symbolic magnitude comparison using a pencil and paper test have certain limitations, as they may be affected by differences in the participants’ hand-eye coordination which may vary significantly across the age range assessed. However, it is important to note that the Numeracy Screener by Nosworthy et al. (2013) used in the current study produced comparable results in multiple studies in different cultural contexts and age groups (Lau et al., 2021). Finally, the developmental context and cognitive, emotional and socio-demographic characteristics are also relevant in the analysis of mathematical performance (Heckman, 2011). Future lines of research in the study of the developmental trajectories of symbolic and non-symbolic magnitudes should investigate whether or not there is a bidirectional relationship between the comparison formats in different or larger subitising ranges (Goffin & Ansari, 2019).
ConclusionsThe findings of this study demonstrate the importance of symbolic processing as a predictor of early mathematical achievement and may have significant implications for assessment and educational practice. Our results suggest that symbolic magnitude comparison skills could potentially be used for early identification of students with mathematical difficulties. Future research could also explore experimentally in greater depth whether an improvement in mathematical performance is achieved following application of symbolic magnitude comparison training programmes for formal school pupils. The possible effect of symbolic processing skills on early development and education suggests that improving these skills could influence overall mathematical performance in later years of schooling.