En muchos estudios médicos, y especialmente en los relacionados con el campo de la pediatría, es muy común que la variable principal que se desea estudiar sea el tiempo que tarda en ocurrir un suceso, ya sea éste beneficioso (tolerancia a la leche, alta hospitalaria) o perjudicial (muerte, recaída), o incluso indiferente (cambio de tratamiento). El conjunto de técnicas estadísticas que se utilizan para analizar este tipo de datos se conoce en medicina como análisis de supervivencia1.
La ventaja que ofrecen estas técnicas es que permiten generalizar el análisis de respuestas binarias (sí/no; fallecido/vivo, etc.), incluyendo el tiempo de seguimiento, es decir, el tiempo transcurrido desde el inicio del seguimiento hasta producirse la respuesta o hasta el final del seguimiento, si la respuesta no se ha producido. Además, este tiempo que se analiza se puede valorar en condiciones muy flexibles, porque la duración del período de observación puede ser muy diferente para cada individuo.
Puntos clave
El análisis de supervivencia es un conjunto de técnicas estadísticas en las que la variable respuesta es el tiempo que transcurre entre el comienzo de seguimiento del individuo en el estudio y la aparición del evento de interés (tolerancia a la leche, muerte, etc.). Con frecuencia suele ocurrir que los individuos abandonen el estudio antes de que presenten el evento, con lo que sólo se obtiene información parcial (censura) de la variable de interés.
El objetivo del análisis de supervivencia es incorporar esta información parcial que proporcionan los individuos censurados mediante métodos desarrollados para este fin.
Los antecedentes más lejanos se pueden situar en el siglo XVII, con la elaboración de tablas de mortalidad de la ciudad de Wroclaw que publicó el astrónomo Edmond Halley. Sin embargo, el análisis de supervivencia, tal como se conoce hoy, tiene sus raíces en la ingeniería, y está encaminado a analizar la duración y la fiabilidad de los diferentes elementos que forman una máquina. La Segunda Guerra Mundial aceleró el desarrollo de estas técnicas. En ciencias de la salud, el auge de estas técnicas empezó hacia los años setenta del siglo XX. Durante las últimas 2 décadas, el análisis de supervivencia se ha convertido en una de las herramientas más importantes de la investigación clínica y epidemiológica2.
Así pues, para realizar un análisis de supervivencia, sólo se necesitan un par de variables: el tiempo de seguimiento del individuo y una variable binaria que indique si se produce o no el evento.
Conceptos básicosLa observación de cada paciente se inicia al diagnosticar la enfermedad, en la intervención quirúrgica, etc. (tiempo = 0), y continua hasta que se produce el evento o hasta que el tiempo de seguimiento se interrumpe. Cuando el tiempo de seguimiento termina antes de producirse el evento, o antes de completar el período de la observación, se habla de individuo censurado.
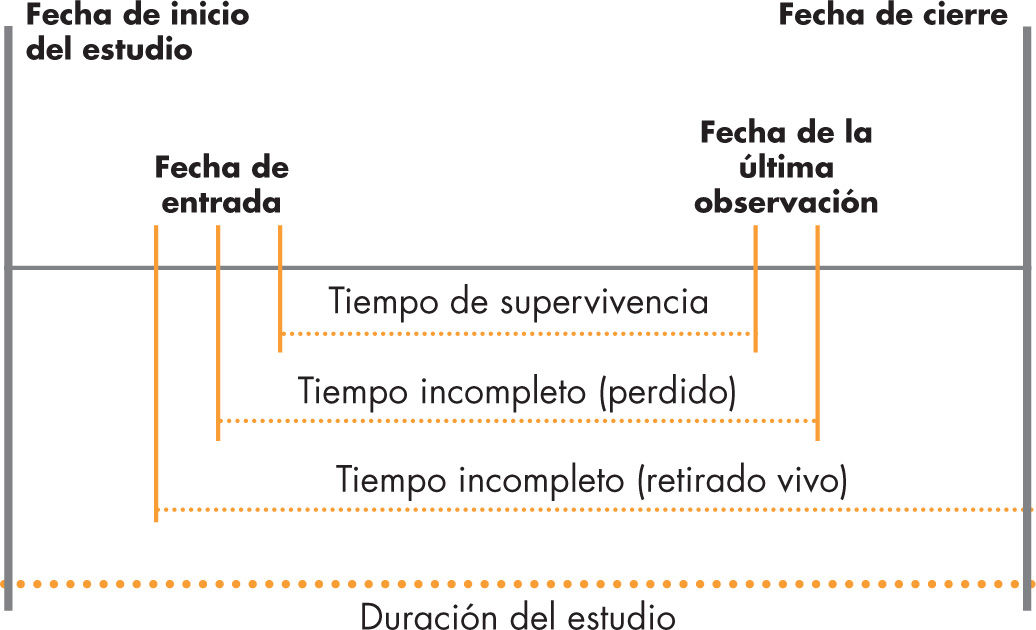
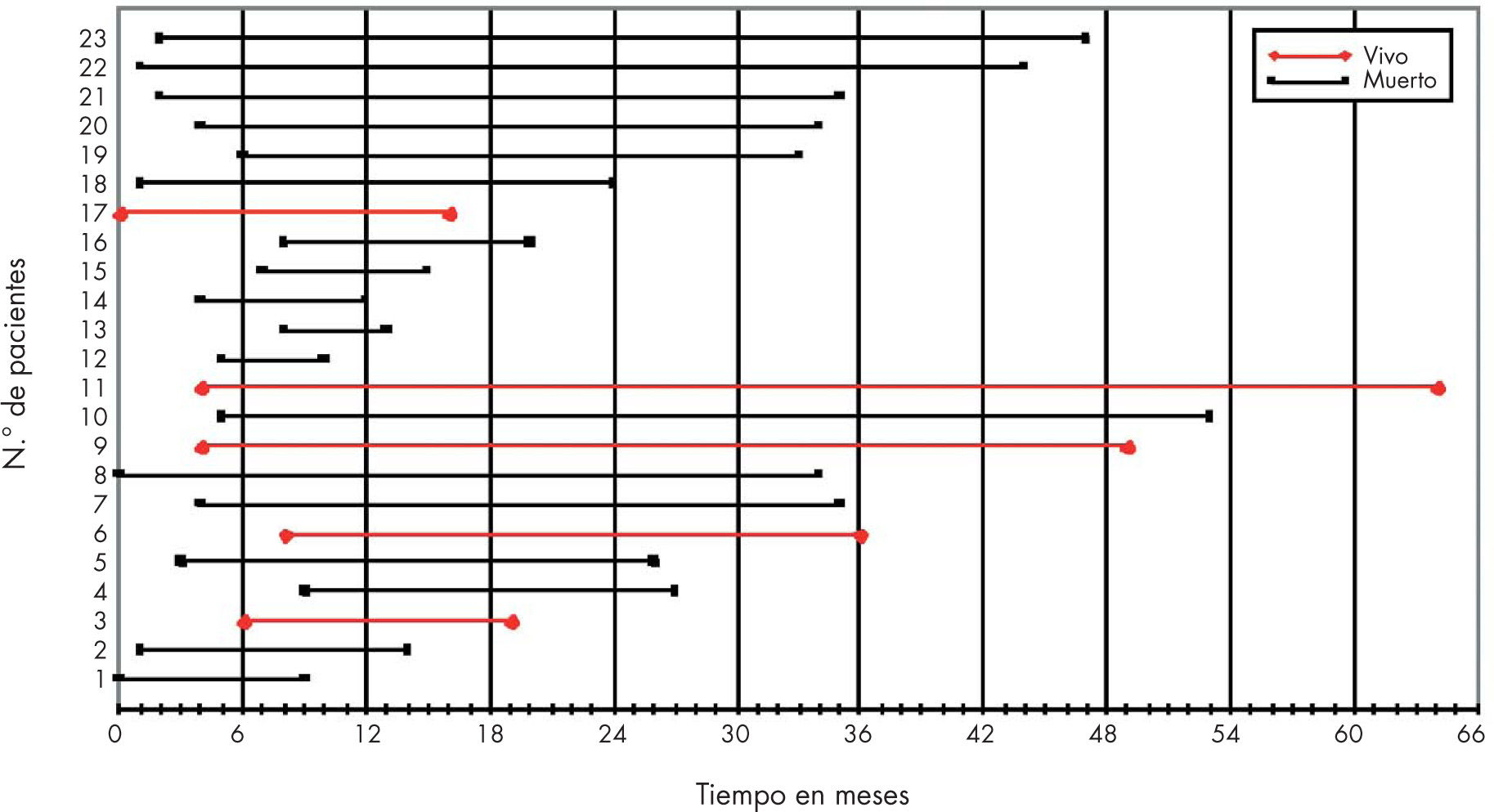
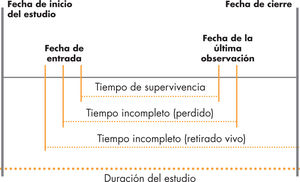
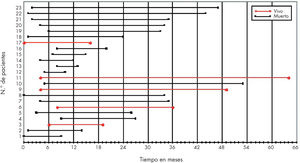
El seguimiento está definido por una fecha de inicio y una fecha de cierre (fig. 1). Estas fechas son distintas para cada individuo, ya que los pacientes incluidos en el estudio se incorporan en momentos diferentes (fig. 2).
El tiempo de supervivencia se define como el tiempo transcurrido desde el estado inicial hasta el estado final.
Este estado inicial debe definirse de manera que la fecha en que se produce el evento pueda conocerse exactamente (fecha de diagnóstico, fecha de nacimiento, etc.).
El acontecimiento o suceso estudiado (episodio) también debe estar perfectamente definido para poder determinar exactamente su fecha. Este episodio está casi siempre asociado a la muerte del paciente, pero no tiene porque ser así, ya que puede hacer referencia también a la fecha del alta, la fecha de remisión de la enfermedad, etc.
En la última observación, se deben registrar 2 variables fundamentales: la primera es el estado del individuo, y la segunda es la fecha de la información de este estado.
Los requisitos necesarios para disponer de datos adecuados para un análisis de supervivencia son:
- —
Definir de forma apropiada el origen o el inicio del seguimiento.
- —
Definir de forma apropiada la escala de tiempo.
- —
Definir de forma apropiada el evento.
Los datos pueden estar sesgados por las censuras o los truncamientos. En el análisis de la supervivencia asumimos un supuesto básico: los mecanismos del evento y la censura son estadísticamente independientes, es decir, los individuos censurados están sujetos a la misma probabilidad de evento que los no censurados1.
CensurasPérdidas de seguimiento o fin del estudio. No se observan los eventos en todos los individuos, ya sea porque el estudio se finalizó antes de la aparición del evento, el paciente decide abandonar y no participar en el estudio, perdemos al paciente por cambio en el lugar de residencia, muerte no relacionada con la investigación, etc.
TruncamientosEntrada en el estudio después del hecho que define el origen. No se observa la ocurrencia de origen en todos los individuos. Se tendría que haber empezado con anterioridad, ya que la enfermedad habría empezado antes.
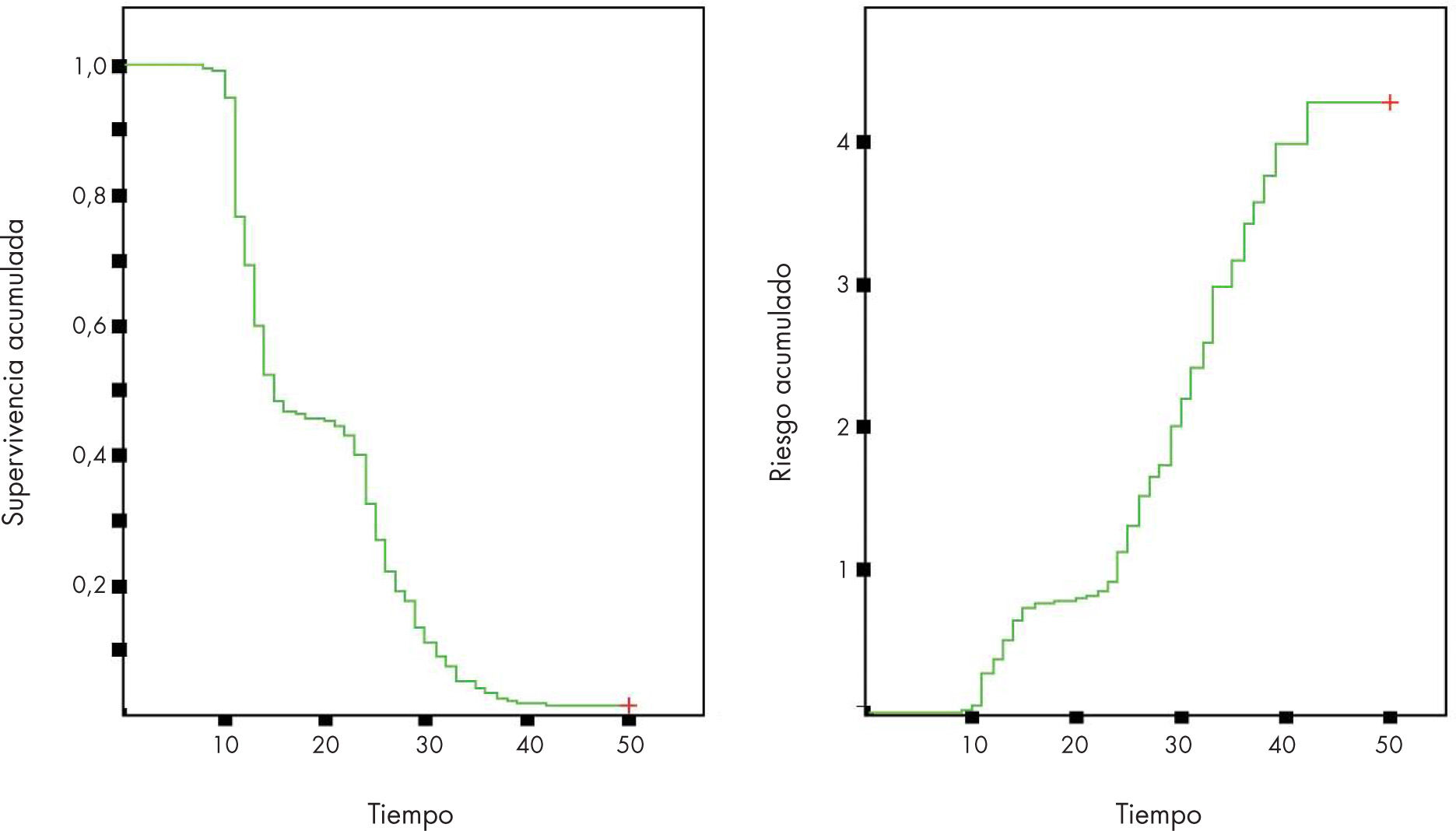
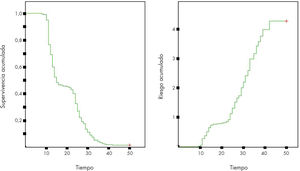
Supervivencia y riesgoHay 2 tipos de probabilidades diferentes para dar y estudiar los datos de supervivencia. Éstas son la supervivencia y el riesgo (figs. 3 y 4).
La supervivencia o función de supervivencia (S[t]) es la probabilidad de que un individuo sobreviva (no ocurra el evento) desde la fecha inicio de seguimiento hasta un momento determinado en el tiempo t.
El riesgo o función de riesgo (λ[t]) es la probabilidad de que un individuo que está siendo observado en el tiempo t muera (suceda el evento) en ese momento.
La diferencia entre ambas probabilidades es que la de supervivencia se centra en la no ocurrencia del evento, mientras que la de riesgo se centra en la ocurrencia del evento. Además, el riesgo proporciona la tasa de incidencia3.
Metodología estadísticaEl problema principal en un análisis de supervivencia es la estimación de la función de supervivencia S(t)3.
El análisis de los datos se puede llevar a cabo utilizando técnicas paramétricas (si la distribución del tiempo de supervivencia es conocida) o no paramétricas (si la distribución no es conocida).
En los estudios médicos, no se suele disponer de la información suficiente para ajustar los datos a una distribución conocida, por lo que es más útil la aplicación de métodos no paramétricos.
Una ventaja de estos métodos es que tienen en cuenta el carácter secuencial de los datos y los ajusta de forma que cada individuo sólo contribuye al estudio mientras está en observación4.
Método de Kaplan-MeierLa estimación de la probabilidad de supervivencia por métodos no paramétricos se realiza mediante el método de Kaplan-Meier (propuesto en 1958)5.
Este método calcula la proporción acumulada que sobrevive para el tiempo individual de cada paciente, cada vez que se produce un evento, y da proporciones exactas de supervivencia (figs. 3 y 4).
La probabilidad de sobrevivir en un tiempo t(i) determinado es igual a la probabilidad de sobrevivir hasta el momento anterior t(i-1) por la probabilidad condicionada de sobrevivir un tiempo t(i) después de haber sobrevivido un tiempo t(i-1)3.
S(t) se representa gráficamente mediante la curva de Kaplan- Meier. Éstas son gráficas escalonadas que comienzan con una supervivencia de 1 que se mantiene hasta el momento de producirse el primer evento. Cada vez que se produce un evento, la gráfica desciende lo mismo que la supervivencia en ese momento.
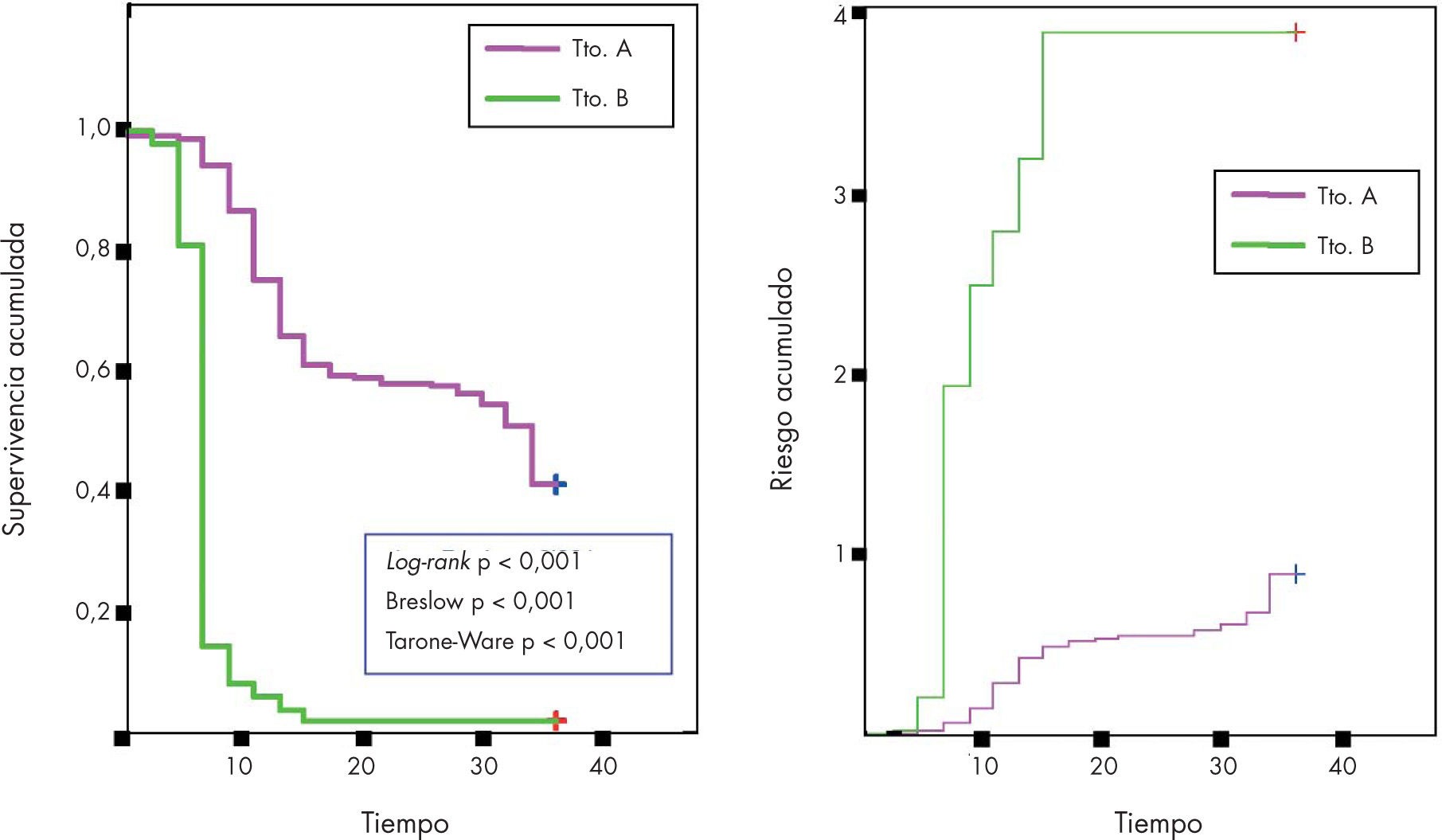
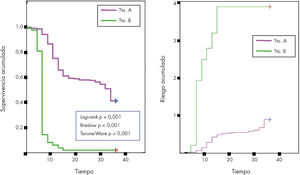
Comparación entre funciones de supervivenciaEn los estudios de supervivencia, es muy frecuente querer saber si 2 o más poblaciones se comportan de forma diferente, es decir, si las funciones de supervivencia difieren desde un punto de vista estadístico, por ejemplo, cuando queremos estudiar si la supervivencia depende del tratamiento administrado a los pacientes (fig. 4).
Para comparar 2 o más funciones de supervivencia, se usan diversas pruebas estadísticas de contraste de hipótesis. La más utilizada es el test de log-rank o test de riesgos proporcionales, que es útil para detectar diferencias a largo plazo. Existe también el test de Breslow que detecta las diferencias al principio de la curva. Un test intermedio entre estos 2 es el test de Tarone-Ware6.
Las características comunes de estos tests son:
- —
Hipótesis nula (H0): las supervivencias de los grupos es la misma
- —
Hipótesis alternativa (H1): al menos uno de los grupos tiene una supervivencia diferente.
- —
Estadístico utilizado: χ2 con k-1 grados de libertad, siendo k el número de grupos que se comparan.
Con frecuencia, nos puede interesar valorar de forma simultánea el efecto de una serie de variables explicativas o factores pronóstico (sexo, tipo de tratamiento, etc.) en la supervivencia o en la tasa de ocurrencia del evento estudiado.
La regresión de Cox es una técnica multivariante que permite identificar y evaluar la relación entre un conjunto de variables explicativas y la tasa de ocurrencia del evento (función de riesgo) en estudio. También permite predecir las probabilidades de supervivencia (o, en general, de permanencia libre del evento) para un determinado individuo a partir de los valores que toman sus variables pronóstico7.
No se trata sólo de saber el efecto en la supervivencia después de un tiempo determinado, sino también de valorar cuál es el efecto en la función de supervivencia durante todo el período de observación de los pacientes, sea cual sea el punto temporal que se elija para la comparación. Sólo la regresión de Cox permite afirmar que una supervivencia más ventajosa puede ser atribuida, por ejemplo, a un determinado tratamiento a igualdad del resto de variables.
La ecuación del modelo de regresión de Cox es: Ln(λt) = β0 + β1x1+ β2x2 + … + βrxr6.
La regresión de Cox asume que la razón de tasas instantáneas es constante a lo largo del tiempo (los riesgos son proporcionales).
La interpretación de una regresión de Cox es muy parecida a la de la regresión logística. En la regresión logística obtenemos el parámetro de asociación odds ratio, mientras que en la regresión de Cox se obtiene una hazard ratio (ratio de riesgos) (HR)6.
El modelo de regresión de Cox promedia de manera ponderada las HR de los distintos momentos en los que se produce algún evento, con lo que así calcula una HR global.
La HR global para una variable explicativa dicotómica xi (que toma el valor 1 para los pacientes expuestos al factor y 0 para los no expuestos) viene dado por: HR = eβi. Una HR > 1 significa que la exposición al factor aumenta la velocidad de aparición del evento (factor de riesgo), mientras que HR < 1 reduce la aparición (factor protector). Si HR = 1 diremos que el factor no afecta a la supervivencia.
La regresión de Cox es una técnica multivariante que permite identificar y evaluar la relación entre un conjunto de variables explicativas y la tasa de ocurrencia del evento (función de riesgo) en estudio, así como predecir las probabilidades de supervivencia de un determinado individuo a partir de los valores que toman sus variables pronóstico.