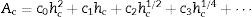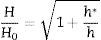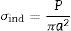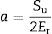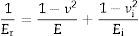Micro-scale mechanical characterization of Inconel cermet coatings deposited by laser cladding

Abstract

In this study, an Inconel 625-Cr₃C₂ cermet coating was deposited on a steel alloy by laser cladding. The elastic and plastic mechanical properties of the cermet matrix were studied by the depth sensing indentation (DSI) in the micro scale. These results were compared with those obtained from an Inconel 600 bulk specimen. The values of Young's modulus and hardness of cermet matrix were higher than those of an Inconel 600 bulk specimen. Meanwhile, the indentation stress–strain curve of the cermet matrix showed a strain hardening value which was more than twice the one obtained for the Inconel 600 bulk. Additionally, the mechanical properties of unmelted Cr₃C₂ ceramic particles, embedded in the cermet matrix were also evaluated by DSI using a spherical indenter.

Resumen

En este estudio, se han depositado recubrimientos cermet de Inconel 625-Cr₃C₂ sobre acero mediante plaqueado láser. Las propiedades mecánicas elasto-plásticas de la matriz de cermet fueron estudiadas mediante el proceso de nanoindentación (DSI) a escala microscópica. Los resultados obtenidos se han comparado con los correspondientes a una muestra masiva de Inconel 600. Los valores del módulo de Young y la dureza de la matriz de cermet son considerablemente mayores que los de la muestra masiva de Inconel 600. La curva de tensión-deformación de la matriz de cermet presenta un valour de endurecimiento por deformación que es más del doble del obtenido para el Inconel 600 en masa. Además, se determinaron las propiedades mecánicas de las partículas cerámicas de Cr₃C₂ sin fundir en la matriz de cermet mediante nanoindentación usando un indentador esférico.

Introduction

Cermet coatings were developed to protect the metallic substrate in high-temperature applications. The idea is to combine the hardness, oxidation resistance and high melting temperature of ceramic particles with the ductility, toughness and high thermal conductivity of metals. Different combinations of metal alloys and ceramics were blended and deposited to obtain cermet coatings [1,2].

Nickel-based superalloys are characterized by high-temperature oxidation and corrosion resistance. The commercial name Inconel is used to identify a group of Ni-based superalloys mainly composed by Ni and Cr. These alloys were demonstrated to be suitable to be deposited as a coating by laser cladding to protect substrate materials, like steel [3–5]. One way to improve the tribological properties of metallic coatings applied by laser cladding is to introduce ceramic particles in the filler material [6]. It has been shown that Inconel 625 and Cr₃C₂ particles could be used for this purpose [7]. The microstructure, the wear behaviour, and the mechanical properties of Inconel coatings have been studied in the literature [4,7–16]. Additionally, a recent study on the fracture and failure mechanisms of Ni-base laser cladding coatings was performed using in situ tensile tests [17]. However, few researches about the local mechanical behaviour in a micro-scale of Inconel cermet coatings have been carried out.

The aim of this work is to study the mechanical properties in the micro-scale of Inconel 625-Cr₃C₂ cermet coatings deposited by laser cladding. The elastic-plastic properties of the cermet matrix obtained by depth-sensing indentation (DSI) were compared with those of an Inconel 600 bulk specimen. In addition, for a more in situ analysis of the coatings, the properties of unmelted Cr₃C₂ ceramic particles, embedded in the in the cermet matrix, were also evaluated by DSI.

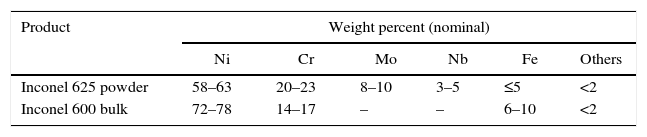
Materials and experimental procedures

Materials

Inconel 625-Cr₃C₂ cermet coating was deposited by laser cladding onto Gr22 ferritic steel (ASTM A387). Inconel 625 and Cr₃C₂ powders were supplied by Sulzer-Metco (MetcoClad 625 and Metco 70C-NS, respectively). The composition of Inconel 625 powder and the Inconel 600 bulk are presented in Table 1. The Inconel 625 powders were mechanically mixed with the 20 wt% of Cr₃C₂ before processing the cermet coatings.

Table 1.

Chemical composition of Inconel 625 powders and the Inconel 600 bulk specimen.

Product	Weight percent (nominal)
	Ni	Cr	Mo	Nb	Fe	Others
Inconel 625 powder	58–63	20–23	8–10	3–5	≤5	<2
Inconel 600 bulk	72–78	14–17	–	–	6–10	<2

Experimental procedure

A Rofin-Dilas High-Power Diode Laser (HPDL) with a wavelength of 940 nm and a maximum output power of 1300 W was used. Argon was applied as a protective and powder carrier gas. In order to deposit the cermet coatings, the laser beam power was fixed at 900 W, the scanning speed at 15 mm/s, the powder feeding rate at 16.5 g/min, and the flux of Ar between 14 and 15 l/min. The substrates were coated by 10 single clad tracks with a 40% overlap between two adjacent tracks [7].

Metallographic samples were prepared in plain-view section. The coated specimens were grounded with SiC paper up to 1200 grit to remove the superficial roughness of the coatings. Successively, they were polished in a diamond slurry of up to 1 μm nominal size. Finally, the polished surfaces were cleaned in deionised water and then by ultrasound in acetone and propanol. The same procedure was followed to obtain a polished surface of the Inconel 600 bulk sample.

Depth sensing indentations tests (DSI) were performed with a Nanoindenter XP (MTS systems Co.), on the polished surfaces of the samples, by using the continuous stiffness measurement methodology (CSM) [18]. Continuous loading and unloading cycles were conducted during the loading branch by imposing a small dynamic oscillation of 2 nm and 45 Hz on the displacement signal and measuring the amplitude and phase of the corresponding force. Consequently, the contact stiffness was continuously measured as a function of the penetration depth during the experiment. Two different batches of indentation tests were carried out on Inconel bulk and cermet samples. For each batch, an indentation matrix of 10 × 10 indentations, spaced 50 microns between them, was performed in displacement control. The first batch of indentation tests was carried out using a Berkovich diamond indenter with a tip radius of 50 nm. A maximum penetration depth of 1000 nm was selected to perform the DSI tests with the Berkovich tip. The aim of these tests was to obtain values of Young's modulus (E) and hardness (H) of the studied materials. Both properties were obtained by following the Oliver–Pharr methodology [19]. The other batch of indentation tests was conducted using a spherical diamond indenter with a tip radius of 10 μm. The aim of these tests was to study the local plastic properties and to obtain the indentation stress–strain curve of both samples. A maximum penetration depth of 1500 nm was selected to perform the DSI tests with the spherical tip. Prior to making the Berkovich indentations, a tip calibration procedure was carried out using the bulk Inconel 600 alloy as the reference material, according to the CSM methodology [3,19,20]. The nominal elastic modulus was set to 214 GPa and the real contact area of the indenter was iteratively obtained through the following equation.

where ci are constants determined by curve fitting procedure. The first term was set to 24.5 for an ideal Berkovich indenter.

In addition, Vicker microhardness indentation tests were carried out on the polished surfaces of the studied materials, with a maximum load of 300 gf and a dwell time of 12 s.

Results and discussion

DSI tests with Berkovich indenter tip

In a previous work [7], the microstructure of the cermet matrix was analyzed by scanning electron microscopy (SEM) and transmission electron microscopy (TEM). Unmelted Cr₃C₂ ceramic particles were randomly distributed in the Inconel matrix. Additionally, Cr-rich carbides of stoichiometry M₇C₃, radially distributed around the unmelted Cr₃C₂ particles, were also observed. They were formed in situ during the laser cladding process.

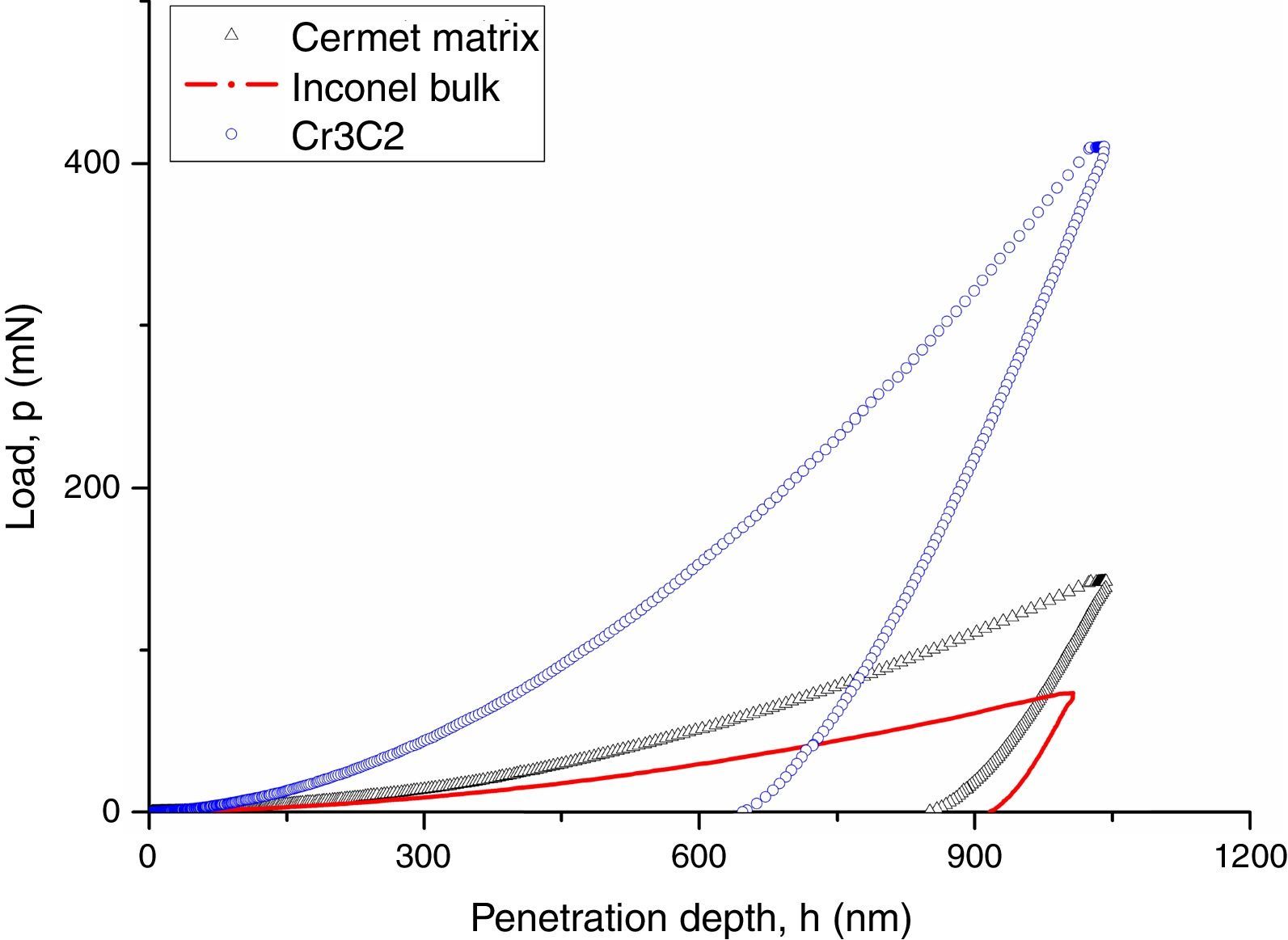
Fig. 1 shows a representative indentation load vs. penetration depth curves obtained from the DSI tests performed with the Berkovich tip. The indentation loads at the maximum penetration of 1000 nm for the tests done in the cermet matrix were twice as much those obtained on Inconel bulk. Additionally, the Cr3C2 carbides showed the highest indentation loads, almost four times those on Inconel bulk.

Fig. 1.

Representative penetration depth vs. load curves obtained from DSI tests performed with the Berkovich tip on the cermet matrix, the Inconel 600 bulk and the unmelted Cr₃C₂ particles.

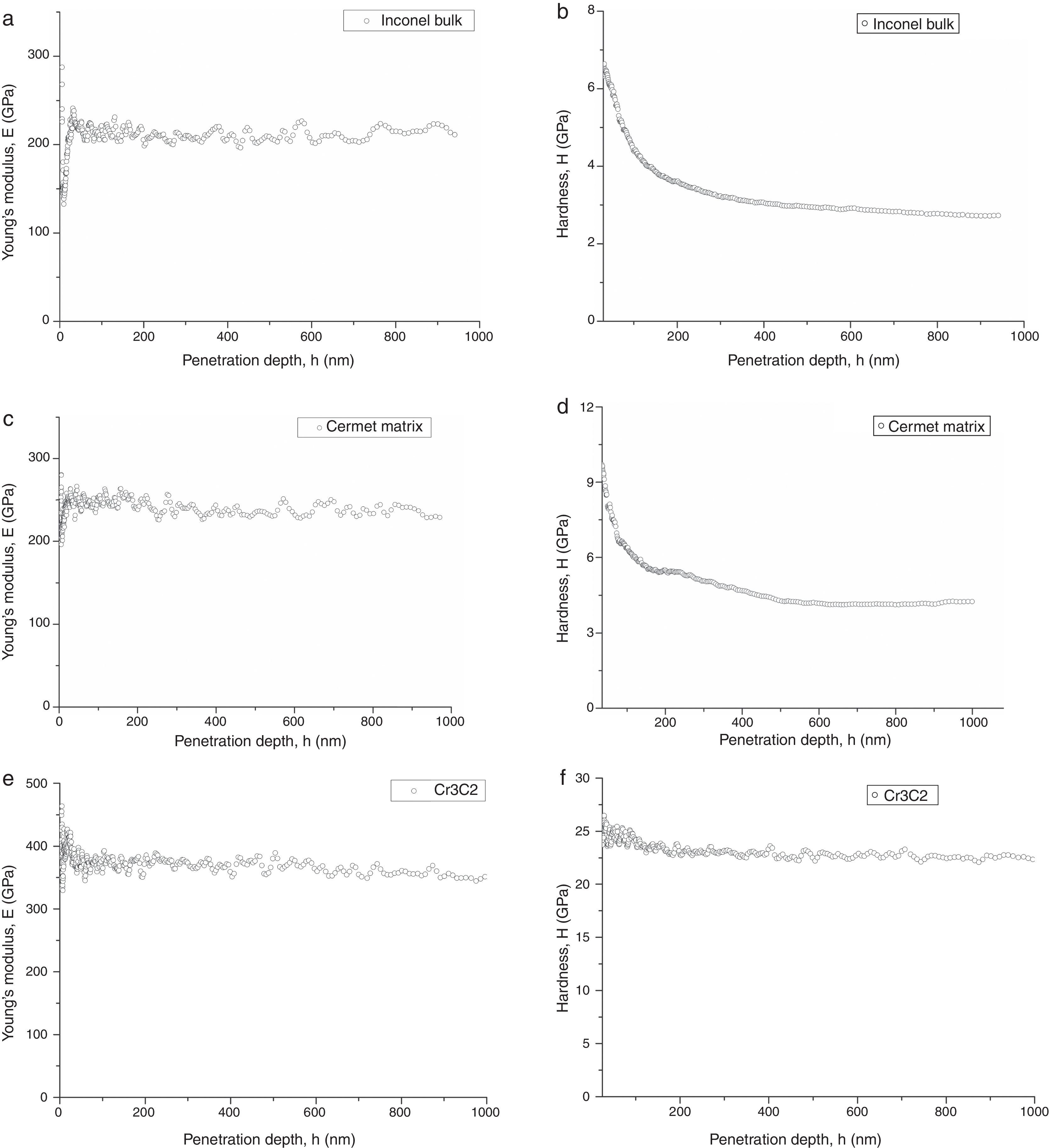
Fig. 2 shows representative examples of Young's modulus vs. penetration depth and hardness vs. penetration depth curves obtained in the DSI tests. The Young's modulus of the studied materials does not change considerably with the penetration depth. Examples of results of the variations of the hardness with the penetration depth are shown in Fig. 2(b), (d), and (f). The unmelted Cr₃C₂ ceramic particles showed almost constant values of hardness with the penetration depth. However, the cermet matrix and the Inconel 600 bulk showed a continuous decreasing tendency of the hardness values with the penetration depth.

Fig. 2.

Representative result of Young's modulus and Hardness variation with penetration depth obtained from the DSI tests with Berkovich tip onto (a and b) Inconel 600 bulk, (c and d) cermet matrix, and (e and f) unmelt Cr₃C₂ particles.

As the values of E remain quite constant, it is possible to discard the occurrence of calibration error in the area function of the indenter tip in Eq. (1). Consequently, the hardness evolution observed with the penetration depth may be a material response to the indentation process. This phenomenon is known as indentation size effect (ISE) [21] and the hardness values obtained on the cermet coating could be affected by this effect. Different models have been developed to analyze the ISE and calculate the asymptotic hardness (H₀) at the fully plastic condition. This value of the hardness is comparable to the Vickers one at macroscale. Nix and Gao [21] proposed a methodology to determine this asymptotic hardness. Due to the very high strain gradient that is induced in the sample during indentation with sharp tips, Geometrically Necessary Dislocations (GNDs) are produced in the indentation volume. The GND's are added to the Statistically Stored Dislocations (SSD's) related to the equivalent strain reached in the test. As a result, the dislocation density increases and thus justifies the hardening effect observed here. Moreover, the smaller the size of the indentation, the more important the strain gradient appears to be. Hence, the hardening effect becomes more noticeable as the indentation size is reduced. By applying the model developed by Nix and Gao, Eq. (2) can be used to describe ISE [22]:

where H represents the apparent hardness; H₀ the asymptotic hardness; h the penetration depth, and h* is a characteristic length that depends on the properties of the indented material and the indenter geometry.

Eq. (2) implies that a plot of H² vs. 1/h results in a straight line that will intercept the y-axis at H₀². Fig. 3 shows a representative plot of H² vs. 1/h for the Inconel 600 bulk (a) and cermet matrix (b), respectively. A very good linear fitting of the data is obtained in accordance with the Nix and Gao model. This behaviour has also been reported in the zirconium [23].

Fig. 3.

Example of H² vs. 1/h curves for the Inconel 600 bulk (a) and cermet matrix (b) obtained from a Berkovich indenter.

Table 2 summarizes the average hardness measured from DSI tests done with the Berkovich indenter, the values of H₀ calculated with the Nix and Gao model, and finally the values of Vicker microhardness (HV) that could be used to verify if the values of H₀ were correctly calculated. The asymptotic hardness values obtained on Inconel bulk and cermet coating are similar to those obtained by Vickers microhardness tests. In addition, the asymptotic hardness value of the cermet matrix is 60% higher than that of the Inconel 600 bulk. The higher hardness value of the cermet matrix may be due to the formation of the M₇C₃ carbides previously described. The Young's modulus of the cermet matrix was 15% higher regarding to that obtained on the Inconel 600 bulk. It is possible to suppose that M₇C₃ carbides, embedded into the Inconel matrix, promote a load distribution phenomena that results in higher values of E measured. The values of E obtained for the Cr₃C₂ particles are similar to those reported by others authors (E = 373 GPa) [24].

Table 2.

Average hardness measured in DSI tests with Berkovich indenter (H), asymptotic hardness (H₀), and Vickers microhardness (HV).

Material	E (GPa)	H (GPa)	H0 (GPa)	HV (GPa)
Inconel 600 bulk	211 ± 7	3.7 ± 0.2	2.4 ± 0.3	2.7 ± 0.1
Cermet matrix	243 ± 12	7.2 ± 0.6	3.85 ± 0.3	4.5 ± 0.07

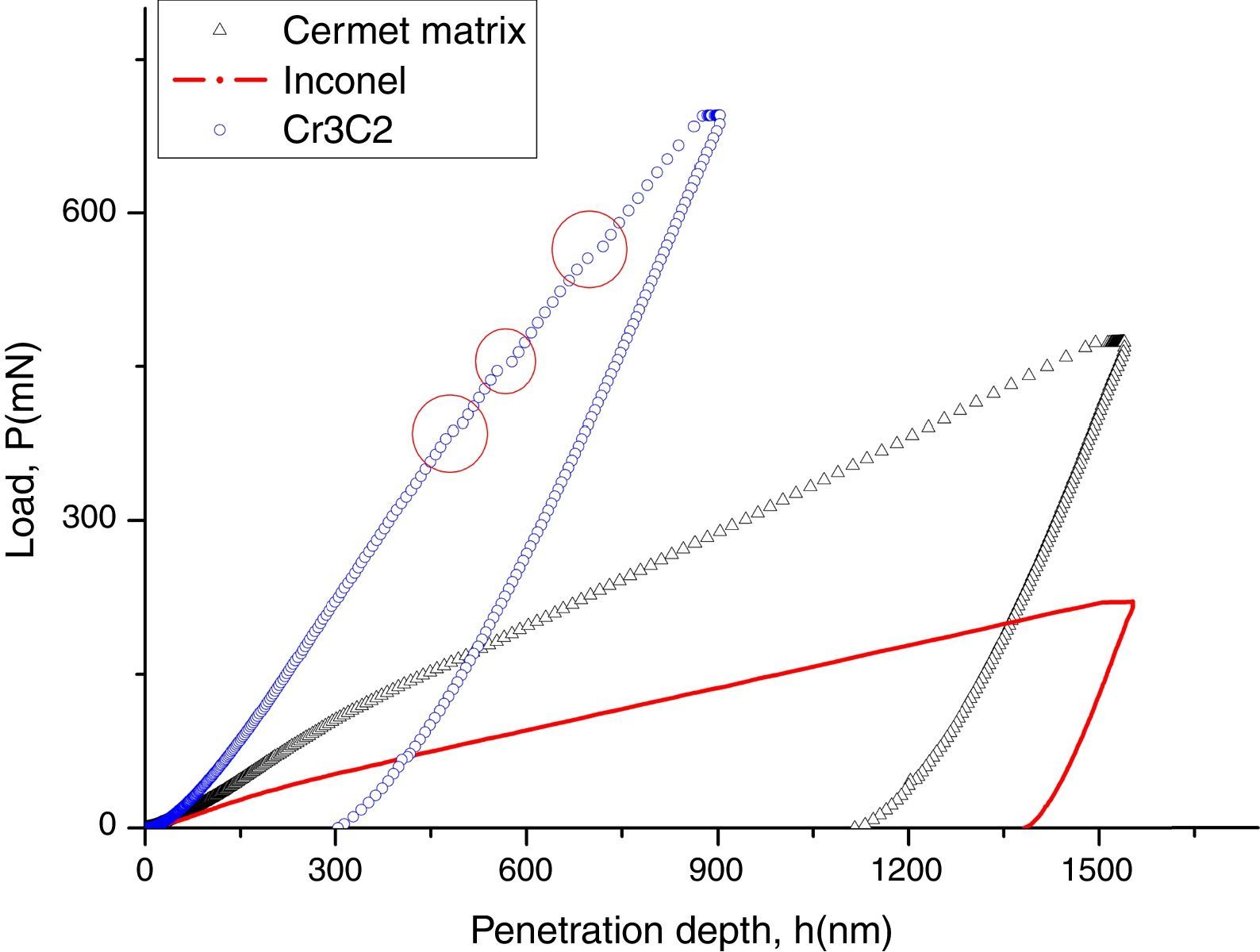
DSI tests with spherical indenter tip

Fig. 4 shows representative load vs. penetration depth curves obtained in DSI tests carried out using the spherical indenter tip. A higher indentation load is needed for the cermet matrix with respect to the Inconel 600 bulk to achieve the same penetration depth, in agreement with the results obtained using the Berkovich tip. It should be noted that there are multiple discontinuities in the curve of the unmelt Cr₃C₂ particle. This phenomenon is known as “pop-in” and it is associated to the formation of cracks in the material during the tests. Materials with hexagonal lattice structure, like the Cr₃C₂ ceramic particles used in this work, may present this behaviour. Others examples of materials showing this phenomena are the sapphire, the GaN, and the ZnO [25]. In the results shown in Fig. 4, the first “pop-in” happens at an indentation depth around 400 nm, the second one at 550 nm, and the third one around 700 nm. There is no pop-in phenomena during the unloading process. For the analysis of the results only the data previous to the first pop-in event were used.

Fig. 4.

Penetration depth versus load from Spherical indentation on Cermet matrix, Inconel bulk and unmelt Cr₃C₂.

Indentation tests with a spherical tip represent the best choice to characterize the strain hardening which offers a gradual transition from elastic to elastic–plastic regime. The indentation stress vs. strain curve can be obtained using the model proposed by S.R. Kalidindi et al. [26]. The indentation stress (σ_ind) and the indentation strain (¿_ind) can be expressed respectively as:

where P is the applied load, a the contact radius, and h is the penetration depth.

The value of Young's modulus of the studied materials was previously measured using the Oliver–Pharr method on the Berkovich indentation data, the contact radius a could be estimated according to the Sneddon's equation [27]:

where S_u represent the harmonic contact stiffness obtained by the CSM methodology and E_r is the reduced Young's modulus, that could be express as a function of the Young's modulus and Poisson's ratios of the studied material (E, ν) and the indenter tip (E_i, ν_i):

The slope of the initial linear part of the indentation stress-strain curves, obtained for the cermet matrix and the Inconel 600 bulk, is approximately equal to the reduced Young's modulus obtained from the Oliver–Pharr analysis of the Berkovich indentation tests (in the zoom parts in Fig. 5). The plastic regime of the indentation stress–strain curves were fitted to a Hollomon equation [28]. The indentation stress–strain curve for cermet matrix shows a strain hardening value which is more than twice the one obtained for the Inconel 600 bulk. Probably, the M₇C₃ carbides, distributed around the unmelted Cr₃C₂ particles, could produce a distortional effect on the cermet matrix and consequently, they may produce a hardening effect. This result is in agreement to the one obtained from the Berkovich tests (Table 2).

Fig. 5.

Indentation stress–strain curve for the cermet matrix and the Inconel 600 bulk.

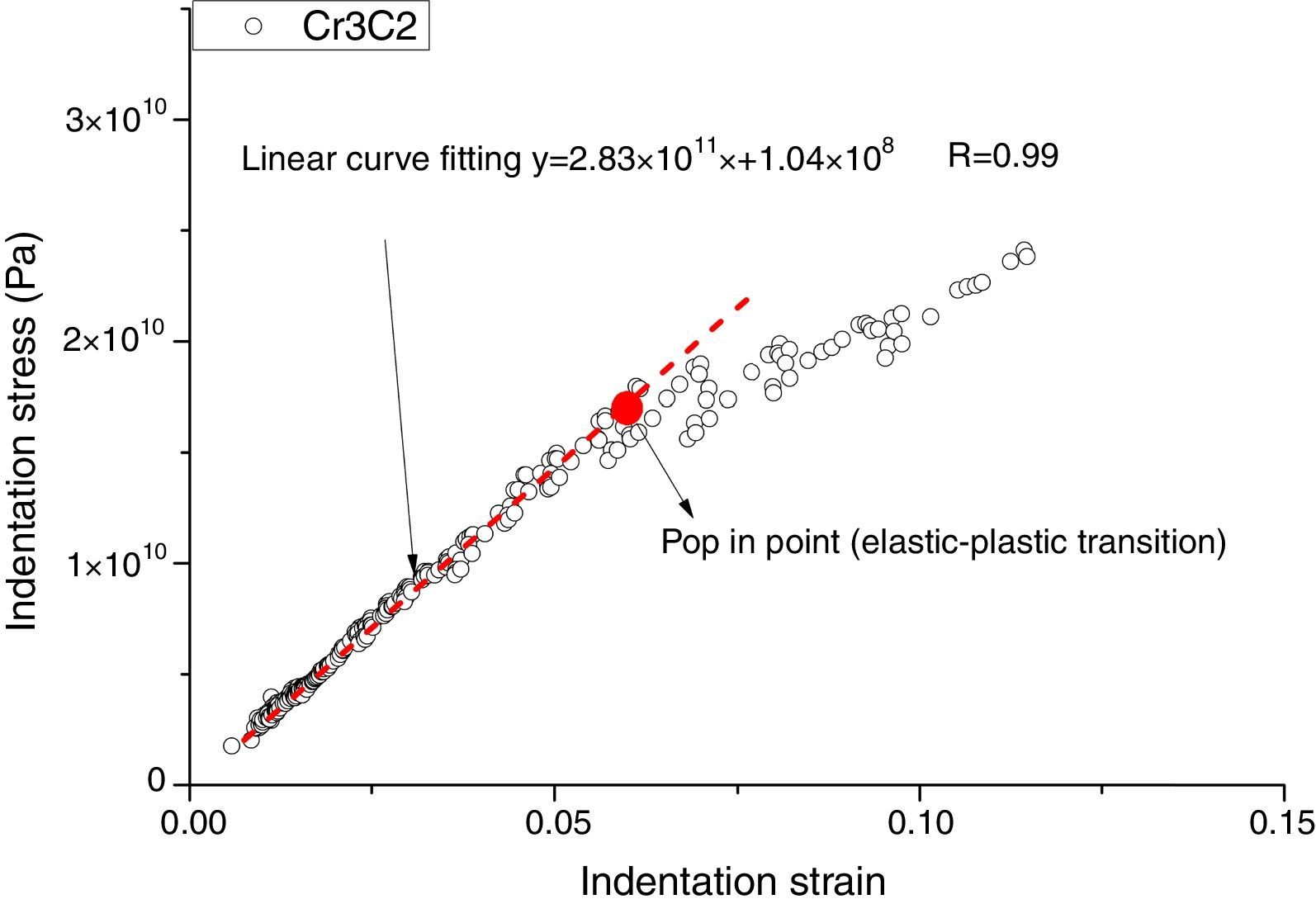
Fig. 6. shows the indentation stress–strain curve for unmelted Cr₃C₂ ceramic particles. The fitting was limited to those under the first “pop-in” event. The indentation stress–strain curve is linear with a slope that corresponds to the Young's modulus (364 GPa) of the unmelted Cr₃C₂ particles. The critical point marked in red in the curve is the first “pop-in” point, at which initial cracking takes place. The mean pressure at this point is about 18 GPa which is consistent with the values of hardness obtained from Vicker indentations in the literature [24,29].

Fig. 6.

Indentation stress–strain curve for unmelt particle Cr₃C₂.

Conclusions

In this study, depth-sensing indentation tests were performed with Berkovich and spherical tips on Inconel 625-Cr₃C₂ cermet coatings in order to evaluate their elastic-plastic properties in the micro-scale. An Inconel 600 bulk specimen was used as reference sample for the calibration of the contact area equation.

The Nix and Gao model has been successfully employed to account for the indentation size effect (ISE) in the hardness measurements on the cermet matrix and the Inconel 600 bulk. The asymptotic hardness of the cermet matrix is equal to 3.85 GPa, which is 60% higher than that of the Inconel 600 bulk (2.4 GPa). The Young's modulus does not depend on the indentation depth and its value for the cermet matrix is 243 GPa, whereas for the Inconel 600 bulk is equal to 211 GPa. The indentation stress–strain curve in the plastic regime for the cermet matrix showed a strain hardening value which is more than twice the one obtained for the Inconel 600 bulk.

The unmelted Cr₃C₂ ceramic particles were also characterized by depth-sensing indentation tests with an spherical tip. In this case, the hardness values (around 23 GPa) did not show any indentation size effect. The Young's modulus was equal to 373 GPa, in agreement with published results. However, there were multiple “pop-in” events in the load–displacement curve associated to crack initiation in the material. The first “pop-in” event was observed at a penetration depth of about 400 nm and the corresponding average pressure (18 GPa) is similar to the hardness measured from Vicker indentations in the literature.

Acknowledgments

One of the authors, Chao Chang, appreciates the financial support provided by the Chinese Scholarship Council (CSC). This work was supported by the project BIA 2014-53314R.