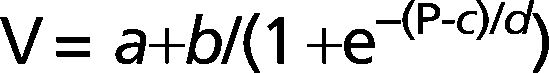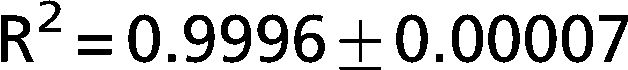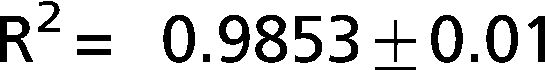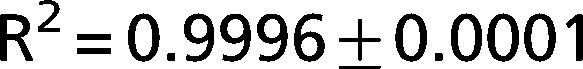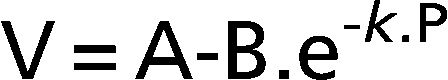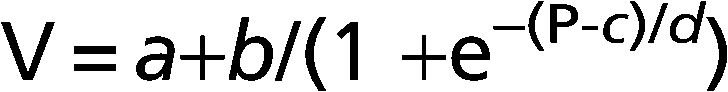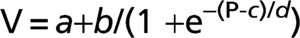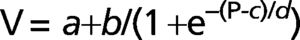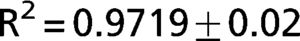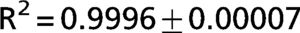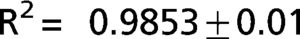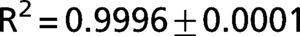A sigmoidal fit for pressure-volume curves of idiopathic pulmonary fibrosis patients on mechanical ventilation: clinical implications

OBJECTIVE:

Respiratory pressure-volume curves fitted to exponential equations have been used to assess disease severity and prognosis in spontaneously breathing patients with idiopathic pulmonary fibrosis. Sigmoidal equations have been used to fit pressure-volume curves for mechanically ventilated patients but not for idiopathic pulmonary fibrosis patients. We compared a sigmoidal model and an exponential model to fit pressure-volume curves from mechanically ventilated patients with idiopathic pulmonary fibrosis.

METHODS:

Six idiopathic pulmonary fibrosis patients and five controls underwent inflation pressure-volume curves using the constant-flow technique during general anesthesia prior to open lung biopsy or thymectomy. We identified the lower and upper inflection points and fit the curves with an exponential equation, V = A-B.e^-k.P, and a sigmoid equation, V = a+b/(1+e^-(P-c)/d).

RESULTS:

The mean lower inflection point for idiopathic pulmonary fibrosis patients was significantly higher (10.5±5.7 cm H₂O) than that of controls (3.6±2.4 cm H₂O). The sigmoidal equation fit the pressure-volume curves of the fibrotic and control patients well, but the exponential equation fit the data well only when points below 50% of the inspiratory capacity were excluded.

CONCLUSION:

The elevated lower inflection point and the sigmoidal shape of the pressure-volume curves suggest that respiratory system compliance is decreased close to end-expiratory lung volume in idiopathic pulmonary fibrosis patients under general anesthesia and mechanical ventilation. The sigmoidal fit was superior to the exponential fit for inflation pressure-volume curves of anesthetized patients with idiopathic pulmonary fibrosis and could be useful for guiding mechanical ventilation during general anesthesia in this condition.

INTRODUCTION

Idiopathic pulmonary fibrosis (IPF) is a chronic, progressive and often fatal lung disease.1,2 Patients often have limited exercise capacity and decreased quality of life.3,4 The pathophysiology and the sequence of events that lead to fibrosis are poorly understood,5 the etiology is unknown, and no effective treatment is available.6 IPF patients who need mechanical ventilation for acute exacerbation of the disease have a high mortality rate,7–11 and even those who receive mechanical ventilation for short periods, while under general anesthesia, may be at an increased risk for respiratory complications and death.12

The pressure-volume (PV) curve of the respiratory system has been used to describe lung mechanics and pulmonary physiology for many years.13–15 Fitting of PV curves in Interstitial Lung Diseases has been done using an exponential equation applied to the upper portion of the deflation limb of the curve of spontaneously breathing patients. Researchers found that parameter k, which describes the slope of the curve, was useful in characterizing changes in lung mechanics16 and the degree of fibrosis.17 The initial portion of the curve, close to Functional Residual Capacity (FRC), deviates from the exponential shape and has been systematically excluded from analyses.16–18

In patients receiving mechanical ventilation, the most commonly used method to generate PV curves is the passive inflation curve.14,15,19 In this case, the exponential model may not be a good fit, and parameter k would be of little use to guide mechanical ventilation. To understand the mechanical properties of the respiratory system in IPF during mechanical ventilation, we performed inflation PV curves in IPF patients and applied a sigmoidal model that included all data points during lung inflation, similar to what has been done to normal patients20 and acute respiratory distress syndrome (ARDS) patients.21–23 We hypothesized that a sigmoidal model would be superior to the exponential model and yield parameters that could be useful for mechanical ventilation adjustments during anesthesia in IPF patients.

MATERIALS AND METHODS

This study was conducted at Hospital das Clinicas, University of Sao Paulo, Brazil and was approved by the Hospital's Ethics Committee. Informed consent was obtained from all the subjects.

Study subjects

From October 2004 to June 2005, consecutive patients with suspected IPF who had been referred for open lung biopsies were invited to participate in the study. Twelve patients met the inclusion criteria and agreed to participate. Six were later excluded because their histological diagnosis was not compatible with usual interstitial pneumonia/idiopathic pulmonary fibrosis.24 Control patients were recruited from a population of nonsmoking myasthenia gravis patients who had been referred for thymectomies. Control patients had no respiratory symptoms or any signs of respiratory compromise, and CT scans of the chest revealed the absence of any respiratory diseases.

Data collection

All curves were obtained from patients who were intubated, anesthetized, paralyzed, and continuously monitored. Mechanical ventilation was performed with volume control ventilation using tidal volumes of 8-10 ml/kg, a positive end-expiratory pressure (PEEP) of 5 cm H₂O and an FIO₂ of 0.3 to 0.4. With the exception of one patient, who was admitted to the intensive care unit (ICU) due to respiratory failure, the PV curves were performed in the operating room immediately prior to surgery. Before the initiation of the PV curve, a volume history was established by performing a recruitment maneuver with a continuous positive airway pressure (CPAP) of 40 cm H₂O for 40 seconds followed by disconnection from the ventilator and exhalation to end-expiratory lung volume (EELV). The inflation curves were performed immediately after EELV was reached (zero flow) using the constant flow technique,25 delivering a 1-5 l/min constant flow of oxygen to the patient's airway from EELV at ZEEP to a peak pressure of 40 cmH₂O. Flow and airway pressures were measured with a pneumotachograph (Hans-Rudolph 3813, Kansas City, MO, USA) and a differential pressure transducer (Validyne DP45, Northridge, CA, USA), placed between the flow-generator and the endotracheal tube. The heat and moisture exchanger was removed from the system to avoid interference.26 Esophageal pressure was monitored with an esophageal balloon (SmartCath Esophageal Catheter, Viasys, Palm Springs, CA, USA), which was placed a few hours before the surgery while the patient was awake. The balloon was filled with 0.5 ml of air, and its position was verified using the occlusion maneuver.27 Analog signals were amplified, digitized (PCI-Mio-16XE-50, National Instruments, Austin, TX, USA), and recorded at 20-50 Hz using a data acquisition system (Labview, National Instruments, Austin, TX, USA) and then stored and analyzed on a computer.

Data Analysis

The lower (LIP) and upper (UIP) inflection points were calculated automatically by a computational program (Labview, National Instruments) using the least squares method. The program fits three lines to the PV curve: the central, linear part of the curve; the initial, concave part and the final, convex part of the curve. The projection on the X axis of the intersection of the central line with the initial line and the final line corresponds to the LIP and UIP, respectively. Initial compliance was calculated by dividing lung inflation volume in mL during the PV curve from EELV until inflation volume reached 8 mL/kg of ideal body weight by the airway pressure at that volume (in cm H₂O). PV curves for the total respiratory system and for the lung were generated.

The curves were fit using Grace software (GNU-General Public License, Boston, MA, USA) with the Levenberg-Marquardt iterative method.28 First, we fit the curves to an exponential equation restricted to data points above 50% of the inflation volume.29 The exponential equation used has three parameters:

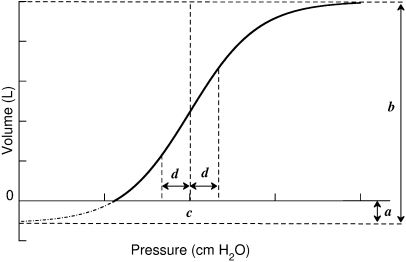
Where V is the absolute lung volume; P is the airway pressure; A is the asymptote approximating total lung capacity (TLC); B is the volume below A at which pressure is zero, thereby approximating inspiratory capacity; and k is the exponential constant that describes the shape of the curve.

Then, we fit the curves to the sigmoidal equation proposed by Paiva and co-workers20 and later modified by Venegas and co-workers21,22 using four parameters (Figure 1):

Where V is absolute lung volume, P is airway pressure, a is the difference in volume between EELV at ZEEP and residual volume, and b is the volume from a to the upper asymptote approximating vital capacity. The parameter c is the pressure at the mathematical sigmoid inflection point and represents the pressure at which compliance is maximal. Parameter d is proportional to the pressure range at which much of the volume change occurs and is measured in cm H₂O. Using parameters c and d, we calculated the pressure of maximal compliance increase (Pmci) as c-1.317*d and the pressure of maximal compliance decrease (Pmcd) as c+1.317*d.22

Figure 1.

Parameters for the sigmoidal equation

. V is absolute lung volume, P is airway pressure, a is the difference in volume between EELV at ZEEP and residual volume, and b is the volume from a to the upper asymptote approximating vital capacity. The parameter c is the pressure at the mathematical sigmoidal inflection point and represents the pressure at which compliance is maximal. Parameter d is proportional to the pressure range at which most of the volume change occurs and is measured in cm H₂O.

Statistical analyses were performed using SPSS 13.0 (SPSS, Chicago, IL, USA). We used a Student's t test to compare the patients and controls and present the data as means and standard deviations. The level of significance was set at p<0.05.

RESULTS

Table 1 shows the characteristics of the six patients included in the study, who had a final diagnosis of IPF according to the European Respiratory Society/American Thoracic Society consensus definition.24 All but one were male, and their mean age (±SD) was 64.5±8.4 years. The mean duration of symptoms was three years, but a diagnosis of interstitial lung disease was recent for all of the patients, and none of them had received specific treatment for IPF. The controls were younger than the patients (mean age of 24 years), and 3 of the 5 were female. The controls also had a lower mean body mass index (BMI) than the IPF patients, but BMI was not significantly correlated to LIP. Table 2 shows the individual respiratory mechanics parameters for the patients and controls.

Table 1.

Demographics and pulmonary function of the study's patients.

Patient #	Gender	Age (years)	Smoking	SpO2	FVC	TLC
1	M	66	20	86%	1.32 (36%)	2.84 (46%)
2	F	49	0	NA	1.97 (62%)	3.71 (72%)
3	M	67	35	93%	3.16 (74%)	5.18 (69%)
4	M	71	0	94%	2.25 (71%)	3.25 (59%)
5	M	62	40	91%	1.80 (63%)	NA
6	M	72	0	95%	3.10 (75%)	5.10 (69%)

M = male; F = female; Smoking = smoking history in pack-years; SpO₂ = pulse oximeter saturation in room air; FVC = forced vital capacity in liters (% = percent of predicted value); TLC = total lung capacity in liters (% = percent of predicted value); NA = data not available.

Table 2.

Demographics and mechanical properties of the respiratory system in patients and controls.

Patient #	Gender	Age (years)	BMI	Comp Initial	LIP	UIP	Diagnosis
1	M	66	28	31	15.1	35.4	IPF
2	F	49	26	40	11.2	37.3	IPF
3	M	67	31	78	3.6	21.8	IPF
4	M	71	28	26	14.5	34.2	IPF
5	M	62	25	15	15.5	37.1	IPF
6	M	72	25	103	3.0	22.8	IPF
N1	M	21	21	108	2.4	18.4	MG
N2	F	31	18	60	5.7	25.7	MG
N3	F	25	23	54	5.2	24.4	MG
N4	M	22	21	60	0.0	22.4	MG
N5	F	23	22	45	4.7	24.1	MG

M = male; F = female; BMI = body mass index in kg/m²; Comp Initial = initial compliance (from EELV to 8 ml/kg predicted body weight) in ml/cm H₂O; LIP = lower inflection point; UIP = upper inflection point; IPF = idiopathic pulmonary fibrosis; MG = myasthenia gravis.

The signal from the esophageal balloon was damped in some patients due to balloon displacement during surgery preparation in the operating room. Because the shapes of the respiratory system PV curves and lung PV curves were similar (see online supplemental material), we present the total respiratory system PV curves.

Table 3 shows the comparisons between the patients and controls. The LIP and UIP were significantly higher in the patients than in the controls (p<0.05). No significant differences were observed in the parameters yielded by the exponential or sigmoidal fit. The Pmci was low (<2 cm H₂O) in all control patients, as was the LIP, whereas it was as high as 15 cm H₂O in the patients; however, no statistical difference was detected between the groups. Parameter c, the point of maximal compliance of the respiratory system, was achieved at higher airway pressures in the patients than in the controls; however, the variability was high, and the difference did not reach statistical significance. Table 4 shows the individual results of the sigmoidal fits for the patients and controls.

Table 3.

Results of the comparison between patients with IPF and controls.

Group	IPF patients	Controls	p-value
LIP	10.5±5.7	3.6±2.38	0.033
UIP	31.4±7.2	23.0±2.8	0.035
Comp initial	49±34	65±25	0.390
Pmci	3.0±11.3	-2.2±4.2	0.339
Pmcd	35.4±9.4	26.6±2.2	0.070
a	-797±610	-969±654	0.662
b	3650±1648	3606±1461	0.964
c	19.2±8.8	12.2±2.9	0.115
d	12.3±4.2	10.9±1.3	0.469
A	3207±1267	3060±1310	0.855
B	5705±3351	3967±1118	0.299
k	0.047±0.024	0.049±0.011	0.877

Values are shown as means ± SD. IPF = Idiopathic pulmonary fibrosis; LIP = lower inflection point; UIP = upper inflection point; Comp initial = initial compliance (from EELV to 8 ml/kg IBW) shown in ml/cm H₂O; Pmci = pressure of maximal compliance increase, mathematically defined as c-1.317d, in cm H₂O ; Pmcd = pressure of maximal compliance decrease, mathematically defined as c+1.317d, in cm H₂O; a = sigmoidal equation parameter representing the difference in volume between EELV and residual volume; b = volume from a to the upper asymptote approximating vital capacity; c = pressure at the mathematical sigmoidal inflection point; d is proportional to the pressure range at which most of the volume change occurs, measured in cm H₂O; A = asymptote approximating total lung capacity; B = volume below A at which the pressure is zero, approximating inspiratory capacity; k = exponential constant that describes the shape of the curve.

Table 4.

Individual results of the sigmoidal fit for patients and controls.

	Diagnosis	a	b	c	d	Pmci	Pmcd
1	IPF	-358	3939	29.0	10.2	15.6	42.3
2	IPF	-1479	3777	10.4	18.4	-13.9	34.6
3	IPF	-1399	4781	11.2	11.5	-4.0	26.4
4	IPF	-180	2467	27.2	9.4	14.9	39.6
5	IPF	-219	1150	25.1	16.5	3.3	46.9
6	IPF	-1149	5785	12.3	8.0	1.7	22.8
N1	MG	-2082.7	6020.6	8.1	12.5	-8.4	24.5
N2	MG	-878.3	3839.5	14.9	11.5	-0.2	30.0
N3	MG	-545.8	2811.1	14.3	10.2	0.8	27.8
N4	MG	-896.0	3073.9	10.5	11.4	-4.5	25.5
N5	MG	-444.3	2286.6	13.4	9.1	1.5	25.4

IPF = idiopathic pulmonary fibrosis; MG = myasthenia gravis; a = sigmoidal equation parameter representing the difference in volume between EELV and residual volume, in mL; b = volume from a to the upper asymptote approximating vital capacity, in mL; c = pressure at the mathematical sigmoidal inflection point, in cm H₂O; d is proportional to the pressure range at which most of the volume change occurs, measured in cm H₂O; Pmci = point of maximal compliance increase, mathematically defined as c-1.317d, in cm H₂O; Pmcd = point of maximal compliance decrease, mathematically defined as c+1.317d, in cm H₂O.

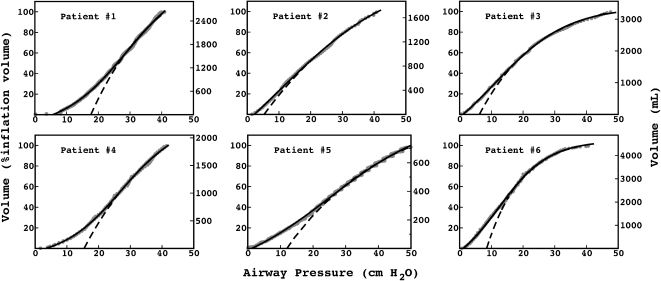
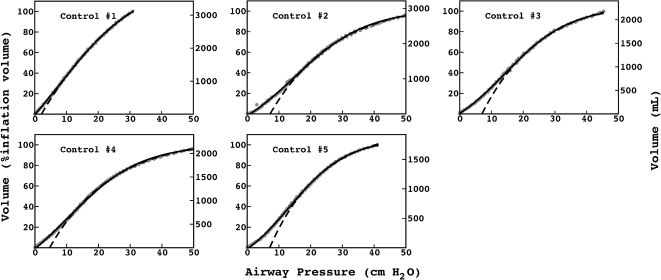
The exponential equation, which was applied only to points above 50% of inspiratory capacity, fit the data well and yielded an adjusted R² = 0.9719±0.02 for the patients and R² = 0.9853±0.01 for the controls. However, this equation could not predict points in the initial part of the inflation curve. The sigmoidal equation, which was applied to the entire data range, also fit the data well and yielded an adjusted R² = 0.9996±0.00007 for the patients (Figure 2) and R² = 0.9996±0.0001 for the controls (Figure 3).

Figure 2.

PV curves from the IPF patients. The data points (gray circles) were fit to an exponential (dashed line) and a sigmoidal equation (solid line). The exponential equation yielded an adjusted

, and the sigmoidal equation yielded an adjusted

. The exponential equation was fit only to data points above 50% of the total inflation volume and clearly misrepresented the initial portion of the curves. The sigmoidal equation fit the entire curve.

Figure 3.

PV curves from the controls. The data points (gray circles) were fit to an exponential (dashed line) and a sigmoidal equation (solid line). The exponential equation yielded an adjusted

, and the sigmoidal equation yielded an adjusted

.

DISCUSSION

To our knowledge, this is the first study to analyze inspiratory PV curves in mechanically ventilated patients with IPF, revealing a sigmoidal shape and the presence of a region of low compliance of the respiratory system at low airway pressures. Despite technical aspects of our study (muscle paralysis and a supine position) that may have interfered with the mechanical behavior of the respiratory system and impacted the shape of the PV curve, the controls had a much less pronounced sigmoidal shape in their PV curves than did the IPF patients.

The lower (LIP) and upper (UIP) inflection points were statiscally higher in the patients than in controls receiving the same level of deep sedation and muscle paralysis and briefly ventilated before the performance of the pressure-volume curve under the same ventilatory conditions: volume control ventilation using low FIO₂ (0.3-0.4) and moderate PEEP (5 cm H₂O). The LIP has been used to titrate PEEP during mechanical ventilation in ARDS30, but more recent studies have suggested that the LIP is not the pressure at which maximal recruitment is achieved and that it may not be the best guide to setting appropriate PEEP in ARDS.14,15,19 Using parameters from the sigmoidal fit could be an alternative. The sigmoidal equation had a good fit to the PV curves of these patients in our study, who had been recently diagnosed with IPF. Parameters a, b, c and d are physiologically meaningful and may be useful for guiding mechanical ventilation, which is particularly challenging in IPF since patients ventilated for acute exacerbations have poor outcomes,7–11 and patients who undergo an open lung biopsy are at increased risk of complications.12

Parameter a estimates how close the lung volume at EELV is to the residual volume. Patients with smaller absolute a had higher LIP, although the correlation did not reach significance (p = 0.064). Parameter b is analogous to vital capacity and could be useful for assessing disease severity in intubated patients in whom standard maneuvers to measure vital capacity cannot be performed. Parameters c and d characterize the shape of the curve, information that is not available from standard tests. Parameter c can be particularly useful during mechanical ventilation because it represents the pressure at which maximal respiratory system compliance is reached. This information could guide the titration of PEEP and inspiratory pressure to generate a mean airway pressure close to c, thereby minimizing both airway and alveolar collapse and hyperinflation. Parameter d estimates the dispersion of the critical opening and hyperinflation pressures for a given patient. Small absolute values indicate that major volume changes occur when the airway pressure is close to c, suggesting avalanche recruiting as the critical opening pressure is achieved. Large values of d suggest that the patient has a heterogeneous distribution of critical opening pressures. These parameters may be useful to guide a protective ventilatory strategy using small tidal volumes to avoid high plateau pressures, similarly to what is recommended for ARDS,30,31 and titrating PEEP to move tidal ventilation to the central, linear part of the curve,32,33 but more study is required before specific guidance can be provided.

The sigmoidal equation had a good fit to the PV curves from the controls; however, unlike the patients, all the controls had LIPs between 0 and 6 cm H₂O and Pmci values lower than 2 cm H₂O. Although a sigmoidal shape was evident, it was less pronounced than in the IPF patients, and a linear pressure-volume relationship is evident at pressures commonly used for mechanical ventilation.

Interestingly, although the LIP and Pmci were consistently low in the controls, for the patients with IPF, the PV curve could either have a linear initial portion, with a low LIP and Pmci, or have a more pronounced sigmoidal shape, with a higher LIP and Pmci. Individual analyses of the PV curve using the sigmoidal fit could help identify each pattern and titrate mechanical ventilation accordingly.

Previous investigators have fit an exponential equation to the deflation PV curves of the lungs of spontaneously breathing patients with fibrotic lung diseases.16–18 However, most of the curves had few points at low lung volumes, close to FRC, where the slope of the curve decreases. By excluding points below 50% of the TLC, researchers were able to fit deflation PV curves from patients with pulmonary fibrosis using an exponential equation; they concluded that this method generated a good fit and that parameter k was useful for characterizing changes in lung mechanics16 and the degree of fibrosis.17 Although this exponential model has been shown to be clinically useful when applied to the deflation limb of the PV curve of spontaneously breathing patients, our results indicate that a sigmoidal model is superior when an inflation PV curve is captured in anesthetized patients and may also be useful for guiding mechanical ventilation.

The finding of a region of low compliance at low lung volumes suggests that small airway and alveolar collapse may be present in IPF patients during mechanical ventilation and general anesthesia, which could be a result of small airways dysfunction. Small airways compromise in early IPF has been previously reported,34–36 but most of the studies of IPF focus on the alveoli, not the airways.5 Recently, Mello and coworkers37 used lung tissues from diagnostic biopsies to show morphological abnormalities in the airways of patients with IPF and overexpression of matrix metalloproteinase (MMP)-7 and MMP-9, suggesting that bronchiolar epithelial cells could contribute to local remodeling of the peribronchial interstitial lung tissue and promote fibrotic activity. Further studies may be warranted to evaluate small airway dysfunction in patients with IPF.37,38

The primary limitation of this study is the number of patients studied. However, despite the small number of patients and the early stage of their disease, a sigmoidal shape of the PV curve was noted in all the patients, and it was more pronounced than in the controls. Our control patients had myasthenia gravis, which is associated with chest wall abnormalities that could impact the shape of a pressure volume curve. This impact, however, would be expected for spontaneously breathing patients who were not under general anesthesia or muscle paralysis. To minimize any concerns about the contribution of the chest wall to the shape of the pressure-volume curve, we used esophageal catheters to monitor chest wall activity during curve recording and found that it was always absent. The controls were younger and had smaller body mass indexes than the patients, a finding that should be kept in mind when interpreting our results.

We studied inflation PV curves of the total respiratory system, which is in contrast to the deflation PV curves of the lung used in previous studies,16,17 a difference that should be considered when comparing results. We used the inflation PV curve because it usually has more points at low lung volumes than does the deflation curve. Total respiratory system PV curves were used instead of lung PV curves because the signal from the esophageal balloon was damped in some cases and because information on the respiratory system as a whole is more commonly used at the bedside to guide mechanical ventilation, given that it does not require an esophageal balloon. In all cases, patient respiratory effort was absent, none of the patients had chest wall abnormalities, and the shapes of the PV curves using airway pressure and transpulmonary pressure were similar (see supplementary material). The PV curves were performed with patients in the supine position while under anesthesia with muscle paralysis, a condition that has been associated with a reduction in the FRC and lung collapse in healthy subjects.39 However, the occurrence of lung collapse during anesthesia is related to mechanical ventilation without PEEP and with a high FIO₂. The use of a recruitment maneuver has been shown to completely reverse anesthesia-induced collapse in supine anesthetized patients, and an FIO₂≤0.4 prevents its recurrence.40 Our patients were ventilated with FIO₂ values between 0.3 and 0.4 and PEEPs of 5 cm H₂O, and a recruitment maneuver was performed immediately before the PV curves. The controls received the same ventilatory strategy and did not demonstrate as pronounced a sigmoidal shape in their PV curves.

In conclusion, our results show that a sigmoidal equation is superior to an exponential equation for fitting inflation PV curves of the respiratory system from IPF patients under general anesthesia. The PV curve's sigmoidal shape reveals, for the first time, that total respiratory system compliance is decreased at low lung volumes during general anesthesia and mechanical ventilation in patients with IPF, a characteristic that should be considered for adjustment of mechanical ventilator settings.